Design and Simulation of a Magnetization Drive Coil Based on the Helmholtz Principle and an Experimental Study
Abstract
:1. Introduction
2. Methods
2.1. Mathematical Model of a Magnetic Field System
2.2. Structural Design and Simulation Setting
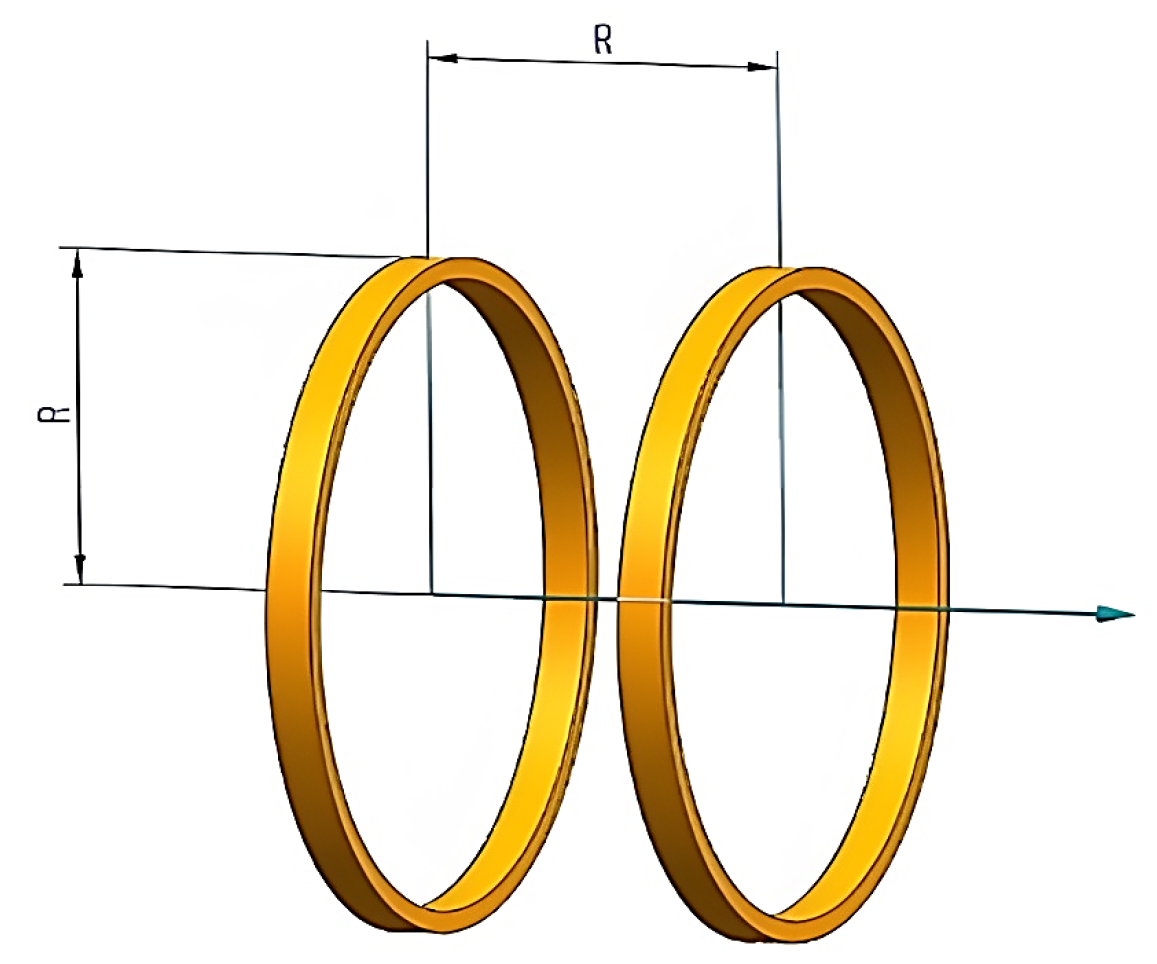
2.2.1. Helmholtz Coil Type Selection
2.2.2. Geometric Model of a Magnetized Drive Coil
- (1)
- For the main coil, the outer diameter and inner diameter are 70 mm and 66 mm, respectively; for the auxiliary coil, the outer diameter and inner diameter are 55 mm and 51 mm, respectively;
- (2)
- The height dimension of each coil is 25 mm;
- (3)
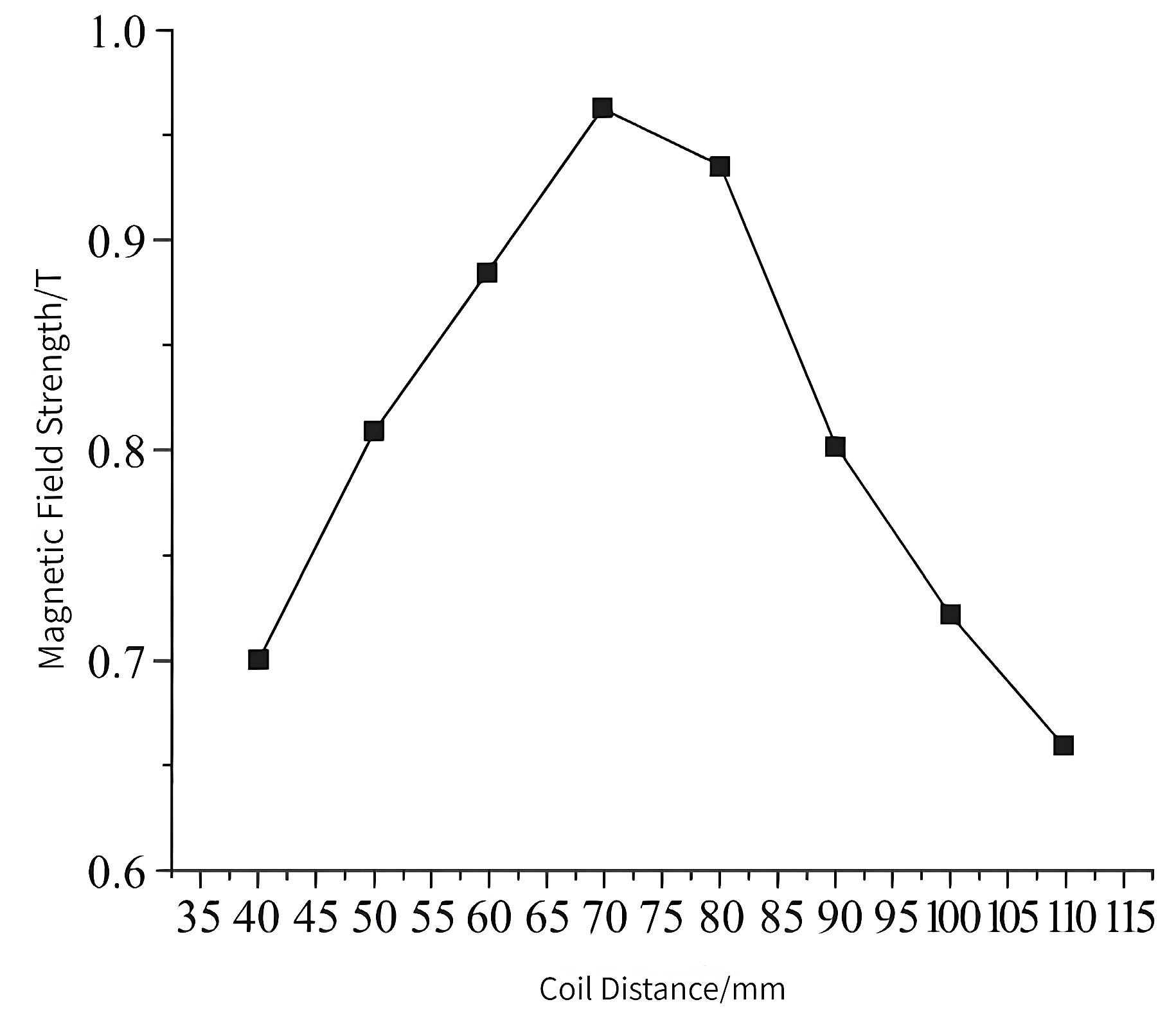
- The distance between the auxiliary coils is set to 80 mm and placed symmetrically on the left and right sides of the main coils. The simplified 3D modeling of the designed magnetic field drive coils in Maxwell software is shown in Figure 5.
2.2.3. Model Meshing and the Associated Parameter Settings
3. Results and Analysis
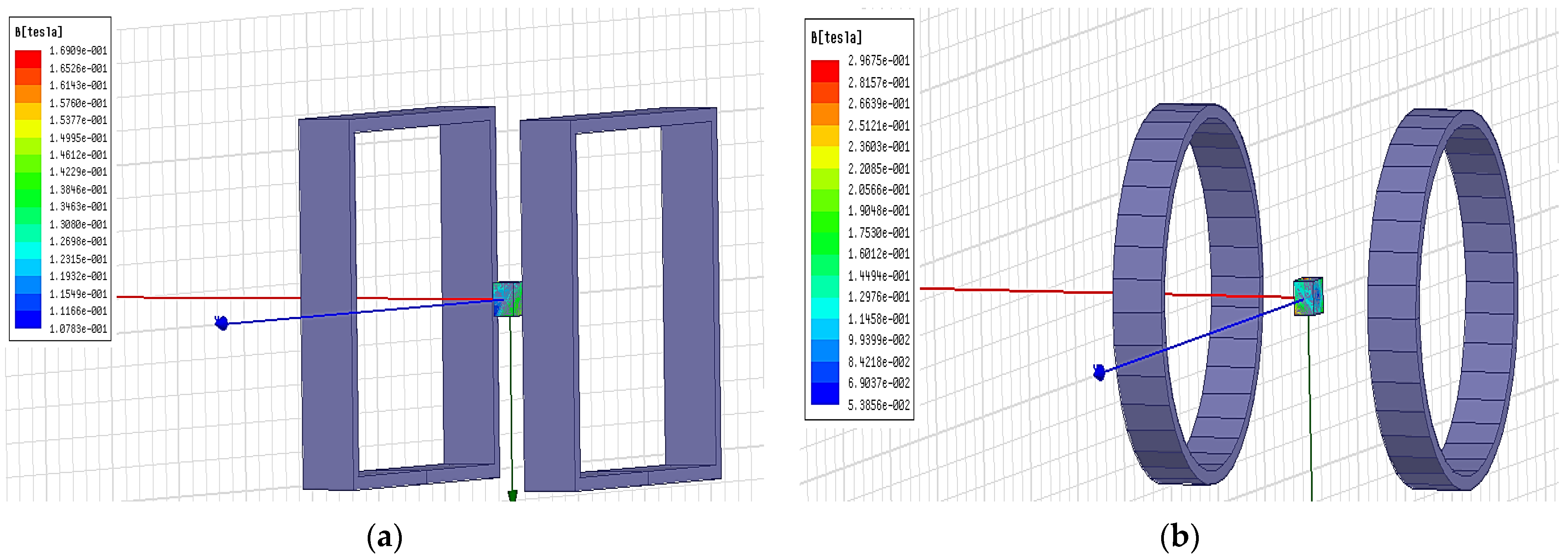
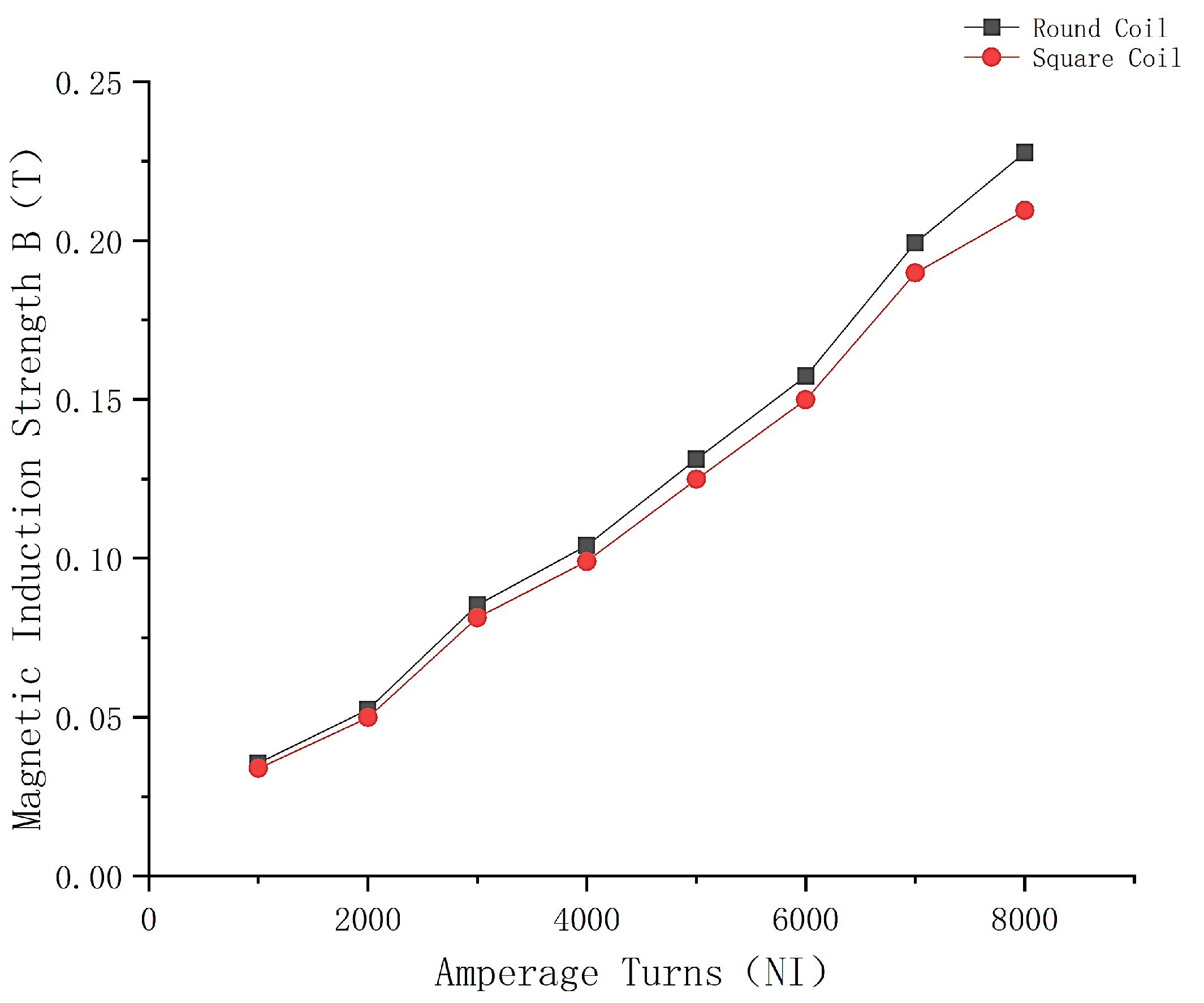
3.1. Simulation Results and Analysis
- (1)
- Simulation analysis of the effect of auxiliary coil distance on the central magnetic induction intensity
- (2)
- The simulation analysis of the influence of Ann turns on the center induction of the Helmholtz coil and magnetized drive coil
- (3)
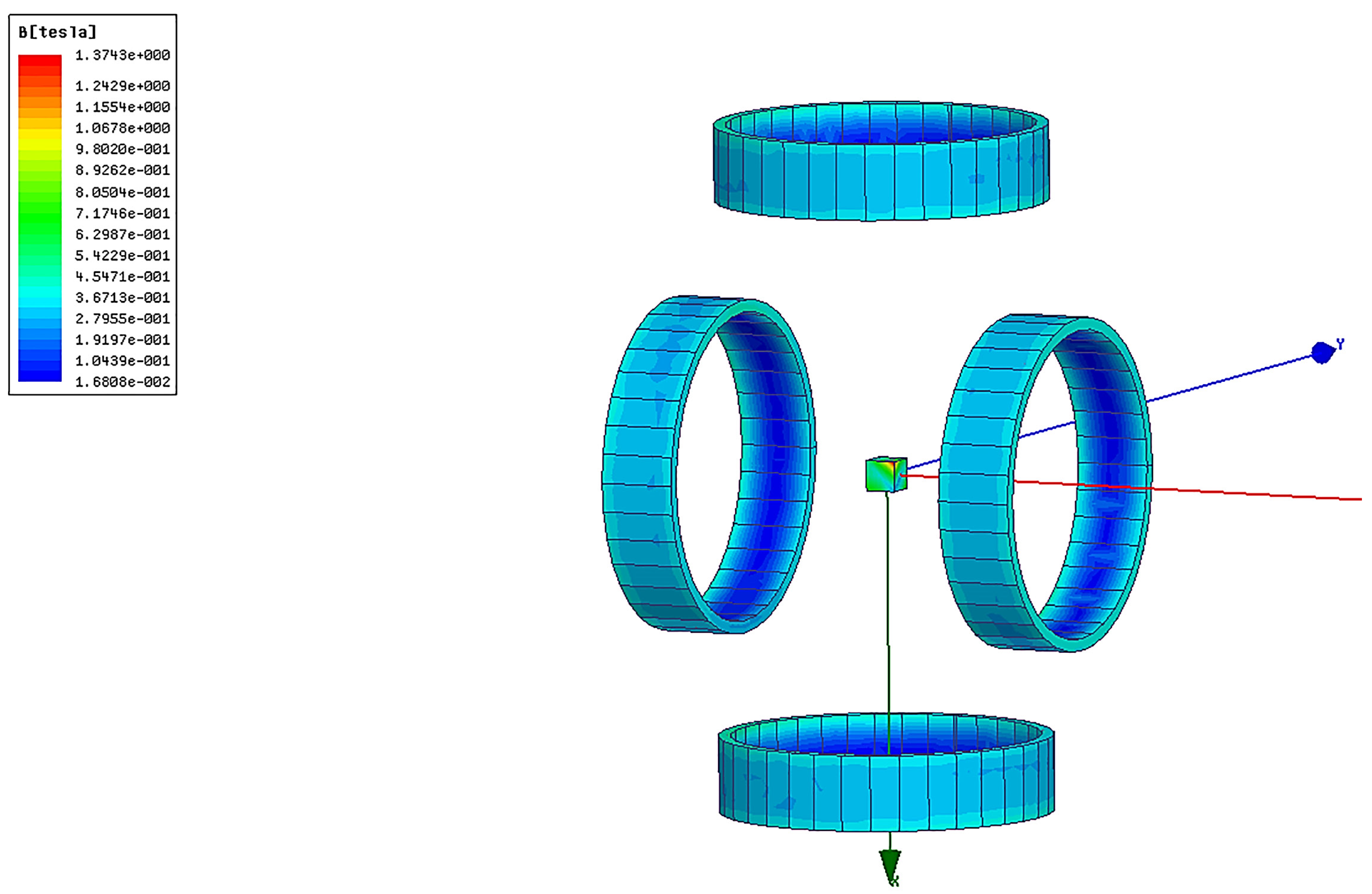
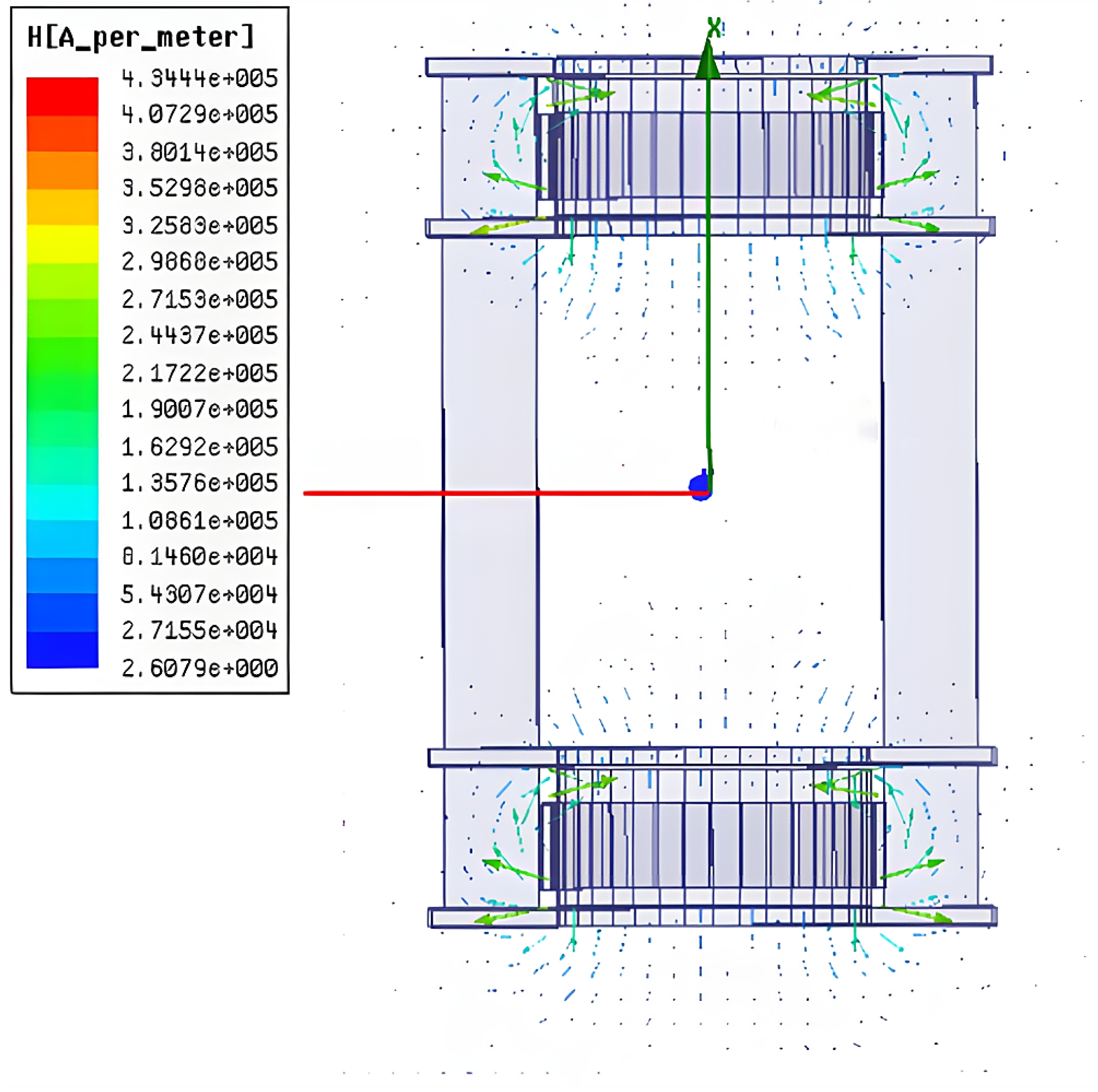
- Distribution of Helmholtz coils and magnetized drive coils
- (4)
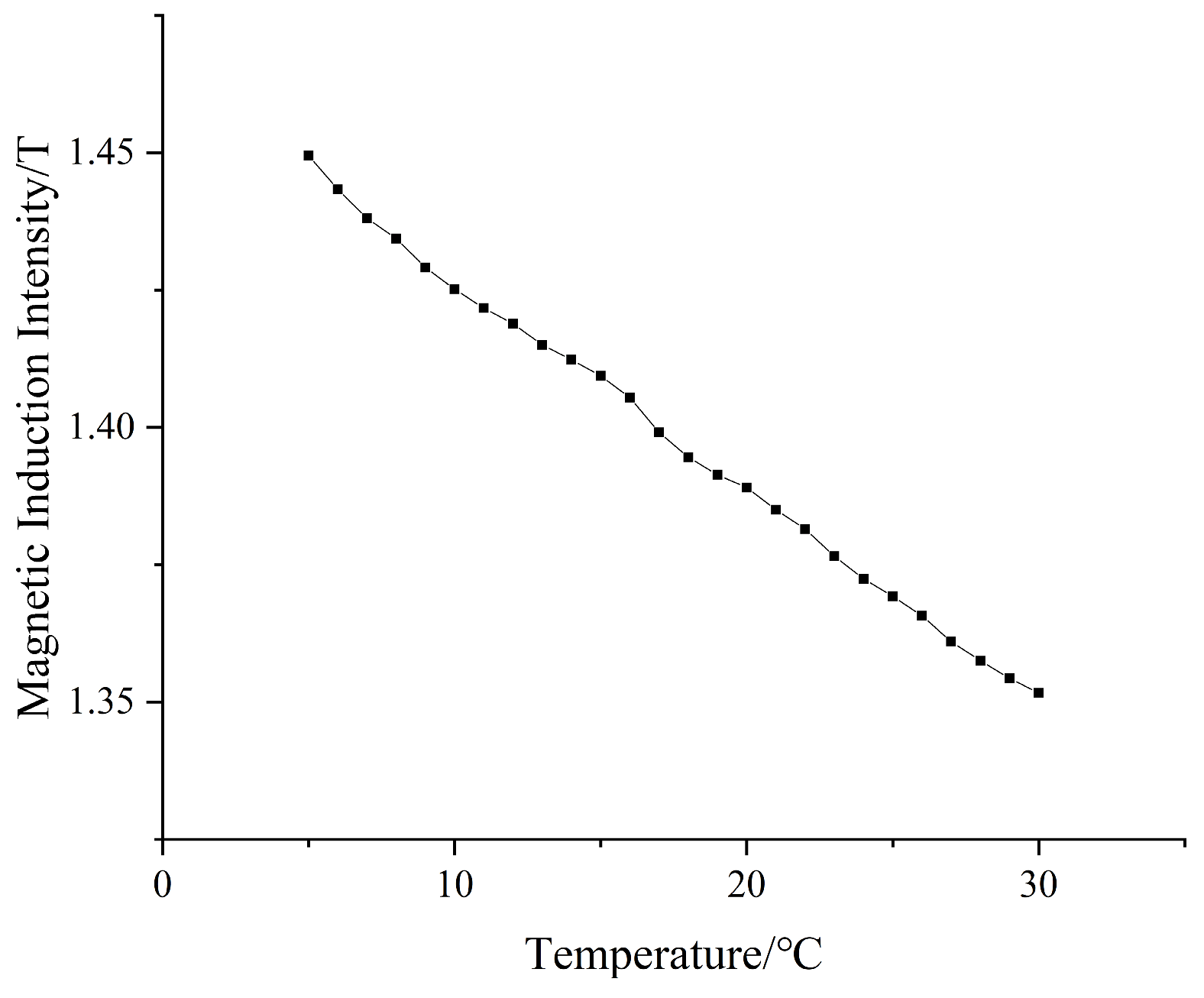
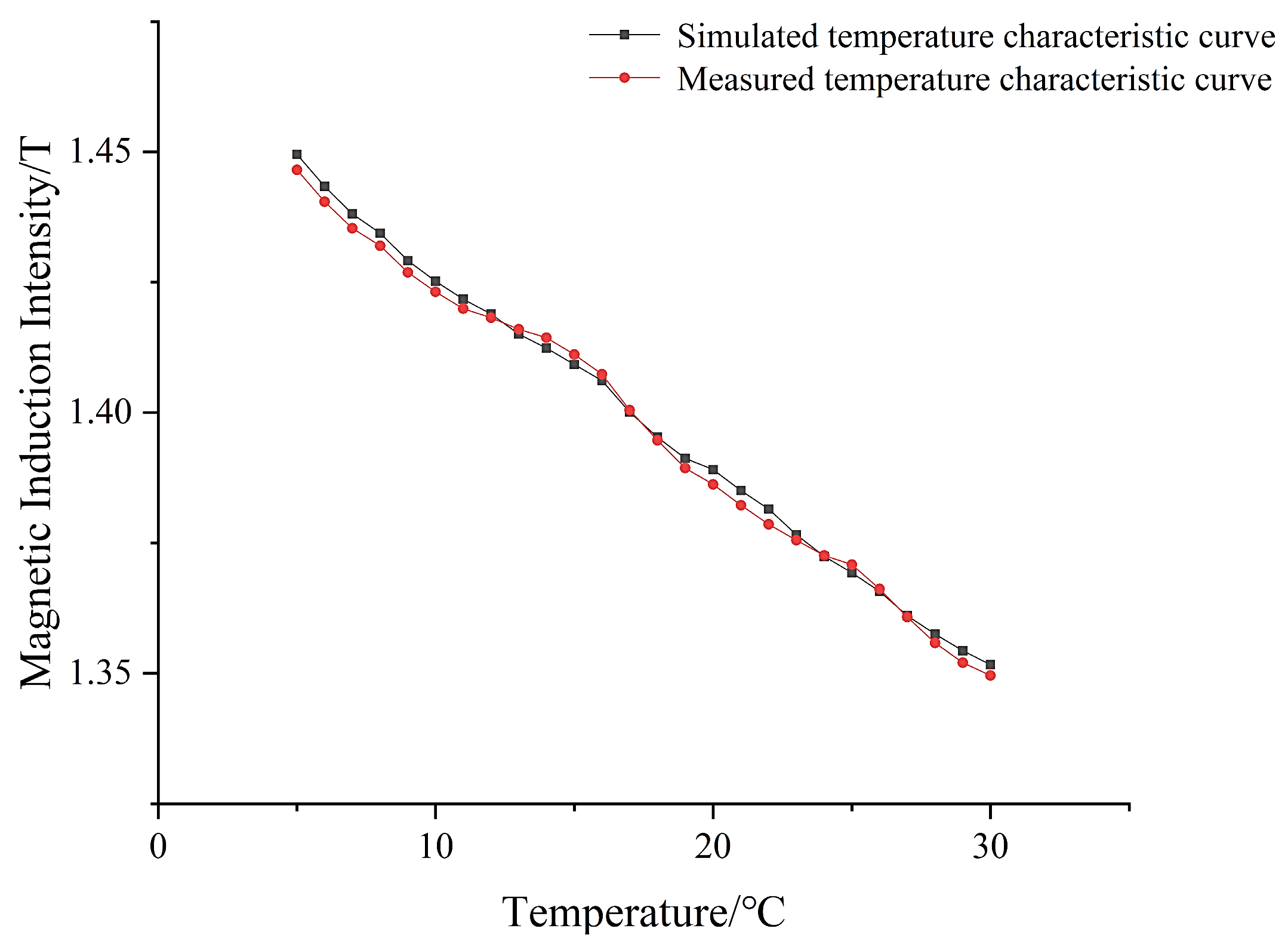
- Temperature characteristics analysis
3.2. Coil Physical Construction and Analysis
- (1)
- Designed with the magnetic potential to meet the magnetic field drive requirements.
- (2)
- Temperature rises at stable operation < limit temperature rises of insulation material.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Invernizzi, M.; Turri, S.; Levi, M.; Suriano, R. 4D printed thermally activated self-healing and shape memory polycaprolactone-based polymers. Eur. Polym. J. 2018, 101, 169–176. [Google Scholar] [CrossRef]
- Simińska-Stanny, J.; Nizioł, M.; Szymczyk-Ziółkowska, P.; Brożyna, M.; Junka, A.; Shavandi, A.; Podstawczyk, D. 4D printing of patterned multimaterial magnetic hydrogel actuators. Addit. Manuf. 2022, 49, 102506. [Google Scholar] [CrossRef]
- Varga, Z.; Filipcsei, G.; Szilágyi, A.; Zrínyi, M. Electric and Magnetic Field-Structured Smart Composites. Macromol. Symp. 2005, 227, 123–134. [Google Scholar] [CrossRef]
- Lian, Q.Y.; Yong, F.Y.; You, G.Y. Effect of Powder Size on Fracture Strength and Magnetic Properties. Rare Metal. Mat. Eng. 2008, 37, 2034–2036. [Google Scholar]
- Kim, S.H.; Ishiyama, K. Magnetic robot and manipulation for active-locomotion with targeted drug release. IEEE/ASME Trans. Mechatron. 2013, 19, 1651–1659. [Google Scholar]
- Fu, Q.; Guo, S.; Huang, Q.; Hirata, H.; Ishihara, H. Development and evaluation of novel magnetic actuated microrobot with spiral motion using electromagnetic actuation system. J. Med. Biol. Eng. 2016, 36, 506–514. [Google Scholar] [CrossRef]
- Jeon, S.; Jang, G.; Choi, H.; Park, S. Magnetic navigation system with gradient and uniform saddle coils for the wireless manipulation of micro-robots in human blood vessels. IEEE Trans. Magn. 2010, 46, 1943–1946. [Google Scholar] [CrossRef]
- Choi, H.; Cha, K.; Choi, J.; Jeong, S.; Jeon, S.; Jang, G.; Park, J.; Park, S. EMA system with gradient and uniform saddle coils for 3D locomotion of microrobot. Sensor Actuat. A-Phys. 2010, 163, 410–417. [Google Scholar] [CrossRef]
- Guo, J.; Bao, Z.; Fu, Q.; Guo, S. Design and implementation of a novel wireless modular capsule robotic system in pipe. MBEC 2020, 58, 2305–2324. [Google Scholar] [CrossRef]
- Jodko-Władzińska, A.; Wildner, K.; Pałko, T.; Władziński, M. Compensation System for Biomagnetic Measurements with Optically Pumped Magnetometers inside a Magnetically Shielded Room. Sensors 2020, 20, 4563. [Google Scholar] [CrossRef]
- Armando, R.S.; Hoon, K.S. Magnetic Force-Propelled 3D Locomotion Control for Magnetic Microrobots via Simple Modified Three-Axis Helmholtz Coil System. Ieee Access 2021, 9, 128755–128764. [Google Scholar]
- Ghaly, S.M.A.; Al-Snaie, K.A.; Ali, A.M. Design and Modeling of a Radio frequency Coil Derived from a Helmholtz Structure. Eng. Technol. Appl. 2019, 9, 4037–4043. [Google Scholar]
- Ghosh, S.; Sonker, P.K.; Chowdhury, S.R. Modeling and Simulation of Low-Cost and Low-Magnetic Field Magnetic Resonance Imaging. Sens. Transducers 2019, 231, 25–30. [Google Scholar]
- Nismayanti, A.; Jannah, H.; Rugayya, S.; Maskur, A.R. Helmholtz coils model as pulsed electromagnetic field therapy devices for fracture healing using comsol multiphysics. J. Phys. Conf. Ser. 2021, 1763, 012060. [Google Scholar] [CrossRef]
- Kittipong, P.; Chalermchai, P.; Waronont, A.; Sumet, S. Design of Three-axis Square Helmholtz Coils for Compact Atomic Magnetometer. In Proceedings of the Fourth International Conference on Photonics Solutions (ICPS2019), Chiang Mai, Thailand, 20–22 November 2019; p. 11331. [Google Scholar]
- Doan, V.D.; Jeng, J.T.; Tsao, T.H.; Pham, T.T.; Huang, G.W.; Dinh, C.H.; Lee, T.H.; Mei, P.I. Development of a Broad Bandwidth Helmholtz Coil for Biomagnetic Application. T-MAG 2020, 57, 1–5. [Google Scholar] [CrossRef]
- Nardelli, N.V.; Krzyzewski, S.P.; Knappe, S.A. Reducing crosstalk in optically-pumped magnetometer arrays. PMB 2019, 64, 21NT03. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Shi, Y. Design and research of electromagnetic generator based on Helmholtz coil. JCPS 2022, 2246, 012052. [Google Scholar] [CrossRef]
- Torres-Osorio, J.; Sabogal-Suárez, D.; Alzate-Cardona, J.D.; Restrepo Parra, E. MFV: Application software for the visualization and characterization of the DC magnetic field distribution in circular coil systems. JCMSE 2021, 21, 511–519. [Google Scholar] [CrossRef]
- Shamseh, M.B.; Yuzurihara, I.; Kawamura, A. A 3.2-kW 13.56-MHz SiC passive rectifier with 94.0% efficiency using commutation capacitor. IEEE Trans. Power Electron. 2016, 31, 6787–6791. [Google Scholar] [CrossRef]
- Saqib, M.; Francis, S.N.; Francis, J.N. Design and development of Helmholtz coils for magnetic field. In Proceedings of the 2020 International Youth Conference on Radio Electronics, Electrical and Power Engineering (REEPE), Moscow, Russia, 12–14 March 2020; pp. 1–5. [Google Scholar]
- Hurtado-Velasco, R.; Gonzalez-Llorente, J. Simulation of the magnetic field generated by square shape Helmholtz coils. Appl. Math. Model. 2016, 40, 9835–9847. [Google Scholar] [CrossRef]
- Abbott, J.J. Parametric design of tri-axial nested Helmholtz coils. Rev. Sci. Instrum. 2015, 86, 054701. [Google Scholar] [CrossRef] [PubMed] [Green Version]


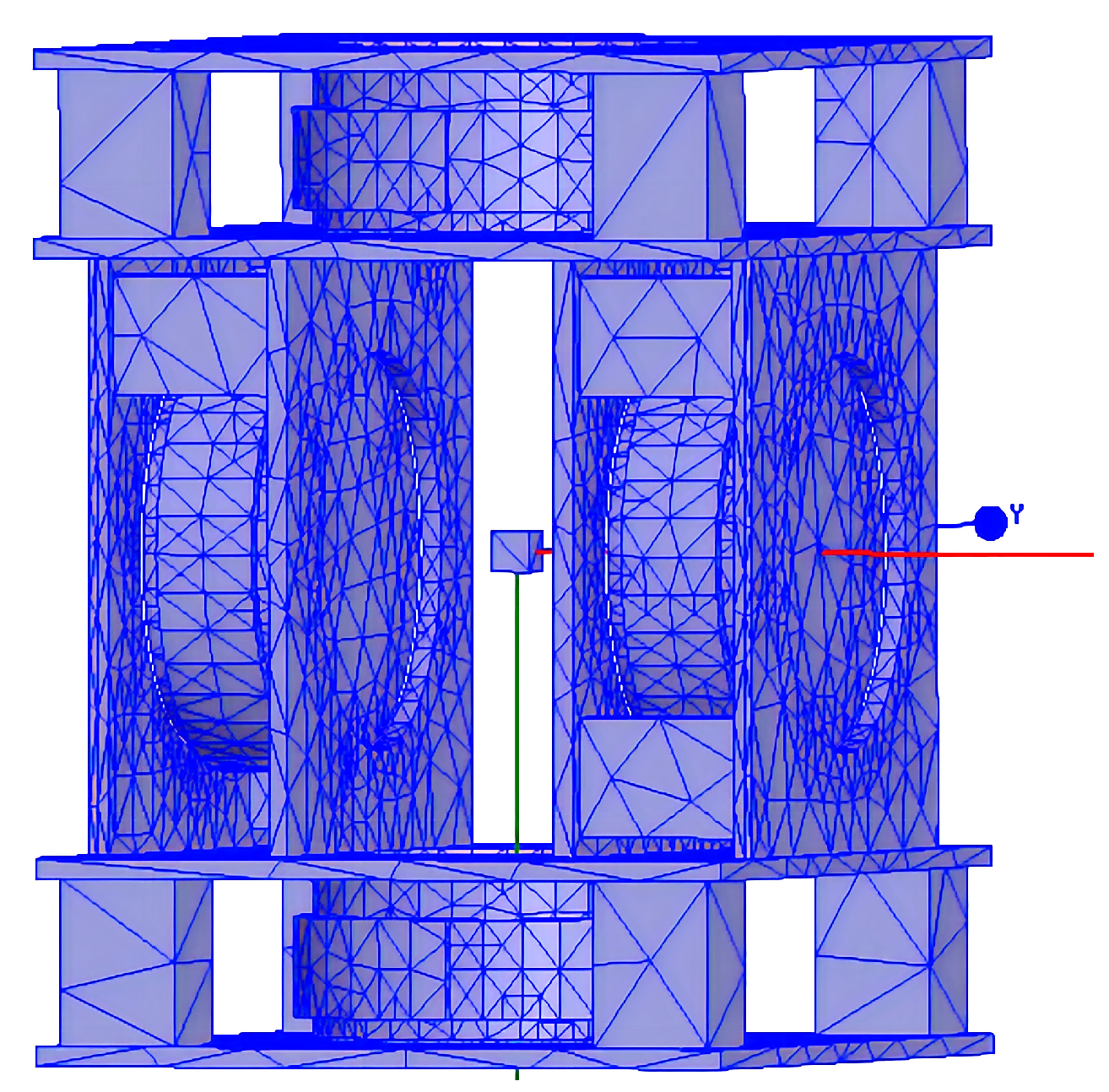
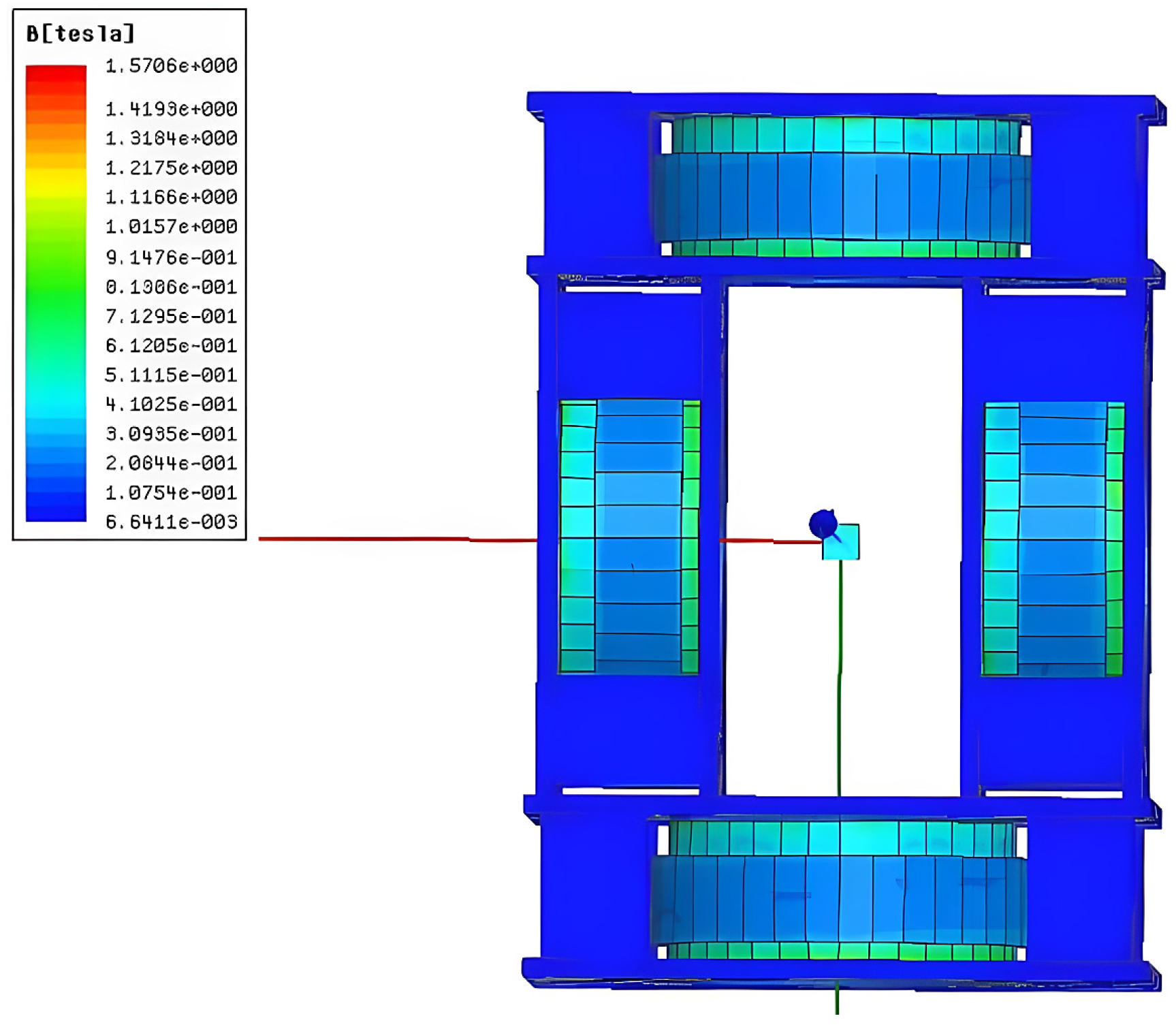
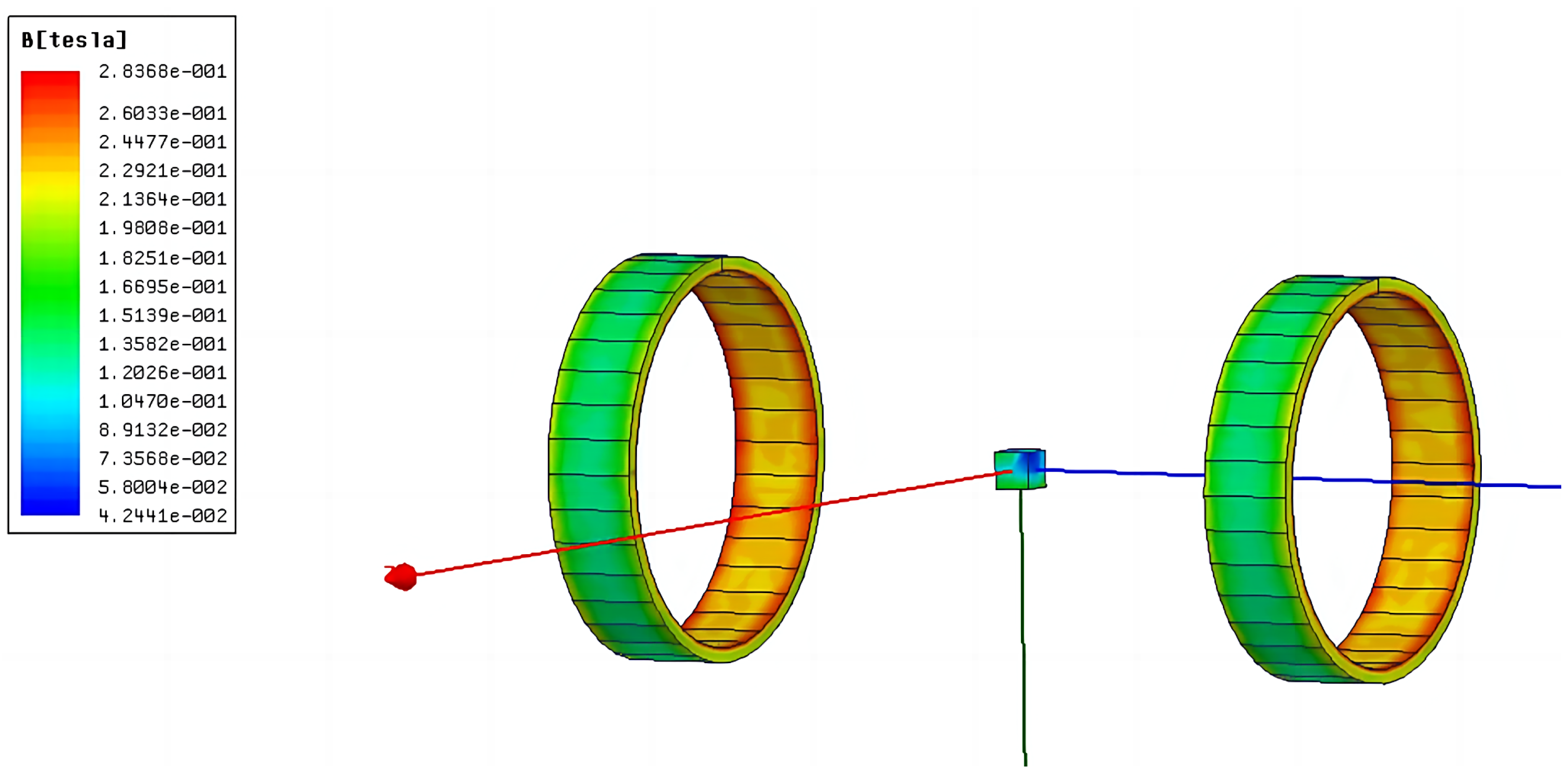





| Parameter | Setting |
|---|---|
| Region | 100% |
| Material | Coil: copper |
| Driving Source | Current source: the number of Ann turns, Direction: Negative |
| Analysis Setup | Maximum number of iterations: 5 Percent Error: 1% Refinement per Pass: 0.3 |
| Parameter | Setting |
|---|---|
| Region | 100% |
| Material | Upper and lower fixed plate, coil fixed column, profile: aluminum Coil: copper |
| Driving Source | Current source: Ann turns, direction: Negative |
| Analysis Setup | Maximum number of iterations: 5 Percent Error: 1% Refinement per Pass: 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Lv, Q.; Yang, J.; Li, M.; Zhao, Q.; Ma, H.; Jia, X. Design and Simulation of a Magnetization Drive Coil Based on the Helmholtz Principle and an Experimental Study. Micromachines 2023, 14, 152. https://doi.org/10.3390/mi14010152
Zhao C, Lv Q, Yang J, Li M, Zhao Q, Ma H, Jia X. Design and Simulation of a Magnetization Drive Coil Based on the Helmholtz Principle and an Experimental Study. Micromachines. 2023; 14(1):152. https://doi.org/10.3390/mi14010152
Chicago/Turabian StyleZhao, Changlong, Qiyin Lv, Junbao Yang, Ming Li, Qinxiang Zhao, Hongnan Ma, and Xiaoyu Jia. 2023. "Design and Simulation of a Magnetization Drive Coil Based on the Helmholtz Principle and an Experimental Study" Micromachines 14, no. 1: 152. https://doi.org/10.3390/mi14010152
APA StyleZhao, C., Lv, Q., Yang, J., Li, M., Zhao, Q., Ma, H., & Jia, X. (2023). Design and Simulation of a Magnetization Drive Coil Based on the Helmholtz Principle and an Experimental Study. Micromachines, 14(1), 152. https://doi.org/10.3390/mi14010152






