SEU Hardened D Flip-Flop Design with Low Area Overhead
Abstract
:1. Introduction
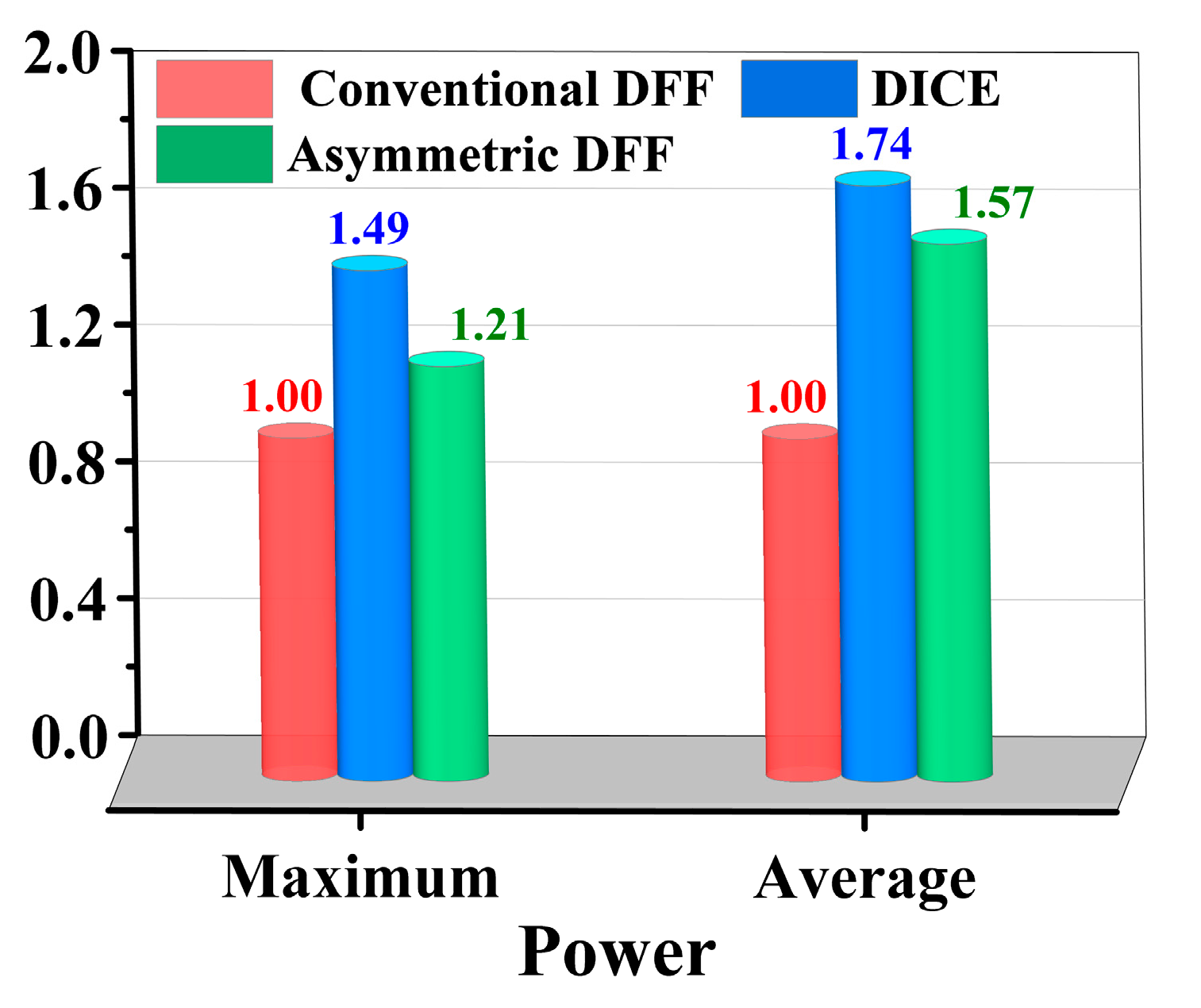
- This DFF utilizes an asymmetric scheme. Different hardening structures are employed for the master and slave latches based on their SEU resistance capabilities. The circuit requires six fewer transistors compared to the DICE structure, effectively reducing the circuit area overhead. Furthermore, the average power consumption and peak power consumption of the circuit are 9.8% and 18.8% lower, respectively, compared to a DICE DFF under identical operating conditions.
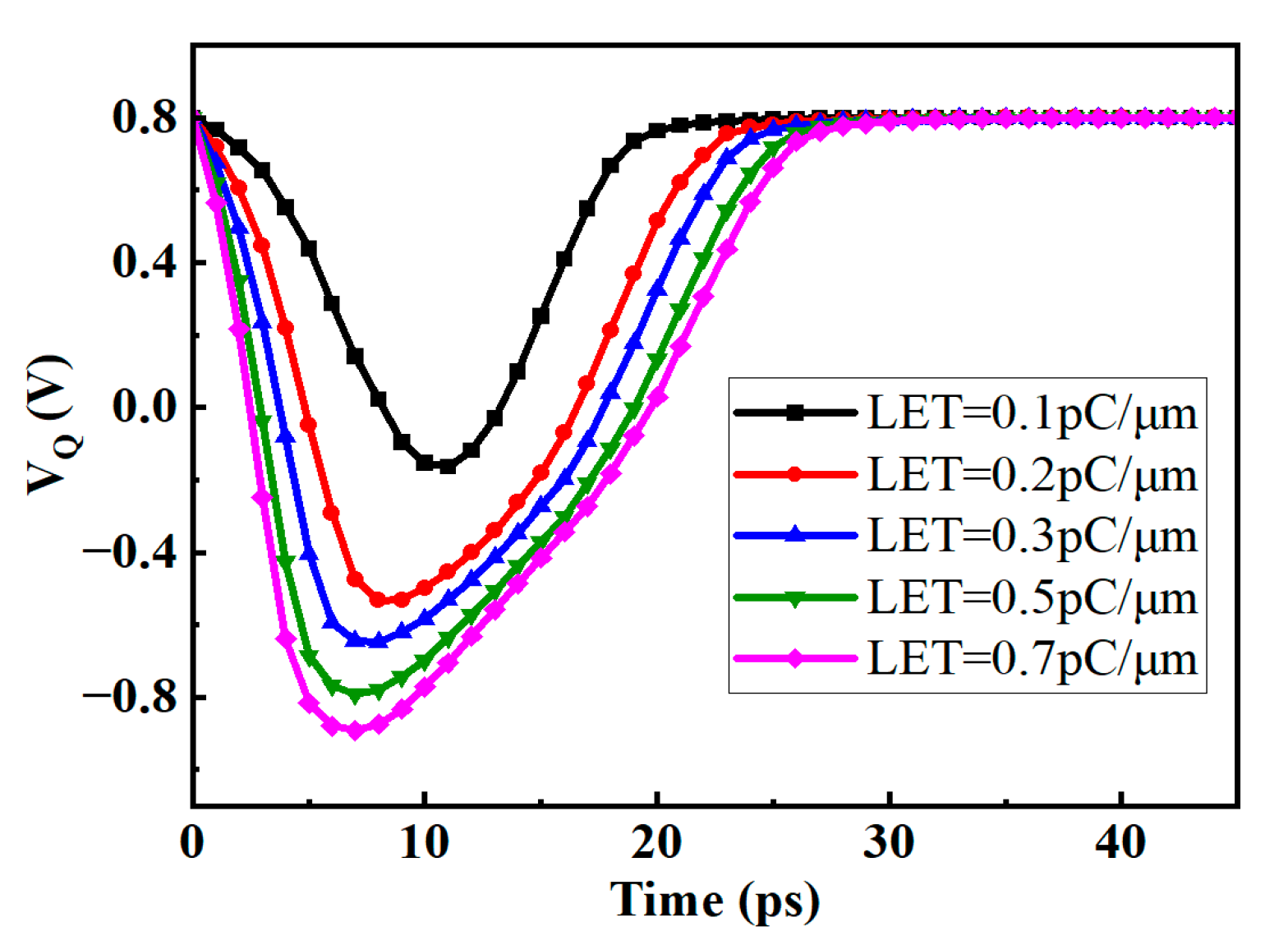
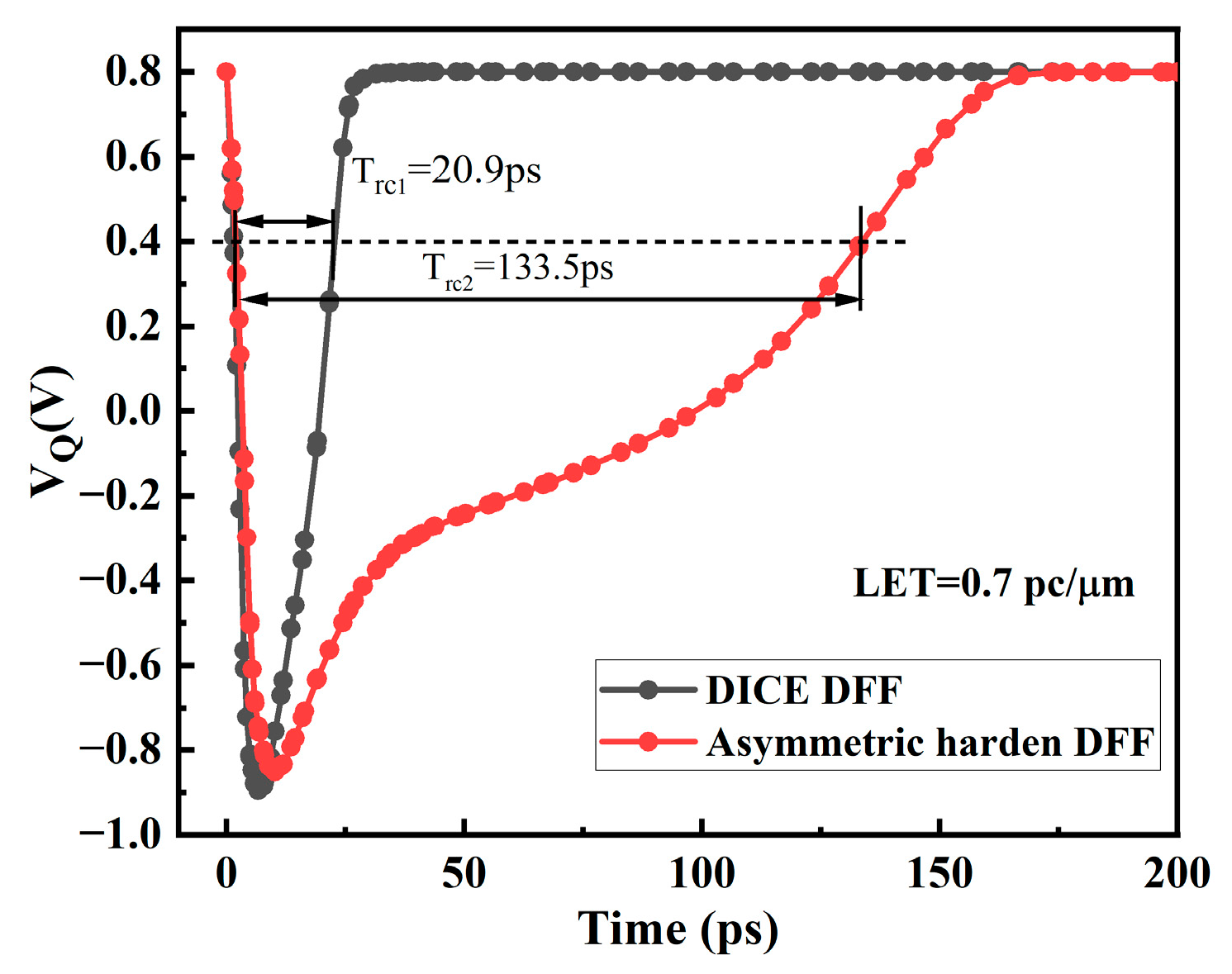
- The structure exhibits strong SEU hardening capabilities. Compared to traditional D-flip-flops, this structure achieves an almost ten-fold increase in the SEU flip threshold. It provides the same hardening effect as DICE under single particle injection with Linear Energy Transfer (LET) ranging from 0 to 0.7 pc/μm.
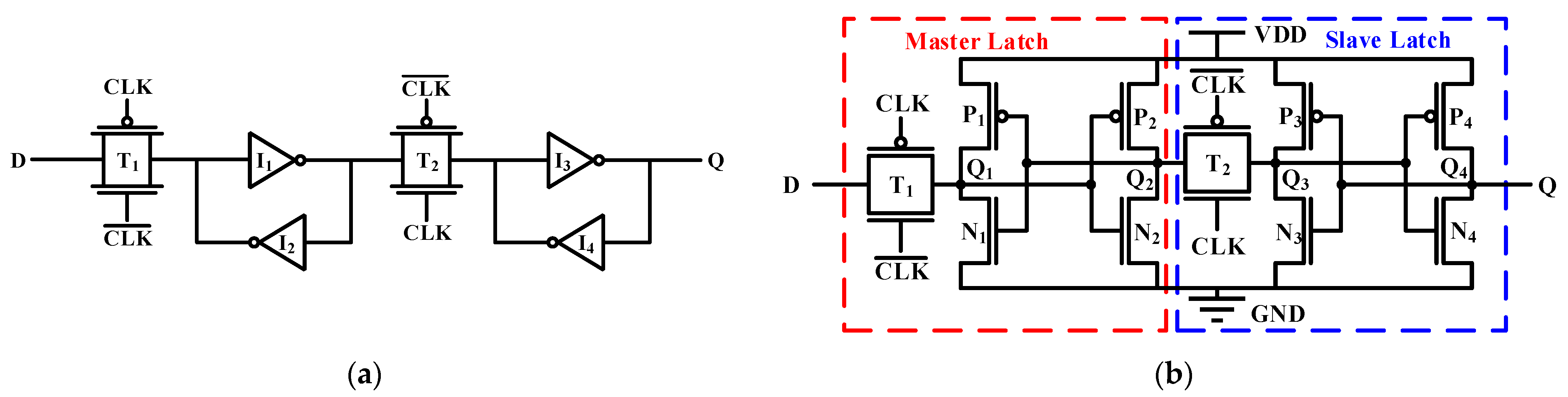
2. Conventional D Flip-Flop
2.1. Working Principle
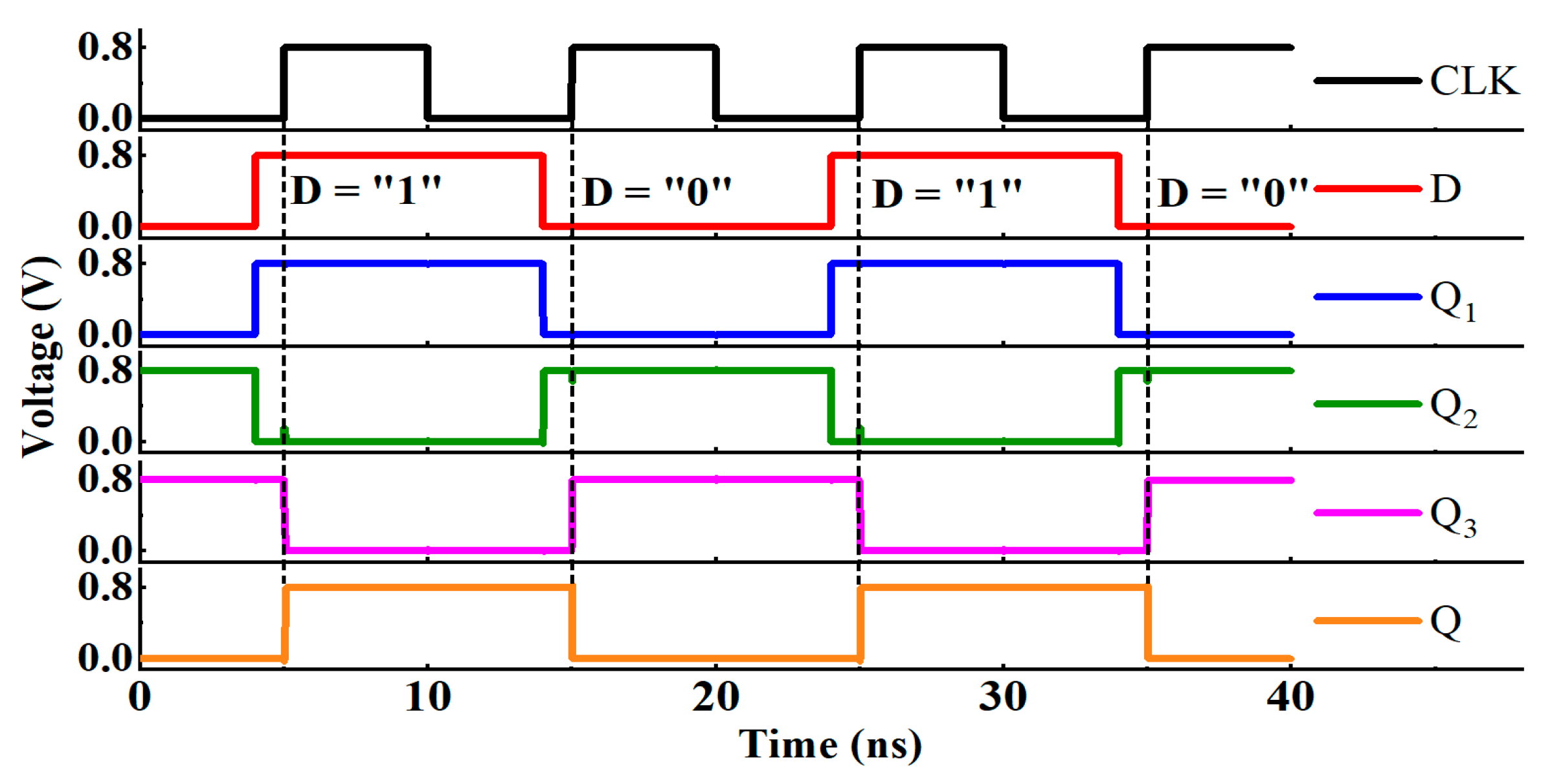
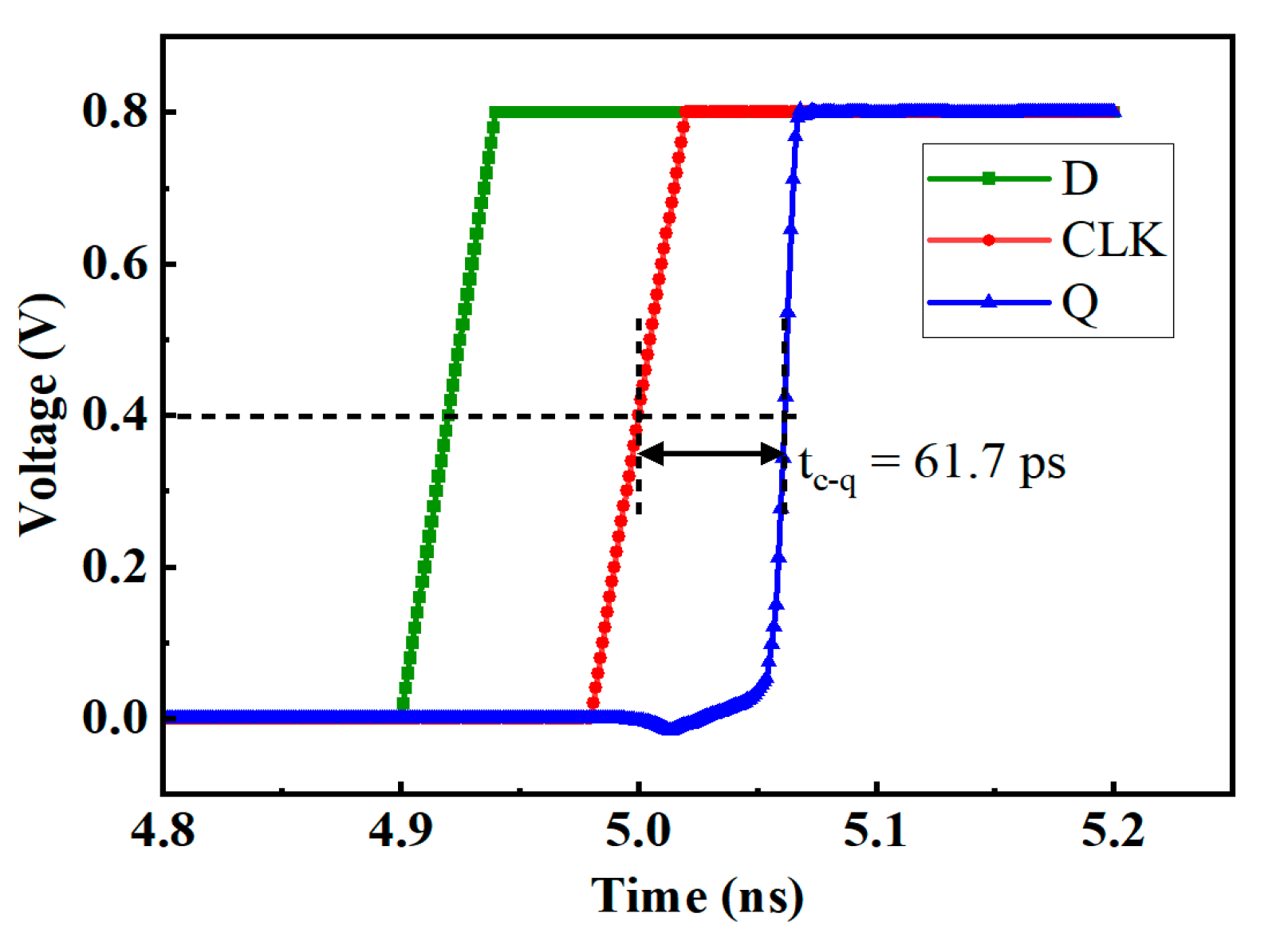
2.2. Simulation of Basic Function
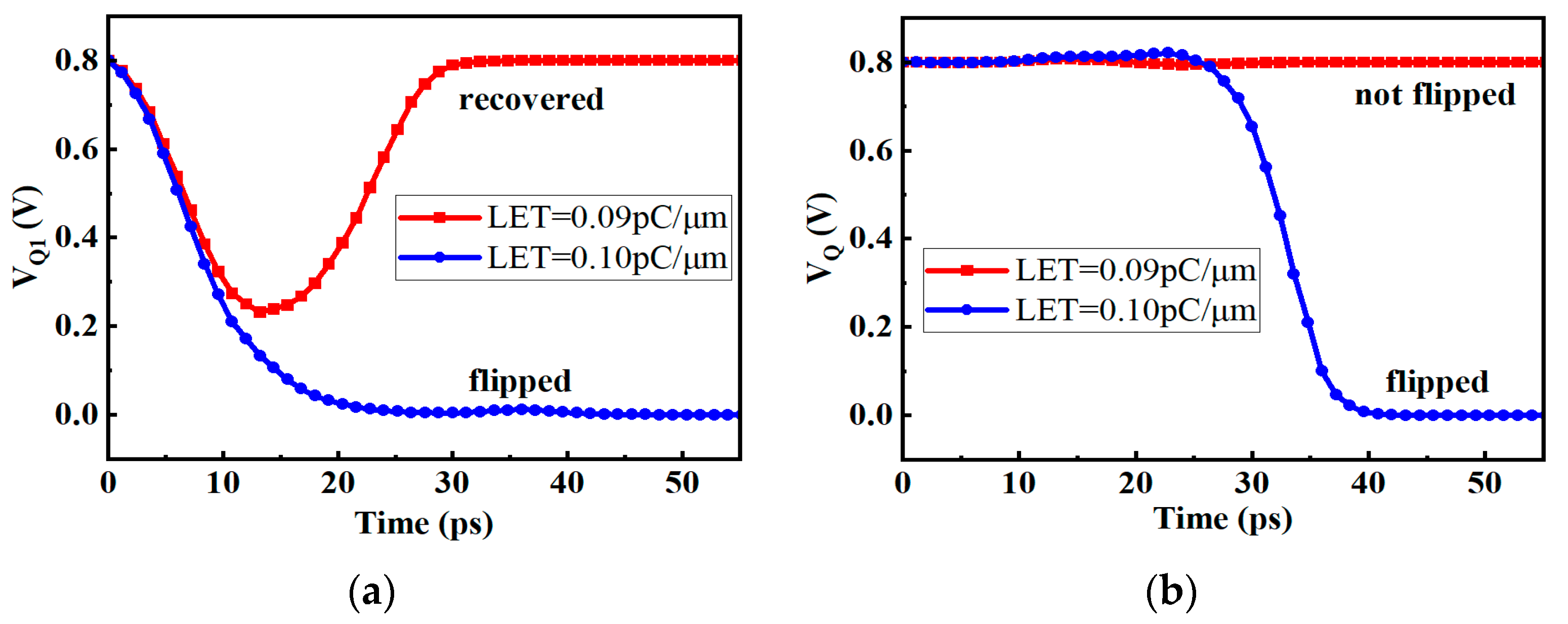
2.3. SEU Simulation
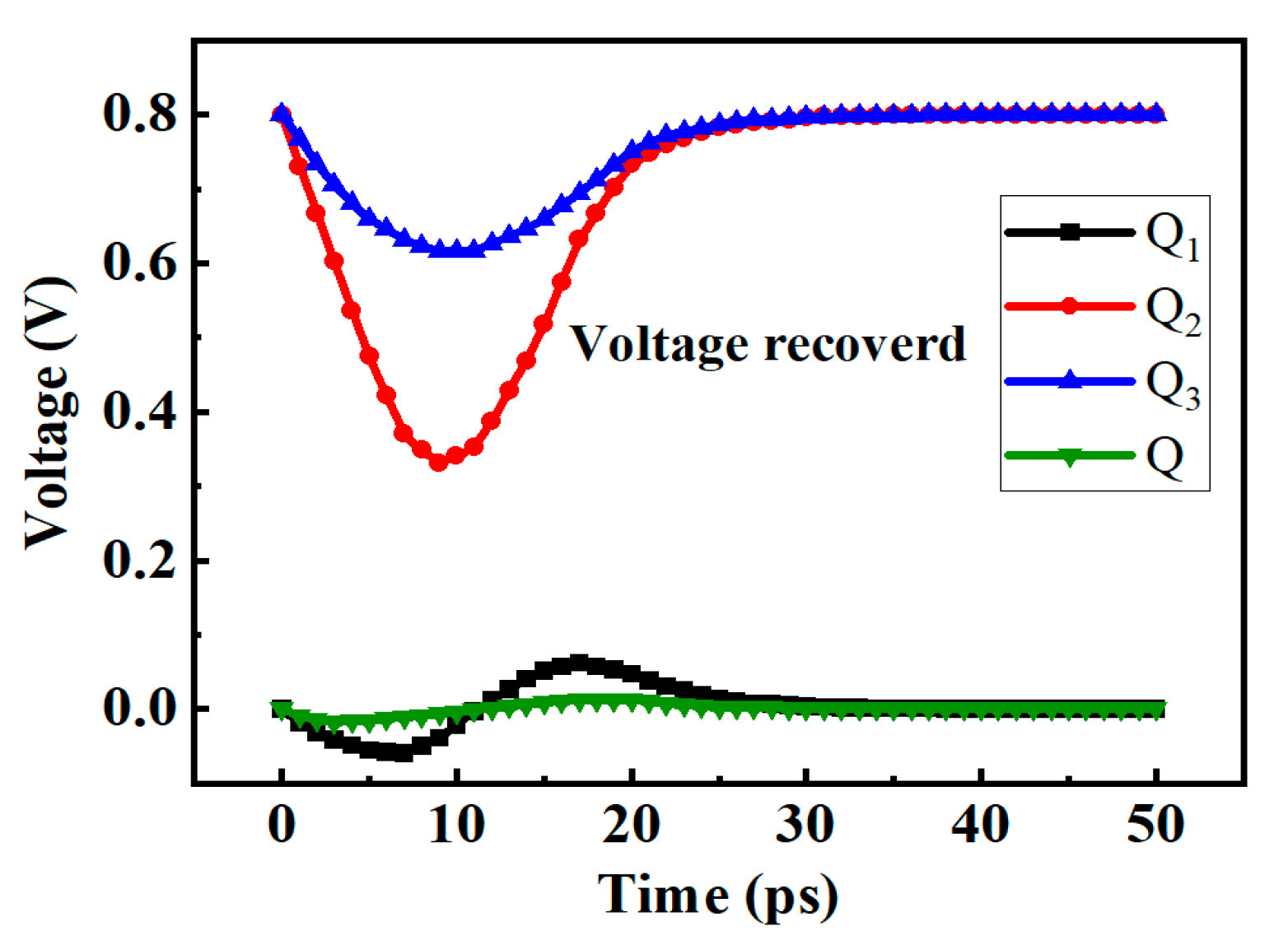
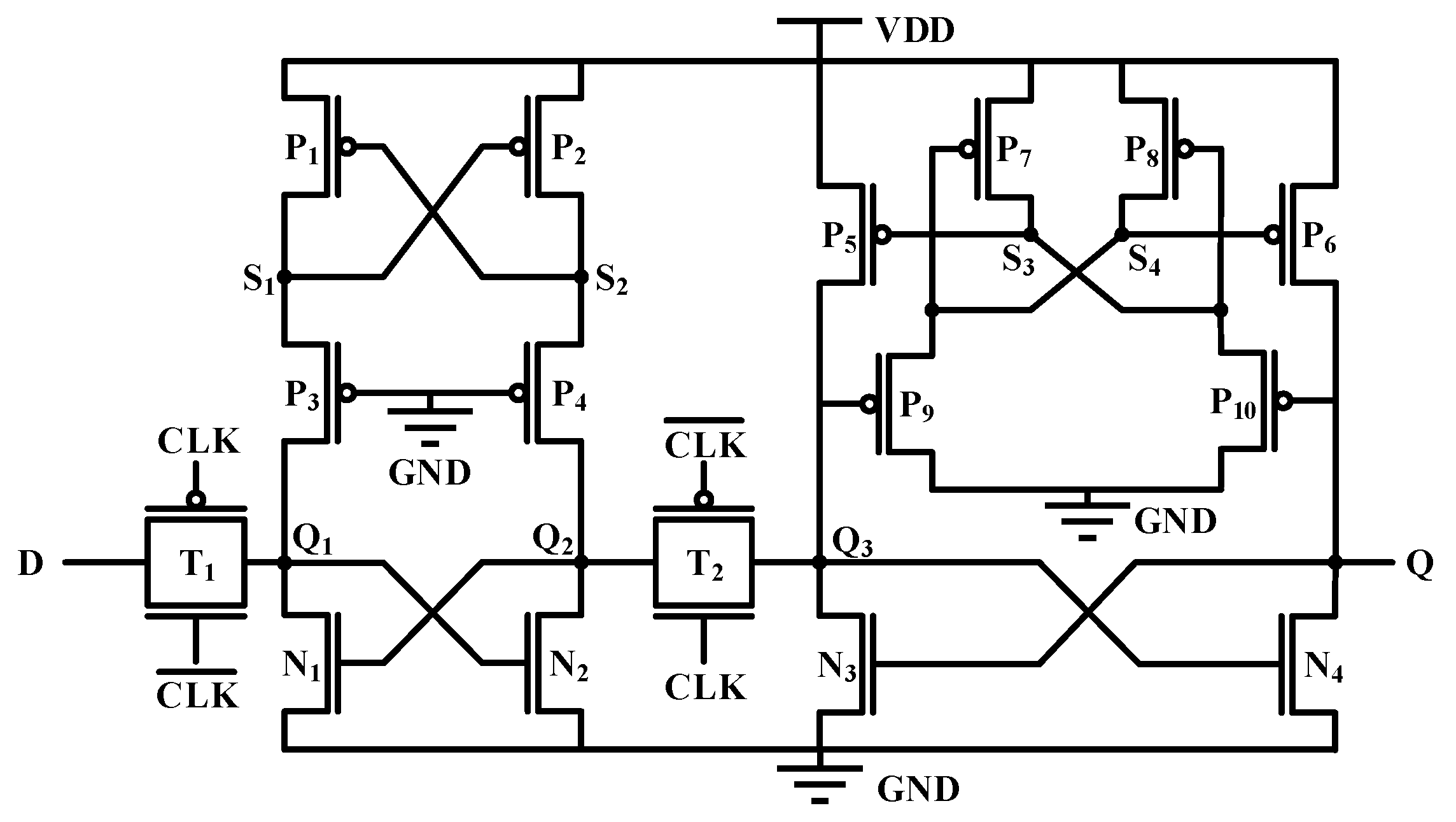
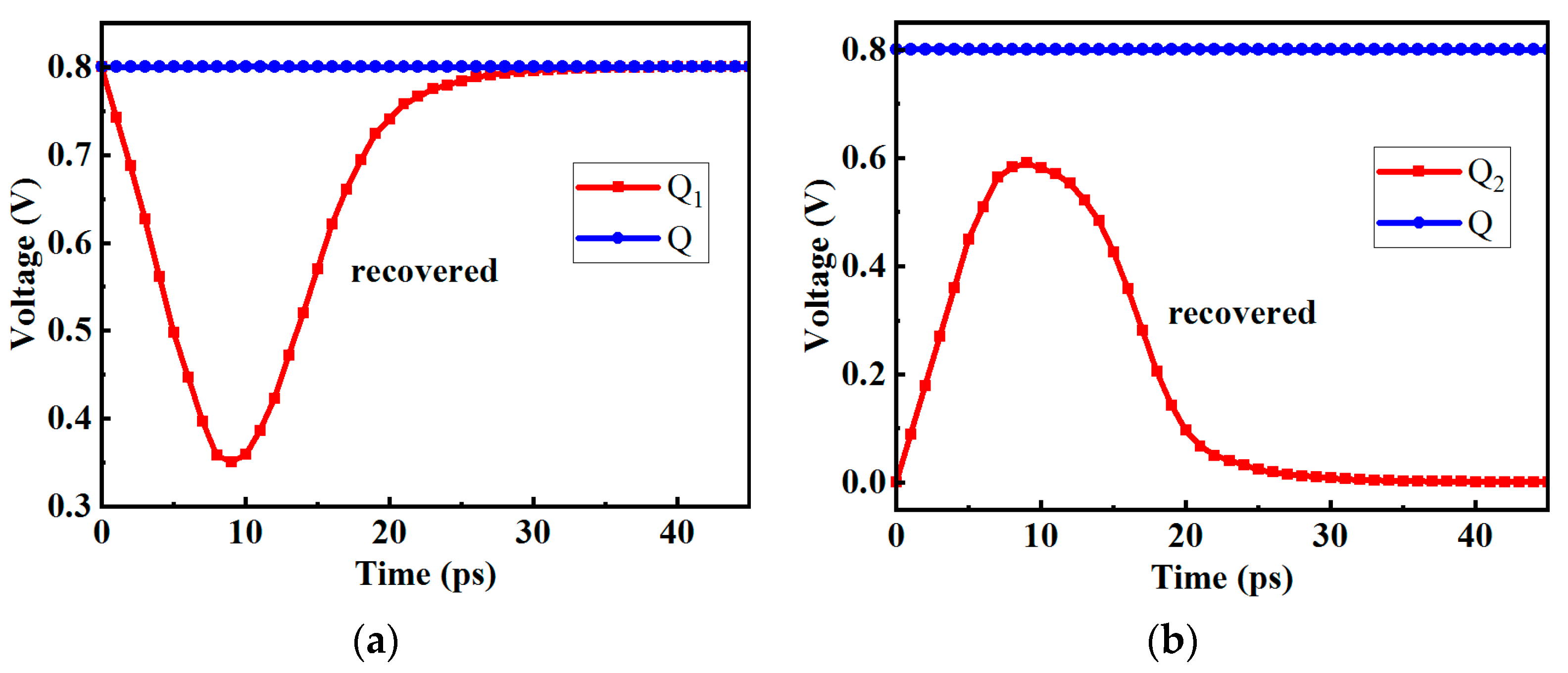
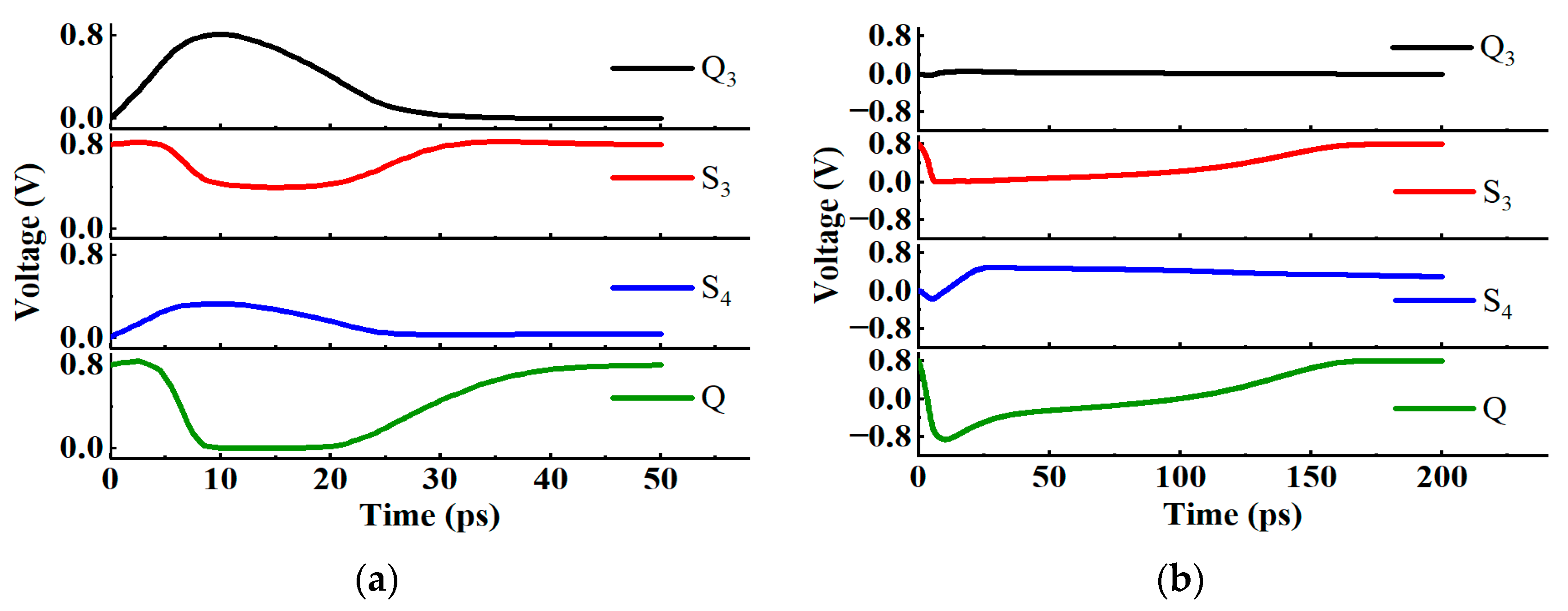
3. Proposed D Flip-Flop
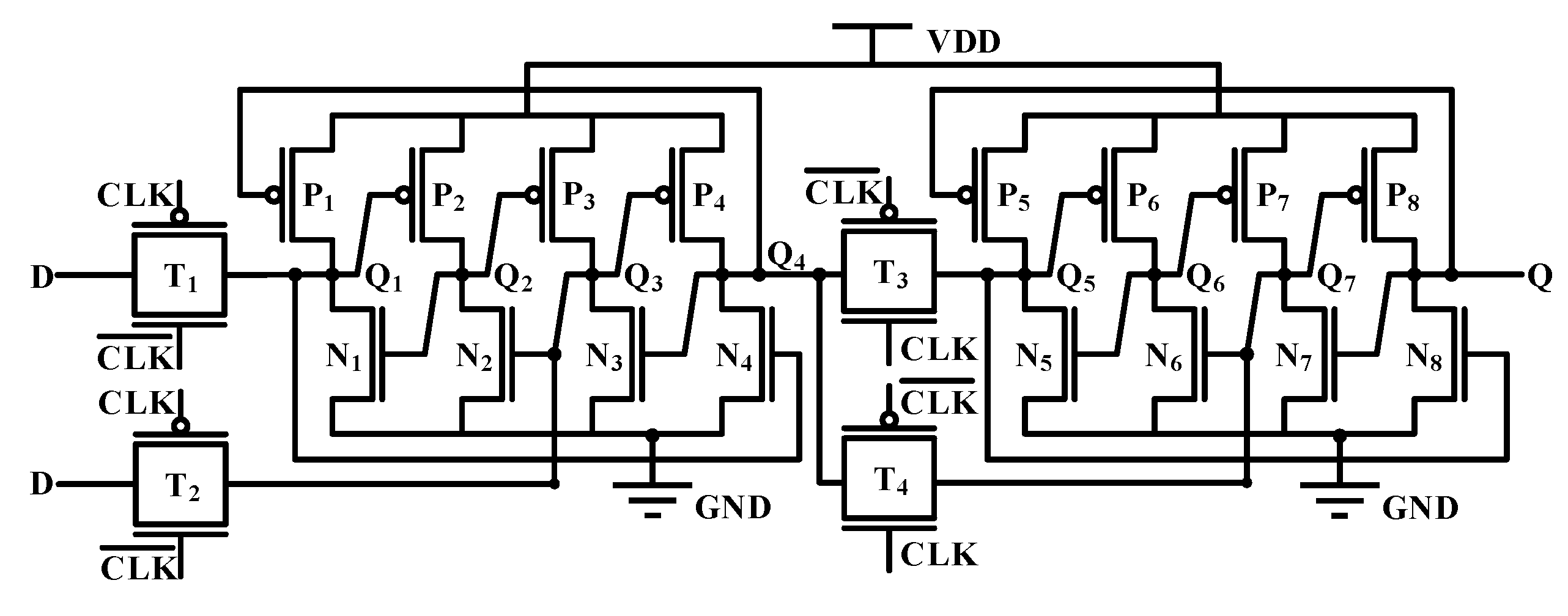
3.1. Asymmetric Reinforcement Circuit Structure
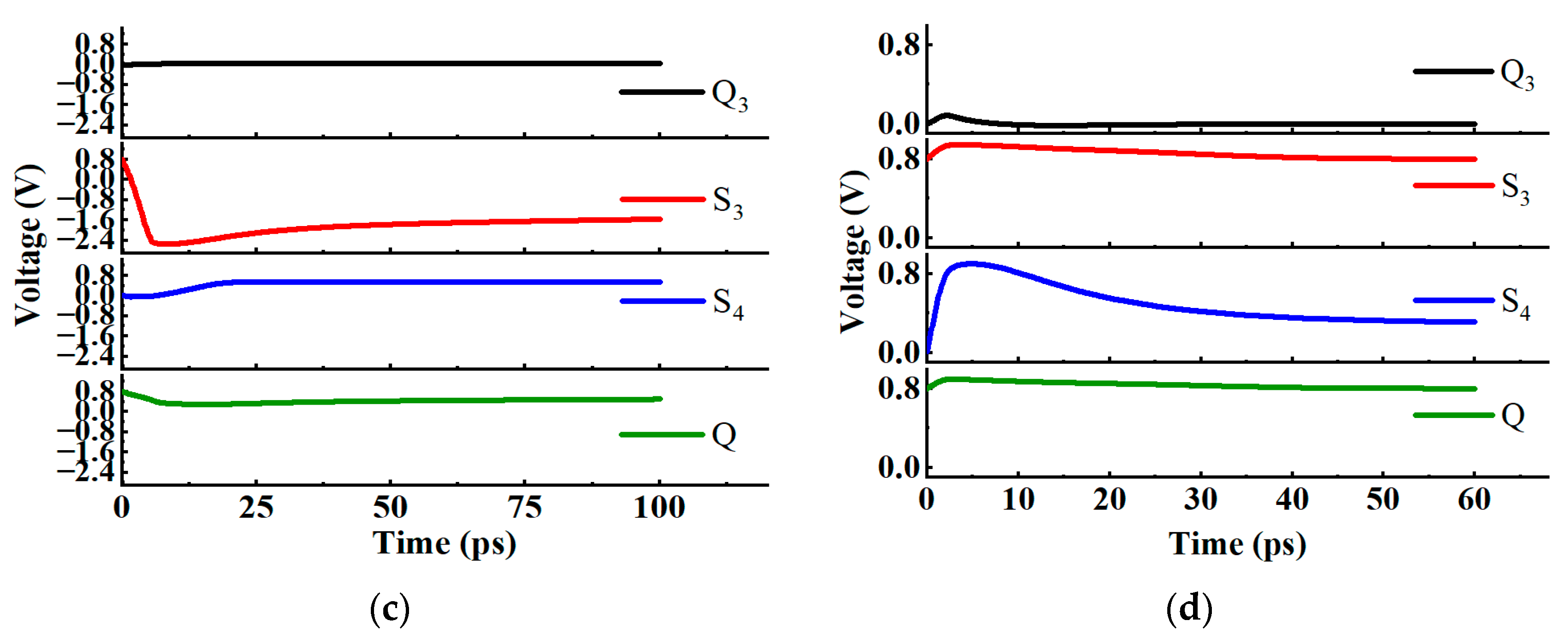
3.2. SEU Simulation
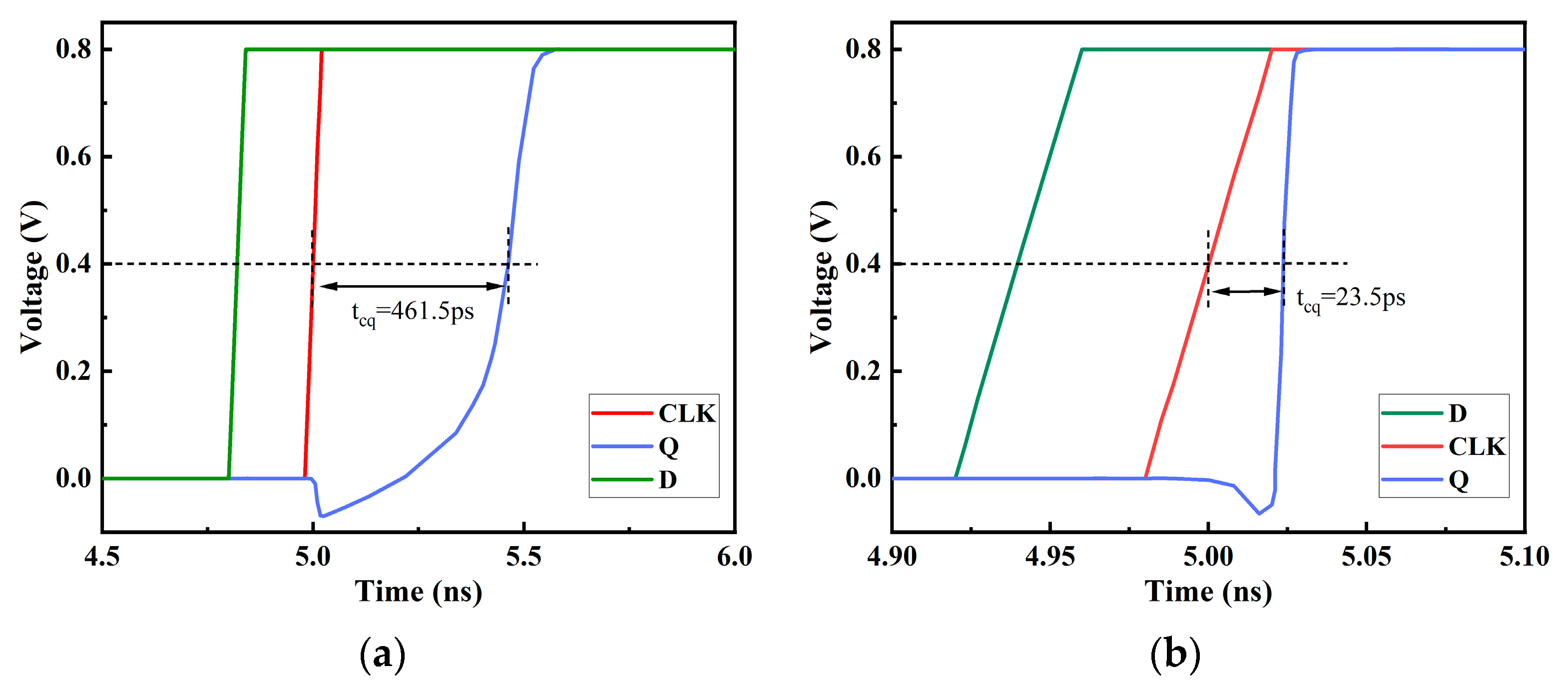
3.3. Circuit Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baumann, R. Soft errors in advanced computer systems. IEEE Des. Test Comput. 2005, 22, 258–266. [Google Scholar] [CrossRef]
- Dodd, P.E.; Massengill, L.W. Basic mechanisms and modeling of single-event upset in digital microelectronics. IEEE Trans. Nucl. Sci. 2003, 50, 583–602. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Jiang, J.; Jia, Y.; Xie, Y.; Zou, S.; Zhang, Z. A High-Performance and Low-Cost Single-Event Multiple-Node-Upsets Resilient Latch Design. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2022, 30, 1867–1877. [Google Scholar] [CrossRef]
- Wilson, A.E.; Wirthlin, M.; Baker, N.G. Neutron Radiation Testing of RISC-V TMR Soft Processors on SRAM-Based FPGAs. IEEE Trans. Nucl. Sci. 2023, 70, 603–610. [Google Scholar] [CrossRef]
- Clark, L.T.; Duvnjak, A.; Young-Sciortino, C.; Cannon, M.; Brunhaver, J.; Agarwal, S.; Neuendank, J.; Wilson, D.; Barnaby, H.; Marinella, M. Self-correcting Flip-flops for Triple Modular Redundant Logic in a 12-nm Technology. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 28 May–1 June 2022; pp. 1205–1209. [Google Scholar]
- Schrape, O.; Breitenreiter, A.; Schulze, C.; Zeidler, S.; Krstić, M. Radiation-Hardness-by-Design Latch-based Triple Modular Redundancy Flip-Flops. In Proceedings of the 2021 IEEE 12th Latin America Symposium on Circuits and System (LASCAS), Arequipa, Peru, 22–25 February 2021; pp. 1–4. [Google Scholar]
- Nassif, N.; Munch, A.O.; Molnar, C.L.; Pasdast, G.; Lyer, S.V.; Yang, Z.; Mendoza, O.; Huddart, M.; Venkataraman, S.; Kandula, S.; et al. Sapphire Rapids: The Next-Generation Intel Xeon Scalable Processor. In Proceedings of the 2022 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 22–26 February 2022; Volume 65, pp. 44–46. [Google Scholar]
- Chen, C.; Xiang, X.; Liu, C.; Shang, Y.; Guo, R.; Liu, D.; Lu, Y.; Hao, Z.; Luo, J.; Chen, Z.; et al. Xuantie-910: A Commercial Multi-Core 12-Stage Pipeline Out-of-Order 64-bit High Performance RISC-V Processor with Vector Extension: Industrial Product. In Proceedings of the 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA), Virtual Event, 30 May–3 June 2020; pp. 52–64. [Google Scholar]
- Azad, Z.; Farbeh, H.; Monazzah, A.M.H.; Miremadi, S.G. AWARE: Adaptive Way Allocation for Reconfigurable ECCs to Protect Write Errors in STT-RAM Caches. IEEE Trans. Emerg. Top. Comput. 2019, 7, 481–492. [Google Scholar] [CrossRef]
- Nakajima, R.; Ioki, K.; Furuta, J.; Kobayashi, K. Radiation Hardened Flip-Flops Minimizing Area, Power, and Delay Overheads with 1/100 Lower α-SER in a 130 nm Bulk Process. In Proceedings of the 2022 IEEE 28th International Symposium on On-Line Testing and Robust System Design (IOLTS), Torino, Italy, 12–14 September 2022; pp. 1–5. [Google Scholar]
- Tajima, S.; Yanagisawa, M.; Shi, Y. Transition Detector-Based Radiation-Hardened Latch for Both Single- and Multiple-Node Upsets. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1114–1118. [Google Scholar] [CrossRef]
- Mori, F.; Ebara, M.; Tsukita, Y.; Furuta, J.; Kobayashi, K. Intrinsic Vulnerability to Soft Errors and a Mitigation Technique by Layout Optimization on DICE Flip Flops in a 65-nm Bulk Process. IEEE Trans. Nucl. Sci. 2021, 68, 1727–1735. [Google Scholar] [CrossRef]
- Rabaey, J.M.; Chandrakasan, A.; Nikolic, B. Digital Integrated Circuits a Design Perspective; Pearson Education: London, UK, 2003. [Google Scholar]
- Calin, T.; Nicolaidis, M.; Velazco, R. Upset hardened memory design for submicron CMOS technology. IEEE Trans. Nucl. Sci. 1996, 43, 2874–2878. [Google Scholar] [CrossRef]
- Kobayashi, K.; Kubota, K.; Masuda, M.; Manzawa, Y.; Furuta, J.; Kanda, S.; Onodera, H. A Low-Power and Area-Efficient Radiation-Hard Redundant Flip-Flop, DICE ACFF, in a 65 nm Thin-BOX FD-SOI. IEEE Trans. Nucl. Sci. 2014, 61, 1881–1888. [Google Scholar] [CrossRef]
- Wang, H.-B.; Kauppila, J.S.; Lilja, K.; Bounasser, M.; Chen, L.; Newton, M.; Li, Y.-Q.; Liu, R.; Bhuva, B.L.; Wen, S.-J.; et al. Evaluation of SEU Performance of 28-nm FDSOI Flip-Flop Designs. IEEE Trans. Nucl. Sci. 2017, 64, 367–373. [Google Scholar] [CrossRef]
- Cai, C.; Liu, T.; Zhao, P.; Fan, X.; Huang, H.; Li, D.; Ke, L.; He, Z.; Xu, L.; Chen, G.; et al. Multiple Layout-Hardening Comparison of SEU-Mitigated Filp-Flops in 22-nm UTBB FD-SOI Technology. IEEE Trans. Nucl. Sci. 2020, 67, 374–381. [Google Scholar] [CrossRef]

| Device | W (nm) | L (nm) | W/L |
|---|---|---|---|
| N1, N3, N4 | 92 | 22 | 4.2 |
| N2, N5~N7, P1, P3, P4 | 184 | 8.4 | |
| P2, P5~P7 | 368 | 16.8 |
| Injection Position | Clock Signal | SEU Hardening Ability (Whether the Q Node Is Flipped) |
|---|---|---|
| Master latch | Low | Can resist SEU |
| High | Q1 is sensitive node | |
| Slave latch | Low | Both Q3 and Q are sensitive nodes |
| High | Can resist SEU |
| Device | W (nm) | L (nm) | W/L |
|---|---|---|---|
| N1, N4 | 92 | 22 | 4.2 |
| N13 | 184 | 8.4 | |
| N2, N11, N12 | 276 | 12.6 | |
| P1, P5~P8, N3 | 46 | 2.1 | |
| P3, P9, P10, P13 | 368 | 16.8 | |
| P2, P4, P11, P12 | 552 | 25.1 |
| Device | W (nm) | L (nm) | W/L |
|---|---|---|---|
| N1~N3, N5~N8, N13 | 100 | 22 | 4.6 |
| N9~N12 | 300 | 13.7 | |
| P5 | 50 | 2.3 | |
| N4, P1~P3, P6~P8, P13 | 200 | 9.1 | |
| P4 | 400 | 18.2 | |
| P9~P12 | 600 | 27.3 |
| Structures | Number of Transistors | Propagation Delay (ps) | SEU Threshold (pc/um) | Average Power | Maximum Power |
|---|---|---|---|---|---|
| Conventional | 12 | 61.7 | 0.06~0.07 | 1 | 1 |
| DICE | 24 | 23.5 | >0.7 | 1.74 | 1.49 |
| Proposed | 18 | 461.5 | >0.7 | 1.57 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Zhou, Y.; Liu, H.; Xiang, Q. SEU Hardened D Flip-Flop Design with Low Area Overhead. Micromachines 2023, 14, 1836. https://doi.org/10.3390/mi14101836
Yin C, Zhou Y, Liu H, Xiang Q. SEU Hardened D Flip-Flop Design with Low Area Overhead. Micromachines. 2023; 14(10):1836. https://doi.org/10.3390/mi14101836
Chicago/Turabian StyleYin, Chenyu, Yulun Zhou, Hongxia Liu, and Qi Xiang. 2023. "SEU Hardened D Flip-Flop Design with Low Area Overhead" Micromachines 14, no. 10: 1836. https://doi.org/10.3390/mi14101836
APA StyleYin, C., Zhou, Y., Liu, H., & Xiang, Q. (2023). SEU Hardened D Flip-Flop Design with Low Area Overhead. Micromachines, 14(10), 1836. https://doi.org/10.3390/mi14101836







