Positive and Negative Photoconductivity in Ir Nanofilm-Coated MoO3 Bias-Switching Photodetector
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Surface Morphology
3.2. EDS Elemental Analysis and Mapping
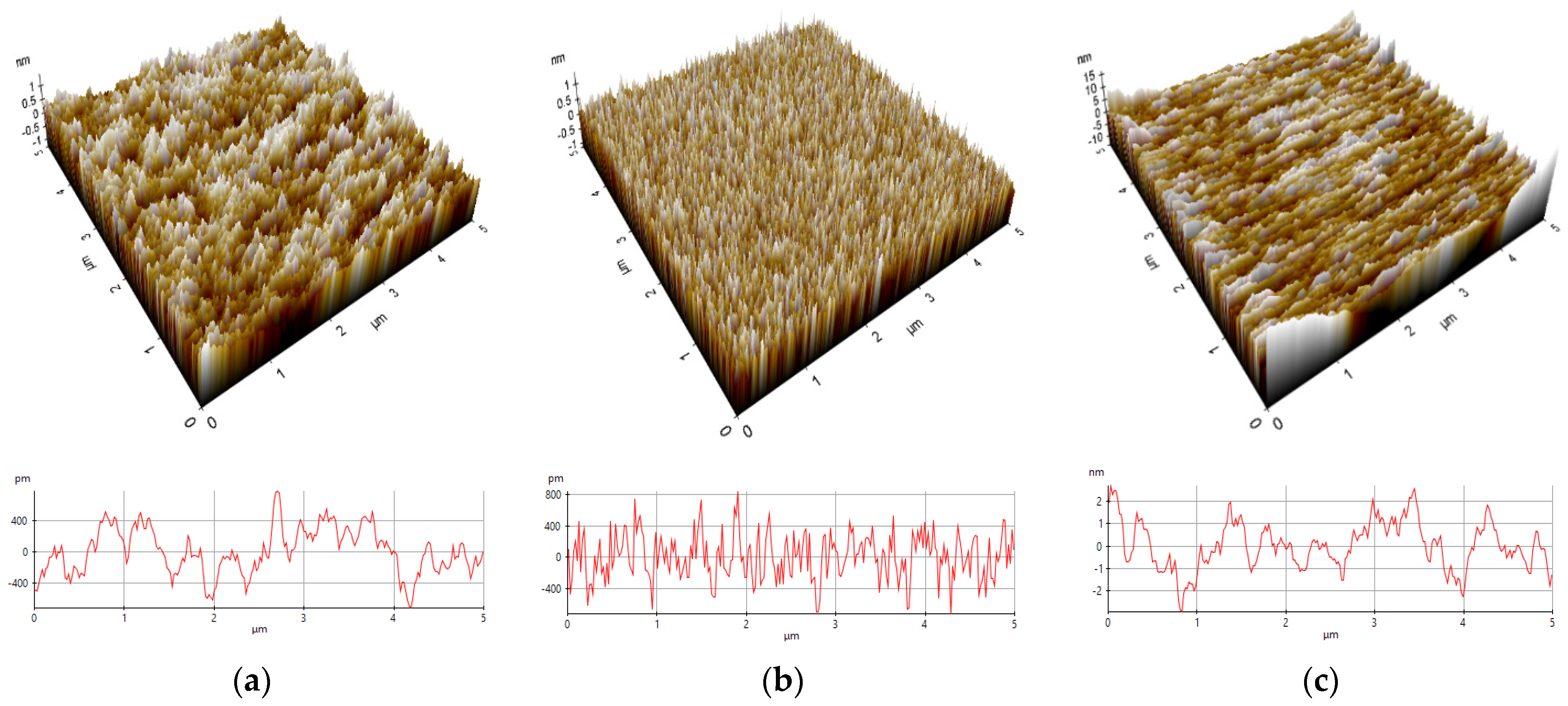
3.3. Surface Topography and Roughness Analysis
3.4. Hall Effect and Carrier Concentrations
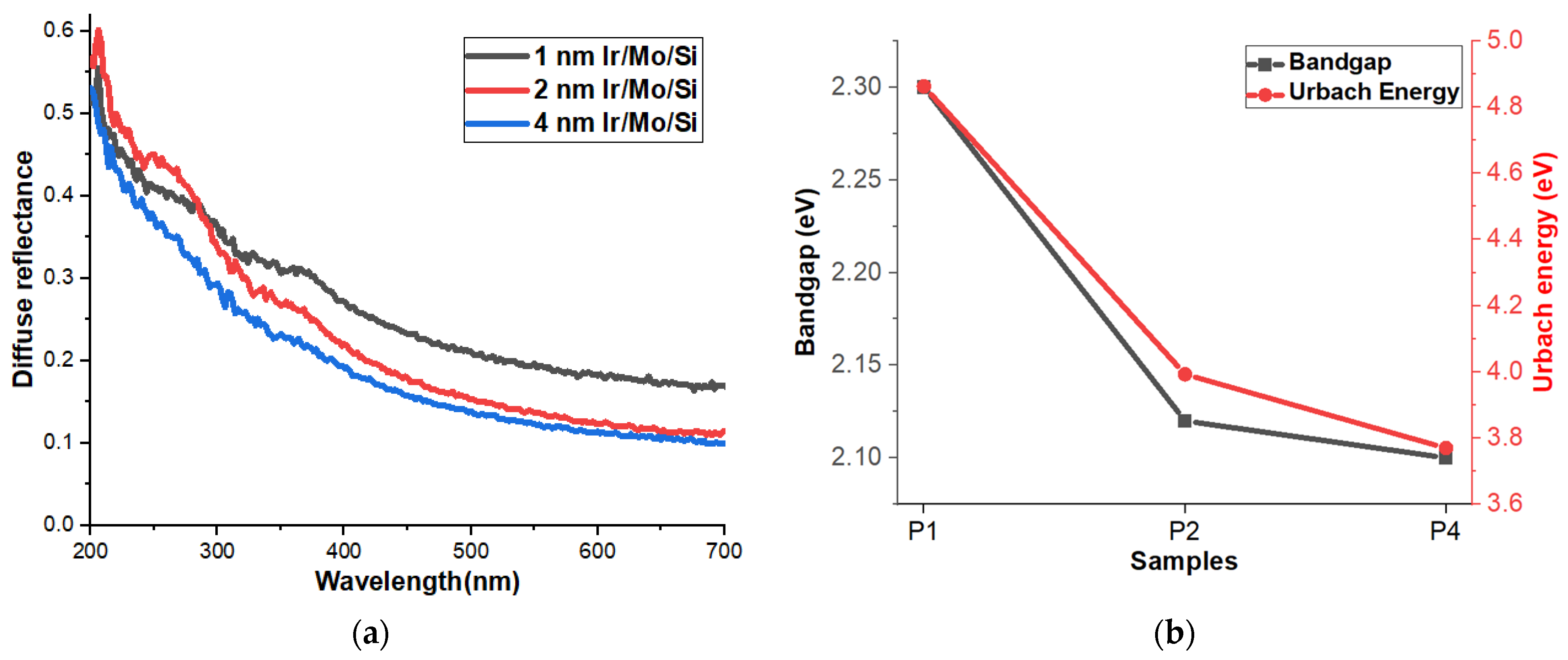
3.5. Reflectance, Bandgap, and Urbach Energy
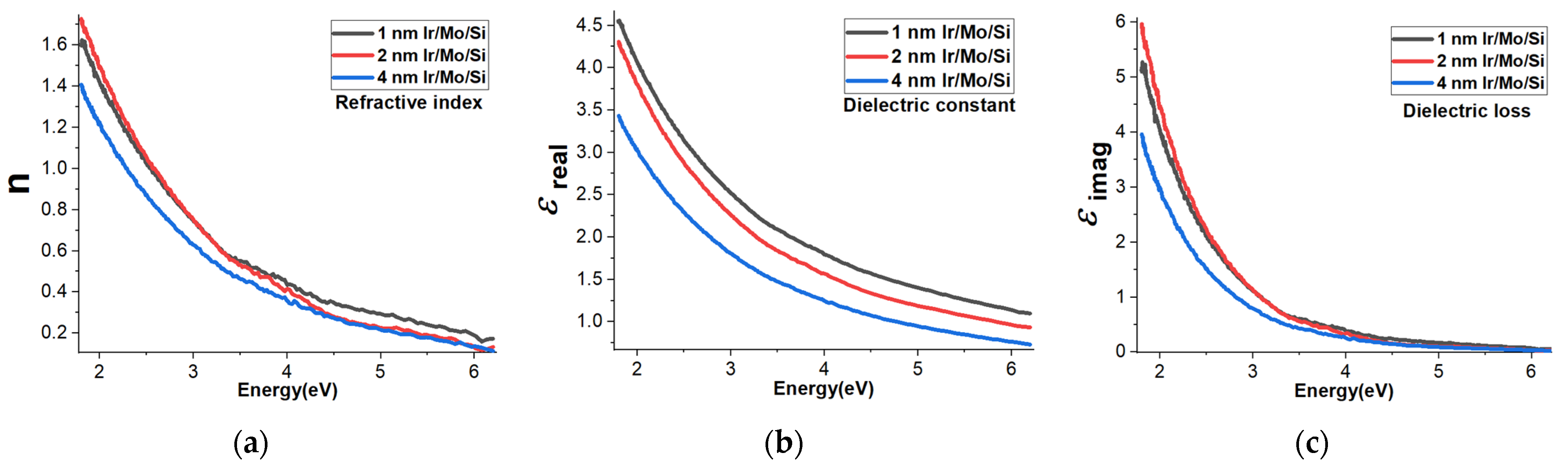
3.6. Refractive Index, Dielectric Constant, and Dielectric Loss
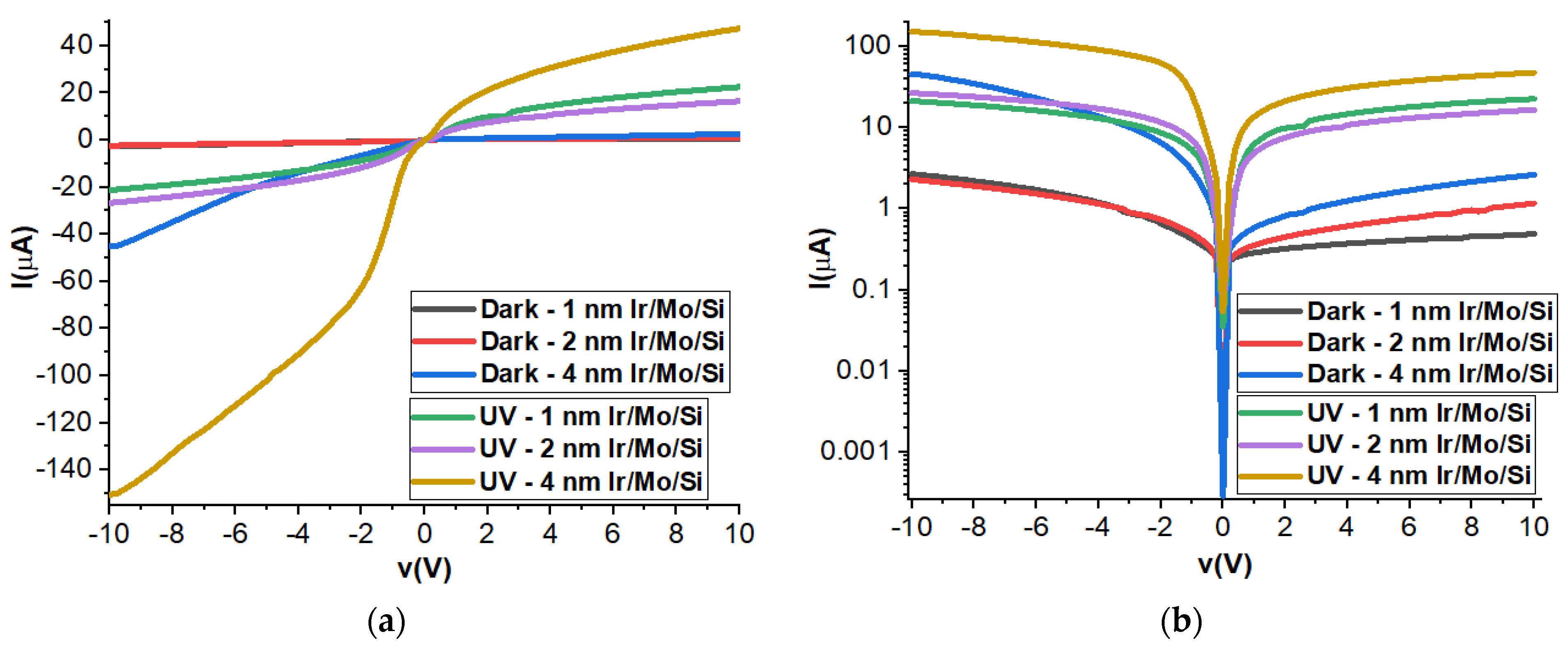
3.7. Current–Voltage Measurements
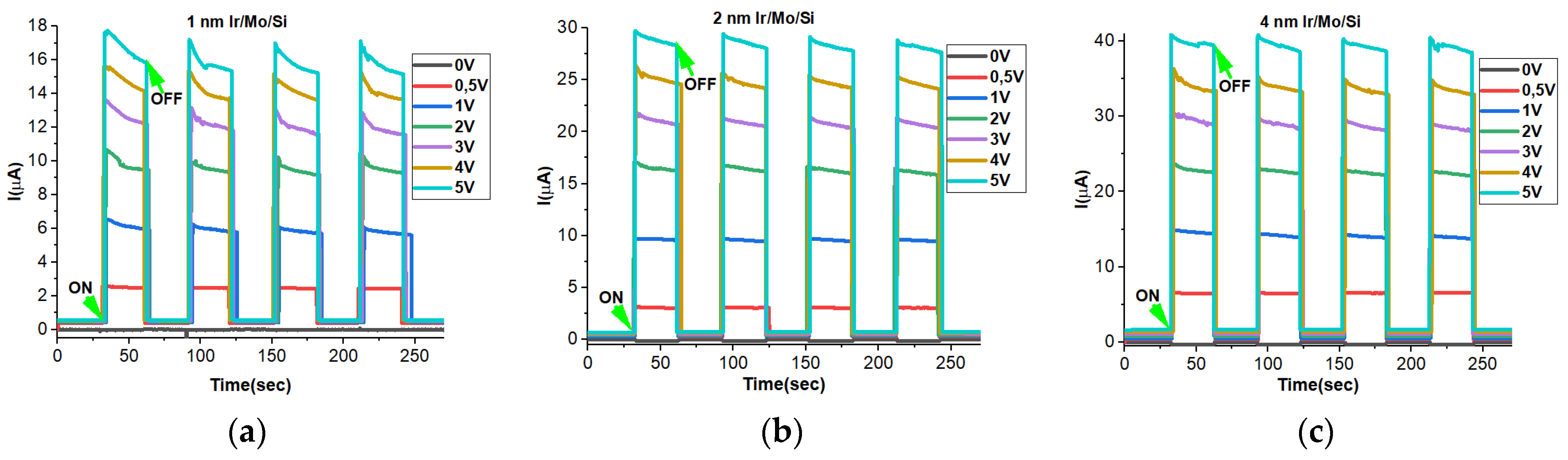
3.8. Transient Photocurrent Properties
3.9. ON–OFF Dynamics
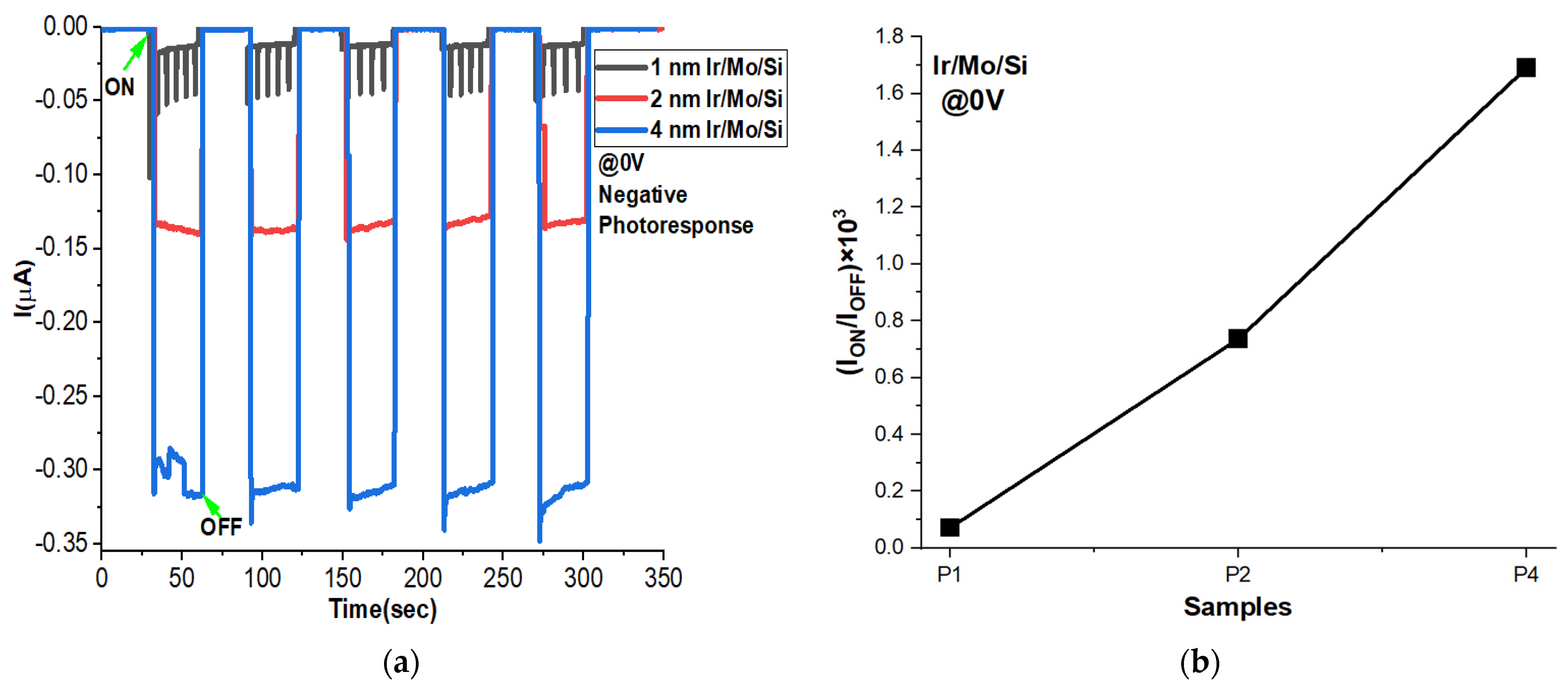
3.10. Negative Photoconductivity at 0 V Bias
3.11. Response and Recovery Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, S.; Liu, Y.; Wu, Y.; Liu, Y.; Guo, F.; Li, S.; Yu, W.; Liu, G.; Hao, J.; Wang, H. Self-powered broadband α-MoO3/Si photodetector based on photo-induced thermoelectric effect. Ceram. Int. 2022, 48, 25079–25085. [Google Scholar] [CrossRef]
- Wang, F.; Li, L.; Huang, W.; Li, L.; Jin, B.; Li, H.; Zhai, T. Submillimeter 2D Bi2Se3 flakes toward high-performance infrared photodetection at optical communication wavelength. Adv. Funct. Mater. 2018, 28, 1802707. [Google Scholar] [CrossRef]
- Buscema, M.; Island, J.O.; Groenendijk, D.J.; Blanter, S.I.; Steele, G.A.; van der Zant, H.S.; Castellanos-Gomez, A. Photocurrent generation with two-dimensional van der Waals semiconductors. Chem. Soc. Rev. 2015, 44, 3691–3718. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Weiss, N.O.; Duan, X.; Cheng, H.-C.; Huang, Y.; Duan, X. Van der Waals heterostructures and devices. Nat. Rev. Mater. 2016, 1, 16042. [Google Scholar] [CrossRef]
- He, R.; Chen, Z.; Lai, H.; Zhang, T.; Wen, J.; Chen, H.; Xie, F.; Yue, S.; Liu, P.; Chen, J.; et al. van der Waals Transition-Metal Oxide for Vis–MIR Broadband Photodetection via Intercalation Strategy. ACS Appl. Mater. Interfaces 2019, 11, 15741–15747. [Google Scholar] [CrossRef]
- Kwak, D.; Wang, M.; Koski, K.J.; Zhang, L.; Sokol, H.; Maric, R.; Lei, Y. Molybdenum trioxide (α-MoO3) nanoribbons for ultrasensitive ammonia (NH3) gas detection: Integrated experimental and density functional theory simulation studies. ACS Appl. Mater. Interfaces 2019, 11, 10697–10706. [Google Scholar] [CrossRef]
- Flannigan, L.; Yoell, L.; Xu, C.-Q. Mid-wave and long-wave infrared transmitters and detectors for optical satellite communications—A review. J. Opt. 2022, 24, 043002. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, S.; Shi, Q.; Hao, S.; Bian, A.; Xie, X.; Liu, Z. Preparation of all-oxide β-Ga2O3/α-MoO3 heterojunction towards self-driven deep ultraviolet photosensor. Phys. Scr. 2021, 96, 125844. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Wang, H.; Chen, P.; Pi, L.; Zhou, X.; Zhai, T. Intercalation strategy in 2D materials for electronics and optoelectronics. Small Methods 2021, 5, 2100567. [Google Scholar] [CrossRef]
- Pligovka, A.; Poznyak, A.; Norek, M. Optical Properties of Porous Alumina Assisted Niobia Nanostructured Films–Designing 2-D Photonic Crystals Based on Hexagonally Arranged Nanocolumns. Micromachines 2021, 12, 589. [Google Scholar] [CrossRef]
- Pligovka, A.; Lazavenka, A.; Turavets, U.; Hoha, A.; Salerno, M. Two-Level 3D Column-like Nanofilms with Hexagonally–Packed Tantalum Fabricated via Anodizing of Al/Nb and Al/Ta Layers—A Potential Nano-Optical Biosensor. Materials 2023, 16, 993. [Google Scholar] [CrossRef] [PubMed]
- Puebla, S.; D’Agosta, R.; Sanchez-Santolino, G.; Frisenda, R.; Munuera, C.; Castellanos-Gomez, A. In-plane anisotropic optical and mechanical properties of two-dimensional MoO3. NPJ 2D Mater. Appl. 2021, 5, 37. [Google Scholar] [CrossRef]
- Lv, X.; Wang, S.; Gong, L.; Chen, Q.; Zhang, Y.; Chen, J.; Xie, W. In-situ investigation on the thermal decomposition of van der Waals MoO3. Chem. Phys. Lett. 2021, 779, 138840. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Y.; Tang, X.; Wang, W.; Li, G. A Self-Powered High-Performance UV Photodetector Based on Core–Shell GaN/MoO3−x Nanorod Array Heterojunction. Adv. Opt. Mater. 2020, 8, 2000197. [Google Scholar] [CrossRef]
- Yang, M.; Han, Q.; Liu, X.; Han, J.; Zhao, Y.; He, L.; Gou, J.; Wu, Z.; Wang, X.; Wang, J. Ultrahigh stability 3D TI Bi2Se3/MoO3 thin film heterojunction infrared photodetector at optical communication waveband. Adv. Funct. Mater. 2020, 30, 1909659. [Google Scholar] [CrossRef]
- Ahmad, H.; Afzal, N.; Rafique, M.; Ahmed, A.A.; Ahmad, R.; Khaliq, Z. Post-deposition annealed MoO3 film based high performance MSM UV photodetector fabricated on Si (100). Ceram. Int. 2020, 46, 20477–20487. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Jit, S. Solution-processed ZnO nanoparticles (NPs)/CH3NH3PbI3/PTB7/MoO3/Ag inverted structure based UV–visible-Near Infrared (NIR) broadband photodetector. Opt. Mater. 2023, 135, 113290. [Google Scholar] [CrossRef]
- Zhang, R.; Ma, X.; An, C.; Zhang, D.; Sun, D.; Hu, X.; Liu, J. Self-powered photodetector based on vertical MoO3/MoS2 hetero-structure with gate tunable photo-response. 2D Mater. 2019, 6, 035033. [Google Scholar] [CrossRef]
- Bhatt, V.; Sahare, S.; Kumar, M.; Lee, S.-L.; Kumar, S.; Yun, J.-H. Pyro-phototronic effect in n-Si/p-MoO3−x heterojunction: An approach to improve the photoresponse of the ultraviolet photodetector. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2023, 10, 2200500. [Google Scholar] [CrossRef]
- Mondal, A.; Reddy, Y.A.K. Influence of Oxygen Partial Pressure on the Performance of MoO3-based Ultraviolet Photodetectors. Surf. Interfaces 2023, 41, 103179. [Google Scholar] [CrossRef]
- Rath, J.; Venkatesh, A.; Moorthy, V. Ultra-Thin Plasmonic Optoelectronic Devices. In Recent Advances in Thin Film Photovoltaics; Springer Nature Singapore: Singapore, 2022; pp. 219–271. [Google Scholar]
- Tang, H.; Chen, C.-J.; Huang, Z.; Bright, J.; Meng, G.; Liu, R.-S.; Wu, N. Plasmonic hot electrons for sensing, photodetection, and solar energy applications: A perspective. J. Chem. Phys. 2020, 152, 220901. [Google Scholar] [CrossRef]
- Chang, X.; Wang, Y.-F.; Zhang, X.; Wang, R.; Liu, Z.; Fu, J.; Zhao, D.; Li, F.; Wang, J.; Wang, W.; et al. Iridium size effects in localized surface plasmon-enhanced diamond UV photodetectors. Appl. Surf. Sci. 2019, 487, 674–677. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Bai, H.; Zhuang, W.; Xu, Y. Effect of iridium doping on electronic structure and optical properties of m-BiVO4 photocatalytic materials: A first principles study. Mol. Phys. 2022, 120, e2002958. [Google Scholar] [CrossRef]
- Weaver, J.H.; Olson, C.G.; Lynch, D.W. Optical investigation of the electronic structure of bulk Rh and Ir. Phys. Rev. B 1977, 15, 4115–4118. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Chang, X.; Li, S.; Zhao, D.; Shao, G.; Zhu, T.; Fu, J.; Zhang, P.; Chen, X.; Li, F.; et al. Ohmic contact between iridium film and hydrogen-terminated single crystal diamond. Sci. Rep. 2017, 7, 12157. [Google Scholar] [CrossRef] [PubMed]
- Hung, S.; Xiao, F.; Hsu, Y.; Suen, N.; Yang, H.; Chen, H.M.; Liu, B. Iridium Oxide-Assisted Plasmon-Induced Hot Carriers: Improvement on Kinetics and Thermodynamics of Hot Carriers. Adv. Energy Mater. 2016, 6, 1501339. [Google Scholar] [CrossRef]
- Xu, X.; Gabor, N.M.; Alden, J.S.; van der Zande, A.M.; McEuen, P.L. Photo-thermoelectric effect at a graphene interface junction. Nano Lett. 2010, 10, 562–566. [Google Scholar] [CrossRef]
- Lemme, M.C.; Koppens, F.H.L.; Falk, A.L.; Rudner, M.S.; Park, H.; Levitov, L.S.; Marcus, C.M. Gate-activated photoresponse in a graphene p–n junction. Nano Lett. 2011, 11, 4134–4137. [Google Scholar] [CrossRef]
- Wang, P.-F.; Liu, Y.; Yin, J.; Ma, W.; Dong, Z.; Zhang, W.; Zhu, J.-L.; Sun, J.-L. A tunable positive and negative photoconductive photodetector based on a gold/graphene/p-type silicon heterojunction. J. Mater. Chem. C 2019, 7, 887–896. [Google Scholar] [CrossRef]
- Miao, J.; Song, B.; Li, Q.; Cai, L.; Zhang, S.; Hu, W.; Dong, L.; Wang, C. Photothermal effect induced negative photoconductivity and high responsivity in flexible black phosphorus transistors. ACS Nano 2017, 11, 6048–6056. [Google Scholar] [CrossRef]
- Singh, S.C.; Peng, Y.; Rutledge, J.; Guo, C. Photothermal and Joule-heating-induced negative-photoconductivity-based ultraresponsive and near-zero-biased copper selenide photodetectors. ACS Appl. Electron. Mater. 2019, 1, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
- Kalanyan, B.; Beams, R.; Katz, M.B.; Davydov, A.V.; Maslar, J.E.; Kanjolia, R.K. MoS2 thin films from a (NtBu)2(NMe2)2Mo and 1-propanethiol atomic layer deposition process. J. Vac. Sci. Technol. A 2019, 37, 010901. [Google Scholar] [CrossRef] [PubMed]
- Bertuch, A.; Sundaram, G.; Saly, M.; Moser, D.; Kanjolia, R. Atomic layer deposition of molybdenum oxide using bis (tert-butylimido) bis (dimethylamido) molybdenum. J. Vac. Sci. Technol. A 2014, 32, 01A119. [Google Scholar] [CrossRef]
- Rossel, R.V.; Glynn, M.; McBratney, A. Determining the composition of mineral-organic mixes using UV–vis–NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Landi, S.; Segundo, I.R.; Freitas, E.; Vasilevskiy, M.; Carneiro, J.; Tavares, C.J. Use and misuse of the Kubelka-Munk function to obtain the band gap energy from diffuse reflectance measurements. Solid State Commun. 2022, 341, 114573. [Google Scholar] [CrossRef]
- Jubu, P.R.; Obaseki, O.; Nathan-Abutu, A.; Yam, F.; Yusof, Y.; Ochang, M. Dispensability of the conventional Tauc’s plot for accurate bandgap determination from UV–vis optical diffuse reflectance data. Results Opt. 2022, 9, 100273. [Google Scholar] [CrossRef]
- Landi, S.; Segundo, I.R.; Afonso, C.; Lima, O.; Costa, M.F.; Freitas, E.; Carneiro, J. Evaluation of band gap energy of TiO2 precipitated from titanium sulphate. Phys. B Condens. Matter 2022, 639, 414008. [Google Scholar] [CrossRef]
- Jamil, H.; Dildar, I.; Ilyas, U.; Hashmi, J.; Shaukat, S.; Sarwar, M.; Khaleeq-Ur-Rahman, M. Microstructural and Optical study of polycrystalline manganese oxide films using Kubelka-Munk function. Thin Solid Films 2021, 732, 138796. [Google Scholar] [CrossRef]
- Tunc, I.; Bruns, M.; Gliemann, H.; Grunze, M.; Koelsch, P. Bandgap determination and charge separation in Ag@ TiO2 core shell nanoparticle films. Surf. Interface Anal. 2010, 42, 835–841. [Google Scholar] [CrossRef]
- Wasim, S.; Rincón, C.; Marín, G.; Bocaranda, P.; Hernández, E.; Bonalde, I.; Medina, E. Effect of structural disorder on the Urbach energy in Cu ternaries. Phys. Rev. B 2001, 64, 195101. [Google Scholar] [CrossRef]
- Tanaka, K. Minimal Urbach energy in non-crystalline materials. J. Non-Cryst. Solids 2014, 389, 35–37. [Google Scholar] [CrossRef]
- Kumar, R.A.; Lekha, P.C.; Sanjeeviraja, C.; Padiyan, D.P. Evolution of structural disorder using Raman spectra and Urbach energy in GeSe0. 5S1. 5 thin films. J. Non-Cryst. Solids 2014, 405, 21–26. [Google Scholar] [CrossRef]
- Chang, Y.; Guha, S.; Grein, C.; Velicu, S.; Flatté, M.; Nathan, V.; Sivananthan, S. Absorption of narrow-gap HgCdTe near the band edge including nonparabolicity and the urbach tail. J. Electron. Mater. 2007, 36, 1000–1006. [Google Scholar] [CrossRef]
- Zhang, C.; Mahadevan, S.; Yuan, J.; Ho, J.K.W.; Gao, Y.; Liu, W.; Zhong, H.; Yan, H.; Zou, Y.; Tsang, S.-W.; et al. Unraveling Urbach tail effects in high-performance organic photovoltaics: Dynamic vs static disorder. ACS Energy Lett. 2022, 7, 1971–1979. [Google Scholar] [CrossRef]
- Archana, K.J.; Preetha, A.C.; Balasubramanian, K. Influence of Urbach energy in enhanced photocatalytic activity of Cu doped ZnO nanoparticles. Opt. Mater. 2022, 127, 112245. [Google Scholar] [CrossRef]
- Moss, T.S.; Burrell, G.J.; Ellis, B. Semiconductor Opto-Electronics; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Shaban, M.; Attia, G.F.; Basyooni, M.A.; Hamdy, H. Synthesis and characterization of Tin oxide thin film, effect of annealing on multilayer film. J. Mod. Trends Phys. Res. 2014, 14, 90–99. [Google Scholar]
- Jiang, T.; Huang, Y.; Meng, X. CdS core-Au/MXene-based photodetectors: Positive deep-UV photoresponse and negative UV–Vis-NIR photoresponse. Appl. Surf. Sci. 2020, 513, 145813. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, Z.; Huang, J.; Shao, L.; Gao, F.; Chen, X.; Khisro, S.N.; Zhang, Y. Bidirectional photoresponse of graphdiyne/graphene heterojunction detector for optical logic gates. Appl. Phys. Lett. 2023, 122, 033501. [Google Scholar] [CrossRef]
- Tailor, N.K.; Aranda, C.A.; Saliba, M.; Satapathi, S. Negative Photoconductivity: Bizarre Physics in Semiconductors. ACS Mater. Lett. 2022, 4, 2298–2320. [Google Scholar] [CrossRef]
- Tailor, N.K.; Maity, P.; Satapathi, S. Observation of Negative Photoconductivity in Lead-Free Cs3Bi2Br9 Perovskite Single Crystal. Acs Photonics 2021, 8, 2473–2480. [Google Scholar] [CrossRef]
- Tran, V.-T.; Wei, Y.; Du, H. On-substrate joule effect heating by printed micro-heater for the preparation of ZnO semiconductor thin film. Micromachines 2020, 11, 490. [Google Scholar] [CrossRef] [PubMed]
- Lalisse, A.; Tessier, G.; Plain, J.; Baffou, G. Quantifying the efficiency of plasmonic materials for near-field enhancement and photothermal conversion. J. Phys. Chem. C 2015, 119, 25518–25528. [Google Scholar] [CrossRef]
- Yang, J.-M.; Pan, Z.-Q.; Qin, F.-F.; Chen, M.; Wang, K.; Xia, X.-H. An in situ SERS study of ionic transport and the Joule heating effect in plasmonic nanopores. Chem. Commun. 2018, 54, 13236–13239. [Google Scholar] [CrossRef] [PubMed]
- Palermo, G.; Guglielmelli, A.; Pezzi, L.; Cataldi, U.; De Sio, L.; Caputo, R.; De Luca, A.; Bürgi, T.; Tabiryan, N.; Umeton, C. A command layer for anisotropic plasmonic photo-thermal effects in liquid crystal. Liq. Cryst. 2018, 45, 2214–2220. [Google Scholar] [CrossRef]




| Presence of Si | Absence of Si | ||||||
|---|---|---|---|---|---|---|---|
| Samples | Si | O | Ir | Mo | O | Ir | Mo |
| P1 | 97.2 | 1.3 | 1.5 | 0.0 | 37.1 | 62.8 | 0.1 |
| P2 | 96.7 | 1.2 | 2.1 | 0.0 | 28.8 | 71.2 | 0.0 |
| P4 | 93.1 | 1.3 | 5.6 | 0.0 | 16.5 | 83.5 | 0.0 |
| Sample | Min (nm) | Max (nm) | Mid (nm) | Rpv (nm) | Rq (nm) | Ra (nm) | Rz (nm) | Rsk | Rku |
|---|---|---|---|---|---|---|---|---|---|
| P1 | −0.76 | 0.56 | −0.10 | 1.33 | 0.25 | 0.19 | 1.09 | 0.22 | 3.05 |
| P2 | −0.72 | 0.84 | 0.06 | 1.56 | 0.29 | 0.23 | 1.37 | 0.02 | 2.82 |
| P4 | −2.94 | 2.69 | −0.12 | 5.63 | 1.07 | 0.85 | 4.56 | −0.07 | 2.81 |
| Sample | Rs (Ω/sq) | Rho (/Ωcm) | VH (V) | RH (m3/C) | Type | Ns (/cm2) | N (/cm3) |
|---|---|---|---|---|---|---|---|
| P1 | 1.028 × 106 | 7.449 × 10−1 | −5.928 × 10−3 | −1.984 × 10−4 | n | −2.277 × 1010 | −3.145 × 1016 |
| P2 | 8.432 × 105 | 5.338 × 10−1 | −5.674 × 10−3 | −4.981 × 10−5 | n | −7.930 × 1010 | −1.252 × 1017 |
| P4 | 2.111 × 105 | 2.584 × 10−1 | −2.410 × 10−5 | −4.092 × 10−7 | n | −1.866 × 1013 | −1.524 × 1019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basyooni-M. Kabatas, M.A.; En-nadir, R.; Rahmani, K.; Eker, Y.R. Positive and Negative Photoconductivity in Ir Nanofilm-Coated MoO3 Bias-Switching Photodetector. Micromachines 2023, 14, 1860. https://doi.org/10.3390/mi14101860
Basyooni-M. Kabatas MA, En-nadir R, Rahmani K, Eker YR. Positive and Negative Photoconductivity in Ir Nanofilm-Coated MoO3 Bias-Switching Photodetector. Micromachines. 2023; 14(10):1860. https://doi.org/10.3390/mi14101860
Chicago/Turabian StyleBasyooni-M. Kabatas, Mohamed A., Redouane En-nadir, Khalid Rahmani, and Yasin Ramazan Eker. 2023. "Positive and Negative Photoconductivity in Ir Nanofilm-Coated MoO3 Bias-Switching Photodetector" Micromachines 14, no. 10: 1860. https://doi.org/10.3390/mi14101860
APA StyleBasyooni-M. Kabatas, M. A., En-nadir, R., Rahmani, K., & Eker, Y. R. (2023). Positive and Negative Photoconductivity in Ir Nanofilm-Coated MoO3 Bias-Switching Photodetector. Micromachines, 14(10), 1860. https://doi.org/10.3390/mi14101860







