Effects of Oxygen Pressure on the Microstructures and Nanomechanical Properties of Samarium-Doped BiFeO3 Thin Films
Abstract
:1. Introduction
2. Materials and Methods
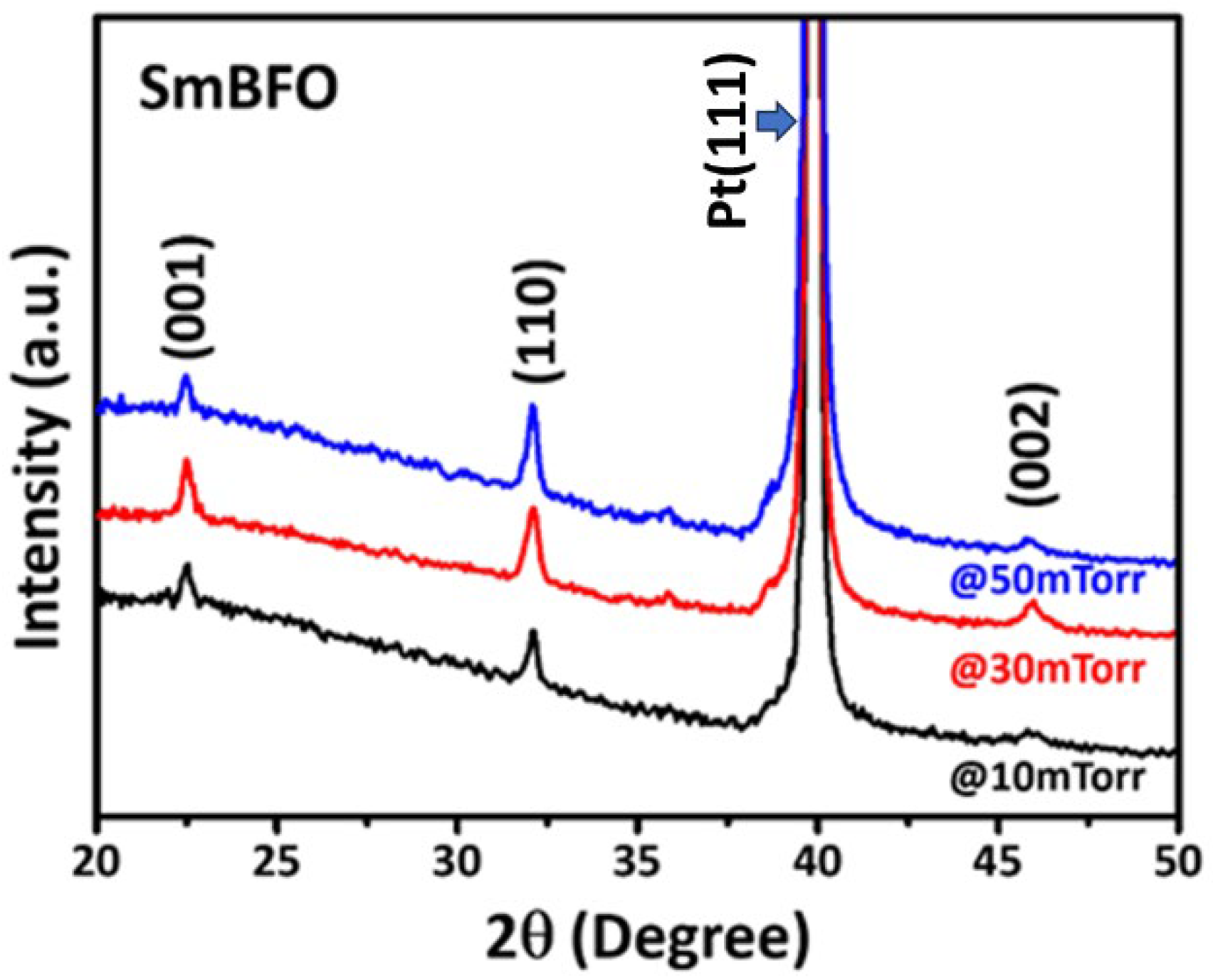
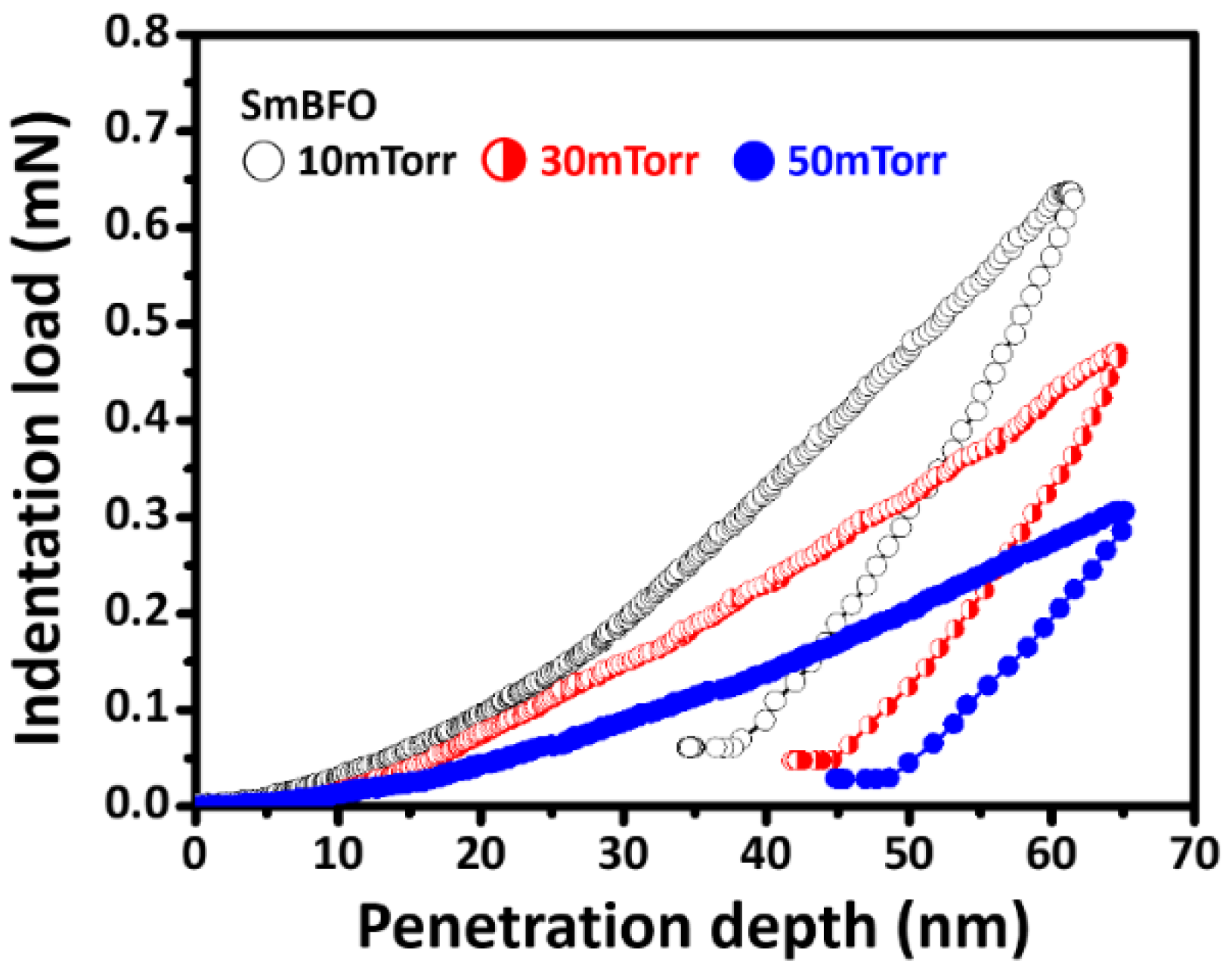
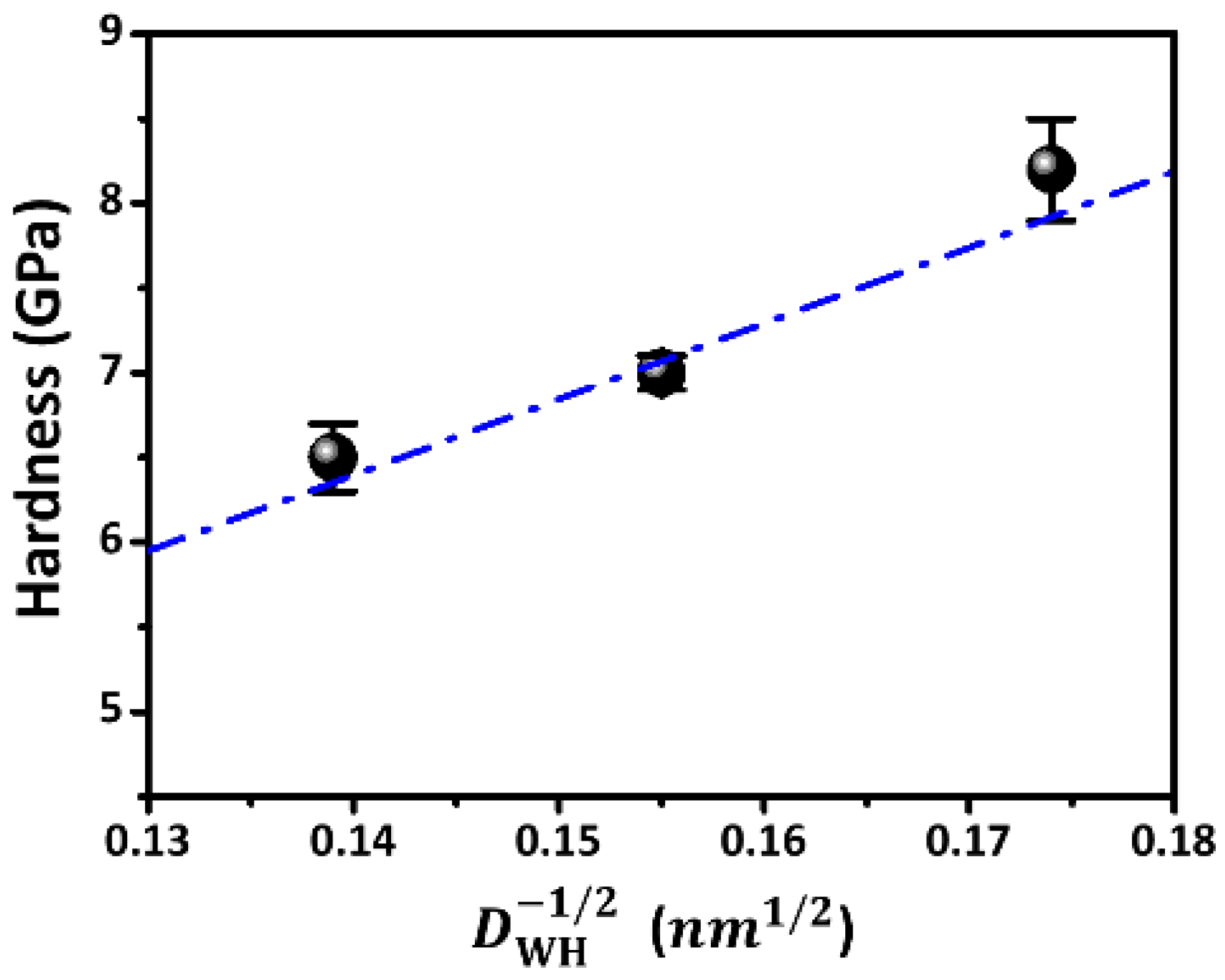
3. Results and Discussion
| Ds (nm) | DWH (nm) | ε (%) | H (GPa) | Ef (GPa) | (GPa) | |
|---|---|---|---|---|---|---|
| BFO thin films [41] | 24.5–51.2 | ― | ― | 6.8–10.6 | 131.4–170.8 | ― |
| BFO thin films [42] | 5.6–10.1 | ― | ― | 7.5–7.9 | 111.1–118.3 | ― |
| La-doped BFO ceramics [43] | ― | ― | ― | 2.5 ± 0.2 | 80 ± 10 | ― |
| SmBFO_10mTorr [#] | 20 | 33 | 0.22 | 8.2 ± 0.3 | 114.3 ± 1.2 | 0.0422 |
| (oxygen partial pressure) | ||||||
| SmBFO_30mTorr [#] | 22 | 41 | 0.24 | 7.1 ± 0.1 | 97.2 ± 2.6 | 0.0378 |
| (oxygen partial pressure) | ||||||
| SmBFO_50mTorr [#] | 25 | 52 | 0.25 | 6.5 ± 0.2 | 85.6 ± 4.3 | 0.0374 |
| (oxygen partial pressure) |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hill, N.A. Why are there so few magnetic ferroelectrics? J. Phys. Chem. B 2000, 104, 6694. [Google Scholar] [CrossRef]
- Kuo, C.-Y.; Hu, Z.; Yang, J.C.; Liao, S.-C.; Huang, Y.L.; Vasudevan, R.K.; Okatan, M.B.; Jesse, S.; Kalinin, S.V.; Li, L.; et al. Single-domain multiferroic BiFeO3 films. Nat. Commun. 2016, 7, 12712. [Google Scholar] [CrossRef]
- Geng, W.R.; Tang, Y.L.; Zhu, Y.L.; Wang, Y.J.; Wu, B.; Yang, L.X.; Feng, Y.P.; Zou, M.J.; Shi, T.T.; Cao, Y.; et al. Magneto-electric-optical coupling in multiferroic BiFeO3-based films. Adv. Mater. 2023, 34, 2106396. [Google Scholar] [CrossRef]
- Yao, L.; Wu, X.; Yang, S.; Zhang, Y. Structural and optical properties of Ca doped BiFeO3 thin films prepared by a sol-gel method. Ceram. Int. 2017, 43, S470–S473. [Google Scholar] [CrossRef]
- Liang, X.L.; Dai, J.Q. Prominent ferroelectric properties in Mn-doped BiFeO3 spin-coated thin films. J. Alloys Compd. 2021, 886, 161168. [Google Scholar] [CrossRef]
- Micard, Q.; Pellegrino, A.L.; Nigro, R.L.; Bartasyte, A.; Condorelli, G.G.; Malandrino, G. Piezoelectric Ba and Ti co-doped BiFeO3 textured films: Selective growth of solid solutions or nanocomposites. J. Mater. Chem. C 2020, 8, 16168–16179. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Wu, J.-M.; Lai, C.-H. Influence of La doping in multiferroic properties of BiFeO3 thin films. Appl. Phys. Lett. 2006, 88, 042903. [Google Scholar] [CrossRef]
- Pan, T.-M.; Chou, Y.-C.; Her, J.-L. Effect of Yb-doping on structural and electrical properties of BiFeO3 thin films. Mater. Chem. Phys. 2022, 278, 125699. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J.; Sun, X.; Jian, J.; Liu, J.; Wang, H. Effective doping control in Sm-doped BiFeO3 thin films via deposition temperature. RSC Adv. 2020, 10, 40229. [Google Scholar] [CrossRef]
- Balmuchu, S.P.; Dobbidi, P. The effect of La doping on multiferroic BiFeO3 ceramic through structural, dielectric, magnetic, ferroelectric, and optical studies. Phys. B 2022, 638, 413937. [Google Scholar] [CrossRef]
- Xue, X.; Tan, G.; Liu, W.; Hao, H. Study on pure and Nd-doped BiFeO3 thin films prepared by chemical solution deposition method. J. Alloys Compd. 2014, 604, 57. [Google Scholar] [CrossRef]
- Hussain, G.; Ahmed, I.; Rehman, A.U.; Subhani, M.U.; Morley, N.; Akhtar, M.; Arshad, M.I.; Anwar, H. Study of the role of dysprosium substitution in tuning structural, optical, electrical, dielectric, ferroelectric, and magnetic properties of bismuth ferrite multiferroic. J. Alloys Compd. 2022, 919, 165743. [Google Scholar] [CrossRef]
- Sheng, Y.; Rui, W.; Qiu, X.; Du, J.; Zhou, S.; Xu, Q. The multiferroic properties of polycrystalline Bi1−xYxFeO3 films. J. Appl. Phys. 2014, 115, 17D902. [Google Scholar] [CrossRef]
- Singh, S.K.; Tomy, C.V.; Era, T.; Itoh, M.; Ishiwara, H. Improved multiferroic properties in Sm-doped BiFeO3 thin films deposited using chemical solution deposition method. J. Appl. Phys. 2012, 111, 102801. [Google Scholar] [CrossRef]
- Singh, S.K.; Maruyama, K.; Ishiwara, H. Reduced leakage current in La and Ni codoped BiFeO3 thin films. Appl. Phys. Lett. 2007, 91, 112913. [Google Scholar] [CrossRef]
- Lin, T.K.; Chang, H.W.; Sung, Y.H.; Wang, C.R.; Wei, D.H.; Tu, C.S.; Chang, W.C. Multiferroic properties of Bi0.95R0.05FeO3 polycrystalline films on the glass substrates (R = La, Pr, Nd, Sm, and Ho). Mater. Lett. 2020, 276, 128216. [Google Scholar] [CrossRef]
- Nalwa, K.S.; Garg, A.; Upadhyaya, A. Effect of samarium doping on the properties of solid-state synthesized multiferroic bismuth ferrite. Mater. Lett. 2008, 62, 878. [Google Scholar] [CrossRef]
- Bouaouina, B.; Besnard, A.; Abaidia, S.E.; Haid, F. Residual stress, mechanical and microstructure properties of multilayer MoS2/CrN coating produced by R.F. magnetron discharge. Appl. Surf. Sci. 2017, 395, 117. [Google Scholar] [CrossRef]
- Chen, G.J.; Jian, S.R. Effects of Cu doping on the structural and nanomechanical properties of ZnO thin films. Appl. Phys. A 2018, 124, 575. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Pan, C.T.; Lu, Y.X.; Jian, S.R.; Chang, H.W.; Juang, J.Y. Influence of post-annealing on the structural and nanomechanical properties of Co thin films. Micromachines 2020, 11, 180. [Google Scholar] [CrossRef]
- Chen, G.J.; Lin, C.M.; Shih, Y.H.; Jian, S.R. The microstructures and characteristics of NiO films: Effects of substrate temperature. Micromachines 2022, 13, 1940. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.-H.; Jian, S.-R.; Juang, J.-Y. Berkovich nanoindentation and deformation mechanisms in GaN thin films. Appl. Surf. Sci. 2008, 254, 1997. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Jian, S.R.; Liu, T.J.; Le, P.H.; Juang, J.Y. Localized deformation and fracture behaviors in InP single-crystals by indentation. Micromachines 2018, 9, 611. [Google Scholar] [CrossRef]
- Sahu, B.P.; Wu, W.; Wang, J.; Misra, A. Deformation behavior of crystalline/amorphous Al-Si nanocomposites with nanolaminate or nanofibrous microstructures. Phys. Rev. Mater. 2022, 6, 094002. [Google Scholar] [CrossRef]
- Maita, J.M.; Rommel, S.; Davis, J.R.; Ryou, H.; Wollmershauser, J.A.; Gorzkowski, E.P.; Feigelson, B.N.; Aindow, M.; Lee, S.-W. Grain size effect on the mechanical properties of nanocrystalline magnesium aluminate spinel. Acta Mater. 2023, 251, 118881. [Google Scholar] [CrossRef]
- Cheng, C.J.; Kan, D.; Lim, S.H.; McKenzie, W.R.; Munroe, P.R.; Salamanca-Riba, L.G.; Withers, R.L.; Takeuchi, I. Structural transition and complex domain structures across a ferroelectric-to-antiferroelectric phase boundary in epitaxial Sm-doped BiFeO3 thin films. Phys. Rev. B 2009, 80, 014109. [Google Scholar] [CrossRef]
- Lin, T.K.; Shen, C.Y.; Kao, C.C.; Chang, C.F.; Chang, H.W.; Wang, C.R.; Tu, C.S. Structural evolution, ferroelectric, and nanomechanical properties of Bi1-xSmxFeO3 films (x = 0.05–0.16) on glass substrates. J. Alloys Compd. 2019, 787, 397. [Google Scholar] [CrossRef]
- Li, X.; Bhushan, B. A review of nanoindentation continuous stiffness measurement technique and its applications. Mater. Charact. 2002, 48, 11. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47. [Google Scholar] [CrossRef]
- Cullity, B.D.; Stock, S.R. Element of X-ray Diffraction; Prentice Hall: Hoboken, NJ, USA, 2001; p. 170. [Google Scholar]
- Panda, P.; Krishna, N.G.; Rajput, P.; Ramaseshan, R. Local crystal structure and mechanical properties of sputtered Ti-doped AlN thin films. Phys. Chem. Chem. Phys. 2018, 20, 29817. [Google Scholar] [CrossRef]
- Li, X.; Gao, H.; Murphy, C.J.; Caswell, K.K. Nanoindentation of silver nanowires. Nano Lett. 2003, 11, 1495. [Google Scholar] [CrossRef]
- Yen, C.-Y.; Jian, S.-R.; Lai, Y.-S.; Yang, P.-F.; Liao, Y.-Y.; Jang, J.S.-C.; Lin, T.-H.; Juang, J.-Y. Mechanical properties of the hexagonal HoMnO3 thin films by nanoindentation. J. Alloys Compd. 2010, 508, 523. [Google Scholar] [CrossRef]
- Jian, S.R.; Lee, Y.H. Nanoindentation-induced interfacial fracture of ZnO thin films deposited on Si(111) substrates by atomic layer deposition. J. Alloys Compd. 2014, 587, 313. [Google Scholar] [CrossRef]
- Jian, S.R.; Chen, G.J.; Juang, J.Y. Nanoindentation-induced phase transformation in (110)-oriented Si single-crystals. Curr. Opin. Solid State Mater. Sci. 2010, 14, 69. [Google Scholar] [CrossRef]
- Wong, S.; Haberl, B.; Williams, J.S.; Bradby, J.E. Phase transformation as the single-mode mechanical deformation of silicon. Appl. Phys. Lett. 2015, 106, 252103. [Google Scholar] [CrossRef]
- Huston, L.Q.; Kiran, M.S.R.N.; Smillie, L.A.; Williams, J.S.; Bradby, J.E. Cold nanoindentation of germanium. Appl. Phys. Lett. 2017, 111, 021901. [Google Scholar] [CrossRef]
- Greer, J.R.; De Hosson, J.T.M. Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 2011, 56, 654. [Google Scholar] [CrossRef]
- Panchasara, A.; Jethva, S.; Savaliya, C.; Jose, P.J.; Keshvani, M.J.; Jivani, M.N.; Ravalia, A. Effect of growth condition on the electrical behavior of BiFeO3/Si thin film devices. Ferroelectrics 2022, 599, 178. [Google Scholar] [CrossRef]
- Jian, S.R.; Chang, H.W.; Tseng, Y.C.; Chen, P.H.; Juang, J.Y. Structural and nanomechanical properties of BiFeO3 thin films deposited by radio frequency magnetron sputtering. Nanoscale Res. Lett. 2013, 8, 297. [Google Scholar] [CrossRef]
- Majtyka, A.; Nowak, A.; Marchand, B.; Chrobak, D.; Ritala, M.; Räisänen, J.; Nowak, R. Structure-dependent mechanical properties of ALD-grown nanocrystalline BiFeO3 multiferroics. J. Nanomater. 2016, 5348471, 5348471. [Google Scholar]
- Abramov, A.S.; Alikin, D.O.; Yuzhakov, V.V.; Nikitin, A.V.; Latushko, S.I.; Karpinsky, D.V.; Shur, V.Y.; Kholkin, A.L. Indentation induced local polarization reversal in La doped BiFeO3 ceramics. Ferroelectrics 2019, 541, 1. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.-S.; Jian, S.-R.; Le, P.H.; Chou, W.-C.; Juang, J.-Y.; Chang, H.-W.; Lin, C.-M. Effects of Oxygen Pressure on the Microstructures and Nanomechanical Properties of Samarium-Doped BiFeO3 Thin Films. Micromachines 2023, 14, 1879. https://doi.org/10.3390/mi14101879
Gao C-S, Jian S-R, Le PH, Chou W-C, Juang J-Y, Chang H-W, Lin C-M. Effects of Oxygen Pressure on the Microstructures and Nanomechanical Properties of Samarium-Doped BiFeO3 Thin Films. Micromachines. 2023; 14(10):1879. https://doi.org/10.3390/mi14101879
Chicago/Turabian StyleGao, Chih-Sheng, Sheng-Rui Jian, Phuoc Huu Le, Wu-Ching Chou, Jenh-Yih Juang, Huang-Wei Chang, and Chih-Ming Lin. 2023. "Effects of Oxygen Pressure on the Microstructures and Nanomechanical Properties of Samarium-Doped BiFeO3 Thin Films" Micromachines 14, no. 10: 1879. https://doi.org/10.3390/mi14101879
APA StyleGao, C.-S., Jian, S.-R., Le, P. H., Chou, W.-C., Juang, J.-Y., Chang, H.-W., & Lin, C.-M. (2023). Effects of Oxygen Pressure on the Microstructures and Nanomechanical Properties of Samarium-Doped BiFeO3 Thin Films. Micromachines, 14(10), 1879. https://doi.org/10.3390/mi14101879









