Nonconventional Tether Structure for Quality Factor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator
Abstract
:1. Introduction
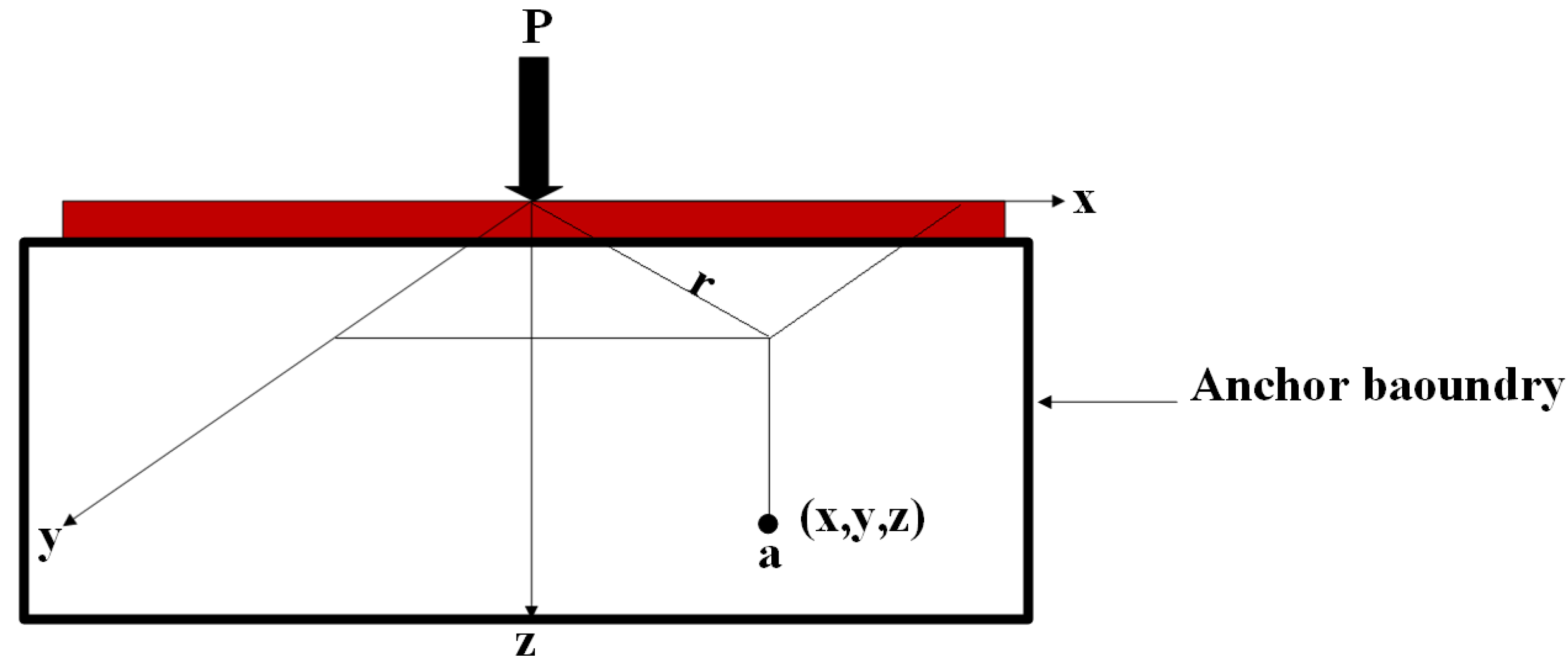
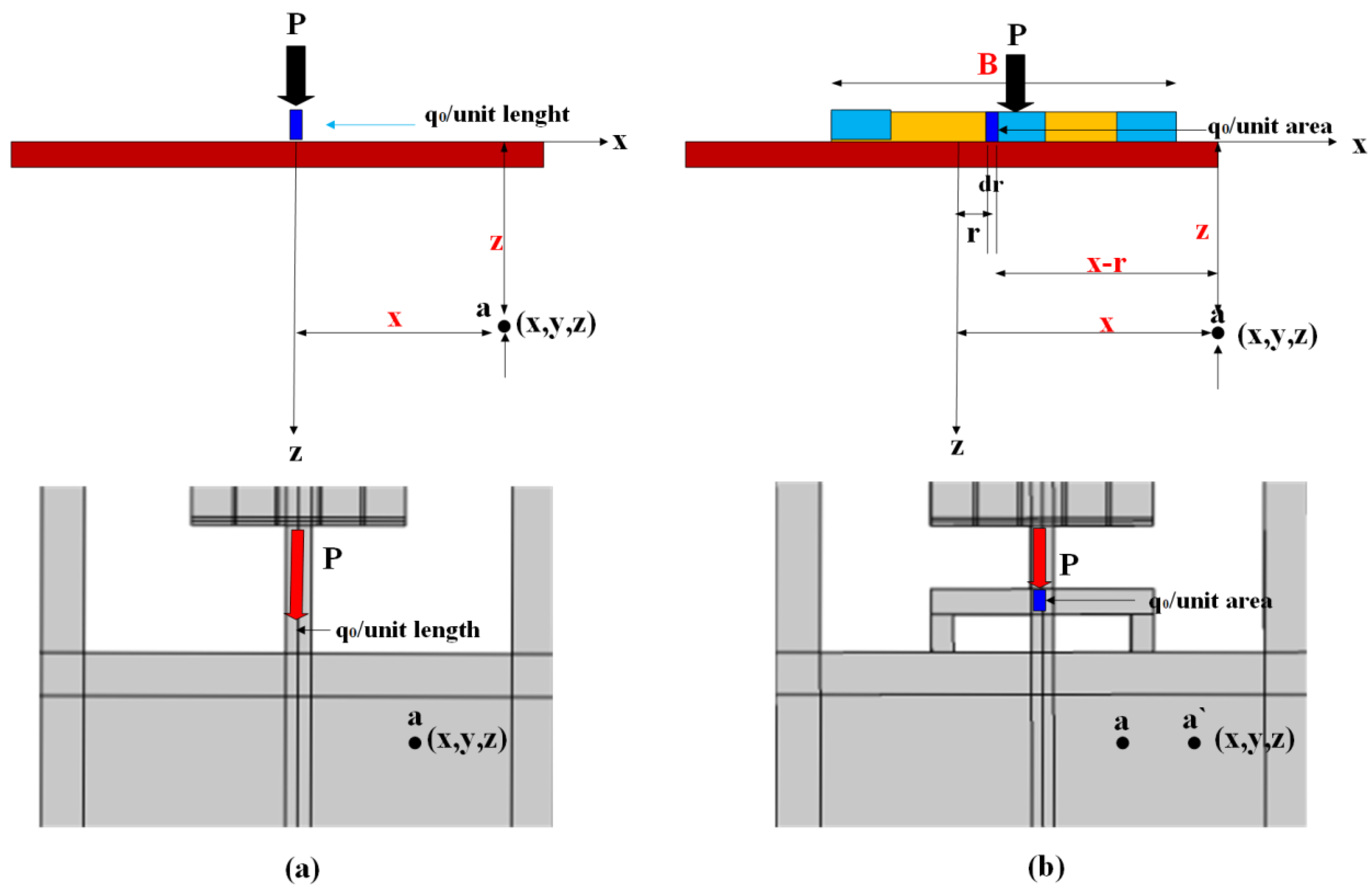
2. Nonconventional Tethers Mechanism
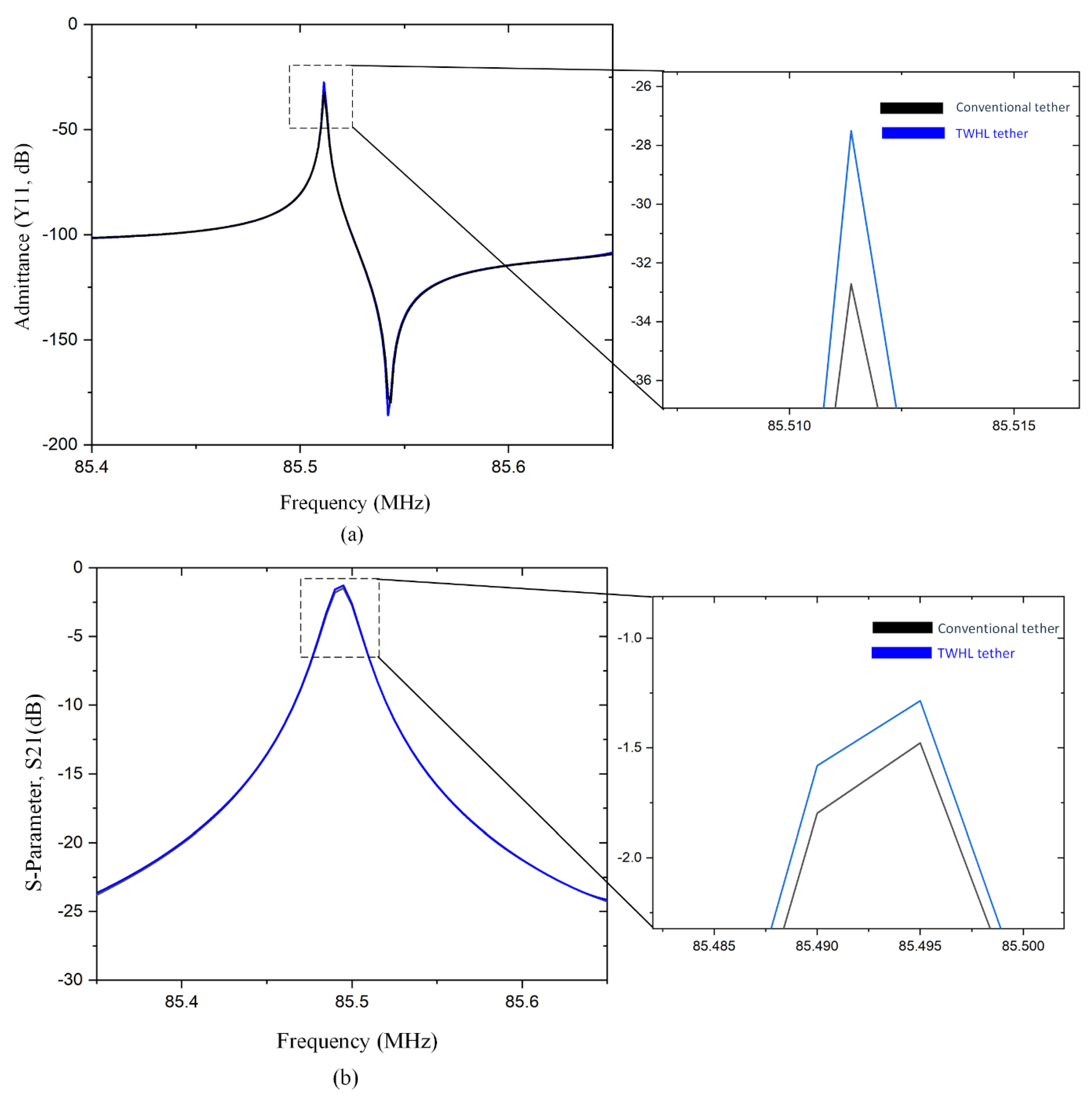
3. Nonconventional Tethers Transmission Characteristics
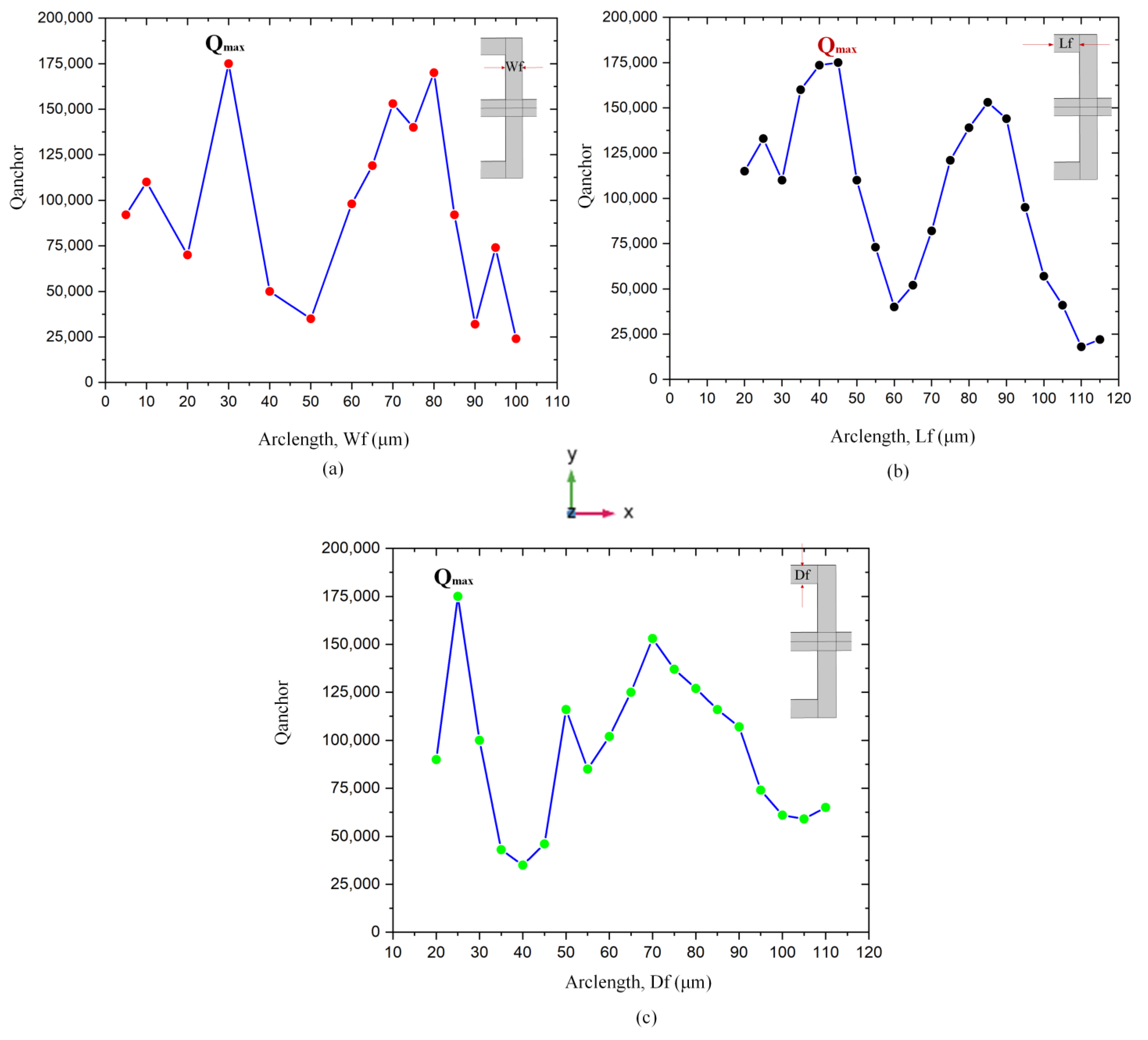
4. Resonator Design
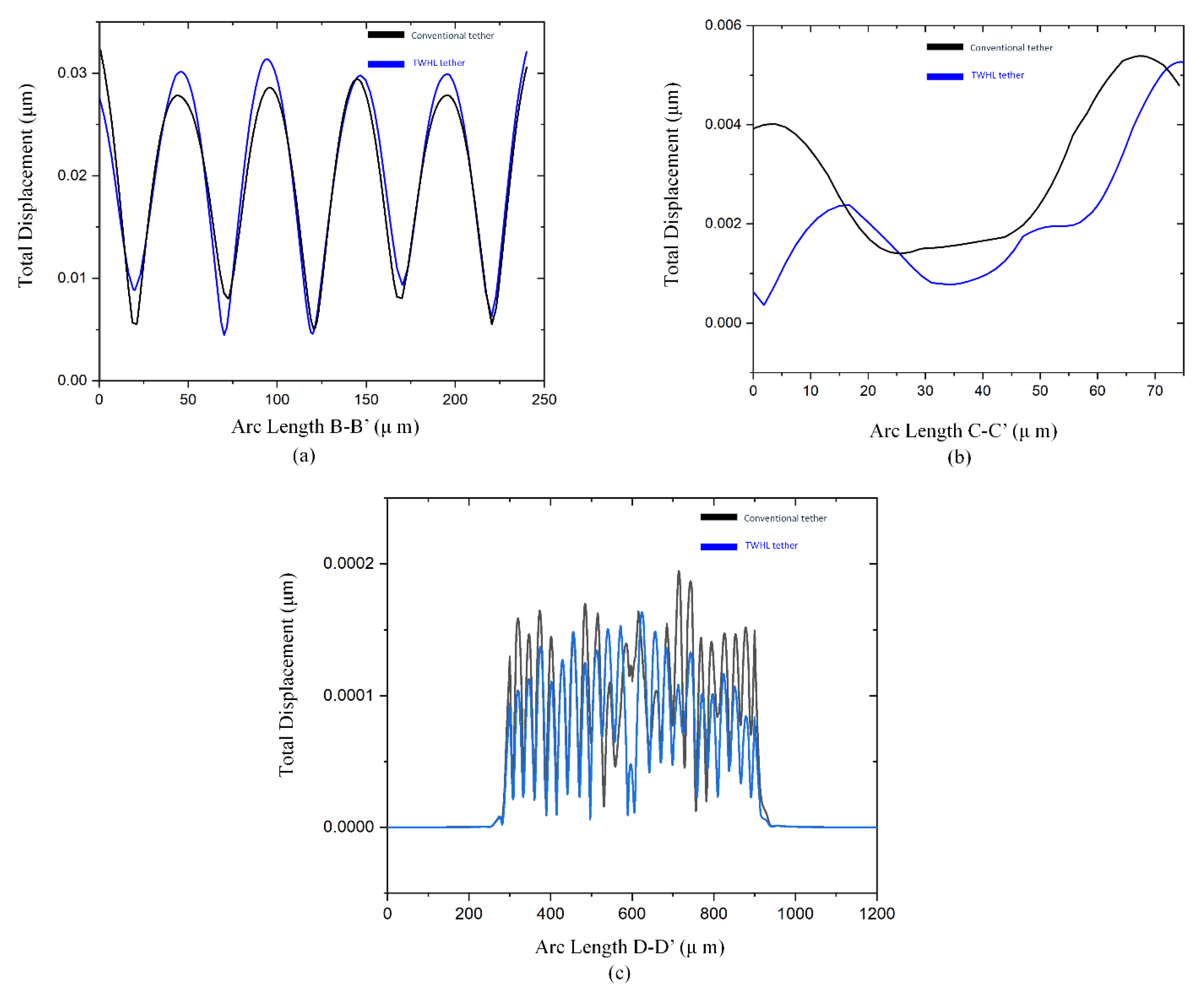
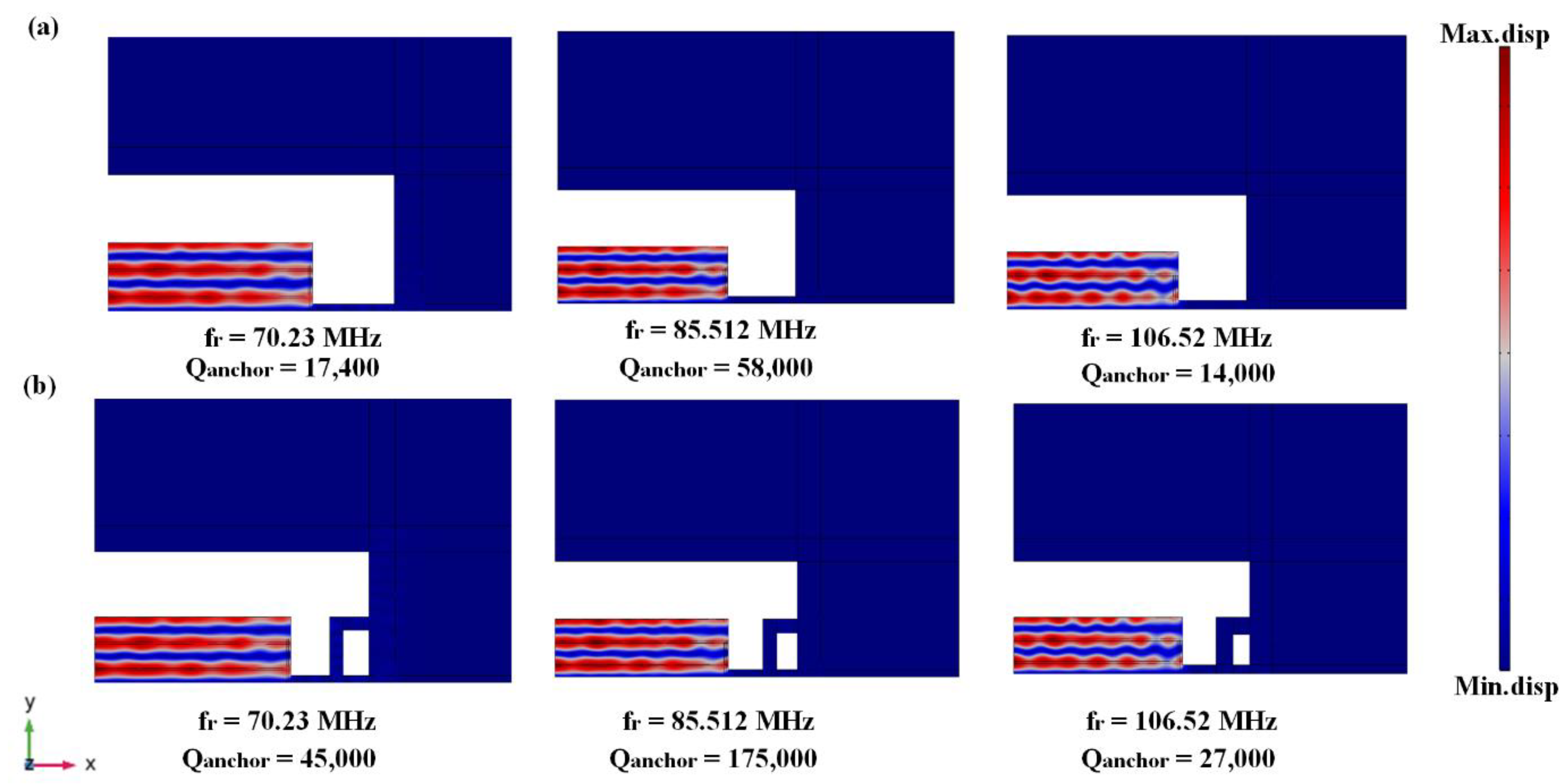
5. Resonator Mode Shapes
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, M.; Han, G.; Si, C.; Zhao, Y.; Ning, J. A review: Aluminum nitride MEMS contour-mode resonator. J. Semicond. 2016, 37, 101001. [Google Scholar] [CrossRef]
- Pillai, G.; Li, S.S. Piezoelectric MEMS resonators: A review. IEEE Sens. J. 2020, 21, 12589–12605. [Google Scholar] [CrossRef]
- Bhugra, H.; Piazza, G. (Eds.) Piezoelectric MEMS Resonators; Springer International Publishing: New York, NY, USA, 2017; p. 103. [Google Scholar]
- Chen, W.; Jia, W.; Xiao, Y.; Wu, G. Anchor Loss Reduction for Square-Extensional Mode MEMS Resonator Using Tethers with Auxiliary Structures. IEEE Sens. J. 2023, 23, 15454–15460. [Google Scholar] [CrossRef]
- Ha, T.D. Boosted anchor quality factor of a thin-film aluminum nitride-on-silicon length extensional mode MEMS resonator using phononic crystal strip. Appl. Phys. A 2021, 127, 738. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Liu, W.; Yang, J.; Zhu, Y.; Yang, F. A novel piezoelectric RF-MEMS resonator with enhanced quality factor. J. Micromech. Microeng. 2022, 32, 035002. [Google Scholar] [CrossRef]
- Bao, F.; Bao, J.; Li, X.; Zhou, X.; Song, Y.; Zhang, X. Reflective strategy based on tether-integrated phononic crystals for 10 MHz MEMS resonator. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Li, L.; He, W.; Tong, Z.; Liu, H.; Xie, M. Q-Factor Enhancement of Coupling Bragg and Local Resonance Band Gaps in Single-Phase Phononic Crystals for TPOS MEMS Resonator. Micromachines 2022, 13, 1217. [Google Scholar] [CrossRef] [PubMed]
- Siddiqi, M.W.U.; Fedeli, P.; Tu, C.; Frangi, A.; Lee, J.E. Numerical analysis of anchor loss and thermoelastic damping in piezoelectric AlN-on-Si Lamb wave resonators. J. Micromech. Microeng. 2019, 29, 105013. [Google Scholar] [CrossRef]
- Bao, F.H.; Bao, J.F.; Lee, J.E.Y.; Bao, L.L.; Khan, M.A.; Zhou, X.; Wu, Q.D.; Zhang, T.; Zhang, X.S. Quality factor improvement of piezoelectric MEMS resonator by the conjunction of frame structure and phononic crystals. Sens. Actuators A Phys. 2019, 297, 111541. [Google Scholar] [CrossRef]
- Workie, T.B.; Wu, T.; Bao, J.F.; Hashimoto, K.Y. Design for high-quality factor of piezoelectric-on-silicon MEMS resonators using resonant plate shape and phononic crystals. Jpn. J. Appl. Phys. 2021, 60, SDDA03. [Google Scholar] [CrossRef]
- Zhu, H.; Lee, J.E.Y. AlN piezoelectric on silicon MEMS resonator with boosted Q using planar patterned phononic crystals on anchors. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; IEEE: New York, NY, USA, 2015; pp. 797–800. [Google Scholar]
- Ha, T.D. Anchor quality factor improvement of a piezoelectrically-excited MEMS resonator using window-like phononic crystal strip. Int. J. Mech. Mater. Des. 2023. [Google Scholar] [CrossRef]
- Awad, M.; Bao, F.; Bao, J.; Zhang, X. Cross-shaped PnC for anchor loss reduction of thin-film ALN-on-silicon high frequency MEMS resonator. In Proceedings of the 2018 IEEE MTT-S International Wireless Symposium (IWS), Chengdu, China, 6–10 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar]
- Zhu, H.; Lee, J.E.Y. Design of phononic crystal tethers for frequency-selective quality factor enhancement in AlN piezoelectric-on-silicon resonators. Procedia Eng. 2015, 120, 516–519. [Google Scholar] [CrossRef]
- Rawat, U.; Nair, D.R.; DasGupta, A. Piezoelectric-on-Silicon array resonators with asymmetric phononic crystal tethering. J. Microelectromech. Syst. 2017, 26, 773–781. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.Y. Enhancing quality factor by etch holes in piezoelectric-on-silicon lateral mode resonators. Sens. Actuators A Phys. 2017, 259, 144–151. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Gorman, J.J. Approaching the intrinsic quality factor limit for micromechanical bulk acoustic resonators using phononic crystal tethers. Appl. Phys. Lett. 2017, 111, 013501. [Google Scholar] [CrossRef]
- Tu, C.; Lee, J.E.Y.; Zhang, X.S. Dissipation analysis methods and Q-enhancement strategies in piezoelectric MEMS laterally vibrating resonators: A review. Sensors 2020, 20, 4978. [Google Scholar] [CrossRef] [PubMed]
- Harrington, B.P. Performance Enhancement of Micromachined Thin-Film Piezoelectric-on-Silicon Lateral-Extensional Resonators through Substrate and Tether Modifications. Ph.D. Thesis, Oklahoma State University, Stillwater, OK, USA, 2013. [Google Scholar]
- Bao, F.H.; Awad, M.; Li, X.Y.; Wu, Z.H.; Bao, J.F.; Zhang, X.S.; Bao, L.L. Suspended frame structure with phononic crystals for anchor loss reduction of MEMS resonator. In Proceedings of the 2018 IEEE International Frequency Control Symposium (IFCS), Olympic Valley, CA, USA, 21–24 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–4. [Google Scholar]
- Ha, T.D. A Two-Square Shaped Phononic Crystal Strip for Anchor Quality Factor Enhancement in a Length Extensional Mode TPoS Resonator. J. Vib. Eng. Technol. 2022, 10, 1073–1080. [Google Scholar] [CrossRef]
- Lv, S.; Zhu, Z.; Long, F.; Sun, H.; Song, C.; Zhang, A.; Tan, F.; Zhao, J. Characterization analysis of quality factor, electro-mechanical coupling and spurious modes for AlN Lamb-wave resonators with fs > 2 GHz. Microelectron. J. 2022, 125, 105466. [Google Scholar] [CrossRef]
- Thakar, V.; Rais-Zadeh, M. Optimization of tether geometry to achieve low anchor loss in Lamé-mode resonators. In Proceedings of the 2013 Joint European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), Prague, Czech Republic, 21–25 July 2013; IEEE: New York, NY, USA, 2013; pp. 129–132. [Google Scholar]
- Khine, L.; Palaniapan, M.; Wong, W.K. 12.9 MHz Lamé-mode differential SOI bulk resonators. In Proceedings of the TRANSDUCERS 2007–2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; IEEE: New York, NY, USA, 2007; pp. 1753–1756. [Google Scholar]
- Elsayed, M.Y.; Nabki, F. Piezoelectric bulk mode disk resonator post-processed for enhanced quality factor performance. J. Microelectromech. Syst. 2016, 26, 75–83. [Google Scholar] [CrossRef]
- Das, B.M.; Sivakugan, N. Principles of Foundation Engineering; Cengage Learning: Boston, MA, USA, 2018. [Google Scholar]
- Awad, M.; Workie, T.B.; Bao, J.F.; Hashimoto, K.Y. Reem-Shape Phononic Crystal for Q Anchor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator. Micromachines 2023, 14, 1540. [Google Scholar] [CrossRef]
- Pillai, G.; Li, S.S. Quality factor boosting of bulk acoustic wave resonators based on a two-dimensional array of high-Q resonant tanks. Appl. Phys. Lett. 2020, 116, 163502. [Google Scholar] [CrossRef]
- Chen, W.; Jia, W.; Xiao, Y.; Wu, G. Design, Modeling and Characterization of High-Performance Bulk-Mode Piezoelectric MEMS Resonators. J. Microelectromech. Syst. 2022, 31, 318–327. [Google Scholar] [CrossRef]
- Workie, T.B.; Wu, Z.; Tang, P.; Bao, J.; Hashimoto, K.Y. Figure of Merit Enhancement of Laterally Vibrating RF-MEMS Resonators via Energy-Preserving Addendum Frame. Micromachines 2022, 13, 105. [Google Scholar] [CrossRef]
- Gokhale, V.J.; Gorman, J.J. Direct measurement of dissipation in phononic crystal and straight tethers for MEMS resonators. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; IEEE: New York, NY, USA, 2017; pp. 958–961. [Google Scholar]
- Tong, Y.; Han, T. Anchor loss reduction of lamb wave resonator by pillar-based phononic crystal. Micromachines 2021, 12, 62. [Google Scholar] [CrossRef]
- Siddiqi, M.W.U.; Lee, J.E.Y. AlN-on-Si MEMS resonator bounded by wide acoustic bandgap two-dimensional phononic crystal anchors. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; IEEE: New York, NY, USA, 2018; pp. 727–730. [Google Scholar]
- Sun, H.; Wang, X.; Zhu, Z.; Zhao, J. Theoretical and experimental analysis of the spurious modes and quality factors for dual-mode AlN lamb-wave resonators. IEICE Trans. Electron. 2023, 106, 76–83. [Google Scholar] [CrossRef]
- Ha, T.D.; Bao, J. A phononic crystal strip based on silicon for support tether applications in silicon-based MEMS resonators and effects of temperature and dopant on its band gap characteristics. AIP Adv. 2016, 6, 045211. [Google Scholar] [CrossRef]
- Liang, J.; Zhang, H.; Zhang, D.; Duan, X.; Zhang, H.; Pang, W. Design and fabrication of aluminum nitride Lamb wave resonators towards high figure of merit for intermediate frequency filter applications. J. Micromech. Microeng. 2015, 25, 035016. [Google Scholar] [CrossRef]
- Bijay, J.; Narayanan, K.B.; Sarkar, A.; DasGupta, A.; Nair, D.R. Optimization of Anchor Placement in TPoS MEMS Resonators: Modeling and Experimental Validation. J. Microelectromech. Syst. 2022, 31, 571–579. [Google Scholar] [CrossRef]
- Qamar, A.; Sherrit, S.; Zheng, X.Q.; Lee, J.; Feng, P.X.L.; Rais-Zadeh, M. Study of energy loss mechanisms in AlN-based piezoelectric length extensional-mode resonators. J. Microelectromech. Syst. 2019, 28, 619–627. [Google Scholar] [CrossRef]
- Workie, T.B.; Liu, J.; Wu, Z.; Tang, P.; Bao, J.F.; Hashimoto, K.Y. Swastika Hole shaped Phononic Crystal for Quality enhancement of Contour Mode Resonators. In Proceedings of the 2021 IEEE MTT-S International Wireless Symposium (IWS), Nanjing, China, 23–26 May 2021; IEEE: New York, NY, USA, 2021; pp. 1–3. [Google Scholar]
- Zhang, Y.; Bao, J.F.; Zhou, X.; Wu, Z.H.; Bao, F.H.; Zhang, X.S. A 10 MHz thin-film piezoelectric-on-silicon MEMS resonator with T-shaped tethers for Q enhancement. Jpn. J. Appl. Phys. 2019, 59, 014002. [Google Scholar] [CrossRef]
- Bao, F.H.; Bao, L.L.; Li, X.Y.; Khan, M.A.; Wu, H.Y.; Qin, F.; Zhang, T.; Zhang, Y.; Bao, J.F.; Zhang, X.S. Multi-stage phononic crystal structure for anchor-loss reduction of thin-film piezoelectric-on-silicon microelectromechanical-system resonator. Appl. Phys. Express 2018, 11, 067201. [Google Scholar] [CrossRef]




| Parameter | Value (μm) |
|---|---|
| Length of resonator, l | 750 |
| Width of resonator, W | 250 |
| Thickness of piezoelectric layer, Pt | 0.5 |
| Thickness of electrode, Ew | 0.5 |
| Length of tether, tl | 1.5λ |
| Width of tether, tw | 12 |
| Electrode thickness | 0.4 |
| Resonant frequency, fr | 85 (MHz) |
| Wavelength, λ | 100 |
| Electrode gap | 4 |
| Silicon substrate high | 10 |
| Perfect matched layer width | 3λ |
| TWHL depth, Df | 25 |
| TWHL length, Lf | 45 |
| TWHL width, Wf | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, M.; Workie, T.B.; Bao, J.; Hashimoto, K.-y. Nonconventional Tether Structure for Quality Factor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator. Micromachines 2023, 14, 1965. https://doi.org/10.3390/mi14101965
Awad M, Workie TB, Bao J, Hashimoto K-y. Nonconventional Tether Structure for Quality Factor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator. Micromachines. 2023; 14(10):1965. https://doi.org/10.3390/mi14101965
Chicago/Turabian StyleAwad, Mohammed, Temesgen Bailie Workie, Jingfu Bao, and Ken-ya Hashimoto. 2023. "Nonconventional Tether Structure for Quality Factor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator" Micromachines 14, no. 10: 1965. https://doi.org/10.3390/mi14101965
APA StyleAwad, M., Workie, T. B., Bao, J., & Hashimoto, K. -y. (2023). Nonconventional Tether Structure for Quality Factor Enhancement of Thin-Film-Piezoelectric-on-Si MEMS Resonator. Micromachines, 14(10), 1965. https://doi.org/10.3390/mi14101965









