Monte Carlo Approach to the Evaluation of Nanoparticles Size Distribution from the Analysis of UV-Vis-NIR Spectra
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Section
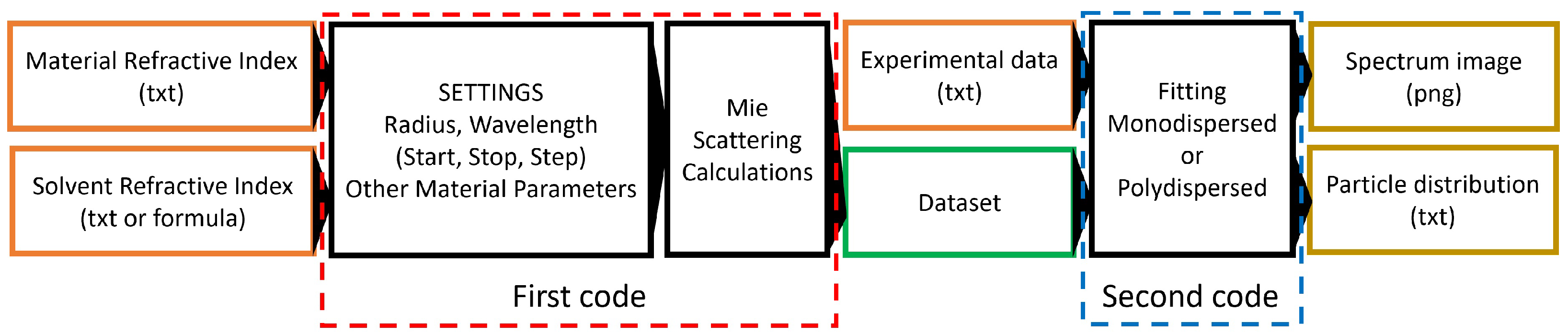
2.2. Computational Section
- Files reading: Experimental data are acquired, sorted, and normalized. The dataset is acquired at the same wavelengths as the experimental points, and it is also rescaled. This automatically leads to the use of the wavelength range in which both the experimental data and the computed dataset are defined.
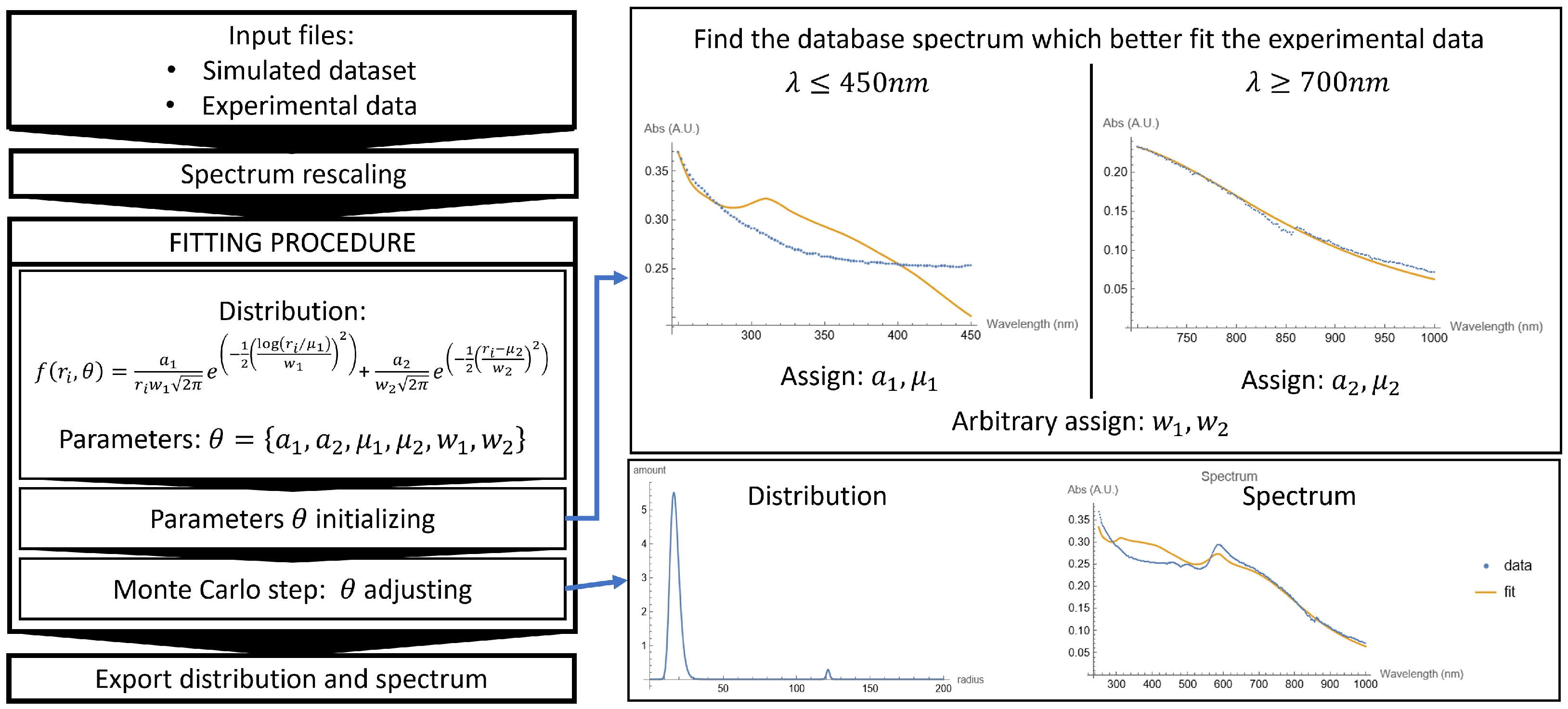
- Assign starting point parameters: choosing the starting point parameters for a function of three or six parameters is crucial. Starting with some random parameters can lead the gradient to descend toward a local minimum without specific physical significance. It is known that “With four parameters I can fit an elephant, and with five I can make him wiggle his trunk—E. Fermi” [25]. To pursue this aim, two strategies are followed:
- Monodisperse NPs: The is evaluated between the experimental data and every spectrum in the dataset. The spectrum that produces the minimum gives the starting point for the distribution centroid and the scale parameter . This evaluation is performed in a small range (a convenient one can be because gold and copper have their plasmonic peak within this range).
- Polydisperse NPs: The is evaluated between the experimental data and every spectrum in the dataset in two different ranges. Small particles strongly contribute in the UV, so and (lognormal distribution) are assigned by finding the minimum among the computed spectra for . Bigger particles and aggregates strongly contribute in the IR, so and (Gaussian distribution) are assigned by finding the minimum among the computed spectra for .
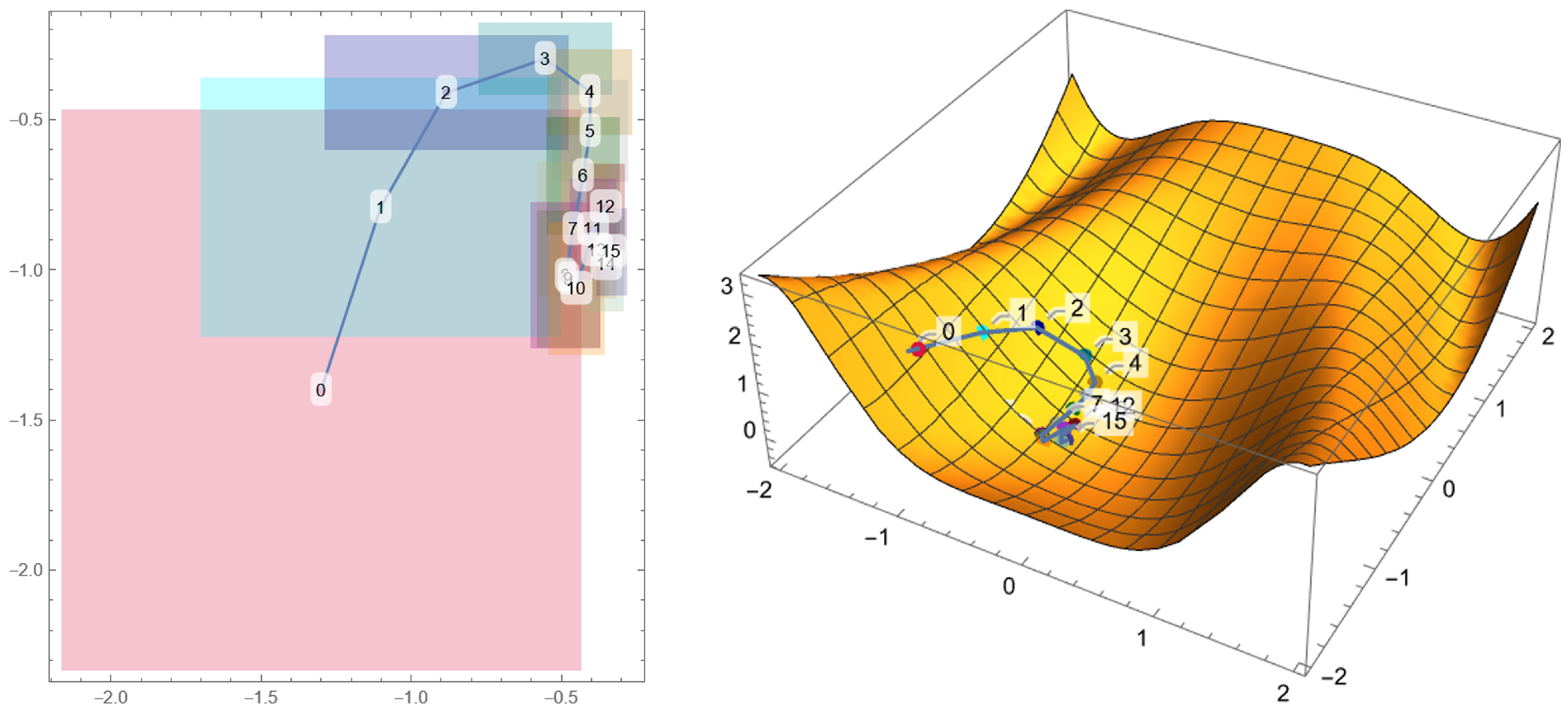
These edge values for are purely indicative and can easily be changed in the code to find the optimal starting point for each sample. The initial values of and are assigned arbitrarily. - Monte Carlo step: A cycle where a new set of parameters is randomly generated each time within a range of the initial parameter. Whenever the obtained with the new set of parameters is lower than the initial , the parameters are updated, and the process is repeated for a fixed number of iterations, but new parameters can now vary in a smaller range than the previous one:where indicates a random number generated between and 1, and is the range in which the new parameter is generated, with that increases at every successful parameter update (the symbol is used to indicate a variable update). A visual representation of this process is given in Figure 3. The relative error associated with each parameter is given by , where m is the number of iterations. At the end of the cycle, a plot and a text file are exported.
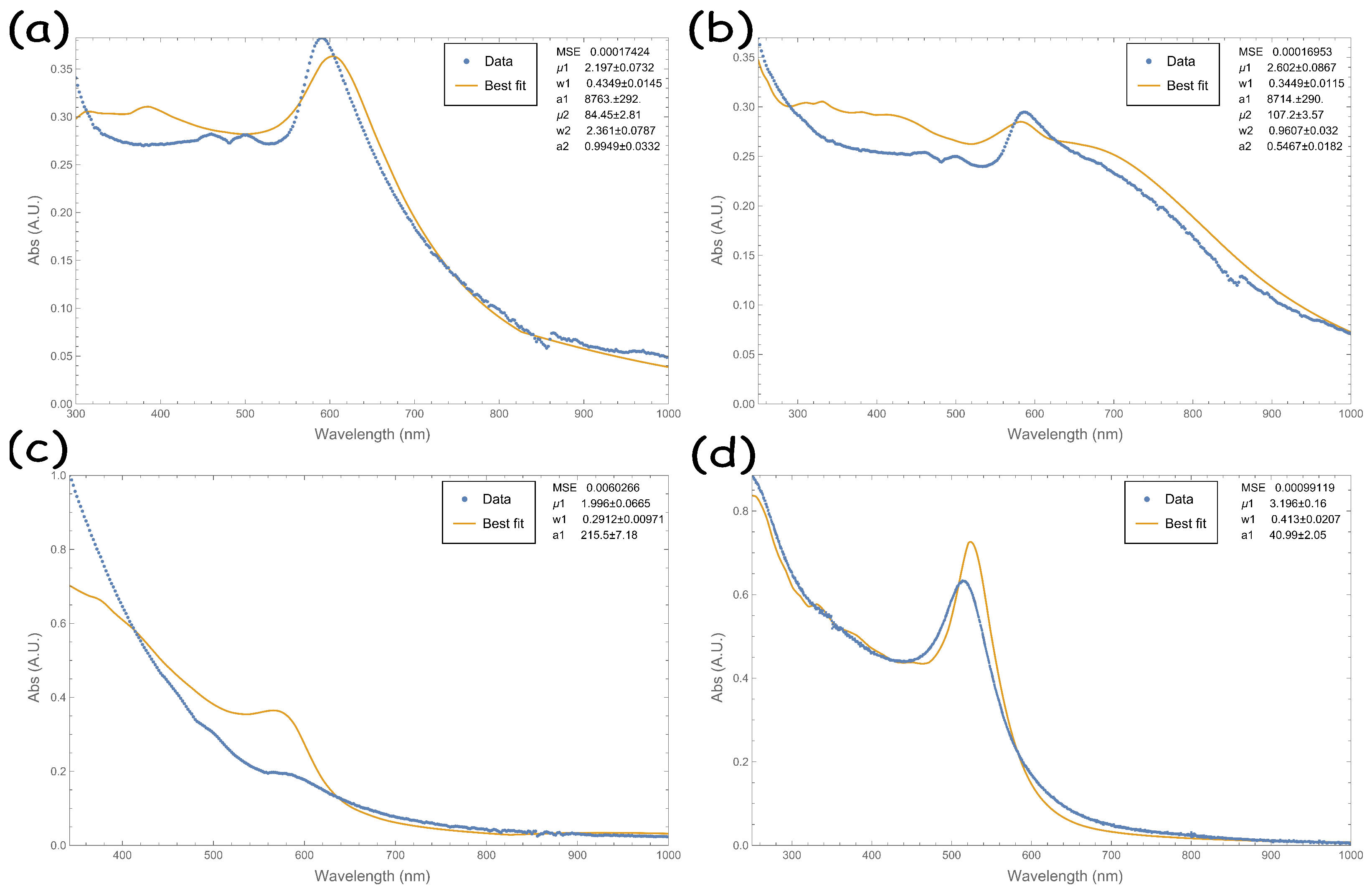
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPs | Nanoparticles |
| PLAL | Pulsed Laser Ablation in Liquid |
| MSE | Mean Squared Error |
| SEM | Scanning Electron Microscopy |
| TEM | Transmission Electron Microscopy |
Appendix A. Copper Refractive Index
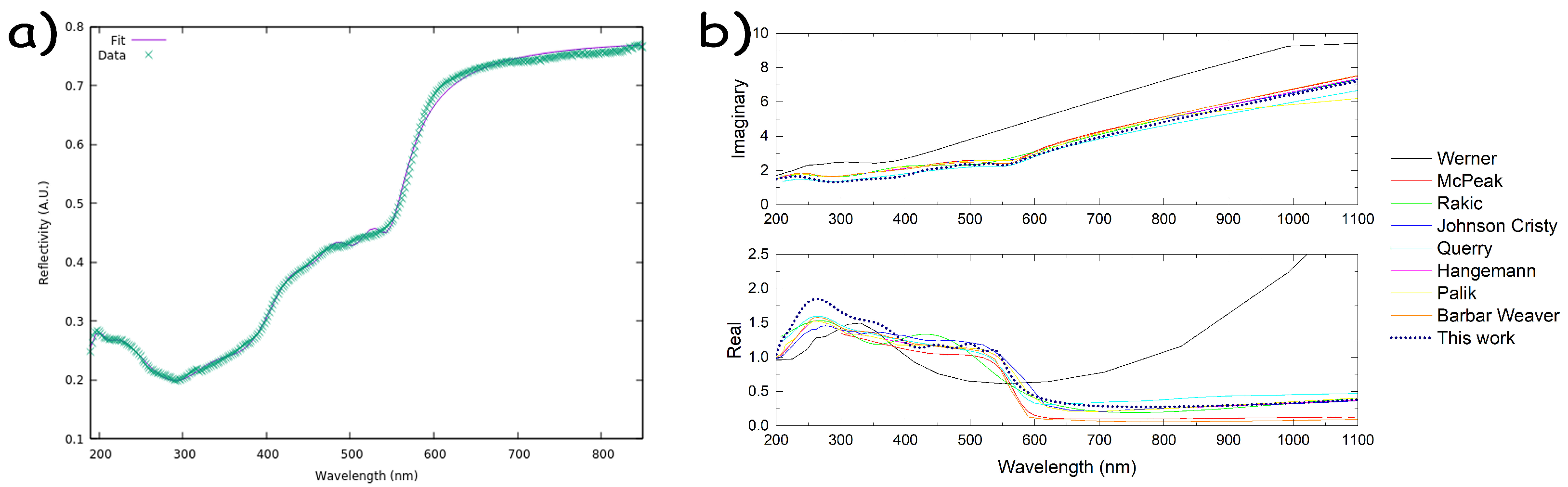
Appendix B. Solvent Refractive Indexes
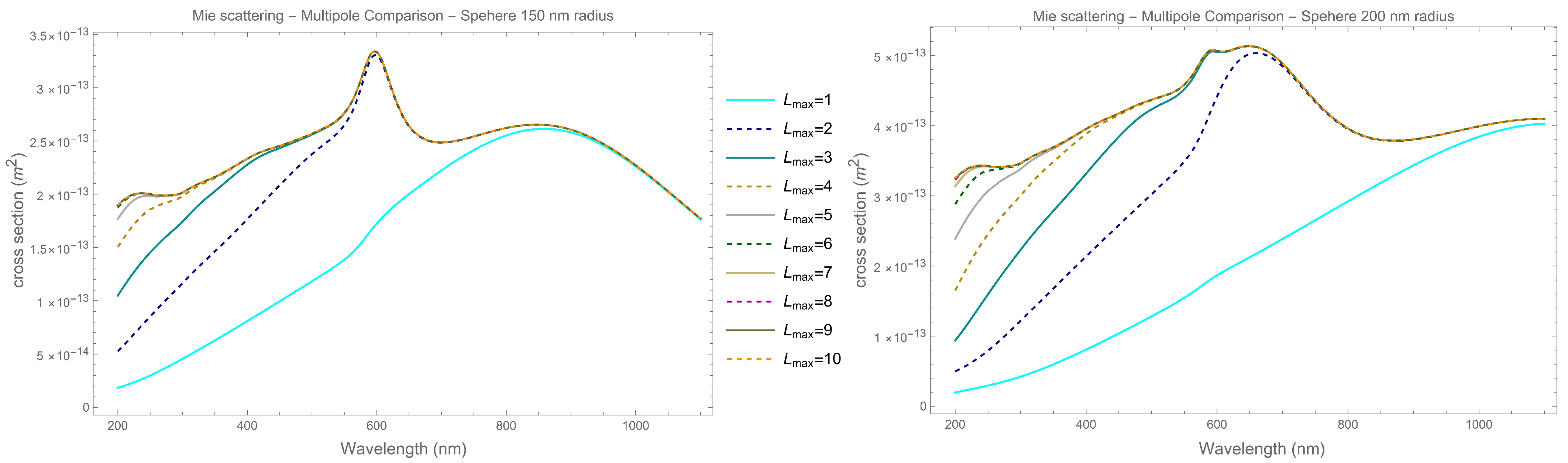
Appendix C. Mie Scattering cross Section Simulation
- The scattering cross section: .
- The extinction cross section: .
- The absorption cross section: .
Appendix D. Results of Fitting with Different Refractive Indexes
| Particle Refractive Index | Dataset Range [nm] (Start:Step:Stop) | Parameter Error | 1 [nm] | 2 [nm] | [nm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| This work | 0.5:0.5:250 | 84 | |||||||
| [22,26] | 0.5:0.5:250 | 83 | |||||||
| [23] | 0.5:0.5:250 | 88 | |||||||
| [22,27] | 0.5:0.5:250 | 83 | |||||||
| This work | 0.1:0.1:30 | ||||||||
| [22,26] | 0.1:0.1:30 | ||||||||
| TEM distribution from Ref. [20] | |||||||||
| Particle Refractive Index | Dataset Range [nm] (Start:Step:Stop) | Parameter Error | 1 [nm] | 2 [nm] | [nm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| This work | 0.5:0.5:250 | 108 | |||||||
| [22,26] | 0.5:0.5:250 | 108 | |||||||
| [23] | 0.5:0.5:250 | 88 | |||||||
| [22,27] | 0.5:0.5:250 | 107 | |||||||
| This work | 0.1:0.1:30 | 310 | |||||||
| [22,26] | 0.1:0.1:30 | ||||||||
| TEM distribution from Ref. [20] | |||||||||
| Particle Refractive Index | Dataset Range [nm] (Start:Step:Stop) | Parameter Error | 1 [nm] | |||
|---|---|---|---|---|---|---|
| This work | 0.1:0.1:30 | 128 | ||||
| [22,26] | 0.1:0.1:30 | 172 | ||||
| [23] | 0.1:0.1:30 | 216 | ||||
| [22,27] | 0.1:0.1:30 | 294 | ||||
| TEM distribution from Ref. [31] | ||||||
| Particle Refractive Index | Dataset Range [nm] (Start:Step:Stop) | Parameter Error | 1 [nm] | |||
|---|---|---|---|---|---|---|
| This work | 0.1:0.1:30 | 90 | ||||
| [22,28] | 0.1:0.1:30 | 72 | ||||
| [22,29] | 0.1:0.1:30 | 119 | ||||
| [22,27] | 0.1:0.1:30 | 41 | ||||
| Fitted with code adapted from Ref. [13] | ||||||
References
- de Aberasturi, D.J.; Serrano-Montes, A.B.; Liz-Marzán, L.M. Modern Applications of Plasmonic Nanoparticles: From Energy to Health. Adv. Opt. Mater. 2015, 3, 602–617. [Google Scholar] [CrossRef]
- Jiang, R.; Li, B.; Fang, C.; Wang, J. Metal/Semiconductor Hybrid Nanostructures for Plasmon-Enhanced Applications. Adv. Mater. 2014, 26, 5274–5309. [Google Scholar] [CrossRef]
- Liu, J.; He, H.; Xiao, D.; Yin, S.; Ji, W.; Jiang, S.; Luo, D.; Wang, B.; Liu, Y. Recent Advances of Plasmonic Nanoparticles and their Applications. Materials 2018, 11, 1833. [Google Scholar] [CrossRef]
- Boscarino, S.; Censabella, M.; Micali, M.; Russo, M.; Terrasi, A.; Grimaldi, M.G.; Ruffino, F. Morphology, Electrical and Optical Properties of Cu Nanostructures Embedded in AZO: A Comparison between Dry and Wet Methods. Micromachines 2022, 13, 247. [Google Scholar] [CrossRef]
- Boscarino, S.; Iacono, V.; Lo Mastro, A.; Tringali, F.; Terrasi, A.; Grimaldi, M.G.; Ruffino, F. Plasmonic and Conductive Structures of TCO Films with Embedded Cu Nanoparticles. Int. J. Mol. Sci. 2022, 23, 11886. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.L.; Liu, R.S.; Tsai, D.P. Plasmonic photocatalysis. Rep. Prog. Phys. 2013, 76, 046401. [Google Scholar] [CrossRef] [PubMed]
- Biagioni, P.; Huang, J.S.; Hecht, B. Nanoantennas for visible and infrared radiation. Rep. Prog. Phys. 2012, 75, 024402. [Google Scholar] [CrossRef]
- Brongersma, M.L.; Halas, N.J.; Nordlander, P. Plasmon-induced hot carrier science and technology. Nat. Nanotechnol. 2015, 10, 25–34. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Gentile, A.; Cacciato, G.; Ruffino, F.; Reitano, R.; Scapellato, G.; Zimbone, M.; Lombardo, S.; Battaglia, A.; Gerardi, C.; Foti, M.; et al. Nanoscale structuration and optical properties of thin gold films on textured FTO. J. Mater. Sci. 2014, 49, 8498–8507. [Google Scholar] [CrossRef]
- Quinten, M. Optical Properties of Nanoparticle Systems; Wiley-VCH Verlag: Weinheim, Germany, 2011. [Google Scholar]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer Series in Materials Science; Springer: Berlin, Germany, 2010. [Google Scholar]
- Amendola, V.; Meneghetti, M. Size Evaluation of Gold Nanoparticles by UV-vis Spectroscopy. J. Phys. Chem. C 2009, 113, 4277–4285. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Nashville, TN, USA, 1998. [Google Scholar]
- Amendola, V.; Polizzi, S.; Meneghetti, M. Laser Ablation Synthesis of Gold Nanoparticles in Organic Solvents. J. Phys. Chem. B 2006, 110, 7232–7237. [Google Scholar] [CrossRef]
- Pashkov, D.M.; Guda, A.A.; Kirichkov, M.V.; Guda, S.A.; Martini, A.; Soldatov, S.A.; Soldatov, A.V. Quantitative Analysis of the UV–Vis Spectra for Gold Nanoparticles Powered by Supervised Machine Learning. J. Phys. Chem. C 2021, 125, 8656–8666. [Google Scholar] [CrossRef]
- Kumar, R.; Binetti, L.; Nguyen, T.H.; Alwis, L.S.M.; Agrawal, A.; Sun, T.; Grattan, K.T.V. Determination of the Aspect-ratio Distribution of Gold Nanorods in a Colloidal Solution using UV-visible absorption spectroscopy. Sci. Rep. 2019, 9, 17469. [Google Scholar] [CrossRef]
- Félidj, N.; Aubard, J.; Lévi, G. Discrete dipole approximation for ultraviolet–visible extinction spectra simulation of silver and gold colloids. J. Chem. Phys. 1999, 111, 1195–1208. [Google Scholar] [CrossRef]
- Andalibi, M.R.; Wokaun, A.; Bowen, P.; Testino, A. Kinetics and Mechanism of Metal Nanoparticle Growth via Optical Extinction Spectroscopy and Computational Modeling: The Curious Case of Colloidal Gold. ACS Nano 2019, 13, 11510–11521. [Google Scholar] [CrossRef]
- Iacono, V.; Lo Pò, C.; Scalese, S.; Boninelli, S.; Condorelli, G.G.; Grimaldi, M.G.; Ruffino, F. Pulsed laser ablation synthesis of Cu-based and Ni-based nanostructured electrodes for highly active alkaline oxygen and hydrogen evolution reactions. APL Mater. 2023, 11, 111102. [Google Scholar] [CrossRef]
- Wolfram Mathematica. Available online: https://www.wolfram.com/mathematica (accessed on 1 November 2023).
- RefractiveIndex.INFO. Available online: https://refractiveindex.info/ (accessed on 1 November 2023).
- Palik, E.D. ; Handbook of Optical Constants of Solids; Handbook of Optical Constants of Solids; Academic Press: San Diego, CA, USA, 1985. [Google Scholar]
- Barcikowski, S.; Amendola, V.; Marzun, G.; Rehbock, C.; Reichenberger, S.; Zhang, D.; Gökce, B. Handbook of Laser Synthesis of Colloids; DuEPublico, Duisburg-Essen: Essen Germany, 2016. [Google Scholar] [CrossRef]
- Dyson, F. A meeting with Enrico Fermi. Nature 2004, 427, 297. [Google Scholar] [CrossRef]
- Hagemann, H.J.; Gudat, W.; Kunz, C. Optical constants from the far infrared to the x-ray region: Mg, Al, Cu, Ag, Au, Bi, C, and Al2O3. J. Opt. Soc. Am. 1975, 65, 742. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Olmon, R.L.; Slovick, B.; Johnson, T.W.; Shelton, D.; Oh, S.H.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of gold. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477. [Google Scholar] [CrossRef]
- Copper—29Cu: Radii of Atoms and Ions. Available online: https://webelements.com/copper/atom_sizes.html (accessed on 1 November 2023).
- Boscarino, S.; Iacono, V.; Mastro, A.L.; Scalese, S.; Boninelli, S.; Lombardo, S.; Corso, R.; Condorelli, G.G.; Reitano, R.; Terrasi, A.; et al. Cu metal nanoparticles in transparent electrodes for light harvesting in solar cells. Unpublished.
- Drude Model Parameters to Fit the Dielectric Function of Free Electron Metals. Available online: http://www.wave-scattering.com/drudefit.html (accessed on 1 November 2023).
- Fermi Energies, Fermi Temperatures, and Fermi Velocities. Available online: http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/fermi.html (accessed on 1 November 2023).
- Gnuplot Homepage. Available online: http://www.gnuplot.info/ (accessed on 1 November 2023).
- Zeman, E.J.; Schatz, G.C. An accurate electromagnetic theory study of surface enhancement factors for silver, gold, copper, lithium, sodium, aluminum, gallium, indium, zinc, and cadmium. J. Phys. Chem. 1987, 91, 634–643. [Google Scholar] [CrossRef]
- Kozma, I.Z.; Krok, P.; Riedle, E. Direct measurement of the group-velocity mismatch and derivation of the refractive-index dispersion for a variety of solvents in the ultraviolet. J. Opt. Soc. Am. B 2005, 22, 1479. [Google Scholar] [CrossRef]
- Rheims, J.; Köser, J.; Wriedt, T. Refractive-index measurements in the near-IR using an Abbe refractometer. Meas. Sci. Technol. 1997, 8, 601–605. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, J. Computation of Special Functions, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Ashcroft, N.W.; Mermin, N. Solid State Physics; Brooks/Cole: Florence, KY, USA, 1976. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pò, C.L.; Iacono, V.; Boscarino, S.; Grimaldi, M.G.; Ruffino, F. Monte Carlo Approach to the Evaluation of Nanoparticles Size Distribution from the Analysis of UV-Vis-NIR Spectra. Micromachines 2023, 14, 2208. https://doi.org/10.3390/mi14122208
Pò CL, Iacono V, Boscarino S, Grimaldi MG, Ruffino F. Monte Carlo Approach to the Evaluation of Nanoparticles Size Distribution from the Analysis of UV-Vis-NIR Spectra. Micromachines. 2023; 14(12):2208. https://doi.org/10.3390/mi14122208
Chicago/Turabian StylePò, Cristiano Lo, Valentina Iacono, Stefano Boscarino, Maria Grazia Grimaldi, and Francesco Ruffino. 2023. "Monte Carlo Approach to the Evaluation of Nanoparticles Size Distribution from the Analysis of UV-Vis-NIR Spectra" Micromachines 14, no. 12: 2208. https://doi.org/10.3390/mi14122208
APA StylePò, C. L., Iacono, V., Boscarino, S., Grimaldi, M. G., & Ruffino, F. (2023). Monte Carlo Approach to the Evaluation of Nanoparticles Size Distribution from the Analysis of UV-Vis-NIR Spectra. Micromachines, 14(12), 2208. https://doi.org/10.3390/mi14122208









