Polishing Approaches at Atomic and Close-to-Atomic Scale
Abstract
:1. Introduction
- (1)
- Era without roughness standard: telescopes and spectacles were invented during the renaissance. Although there was no standard for roughness at that time, as early as 1634, it was already realized that polishing was not just cleaning the glass, but reducing the roughness, such as the cloth is shaved by the cropper [4]. The manufacture of lenses, prisms, and mirrors laid the groundwork for the development of polishing technology. In the 19th century, the “trial and error” production method is common to fabricate microscopes. Carl Zeiss and Ernst Abbe introduced diffraction limit, Abbe number and measured Abbe error to measurements, which led to a qualitative change in microscope polishing technology [5,6].
- (2)
- Sub-micro scale era: after the second industrial revolution, optical theory and measuring technologies have propelled polishing into the era of standardization. The first roughness standard, ASA B46.1, was issued in 1940. Hereafter, roughness down to 9 µin in Ra (0.23 μm) [7] and 30 µin in RMS (0.76 μm) [8] were realized for rubberized seal and cast dental gold alloy, respectively. In this period, µin is a common unit for evaluating roughness and the highest precision of roughness in polishing was considered to be 0.5~5 µin [9]. It should be noted that Ra and Rz were not used as roughness parameters in the mid-twentieth century. Instead, they used have and hmax, where have is similar to Ra and hmax is similar to Rz.
- (3)
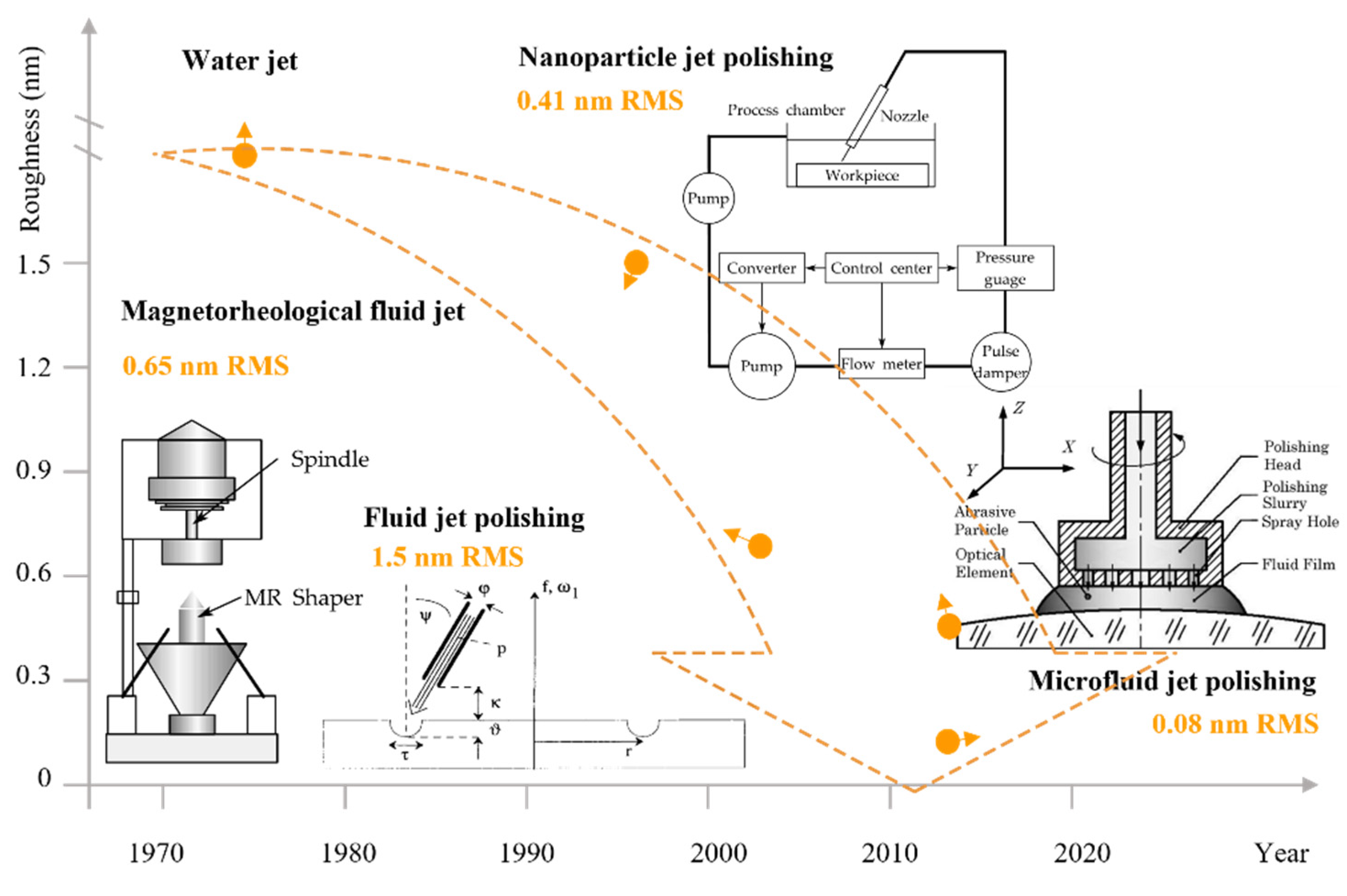
- Nanometre scale era: in the second half of the 20th century, the invention of precision polishing technologies including chemical mechanical polishing (CMP), ion beam figuring (IBF), magnetorheological finishing (MRF), fluid jet polishing (FJP), and bonnet polishing (BP) allowed the roughness achieved by polishing to reach the nanometre scale, achieving 3.4 nm in Ra for diamond [10], 2 nm in Rmax for metal mirror surfaces made from Cu/Al alloys [11], and 1.6 nm in RMS for BK7 [12].
- (4)
- Atomic and close-to-atomic scale (ACS) era: the maturation of computer numerical control (CNC) technology and the diversification of measurement techniques have led to a quantum jump in polishing technology at the sub-nanometer scale. Roughness values of 0.5 nm in RMS for tungsten [13], 0.5 nm in Ra for silicon nitride [14], and 0.15 nm in RMS for polysilicon [15] were realized. The sub-nanometer roughness indicates an upgrade from precision polishing to what we may define as “ultra-precision” polishing and entered the era of ACS [16,17].

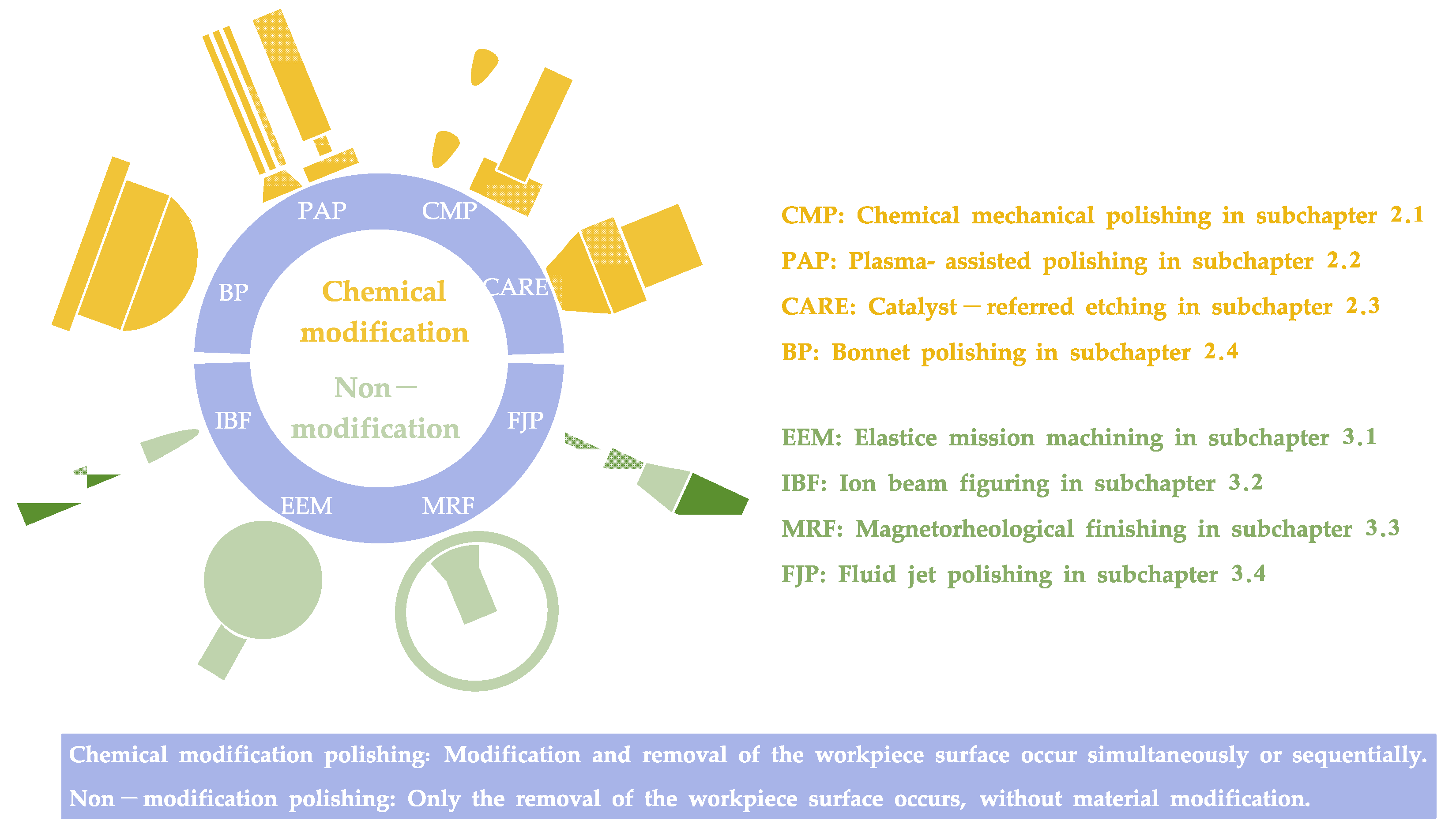
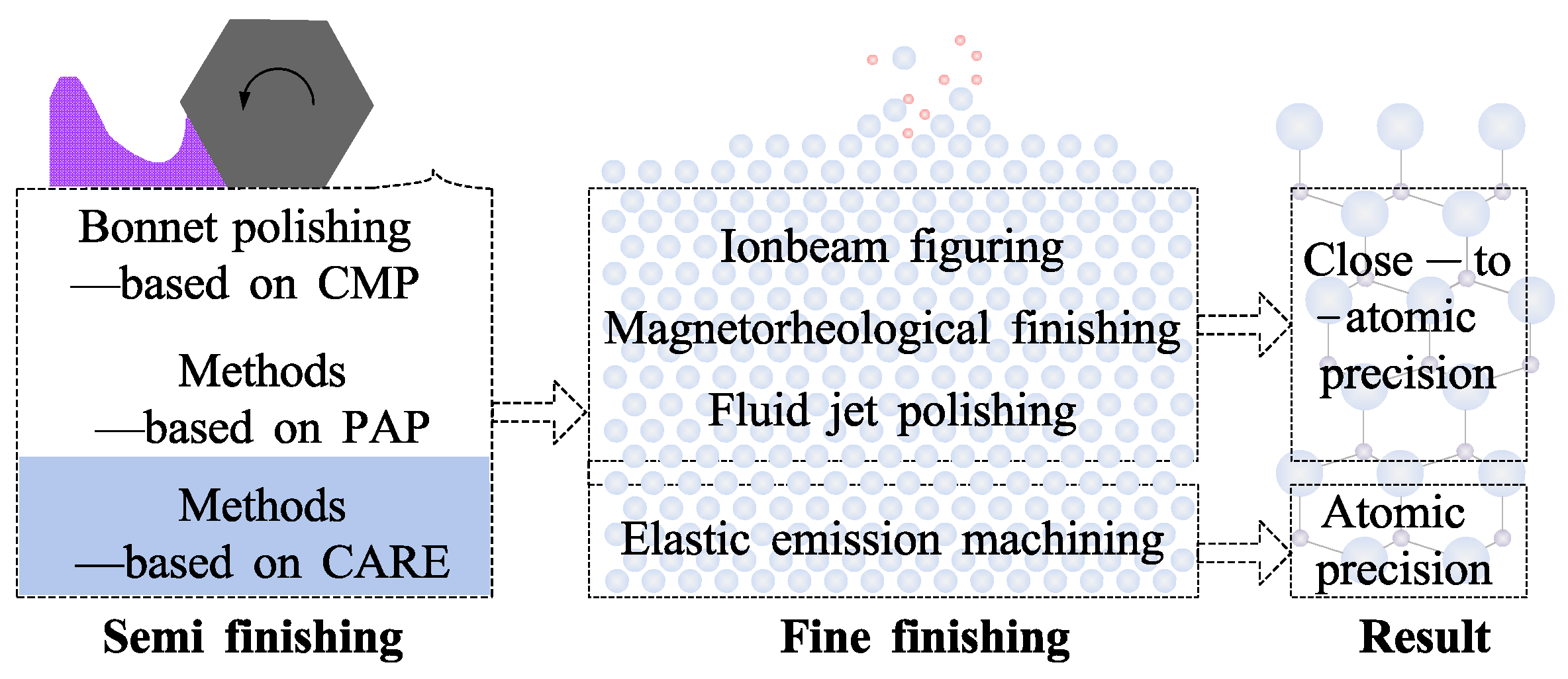
2. Chemical Modification Polishing Approaches
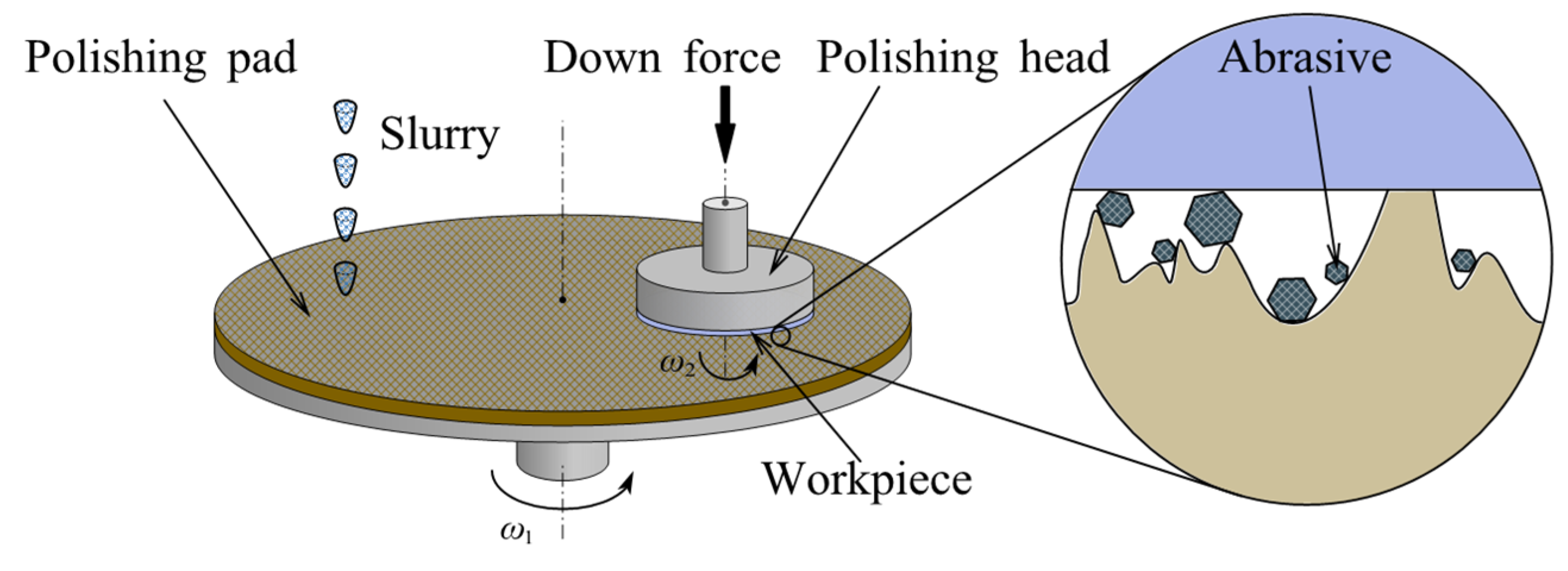
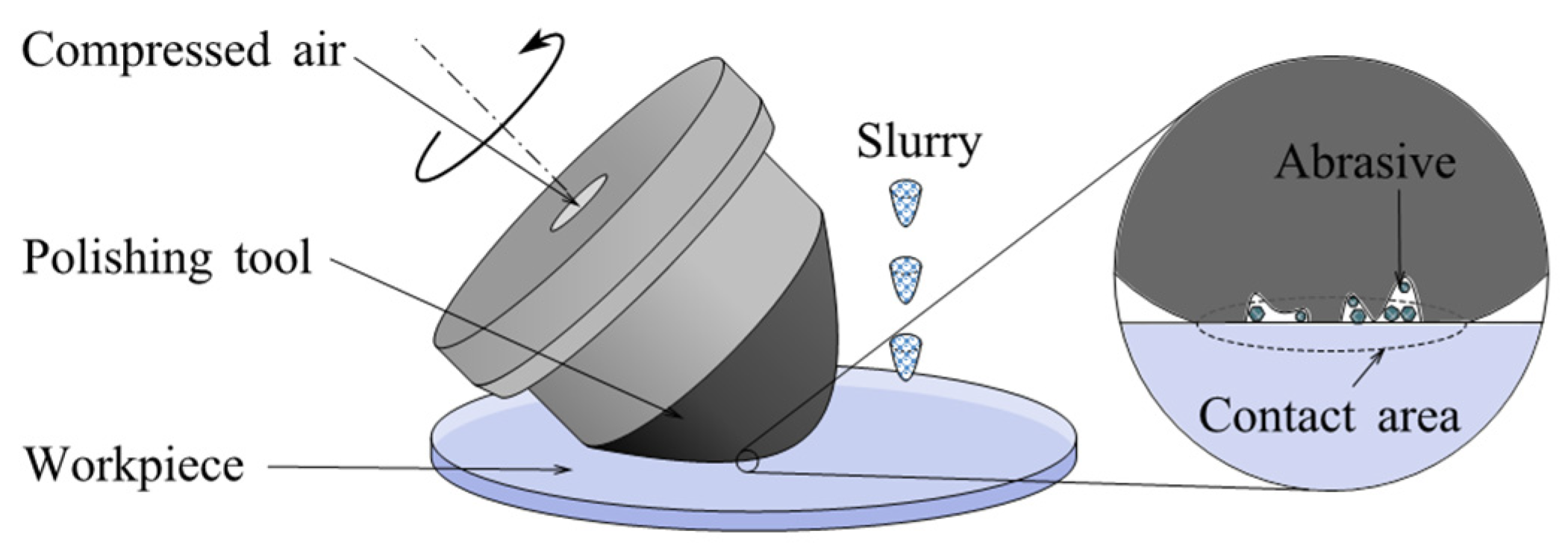
2.1. Chemical Mechanical Polishing
2.1.1. Removal Mechanism

2.1.2. Chemical Reaction Factors
2.1.3. Mechanical Interaction Factors
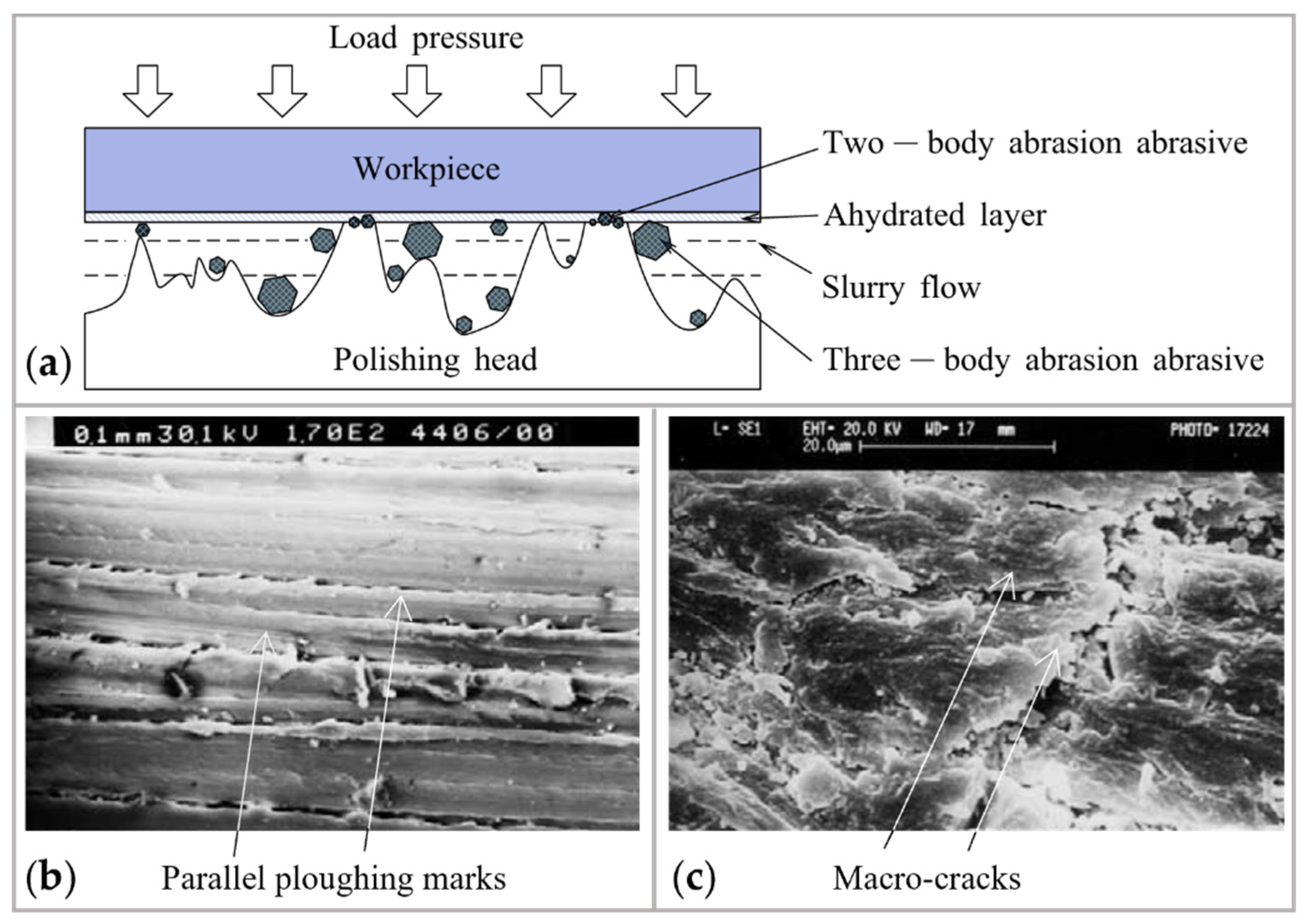
2.1.4. Characteristics
- (1)
- While softening the workpiece surface, the polishing slurry also has a corrosive effect on the polishing pads, resulting in more frequent replacement of polishing pads and higher costs.
- (2)
- (3)
- Low contact pressure is necessary to achieve low roughness, but unavoidably affects removal efficiency. As loose abrasive particles rarely slide on the workpiece surface under low contact pressure, they spend about 90% of their time rolling according to the three-body abrasion mode [77].
- (4)
- The workpiece roughness under three-body abrasion is sensitive to the abrasive size. When the abrasive size is not uniform, the mechanical material removal is carried out by a small number of large abrasives, probably resulting in the formation of scratches, pits, and other damage.
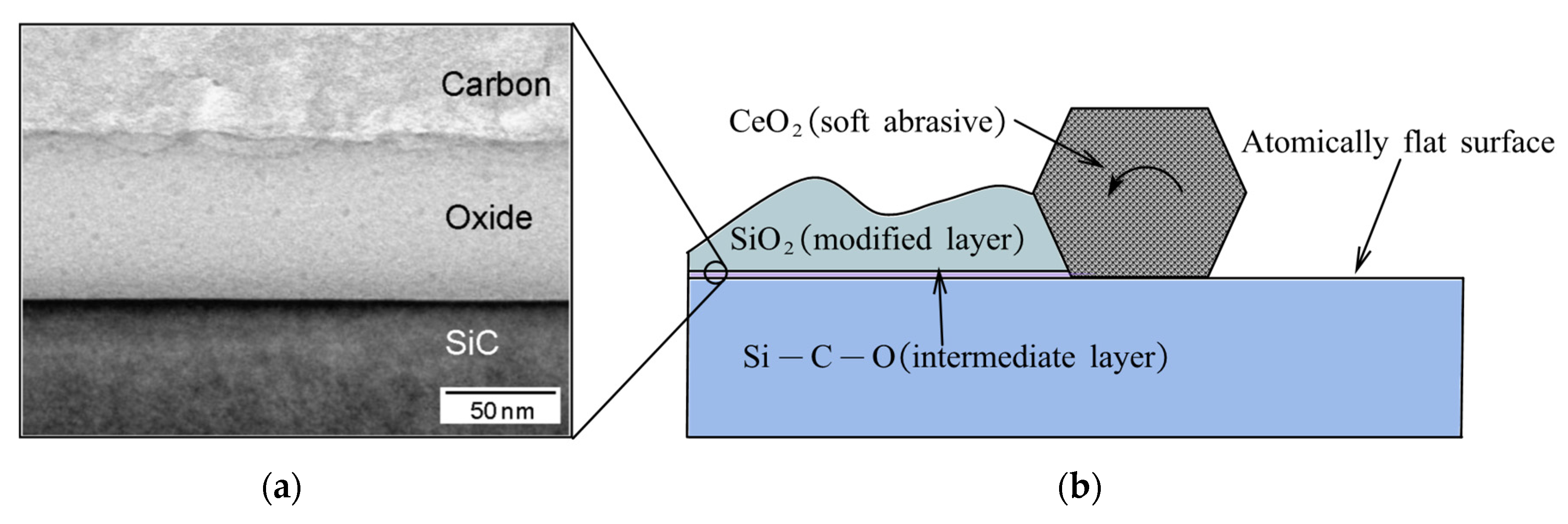
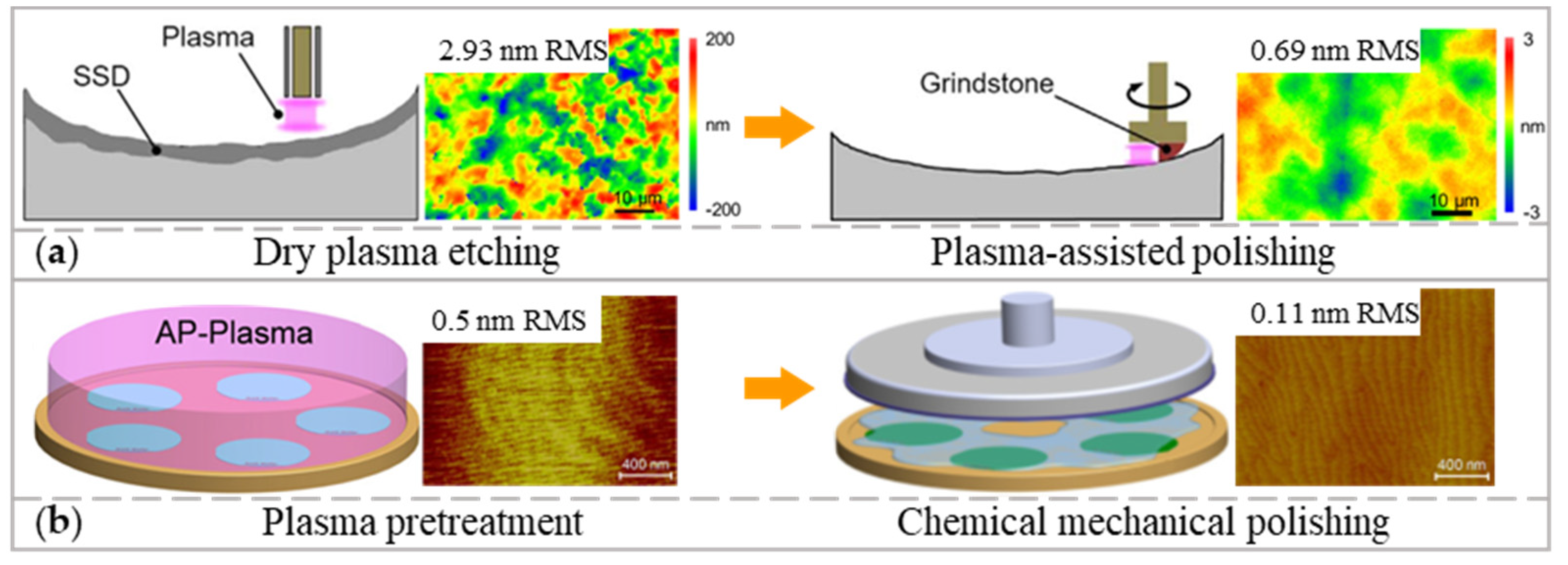
2.2. Plasma-Assisted Polishing
2.2.1. Removal Mechanism
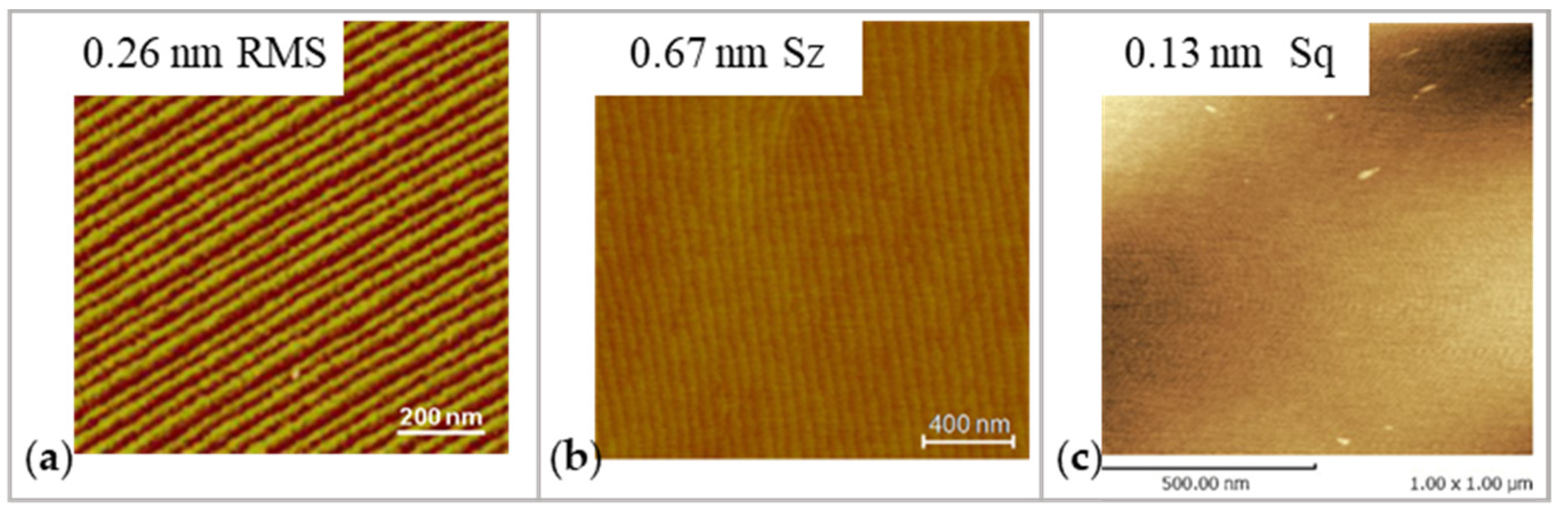
2.2.2. Processing Parameter in PAP

2.2.3. Combination with Other Polishing Approaches
2.2.4. Characteristics
- (1)
- The atomically flat interface between the modified layer and bulk material is the key to obtaining ACS precision. Although an atomically flat interface has been observed by cross sectional transmission electron microscopy [95], there is a lack of specific research as to why this interface forms, as well as about the types or interfaces that can be formed on various materials. This severely limits the application of PAP. For example, the achievable roughness is only 3 nm in Sa when applied to AIN [110].
- (2)
- The grinding stone surface in the PAP setup is planar, which limits the polishing of sloped surfaces.
- (3)
- In the modification process of PAP, the precursor gas is one of the necessary factors. However, the stability of the gas flow is difficult to control in practice. The difficulty in controlling the chemical concentration limits the stability of the polishing.
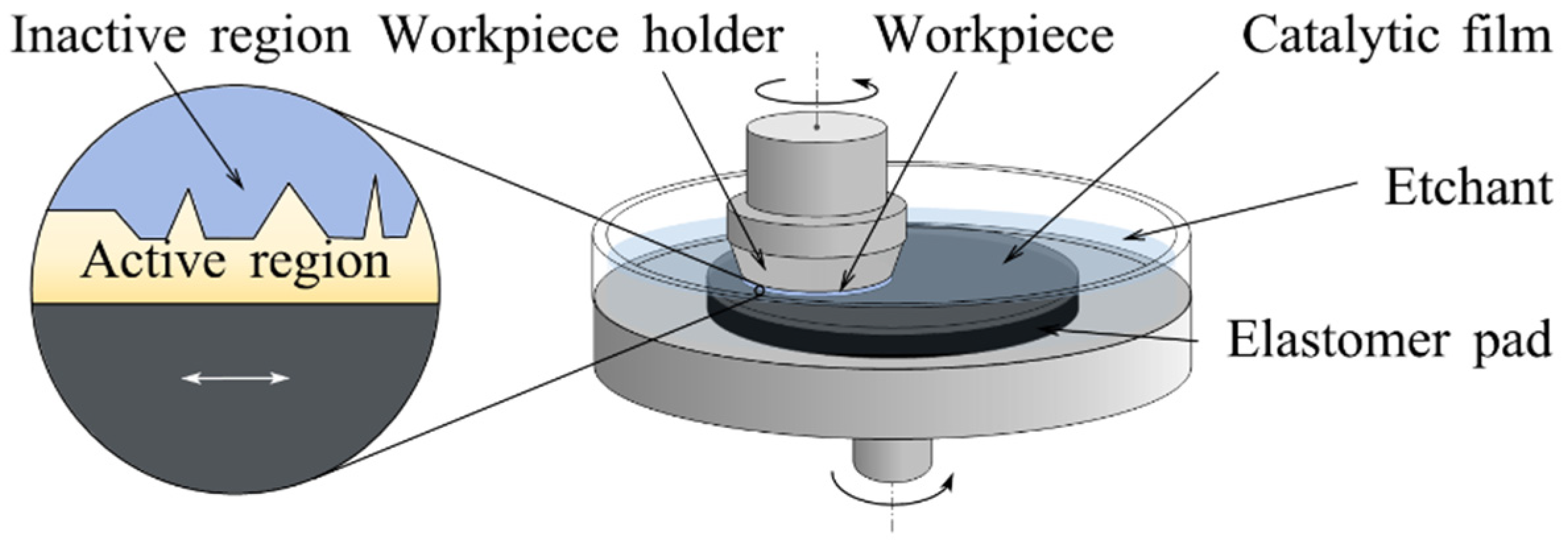
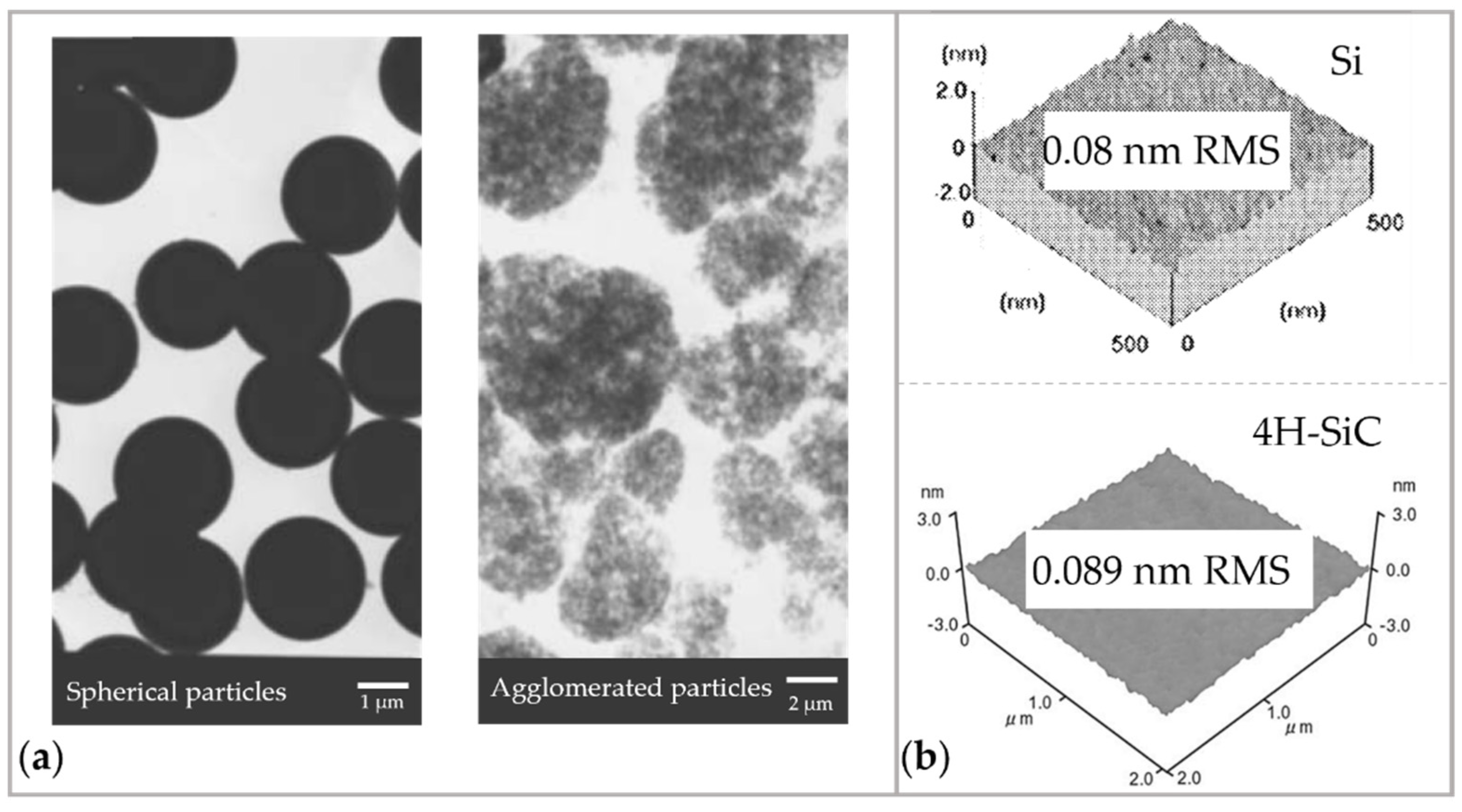
2.3. Catalyst-Referred Etching
2.3.1. Removal Mechanism
2.3.2. Expanding the Application
| Material. | Catalyst (Nobel Metal) | Etchant and Oxidant |
|---|---|---|
| Si | Au, Pt | HF and H2O2 [126] |
| Si | Pt | HF and H2O2 [127] |
| Si | Cu | HF and H3PO3 [128] |
| GaAs | Ag | HF and H2O2 [129] |
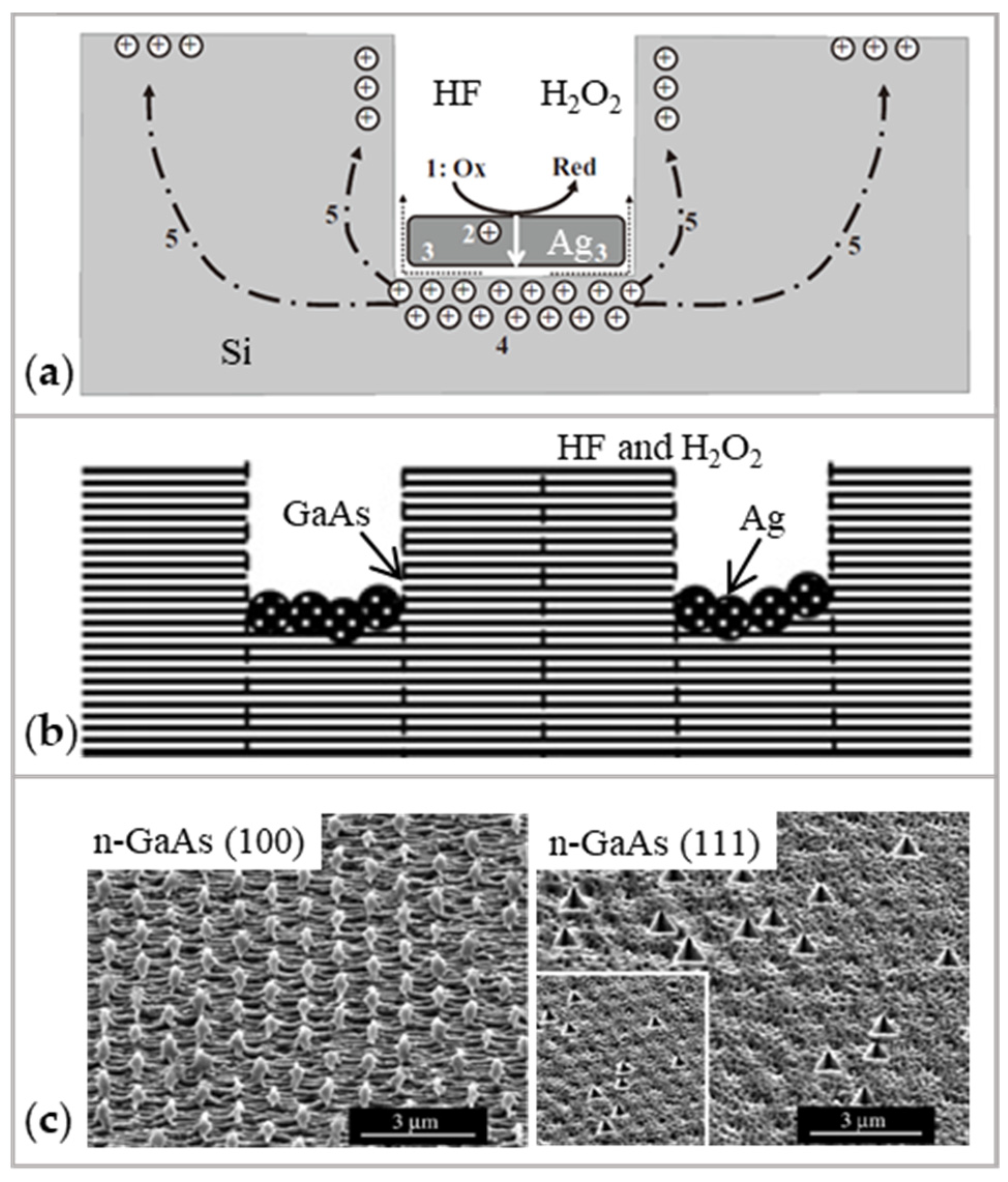
2.3.3. Characteristics
- (1)
- Currently, noble metals (catalyst) and HF (etchant) are fundamental in CARE. The use of noble metals increases the cost of CARE. The use of environment-hazardous HF makes CARE difficult to be applied in industry [122]. Although some researchers applied pure water instead of HF, the material removal rate is 2 nm/h [122], which is very low compared with material removal rate 500 nm/h using HF [114].
- (2)
- The ability to achieve sub-nanometer roughness in CARE relies on the accuracy of the catalyst film surface. While polishing off-axis SiC, the researchers have to lap the catalyst film by hand to minimize the degree of convexity [119]. Human intervention leaves uncertainty about the accuracy of CARE.
- (3)
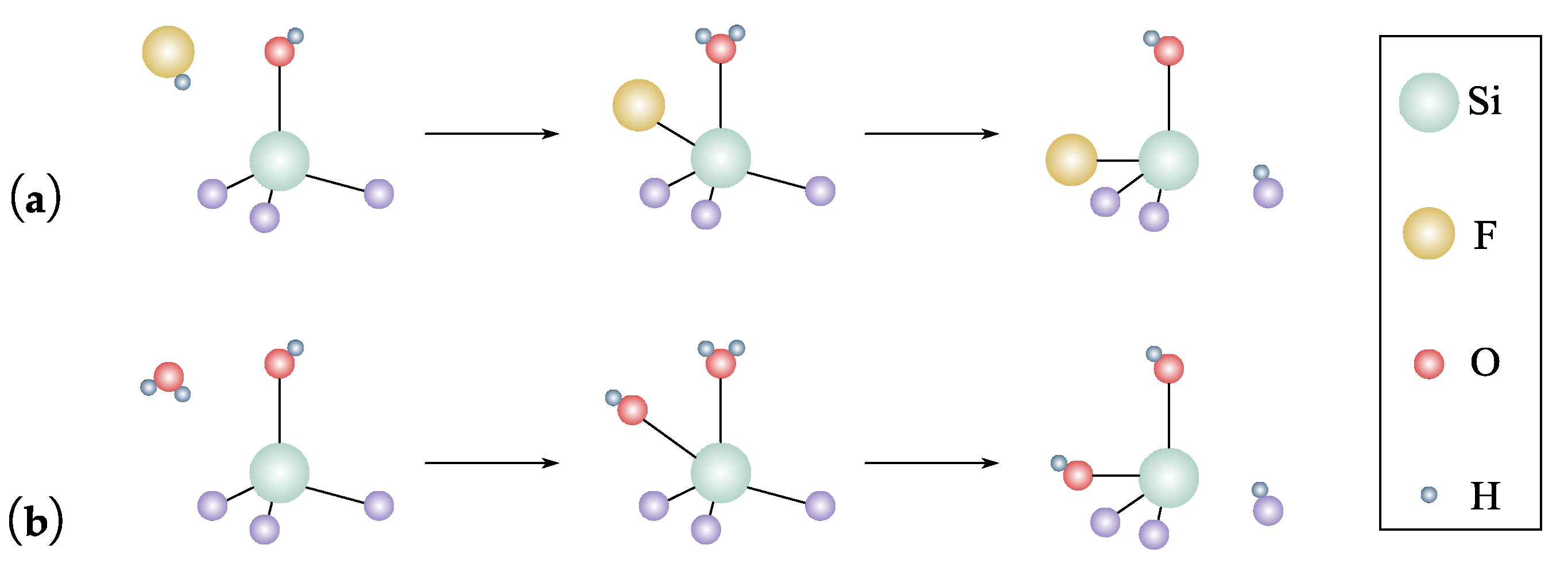
- Two difficulties arise if CARE is applied to curved surfaces: (a) The material exhibits anisotropy during etching [129], thus decreasing the precision, as shown in Figure 16c. (b) The direction of material removal depends on the crystal orientation of the workpiece [131], it is difficult to form a Gaussian distribution which could be used for surface figure error correction.
2.4. Bonnet Polishing
2.4.1. Removal Mechanism
2.4.2. Polishing System Development
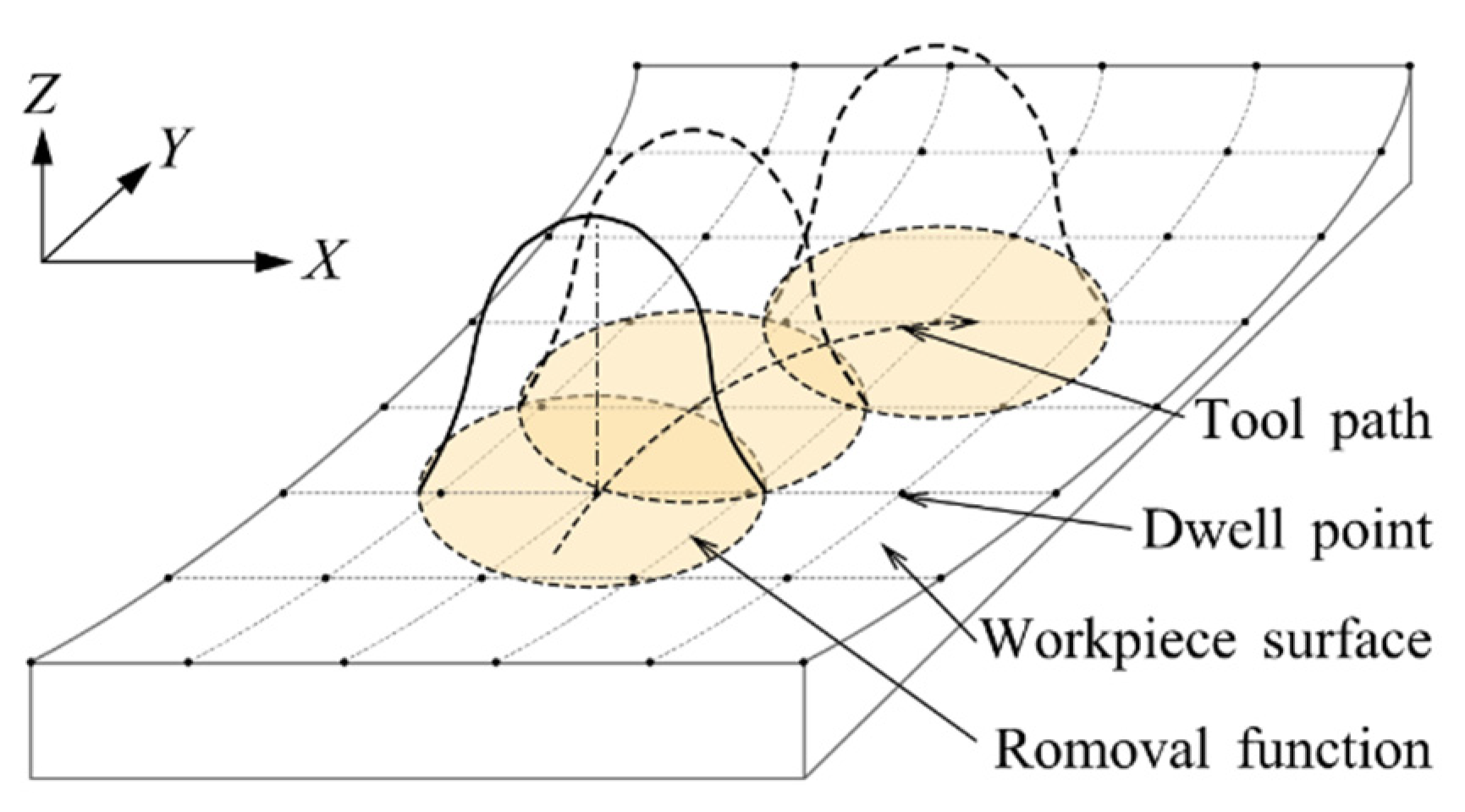
2.4.3. Tool Path Planning Approach
2.4.4. Characteristics
- (1)
- Polyurethane is a common polishing cloth in BP, which is extremely easy to wear during polishing. Therefore, the material removal function may not be constant.
- (2)
- Due to the poor rigidity of the soft polishing tool, mid-spatial frequencies are generated by process kinematics [151], limiting the realization of the sub-nanometer roughness.
- (3)
- The BP may be not the optimal choice when polishing small components [136] or workpieces with complex optical surfaces. This is because the bulged bonnet probably interferes with the workpiece surface.
2.5. Discussion on the Chemical Modification Polishing Approaches
3. Non-Modification Polishing Approaches
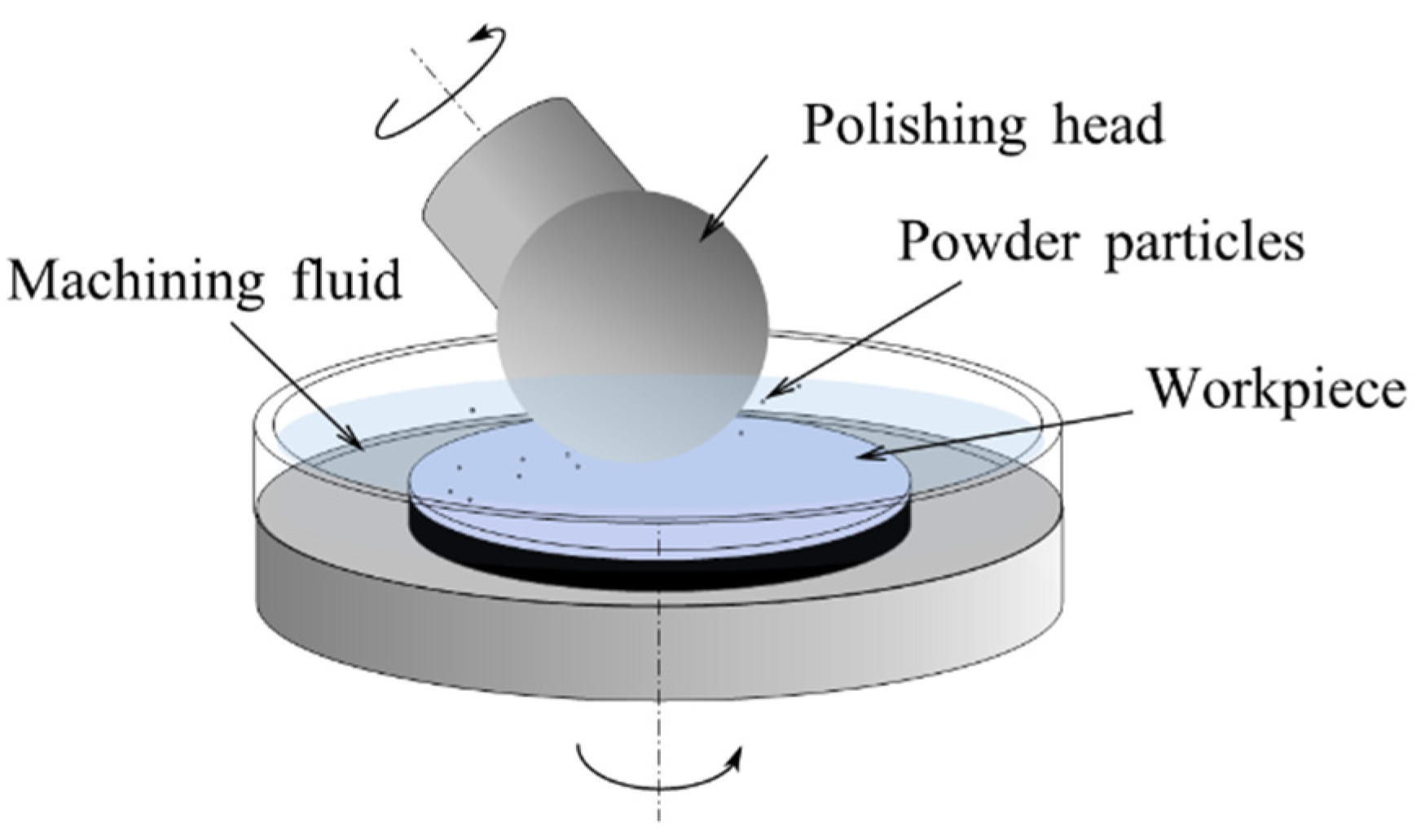
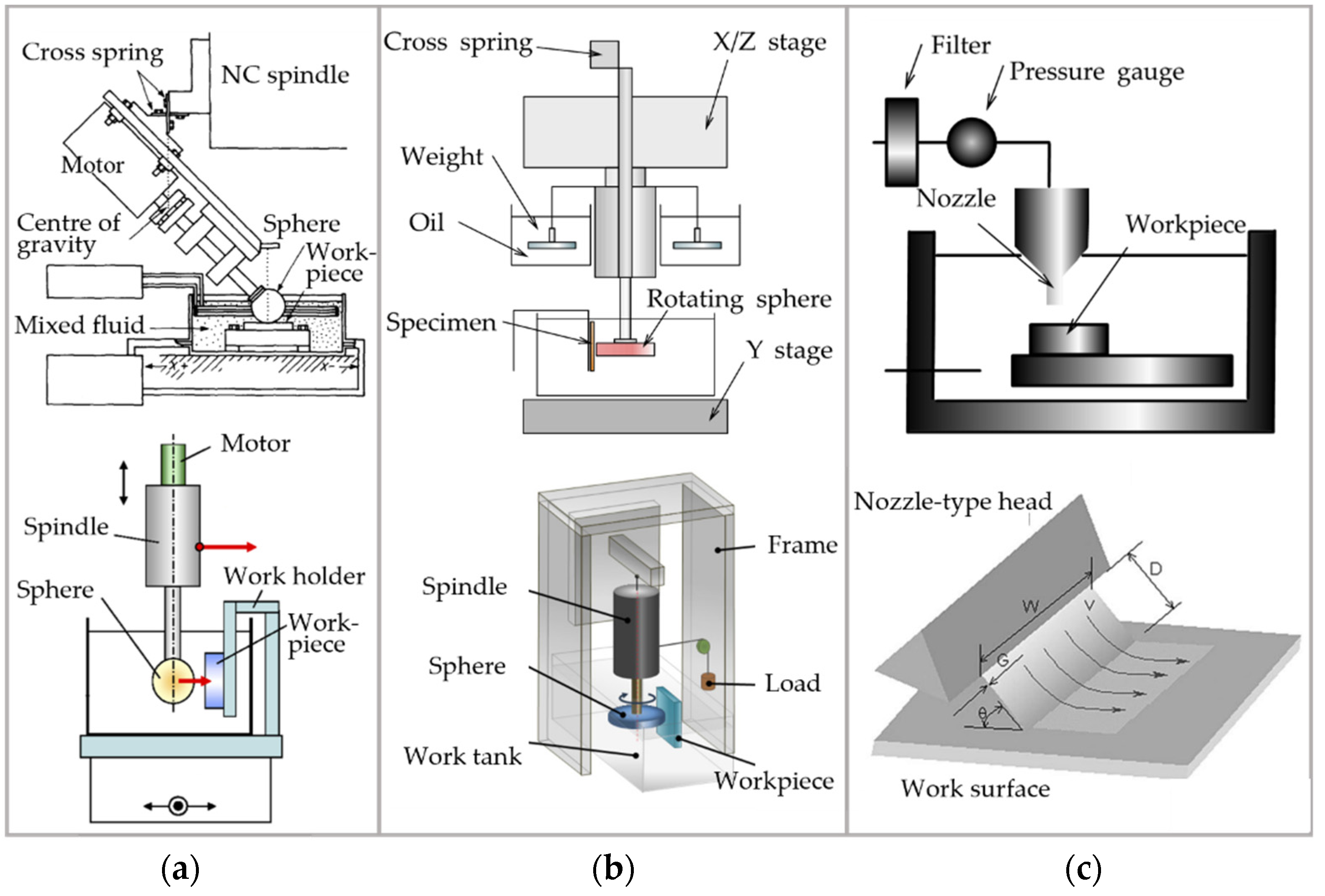
3.1. Elastic Emission Machining
3.1.1. Removal Mechanism
3.1.2. Equipment Development
3.1.3. Expanding Application
3.1.4. Characteristics
- (1)
- There is a high frequency of collision between powder particles and between the powder particles and the polishing head. The energy is wasted by this ineffective collisional process.
- (2)
- To achieve atomic-level removal, the thickness of the fluid film between the workpiece and polishing head needs to be tightly controlled at the micron scale to keep a small processing area. A too-small processing area causes an increase in polishing time.
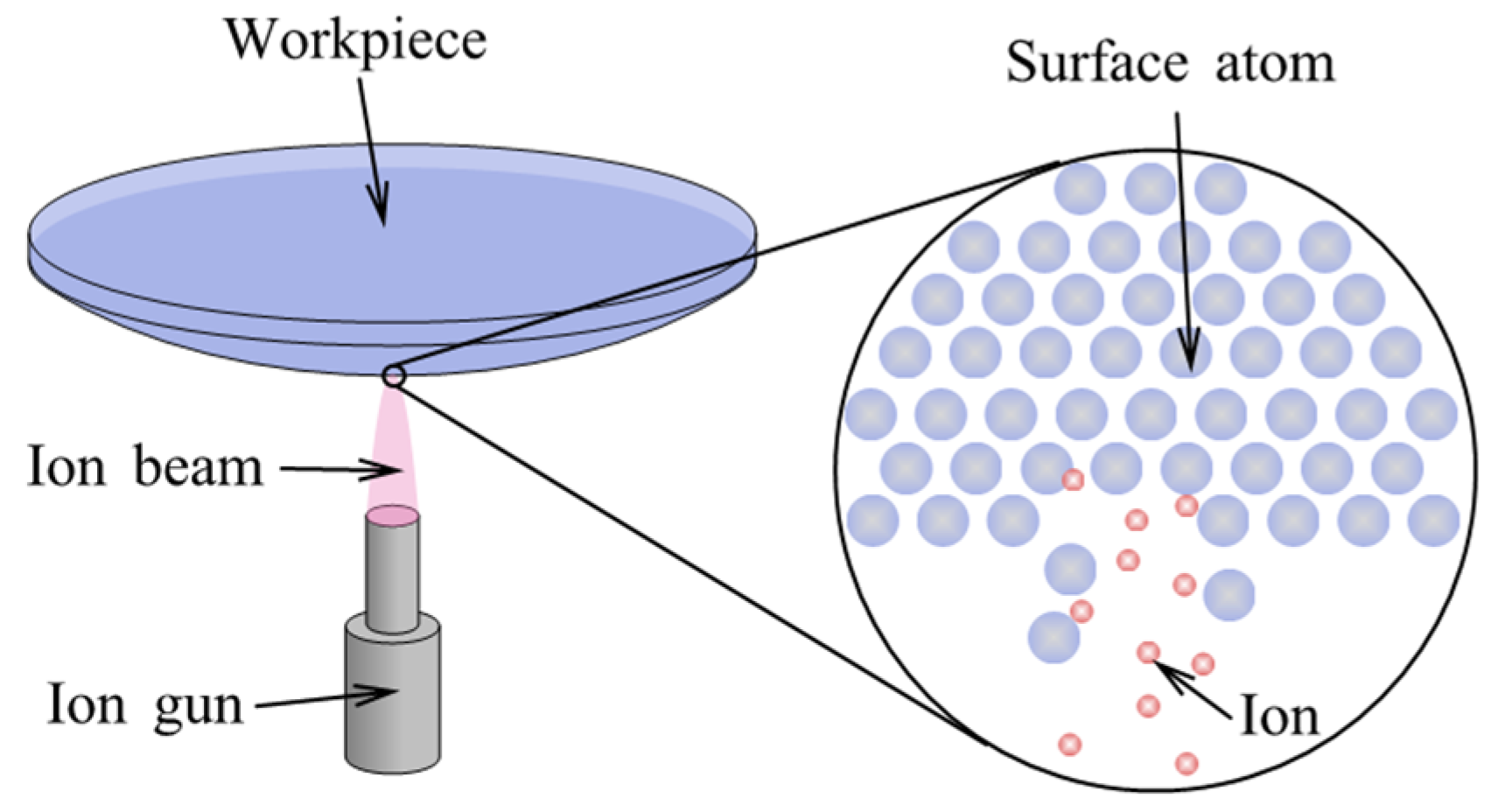
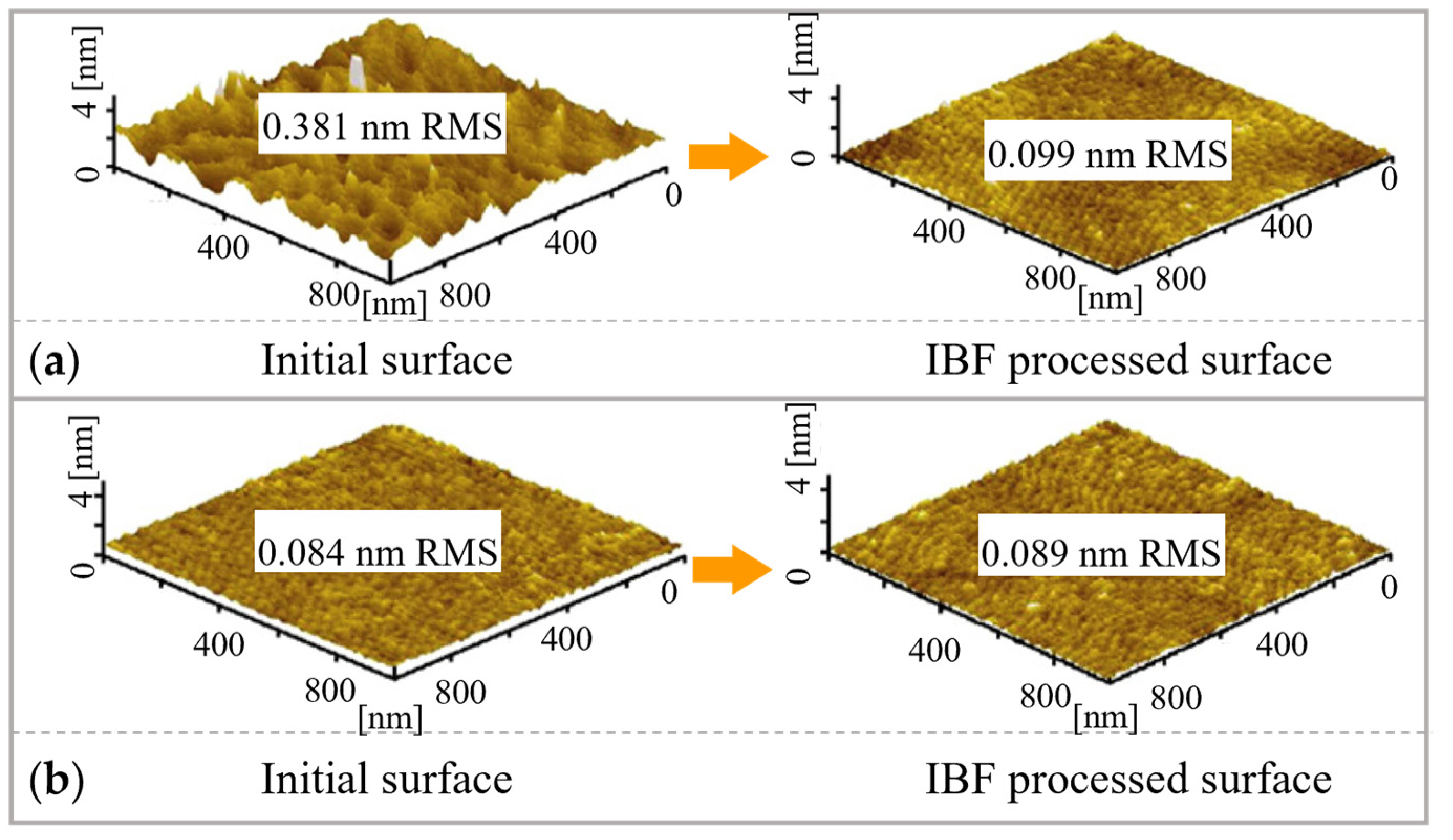
3.2. Ion Beam Figuring
3.2.1. Removal Mechanism
3.2.2. Equipment Development
3.2.3. Effect of Original Roughness
3.2.4. Characteristics
- (1)
- The aperture of the workpieces is limited by the size of the essential vacuum chamber.
- (2)
- The material sputtering phenomenon ensures the atomic-level material removal, resulting in the difficulty of improving the machining efficiency and the limitation of brittle materials with a high coefficient of expansion.
- (3)
- The requirements for the original roughness of the workpiece make IBF costly [24].
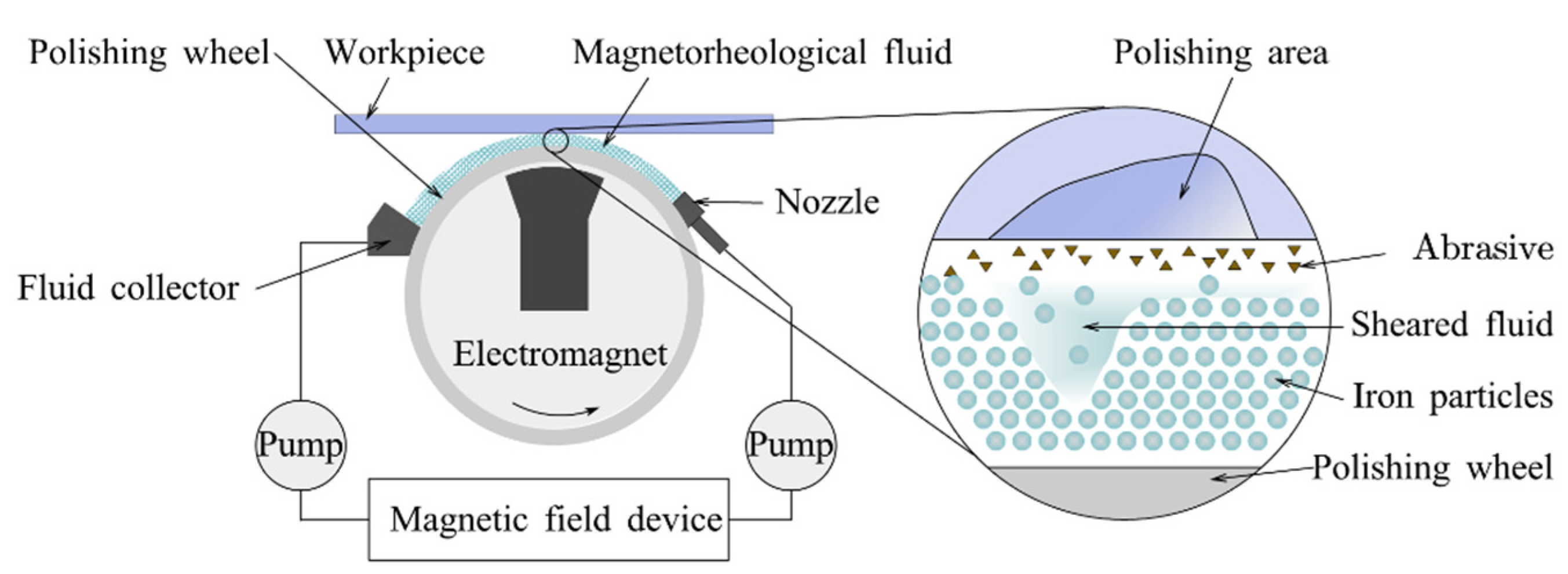
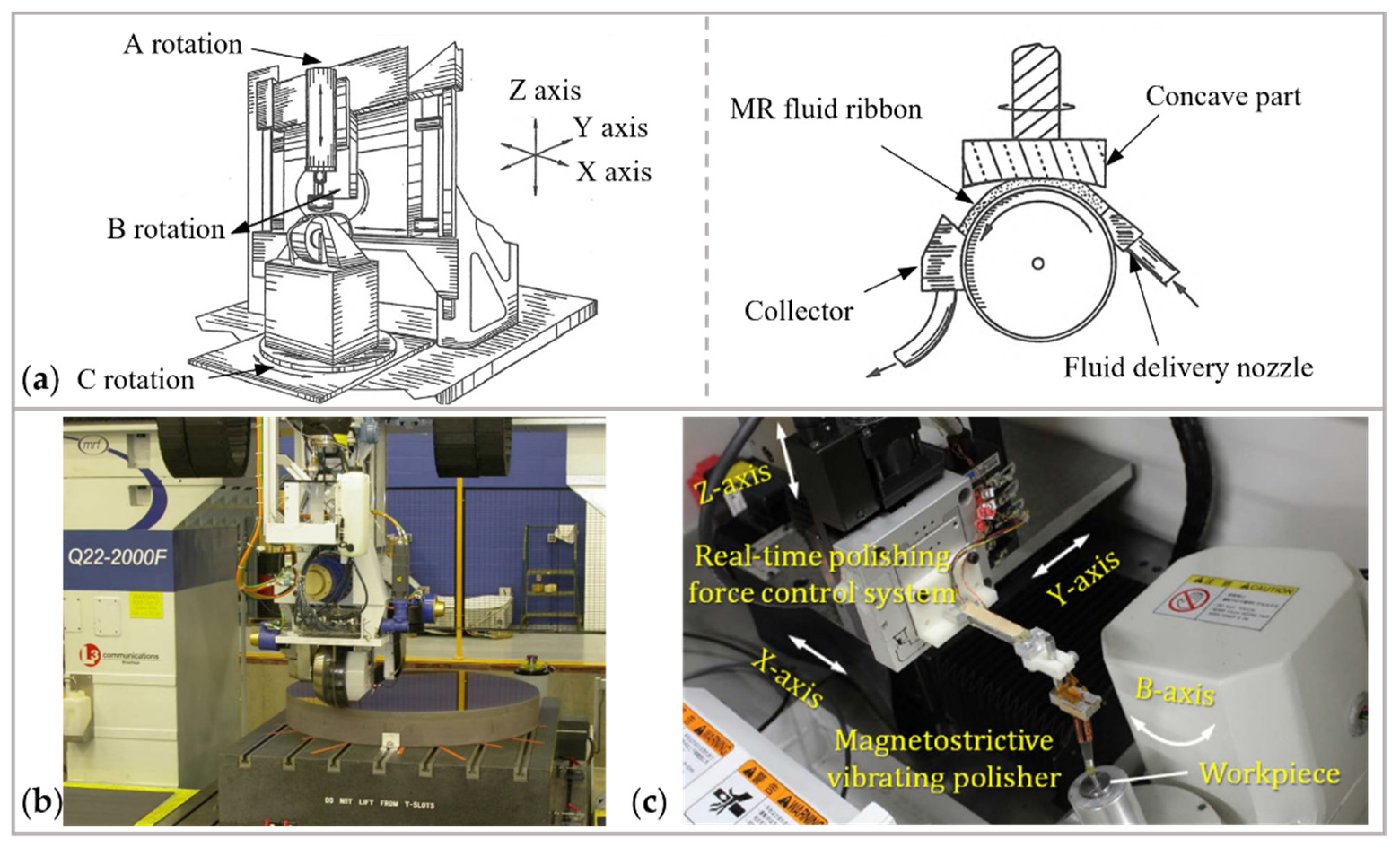
3.3. Magnetorheological Finishing
3.3.1. Removal Mechanism
3.3.2. Equipment Development
3.3.3. Magnetorheological Fluid Development
3.3.4. Characteristics
- (1)
- MRF equipment with special magnetorheological fluid requires a suitable gradient magnetic field generator and high accuracy of the kinematic system, resulting in high cost.
- (2)
- During the MRF process, there is 1~2 mm clearance between the large polishing wheel and the workpiece. When polishing concave surfaces with a small radius of curvature and the internal surface of the workpiece, collisions may occur. This small converging gap limits the curvature and complexity of the workpiece.
- (3)
- MRF cannot be applied to ferromagnetic materials. Due to the presence of the electromagnet, the ferromagnetic workpiece may interrupt the processing stability.
- (4)
- The sedimentation of micron-sized magnetic powder is a common problem, which is the key issue limiting the prolonged utilization in MRF [239].
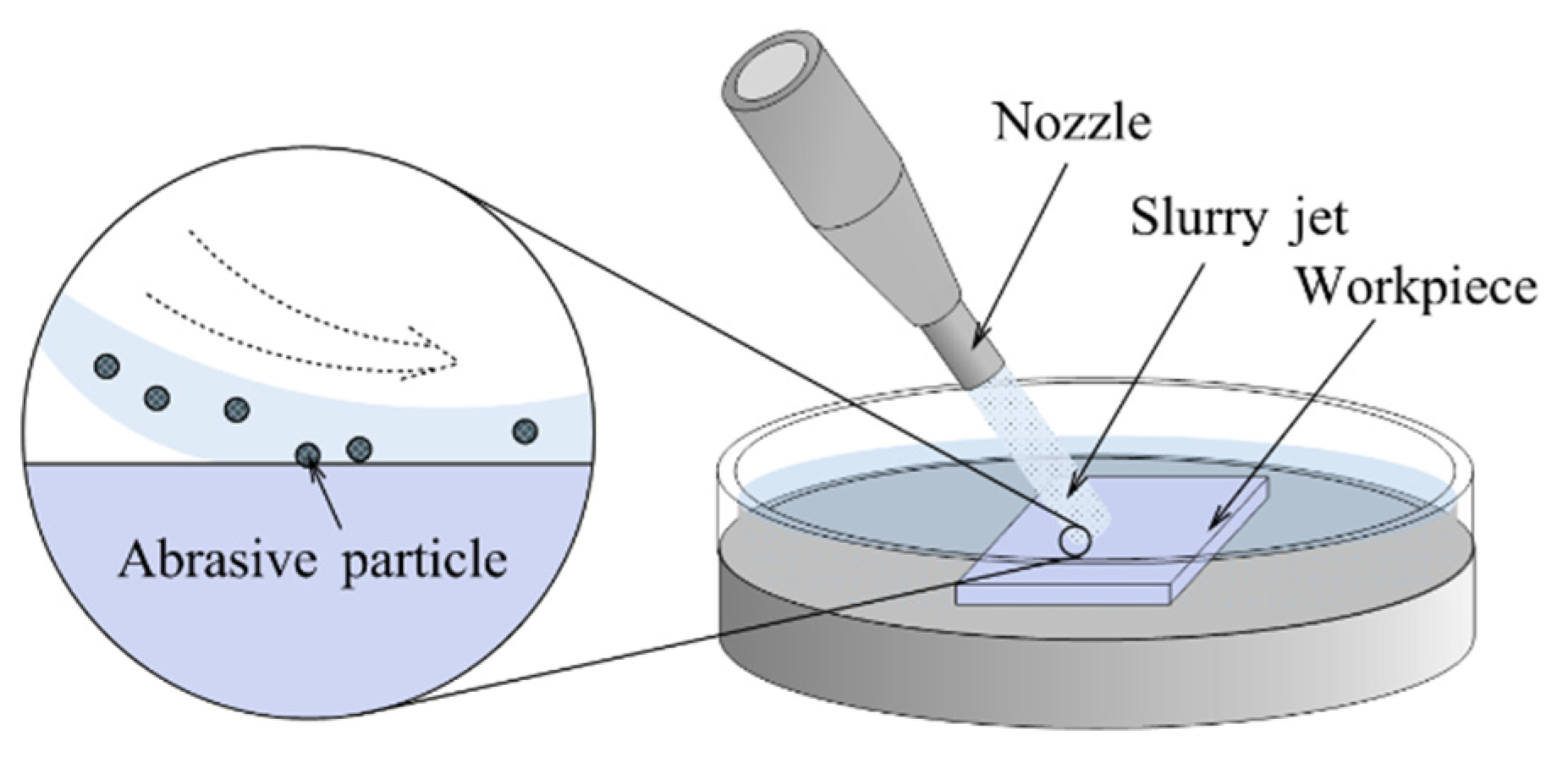
3.4. Fluid Jet Polishing
3.4.1. Removal Mechanism
3.4.2. Development of Roughness Reduction
3.4.3. Gaussian Removal Function
3.4.4. Characteristics
3.5. Discussion on “Non-Modification” Polishing Approaches
3.5.1. Characteristics
3.5.2. Processing Chain for Non-Planar Surface
4. Conclusions and Perspective
- (1)
- Limited range of processing materials
- (2)
- Limited range of workpiece shapes
- (3)
- High processing costs
- (4)
- Environmental pollution
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Zucuni, C.P.; Dapieve, K.S.; Rippe, M.P.; Pereira, G.K.R.; Bottino, M.C.; Valandro, L.F. Influence of finishing/polishing on the fatigue strength, surface topography, and roughness of an yttrium-stabilized tetragonal zirconia polycrystals subjected to grinding. J. Mech. Behav. Biomed. Mater. 2019, 93, 222–229. [Google Scholar] [CrossRef] [PubMed]
- Ettl, P.; Schmidt, B.E.; Schenk, M.; Laszlo, I.; Haeusler, G. Roughness parameters and surface deformation measured by coherence radar. Int. Conf. Appl. Opt. Metrol. 1998, 3407, 133–140. [Google Scholar]
- Kriiska, A. Excavations of the Stone Age site at Vihasoo III. Arheol. Välitööd Eest. 1996, 7, 19–28. [Google Scholar]
- Helden, V.; Albert; Dupré, S.; Gent, R.V. The Origins of the Telescope; Amsterdam University Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Masters, B.R. Ernst Abbe and the Foundation of Scientific Microscopes. Opt. Photonics News 2007, 18, 18. [Google Scholar] [CrossRef]
- Carl Zeiss, Ernst Abbe and Otto Schott–A Winning Team. 2002. Available online: https://www.zeiss.com/vision-care/int/better-vision/understanding-vision/carl-zeiss-ernst-abbe-and-otto-schott-a-winning-team.html (accessed on 15 December 2022).
- Clay, W. Surface Finish. Proc. Inst. Automob. Eng. 1944, 38, 43–73. [Google Scholar]
- Pomes, C.; Slack, G.; Wise, M. Surface roughness of dental castings. J. Am. Dent. Assoc. 1950, 41, 545–556. [Google Scholar] [CrossRef]
- Schlesinger, G. Surface finish and the function of part. Proc. Inst. Mech. Eng. 1944, 151, 153–178. [Google Scholar] [CrossRef]
- Pimenov, S.M.; Kononenko, V.V.; Ralchenko, V.G.; Konov, V.I.; Gloor, S.; Lüthy, W.; Weber, H.P.; Khomich, A.V. Laser polishing of diamond plates. Appl. Phys. A: Mater. Sci. Process. 1999, 69, 81–88. [Google Scholar] [CrossRef]
- Higashi, Y.; Meike, T.; Suzuki, J.; Mori, Y.; Yamauchi, K.; Endo, K.; Namba, H. New machining method for making precise and very smooth mirror surfaces made from Cu and Al alloys for synchrotron radiation optics. Rev. Sci. Instrum. 1989, 60, 2120–2123. [Google Scholar] [CrossRef]
- Fähnle, O.W.; van Brug, H.H. Fluid jet polishing: Removal process analysis. Opt. Fabr. Test. 1999, 3739, 68–77. [Google Scholar]
- Basim, G.; Adler, J.; Mahajan, U.; Singh, R.; Moudgil, B. Effect of particle size of chemical mechanical polishing slurries for enhanced polishing with minimal defects. J. Electrochem. Soc. 2000, 147, 3523. [Google Scholar] [CrossRef]
- Muratov, V.A.; Fischer, T.E. Tribochemical polishing. Annu. Rev. Mater. Sci. 2000, 30, 27–51. [Google Scholar] [CrossRef]
- Lee, B.; Quinn, L.; Baine, P.; Mitchell, S.; Armstrong, B.; Gamble, H. Investigation of the role of chemical-mechanical polishing in improving the performance of polysilicon TFTs. MRS Online Proc. Libr. (OPL) 1999, 558, 257–262. [Google Scholar] [CrossRef]
- Mathew, P.T.; Rodriguez, B.J.; Fang, F.Z. Atomic and Close-to-Atomic Scale Manufacturing: A Review on Atomic Layer Removal Methods Using Atomic Force Microscopy. Nanomanufacturing Metrol. 2020, 3, 167–186. [Google Scholar] [CrossRef]
- Fang, F.Z. On Atomic and Close-to-atomic Scale Manufacturing—Development Trend of Manufacturing Technology. China Mech. Eng. 2020, 31, 1009–1021. [Google Scholar]
- Betancourt-Parra, S. Leonardo da Vinci’s tribological intuitions. Tribol. Int. 2021, 153, 106664. [Google Scholar] [CrossRef]
- Molesini, G.; Greco, V. Galileo Galilei: Research and development of the telescope. Trends Opt. 1996, 23, 423–438. [Google Scholar]
- Brinksmeier, E.; Riemer, O.; Gessenharter, A. Finishing of structured surfaces by abrasive polishing. Precis. Eng. 2006, 30, 325–336. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, G.; Shi, X.; Zhang, S.; Gong, H.; Luo, G. Effects of ultra-smooth surface atomic step morphology on chemical mechanical polishing (CMP) performances of sapphire and SiC wafers. Tribol. Int. 2015, 87, 145–150. [Google Scholar] [CrossRef]
- Chen, L.; Wen, J.; Zhang, P.; Yu, B.; Chen, C.; Ma, T.; Lu, X.; Kim, S.H.; Qian, L. Nanomanufacturing of silicon surface with a single atomic layer precision via mechanochemical reactions. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, N. Current Status in, and Future Trends of, Ultraprecision Machining and Ultrafine Materials Processing. CIRP Ann. 1983, 32, 573–582. [Google Scholar] [CrossRef]
- Zhang, Z.; Yan, J.; Kuriyagawa, T. Manufacturing technologies toward extreme precision. Int. J. Extrem. Manuf. 2019, 1, 022001. [Google Scholar] [CrossRef] [Green Version]
- Fang, F.Z. Atomic and close-to-atomic scale manufacturing: Perspectives and measures. Int. J. Extrem. Manuf. 2020, 2, 030201. [Google Scholar] [CrossRef]
- Fang, F.Z.; Zhang, X.; Gao, W.; Guo, Y.; Byrne, G.; Hansen, H.N. Nanomanufacturing—Perspective and applications. CIRP Ann. 2017, 66, 683–705. [Google Scholar] [CrossRef] [Green Version]
- Assoufid, L.; Ohashi, H.; Asundi, A.K.; Yumoto, H.; Koyama, T.; Matsuyama, S.; Yamauchi, K.; Ohashi, H. Ultra-high-precision surface processing techniques for nanofocusing ellipsoidal mirrors in hard x-ray region. Adv. Metrol. X-Ray EUV Opt. V 2014, 9206, 27–37. [Google Scholar]
- Usuki, K.; Mazuray, L.; Kitayama, T.; Wartmann, R.; Wood, A.P.; Matsumura, H.; Kojima, T.; de la Fuente, M.C.; Tissot, J.-L.M.; Uchikoshi, J.; et al. Development of a nanoprofiler using the follow-up normal vector to the surface for next-generation ultraprecise mirrors. Optical Systems Design 2012 2012, 8550, 220–227. [Google Scholar]
- Kurashima, Y.; Miyachi, S.; Miyamoto, I.; Ando, M.; Numata, A. Evaluation of surface roughness of ULE® substrates machined by Ar+ ion beam. Microelectron. Eng. 2008, 85, 1193–1196. [Google Scholar] [CrossRef]
- Kanaoka, M.; Liu, C.; Nomura, K.; Ando, M.; Takino, H.; Fukuda, Y.; Mori, Y.; Mimura, H.; Yamauchi, K. Processing efficiency of elastic emission machining for low-thermal-expansion material. Surf. Interface Anal. 2008, 40, 1002–1006. [Google Scholar] [CrossRef]
- Hasan, R.M.M.; Luo, X. Promising Lithography Techniques for Next-Generation Logic Devices. Nanomanufacturing Metrol. 2018, 1, 67–81. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Luo, J.; Lu, X.; Zhang, C.; Pan, G. Progress in material removal mechanisms of surface polishing with ultra precision. Chin. Sci. Bull. 2004, 49, 1687–1693. [Google Scholar] [CrossRef]
- Yin, S.H.; Wang, Y.Q.; Li, Y.P.; Gong, S. Experimental Study on Effects of Translational Movement on Surface Planarity in Magnetorheological Planarization Process. Adv. Mater. Res. 2016, 1136, 293–296. [Google Scholar] [CrossRef]
- Gautam, G.D.; Pandey, A.K. Pulsed Nd:YAG laser beam drilling: A review. Opt. Laser Technol. 2018, 100, 183–215. [Google Scholar] [CrossRef]
- Schuelke, T.; Grotjohn, T.A. Diamond polishing. Diam. Relat. Mater. 2013, 32, 17–26. [Google Scholar] [CrossRef]
- Chkhalo, N.I.; Kaskov, I.A.; Malyshev, I.V.; Mikhaylenko, M.S.; Pestov, A.E.; Polkovnikov, V.N.; Salashchenko, N.N.; Toropov, M.N.; Zabrodin, I.G. High-performance facility and techniques for high-precision machining of optical components by ion beams. Precis. Eng. 2017, 48, 338–346. [Google Scholar] [CrossRef]
- Kohn, E.; Adamschik, M.; Schmid, P.; Denisenko, A.; Aleksov, A.; Ebert, W. Prospects of diamond devices. J. Phys. D Appl. Phys. 2001, 34, 77–85. [Google Scholar] [CrossRef]
- Yamauchi, K.; Mimura, H.; Inagaki, K.; Mori, Y. Figuring with subnanometer-level accuracy by numerically controlled elastic emission machining. Rev. Sci. Instrum. 2002, 73, 4028–4033. [Google Scholar] [CrossRef]
- Khounsary, A.; Takei, Y.; Kume, T.; Motoyama, H.; Hiraguri, K.; Hashizume, H.; Mimura, H.; Goto, S.; Morawe, C. Development of a numerically controlled elastic emission machining system for fabricating mandrels of ellipsoidal focusing mirrors used in soft x-ray microscopy. Adv. X-Ray/EUV Opt. Compon. VIII 2013, 8848, 71–80. [Google Scholar]
- Hashimoto, T.; Maeya, J.; Fujita, T.; Maenaka, K. Concept of MEMS Ring Laser Gyroscope with Movable Optical Parts. Procedia Chem. 2009, 1, 564–567. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Lin, Z.; Zhu, W.; Lezec, H.J.; Xu, T.; Agrawal, A.; Zhang, C.; Huang, K. Recent advances in ultraviolet nanophotonics: From plasmonics and metamaterials to metasurfaces. Nanophotonics 2021, 10, 2283–2308. [Google Scholar] [CrossRef]
- Zhang, B.; Gardner, D.F.; Seaberg, M.D.; Shanblatt, E.R.; Kapteyn, H.C.; Murnane, M.M.; Adams, D.E. High contrast 3D imaging of surfaces near the wavelength limit using tabletop EUV ptychography. Ultramicroscopy 2015, 158, 98–104. [Google Scholar] [CrossRef] [Green Version]
- de Jonge, M.D.; Vogt, S. Hard X-ray fluorescence tomography--an emerging tool for structural visualization. Curr. Opin. Struct. Biol. 2010, 20, 606–614. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, M.; Singh, J.; Mishra, D.K.; Singh, R.P. Review on the various strategies adopted for the polishing of silicon wafer—A chemical perspective. Mater. Today: Proc. 2022, 63, 62–68. [Google Scholar] [CrossRef]
- Li, Z.; Pei, Z.; Funkenbusch, P. Machining processes for sapphire wafers: A literature review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 975–989. [Google Scholar] [CrossRef]
- Shao, Q.; Duan, S.; Fu, L.; Lyu, B.; Zhao, P.; Yuan, J. Shear Thickening Polishing of Quartz Glass. Micromachines 2021, 12, 956. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, A.; Fang, F.Z. Review on mechanism and process of surface polishing using lasers. Front. Mech. Eng. 2019, 14, 299–319. [Google Scholar] [CrossRef] [Green Version]
- Ermergen, T.; Taylan, F. Review on Surface Quality Improvement of Additively Manufactured Metals by Laser Polishing. Arab. J. Sci. Eng. 2021, 46, 7125–7141. [Google Scholar] [CrossRef]
- Li, M.; Lyu, B.; Yuan, J.; Dong, C.; Dai, W. Shear-thickening polishing method. Int. J. Mach. Tools Manuf. 2015, 94, 88–99. [Google Scholar] [CrossRef]
- Mohammad, A.E.K.; Wang, D. Electrochemical mechanical polishing technology: Recent developments and future research and industrial needs. Int. J. Adv. Manuf. Technol. 2016, 86, 1909–1924. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Beaucamp, A. Compliant grinding and polishing: A review. Int. J. Mach. Tools Manuf. 2020, 158, 103634. [Google Scholar] [CrossRef]
- Marks, M.R.; Hassan, Z.; Cheong, K.Y. Ultrathin wafer pre-assembly and assembly process technologies: A review. Crit. Rev. Solid State Mater. Sci. 2015, 40, 251–290. [Google Scholar] [CrossRef]
- Walsh, R.J.; Arno, H.H. Process for Polishing Semi-conductor Materials. U.S. Pat. Trademark Off. 1965, 3, 273. [Google Scholar]
- Fury, M.A. The early days of CMP. Solid State Technol. 1997, 40, 81–84. [Google Scholar]
- Zantye, P.B.; Kumar, A.; Sikder, A.K. Chemical mechanical planarization for microelectronics applications. Mater. Sci. Eng. R Rep. 2004, 45, 89–220. [Google Scholar] [CrossRef]
- Pan, B.; Kang, R.; Guo, J.; Fu, H.; Du, D.; Kong, J. Precision Fabrication of Thin Copper Substrate by Double-sided Lapping and Chemical Mechanical Polishing. J. Manuf. Process. 2019, 44, 47–54. [Google Scholar] [CrossRef]
- Guo, J.; Shi, X.; Song, C.; Niu, L.; Cui, H.; Guo, X.; Tong, Z.; Yu, N.; Jin, Z.; Kang, R. Theoretical and experimental investigation of chemical mechanical polishing of W–Ni–Fe alloy. Int. J. Extrem. Manuf. 2021, 3, 025103. [Google Scholar] [CrossRef]
- Geng, Z.; Zhou, P.; Meng, L.; Yan, Y.; Guo, D. Prediction of Surface Profile Evolution of Workpiece and Lapping Plate in Lapping Process. J. Manuf. Sci. Eng. 2022, 144, 081001. [Google Scholar] [CrossRef]
- Cook, L.M. Chemical processes in glass polishing. J. Non-Cryst. Solids 1990, 120, 152–171. [Google Scholar] [CrossRef]
- Onodera, T.; Takahashi, H.; Nomura, S. First-principles molecular dynamics investigation of ceria/silica sliding interface toward functional materials design for chemical mechanical polishing process. Appl. Surf. Sci. 2020, 530, 147259. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Z.; Guo, J. The effect of the interface reaction mode on chemical mechanical polishing. CIRP J. Manuf. Sci. Technol. 2020, 31, 539–547. [Google Scholar] [CrossRef]
- Preston, F. The theory and design of plate glass polishing machines. J. Glass Technol. 1927, 11, 214–256. [Google Scholar]
- Li, W.; Zhou, P.; Geng, Z.; Yan, Y.; Guo, D. A Global Correction Process for Flat Optics with Patterned Polishing Pad. J. Manuf. Sci. Eng. 2019, 141, 091012. [Google Scholar] [CrossRef]
- Pan, J.; Yan, Q. Material removal mechanism of cluster magnetorheological effect in plane polishing. Int. J. Adv. Manuf. Technol. 2015, 81, 2017–2026. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, H. A wafer-scale material removal rate profile model for copper chemical mechanical planarization. Int. J. Mach. Tools Manuf. 2011, 51, 395–403. [Google Scholar] [CrossRef]
- Lin, J.F.; Chern, J.D.; Chang, Y.H.; Kuo, P.L.; Tsai, M.S. Analysis of the tribological mechanisms arising in the chemical mechanical polishing of copper-film wafers. J. Tribol. 2004, 126, 185–199. [Google Scholar] [CrossRef]
- Reynolds, O., IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 1, 157–234. [Google Scholar]
- Zhao, D.; Wang, T.; He, Y.; Lu, X. Experimental studies on interfacial fluid lubrication and wafer status during chemical mechanical polishing of 12-inch wafer. In Proceedings of the ICPT 2012-International Conference on Planarization/CMP Technology, Grenoble, France, 15–17 October 2012; pp. 1–6. [Google Scholar]
- Li, J.; Liu, Y.; Dai, Y.; Yue, D.; Lu, X.; Luo, J. Achievement of a near-perfect smooth silicon surface. Sci. China Technol. Sci. 2013, 56, 2847–2853. [Google Scholar] [CrossRef]
- Mc Kay, J.M.N. Chemical Mechanical polishing and Direct Bonding of YAG and Y2O3; University of California: Los Angeles, CA, USA, 2016. [Google Scholar]
- Zhang, Z.; Jin, Z.; Guo, J.; Han, X.; Mu, Q.; Zhu, X. A novel chemical mechanical polishing slurry for yttrium aluminum garnet crystal. Appl. Surf. Sci. 2019, 496, 143601. [Google Scholar] [CrossRef]
- Liu, Z.; Gong, J.; Xiao, C.; Shi, P.; Kim, S.H.; Chen, L.; Qian, L. Temperature-dependent mechanochemical wear of silicon in water: The role of Si–OH surfacial groups. Langmuir 2019, 35, 7735–7743. [Google Scholar] [CrossRef] [PubMed]
- Kay, J.M.; Bai, T.; Goorsky, M.S. Chemical Mechanical Polishing and Direct Bonding of YAG. ECS Trans. 2018, 86, 217–222. [Google Scholar]
- Li, J.; Zhu, Y.; Chen, C.T. Chemical Mechanical Polishing of Transparent Nd:YAG Ceramics. Key Eng. Mater. 2008, 375–376, 278–282. [Google Scholar] [CrossRef]
- Katsuki, F.; Kamei, K.; Saguchi, A.; Takahashi, W.; Watanabe, J. AFM studies on the difference in wear behavior between Si and SiO2 in KOH solution. J. Electrochem. Soc. 2000, 147, 2328. [Google Scholar] [CrossRef]
- Guo, J.; Song, C.; Niu, L.; Shi, X.; Jin, Z.; Guo, C.; Namba, Y. Suppression of grain boundary steps in chemical mechanical polishing of W-Ni-Fe alloy by a citric acid-based slurry. Manuf. Lett. 2020, 25, 40–43. [Google Scholar] [CrossRef]
- Harsha, A.; Tewari, U. Two-body and three-body abrasive wear behaviour of polyaryletherketone composites. Polym. Test. 2003, 22, 403–418. [Google Scholar] [CrossRef]
- Gahr, K.-H.Z. Wear by hard particles. Tribol. Int. 1998, 31, 587–596. [Google Scholar] [CrossRef]
- Lin, Y.-Y.; Lo, S.-P. Finite element modeling for chemical mechanical polishing process under different back pressures. J. Mater. Process. Technol. 2003, 140, 646–652. [Google Scholar] [CrossRef]
- Chen, Y.; Liangchi, Z. Polishing of Diamond Materials: Mechanisms, Modeling and Implementation; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kubota, A.; Nagae, S.; Touge, M. Improvement of material removal rate of single-crystal diamond by polishing using H2O2 solution. Diam. Relat. Mater. 2016, 70, 39–45. [Google Scholar] [CrossRef]
- Kubota, A.; Fukuyama, S.; Ichimori, Y.; Touge, M. Surface smoothing of single-crystal diamond (100) substrate by polishing technique. Diam. Relat. Mater. 2012, 24, 59–62. [Google Scholar] [CrossRef]
- Kubota, A.; Nagae, S.; Motoyama, S.; Touge, M. Two-step polishing technique for single crystal diamond (100) substrate utilizing a chemical reaction with iron plate. Diam. Relat. Mater. 2015, 60, 75–80. [Google Scholar] [CrossRef]
- Thomas, E.L.; Mandal, S.; Brousseau, E.B.; Williams, O.A. Silica based polishing of {100} and {111} single crystal diamond. Sci. Technol. Adv. Mater. 2014, 15, 035013. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, T.; Kurokawa, S.; Umezaki, Y.; Ohnishi, O.; Akagami, Y.; Yamaguchi, Y.; Kishii, S. Study on the Development of Resource-Saving High Performance Slurry-Polishing/CMP for glass substrates in a radical polishing environment, using manganese oxide slurry as an alternative for ceria slurry. Adv. Sci. Technol. 2010, 64, 65–70. [Google Scholar]
- Aida, H.; Doi, T.; Takeda, H.; Katakura, H.; Kim, S.-W.; Koyama, K.; Yamazaki, T.; Uneda, M. Ultraprecision CMP for sapphire, GaN, and SiC for advanced optoelectronics materials. Curr. Appl. Phys. 2012, 12, S41–S46. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, G.; Shi, X.; Gong, H.; Luo, G.; Gu, Z. Chemical mechanical planarization (CMP) of on-axis Si-face SiC wafer using catalyst nanoparticles in slurry. Surf. Coat. Technol. 2014, 251, 48–55. [Google Scholar] [CrossRef]
- Shi, X.; Pan, G.; Zhou, Y.; Xu, L.; Zou, C.; Gong, H. A study of chemical products formed on sapphire (0001) during chemical–mechanical polishing. Surf. Coat. Technol. 2015, 270, 206–220. [Google Scholar] [CrossRef]
- Shi, X.; Chen, G.; Xu, L.; Kang, C.; Luo, G.; Luo, H.; Zhou, Y.; Dargusch, M.S.; Pan, G. Achieving ultralow surface roughness and high material removal rate in fused silica via a novel acid SiO2 slurry and its chemical-mechanical polishing mechanism. Appl. Surf. Sci. 2020, 500, 144041. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Chen, A.; Ma, X. Composite particles with dendritic mesoporous-silica cores and nano-sized CeO2 shells and their application to abrasives in chemical mechanical polishing. Mater. Chem. Phys. 2020, 240, 122279. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, L.; Yang, F.; Cao, H. Influence of slurry components on copper CMP performance in alkaline slurry. Microelectron. Eng. 2017, 183, 1–11. [Google Scholar] [CrossRef]
- Lei, H.; Jiang, L.; Chen, R. Preparation of copper-incorporated mesoporous alumina abrasive and its CMP behavior on hard disk substrate. Powder Technol. 2012, 219, 99–104. [Google Scholar] [CrossRef]
- Liao, C.; Guo, D.; Wen, S.; Luo, J. Effects of chemical additives of CMP slurry on surface mechanical characteristics and material removal of copper. Tribol. Lett. 2012, 45, 309–317. [Google Scholar] [CrossRef]
- Yamamura, K.; Takiguchi, T.; Ueda, M.; Hattori, A.N.; Zettsu, N. High-Integrity Finishing of 4H-SiC (0001) by Plasma-Assisted Polishing. Adv. Mater. Res. 2010, 126, 423–428. [Google Scholar] [CrossRef] [Green Version]
- Deng, H. Development of Plasma-Assisted Polishing for Highly Efficient and Damage-Free Finishing of Single-Crystal SiC, GaN and VD-SiC; Osaka University: Osaka, Japan, 2016. [Google Scholar]
- Sun, R.; Yang, X.; Watanabe, K.; Miyazaki, S.; Fukano, T.; Kitada, M.; Arima, K.; Kawai, K.; Yamamura, K. Etching Characteristics of Quartz Crystal Wafers Using Argon-Based Atmospheric Pressure CF4 Plasma Stabilized by Ethanol Addition. Nanomanufacturing Metrol. 2019, 2, 168–176. [Google Scholar] [CrossRef]
- Deng, H.; Yamamura, K. Atomic-scale flattening mechanism of 4H-SiC (0 0 0 1) in plasma assisted polishing. CIRP Ann. 2013, 62, 575–578. [Google Scholar] [CrossRef]
- Deng, H.; Takiguchi, T.; Ueda, M.; Hattori, A.N.; Zettsu, N.; Yamamura, K. Damage-Free Dry Polishing of 4H-SiC Combined with Atmospheric-Pressure Water Vapor Plasma Oxidation. Jpn. J. Appl. Phys. 2011, 50, 08JG05. [Google Scholar] [CrossRef]
- Deng, H.; Endo, K.; Yamamura, K. Plasma-assisted polishing of gallium nitride to obtain a pit-free and atomically flat surface. CIRP Ann. 2015, 64, 531–534. [Google Scholar] [CrossRef] [Green Version]
- Yamamura, K.; Emori, K.; Sun, R.; Ohkubo, Y.; Endo, K.; Yamada, H.; Chayahara, A.; Mokuno, Y. Damage-free highly efficient polishing of single-crystal diamond wafer by plasma-assisted polishing. CIRP Ann. 2018, 67, 353–356. [Google Scholar] [CrossRef]
- Deng, H.; Endo, K.; Yamamura, K. Competition between surface modification and abrasive polishing: A method of controlling the surface atomic structure of 4H-SiC (0001). Sci. Rep. 2015, 5, 8947. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Endo, K.; Yamamura, K. Damage-free finishing of CVD-SiC by a combination of dry plasma etching and plasma-assisted polishing. Int. J. Mach. Tools Manuf. 2017, 115, 38–46. [Google Scholar] [CrossRef]
- Deng, H.; Endo, K.; Yamamura, K. Atomic-scale and pit-free flattening of GaN by combination of plasma pretreatment and time-controlled chemical mechanical polishing. Appl. Phys. Lett. 2015, 107, 051602. [Google Scholar] [CrossRef]
- Lyu, P.; Lai, M.; Fang, F.Z. Nanometric polishing of lutetium oxide by plasma-assisted etching. Adv. Manuf. 2020, 8, 440–446. [Google Scholar] [CrossRef]
- Lyu, P.; Lai, M.; Liu, Z.; Fang, F.Z. Ultra-smooth finishing of single-crystal lutetium oxide by plasma-assisted etching. Precis. Eng. 2021, 67, 77–88. [Google Scholar] [CrossRef]
- Mori, Y.; Yamamura, K.; Sano, Y. Thinning of silicon-on-insulator wafers by numerically controlled plasma chemical vaporization machining. Rev. Sci. Instrum. 2004, 75, 942–946. [Google Scholar] [CrossRef]
- Sano, Y.; Yamamura, K.; Mimura, H.; Yamauchi, K.; Mori, Y. Fabrication of ultrathin and highly uniform silicon on insulator by numerically controlled plasma chemical vaporization machining. Rev. Sci. Instrum. 2007, 78, 086102. [Google Scholar] [CrossRef] [PubMed]
- Yamamura, K.; Takiguchi, T.; Ueda, M.; Deng, H.; Hattori, A.N.; Zettsu, N. Plasma assisted polishing of single crystal SiC for obtaining atomically flat strain-free surface. CIRP Ann. 2011, 60, 571–574. [Google Scholar] [CrossRef]
- Shen, X.; Tu, Q.; Deng, H.; Jiang, G.; He, X.; Liu, B.; Yamamura, K. Comparative analysis on surface property in anodic oxidation polishing of reaction-sintered silicon carbide and single-crystal 4H silicon carbide. Appl. Phys. A 2016, 122, 354. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Yang, X.; Arima, K.; Kawai, K.; Yamamura, K. High-quality plasma-assisted polishing of aluminum nitride ceramic. CIRP Ann. 2020, 69, 301–304. [Google Scholar] [CrossRef]
- Okamoto, T.; Sano, Y.; Hara, H.; Hatayama, T.; Arima, K.; Yagi, K.; Murata, J.; Sadakuni, S.; Tachibana, K.; Shirasawa, Y.; et al. Reduction of Surface Roughness of 4H-SiC by Catalyst-Referred Etching. Mater. Sci. Forum 2010, 648, 775–778. [Google Scholar] [CrossRef]
- Hara, H.; Sano, Y.; Mimura, H.; Arima, K.; Kubota, A.; Yagi, K.; Murata, J.; Yamauch, K. Novel abrasive-free planarization of 4H-SiC (0001) using catalyst. J. Electron. Mater. 2006, 35, L11–L14. [Google Scholar] [CrossRef]
- Bui, P.V.; Sano, Y.; Morikawa, Y.; Yamauchi, K. Characteristics and Mechanism of Catalyst-Referred Etching Method: Application to 4H-SiC. Int. J. Autom. Technol. 2018, 12, 154–159. [Google Scholar] [CrossRef]
- Okamoto, T.; Sano, Y.; Tachibana, K.; Pho, B.V.; Arima, K.; Inagaki, K.; Yagi, K.; Murata, J.; Sadakuni, S.; Asano, H.; et al. Improvement of Removal Rate in Abrasive-Free Planarization of 4H-SiC Substrates Using Catalytic Platinum and Hydrofluoric Acid. Jpn. J. Appl. Phys. 2012, 51, 046501. [Google Scholar] [CrossRef]
- Hara, H.; Sano, Y.; Mimura, H.; Arima, K.; Kubota, A.; Yagi, K.; Murata, J.; Yamauchi, K. Damage-Free Planarization of 4H-SiC (0001) by Catalyst-Referred Etching. Mater. Sci. Forum 2007, 556, 749–751. [Google Scholar] [CrossRef]
- Pho, B.V.; Sadakuni, S.; Okamoto, T.; Sagawa, R.; Arima, K.; Sano, Y.; Yamauchi, K. High-Resolution TEM Observation of 4H-SiC (0001) Surface Planarized by Catalyst-Referred Etching. Mater. Sci. Forum 2012, 717, 873–876. [Google Scholar] [CrossRef]
- Murata, J.; Kubota, A.; Yagi, K.; Sano, Y.; Hara, H.; Arima, K.; Okamoto, T.; Mimura, H.; Yamauchi, K. New Chemical Planarization of SiC and GaN Using an Fe Plate in H2O2 Solution. Mater. Sci. Forum 2008, 600, 815–818. [Google Scholar] [CrossRef]
- Arima, K.; Hara, H.; Murata, J.; Ishida, T.; Okamoto, R.; Yagi, K.; Sano, Y.; Mimura, H.; Yamauchi, K. Atomic-scale flattening of SiC surfaces by electroless chemical etching in HF solution with Pt catalyst. Appl. Phys. Lett. 2007, 90, 202106. [Google Scholar] [CrossRef]
- Okamoto, T.; Sano, Y.; Hara, H.; Arima, K.; Yagi, K.; Murata, J.; Mimura, H.; Yamauchi, K. Damage-Free Planarization of 2-Inch 4H-SiC Wafer Using Pt Catalyst Plate and HF Solution. Mater. Sci. Forum 2008, 600, 835–838. [Google Scholar] [CrossRef]
- Okamoto, T.; Sano, Y.; Tachibana, K.; Arima, K.; Hattori, A.N.; Yagi, K.; Murata, J.; Sadakuni, S.; Yamauchi, K. Dependence of process characteristics on atomic-step density in catalyst-referred etching of 4H-SiC(0001) surface. J. Nanosci. Nanotechnol. 2011, 11, 2928–2930. [Google Scholar] [CrossRef] [PubMed]
- Bui, P.V.; Inagaki, K.; Sano, Y.; Yamauchi, K.; Morikawa, Y. Adsorption of hydrogen fluoride on SiC surfaces: A density functional theory study. Curr. Appl. Phys. 2012, 12, S42–S46. [Google Scholar] [CrossRef]
- Isohashi, A.; Sano, Y.; Sadakuni, S.; Yamauchi, K. 4H-SiC Planarization Using Catalyst-Referred Etching with Pure Water. Mater. Sci. Forum 2014, 778, 722–725. [Google Scholar] [CrossRef]
- Isohashi, A.; Bui, P.; Toh, D.; Matsuyama, S.; Sano, Y.; Inagaki, K.; Morikawa, Y.; Yamauchi, K. Chemical etching of silicon carbide in pure water by using platinum catalyst. Appl. Phys. Lett. 2017, 110, 201601. [Google Scholar] [CrossRef] [Green Version]
- Isohashi, A.; Sano, Y.; Yamauchi, K. Planarization of 4H-SiC (0001) by catalyst-referred etching using pure water etchant. Proceedings of International Conference on Planarization/CMP Technology, Kobe, Japan, 19–21 November 2014; pp. 273–274. [Google Scholar]
- Huang, Z.; Geyer, N.; Werner, P.; De Boor, J.; Gösele, U. Metal-assisted chemical etching of silicon: A review: In memory of Prof. Ulrich Gösele. Adv. Mater. 2011, 23, 285–308. [Google Scholar] [CrossRef]
- Li, X.; Bohn, P. Metal-assisted chemical etching in HF/H 2 O 2 produces porous silicon. Appl. Phys. Lett. 2000, 77, 2572–2574. [Google Scholar] [CrossRef]
- Tsujino, K.; Matsumura, M. Helical nanoholes bored in silicon by wet chemical etching using platinum nanoparticles as catalyst. Electrochem. Solid-State Lett. 2005, 8, C193. [Google Scholar] [CrossRef]
- YLu, T.; Barron, A.R. Anti-reflection layers fabricated by a one-step copper-assisted chemical etching with inverted pyramidal structures intermediate between texturing and nanopore-type black silicon. J. Mater. Chem. A 2014, 2, 12043–12052. [Google Scholar]
- Yasukawa, Y.; Asoh, H.; Ono, S. Site-selective chemical etching of GaAs through a combination of self-organized spheres and silver particles as etching catalyst. Electrochem. Commun. 2008, 10, 757–760. [Google Scholar] [CrossRef]
- Hara, H.; Sano, Y.; Mimura, H.; Arima, K.; Kubota, A.; Yagi, K.; Murata, J.; Yamauchi, K. Novel abrasive-free planarization of Si and SiC using catalyst. In Towards Synthesis of Micro-/Nano-Systems; Springer: London, UK, 2007. [Google Scholar]
- Peng, K.; Lu, A.; Zhang, R.; Lee, S.T. Motility of metal nanoparticles in silicon and induced anisotropic silicon etching. Adv. Funct. Mater. 2008, 18, 3026–3035. [Google Scholar] [CrossRef]
- Bingham, R.G.; Walker, D.D.; Kim, D.-H.; Brooks, D.; Freeman, R.; Riley, D. Novel automated process for aspheric surfaces. Curr. Dev. Lens Des. Opt. Syst. Eng. 2000, 4093, 445–450. [Google Scholar]
- Cao, Z.; Cheung, C. Multi-scale modeling and simulation of material removal characteristics in computer-controlled bonnet polishing. Int. J. Mech. Sci. 2016, 106, 147–156. [Google Scholar] [CrossRef]
- Stahl, H.P.; Walker, D.D.; Beaucamp, A.T.H.; Doubrovski, V.; Dunn, C.; Freeman, R.; McCavana, G.; Morton, R.; Riley, D.; Simms, J.; et al. New results extending the Precessions process to smoothing ground aspheres and producing freeform parts. Opt. Manuf. Test. VI 2005, 5869, 79–87. [Google Scholar]
- Wang, C.; Yang, W.; Wang, Z.; Yang, X.; Hu, C.; Zhong, B.; Guo, Y.; Xu, Q. Dwell-time algorithm for polishing large optics. Appl. Opt. 2014, 53, 4752–4760. [Google Scholar] [CrossRef]
- Xia, Z.; Fang, F.Z.; Ahearne, E.; Tao, M. Advances in polishing of optical freeform surfaces: A review. J. Mater. Process. Technol. 2020, 286, 116828. [Google Scholar] [CrossRef]
- Pan, R.; Zhong, B.; Chen, D.; Wang, Z.; Fan, J.; Zhang, C.; Wei, S. Modification of tool influence function of bonnet polishing based on interfacial friction coefficient. Int. J. Mach. Tools Manuf. 2018, 124, 43–52. [Google Scholar] [CrossRef]
- Bo, Z.; Xianhua, C.; Ri, P.; Jian, W.; Hongzhong, H.; Wenhui, D.; Zhenzhong, W.; Ruiqing, X.; Defeng, L. The effect of tool wear on the removal characteristics in high-efficiency bonnet polishing. Int. J. Adv. Manuf. Technol. 2017, 91, 3653–3662. [Google Scholar] [CrossRef]
- Shi, C.; Peng, Y.; Hou, L.; Wang, Z.; Guo, Y. Micro-analysis model for material removal mechanisms of bonnet polishing. Appl. Opt. 2018, 57, 2861–2872. [Google Scholar] [CrossRef] [PubMed]
- Oh, S.; Seok, J. Modeling of chemical–mechanical polishing considering thermal coupling effects. Microelectron. Eng. 2008, 85, 2191–2201. [Google Scholar] [CrossRef]
- Walker, D.D.; Freeman, R.; McCavana, G.; Morton, R.; Riley, D.; Simms, J.; Brooks, D.; Kim, E.; King, A. Zeeko/UCL process for polishing large lenses and prisms. Large Lenses Prism. 2002, 4411, 106–111. [Google Scholar]
- Cheung, C.F.; Kong, L.B.; Ho, L.T.; To, S. Modelling and simulation of structure surface generation using computer controlled ultra-precision polishing. Precis. Eng. 2011, 35, 574–590. [Google Scholar] [CrossRef]
- Dunn, C.R.; Walker, D.D. Pseudo-random tool paths for CNC sub-aperture polishing and other applications. Opt. Express 2008, 16, 18942–18949. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.; Yu, G.; Li, H.; Messelink, W.; Evans, R.; Beaucamp, A. Edges in CNC polishing: From mirror-segments towards semiconductors, paper 1: Edges on processing the global surface. Opt. Express 2012, 20, 19787–19798. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Walker, D.; Yu, G.; Sayle, A.; Messelink, W.; Evans, R.; Beaucamp, A. Edge control in CNC polishing, paper 2: Simulation and validation of tool influence functions on edges. Opt. Express 2013, 21, 370–381. [Google Scholar] [CrossRef] [PubMed]
- Bentley, J.L.; Stoebenau, S.; Stephenson, D.; Kumler, J. Optical design constraints for the successful fabrication and testing of aspheres. Optifab 2015, 9633, 209–218. [Google Scholar]
- Atkins, C.; Ramsey, B.; Kilaru, K.; Gubarev, M.; ODell, S.; Elsner, R.; Swartz, D.; Gaskin, J.; Weisskopf, M. X-ray optic developments at NASA’s MSFC. In Damage to VUV, EUV, and X-ray Optics IV; and EUV and X-ray Optics: Synergy between Laboratory and Space III; SPIE: Bellingham, WA, USA, 2013; Volume 8777, pp. 185–193. [Google Scholar]
- Yu, G.; Walker, D.; Li, H. Implementing a grolishing process in Zeeko IRP machines. Appl. Opt. 2012, 51, 6637–6640. [Google Scholar] [CrossRef]
- Yu, G.; Walker, D.; Li, H. Research on fabrication of mirror segments for E-ELT. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Xiamen, China, 26–29 April 2012; Volume 8416, pp. 19–24. [Google Scholar]
- Han, Y.; Zhang, L.; Guo, M.; Fan, C.; Liang, F. Tool paths generation strategy for polishing of freeform surface with physically uniform coverage. Int. J. Adv. Manuf. Technol. 2017, 95, 2125–2144. [Google Scholar] [CrossRef]
- Kovacicinova, J.; Procháska, F.; Poláková, I.; Polák, J.; Matoušek, O.; Tomka, D. Zeeko precession for free-form polishing. In Proceedings of the Optics and Measurement International Conference 2016, Liberec, Czech Republic, 11–14 October 2016; Volume 10151, pp. 172–178. [Google Scholar]
- Walker, D.D.; Brooks, D.; King, A.; Freeman, R.; Morton, R.; McCavana, G.; Kim, S.-W. The ‘Precessions’ tooling for polishing and figuring flat, spherical and aspheric surfaces. Opt. Express 2003, 11, 958–964. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P. The Application of Zeeko Polishing Technology to Freeform Femoral Knee Replacement Component Manufacture. Doctoral Dissertation, University of Huddersfield, Queensgate, UK, 2011. [Google Scholar]
- Walker, D.D.; Beaucamp, A.T.H.; Brooks, D.; Doubrovski, V.; Cassie, M.; Dunn, C.; Freeman, R.; King, A.; Libert, M.; McCavana, G.; et al. New results from the Precessions polishing process scaled to larger sizes. Opt. Fabr. Metrol. Mater. Adv. Telesc. 2004, 5494, 71–80. [Google Scholar]
- Walker, D.D.; Beaucamp, A.; Bingham, R.G.; Brooks, D.; Freeman, R.; Kim, S.; King, A.; McCavana, G.; Morton, R.; Riley, D. Precessions process for efficient production of aspheric optics for large telescopes and their instrumentation. Spec. Opt. Dev. Astron. 2003, 4842, 73–84. [Google Scholar]
- Wan, Y.; Russell, A.; Luo, X.; Fan, B.; Ma, X.; Yang, Y. Study of ultra-precision polishing of electroless nickel molding dies. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes, Chengdu, China, 26–29 June 2019; Volume 10837, pp. 353–364. [Google Scholar]
- Arcangeli, L.; Bianucci, G.; Marioni, F.; Mazzoleni, R.; Rossi, M.; Terraneo, M.; Zocchi, F.E.; Meini, M.; Galeotti, F.; Gabrieli, R.; et al. Manufacturing and qualification of the QM mirror for the high-resolution spectrometer of the FLEX mission. In Proceedings of the International Conference on Space Optics—ICSO 2018, Crete, Greece, 9–12 October 2018; Volume 11180, pp. 3065–3071. [Google Scholar]
- Han, W.; Mathew, P.T.; Kolagatla, S.; Rodriguez, B.J.; Fang, F.Z. Toward Single-Atomic-Layer Lithography on Highly Oriented Pyrolytic Graphite Surfaces Using AFM-Based Electrochemical Etching. Nanomanufacturing Metrol. 2022, 5, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Pelaez, M.; Nolan, N.T.; Pillai, S.C.; Seery, M.K.; Falaras, P.; Kontos, A.G.; Dunlop, P.S.M.; Hamilton, J.W.J.; Byrne, J.A.K.; O’Shea; et al. A review on the visible light active titanium dioxide photocatalysts for environmental applications. Appl. Catal. B Environ. 2012, 125, 331–349. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; TSuwa, H.; Sugiyama, K. EEM (Elastic Emission Machining) (1st Report): Concept of EEM and its feasibility. J. Jpn. Soc. Precis. Eng. 1977, 43, 542–548. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Yamamura, K.; Endo, K.; Yamauchi, K.; Yasutake, K.; Goto, H.; Kakiuchi, H.; Sano, Y.; Mimura, H. Creation of perfect surfaces. J. Cryst. Growth 2005, 275, 39–50. [Google Scholar] [CrossRef]
- Mori, Y.; Yamauchi, K.; Endo, K. Elastic emission machining. Precis. Eng. 1987, 9, 123–128. [Google Scholar] [CrossRef]
- Kim, J.-D. Motion analysis of powder particles in EEM using cylindrical polyurethane wheel. Int. J. Mach. Tools Manuf. 2002, 42, 21–28. [Google Scholar] [CrossRef]
- Cao, Z.; Jiang, B.X.; Li, Y. Flow field analysis of the thin fluid film in disc hydrodynamic polishing. Procedia CIRP 2018, 77, 363–366. [Google Scholar] [CrossRef]
- Inagaki, K.; Yamauchi, K.; Mimura, H.; Sugiyama, K.; Hirose, K.; Mori, Y. First-principles evaluations of machinability dependency on powder material in elastic emission machining. Mater. Trans. 2001, 42, 2290–2294. [Google Scholar] [CrossRef] [Green Version]
- Yamauchi, K.; Hirose, K.; Goto, H.; Sugiyama, K.; Inagaki, K.; Yamamura, K.; Sano, Y.; Mori, Y. First-principles simulations of removal process in EEM (elastic emission machining). Comput. Mater. Sci. 1999, 14, 232–235. [Google Scholar] [CrossRef]
- Peng, W.; Guan, C.; Li, S. Ultrasmooth surface polishing based on the hydrodynamic effect. Appl. Opt. 2013, 52, 6411–6416. [Google Scholar] [CrossRef]
- Kanaoka, M.; Nomura, K.; Yamauchi, K.; Mori, Y. Efficiency-enhanced elastic emission machining on the basis of processing mechanism. In Proceedings of the 12th Euspen International Conference, Stockholm, Sweden, 4–8 June 2012; p. 193196. [Google Scholar]
- Peng, W.; Guan, C.; Li, S. Defect-free surface of quartz glass polished in elastic mode by chemical impact reaction. J. Cent. South Univ. 2014, 21, 4438–4444. [Google Scholar] [CrossRef]
- Kanaoka, M.; Takino, H.; Nomura, K.; Mori, Y.; Mimura, H.; Yamauchi, K. Removal properties of low-thermal-expansion materials with rotating-sphere elastic emission machining. Sci. Technol. Adv. Mater. 2016, 8, 170–172. [Google Scholar] [CrossRef]
- Hirata, T.; Takei, Y.; Mimura, H. Machining Property in Smoothing of Steeply Curved Surfaces by Elastic Emission Machining. Procedia CIRP 2014, 13, 198–202. [Google Scholar] [CrossRef] [Green Version]
- Kubota, A.; Mimura, H.; Inagaki, K.; Arima, K.; Mori, Y.; Yamauchi, K. Preparation of ultrasmooth and defect-free 4H-SiC (0001) surfaces by elastic emission machining. J. Electron. Mater. 2005, 34, 439–443. [Google Scholar] [CrossRef]
- Takei, Y.; Mimura, H. 100 μm-size stationary spot machining in elastic emission machining. Int. J. Nanomanufacturing 2014, 10, 244–253. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Zhang, J. Super-smooth surface fabrication technique and experimental research. Appl. Opt. 2012, 51, 6612–6617. [Google Scholar] [CrossRef]
- Kubota, A.; Mimura, H.; Inagaki, K.; Mori, Y.; Yamauchi, K. Effect of Particle Morphology on Removal Rate and Surface Topography in Elastic Emission Machining. J. Electrochem. Soc. 2006, 153, G874. [Google Scholar] [CrossRef]
- Mori, Y.; Yamauchi, K.; Yamamura, K.; Sano, Y. Development of plasma chemical vaporization machining. Rev. Sci. Instrum. 2000, 71, 4627–4632. [Google Scholar] [CrossRef]
- Yamamura, K.; Mimura, H.; Yamauchi, K.; Sano, Y.; Saito, A.; Kinoshita, T.; Endo, K.; Mori, Y.; Souvorov, A.; Yabashi, M. Aspheric surface fabrication in nanometer-level accuracy by numerically controlled plasma chemical vaporization machining (CVM) and elastic emission machining (EEM). X-Ray Mirrors Cryst. Multilayers II 2002, 4782, 265–270. [Google Scholar]
- Qingyu, L. Study on the Technology of Elastic Emission Machining with Dual-Rotor Based on Hydrodynamic Lubrication. Master’s Thesis, National University of Defense Technology, Changsha, China, 2015. [Google Scholar]
- Xie, M.; Pan, Y.; An, Z.; Huang, S.; Dong, M.; Xie, G. Review on Surface Polishing Methods of Optical Parts. Adv. Mater. Sci. Eng. 2022, 2022, 1–30. [Google Scholar] [CrossRef]
- Allen, L.N.; Romig, H.W. Demonstration of an ion-figuring process. Adv. Opt. Manuf. Test. 1990, 1333, 22–33. [Google Scholar]
- Kaufman, H.R.; Reader, P.D.; Isaacson, G.C. Ion Sources for Ion Machining Applications. AIAA J. 1977, 15, 843–847. [Google Scholar] [CrossRef]
- Wilson, S.; McNeil, J. Neutral ion beam figuring of large optical surfaces. Curr. Dev. Opt. Eng. II 1987, 818, 320–324. [Google Scholar]
- Haensel, T.; Nickel, A.; Schindler, A. Ion beam figuring of strongly curved surfaces with a (x, y, z) linear three-axes system. In Plasmonics and Metamaterials; Optica Publishing Group: Washington, DC, USA, 2008; p. JWD6. [Google Scholar]
- MZeuNer; Kiontke, S. Ion Beam Figuring Technology in Optics Manufacturing An established alternative for commercial applications. Opt. Photonik 2012, 7, 56–58. [Google Scholar] [CrossRef]
- Mantenieks, O.; Duchemin, J.; Brophy, C.; Garner, P.; Ray, V.; Shutthanandan, M. A Review of Low Energy Sputtering Theory and Experiments. In Proceedings of the 25th International Electric Propulsion Conference, Cleveland, OH, USA, 24–28 August 1997; pp. 1–9. [Google Scholar]
- Meinel, A.; Bashkin, S.; Loomis, D. Controlled Figuring of Optical Surfaces by Energetic Ionic Beams. Appl. Opt. 1965, 4, 1674. [Google Scholar] [CrossRef]
- Sigmund, P. Theory of sputtering. I. Sputtering yield of amorphous and polycrystalline targets. Phys. Rev. 1969, 184, 383. [Google Scholar] [CrossRef]
- Allen, L.N.; Keim, R.E. An ion figuring system for large optic fabrication. Adv. Opt. Manuf. Test. 1989, 1168, 33–50. [Google Scholar]
- Demmler, M.; Zeuner, M.; Allenstein, F.; Dunger, T.; Nestler, M.; Kiontke, S. Ion beam figuring (IBF) for high precision optics. Adv. Fabr. Technol. Micro/Nano Opt. Photonics III 2010, 7591, 203–211. [Google Scholar]
- Schindler, A.; Hänsel, T.; Frost, F.; Fechner, R.; Seidenkranz, G.; Nickel, A.; Thomas, H.-J.; Neumann, H.; Hirsch, D.; Schwabe, R. Ion beam finishing technology for high precision optics production. In Optical Fabrication and Testing; Optica Publishing Group: Washington, DC, USA, 2002; p. OTuB5. [Google Scholar]
- TKamimura; Nakai, K.; Mori, Y.; Sasaki, T.; Yoshida, H.; Nakatuka, M.; Tanaka, M.; Toda, S.; Tanaka, M.; Yoshida, K. Improvement of laser-induced surface damage in UV optics by ion beam etching (CsLiB6O10 and fused silica). Laser-Induc. Damage Opt. Mater. 1999, 3578, 695–701. [Google Scholar]
- Mahmud, S.F.; Fukabori, T.; Pahlovy, S.A.; Miyamoto, I. Low energy ion beam smoothening of artificially synthesized single crystal diamond chips with initial surface roughness of 0.08–0.4nm rms. Diam. Relat. Mater. 2012, 24, 116–120. [Google Scholar] [CrossRef]
- Allen, L.N.; Hannon, J.J.; Wambach, R., Jr. Final surface error correction of an off—Axis aspheric petal by ion figuring. Curr. Dev. Opt. Eng. Commer. Opt. 1992, 1543, 190–200. [Google Scholar]
- Drueding, T.W.; Fawcett, S.C.; Wilson, S.R.; Bifano, T.G. Ion beam figuring of small optical components. Opt. Eng. 1995, 34, 3565–3571. [Google Scholar]
- Xie, X.; Hao, Y.; Zhou, L.; Dai, Y.; Li, S. High thermal expansion optical component machined by ion beam figuring. Opt. Eng. 2012, 51, 013401. [Google Scholar] [CrossRef]
- Yin, X.; Deng, W.; Tang, W.; Zhang, B.; Xue, D.; Zhang, F.; Zhang, X. Ion beam figuring approach for thermally sensitive space optics. Appl. Opt. 2016, 55, 8049–8055. [Google Scholar] [CrossRef]
- Schindler, A.; Haensel, T.; Flamm, D.; Frank, W.; Boehm, G.; Frost, F.; Fechner, R.; Bigl, F.; Rauschenbach, B. Ion beam and plasma jet etching for optical component fabrication. Lithogr. Micromach. Tech. Opt. Compon. Fabr. 2001, 4440, 217–227. [Google Scholar]
- Li, X.; Goodhue, W.; Santeufeimio, C.; Tetreault, T.; MacCrimmon, R.; Allen, L.; Bliss, D.; Krishnaswami, K.; Sung, C. Gas cluster ion beam processing of gallium antimonide wafers for surface and sub-surface damage reduction. Appl. Surf. Sci. 2003, 218, 251–258. [Google Scholar] [CrossRef]
- Arnold, T.; Böhm, G.; Fechner, R.; Meister, J.; Nickel, A.; Frost, F.; Hänsel, T.; Schindler, A. Ultra-precision surface finishing by ion beam and plasma jet techniques—Status and outlook. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2010, 616, 147–156. [Google Scholar] [CrossRef]
- Chkhalo, N.I.; Churin, S.A.; Pestov, A.E.; Salashchenko, N.N.; Vainer, Y.A.; Zorina, M.V. Roughness measurement and ion-beam polishing of super-smooth optical surfaces of fused quartz and optical ceramics. Opt. Express 2014, 22, 20094–20106. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, L.; Fang, Y.; Dun, A.; Zhao, J.; Xu, X.; Zhu, X. Application of Flow Field Analysis in Ion Beam Figuring for Ultra-Smooth Machining of Monocrystalline Silicon Mirror. Micromachines 2022, 13, 318. [Google Scholar] [CrossRef]
- Golini, D. 60. A Brief History of QED Technologies. Photonics Spectra 1993, 60, 313–318. [Google Scholar]
- Kordonski, W.; Golini, D. Multiple Application of Magnetorheological Effect in High Precision Finishing. J. Intell. Mater. Syst. Struct. 2016, 13, 401–404. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, X.; Tao, R.; Rong, Y. Structure-enhanced yield stress of magnetorheological fluids. J. Appl. Phys. 2000, 87, 2634–2638. [Google Scholar] [CrossRef] [Green Version]
- Bossis, G.; Lemaire, E.; Volkova, O.; Clercx, H. Yield stress in magnetorheological and electrorheological fluids: A comparison between microscopic and macroscopic structural models. J. Rheol. 1997, 41, 687–704. [Google Scholar] [CrossRef] [Green Version]
- Tustison, R.W.; Harris, D.C. History of magnetorheological finishing. Window Dome Technol. Mater. XII 2011, 8016, 206–227. [Google Scholar]
- Kordonski, W.I.; Jacobs, S.D. Magnetorheological Finishing. Int. J. Mod. Phys. B 1996, 10, 2837–2848. [Google Scholar] [CrossRef]
- Tingzhang, W.; Mingjun, C.; Henan, L.; Jiang, X. Development of a Magnetorheological Finishing Machine for Small-Bore Part of Irregular Shape and Experimental Study. Am. J. Eng. Appl. Sci. 2015, 8, 399–404. [Google Scholar] [CrossRef] [Green Version]
- Hull, T.; Hartmann, P.; Clarkson, A.R.; Barentine, J.M.; Jedamzik, R.; Westerhoff, T. Lightweight high-performance 1-4 m class spaceborne mirrors: Emerging technology for demanding spaceborne requirements. Mod. Technol. Space-Ground-Based Telesc. Instrum. 2010, 7739, 104–117. [Google Scholar]
- Guo, J.; Suzuki, H.; Higuchi, T. Finishing of Micro Aspheric Molds by Vibration Assisted Polishing Using Magnetostrictive Material. In Proceedings of the 11th euspen International Conference, Como, Italy, 23–26 May 2011; Volume 1, pp. 275–278. [Google Scholar]
- Guo, J.; Suzuki, H.; Morita, S.; Yamagata, Y.; Higuchi, T. Micro-Aspheric Mold Polishing Utilizing Magnetostrictive Vibration-Assisted Polishing Machine. Key Eng. Mater. 2012, 523, 768–773. [Google Scholar] [CrossRef]
- Guo, J. Corrective finishing of a micro-aspheric mold made of tungsten carbide to 50 nm accuracy. Appl. Opt. 2015, 54, 5764–5770. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Morita, S.-y.; Hara, M.; Yamagata, Y.; Higuchi, T. Ultra-precision finishing of micro-aspheric mold using a magnetostrictive vibrating polisher. CIRP Ann. 2012, 61, 371–374. [Google Scholar] [CrossRef]
- Kordonski, W.I.; Jacobs, S.D.; Golini, D.; Fess, E.; Strafford, R.D.J.; Bechtold, M. Vertical Wheel Magnetorheological Finishing Machine for Flats, Convex, and Concave Surfaces. In Optical Fabrication and Testing; Optica Publishing Group: Washington, DC, USA, 1996; p. OFC-1. [Google Scholar]
- Piché, F.; Clarkson, A.R. One Year of Finishing Meter-Class Optics with MRF® at L-3 IOS Brashear Optics. In Optical Fabrication and Testing; Optica Publishing Group: Washington, DC, USA, 2010; p. OThB6. [Google Scholar]
- Zhang, Y.; Fang, F.Z.; Huang, W.; Wang, C.; Fan, W. Polishing technique for potassium dihydrogen phosphate crystal based on magnetorheological finishing. Procedia CIRP 2018, 71, 21–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, F.Z.; Wang, L.; Li, X.; Liu, J.; Ye, Z.; Tian, D.; Huang, W.; Yu, M.; Ye, M.; et al. Effects of functional alkali in magnetorheological finishing fluid. Smart Mater. Struct. 2020, 30, 024001. [Google Scholar] [CrossRef]
- Lee, J.W.; Hong, K.P.; Cho, M.W.; Kwon, S.H.; Choi, H.J. Polishing characteristics of optical glass using PMMA-coated carbonyl-iron-based magnetorheological fluid. Smart Mater. Struct. 2015, 24, 065002. [Google Scholar] [CrossRef]
- Morillas, J.R.; de Vicente, J. Magnetorheology: A review. Soft Matter. 2020, 16, 9614–9642. [Google Scholar] [CrossRef]
- Davis, L. Model of magnetorheological elastomers. J. Appl. Phys. 1999, 85, 3348–3351. [Google Scholar] [CrossRef]
- Jolly, M.R.; Carlson, J.D.; Munoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 607. [Google Scholar] [CrossRef]
- MRF™ POLISHING MR FLUIDS. 2022. Available online: https://qedmrf.com/mrf-polishing/mrf-fluids/ (accessed on 15 December 2022).
- Faure, T.B.; Dumas, P.; Jenkins, R.; McFee, C.; Kadaksham, A.J.; Balachandran, D.K.; Teki, R.; Ackmann, P.W. Ultra-low roughness magneto-rheological finishing for EUV mask substrates. Photomask Technol. 2013, 8880, 13–20. [Google Scholar]
- Maloney, C.; Lormeau, J.P.; Dumas, P. Improving low, mid and high-spatial frequency errors on advanced aspherical and freeform optics with MRF. Third Eur. Semin. Precis. Opt. Manuf. 2016, 10009, 147–154. [Google Scholar]
- Olabi, A.G.; Grunwald, A. Design and application of magneto-rheological fluid. Mater. Des. 2007, 28, 2658–2664. [Google Scholar] [CrossRef] [Green Version]
- Carlson, J.D.; Jolly, M.R. MR fluid, foam and elastomer devices. mechatronics 2000, 10, 555–569. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A.; Bharti, R.K.; Yadav, H.N.S.; Das, M. A review on rheological properties of magnetorheological fluid for engineering components polishing. Mater. Today: Proc. 2022, 56, A6–A12. [Google Scholar] [CrossRef]
- Kordonski, W.I.; Golini, D. Fundamentals of Magnetorheological Fluid Utilization in High Precision Finishing. J. Intell. Mater. Syst. Struct. 2016, 10, 683–689. [Google Scholar] [CrossRef]
- Geyl, R.; Di Luzio, S.; Rimmer, D.; Gagnaire, H.; Revel, P.; Wang, L.; Feraud, B.; Tirvaudey, C. Industrial process of aspherical lens surfaces manufacturing. Opt. Fabr. 2004, 5252, 496–507. [Google Scholar]
- Kumar, M.; Kumar, A.; Alok, A.; Das, M. Magnetorheological method applied to optics polishing: A review. IOP Conf. Ser. Mater. Sci. Eng. 2020, 804, 012012. [Google Scholar] [CrossRef]
- Bentley, J.L.; Beier, M.; Scheiding, S.; Gebhardt, A.; Loose, R.; Risse, S.; Eberhardt, R.; Tünnermann, A.; Pfaff, M. Fabrication of high precision metallic freeform mirrors with magnetorheological finishing (MRF). Optifab 2013, 8884, 139–152. [Google Scholar]
- Navarro, R.; Burge, J.H.; Hu, H.; Song, C.; Xie, X. Combined fabrication technique for high-precision aspheric optical windows. Adv. Opt. Mech. Technol. Telesc. Instrum. II 2016, 9912, 99123W. [Google Scholar]
- Singh, A.K.; Jha, S.; Pandey, P.M. Magnetorheological Ball End Finishing Process. Mater. Manuf. Process. 2012, 27, 389–394. [Google Scholar] [CrossRef]
- Shi, F.; Shu, Y.; Dai, Y.; Peng, X.; Li, S. Magnetorheological elastic super-smooth finishing for high-efficiency manufacturing of ultraviolet laser resistant optics. Opt. Eng. 2013, 52, 075104. [Google Scholar] [CrossRef]
- Khounsary, A.M.; Shorey, A.B.; Dinger, U.; Kordonski, W.; Tricard, M.; Ota, K. Magnetorheological finishing of large and lightweight optics. Adv. Mirror Technol. X-Ray EUV Lithogr. Laser Other Appl. II 2004, 5533, 99–107. [Google Scholar]
- Tricard, M.; Kordonski, W.I.; Shorey, A.B.; Evans, C. Magnetorheological Jet Finishing of Conformal, Freeform and Steep Concave Optics. CIRP Ann. 2006, 55, 309–312. [Google Scholar] [CrossRef]
- Khounsary, A.M.; Goto, S.; Morawe, C.; Zhong, X.; Hou, X.; Yang, J. Super-smooth processing x-ray telescope application research based on the magnetorheological finishing (MRF) technology. Adv. X-Ray/EUV Opt. Compon. XI 2016, 9963, 80–85. [Google Scholar]
- Sugawara, J.; Kamiya, T.; Mikashima, B. Polishing Aspheric Mirrors of Zero-Thermal Expansion Cordierite Ceramics (NEXCERA) for Space Telescope. Mater. Technol. Appl. Opt. Struct. Compon. Sub-Syst. III 2017, 10372, 125–133. [Google Scholar]
- Nejatpour, M.; Unal, U.; Acar, H.Y. Bidisperse magneto-rheological fluids consisting of functional SPIONs added to commercial MRF. J. Ind. Eng. Chem. 2020, 91, 110–120. [Google Scholar] [CrossRef]
- Fähnle, O.W.; Van Brug, H.; Frankena, H.J. Fluid jet polishing of optical surfaces. Appl. Opt. 1998, 37, 6771–6773. [Google Scholar] [CrossRef] [Green Version]
- Stahl, H.P.; Messelink, W.A.C.M.; Waeger, R.; Wons, T.; Meeder, M.; Heiniger, K.C.; Faehnle, O.W. Prepolishing and finishing of optical surfaces using fluid jet polishing. Opt. Manuf. Test. VI 2005, 5869, 38–43. [Google Scholar]
- Cao, Z.C.; Cheung, C.F. An Experimental Investigation of Effect of Process Parameters on Materials Removal Characteristics in Fluid Jet Polishing. Key Eng. Mater. 2016, 679, 91–96. [Google Scholar] [CrossRef]
- Booij, S.M. Nanometer deep shaping with fluid jet polishing. Opt. Eng. 2002, 41, 1926. [Google Scholar] [CrossRef]
- Zhang, F.; Song, X.; Zhang, Y.; Luan, D. Figuring of an ultra-smooth surface in nanoparticle colloid jet machining. J. Micromechanics Microengineering 2009, 19, 054009. [Google Scholar] [CrossRef]
- Bitter, J. A study of erosion phenomena part I. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Bitter, J. A study of erosion phenomena: Part II. Wear 1963, 6, 169–190. [Google Scholar] [CrossRef]
- Finnie, I.; McFadden, D. On the velocity dependence of the erosion of ductile metals by solid particles at low angles of incidence. Wear 1978, 48, 181–190. [Google Scholar] [CrossRef] [Green Version]
- Hutchings, I. A model for the erosion of metals by spherical particles at normal incidence. Wear 1981, 70, 269–281. [Google Scholar] [CrossRef] [Green Version]
- DuPlessis, M.; Hashish, M. High energy water jet cutting equations for wood. J. Manuf. Sci. Eng. 1978, 100, 452–458. [Google Scholar] [CrossRef]
- Kordonski, W.; Shorey, A.B.; Sekeres, A. New magnetically assisted finishing method: Material removal with magnetorheological fluid jet. Opt. Manuf. Test. V 2003, 5180, 107–114. [Google Scholar]
- Ma, Z.; Peng, L.; Wang, J. Ultra-smooth polishing of high-precision optical surface. Optik 2013, 124, 6586–6589. [Google Scholar] [CrossRef]
- Peng, W.; Li, S.; Guan, C.; Shen, X.; Dai, Y.; Wang, Z. Improvement of magnetorheological finishing surface quality by nanoparticle jet polishing. Opt. Eng. 2013, 52, 043401. [Google Scholar] [CrossRef]
- Horiuchi, O.; Ikeno, J.; Shibutani, H.; Suzuki, H.; Mizukami, Y. Nano-abrasion machining of brittle materials and its application to corrective figuring. Precis. Eng. 2007, 31, 47–54. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, H.-B.; Dong, Z.-C.; Tam, H.-Y. Removal character of vertical jet polishing with eccentric rotation motion using magnetorheological fluid. J. Mater. Process. Technol. 2013, 213, 1532–1537. [Google Scholar] [CrossRef]
- Fang, H.; Guo, P.; Yu, J. Optimization of the material removal in fluid jet polishing. Opt. Eng. 2006, 45, 053401. [Google Scholar] [CrossRef]
- Burge, J.H.; Yu, Z.-R.; Fähnle, O.W.; Kuo, C.-H.; Chen, C.-C.; Williamson, R.; Hsu, W.-Y.; Tsai, D.P. Study of air-driving fluid jet polishing. Opt. Manuf. Test. IX 2011, 8126, 298–303. [Google Scholar]
- Shi, C.; Yuan, J.; Wu, F.; Wan, Y. Ultra-precision figuring using submerged jet polishing. Chin. Opt. Lett. 2011, 9, 092201–92203. [Google Scholar]
- Beaucamp, A.; Namba, Y.; Freeman, R. Dynamic multiphase modeling and optimization of fluid jet polishing process. CIRP Ann. 2012, 61, 315–318. [Google Scholar] [CrossRef]
- Peng, W.; Guan, C.; Li, S. Material removal mode affected by the particle size in fluid jet polishing. Appl. Opt. 2013, 52, 7927–7933. [Google Scholar] [CrossRef]
- Beaucamp, A.; Namba, Y. Super-smooth finishing of diamond turned hard X-ray molding dies by combined fluid jet and bonnet polishing. CIRP Ann. 2013, 62, 315–318. [Google Scholar] [CrossRef]
- Fang, F.Z.; Zhang, X.; Weckenmann, A.; Zhang, G.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Fang, F.Z. The three paradigms of manufacturing advancement. J. Manuf. Syst. 2022, 63, 504–505. [Google Scholar] [CrossRef]
- Beaucamp, A.T.; Namba, Y.; Charlton, P.; Jain, S.; Graziano, A.A. Finishing of additively manufactured titanium alloy by shape adaptive grinding (SAG). Surf. Topogr. Metrol. Prop. 2015, 3, 024001. [Google Scholar] [CrossRef]
- Beaucamp, A.; Namba, Y.; Combrinck, H.; Charlton, P.; Freeman, R. Shape adaptive grinding of CVD silicon carbide. CIRP Ann. 2014, 63, 317–320. [Google Scholar] [CrossRef]
- Carlson, J.D. What Makes a Good MR Fluid? Journal of intelligent material systems and structures. 2002, 13, 431–435. [Google Scholar] [CrossRef]
- Li, S.; Dai, Y. Large and Middle-Scale Aperture Aspheric Surfaces: Lapping, Polishing and Measurement; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Zhang, Y.; Fang, F.Z.; Huang, W.; Fan, W. Dwell Time Algorithm Based on Bounded Constrained Least Squares Under Dynamic Performance Constraints of Machine Tool in Deterministic Optical Finishing. Int. J. Precis. Eng. Manuf. -Green Technol. 2021, 8, 1415–1427. [Google Scholar] [CrossRef]
- Jones, R.A. Optimization of computer controlled polishing. Appl. Opt. 1977, 16, 218–224. [Google Scholar] [CrossRef]
- Shanbhag, P.M.; Feinberg, M.R.; Sandri, G.; Horenstein, M.N.; Bifano, T.G. Ion-beam machining of millimeter scale optics. Appl. Opt. 2000, 39, 599–611. [Google Scholar] [CrossRef] [PubMed]
- Wilson, S.; Reicher, D.; McNeil, J. Surface figuring using neutral ion beams. Adv. Fabr. Metrol. Opt. Large Opt. 1989, 966, 74–81. [Google Scholar]
- Allen, L.N.; Keim, R.E.; Lewis, T.S.; Ullom, J.R. Surface error correction of a Keck 10-m telescope primary mirror segment by ion figuring. Adv. Opt. Manuf. Test. II 1992, 1531, 195–204. [Google Scholar]
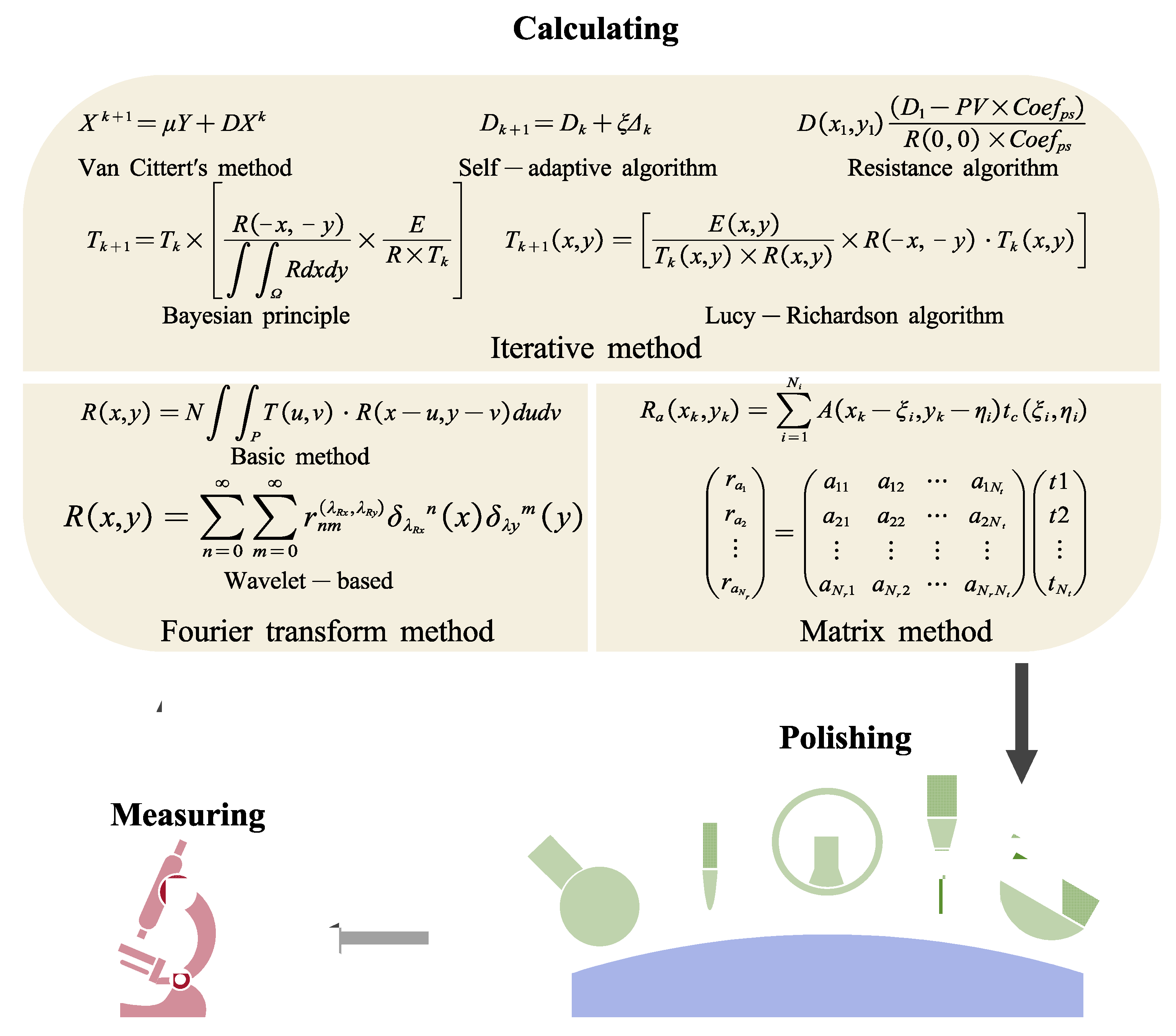
- Jiao, C. Bayesian Principle Based Dwell Time Algorithm for Ion Beam Figuring of Low Gradient Mirrors. J. Mech. Eng. 2009, 45, 253. [Google Scholar] [CrossRef]
- Xu, C.; Aissaoui, I.; Jacquey, S. Algebraic analysis of the Van Cittert iterative method of deconvolution with a general relaxation factor. J. Opt. Soc. Am. A 1994, 11, 2804–2808. [Google Scholar] [CrossRef]
- Chen, J.; Jia, G.; Li, B.; Zhang, J.; Luo, X. Deterministic removal of atmospheric pressure plasma polishing based on the lucy–richardson algorithm. Mach. Sci. Technol. 2018, 22, 953–967. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, L.; Shi, Y.; Wang, X.; Zhang, X. Dwell-time algorithm based on matrix algebra and regularization method. Opt. Precis. Eng. 2007, 15, 1009–1015. [Google Scholar]
- Mouroulis, P.Z.; Zheng, L.; Smith, W.J.; Zhang, X.; Johnson, R.B. A novel resistance iterative algorithm for CCOS. Curr. Dev. Lens Des. Opt. Eng. VII 2006, 6288, 212–220. [Google Scholar]
- Carnal, C.L.; Egert, C.M.; Hylton, K.W. Advanced matrix-based algorithm for ion-beam milling of optical components. Curr. Dev. Opt. Des. Opt. Eng. II 1992, 1752, 54–62. [Google Scholar]
- Wu, J.F.; Lu, Z.W.; Zhang, H.X.; Wang, T.S. Dwell time algorithm in ion beam figuring. Appl. Opt. 2009, 48, 3930–3937. [Google Scholar] [CrossRef]
- Yang, M. Dwell time algorithm for computer-controlled polishing of small axis-symmetrical aspherical lens mold. Opt. Eng. 2001, 40, 1936. [Google Scholar] [CrossRef]
- Li, L.; Deng, W.; Zhang, B.; Bai, Y.; Zheng, L.; Zhang, X. Dwell time algorithm for large aperture optical element in magnetorheological finishing. Acta Opt. Sin. 2014, 34, 0522001. [Google Scholar]
- Bouvier, C. Investigation of Polishing Algorithms and Removal Processes for Deterministic Subaperture Polisher; University of Rochester: Rochester, UK, 2008. [Google Scholar]
- Dong, Z.; Cheng, H.; Tam, H.Y. Robust linear equation dwell time model compatible with large scale discrete surface error matrix. Appl. Opt. 2015, 54, 2747–2756. [Google Scholar] [CrossRef]
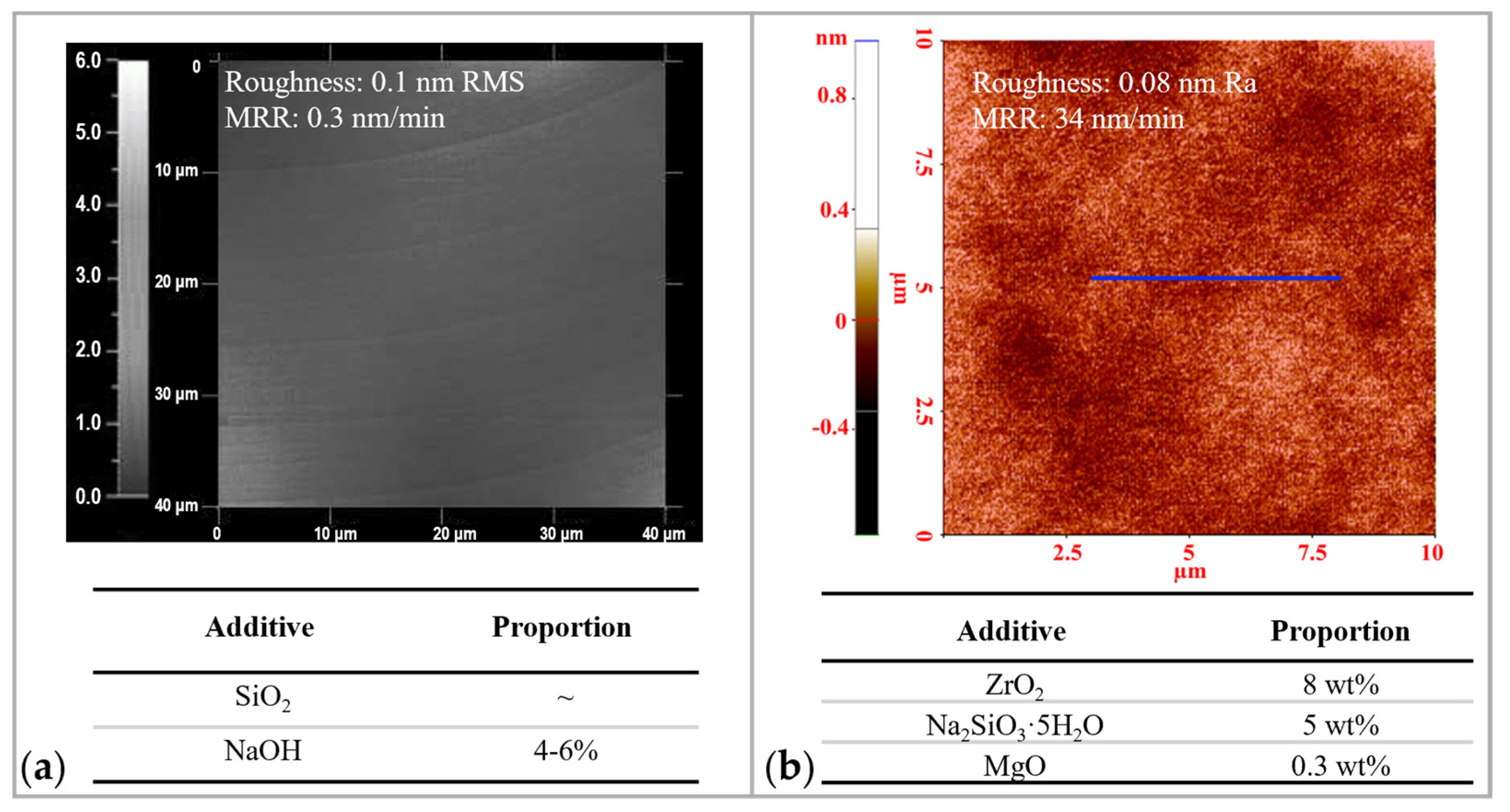



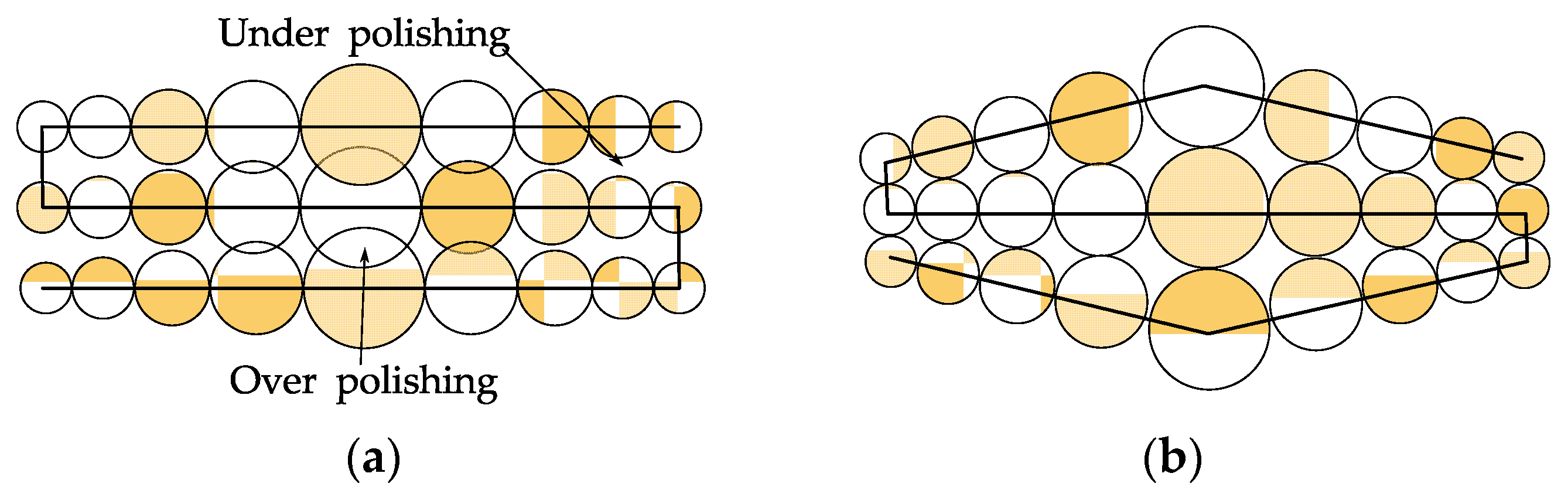







| Material | Roughness (nm) | Year |
|---|---|---|
| Glass | Ra 0.8 | 2010 [85] |
| GaN | Ra 0.18 | 2012 [86] |
| SCD | Ra 0.09 | 2014 [84] |
| SiC | Ra 0.05 | 2014 [87] |
| Sapphire | Ra 0.065 | 2015 [88] |
| SiO2 | Ra 0.193 | 2019 [89] |
| YAG | Sa 0.45 | 2019 [61] |
| Oxide silicon | RMS 0.15 | 2020 [90] |
| Material | SiC [94] | GaN [99] | SCD [100] |
|---|---|---|---|
| Modified material | SiO2 | GaF3 | ~ |
| Process gas | He, 1.7% H2O | He, CF4 | Ar, 0.67% H2O |
| Radicals | OH molecules | F molecule | OH molecules |
| Flow rate (L/min) | 1.5 | ~ | 0.1 |
| RF power (W) | 6 | 18 | ~ |
| Abrasive | CeO2 (Φ 0.5 μm) | CeO2 (Φ 1.2 μm) | ~ |
| Material | Roughness (nm) | Year |
|---|---|---|
| RS-SiC | Ra 0.48 | 2013 [109] |
| 4H-SiC | RMS 0.1 | 2013 [97] |
| GaN | Sq 0.1 | 2015 [99] |
| CVD-SiC | RMS 0.69 | 2017 [102] |
| SCD | Sq 0.13 | 2018 [100] |
| Material | Roughness (nm) | Year |
|---|---|---|
| On-axis 4H-SiC (0001) | RMS 0.093 | 2007 [115] |
| GaN | RMS 0.198 | 2008 [117] |
| 8° off-axis 4H-SiC (0001) | RMS 0.044 | 2008 [119] |
| 4° off-axis 4H-SiC (0001) | RMS 0.051 | 2017 [123] |
| Material | Roughness (nm) | Year |
|---|---|---|
| BK7 | Ra 0.5 | 2002 [141] |
| Nickel-coated aluminum | Ra 1 | 2003 [155] |
| Stavax stainless steel | Ra 1 | 2003 [155] |
| Electroless nickel | Ra 0.316 | 2019 [156] |
| Aluminum alloy | RMS 0.58 | 2019 [157] |
| Material | Roughness (nm) | Year |
|---|---|---|
| SiC | RMS 0.089 | 2005 [172] |
| Zerodur | RMS 0.116 | 2007 [170] |
| Si | RMS 0.050 | 2012 [168] |
| Quartz glass | RMS 0.080 | 2015 [178] |
| Monocrystalline Si | RMS 0.151 | 2022 [179] |
| Material | Roughness (nm) | Year |
|---|---|---|
| Fused silica | RMS 0.08 | 2001 [197] |
| GaSb | RMS 0.18 | 2003 [198] |
| SiC | Rq 0.54 | 2010 [199] |
| SCD | RMS 0.1 | 2012 [192] |
| ULE | RMS 0.18 | 2014 [200] |
| Si | RMS 0.5 | 2022 [201] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Z.; Huang, N.; Castelli, M.; Fang, F. Polishing Approaches at Atomic and Close-to-Atomic Scale. Micromachines 2023, 14, 343. https://doi.org/10.3390/mi14020343
Geng Z, Huang N, Castelli M, Fang F. Polishing Approaches at Atomic and Close-to-Atomic Scale. Micromachines. 2023; 14(2):343. https://doi.org/10.3390/mi14020343
Chicago/Turabian StyleGeng, Zhichao, Ning Huang, Marco Castelli, and Fengzhou Fang. 2023. "Polishing Approaches at Atomic and Close-to-Atomic Scale" Micromachines 14, no. 2: 343. https://doi.org/10.3390/mi14020343







