Aggregation of ODC(I) and POL Defects in Bismuth Doped Silica Fiber
Abstract
:1. Introduction
2. Model and Calculation Method
3. Calculation Results and Discussion
3.1. Calculation of Doping Position
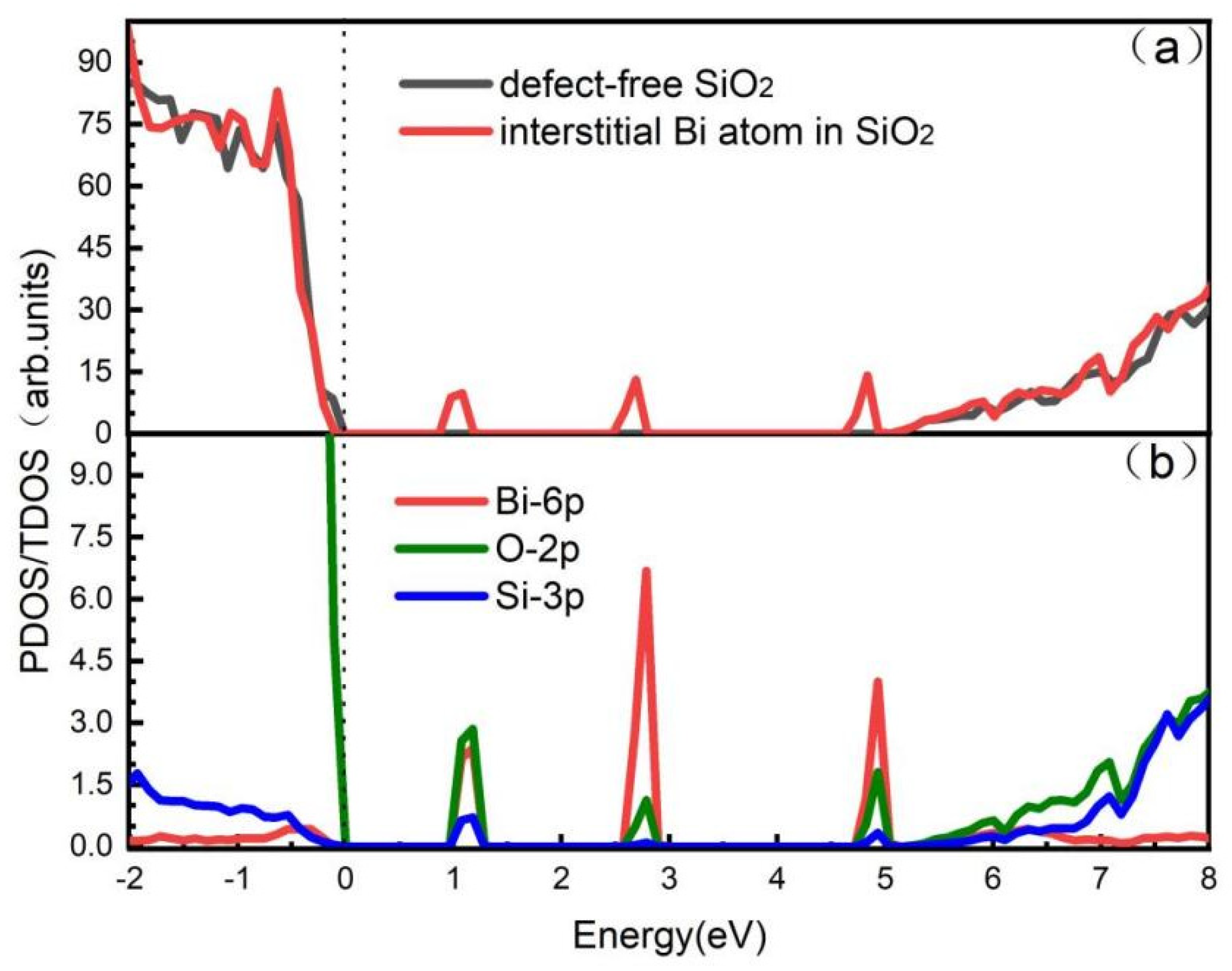
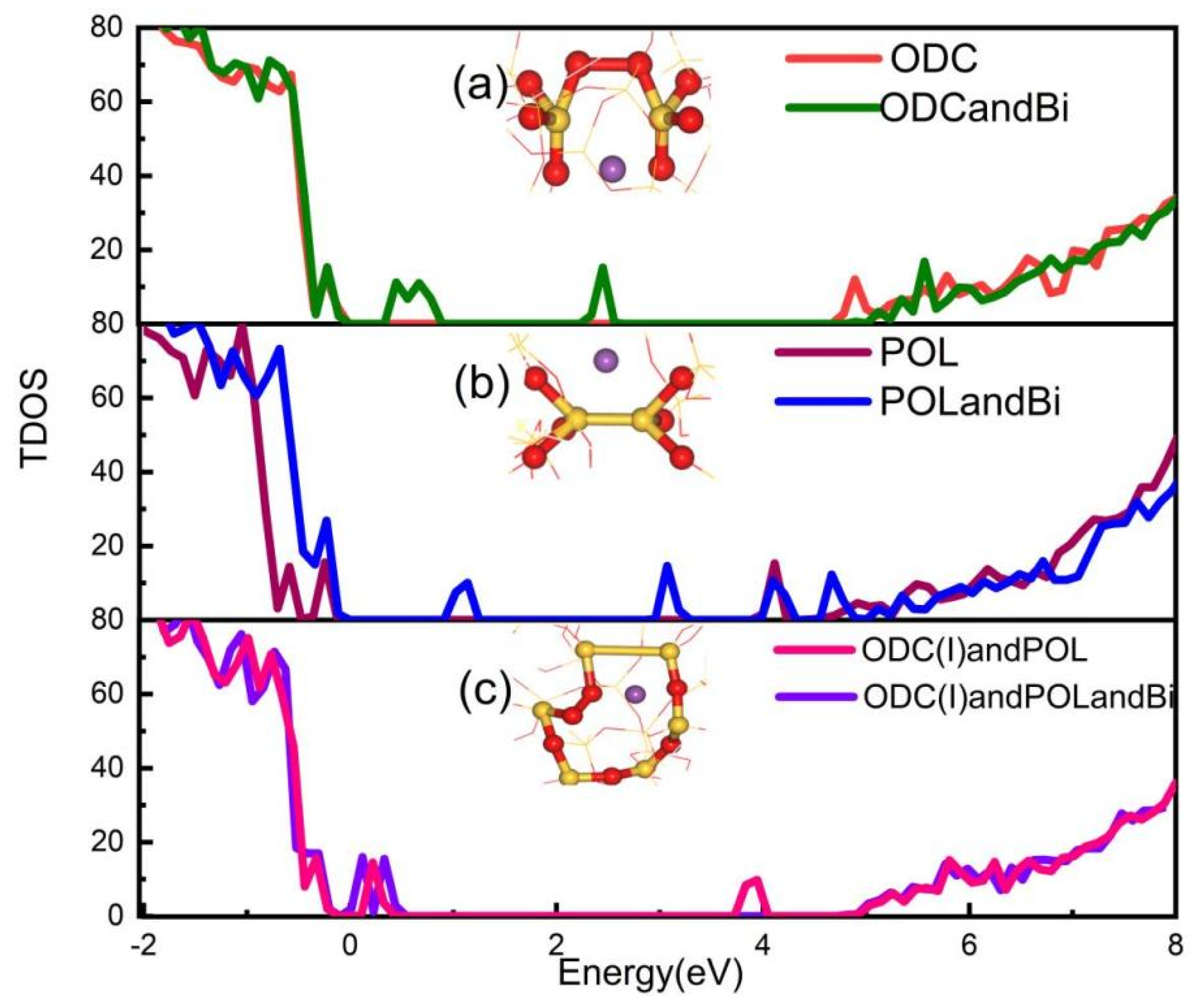
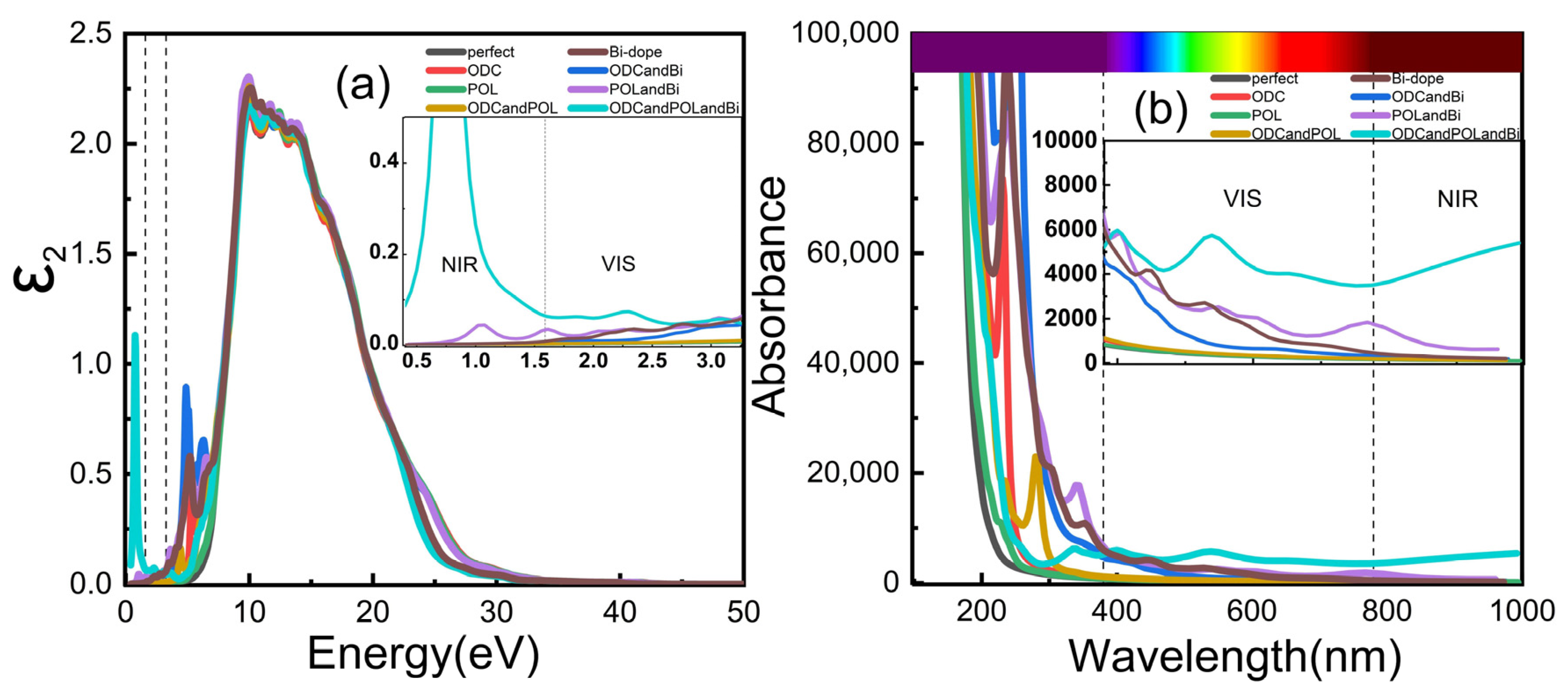
3.2. Analysis of Electronic and Optical Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fujimoto, Y.F.Y.; Nakatsuka, M.N.M. Infrared luminescence from bismuth-doped silica glass. Jpn. J. Appl. Phys. 2001, 40, L279. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Nakatsuka, M. Optical amplification in bismuth-doped silica glass. Appl. Phys. Lett. 2003, 82, 3325–3326. [Google Scholar] [CrossRef]
- Dianov, E.M.; Dvoyrin, V.V.; Mashinsky, V.M.; Umnikov, A.A.; Yashkov, M.V.; Gur’yanov, A.N. CW bismuth fibre laser. Quantum Electron. 2005, 35, 1083. [Google Scholar] [CrossRef]
- Lu, K.; Dutta, N.K. Spectroscopic properties of Yb-doped silica glass. J. Appl. Phys. 2002, 91, 576–581. [Google Scholar] [CrossRef]
- Snoeks, E.; van den Hoven, G.N.; Polman, A. Optimization of an Er-doped silica glass optical waveguide amplifier. IEEE J. Quantum Electron. 1996, 32, 1680–1684. [Google Scholar] [CrossRef]
- Aitken, B.G.; Dejneka, M.J.; Powley, M.L. Tm-doped alkaline earth aluminate glass for optical amplification at 1460 nm. J. Non-Cryst. Solids 2004, 349, 115–119. [Google Scholar] [CrossRef]
- Watekar, P.R.; Ju, S.; Han, W.T. Optical properties of Ho-doped alumino–germano-silica glass optical fiber. J. Non-Cryst. Solids 2008, 354, 1453–1459. [Google Scholar] [CrossRef]
- Tagaya, A.; Teramoto, S.; Yamamoto, T.; Fujii, K.; Nihei, E.; Koike, Y.; Sasaki, K. Theoretical and experimental investigation of rhodamine B-doped polymer optical fiber amplifiers. IEEE J. Quantum Electron. 1995, 31, 2215–2220. [Google Scholar] [CrossRef]
- Zhang, J.; Han, L.; Guan, Z.; Jia, B.; Peng, Z.; Guan, X.; Yan, B.; Peng, G.-D.; Lu, P. Electronic and luminescence characteristics of interstitial Bi0 atom in bismuth-doped silica optical fiber. J. Lumin. 2018, 207, 346–350. [Google Scholar] [CrossRef]
- Jia, B.; Zhu, P.; Sun, S.; Han, L.; Liu, G.; Wang, Y.; Peng, G.-D.; Lu, P. Conversion mechanism from trivalent bismuth to bivalent bismuth defect center in Bi-doped silica optical fiber. IEEE J. Sel. Top. Quantum Electron. 2019, 26, 1–6. [Google Scholar] [CrossRef]
- Bufetov, I.A.; Firstov, S.V.; Khopin, V.F.; Medvedkov, O.I.; Guryanov, A.N.; Dianov, E.M. Bi-doped fiber lasers and amplifiers for a spectral region of 1300–1470 nm. Opt. Lett. 2008, 33, 2227–2229. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, V.O.; Plotnichenko, V.G.; Dianov, E.M. Interstitial BiO molecule as a broadband IR luminescence centre in bismuth-doped silica glass. Quantum Electron. 2011, 41, 1080. [Google Scholar] [CrossRef]
- Sokolov, V.O.; Plotnichenko, V.G.; Dianov, E.M. Origin of broadband near-infrared luminescence in bismuth-doped glasses. Opt. Lett. 2008, 33, 1488–1490. [Google Scholar] [CrossRef] [Green Version]
- Sokolov, V.O.; Plotnichenko, V.G.; Koltashev, V.V.; Dianov, E.M. Centres of broadband near-IR luminescence in bismuth-doped glasses. J. Phys. D Appl. Phys. 2009, 42, 095410. [Google Scholar] [CrossRef]
- Romanov, A.N.; Fattakhova, Z.T.; Veber, A.A.; Usovich, O.V.; Haula, E.V.; Korchak, V.N.; Tsvetkov, V.B.; Trusov, L.A.; Kazin, P.E.; Sulimov, V.B. On the origin of near-IR luminescence in Bi-doped materials (II). Subvalent monocation Bi+ and cluster Bi53+ luminescence in AlCl3/ZnCl2/BiCl3 chloride glass. Opt. Express 2012, 20, 7212–7220. [Google Scholar] [CrossRef]
- Wen, J.; Wang, T.; Pang, F.; Zeng, X.; Chen, Z.; Peng, G.-D. Photoluminescence Characteristics of Bi(m+)-Doped Silica Optical Fiber: Structural Model and Theoretical Analysis. Jpn. J. Appl. Phys. 2013, 52, 122501. [Google Scholar] [CrossRef]
- Jia, B.; Lu, P.; Zhang, J.; Peng, Z.; Yan, B.; Wang, Y.; Peng, G.-D. Influence of ring structures on optical properties of trivalent bismuth in Bi-doped silica optical fiber. J. Clust. Sci. 2018, 29, 861–865. [Google Scholar] [CrossRef]
- Lu, P.; Ren, T.; Jia, B.; Yan, B.; Liu, G.; Guo, M.; Wang, Y.; Peng, G.-D. Atomic structures and electronic states of divalent bismuth in Bi-doped silica optical fiber. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 1–5. [Google Scholar] [CrossRef]
- Sokolov, V.O.; Plotnichenko, V.G.; Dianov, E.M. The origin of near-IR luminescence in bismuth-doped silica and germania glasses free of other dopants: First-principle study. Opt. Mater. Express 2013, 3, 1059–1074. [Google Scholar] [CrossRef]
- Romanov, A.N.; Fattakhova, Z.T.; Veber, A.A.; Usovich, O.V.; Haula, E.V.; Korchak, V.N.; Tsvetkov, V.B.; Trusov, L.A.; Kazin, P.E.; Sulimov, V.B. On the origin of near-IR luminescence in Bi-doped materials (I). Generation of low-valence bismuth species by Bi3+ and Bi0 synproportionation. Opt. Mater. 2011, 33, 631–634. [Google Scholar] [CrossRef]
- Romanov, A.N.; Haula, E.V.; Fattakhova, Z.T.; Veber, A.A.; Tsvetkov, V.B.; Zhigunov, D.M.; Korchak, V.N.; Sulimov, V.B. Near-IR luminescence from subvalent bismuth species in fluoride glass. Opt. Mater. 2011, 34, 155–158. [Google Scholar] [CrossRef]
- Veber, A.A.; Romanov, A.N.; Usovich, O.V.; Fattakhova, Z.T.; Haula, E.V.; Korchak, V.N.; Trusov, L.A.; Kazin, P.E.; Sulimov, V.B.; Tsvetkov, V.B. Luminescent properties of Bi-doped polycrystalline KAlCl4. Appl. Phys. B 2012, 108, 733–736. [Google Scholar] [CrossRef] [Green Version]
- Romanov, A.N.; Veber, A.A.; Vtyurina, D.N.; Fattakhova, Z.T.; Haula, E.V.; Shashkin, D.P.; Sulimov, V.B.; Tsvetkov, V.B.; Korchak, V.N. Near infrared photoluminescence of the univalent bismuth impurity center in leucite and pollucite crystal hosts. J. Mater. Chem. C 2015, 3, 3592–3598. [Google Scholar] [CrossRef] [Green Version]
- Romanov, A.N.; Veber, A.A.; Fattakhova, Z.T.; Vtyurina, D.N.; Usovich, O.V.; Grigoriev, F.V.; Haula, E.V.; Trusov, L.A.; Kazin, P.E.; Korchak, V.N.; et al. New route to Bi+-doped crystals: Preparation and NIR luminescence of K, Rb and Cs ternary chlorides, containing univalent bismuth. In The European Conference on Lasers and Electro-Optics; Optical Society of America: New York, NY, USA, 2013; p. CE_P_21. [Google Scholar]
- Han, L.; Xiao, W.; Zhang, J.; Jia, B.; Liu, G.; Chen, X.; Lu, P. Investigations of interstitial Bi0 interacting with intrinsic defects in bismuth-doped silica optical fiber. Appl. Phys. A 2019, 125, 482. [Google Scholar] [CrossRef]
- Liu, M.; Lu, P.F.; Yang, Y.; Wu, L.Y.; Su, R.; Chen, J. Structural and Optical Properties of Point Defects in α-SiO2 Cluster. Commun. Theor. Phys. 2015, 64, 244. [Google Scholar] [CrossRef]
- Imai, H.; Arai, K.; Imagawa, H.; Hosono, H.; Abe, Y. Two types of oxygen-deficient centers in synthetic silica glass. Phys. Rev. B 1988, 38, 12772–12775. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Jia, B.; Yan, B.; Li, S.; Gao, C.; Wang, J.; Yang, B.; Lu, P. Optical absorption of Bi2+-ODC(II) active center in Bi-doped silica optical fiber. J. Lumin. 2019, 213, 304–309. [Google Scholar] [CrossRef]
- Skuja, L.; Hirano, M.; Hosono, H.; Kajihara, K. Defects in oxide glasses. Phys. Status Solidi C 2005, 2, 15–24. [Google Scholar] [CrossRef]
- Furukawa, Y.; Matsushita, Y. Analysis of single and composite structural defects in pure amorphous silicon: A first-principles study. J. Non-Cryst. Solids 2017, 473, 64–73. [Google Scholar] [CrossRef] [Green Version]
- Sulimov, V.B.; Kutov, D.C.; Sulimov, A.V.; Grigoriev, F.V.; Tikhonravov, A.V. Density functional modeling of structural and electronic properties of amorphous high temperature oxides. J. Non-Cryst. Solids 2022, 578, 121170. [Google Scholar] [CrossRef]
- Sulimov, A.V.; Kutov, D.C.; Grigoriev, F.V.; Tikhonravov, A.V.; Sulimov, V.B. Generation of Amorphous Silicon Dioxide Structures via Melting-Quenching Density Functional Modeling. Lobachevskii J. Math. 2020, 41, 1581–1590. [Google Scholar] [CrossRef]
- Zheng, G.P. A density functional theory study on the deformation behaviors of Fe-Si-B metallic glasses. Int. J. Mol. Sci. 2012, 13, 10401–10409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Munde, M.S.; Gao, D.Z.; Shluger, A.L. Diffusion and aggregation of oxygen vacancies in amorphous silica. J. Phys. Condens. Matter 2017, 29, 245701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, B.; Lu, P.; Peng, Z.; Yan, B.; Yang, B.; Wang, Y.; Peng, G.-D. Near-IR luminescence characteristics of monovalent bismuth in Bi-doped pure silica optical fiber: First-principle study. J. Lumin. 2018, 198, 384–388. [Google Scholar] [CrossRef]
- Liu, G.; Wang, F.; Guan, X.; Jia, B.; Han, L.; Yan, B.; Peng, G.-D.; Lu, P. Geometric and optical properties of Bi/Er co-doped silica optical fiber. Opt. Mater. 2020, 107, 110030. [Google Scholar] [CrossRef]
- Kong, B.; Zeng, T.; Wang, W. The n-type and p-type conductivity mechanisms of the bulk BiOCl photocatalyst from hybrid density functional theory calculations. Phys. Chem. Chem. Phys. 2021, 23, 19841–19853. [Google Scholar] [CrossRef]
- Jia, B.; Guan, Z.; Peng, Z.; Zhang, J.; Guan, X.; Guan, P.; Yang, B.; Wang, Y.; Lu, P. Structural disorder in fused silica with ODC(I) defect. Appl. Phys. A 2018, 124, 696. [Google Scholar] [CrossRef]
- Wang, W.; Lu, P.; Han, L.; Zhang, C.; Wu, L.; Guan, P.; Su, R.; Chen, J. Structural and electronic properties of peroxy linkage defect and its interconversion in fused silica. J. Non-Cryst. Solids 2016, 434, 96–101. [Google Scholar] [CrossRef]
- Nor, R.M.; Halim, S.N.M.; Taib, M.F.M.; Abd-Rahman, M.K. First principles investigation on the structural, electronic and optical properties of amorphous silica glass. In Solid State Phenomena; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2017; Volume 268, pp. 92–96. [Google Scholar]
- Skuja, L. Optically active oxygen-deficiency-related centers in amorphous silicon dioxide. J. Non-Cryst. Solids 1998, 239, 16–48. [Google Scholar] [CrossRef]
- Galiulina, J.S.; Mamonov, A.P.; Koubisy MS, I.; Shtang, T.V.; Biryukov, D.Y.; Gavrilov, N.V.; Zatsepin, A.F. The formation of optically active centers in silica glass during implantation of bismuth ions. In AIP Conference Proceedings; AIP Publishing LLC of America: Melville, NY, USA, 2020; Volume 2313, p. 030015. [Google Scholar]
- Winkler, B.; Martin-Samos, L.; Richard, N.; Giacomazzi, L.; Alessi, A.; Girard, S.; Boukenter, A.; Ouerdane, Y.; Valant, M. Correlations between Structural and Optical Properties of Peroxy Bridges from First Principles. J. Phys. Chem. C 2017, 121, 4002–4010. [Google Scholar] [CrossRef]
- Cheng, Y.; Ren, D.; Zhang, H.; Cheng, X. First-principle study of the structural, electronic and optical properties of defected amorphous silica. J. Non-Cryst. Solids 2015, 416, 36–43. [Google Scholar] [CrossRef]
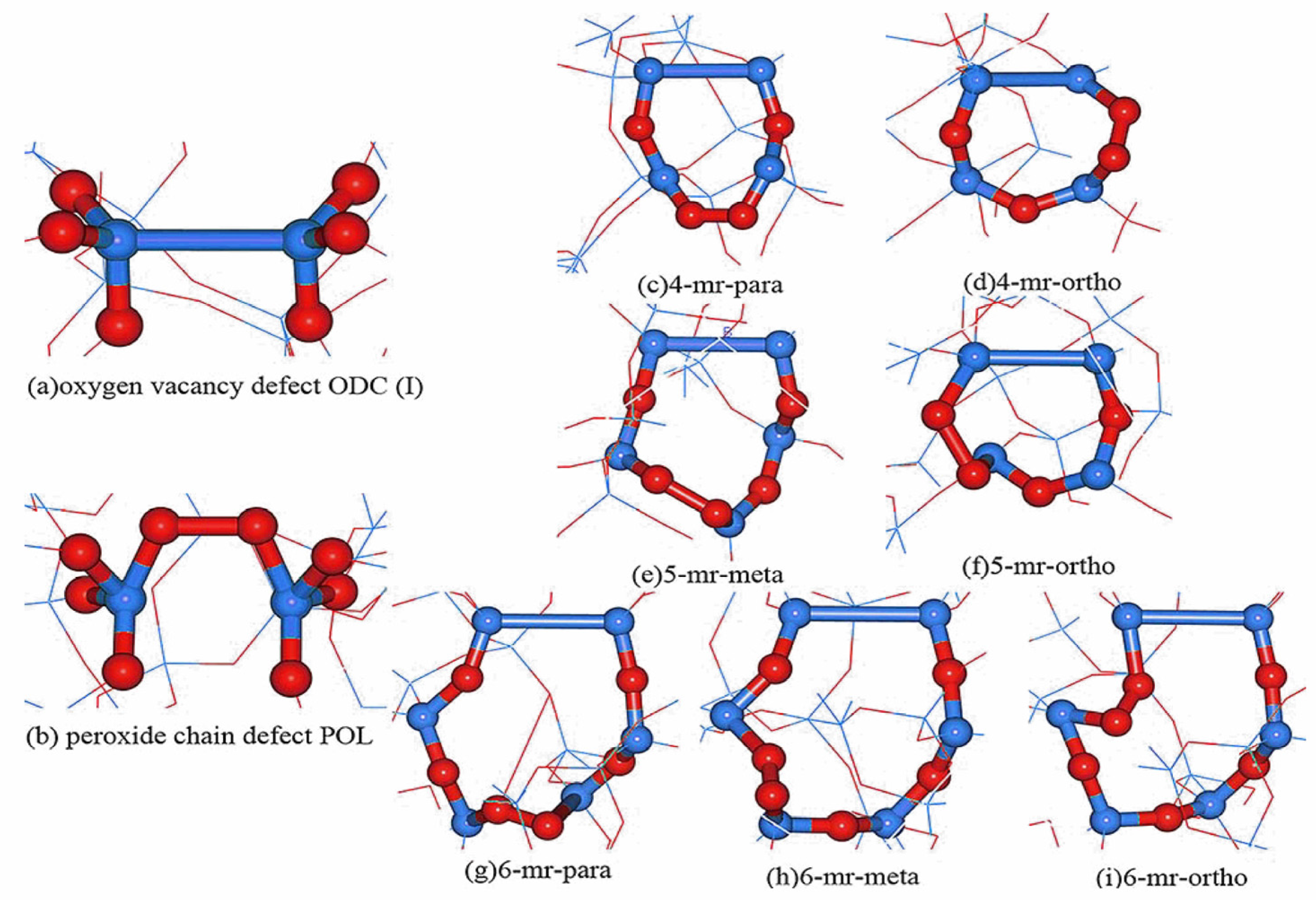
| n-Membered Rings | 3-MR | 4-MR | 5-MR | 6-MR |
|---|---|---|---|---|
| Formation Energy (eV) | 9.16 | 14.32 | 4.5 | 3.81 |
| Meta Ring | Model | Forming Energy (eV) | Si-Si (Å) | O-O (Å) |
|---|---|---|---|---|
| 4MR | Para-position Ortho-position | 7.13 7.02 | 2.424 2.481 | 1.514 1.520 |
| 5MR | Meta-position Ortho-position | 6.84 6.94 | 2.430 2.412 | 1.474 1.479 |
| 6MR | Para-position Ortho-position Meta-position | 7.91 6.43 7.85 | 2.561 2.464 2.534 | 1.476 1.510 1.490 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, B.; Song, T.; Zhang, M.; Zeng, T.; Chen, J.; Zhang, F. Aggregation of ODC(I) and POL Defects in Bismuth Doped Silica Fiber. Micromachines 2023, 14, 358. https://doi.org/10.3390/mi14020358
Li X, Wang B, Song T, Zhang M, Zeng T, Chen J, Zhang F. Aggregation of ODC(I) and POL Defects in Bismuth Doped Silica Fiber. Micromachines. 2023; 14(2):358. https://doi.org/10.3390/mi14020358
Chicago/Turabian StyleLi, Xiaofei, Binbin Wang, Tingting Song, Min Zhang, Tixian Zeng, Jiang Chen, and Feiquan Zhang. 2023. "Aggregation of ODC(I) and POL Defects in Bismuth Doped Silica Fiber" Micromachines 14, no. 2: 358. https://doi.org/10.3390/mi14020358
APA StyleLi, X., Wang, B., Song, T., Zhang, M., Zeng, T., Chen, J., & Zhang, F. (2023). Aggregation of ODC(I) and POL Defects in Bismuth Doped Silica Fiber. Micromachines, 14(2), 358. https://doi.org/10.3390/mi14020358






