A Novel Bird-Shape Broadband Piezoelectric Energy Harvester for Low Frequency Vibrations
Abstract
:1. Introduction
2. Designing Process and Working Principle of the Harvester
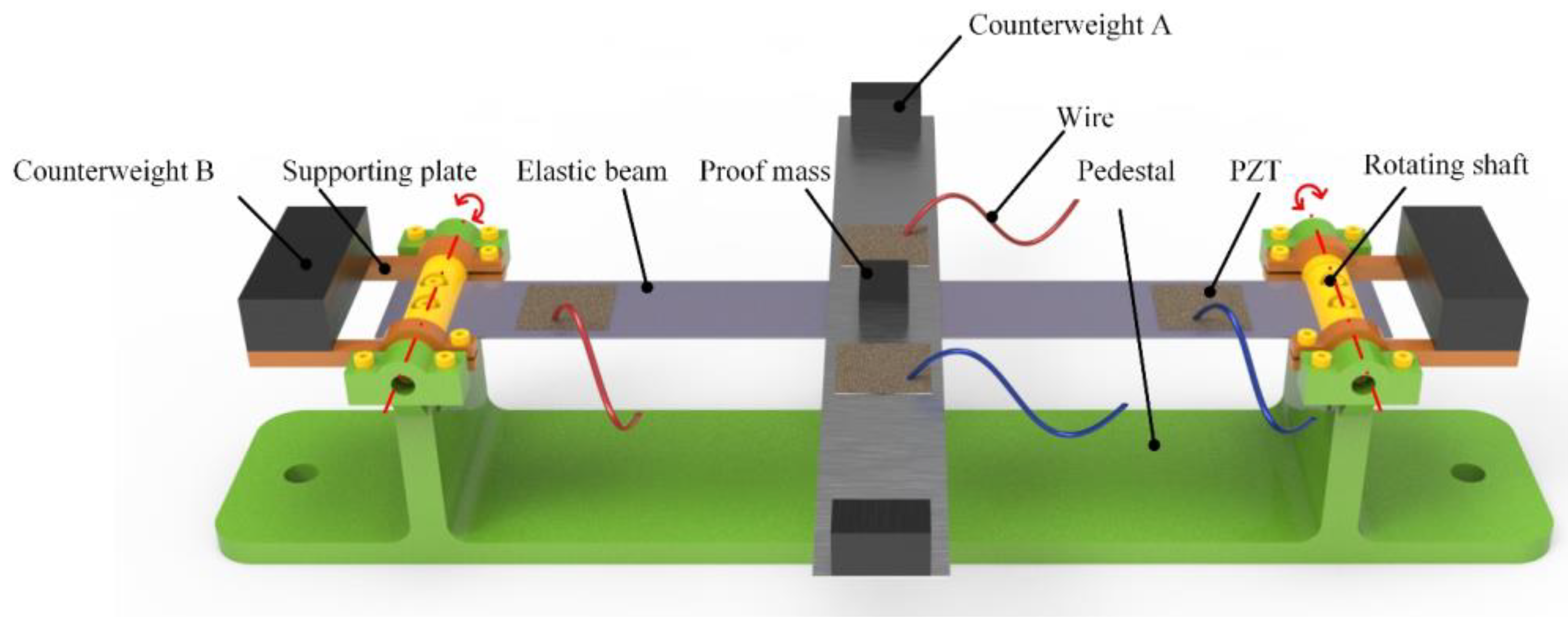
2.1. Structural Design
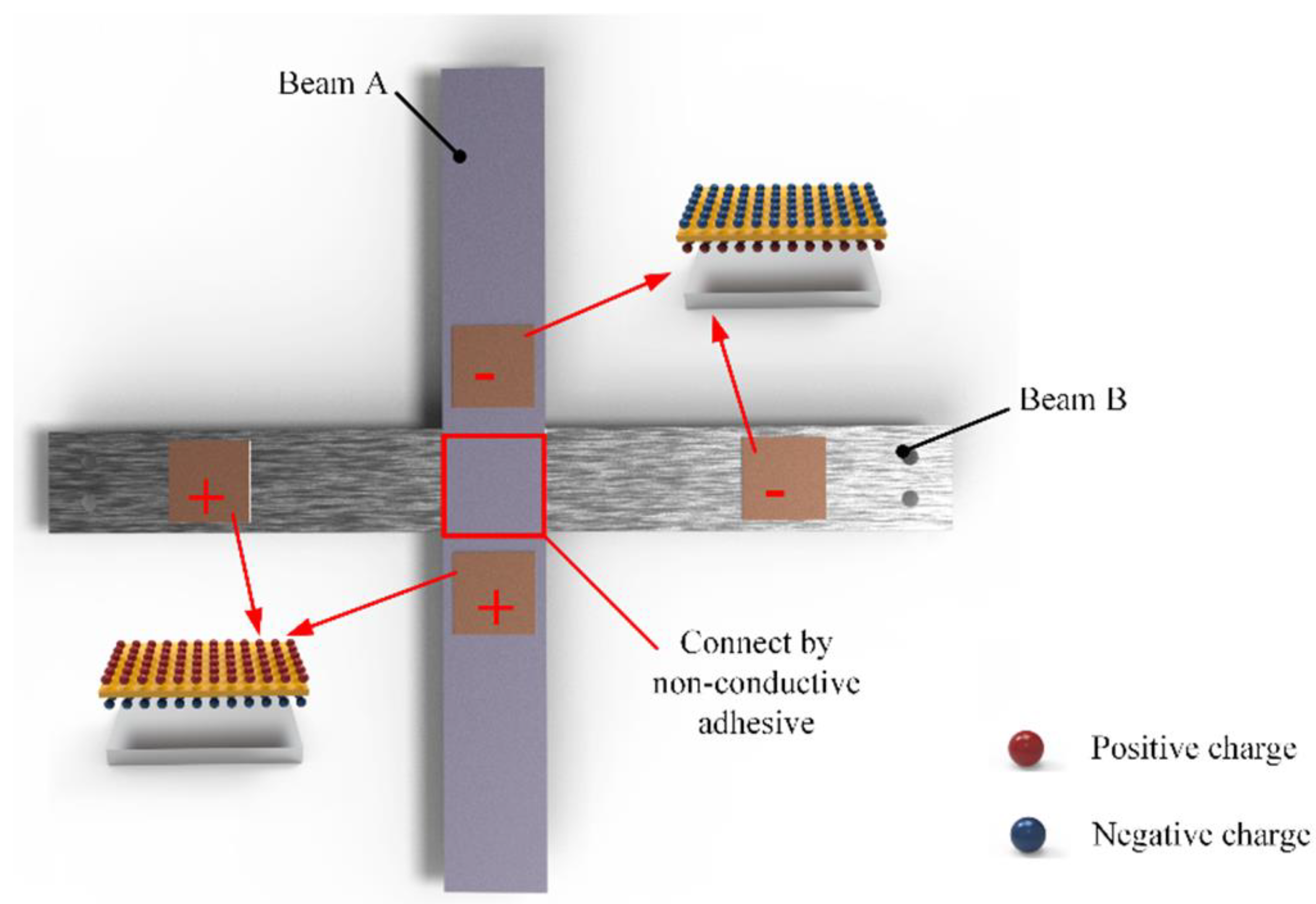
2.2. Working Principle
3. Finite Element Method
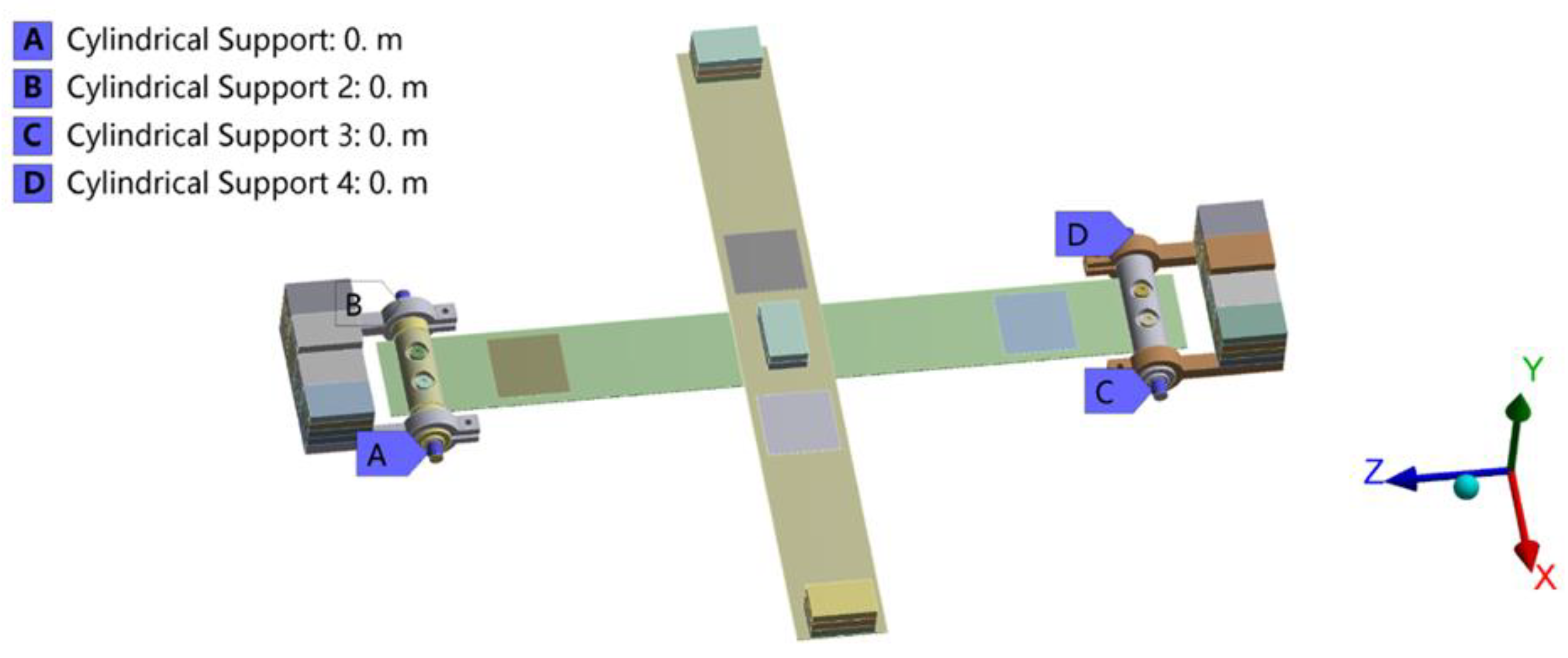
3.1. Finite Element Modeling
3.2. Modal Analysis
3.3. Harmonic Response Analysis
4. Experimental Setup
5. Results and Discussion
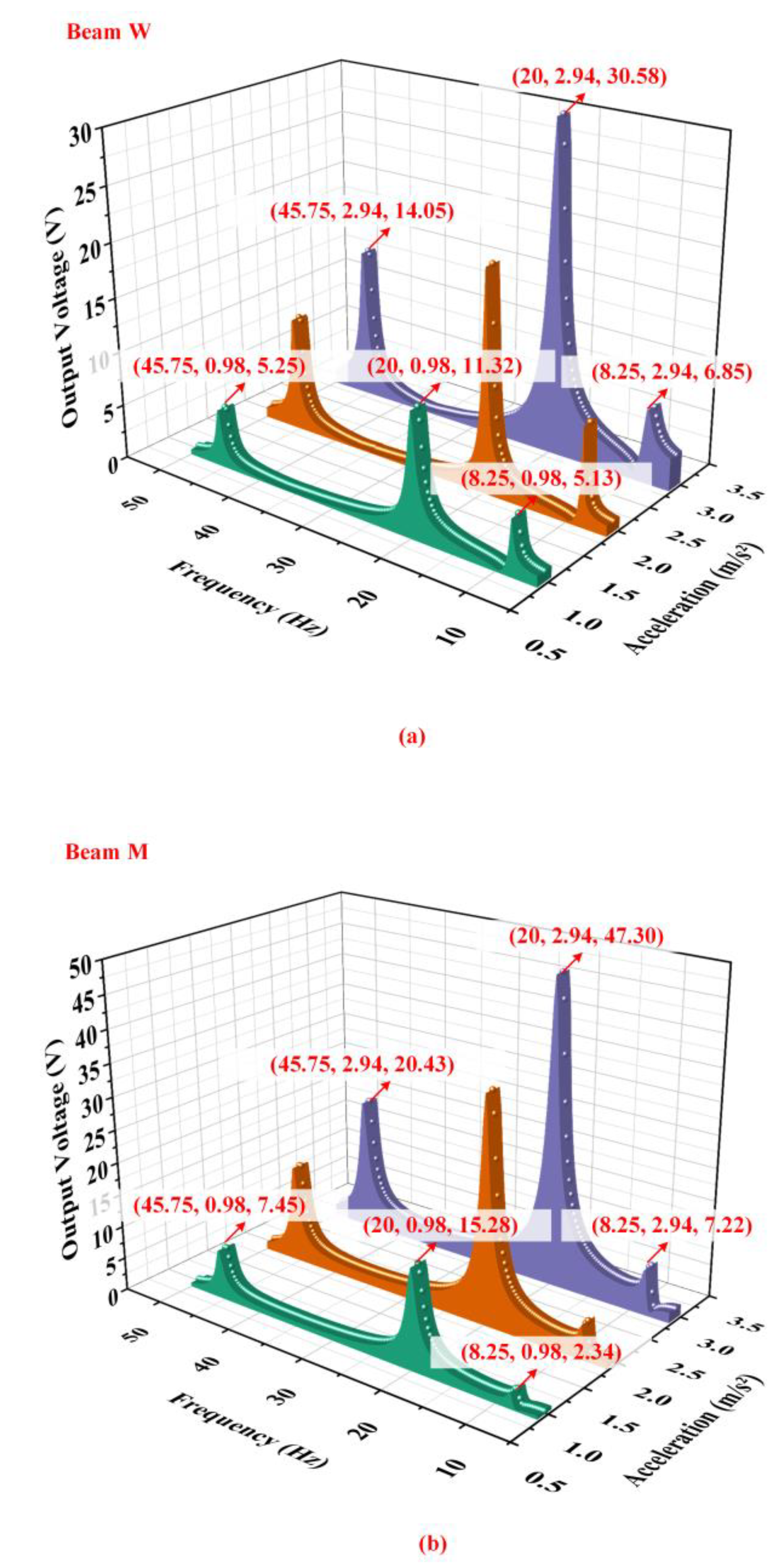
5.1. Effects of the Base Acceleration
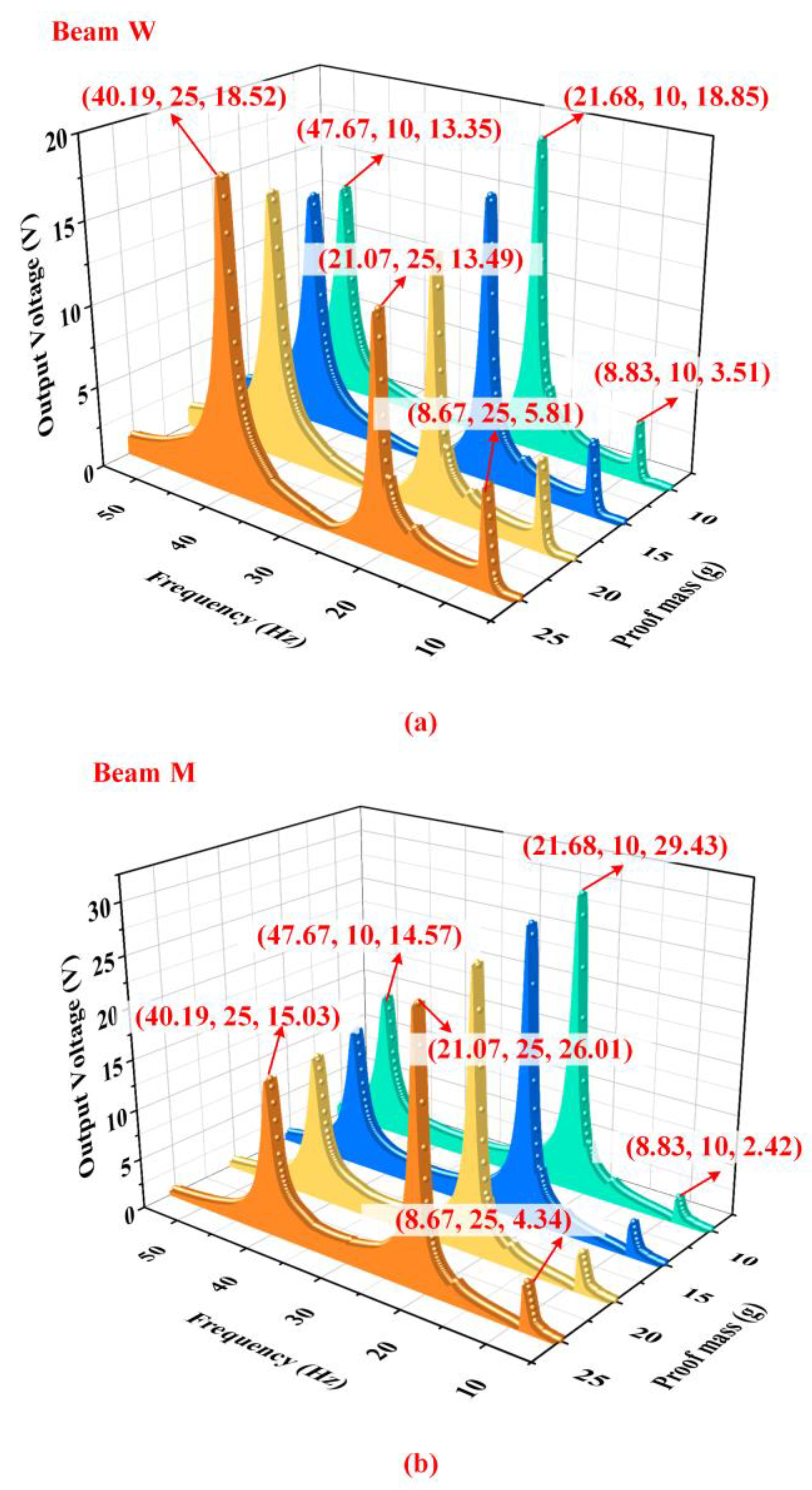
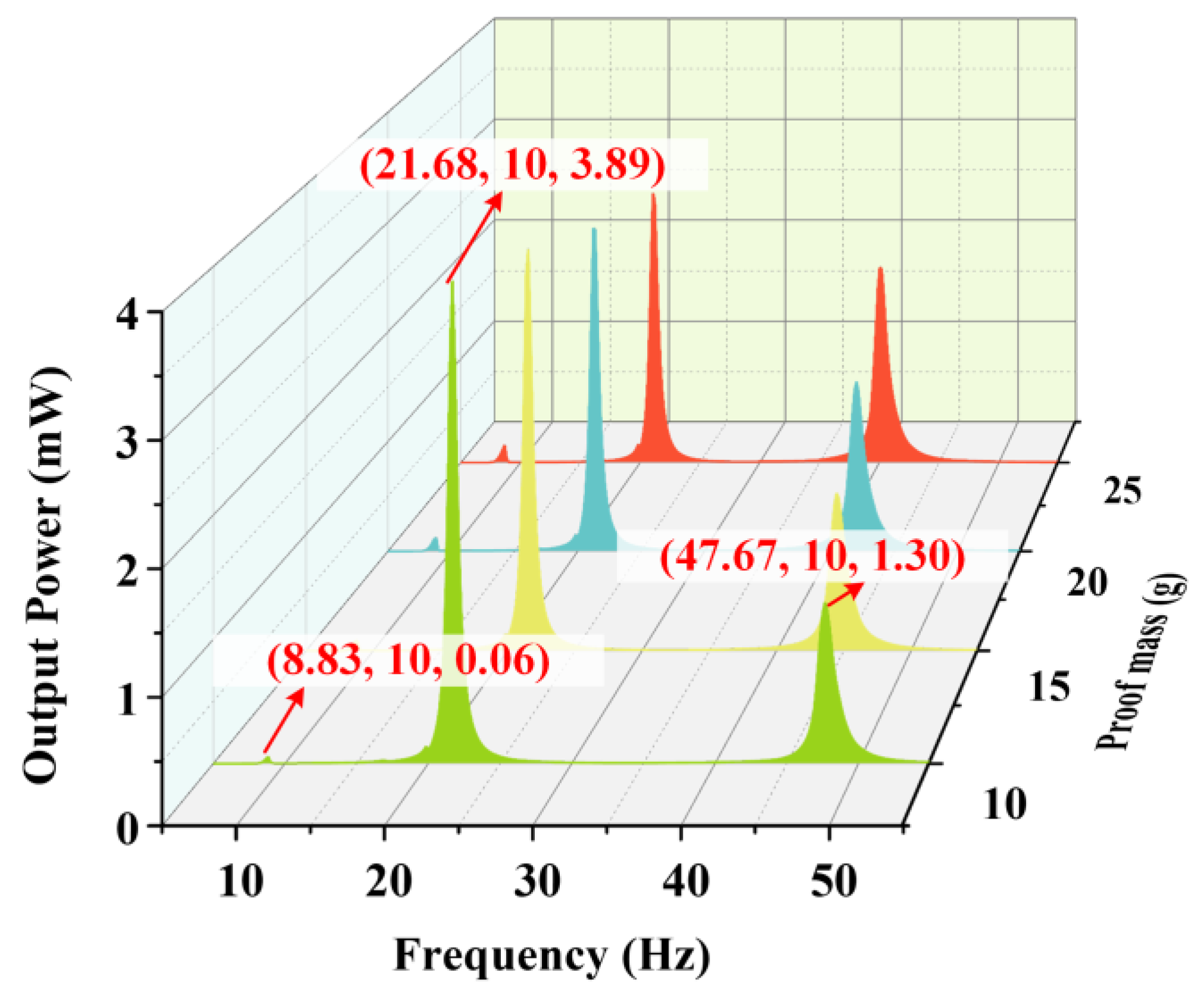
5.2. Effects of the Proof Mass
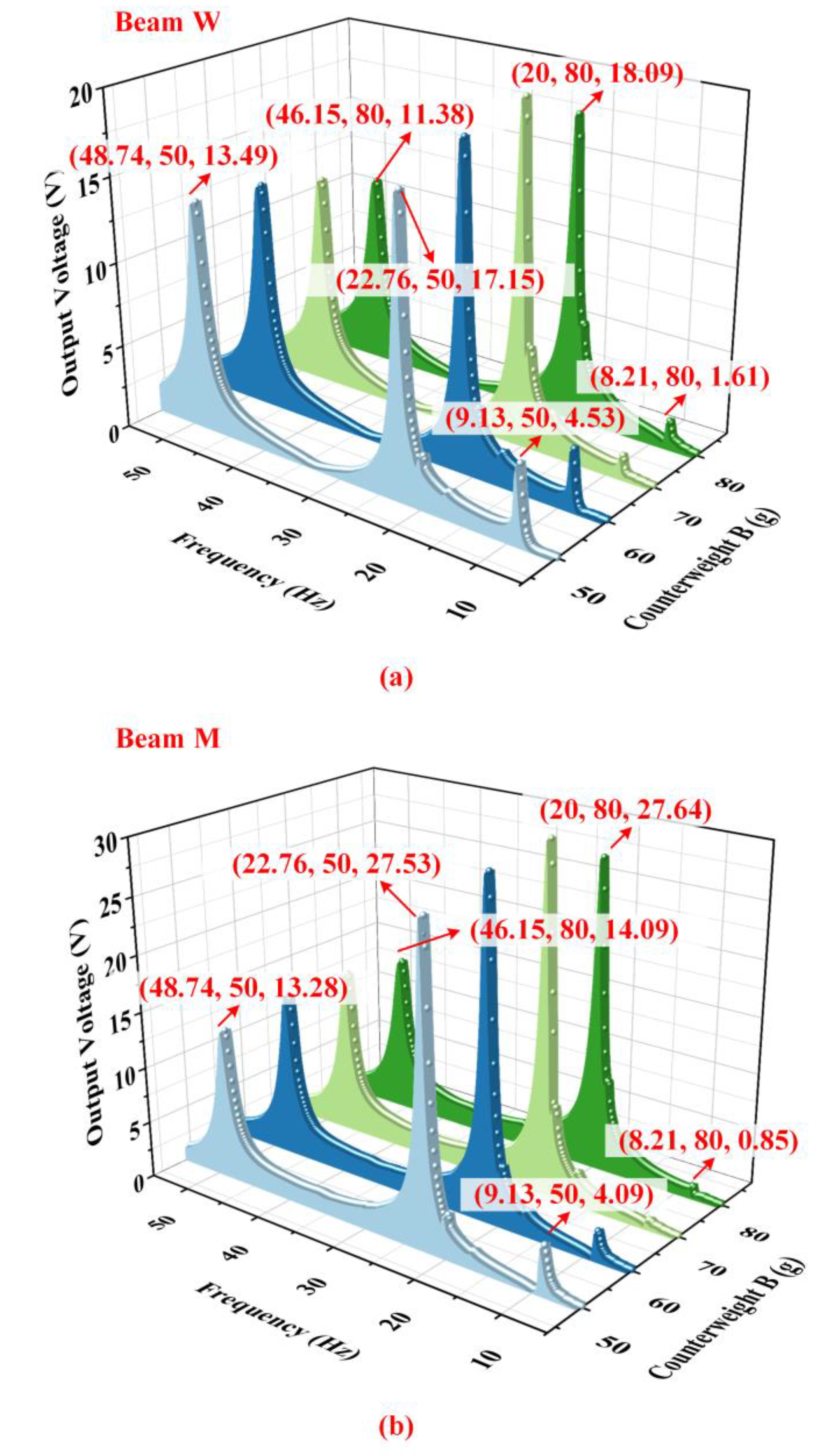
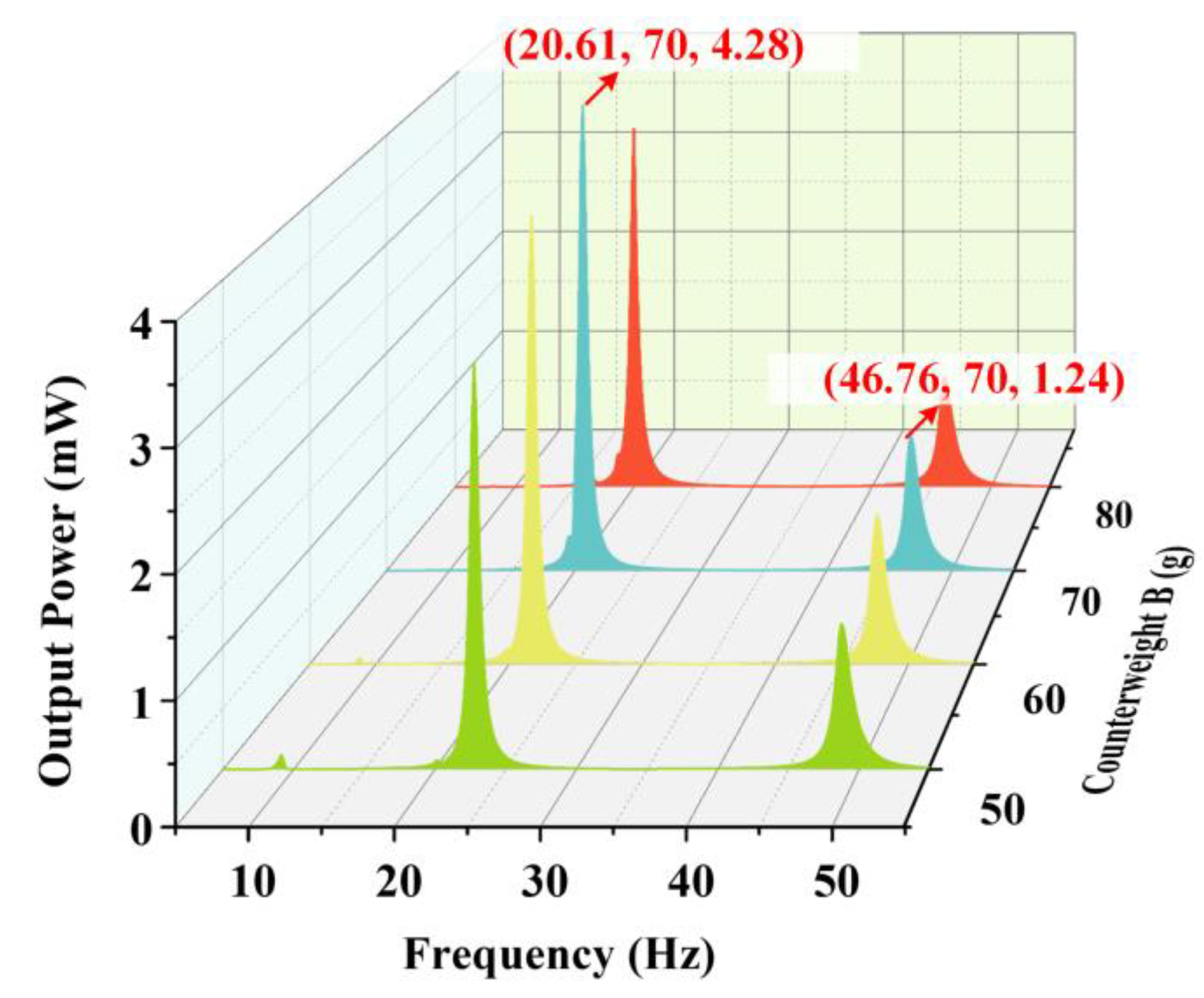
5.3. Effects of Counterweight A and Counterweight B
5.4. Discussion and Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, L.; Tang, L.; Yang, T. Piezoelectric passive self-tuning energy harvester based on a beam-slider structure. J. Sound Vib. 2020, 489, 115689. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Yan, G.; Liu, F.-R.; Tan, T.; Zhang, W.-M.; Peng, Z.-K.; Meng, G. A water-proof magnetically coupled piezoelectric-electromagnetic hybrid wind energy harvester. Appl. Energy 2019, 239, 735–746. [Google Scholar] [CrossRef]
- Meng, D.; Huang, K.; Xu, W. Impacts of Small-Scale Effect and Nonlinear Damping on the Nonlinear Vibrations of Electrostatic Microresonators. Micromachines 2023, 14, 170. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gu, S.; Abdelkefi, A.; Bose, C. Enhancing piezoelectric energy harvesting from the flow-induced vibration of a circular cylinder using dual splitters. Smart Mater. Struct. 2021, 30, 05LT01. [Google Scholar] [CrossRef]
- Zhang, Y.; Tu, Z.; Lu, T.-F.; Al-Sarawi, S. A simplified transfer matrix of multi-layer piezoelectric stack. J. Intell. Mater. Syst. Struct. 2017, 28, 595–603. [Google Scholar] [CrossRef]
- Cao, Y.; Zong, R.; Wang, J.; Xiang, H.; Tang, L. Design and performance evaluation of piezoelectric tube stack energy harvesters in railway systems. J. Intell. Mater. Syst. Struct. 2022, 33, 2305–2320. [Google Scholar] [CrossRef]
- Li, Y.; Yin, D.; Cheng, X.; Chen, J.; Zhou, A.; Ji, X.; Li, Y. Vibration energy harvesting with piezoelectric ceramics working in d33 mode by using a spring-mass-spring oscillator. J. Appl. Phys. 2020, 127, 064104. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.-H. A device capable of customizing nonlinear forces for vibration energy harvesting, vibration isolation, and nonlinear energy sink. Mech. Syst. Signal Process. 2021, 147, 107101. [Google Scholar] [CrossRef]
- Mohamed, K.; Elgamal, H.; Kouritem, S.A. An experimental validation of a new shape optimization technique for piezoelectric harvesting cantilever beams. Alex. Eng. J. 2021, 60, 1751–1766. [Google Scholar] [CrossRef]
- Ferguson, W.J.; Kuang, Y.; Evans, K.E.; Smith, C.W.; Zhu, M. Auxetic structure for increased power output of strain vibration energy harvester. Sens. Actuators A: Phys. 2018, 282, 90–96. [Google Scholar] [CrossRef]
- Ting, R.Y. Composite piezoelectric materials for transduction. Appl. Acoust. 1994, 41, 325–335. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Civalek, Ö. Application of Chebyshev–Ritz method for static stability and vibration analysis of nonlocal microstructure-dependent nanostructures. Eng. Comput. 2020, 36, 953–964. [Google Scholar] [CrossRef]
- Umeda, M.; Nakamura, K.; Ueha, S. Analysis of the transformation of mechanical impact energy to electric energy using piezoelectric vibrator. Jpn. J. Appl. Phys. 1996, 35, 3267. [Google Scholar] [CrossRef]
- Jalaei, M.; Thai, H.; Civalek, Ö. On viscoelastic transient response of magnetically imperfect functionally graded nanobeams. Int. J. Eng. Sci. 2022, 172, 103629. [Google Scholar] [CrossRef]
- Goldfarb, M.; Jones, L.D. On the efficiency of electric power generation with piezoelectric ceramic. J. Dyn. Sys. Meas. Control. 1999, 121, 566–571. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Wu, Z.-Y.; Gao, Q.-H.; Yan, G.; Liu, F.-R.; Wei, K.-X.; Zhang, W.-M. Dynamically synergistic regulation mechanism for rotation energy harvesting. Mech. Syst. Signal Process. 2022, 169, 108637. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Liu, J.; Deng, J.; Liu, Y. A review of recent studies on non-resonant piezoelectric actuators. Mech. Syst. Signal Process. 2019, 133, 106254. [Google Scholar] [CrossRef]
- Güleç, H.; Gurbuz, M.; Toktas, A.G.; Gul, M.; Koc, B.; Dogan, A. A new design to improve bandwidth of piezoelectric energy harvester. J. Aust. Ceram. Soc. 2020, 56, 117–126. [Google Scholar] [CrossRef]
- Zhang, H.; Afzalul, K. Design and analysis of a connected broadband multi-piezoelectric-bimorph-beam energy harvester. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014, 61, 1016–1023. [Google Scholar] [CrossRef]
- Chen, K.; Gao, Q.; Fang, S.; Zou, D.; Yang, Z.; Liao, W.-H. An auxetic nonlinear piezoelectric energy harvester for enhancing efficiency and bandwidth. Appl. Energy 2021, 298, 117274. [Google Scholar] [CrossRef]
- Li, Q.; Kuang, Y.; Zhu, M. Auxetic piezoelectric energy harvesters for increased electric power output. AIP Adv. 2017, 7, 015104. [Google Scholar] [CrossRef]
- Farhangdoust, S.; Georgeson, G.; Ihn, J.-B.; Chang, F.-K. Kirigami auxetic structure for high efficiency power harvesting in self-powered and wireless structural health monitoring systems. Smart Mater. Struct. 2020, 30, 015037. [Google Scholar] [CrossRef]
- Chen, K.; Fang, S.; Gao, Q.; Zou, D.; Cao, J.; Liao, W.-H. An enhanced nonlinear piezoelectric energy harvester with multiple rotating square unit cells. Mech. Syst. Signal Process. 2022, 173, 109065. [Google Scholar] [CrossRef]
- Eghbali, P.; Younesian, D.; Farhangdoust, S. Enhancement of piezoelectric vibration energy harvesting with auxetic boosters. Int. J. Energy Res. 2020, 44, 1179–1190. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, H.; Gao, Q.; Yan, G.; Wu, Z.; Liu, F.; Wei, K.; Yang, B.; Zhang, W. Design, modeling and experimental investigation of a magnetically modulated rotational energy harvester for low frequency and irregular vibration. Sci. China Technol. Sci. 2020, 63, 2051–2062. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Bowen, C.R.; Litak, G. Probability and output analysis of asymmetric bistable energy harvesters subjected to Gaussian white noise. Eur. Phys. J. Plus 2019, 134, 558. [Google Scholar] [CrossRef]
- Qian, F.; Hajj, M.R.; Zuo, L. Bio-inspired bi-stable piezoelectric harvester for broadband vibration energy harvesting. Energy Convers. Manag. 2020, 222, 113174. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design of a structure-based bistable piezoelectric energy harvester for scavenging vibration energy in gravity direction. Mech. Syst. Signal Process. 2022, 162, 108043. [Google Scholar] [CrossRef]
- Sun, S.; Leng, Y.; Su, X.; Zhang, Y.; Chen, X.; Xu, J. Performance of a novel dual-magnet tri-stable piezoelectric energy harvester subjected to random excitation. Energy Convers. Manag. 2021, 239, 114246. [Google Scholar] [CrossRef]
- Atmeh, M.; Ibrahim, A.; Ramini, A. Static and Dynamic Analysis of a Bistable Frequency Up-Converter Piezoelectric Energy Harvester. Micromachines 2023, 14, 261. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, J.; Hu, S.; Rao, J.; Theodossiades, S. A multi-stable ultra-low frequency energy harvester using a nonlinear pendulum and piezoelectric transduction for self-powered sensing. Mech. Syst. Signal Process. 2023, 189, 110034. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Dai, K. A multi-mode broadband vibration energy harvester composed of symmetrically distributed u-shaped cantilever beams. Micromachines 2021, 12, 203. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, L. Investigation on the characteristics of a novel internal resonance galloping oscillator for concurrent aeroelastic and base vibratory energy harvesting. Mech. Syst. Signal Process. 2022, 173, 109022. [Google Scholar] [CrossRef]
- Micek, P.; Grzybek, D. Experimental Analysis of the Arrays of Macro Fiber Composite Patches for Rotational Piezoelectric Energy Harvesting from a Shaft. Energies 2021, 14, 4815. [Google Scholar] [CrossRef]
- Lan, C.; Tang, L.; Qin, W.; Xiong, L. Magnetically coupled dual-beam energy harvester: Benefit and trade-off. J. Intell. Mater. Syst. Struct. 2018, 29, 1216–1235. [Google Scholar] [CrossRef]
- Shim, H.-K.; Sun, S.; Kim, H.-S.; Lee, D.-G.; Lee, Y.-J.; Jang, J.-S.; Cho, K.-H.; Baik, J.M.; Kang, C.-Y.; Leng, Y. On a nonlinear broadband piezoelectric energy harvester with a coupled beam array. Appl. Energy 2022, 328, 120129. [Google Scholar] [CrossRef]
- Ding, J.; Lu, M.; Deng, A.; Jiang, S. A piezoelectric energy harvester using an arc-shaped piezoelectric cantilever beam array. Microsyst. Technol. 2022, 28, 1947–1958. [Google Scholar] [CrossRef]
- Fan, K.; Cai, M.; Liu, H.; Zhang, Y. Capturing energy from ultra-low frequency vibrations and human motion through a monostable electromagnetic energy harvester. Energy 2019, 169, 356–368. [Google Scholar] [CrossRef]
- Wang, J.; Xue, Z.; Cai, C.; Wang, D. A Novel Piezoelectric Energy Harvester With Different Circular Arc Spiral Cantilever Beam. IEEE Sens. J. 2022, 22, 11016–11022. [Google Scholar] [CrossRef]
- Wang, H.; Li, B.; Liu, Y.; Zhao, W. Low-frequency, broadband piezoelectric vibration energy harvester with folded trapezoidal beam. Rev. Sci. Instrum. 2019, 90, 035001. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Dong, G.; Zhou, M. Low-Frequency Broadband Piezoelectric Vibration Energy Harvester Based on Double L-shaped Beam Structures. J. Vib. Eng. Technol. 2022, 10, 3179–3189. [Google Scholar] [CrossRef]





| Parameters | Units | Values |
|---|---|---|
| The density of beam M and beam W | 2770 | |
| Young’s Modulus of beam M and beam W | GPa | 71 |
| Poisson’s Ratio of beam M and beam W | ------ | 0.33 |
| The thickness of the beam M and beam W | mm | 0.6 |
| Width of the beam M and beam W | mm | 25 |
| Density of shaft | 1130 | |
| Young’s Modulus of shaft | MPa | 2589 |
| Poisson’s Ratio of shaft | ------ | 0.4 |
| Density of counterweight | 8000 | |
| Young’s Modulus of counterweight | GPa | 200 |
| Poisson’s Ratio of counterweight | ------ | 0.3 |
| The density of PZT sheets | 7500 | |
| Piezoelectric tensor | ||
| Stiffness tensor | GPa | |
| Permittivity tensor | ------ | |
| The thickness of PZT sheets | mm | 0.3 |
| Width of PZT sheets | mm | 20 |
| Length of PZT sheets | mm | 20 |
| Length of beam M | mm | 200 |
| Length of beam W | mm | 220 |
| Reference | Piezoelectric Material | Dimension of Piezoelectric Materials (mm) | Resonant Frequency (Hz) | Configuration | ||
|---|---|---|---|---|---|---|
| Wang et al. [40] | PZT | 30 × 6 × 1 | 52 | 0.42 | --- |  |
| Wang et al. [41] | PZT | 22 × 19.5 × 0.35 | 10 | 1.45 | 4.9 |  |
| Huang et al. [42] | PZT | 30 × 20 × 0.2 | 1–15 | 11.08 | 0.98 | 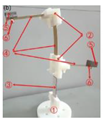 |
| This work | PZT | 20 × 20 × 0.3 | 19.23 | 19.85 | 2.94 | 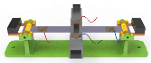 |
| 45.38 | 3.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Zhang, X.; Shan, X.; Hu, L.; Zhang, X.; Hou, C.; Xie, T. A Novel Bird-Shape Broadband Piezoelectric Energy Harvester for Low Frequency Vibrations. Micromachines 2023, 14, 421. https://doi.org/10.3390/mi14020421
Yu H, Zhang X, Shan X, Hu L, Zhang X, Hou C, Xie T. A Novel Bird-Shape Broadband Piezoelectric Energy Harvester for Low Frequency Vibrations. Micromachines. 2023; 14(2):421. https://doi.org/10.3390/mi14020421
Chicago/Turabian StyleYu, Han, Xiaofan Zhang, Xiaobiao Shan, Liangxing Hu, Xingxu Zhang, Chengwei Hou, and Tao Xie. 2023. "A Novel Bird-Shape Broadband Piezoelectric Energy Harvester for Low Frequency Vibrations" Micromachines 14, no. 2: 421. https://doi.org/10.3390/mi14020421
APA StyleYu, H., Zhang, X., Shan, X., Hu, L., Zhang, X., Hou, C., & Xie, T. (2023). A Novel Bird-Shape Broadband Piezoelectric Energy Harvester for Low Frequency Vibrations. Micromachines, 14(2), 421. https://doi.org/10.3390/mi14020421





