The Study of the Reliability of Complex Components during the Electromigration Process
Abstract
:1. Introduction
2. Simulation and Experimental Procedures
2.1. Simulation Approaches
2.2. Electromigration Test
3. Results and Discussion
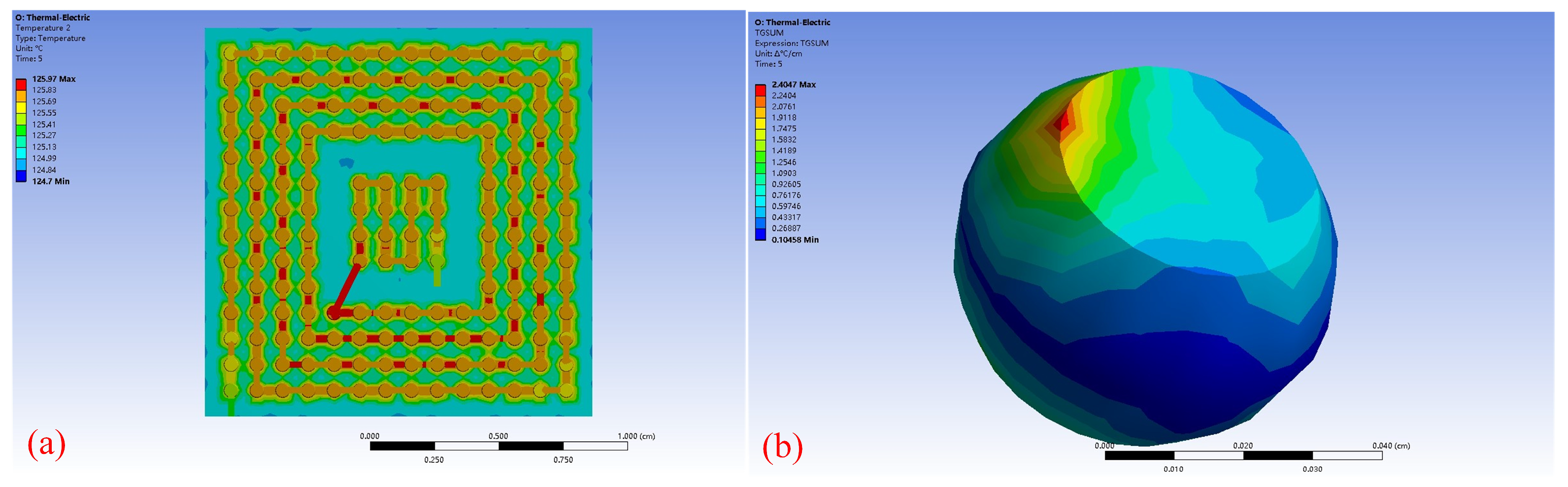
3.1. Thermo-Electric Coupling Analysis
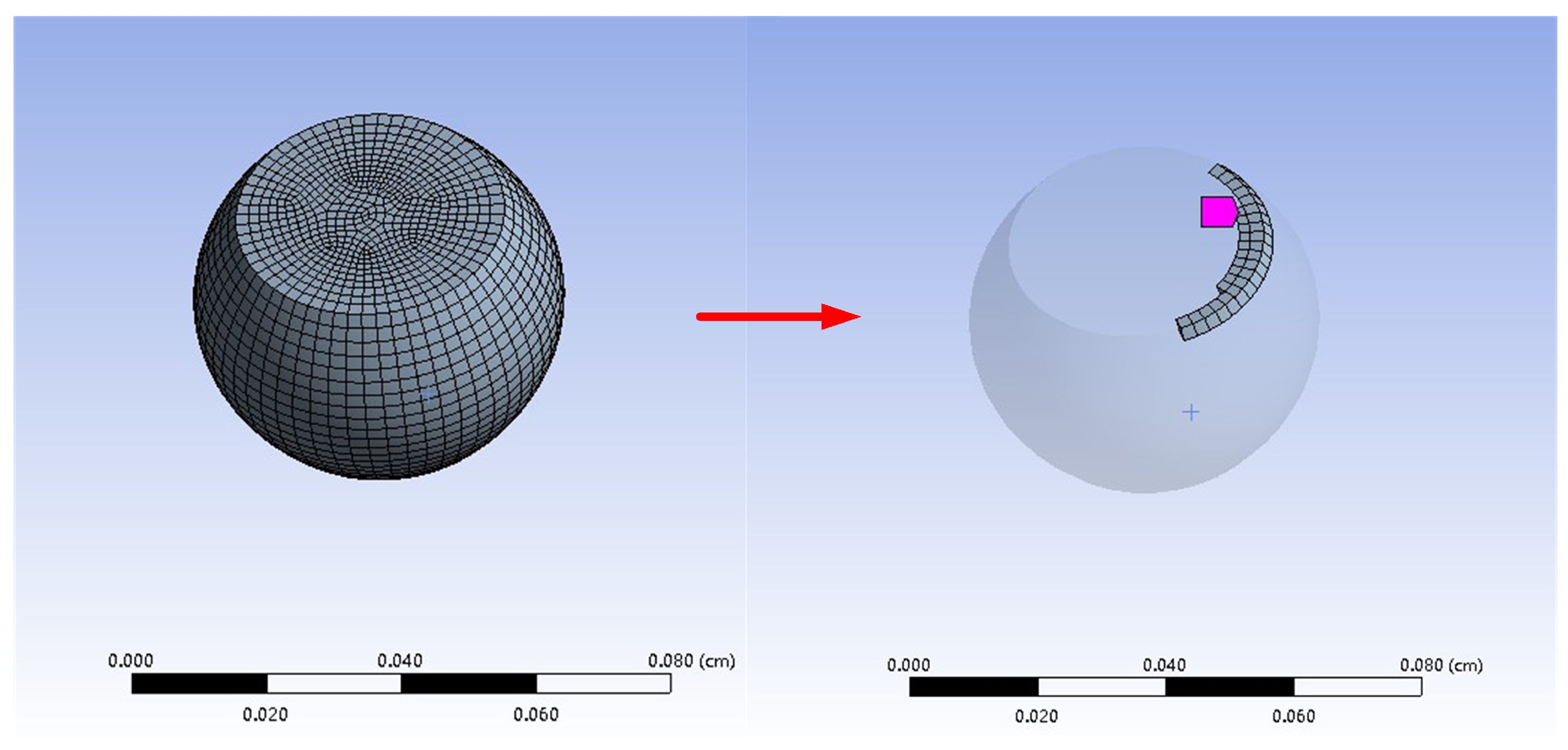
3.2. Failure Time Calculation Based on Black’s Equation and Atomic Flux Divergence Method
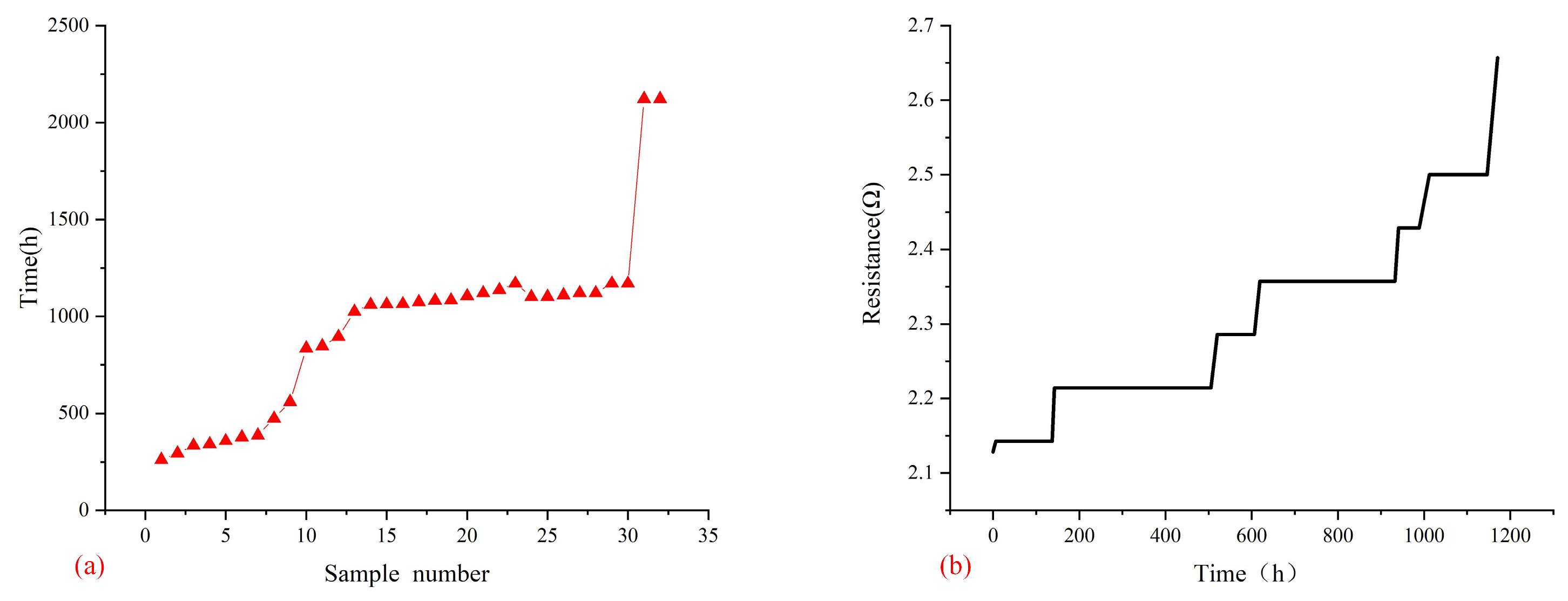
3.3. Failure Time Based on Experiment Results
3.4. Kinetics of IMC Growth during the EM Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Annuar, S.; Mahmoodian, R.; Hamdi, M.; Tu, K.-N. Intermetallic compounds in 3D integrated circuits technology: A brief review. Sci. Technol. Adv. Mater. 2017, 18, 693–703. [Google Scholar] [CrossRef] [Green Version]
- Tian, W.; Cui, H.; Yu, W. Analysis and Experimental Test of Electrical Characteristics on Bonding Wire. Electronics 2019, 8, 365. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Fu, G.; Wan, B.; Wu, Z.; Yan, X.; Zhang, W. A study on the effects of electrical and thermal stresses on void formation and migration lifetime of Sn3.0Ag0.5Cu solder joints. Solder. Surf. Mt. Technol. 2022, 34, 162–173. [Google Scholar] [CrossRef]
- He, Y.-f.; Wang, F.; Lu, T.j. Current Situation and Prospect of Lead-free Electroplating Technology in Electronic Industry. Surf. Technol. 2017, 46, 287–292. [Google Scholar]
- Liu, Y.; Li, M.; Kim, D.W.; Gu, S.; Tu, K.N. Synergistic effect of electromigration and Joule heating on system level weak-link failure in 2.5D integrated circuits. J. Appl. Phys. 2015, 118, 135304. [Google Scholar] [CrossRef]
- Huang, Y.T.; Hsu, H.H.; Wu, A.T. Electromigration-induced back stress in critical solder length for three-dimensional integrated circuits. J. Appl. Phys. 2014, 115, 034904. [Google Scholar] [CrossRef]
- Liang, L.; Zhang, Y.; Liu, Y. Prediction of Electromigration Failure of Solder Joints and Its Sensitivity Analysis. J. Electron. Packag. 2011, 133, 031002. [Google Scholar] [CrossRef]
- An, R.; Tian, Y.; Zhang, R.; Wang, C. Electromigration-induced intermetallic growth and voids formation in symmetrical Cu/Sn/Cu and Cu/Intermetallic compounds (IMCs)/Cu joints. J. Mater. Sci. Mater. Electron. 2015, 26, 2674–2681. [Google Scholar] [CrossRef]
- Wang, F.; Li, D.; Tian, S.; Zhang, Z.; Wang, J.; Yan, C. Interfacial behaviors of Sn-Pb, Sn-Ag-Cu Pb-free and mixed Sn-Ag-Cu/Sn-Pb solder joints during electromigration. Microelectron. Reliab. 2017, 73, 106–115. [Google Scholar] [CrossRef]
- Jin, Z.; Shen, Y.A.; He, S.; Zhou, S.; Nishikawa, H. Novel polarity effect on intermetallic compound thickness changes during electromigration in Cu/Sn-3.0Ag-0.5Cu/Cu solder joints. J. Appl. Phys. 2019, 126, 185109. [Google Scholar] [CrossRef]
- Lin, T.W.; Shie, K.C.; Chen, C.; Tu, K.N. Study of Electromigration of Solder Microbumps by 3D X-ray Microscopy. In Proceedings of the 2020 15th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 21–23 October 2020; pp. 76–78. [Google Scholar]
- AbdelAziz, M.; Xu, D.E.; Wang, G.; Mayer, M. Electromigration in solder joints: A cross-sectioned model system for real-time observation. Microelectron. Reliab. 2021, 119, 114068. [Google Scholar] [CrossRef]
- Qin, H.; Liu, T.; Li, W.; Yue, W.; Yang, D. Influence of microstructure inhomogeneity on the current density and temperature gradient in microscale line-type Sn58Bi solder joints under current stressing. Microelectron. Reliab. 2020, 115, 113995. [Google Scholar] [CrossRef]
- Xu, K.; Fu, X.; Wang, X.; Fu, Z.; Yang, X.; Chen, S.; Shi, Y.; Huang, Y.; Chen, H. The Effect of Grain Orientation of β-Sn on Copper Pillar Solder Joints during Electromigration. Materials 2022, 15, 108. [Google Scholar] [CrossRef]
- Madanipour, H.; Kim, Y.R.; Kim, C.U.; Mishra, D.; Thompson, P. Study of electromigration in Sn-Ag-Cu micro solder joint with Ni interfacial layer. J. Alloys Compd. 2021, 862, 158043. [Google Scholar] [CrossRef]
- Mao, X.; Zhang, R.; Hu, X. Influence of Ni foam/Sn composite solder foil on IMC growth and mechanical properties of solder joints bonded with solid-liquid electromigration. Intermetallics 2021, 131, 107107. [Google Scholar] [CrossRef]
- Weide-Zaage, K.; Dalleau, D.; Yu, X. Static and dynamic analysis of failure locations and void formation in interconnects due to various migration mechanisms. Mater. Sci. Semicond. Process. 2003, 6, 85–92. [Google Scholar] [CrossRef]
- Hu, S.H.; Lin, T.C.; Kao, C.L.; Huang, F.Y.; Tsai, Y.Y.; Hsiao, S.C.; Kuo, J.C. Effects of bismuth additions on mechanical property and microstructure of SAC-Bi solder joint under current stressing. Microelectron. Reliab. 2021, 117, 114041. [Google Scholar] [CrossRef]
- Yao, W. Damage Mechanics of Electromigration and Thermomigration in Electronics Packaging Solder Joints under Time Varying Current Loading. Ph.D. Thesis, State University of New York at Buffalo, Buffalo, NY, USA, 2013. [Google Scholar]
- Basaran, C.; Lin, M. Damage mechanics of electromigration induced failure. Mech. Mater. 2008, 40, 66–79. [Google Scholar] [CrossRef]
- Park, M.S.; Gibbons, S.L.; Arróyave, R. Phase-field simulations of intermetallic compound evolution in Cu/Sn solder joints under electromigration. Acta Mater. 2013, 61, 7142–7154. [Google Scholar] [CrossRef]
- Dalleau, D.; Weide-Zaage, K. Three-Dimensional Voids Simulation in chip Metallization Structures: A Contribution to Reliability Evaluation. Microelectron. Reliab. 2001, 41, 1625–1630. [Google Scholar] [CrossRef]
- Tu, K.N.; Gusak, A.M. A unified model of mean-time-to-failure for electromigration, thermomigration, and stress-migration based on entropy production. J. Appl. Phys. 2019, 126, 075109. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, Y.; Chen, Y.; Chen, S.; Cui, H. Simulation Research on Electromigration of BGA Devices. In Proceedings of the 2021 22nd International Conference on Electronic Packaging Technology (ICEPT), Xiamen, China, 14–17 September 2021; pp. 1–5. [Google Scholar]
- Choi, W.J.; Yeh, E.C.C.; Tu, K.N. Mean-time-to-failure study of flip chip solder joints on Cu/Ni(V)/Al thin-film under-bump-metallization. J. Appl. Phys. 2003, 94, 5665–5671. [Google Scholar] [CrossRef] [Green Version]
- Hsu, Y.-C.; Chou, C.-K.; Liu, P.C.; Chen, C.; Yao, D.J.; Chou, T.; Tu, K.N. Electromigration in Pb-free SnAg3.8Cu0.7 solder stripes. J. Appl. Phys. 2005, 98, 033523. [Google Scholar] [CrossRef] [Green Version]
- Blech, I.A. Electromigration in thin aluminum films on titanium nitride. J. Appl. Phys. 1976, 47, 1203–1208. [Google Scholar] [CrossRef]
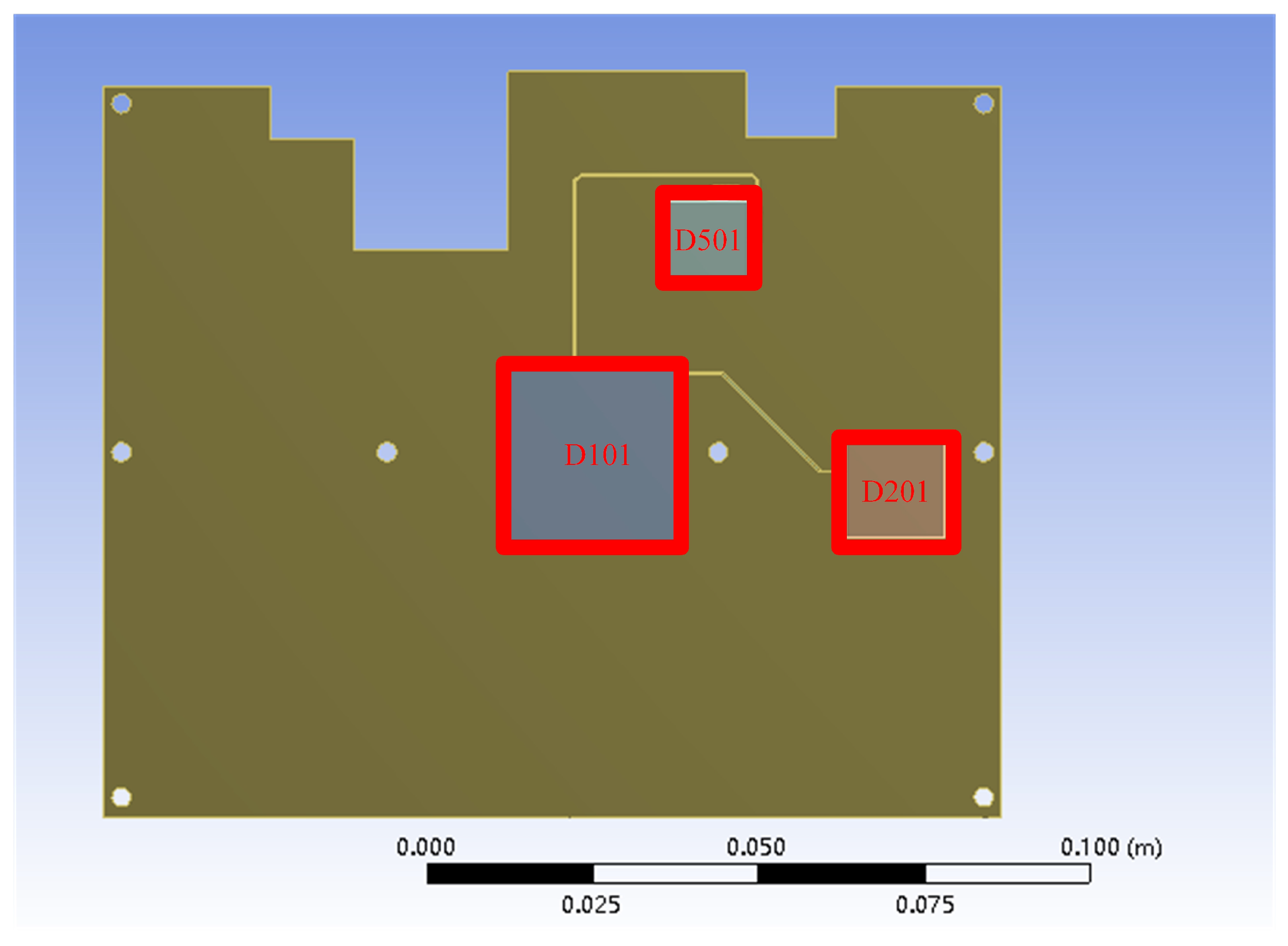








| Materials | ρ (g/cm3) | E (Gpa) | v | A (1 × 10−6/K) |
|---|---|---|---|---|
| Solder | 8.4 | 30 | 0.36 | 24.7 |
| FR4 | 1.859 | 11 | 0.28 | 13.6 |
| EMC | 1.820 | 8.7 | 0.3 | 12.4 |
| BT | 1.7 | 23.1 | 0.21 | 12.4 |
| Cu | 8.92 | 117 | 0.34 | 16.6 |
| Component | Parameter | Value (mm) |
|---|---|---|
| D101 | Length | 27 |
| Width | 27 | |
| Height | 0.6 | |
| D201 | Length | 15 |
| Width | 15 | |
| Height | 0.56 | |
| D501 | Length | 12.3 |
| Width | 11.5 | |
| Height | 1 |
| Step | Total Mass Flux Divergence (atoms/m3·s) | Average Life of Element (h) |
|---|---|---|
| 1 | 1.70 × 10−4 | 3.76 |
| 2 | 1.78 × 10−4 | 3.59 |
| 3 | 1.88 × 10−4 | 3.40 |
| 4 | 2.00 × 10−4 | 3.20 |
| 5 | 2.41 × 10−4 | 2.65 |
| 6 | 2.71 × 10−4 | 2.36 |
| 7 | 2.99 × 10−4 | 2.14 |
| 8 | 3.20 × 10−4 | 2.00 |
| 9 | 3.51 × 10−4 | 1.82 |
| 10 | 4.01 × 10−4 | 1.60 |
| Method | Failure Time (h) | Error |
|---|---|---|
| Experiment | 1065 h | / |
| Black’s equation | 588 h | 44.78% |
| AFD | 954.91 h | 10.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Tian, W.; Zhang, Y.; Chen, Z. The Study of the Reliability of Complex Components during the Electromigration Process. Micromachines 2023, 14, 499. https://doi.org/10.3390/mi14030499
Cui H, Tian W, Zhang Y, Chen Z. The Study of the Reliability of Complex Components during the Electromigration Process. Micromachines. 2023; 14(3):499. https://doi.org/10.3390/mi14030499
Chicago/Turabian StyleCui, Hao, Wenchao Tian, Yiming Zhang, and Zhiqiang Chen. 2023. "The Study of the Reliability of Complex Components during the Electromigration Process" Micromachines 14, no. 3: 499. https://doi.org/10.3390/mi14030499
APA StyleCui, H., Tian, W., Zhang, Y., & Chen, Z. (2023). The Study of the Reliability of Complex Components during the Electromigration Process. Micromachines, 14(3), 499. https://doi.org/10.3390/mi14030499





