Measurement of Complex Permittivity for Rapid Detection of Liquid Concentration Using a Reusable Octagon-Shaped Resonator Sensor
Abstract
1. Introduction
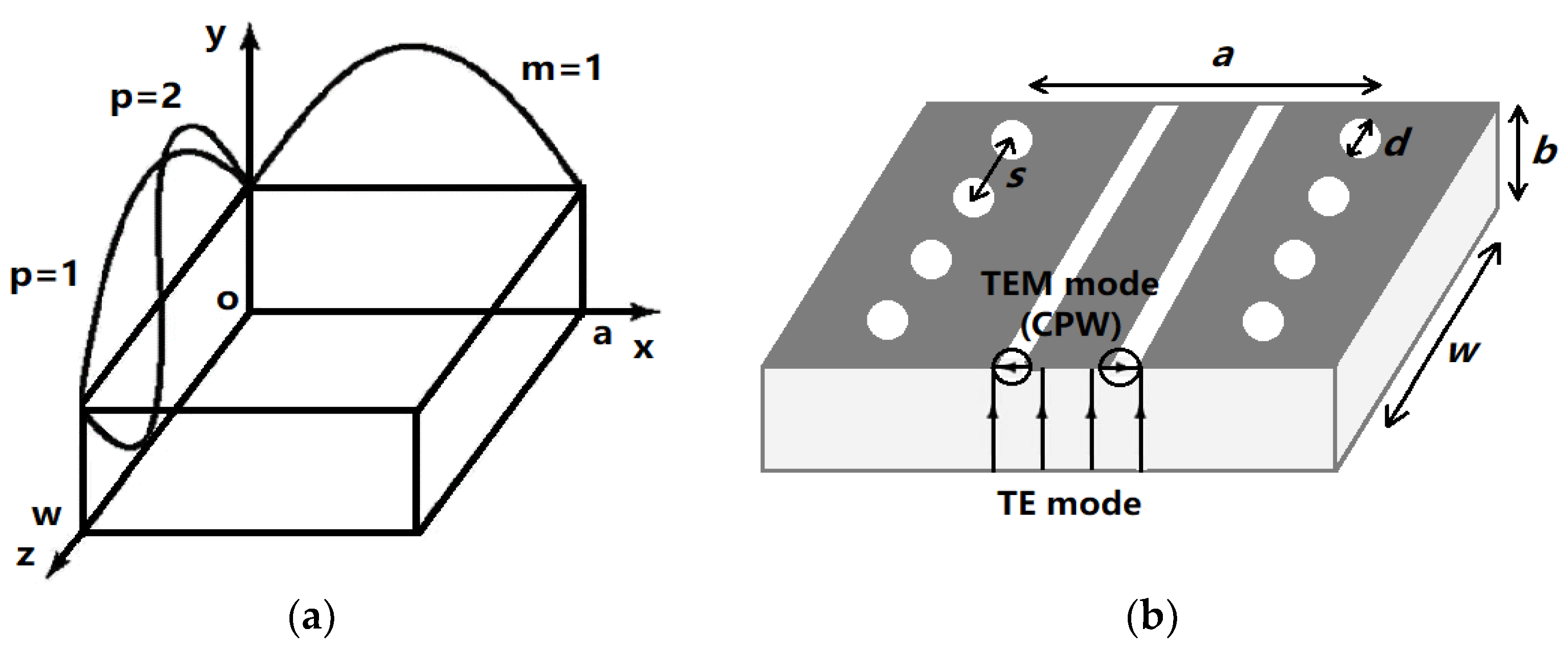
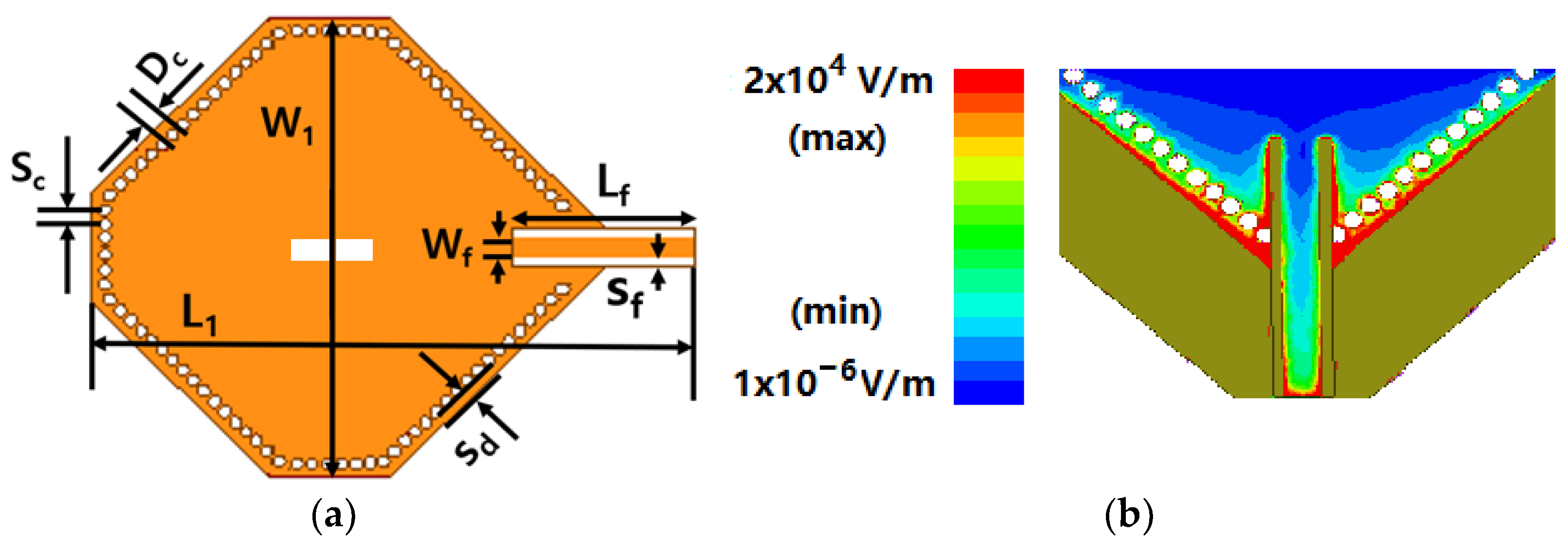
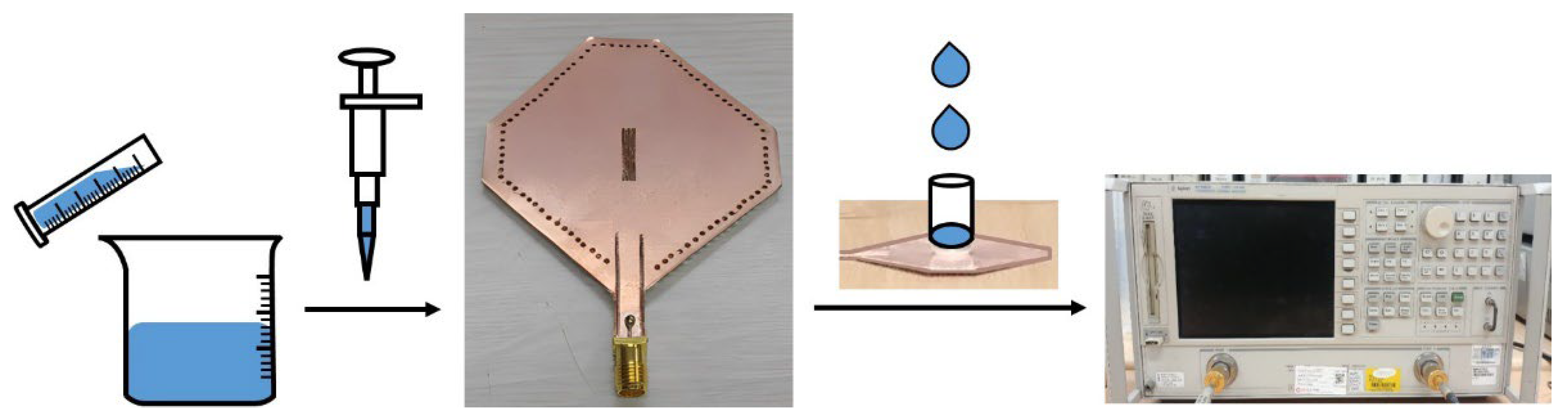
2. Materials and Methods
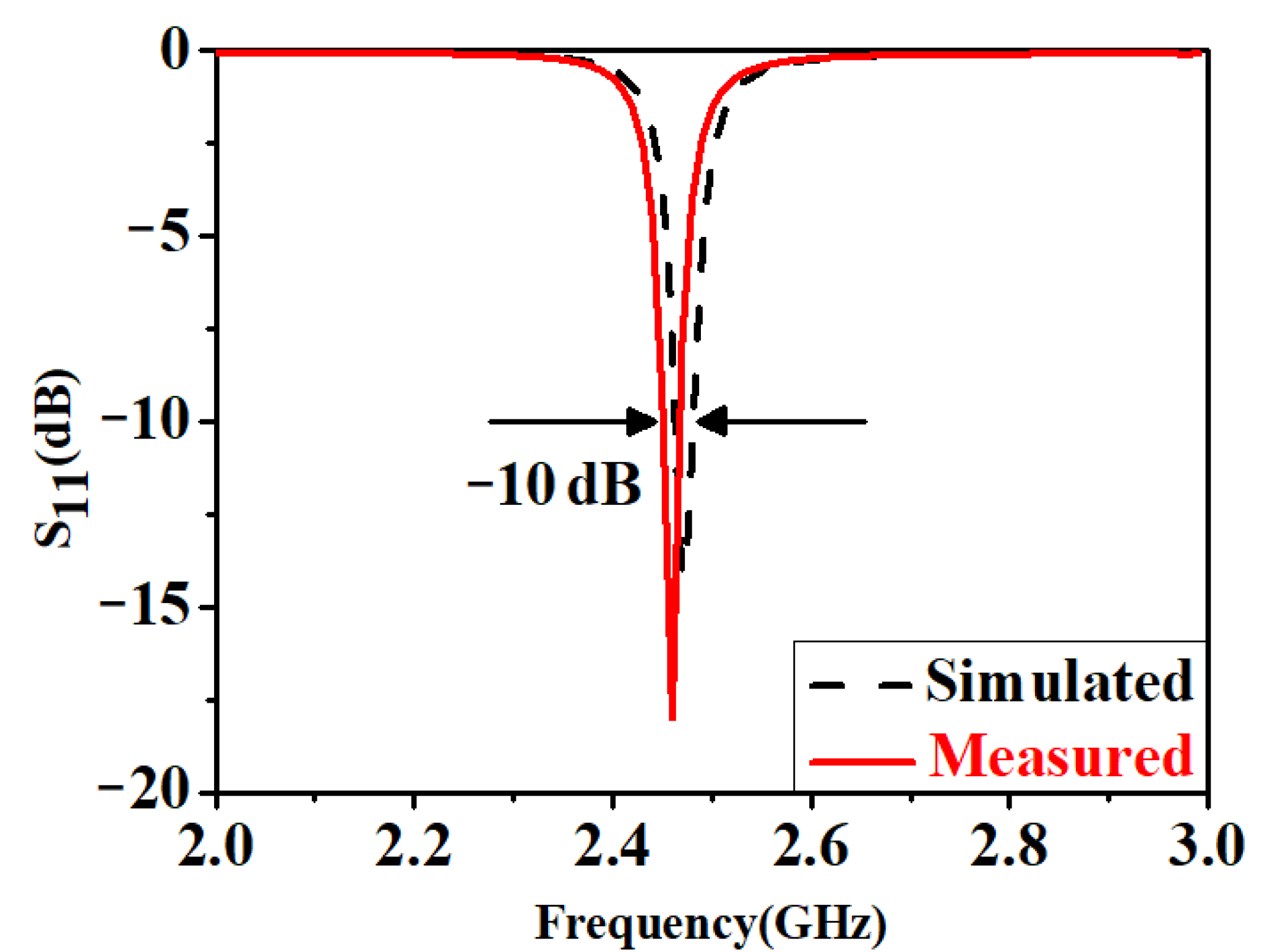
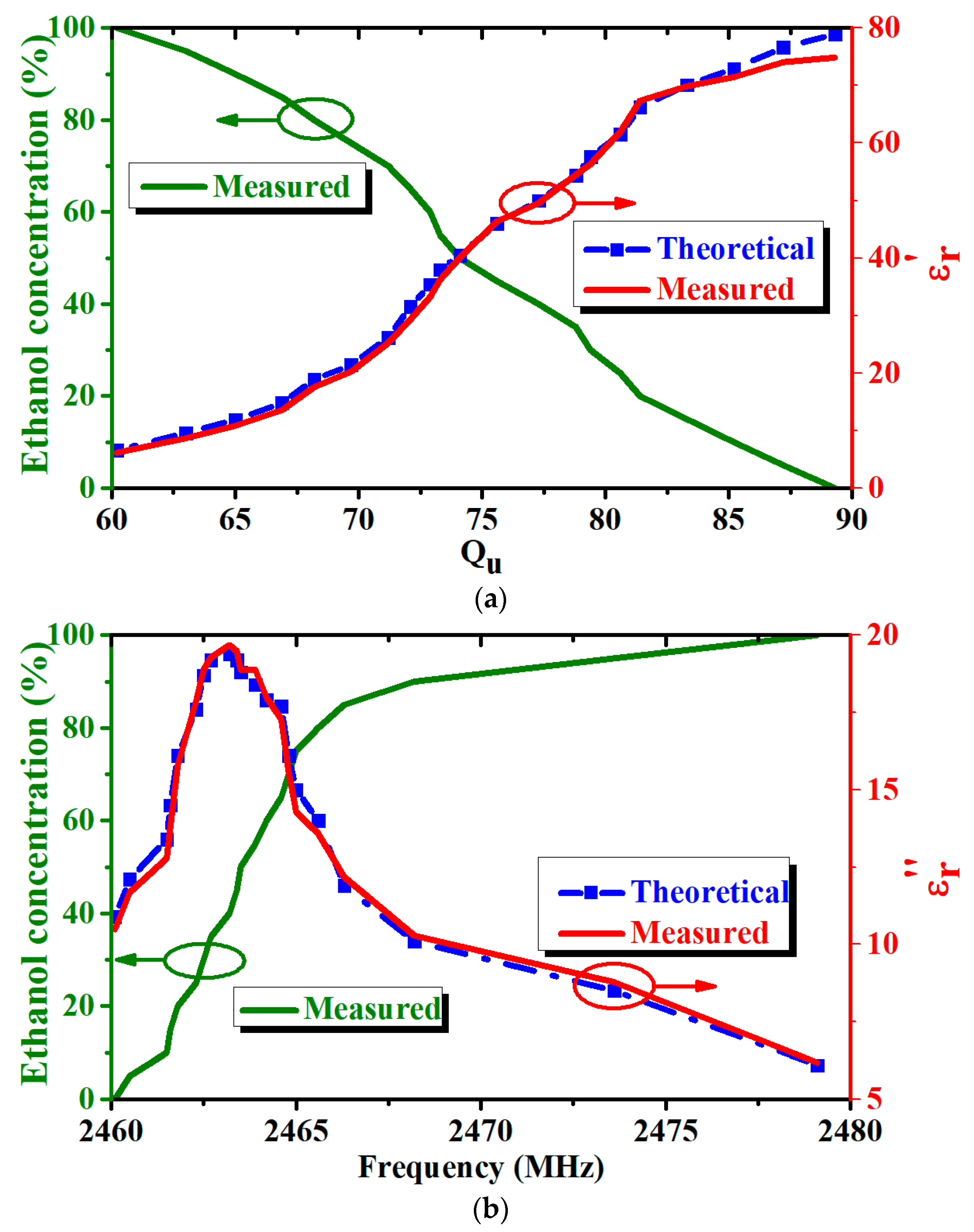
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fleming, W.J. New automotive sensors—A review. IEEE Sens. J. 2008, 8, 1900–1921. [Google Scholar] [CrossRef]
- Uddin, M.J.; Ullah, M.H. The effective periodic homogeneous metamaterials for infinite complementary dielectric slab characteristics. Int. J. Appl. Electromagn. Mech. 2016, 50, 255–262. [Google Scholar] [CrossRef]
- de Graaf, G.; Lacerenza, G.; Wolffenbuttel, R.; Visser, J. Dielectric spectroscopy for measuring the composition of gasoline/water/ethanol mixtures. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Pisa, Italy, 11–14 May 2015; pp. 154–158. [Google Scholar] [CrossRef]
- Rocco, G.M.; Bozzi, M.; Schreurs, D.; Perregrini, L.; Marconi, S.; Alaimo, G.; Auricchio, F. 3-D printed microfluidic sensor in SIW technology for liquids’ characterization. IEEE Trans. Microw. Theory Tech. 2019, 68, 1175–1784. [Google Scholar] [CrossRef]
- Houtz, D.A.; Gu, D.; Walker, D.K. An improved two-port transmission line permittivity and permeability determination method with shorted sample. IEEE Trans. Microw. Theory Tech. 2016, 64, 3820–3827. [Google Scholar] [CrossRef]
- Siddiqui, O.; Ramzan, R.; Amin, M.; Ramahi, O.M. A non-invasive phase sensor for permittivity and moisture estimation based on anomalous dispersion. Sci. Rep. 2016, 6, 28626. [Google Scholar] [CrossRef]
- Venkatesh, M.S.; Raghavan, G.S.V. An overview of dielectric properties measuring techniques. Can. Biosyst. Eng. 2005, 47, 15–30. [Google Scholar]
- Piekarz, I.; Sorocki, J.; Wincza, K.; Gruszczynski, S. Liquids permittivity measurement using two-wire transmission line sensor. IEEE Sens. J. 2018, 18, 7458–7466. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, C.; Haq, T.U.; Chen, K. High-sensitivity microwave sensor for liquid characterization using a complementary circular spiral resonator. Sensors 2019, 19, 787. [Google Scholar] [CrossRef]
- Wang, Y.; Quan, C.H.; Liu, F.X.; Zhang, X.Y.; Lee, J.C. A new chipless RFID permittivity sensor system. IEEE Access 2021, 9, 35027–35033. [Google Scholar] [CrossRef]
- Liu, C.J.; Tong, F. An SIW resonator sensor for liquid permittivity measurements at C band. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 751–753. [Google Scholar] [CrossRef]
- Wei, Z.; Huang, J.; Li, J.; Xu, G.; Ju, Z.; Liu, X.; Ni, X. A high-sensitivity microfluidic sensor based on a substrate integrated waveguide re-entrant cavity for complex permittivity measurement of liquids. Sensors 2018, 18, 4005. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Long, Z.; Shinohara, N.; Liu, C. A substrate integrated waveguide resonator sensor for dual-band complex permittivity measurement. Processes 2022, 10, 708. [Google Scholar] [CrossRef]
- Bozzi, M.; Georgiadis, A.; Wu, K. Review of substrate-integrated waveguide circuits and antennas. IET Microw. Antennas Propag. 2011, 5, 909–920. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 272–297. [Google Scholar]
- Varshney, P.K.; Akhtar, M.J. Permittivity estimation of dielectric substrate materials via enhanced SIW sensor. IEEE Sens. J. 2021, 21, 12104–12112. [Google Scholar] [CrossRef]
- Khan, A.A.; Mandal, M.K.; Sanyal, S. Unloaded quality factor of a substrate integrated wave guide resonator and its variation with the substrate parameters. In Proceedings of the 2013 International Conference on Microwave and Photonics, Dhanbad, India, 13–15 December 2013. [Google Scholar]
- Sekar, V.; Torke, W.J.; Palermo, S.; Entesari, K. A self-sustained microwave system for dielectric-constant measurement of lossy organic liquids. IEEE Trans. Microw. Theory Tech. 2012, 60, 1444–1455. [Google Scholar] [CrossRef]
- Liu, C.J.; Pu, Y. A microstrip resonator with slotted ground plane for complex permittivity measurements of liquids. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 257–259. [Google Scholar] [CrossRef]
- Kitahara, H.; Yagi, T.; Mano, K.; Takeda, M.W. Dielectric characteristics of water solutions of ethanol in the terahertz region. J. Korean Phys. Soc. 2005, 46, 82–85. [Google Scholar]
- Paleczek, A.; Grochala, D.; Rydosz, A. Artificial breath classification using XGBoost algorithm for diabetes detection. Sensors 2021, 21, 4187. [Google Scholar] [CrossRef]
- Sharma, P.K.; Kim, E.S.; Mishra, S.; Ganbold, E.; Seong, R.S.; Kaushik, A.K.; Kim, N.Y. Ultrasensitive and reusable graphene oxide-modified double-interdigitated capacitive (DIDC) sensing chip for detecting SARS-CoV-2. ACS Sens. 2021, 6, 3468–3476. [Google Scholar] [CrossRef]
- Podlepetsky, B.; Kovalenko, A. Errors of integrated hydrogen sensors based on FETs with structure Pd (Ag)-Ta2O5-SiO2-Si. J. Electrochem. Soc. 2020, 167, 167524. [Google Scholar] [CrossRef]
- Sato, T.; Chiba, A.; Nozaki, R. Dynamical aspects of mixing schemes in ethanol-water mixtures in terms of the excess partial molar activation free energy, enthalpy, and entropy of the dielectric relaxation process. J. Chem. Phys. 1999, 110, 2508–2521. [Google Scholar] [CrossRef]
- Sato, T.; Chiba, A.; Nozaki, R. Composition-dependent dynamical structures of monohydric alcohol-water mixtures studied by microwave dielectric analysis. J. Mol. Liq. 2002, 96–97, 327–339. [Google Scholar] [CrossRef]
- Webb, W.E.; Church, R.H. Measurement of dielectric properties of minerals at microwave frequencies; US Department of the Interior, Bureau of Mines: Washington, DC, USA, 1986; pp. 1–8. [Google Scholar]
- Ramos, A.; Girbau, D.; Lazaro, A.; Villarino, R. Wireless concrete mixture composition sensor based on time-coded UWB RFID. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 681–683. [Google Scholar] [CrossRef]
- Biswas, M.; Dam, M. Investigation of equilateral triangular patch antenna covered with several dielectric layers: Theoretical and experimental study. J. Electromagn. Waves Appl. 2021, 35, 1770–1801. [Google Scholar] [CrossRef]
- Mohd Bahar, A.A.; Zakaria, Z.; Isa, M.M.; Dasril, Y.; Alahnomi, R.A. Real time microwave biochemical sensor based on circular SIW approach for aqueous dielectric detection. Sci. Rep. 2019, 9, 5467. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-sensitivity microwave sensor for microfluidic complex permittivity measurement. IEEE Trans. Microw. Theory Tech. 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
- Salim, A.; Memon, M.U.; Jeong, H.; Lim, S. Simplified approach to detect dielectric constant using a low-cost microfluidic quarter mode substrate-integrated waveguide. Sensors 2020, 20, 4985. [Google Scholar] [CrossRef]
- Hamzah, H.; Lees, J.; Porch, A. Split ring resonator with optimised sensitivity for microfluidic sensing. Sens. Actuators A Phys. 2018, 276, 1–10. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly enhanced sensitivity in planar microwave sensors based on metamaterial coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef]
- Javed, A.; Arif, A.; Zubair, M.; Mehmood, M.Q.; Riaz, K. A low-cost multiple complementary split-ring resonator based microwave sensor for contactless dielectric characterization of liquids. IEEE Sens. J. 2020, 20, 11326–11334. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Xiang, Y.; Fu, L.; Gu, W.; Wu, F. A modified SIW re-entrant microfluidic microwave sensor for characterizing complex permittivity of liquids. IEEE Sens. J. 2021, 21, 14838–14846. [Google Scholar] [CrossRef]
- Cao, Q.; Al-Qadi, I.L. Development of a numerical model to predict the dielectric properties of heterogeneous asphalt concrete. Sensors 2021, 21, 2643. [Google Scholar] [CrossRef] [PubMed]
- Roshani, S.; Dehghani, K.; Roshani, S. A lowpass filter design using curved and fountain shaped resonators. Frequenz 2019, 73, 267–272. [Google Scholar] [CrossRef]
- Hookari, M.; Roshani, S.; Roshani, S. Design of a low pass filter using rhombus-shaped resonators with an analyticalLC equivalent circuit. Turk. J. Electr. Eng. Comp. Sci. 2020, 28, 865–874. [Google Scholar] [CrossRef]
- Zhu, L.; Li, X.; Kasuga, T.; Uetani, K.; Nogi, M.; Koga, H. All-cellulose-derived humidity sensor prepared via direct laser writing of conductive and moisture-stable electrodes on TEMPO-oxidized cellulose paper. J. Mater. Chem. C 2022, 10, 3712–3719. [Google Scholar] [CrossRef]
- You, J. Lessons from South Korea’s COVID-19 policy response. Am. Rev. Public Adm. 2020, 50, 801–808. [Google Scholar] [CrossRef]
- Ullah, M.H.; Uddin, M.J.; Latef, T.A.; Mahadi, W.N.L.; Ahsan, M.R.; Islam, M.T. Constitutive parameter analysis of left-handed dual-star split-ring resonator metamaterial for homogeneous infinite slab. IET Microw. Antennas Propag. 2015, 9, 1740–1746. [Google Scholar] [CrossRef]


| Temperature (℃) | f0 (MHz) | Qu |
|---|---|---|
| 30 | 2453.7 | 87.5 |
| 25 | 2460.0 | 89.2 |
| 20 | 2467.2 | 92.1 |
| Reference | Structure | Frequency (GHz) | Relative Size (λ0 × λ0) | Error |
|---|---|---|---|---|
| [32] | Split-ring resonator | 2.5 | 0.15 × 0.15 | 6.5% |
| [33] | Open-loop resonator | 2.6 | >0.18 × 0.09 | 6.3% |
| [12] | Square SIW | 2.19 | 0.4 × 0.36 | 3.2% |
| [29] | Circular SIW | 4.4 | 1.17 × 1.17 | 0.9% |
| [30] | Stepped impedance resonator | 1.91 | 0.26 × 0.2 [33] | 4.5% |
| [4] | SIW using 3-D printing | 3.82 | 0.66 × 0.66 | 11.6% |
| [34] | Multiple complementary split-ring | 2.45 | 0.27 × 0.2 | 4.9% |
| [31] | Quarter mode SIW | 4.55 | 0.91 × 091 | 3.9% |
| [35] | SIW re-entrant cavity resonator | 2.29 | 0.49 × 0.49 | 7.8% |
| [13] | Dual-band SIW | 2.45/5.85 | >1.05 × 0.72 | 2.7% |
| This work | Octagon-shaped SIW | 2.45 | 0.65 × 0.49 | 3.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, C.-H.; Zhang, X.-Y.; Lee, J.-C. Measurement of Complex Permittivity for Rapid Detection of Liquid Concentration Using a Reusable Octagon-Shaped Resonator Sensor. Micromachines 2023, 14, 542. https://doi.org/10.3390/mi14030542
Quan C-H, Zhang X-Y, Lee J-C. Measurement of Complex Permittivity for Rapid Detection of Liquid Concentration Using a Reusable Octagon-Shaped Resonator Sensor. Micromachines. 2023; 14(3):542. https://doi.org/10.3390/mi14030542
Chicago/Turabian StyleQuan, Chun-He, Xiao-Yu Zhang, and Jong-Chul Lee. 2023. "Measurement of Complex Permittivity for Rapid Detection of Liquid Concentration Using a Reusable Octagon-Shaped Resonator Sensor" Micromachines 14, no. 3: 542. https://doi.org/10.3390/mi14030542
APA StyleQuan, C.-H., Zhang, X.-Y., & Lee, J.-C. (2023). Measurement of Complex Permittivity for Rapid Detection of Liquid Concentration Using a Reusable Octagon-Shaped Resonator Sensor. Micromachines, 14(3), 542. https://doi.org/10.3390/mi14030542






