Analysis of Von Kármán Swirling Flows Due to a Porous Rotating Disk Electrode
Abstract
:1. Introduction
2. Mathematical Formulation of the Problems
3. Analytical Expressions of Velocity Components Using the Homotopy Analysis Method
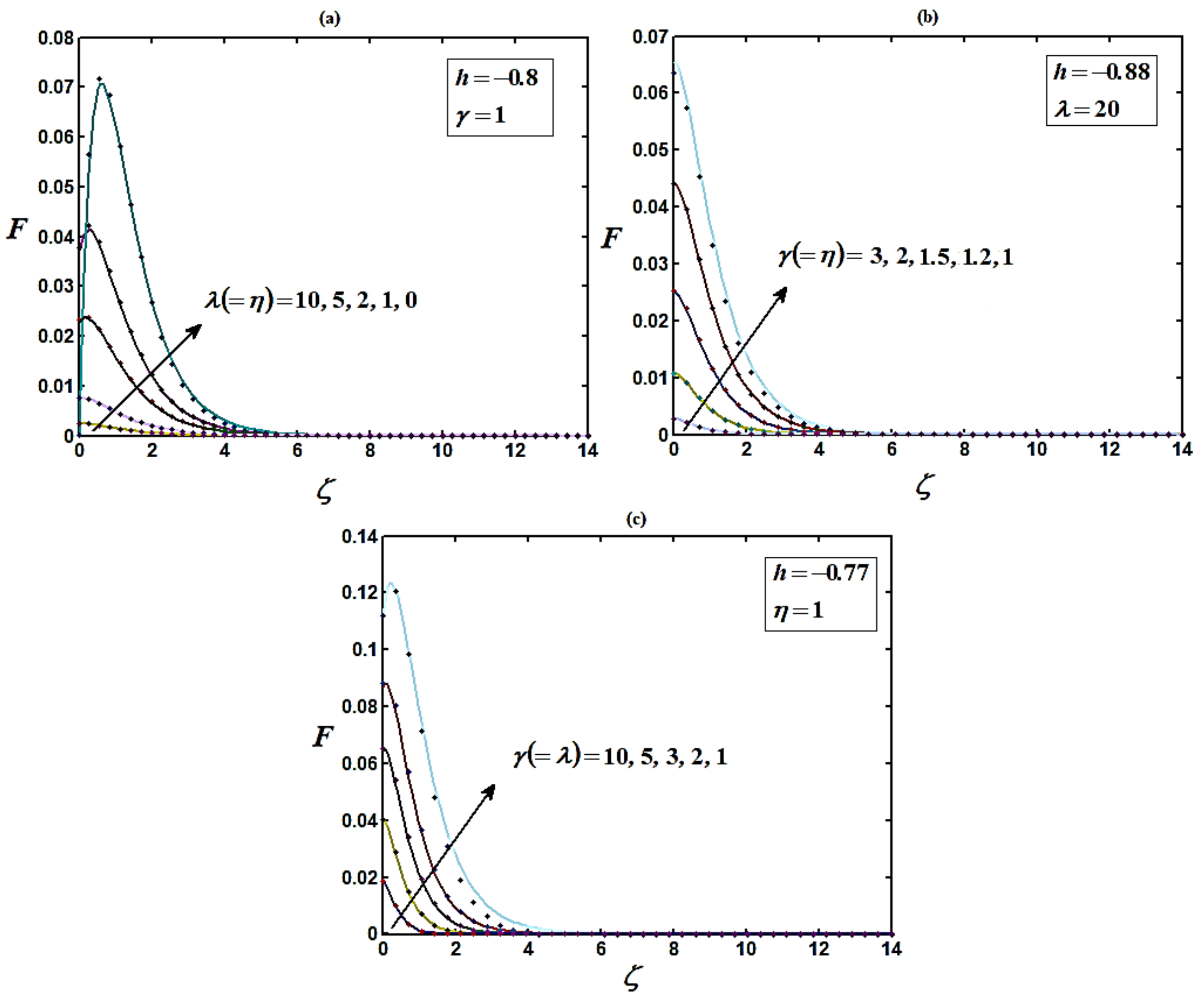
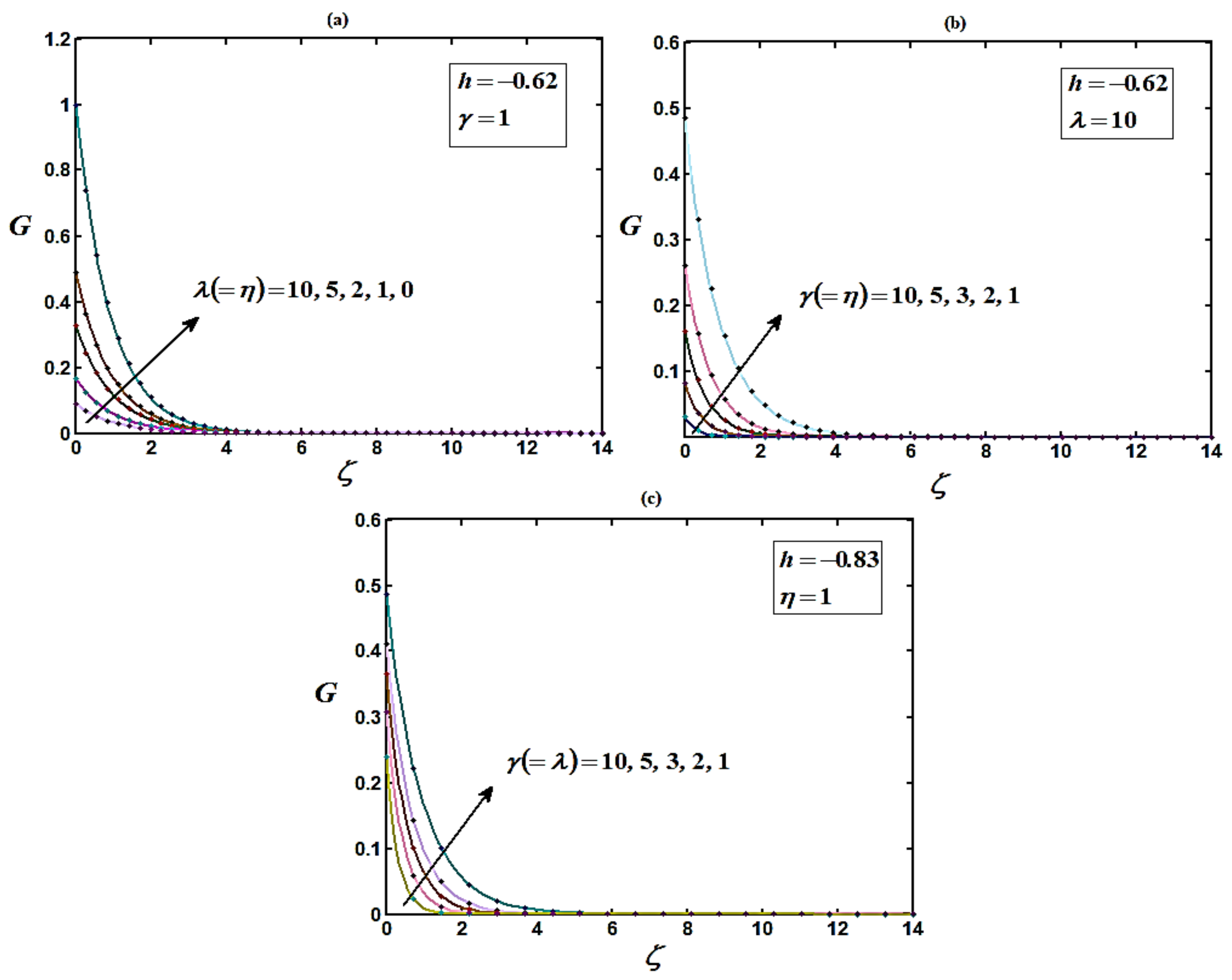
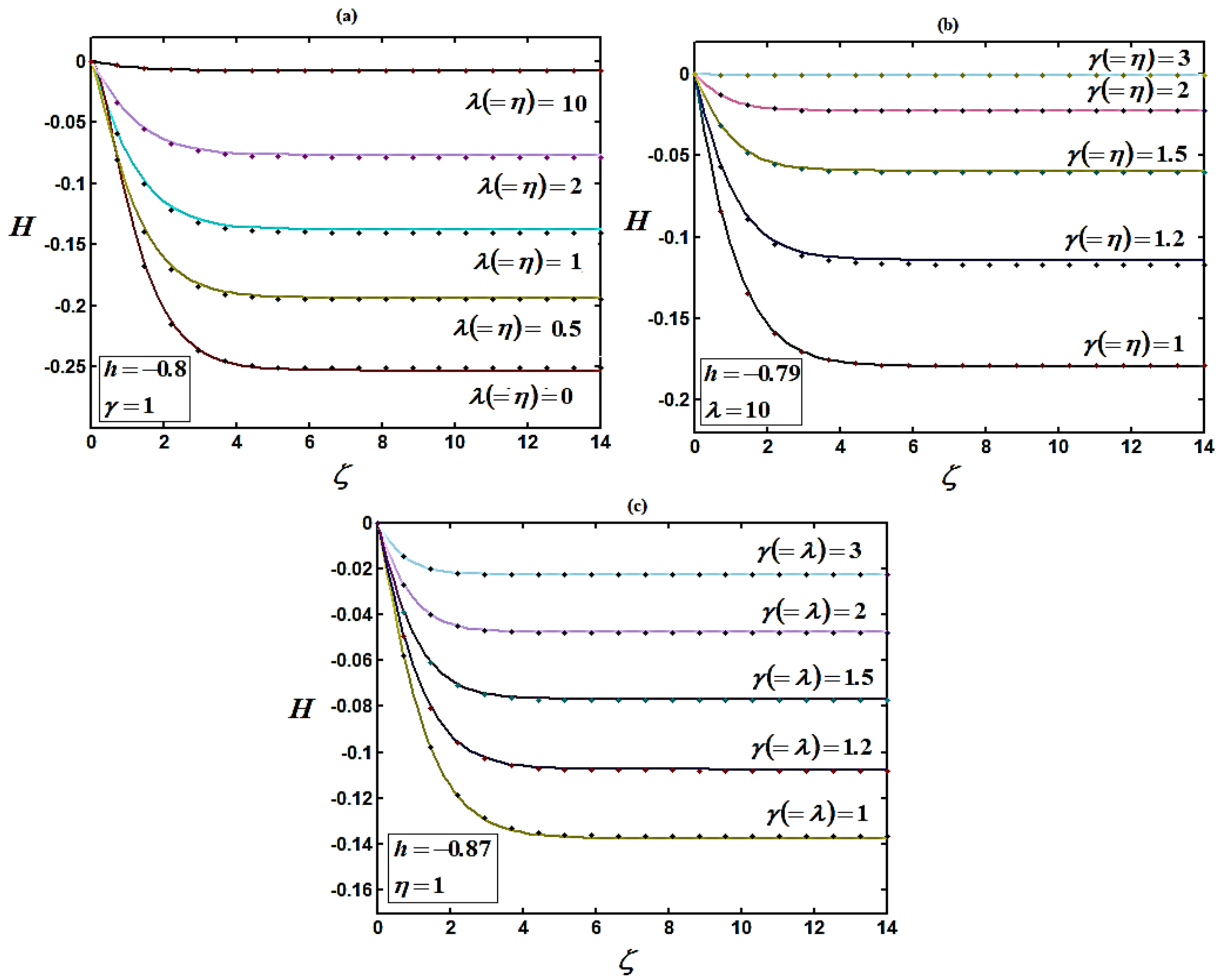
4. Numerical Simulations
5. Discussion
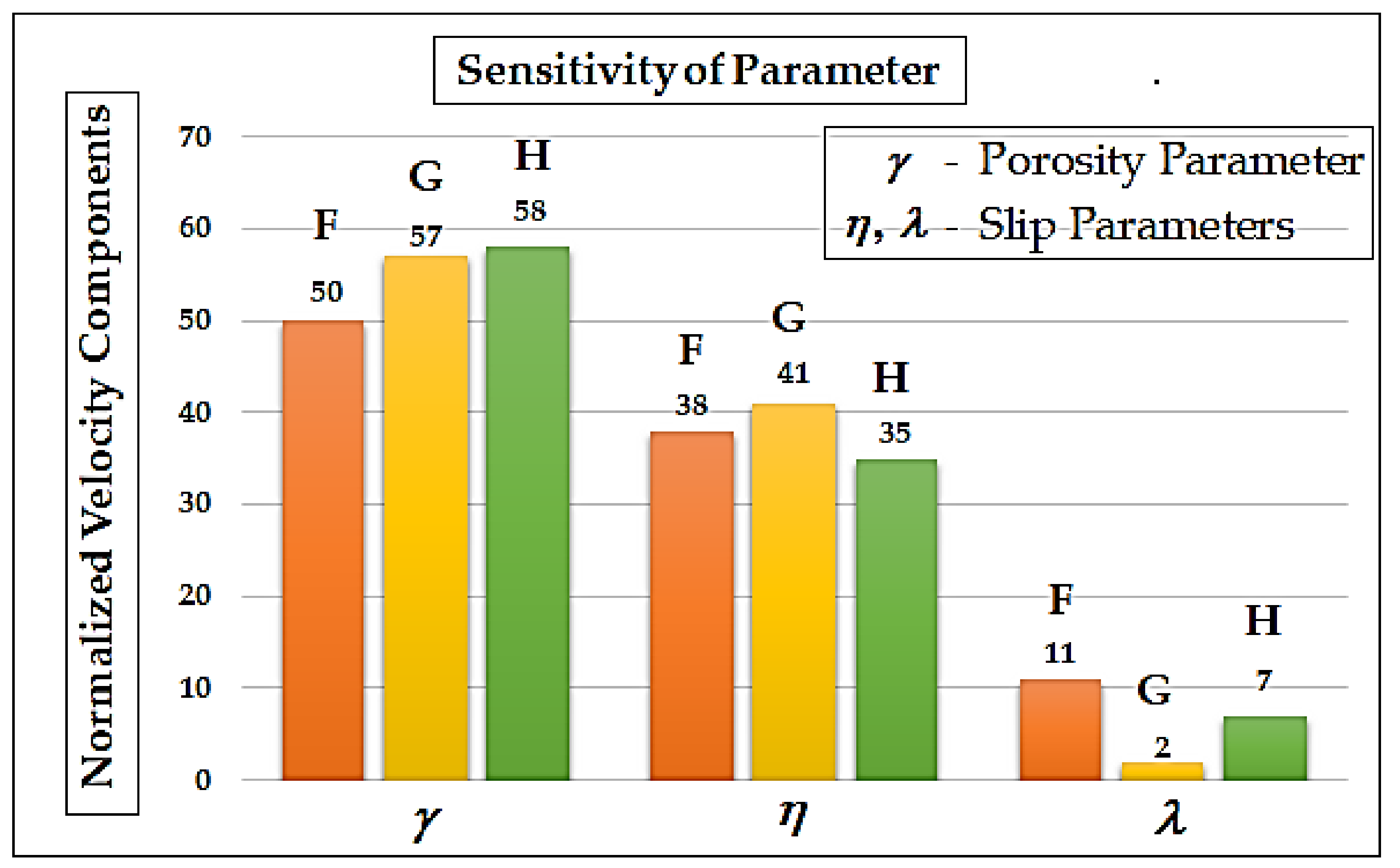
6. Differential Sensitivity Analysis of Parameters
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cm | dimensionless moment coefficient (−); |
| cp | heat capacity of the fluid at constant pressure (J/kg/K); |
| F, G, H | normalized radial, tangential, and axial velocity components (−); |
| K | Darcy permeability (m2); |
| Nu | Nusselt number (−); |
| p, P | pressure (Pa) and normalized pressure (−); |
| Pr | Prandtl number (−); |
| q | heat flux supplied to the disk (W/m2); |
| r, φ, z | cylindrical coordinates (m); |
| Re | rotational Reynolds number (−); |
| T | temperature (K); |
| u, v, w | radial, tangential, and axial velocity components (m/s); |
| β | normalized temperature slip factor (−); |
| β1 | proportionality constant (−); |
| ε | porosity (−); |
| γ | normalized porosity parameter (−); |
| κ | thermal conductivity of the fluid (W/(m K)); |
| λ, η | normalized velocity slip parameters (−); |
| µ, ν | dynamic (Pa.s) and kinematic (m2/s) fluid viscosities; |
| Ω | rotation rate of the disk (rad/s); |
| ρ | voluminal mass of the fluid (kg/m3); |
| ζ | normalized distance from the disk (−); |
| θ | normalized temperature (−); |
| w | denotes a quantity evaluated at the wall; |
| denotes a quantity evaluated at infinity; | |
| ‘ | denotes a derived quantity according to the axial direction. |
Appendix A
Analytical Solution of Equations (7)–(9) Using the Homotopy Analysis Method
References
- Kataoka, H.; Tomiyama, A.; Hosokawa, S.; Sou, A.; Chaki, M. Two-phase swirling flow in a gas-liquid separator. J. Power Energy Sys. 2008, 2, 1120–1131. [Google Scholar] [CrossRef] [Green Version]
- Bonnecaze, R.; Mano, N.; Nam, B.; Heller, A. On the behavior of the porous rotating disc electrode. J. Electrochem. Soc. 2007, 154, F44–F47. [Google Scholar] [CrossRef]
- Vargas, R.; Borrás, C.; Mostanya, J.; Scharifker, B.R. Kinetics of surface reactions on rotating disk electrodes. Electrochim. Acta 2012, 80, 326–333. [Google Scholar] [CrossRef]
- Miklavcic, M.M.; Wang, C.Y. The Flow due to a Rough Rotating Disk. J. ApplMath. Phys. 2004, 55, 235–246. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Therm. Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Kármán, T.V. Über laminare und turbulente Reibung. ZAMM 1921, 1, 233–252. [Google Scholar] [CrossRef] [Green Version]
- Cochran, W.G. Flow due to a rotating disc. Proc. Camb. Philos. Soc. 1934, 30, 365–375. [Google Scholar] [CrossRef]
- Benton, E.R. On the flow due to a rotating disk. J. Fluid. Mech. 1966, 24, 781–800. [Google Scholar] [CrossRef]
- Millsaps, K.; Pohlhausen, K. Heat transfer by laminar flow from a rotating disk. J. Aeronaut. Sci. 1952, 19, 120–126. [Google Scholar] [CrossRef]
- Attia, H.A. Unsteady MHD flow near a rotating porous disk with uniform suction or injection. J. Fluid Dynam. Res. 1998, 23, 283–290. [Google Scholar] [CrossRef]
- Attia, H.A.; Aboul-Hassan, A.L. Effect of Hall Current on the Unsteady MHD Flow Due to a Rotating Disk with Uniform Suction or Injection. Appl. Math. Model. 2001, 25, 1089–1098. [Google Scholar] [CrossRef]
- Attia, H.A. On the effectiveness of uniform suction-injection on the unsteady flow due to a rotating disk with heat transfer. Int. Commun. Heat Mass 2002, 29, 653–661. [Google Scholar] [CrossRef]
- Stuart, J.T. On the effects of uniform suction on the steady flow due to a rotating disk Quart. J. Mech. Appl. Math. 1954, 7, 446–457. [Google Scholar] [CrossRef]
- Kuiken, H.K. The effect of normal blowing on the flow near a rotating disk of infinite extent. J. Fluid Mech. 1971, 47, 789–798. [Google Scholar] [CrossRef]
- Ockendon, H. An asymptotic solution for steady flow above an infinite rotating disk with suction Quart. J. Mech. Appl. Math. 1972, 25, 291–301. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Mohimanian Pour, S.A.; Hayat, T.; Obaidat, S. Analytic Approximate Solutions for Steady Flow over a Rotating Disk in Porous Medium with Heat Transfer by Homotopy Analysis Method. Comput. Fluids 2012, 54, 1–9. [Google Scholar] [CrossRef]
- Attia, H. Steady flow over a rotating disk in porous medium with heat transfer. Nonlinear Anal. Model. Cont. 2009, 14, 21–26. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.-S.; Bilal, M.; Khan, M.A.; Muhammad, T. Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk. Micromachines 2021, 12, 540. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Alotaibi, H.; Aljohani, H.M.; Wakif, A.; Khan, I.; Akram, S. Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field. Micromachines 2021, 12, 605. [Google Scholar] [CrossRef]
- Alotaibi, H.; Rafique, K. Numerical Analysis of Micro-Rotation Effect on Nanofluid Flow for Vertical Riga Plate. Crystals 2021, 11, 1315. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Alqarni, M.S.; Wakif, A.; Khan, I.; Bhutta, M.S. Numerical Scrutinization of Darcy-Forchheimer Relation in Convective Magnetohydrodynamic Nanofluid Flow Bounded by Nonlinear Stretching Surface in the Perspective of Heat and Mass Transfer. Micromachines 2021, 12, 374. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Wang, J.; Wang, C.; Yu, R.; Shi, L.; Xiao, L. Optical microfibers integrated with evanescent field triggered self-growing polymer nanofilms. Opt. Express 2022, 30, 18044–18053. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, A.; Chen, S.; Lum, G.Z.; Zhang, X. A perspective on magnetic microfluidics: Towards an intelligent future. Biomicrofluidics 2022, 16, 011301. [Google Scholar] [CrossRef] [PubMed]
- Shin, D.J.; Zhang, Y.; Wang, T.H. A droplet microfluidic approach to single-stream nucleic acid isolation and mutation detection. Microfluid. Nanofluidics 2014, 17, 425–430. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, T.H. Micro magnetic gyromixer for speeding up reactions in droplets. Microfluid. Nanofluidics 2012, 12, 787–794. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, S.; Lee, M.; Prakash, R.; Kim, H.; Cho, G.; Lee, J. Enhancing Mixing Performance in a Rotating Disk Mixing Chamber: A Quantitative Investigation of the Effect of Euler and Coriolis Forces. Micromachines 2022, 13, 1218. [Google Scholar] [CrossRef]
- Dehghan, M.; Heris, J.M.; Saadatmandi, A. Application of semi-analytic methods for the Fitzhugh-Nagumo equation, which models the transmission of nerve impulses. J. Math. Methods Appl. Sci. 2010, 33, 1384–1398. [Google Scholar] [CrossRef]
- Liao, S.J. On the Analysis of Variable Thermophysical Properties of Thermophoretic Viscoelastic Fluid Flow Past a Vertical Surface with nth Order of Chemical Reaction. Beyond Perturbation, An Introduction to Homotopy Analysis Method; Boca Raton Chapman Hall, CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Dehghan, M.; Salehi, R. Analytical Approach to Differential Equations with Piecewise Continuous Arguments via Modified Piecewise Variational Iteration Method. Comput. Phys. Commun. 2010, 181, 1255–1265. [Google Scholar] [CrossRef]
- Wang, Z.K.; Cao, T.A. An Introduction to Homotopy Methods; Chongqing Publishing House: Chongqing, China, 1991. [Google Scholar]
- Kamal, M.M.; Mohamad, A. Effect of Swirl on Performance of Foam Porous Medium Burners. J. Combust. Sciand. Tech. 2006, 178, 729–761. [Google Scholar] [CrossRef]
- Visuvasam, J.; Molina, A.; Laborda, E.; Rajendran, L. Mathematical Models of the Infinite Porous Rotating Disk Electrode. Int. J. Electrochem. Sci. 2018, 13, 9999–10022. [Google Scholar] [CrossRef]
- Muhammad, S.; Ghania, X.; Kottakkaran, S.N.; Muhammad, A.Z.R.; Muhammad, I.K.; Punith Gowda, R.J.; Prasannakumara, B.C. Ohmic heating effects and entropy generation for nanofluidic system of Ree-Eyring fluid: Intelligent computing paradigm. Int. Commun. Heat Mass Transf. 2021, 129, 105683. [Google Scholar]
- Yun, -J.X.; Faisal, S.; Ijaz, K.M.; Naveen Kumar, R.; Punith Gowda, R.J.; Prasannakumara, B.C.; Malik, M.Y.; Sami, U.K. New modeling and analytical solution of fourth grade (non-Newtonian) fluid by a stretchable magnetized Riga device. Int. J. Modern Phy. C 2022, 33, 2250013. [Google Scholar]
- Sunitha, M.; Gamaoun, F.; Abdulrahman, A.; Malagi, N.S.; Singh, S.; Gowda, R.J.; Gowda, R.J.P. An efficient analytical approach with novel integral transform to study the two-dimensional solute transport problem. Ain Shams Eng. J. 2022, 14, 101878. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Naveenkumar, R.; Madhukesh, J.K.; Prasannakumara, B.C.; Gorla, R.S.R. Theoretical analysis of SWCNT- MWCNT/H2O hybrid flow over an upward/downward moving rotating disk. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2021, 235, 97–106. [Google Scholar] [CrossRef]
- Naveen Kumar, R.; Hogarehally, B.M.; Nirmala, T.; Punith Gowda, R.J.; Deepak, U.S. Carbon nanotubes suspended dusty nanofluid flow over stretching porous rotating disk with non-uniform heat source/sink. Int. J. Comput. Methods Eng. Sci. Mech. 2022, 23, 119–128. [Google Scholar] [CrossRef]
- Naveen Kumar, R.; Gowda, R.J.P.; Gireesha, B.J. Non-Newtonian hybrid nanofluid flow over vertically upward/downward moving rotating disk in a Darcy–Forchheimer porous medium. Eur. Phys. J. Spec. Top. 2021, 230, 1227–1237. [Google Scholar] [CrossRef]
- Anwar Bég, O.; Mahabaleshwar, U.S.; Rashidi, M.M.; Rahimzadeh, N.; Curiel Sosa, J.L.; Sarris, I.; Laraqi, N. Homotopy analysis of magnetohydrodynamic convection flow in manufacture of a viscoelastic fabric for space applications. Int. J. Appl. Math. Mech. 2014, 10, 9–49. [Google Scholar]
- Sowmya, G.; Varun Kumar, R.S.; Alsulami, M.D.; Prasannakumara, B.C. Thermal stress and temperature distribution of an annular fin with variable temperature-dependent thermal properties and magnetic field using DTM-Pade approximant. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Jayaprakash, M.C.; Alsulami, M.D.; Shanker, B.; Varun Kumar, R.S. Investigation of Arrhenius activation energy and convective heat transfer efficiency in radiative hybrid nanofluid flow. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Benos, L.T.; Polychronopoulos, N.D.; Mahabaleshwar, U.S. Thermal and flow investigation of MHD natural convection in a nanofluid-saturated porous enclosure: An asymptotic analysis. J. Therm. Anal Calorim. 2021, 143, 751–765. [Google Scholar] [CrossRef]
- Sowmya, G.; Sarris, I.E.; Vishalakshi, C.S.; Kumar, R.S.V.; Prasannakumara, B.C. Analysis of Transient Thermal Distribution in a Convective–Radiative Moving Rod Using Two-Dimensional Differential Transform Method with Multivariate Pade Approximant. Symmetry 2021, 13, 1793. [Google Scholar] [CrossRef]
- Sahoo, B.; Poncet, S.; Labropulu, F. Effects of slip on the Von Kármán swirling flow and heat transfer in a porous medium. Trans. Can. Soc. Mech. Eng. 2015, 39, 357–366. [Google Scholar] [CrossRef]
- Liao, S.J. Series Solution of Non-Similarity Boundary-Layer Flow in Porous Medium. The Proposed Homotopy Analysis Technique for the Solution of Non-Linear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comp. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S.J. Analytic Solution for Fluid Flow over an Exponentially Stretching Porous Sheet with Surface Heat Flux in Porous Medium by Means of Homotopy Analysis Method. Appl. Math. Comp. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy analysis method: A new analytical technique for nonlinear problems. Commun. Nonlinear. Sci. Numer. Simul. 1997, 2, 95–100. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, T.; Sajid, M. Analytic solution for rotating flow and heat transfer analysis of a third-grade fluid. Acta Mechanica. 2007, 191, 219–229. [Google Scholar] [CrossRef]
- Abbasbandy, S. Solving Nonlinear Stochastic Diffusion Models with Nonlinear Losses Using the Homotopy Analysis Method. Nonlinear Dyn. 2008, 51, 83–87. [Google Scholar] [CrossRef]
- Zhu, S.P. An Exact and Explicit Solution for the Valuation of American Put Options. Quant. Financ. 2006, 6, 229–242. [Google Scholar] [CrossRef]
- Effati, S.; SaberiNik, H.; Shirazian, M. Analytic-approximate solution for a class of nonlinear optimal control problems by Homotopy analysis method Asian-Euro. J. Math. 2013, 6, 1–22. [Google Scholar]
- Ahlersten, K. An Introduction to MATLAB; Bookboon: Copenhagen, Denmark, 2015. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Visuvasam, J.; Alotaibi, H. Analysis of Von Kármán Swirling Flows Due to a Porous Rotating Disk Electrode. Micromachines 2023, 14, 582. https://doi.org/10.3390/mi14030582
Visuvasam J, Alotaibi H. Analysis of Von Kármán Swirling Flows Due to a Porous Rotating Disk Electrode. Micromachines. 2023; 14(3):582. https://doi.org/10.3390/mi14030582
Chicago/Turabian StyleVisuvasam, James, and Hammad Alotaibi. 2023. "Analysis of Von Kármán Swirling Flows Due to a Porous Rotating Disk Electrode" Micromachines 14, no. 3: 582. https://doi.org/10.3390/mi14030582





