Estimation of Particle Location in Granular Materials Based on Graph Neural Networks
Abstract
1. Introduction
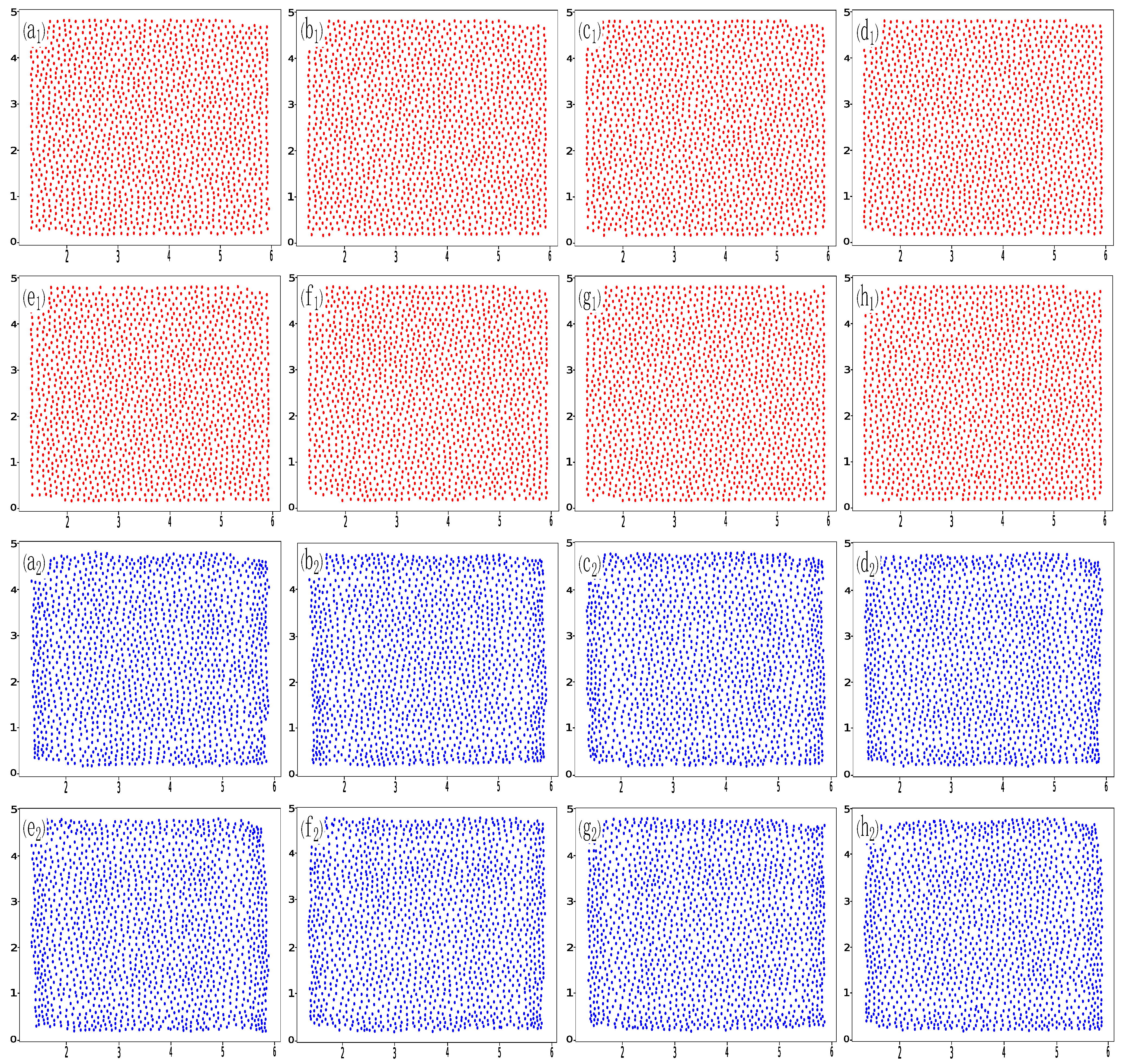
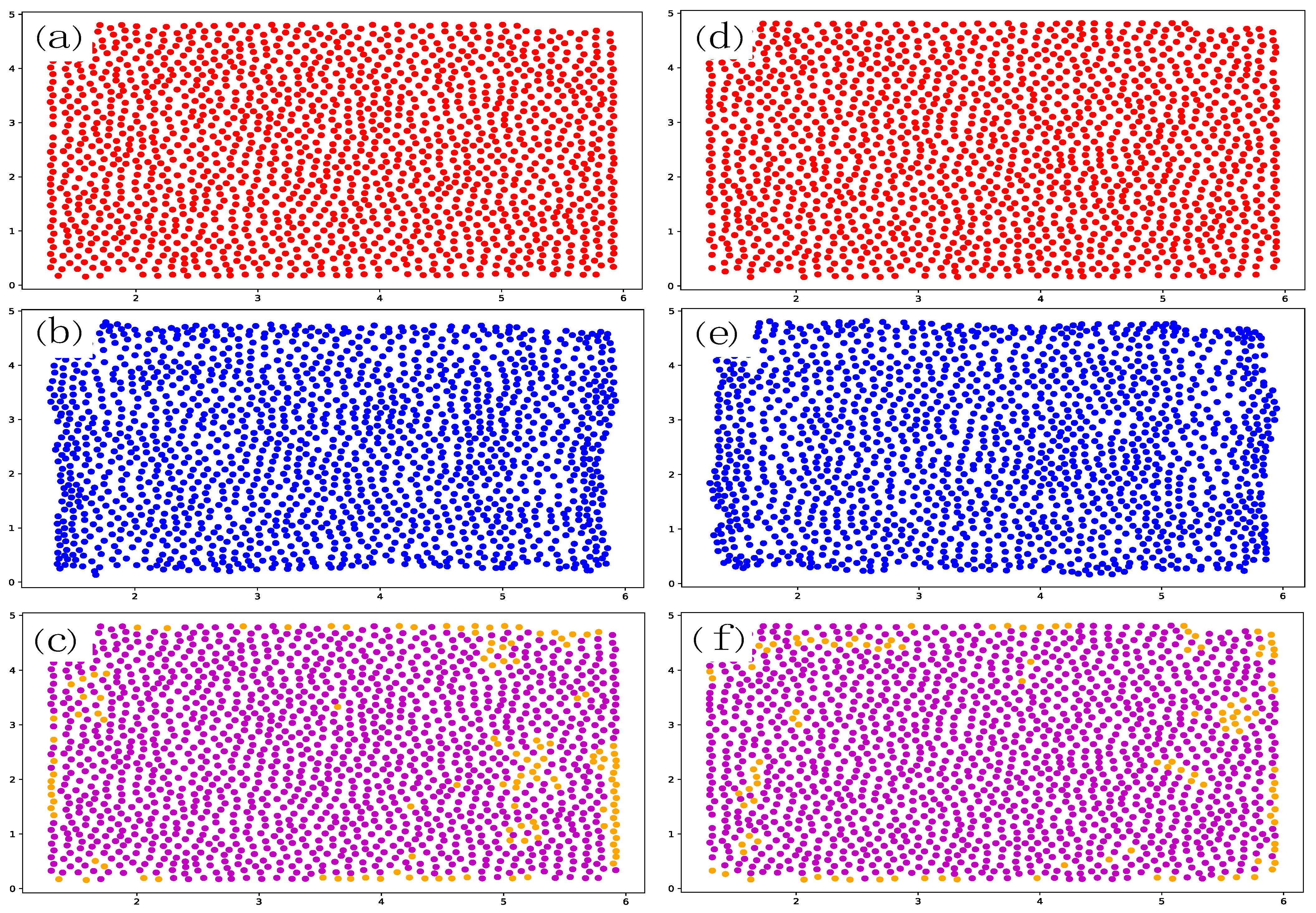
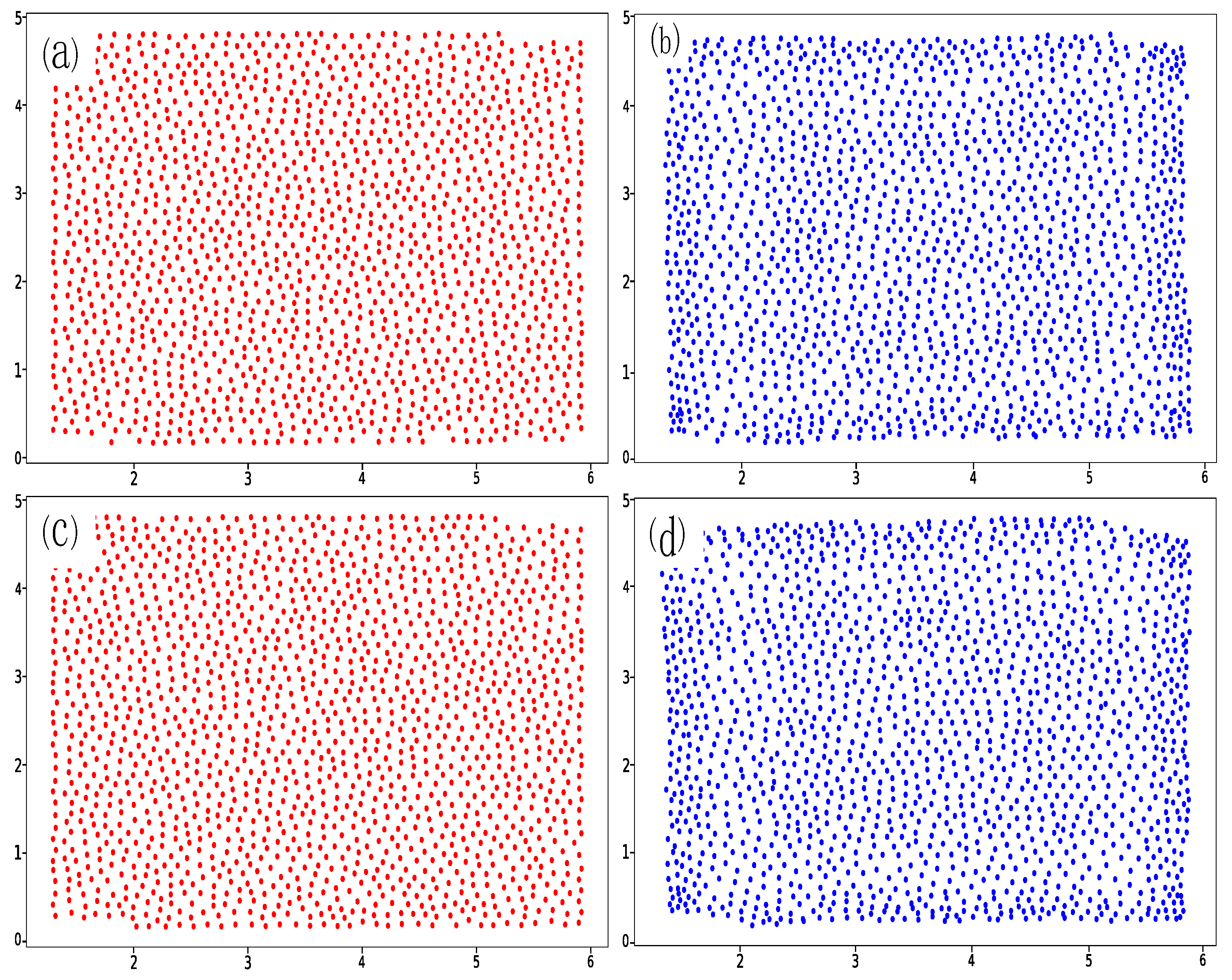
2. Data Set
3. Distance Estimation
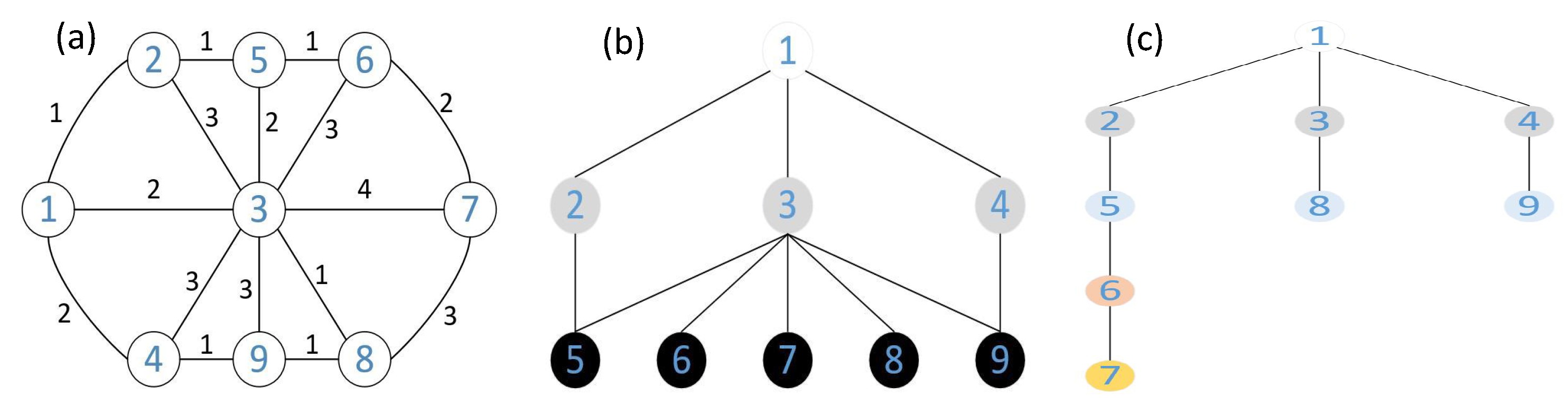
3.1. Building a Graph Network
3.2. Calculation of Shortest Path and Hop Counts
3.3. Estimation of the Distance between Nodes
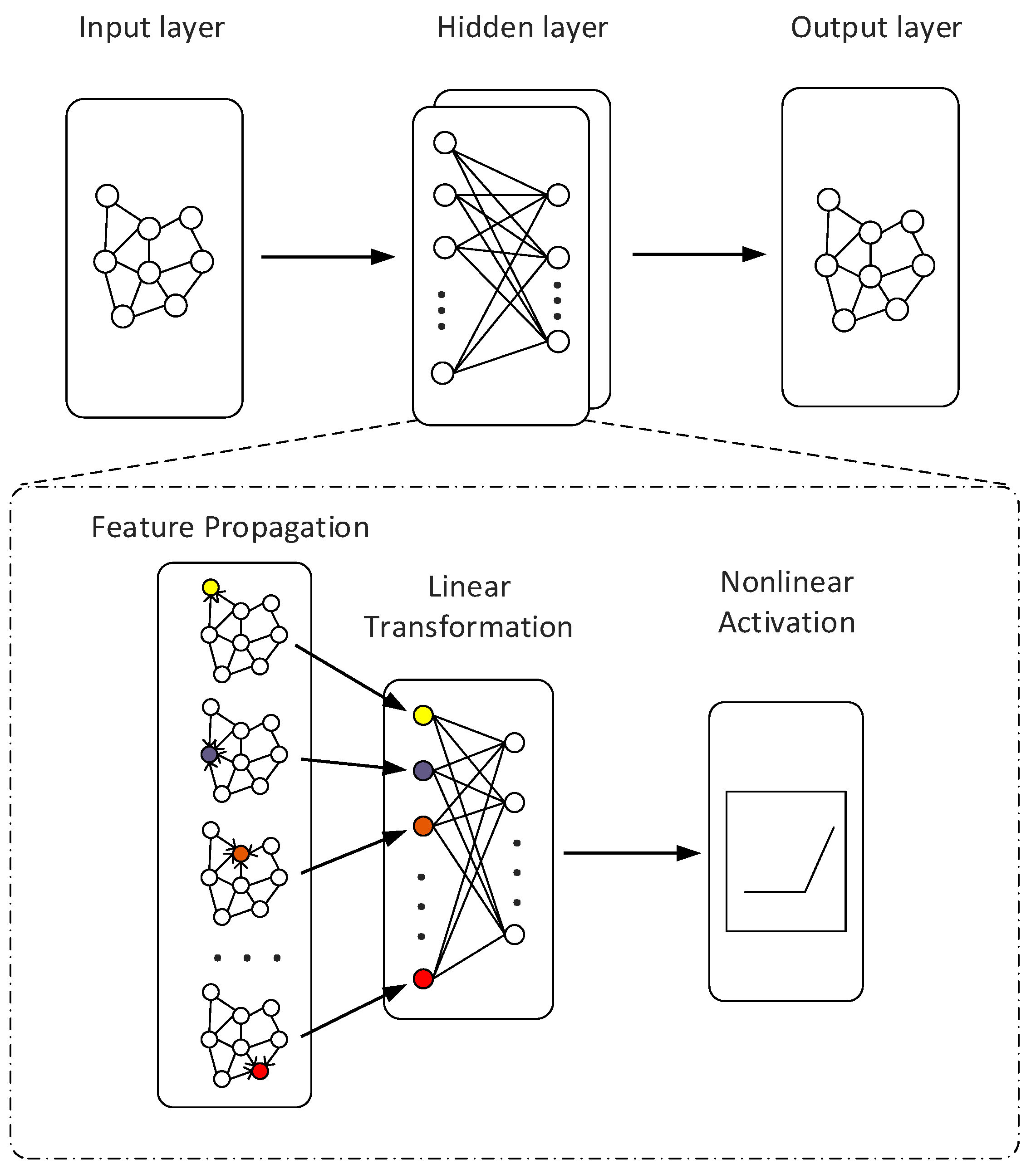
4. GCN Model
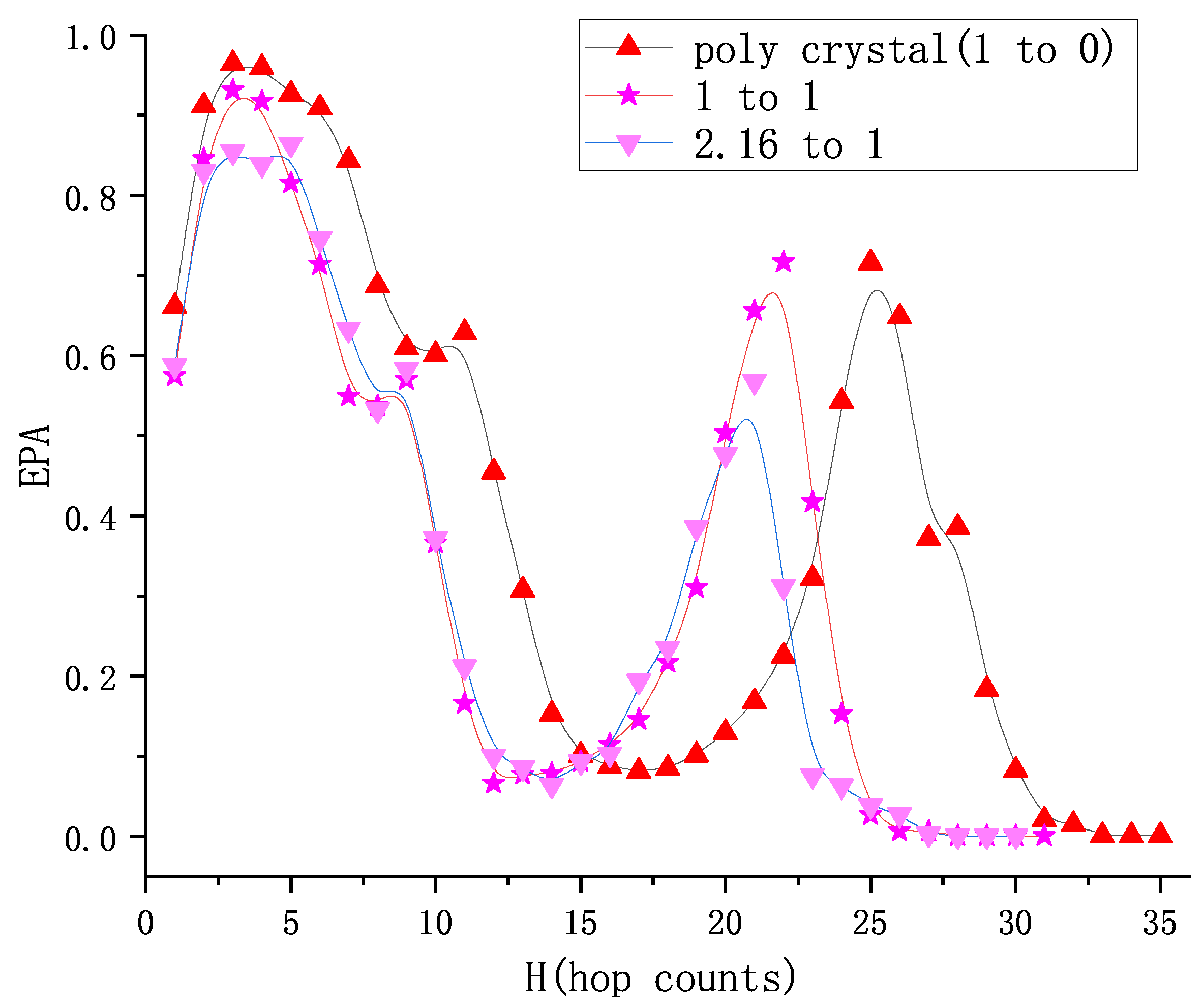
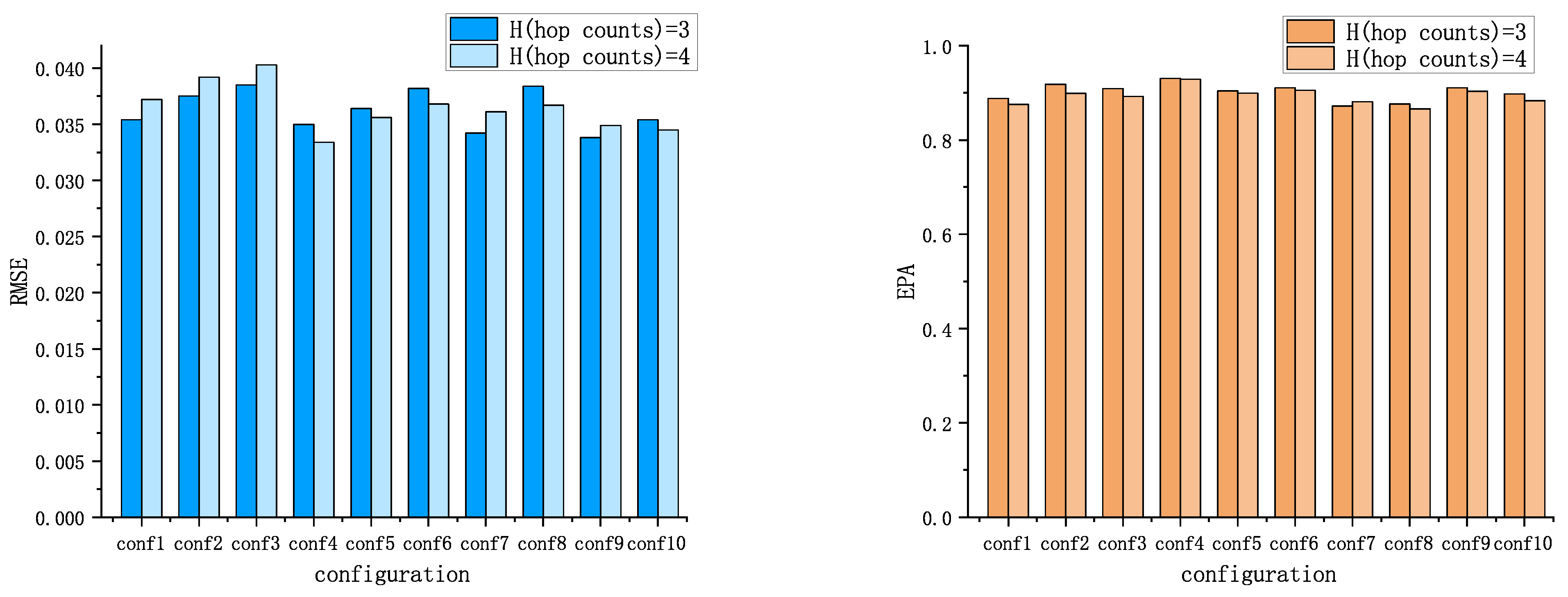
5. Results
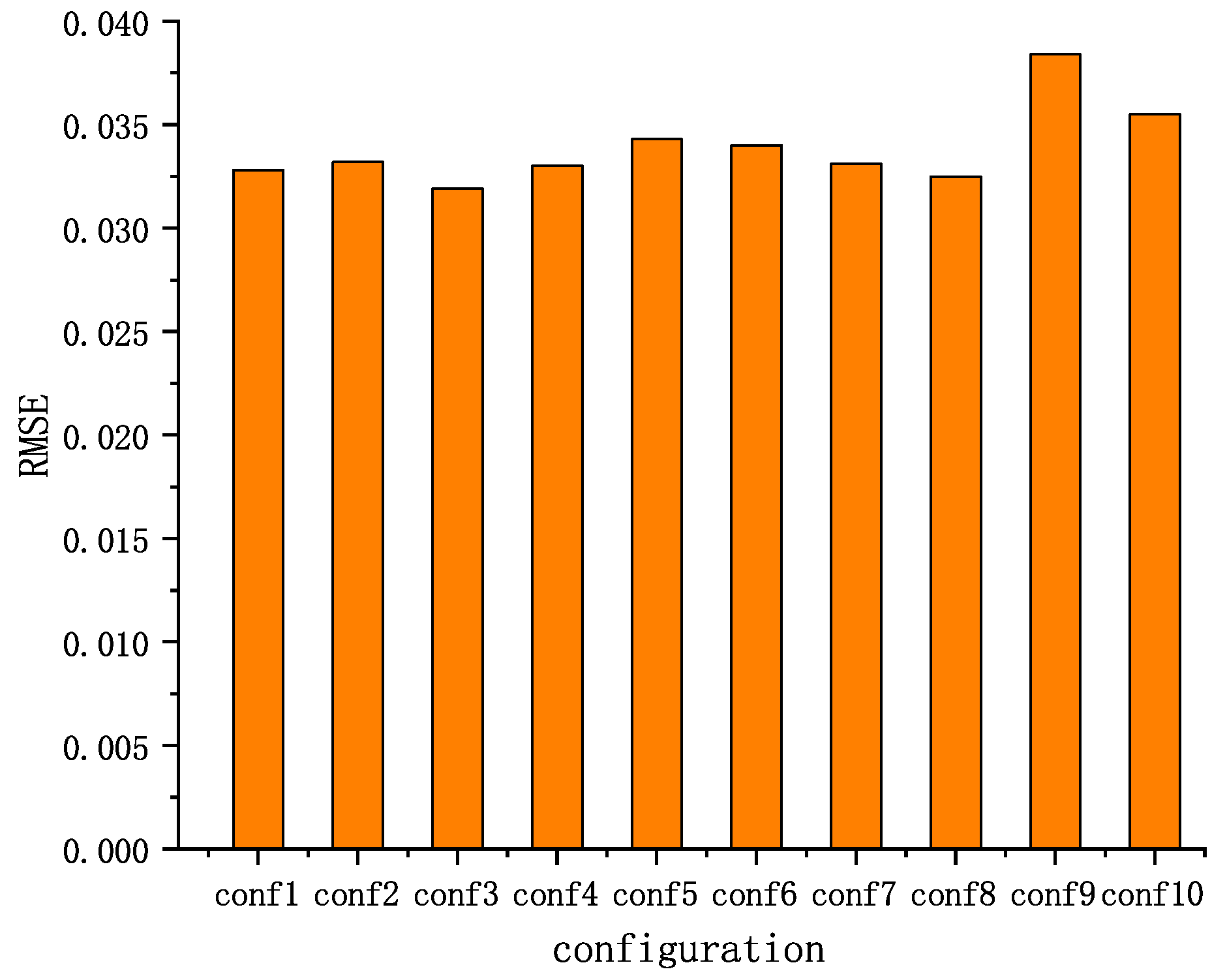
5.1. Positioning Accuracy
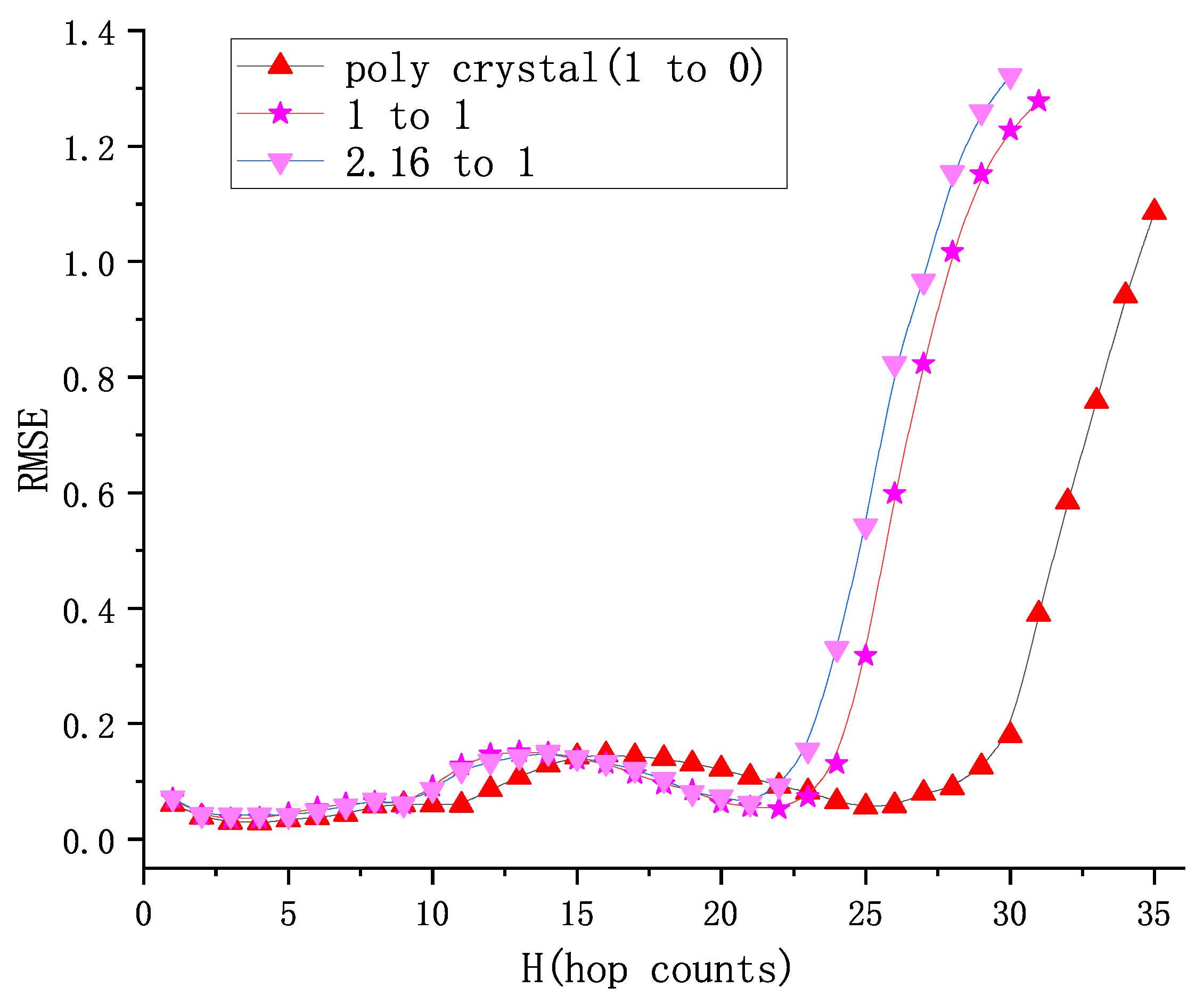
5.1.1. The Root-Mean-Squared Error (RMSE)
5.1.2. The Effective Prediction Accuracy (EPA)
5.2. Prediction of 1:1 Granular System
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Two-Dimensional Disk Experiment
Appendix B. Over-Smoothing
Appendix C. Additional Prediction Results
References
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259. [Google Scholar] [CrossRef]
- de Gennes, P.G. Granular matter: A tentative view. Rev. Mod. Phys. 1999, 71, S374. [Google Scholar] [CrossRef]
- Wang, Y. Granular packing as model glass formers. Chin. Phys. 2017, 26, 014503. [Google Scholar] [CrossRef]
- Tapia-Ignacio, C.; Garcia-Serrano, J.; Donado, F. Nonvibrating granular model for a glass-forming liquid: Equilibration and aging. Phys. Rev. 2016, 94, 062902. [Google Scholar] [CrossRef] [PubMed]
- Sperl, M.; Zippelius, A. Driven granular fluids: Glass transition and microrheology. Eur. Phys. J. Spec. Top. 2017, 226, 3079–3094. [Google Scholar] [CrossRef]
- Majmudar, T.; Sperl, M.; Luding, S.; Behringer, R.P. Jamming transition in granular systems. Phys. Rev. Lett. 2007, 98, 058001. [Google Scholar] [CrossRef]
- Silbert, L.E.; Liu, A.J.; Nagel, S.R. Structural signatures of the unjamming transition at zero temperature. Phys. Rev. 2006, 73, 89–132. [Google Scholar] [CrossRef]
- Mizuno, H.; Shiba, H.; Ikeda, A. Continuum limit of the vibrational properties of amorphous solids. Proc. Natl. Acad. Sci. USA 2017, 114, E9767–E9774. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, J.; Wang, Y.; Zhang, L.; Jin, Z.; Hong, L.; Wang, Y.; Zhang, J. Experimental studies of vibrational modes in a two-dimensional amorphous solid. Nat. Commun. 2017, 8, 67. [Google Scholar] [CrossRef]
- Gartner, L.; Lerner, E. Nonlinear plastic modes in disordered solids. Phys. Rev. 2016, 93, 011001. [Google Scholar] [CrossRef]
- Cao, Y.; Li, J.; Kou, B.; Xia, C.; Li, Z.; Chen, R.; Xie, H.; Xiao, T.; Kob, W.; Hong, L.; et al. Structural and topological nature of plasticity in sheared granular materials. Nat. Commun. 2018, 9, 2911. [Google Scholar] [CrossRef]
- Johnson, P.A.; Jia, X. Nonlinear dynamics, granular media and dynamic earthquake triggering. Nature 2005, 437, 871–874. [Google Scholar] [CrossRef]
- Xia, C.; Li, J.; Cao, Y.; Kou, B.; Xiao, X.; Fezzaa, K.; Xiao, T.; Wang, Y. The structural origin of the hard-sphere glass transition in granular packing. Nat. Commun. 2015, 6, 8409. [Google Scholar] [CrossRef] [PubMed]
- Denisov, D.; Lörincz, K.; Uhl, J.; Dahmen, K.A.; Schall, P. Universality of slip avalanches in flowing granular matter. Nat. Commun. 2016, 7, 10641. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Shi, Z.; Zhang, Q.; Liu, W.; Peng, M.; Wu, C. 3D DEM investigation on the morphology and structure of landslide dams formed by dry granular flows. Eng. Geol. 2019, 258, 105151. [Google Scholar] [CrossRef]
- Lai, Z.; Vallejo, L.E.; Zhou, W.; Ma, G.; Espitia, J.M.; Caicedo, B.; Chang, X. Collapse of granular columns with fractal particle size distribution: Implications for understanding the role of small particles in granular flows. Geophys. Res. Lett. 2017, 44, 12,181–12,189. [Google Scholar] [CrossRef]
- Biswas, P.; Sen, D.; Bouwman, W. Structural characterization of spray-dried microgranules by spin-echo small-angle neutron scattering. Powder Technol. 2021, 378, 680–684. [Google Scholar] [CrossRef]
- Wang, L.; Frost, J.; Lai, J. Three-dimensional digital representation of granular material microstructure from X-ray tomography imaging. J. Comput. Civ. Eng. 2004, 18, 28–35. [Google Scholar] [CrossRef]
- Pokrovskaya, I.D.; Yadav, S.; Rao, A.; McBride, E.; Kamykowski, J.A.; Zhang, G.; Aronova, M.A.; Leapman, R.D.; Storrie, B. 3D ultrastructural analysis of α-granule, dense granule, mitochondria, and canalicular system arrangement in resting human platelets. Res. Pract. Thromb. Haemost. 2020, 4, e12260. [Google Scholar] [CrossRef]
- Lherminier, S.; Planet, R.; Simon, G.; Vanel, L.; Ramos, O. Revealing the structure of a granular medium through ballistic sound propagation. Phys. Rev. Lett. 2014, 113, 098001. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Gittings, A.; Suh, S.; Dixon, P.; Durian, D.J. Speckle-visibility spectroscopy: A tool to study time-varying dynamics. Rev. Sci. Instrum. 2005, 76, 093110. [Google Scholar] [CrossRef]
- Yang, H.; Li, R.; Kong, P.; Sun, Q.; Biggs, M.J.; Zivkovic, V. Avalanche dynamics of granular materials under the slumping regime in a rotating drum as revealed by speckle visibility spectroscopy. Phys. Rev. 2015, 91, 042206. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Li, L.; Cai, H.; Zhu, X.; Shi, Q.; Zheng, N. Computational imaging of moving objects obscured by a random corridor via speckle correlations. Nat. Commun. 2022, 13, 4081. [Google Scholar] [CrossRef]
- Pradhyumna, P.; Shreya, G.P. Graph neural network (GNN) in image and video understanding using deep learning for computer vision applications. In Proceedings of the 2021 IEEE, Second International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 4–6 August 2021; pp. 1183–1189. [Google Scholar]
- Gupta, A.; Matta, P.; Pant, B. Graph neural network: Current state of Art, challenges and applications. Mater. Today Proc. 2021, 46, 10927–10932. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30, 671. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Ortega, A.; Frossard, P.; Kovačević, J.; Moura, J.M.; Vandergheynst, P. Graph signal processing: Overview, challenges, and applications. Proc. IEEE 2018, 106, 808–828. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liang, L.; Liu, L.; Tang, M.J. Graph neural networks and their current applications in bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef]
- Gao, W.; Mahajan, S.P.; Sulam, J.; Gray, J.J. Deep learning in protein structural modeling and design. Patterns 2020, 1, 100142. [Google Scholar] [CrossRef]
- Strokach, A.; Becerra, D.; Corbi-Verge, C.; Perez-Riba, A.; Kim, P.M. Fast and flexible protein design using deep graph neural networks. Cell Syst. 2020, 11, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wellawatte, G.P.; Chakraborty, M.; Gandhi, H.A.; Xu, C.; White, A.D. Graph neural network based coarse-grained mapping prediction. Chem. Sci. 2020, 11, 9524–9531. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Li, Z.; Zhang, S.; Wang, S.; Wang, X.; Yuan, Q.; Wei, Z. Drug–target affinity prediction using graph neural network and contact maps. RSC Adv. 2020, 10, 20701–20712. [Google Scholar] [CrossRef]
- Sun, Z.; Yin, H.; Chen, H.; Chen, T.; Cui, L.; Yang, F. Disease prediction via graph neural networks. IEEE J. Biomed. Health Inf. 2020, 25, 818–826. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Zhu, Z.; Liu, Z.; Guo, Z.; Liu, Y.; Yang, Y.; Zhao, Y. Multi-modal Graph Learning for Disease Prediction. IEEE Trans. Med. Imaging 2022, 41, 2207–2216. [Google Scholar] [CrossRef]
- Meng, Y.; Zhang, H.; Zhao, Y.; Yang, X.; Qiao, Y.; MacCormick, I.J.; Huang, X.; Zheng, Y. Graph-based region and boundary aggregation for biomedical image segmentation. IEEE Trans. Med. Imaging 2021, 41, 690–701. [Google Scholar] [CrossRef] [PubMed]
- Shlomi, J.; Battaglia, P.; Vlimant, J.R. Graph neural networks in particle physics. Mach. Learn. Sci. Technol. 2020, 2, 021001. [Google Scholar] [CrossRef]
- Thais, S.; Calafiura, P.; Chachamis, G.; DeZoort, G.; Duarte, J.; Ganguly, S.; Kagan, M.; Murnane, D.; Neubauer, M.S.; Terao, K. Graph neural networks in particle physics: Implementations, innovations, and challenges. arXiv 2022, arXiv:2203.12852. [Google Scholar]
- Bapst, V.; Keck, T.; Grabska-Barwińska, A.; Donner, C.; Cubuk, E.D.; Schoenholz, S.S.; Obika, A.; Nelson, A.W.; Back, T.; Hassabis, D.; et al. Unveiling the predictive power of static structure in glassy systems. Nat. Phys. 2020, 16, 448–454. [Google Scholar] [CrossRef]
- Sanchez-Gonzalez, A.; Godwin, J.; Pfaff, T.; Ying, R.; Leskovec, J.; Battaglia, P. Learning to simulate complex physics with graph networks. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 8459–8468. [Google Scholar]
- Jang, J.; Gu, G.H.; Noh, J.; Kim, J.; Jung, Y. Structure-based synthesizability prediction of crystals using partially supervised learning. J. Am. Chem. Soc. 2020, 142, 18836–18843. [Google Scholar] [CrossRef]
- Omee, S.S.; Louis, S.Y.; Fu, N.; Wei, L.; Dey, S.; Dong, R.; Li, Q.; Hu, J. Scalable deeper graph neural networks for high-performance materials property prediction. Patterns 2022, 3, 100491. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Zhang, C.; Dong, L. A geometric-information-enhanced crystal graph network for predicting properties of materials. Commun. Mater. 2021, 2, 92. [Google Scholar] [CrossRef]
- Court, C.J.; Yildirim, B.; Jain, A.; Cole, J.M. 3-D inorganic crystal structure generation and property prediction via representation learning. J. Chem. Inf. Model. 2020, 60, 4518–4535. [Google Scholar] [CrossRef] [PubMed]
- Mandal, R.; Casert, C.; Sollich, P. Robust prediction of force chains in jammed solids using graph neural networks. Nat. Commun. 2022, 13, 4424. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Wang, J. Estimation of contact forces of granular materials under uniaxial compression based on a machine learning model. Granul. Matter 2022, 24, 17. [Google Scholar] [CrossRef]
- Yan, W.; Jin, D.; Lin, Z.; Yin, F. Graph neural network for large-scale network localization. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 5250–5254. [Google Scholar]
- Khalaf-Allah, M. Time of arrival (TOA)-based direct location method. In Proceedings of the 2015 IEEE, 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 812–815. [Google Scholar]
- Kovavisaruch, L.O.; Ho, K. Alternate source and receiver location estimation using TDOA with receiver position uncertainties. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Proceedings (ICASSP’05), Philadelphia, PA, USA, 18–23 March 2005; Volume 4, pp. iv/1065–iv/1068. [Google Scholar]
- Watanabe, F. Wireless sensor network localization using AoA measurements with two-step error variance-weighted least squares. IEEE Access 2021, 9, 10820–10828. [Google Scholar] [CrossRef]
- Jian Yin, L. A new distance vector-hop localization algorithm based on half-measure weighted centroid. Mob. Inf. Syst. 2019, 2019, 9892512. [Google Scholar] [CrossRef]
- He, T.; Huang, C.; Blum, B.M.; Stankovic, J.A.; Abdelzaher, T. Range-free localization schemes for large scale sensor networks. In Proceedings of the 9th Annual International Conference on Mobile Computing and Networking, San Diego, CA, USA, 14–19 September 2003; pp. 81–95. [Google Scholar]
- Kazemi, S.A.R.; Amiri, R.; Behnia, F. Efficient convex solution for 3-D localization in MIMO radars using delay and angle measurements. IEEE Commun. Lett. 2019, 23, 2219–2223. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Z. Improved DV-hop localization algorithm based on dynamic anchor node set for wireless sensor networks. IEEE Access 2019, 7, 124876–124890. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Chen, Y.; Shang, J.; Sun, A.; Sun, X.; Yu, S.; Zheng, J.; Wang, Y.; Schirmacher, W.; et al. Disorder-induced vibrational anomalies from crystalline to amorphous solids. Phys. Rev. Res. 2021, 3, L032067. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, X.; Li, Z.; Huang, D.; Zhang, L. Estimation of Particle Location in Granular Materials Based on Graph Neural Networks. Micromachines 2023, 14, 714. https://doi.org/10.3390/mi14040714
Zhang H, Li X, Li Z, Huang D, Zhang L. Estimation of Particle Location in Granular Materials Based on Graph Neural Networks. Micromachines. 2023; 14(4):714. https://doi.org/10.3390/mi14040714
Chicago/Turabian StyleZhang, Hang, Xingqiao Li, Zirui Li, Duan Huang, and Ling Zhang. 2023. "Estimation of Particle Location in Granular Materials Based on Graph Neural Networks" Micromachines 14, no. 4: 714. https://doi.org/10.3390/mi14040714
APA StyleZhang, H., Li, X., Li, Z., Huang, D., & Zhang, L. (2023). Estimation of Particle Location in Granular Materials Based on Graph Neural Networks. Micromachines, 14(4), 714. https://doi.org/10.3390/mi14040714







