Dynamic Beam Steering and Focusing Graphene Metasurface Mirror Based on Fermi Energy Control
Abstract
:1. Introduction
2. Structure Design
3. Results
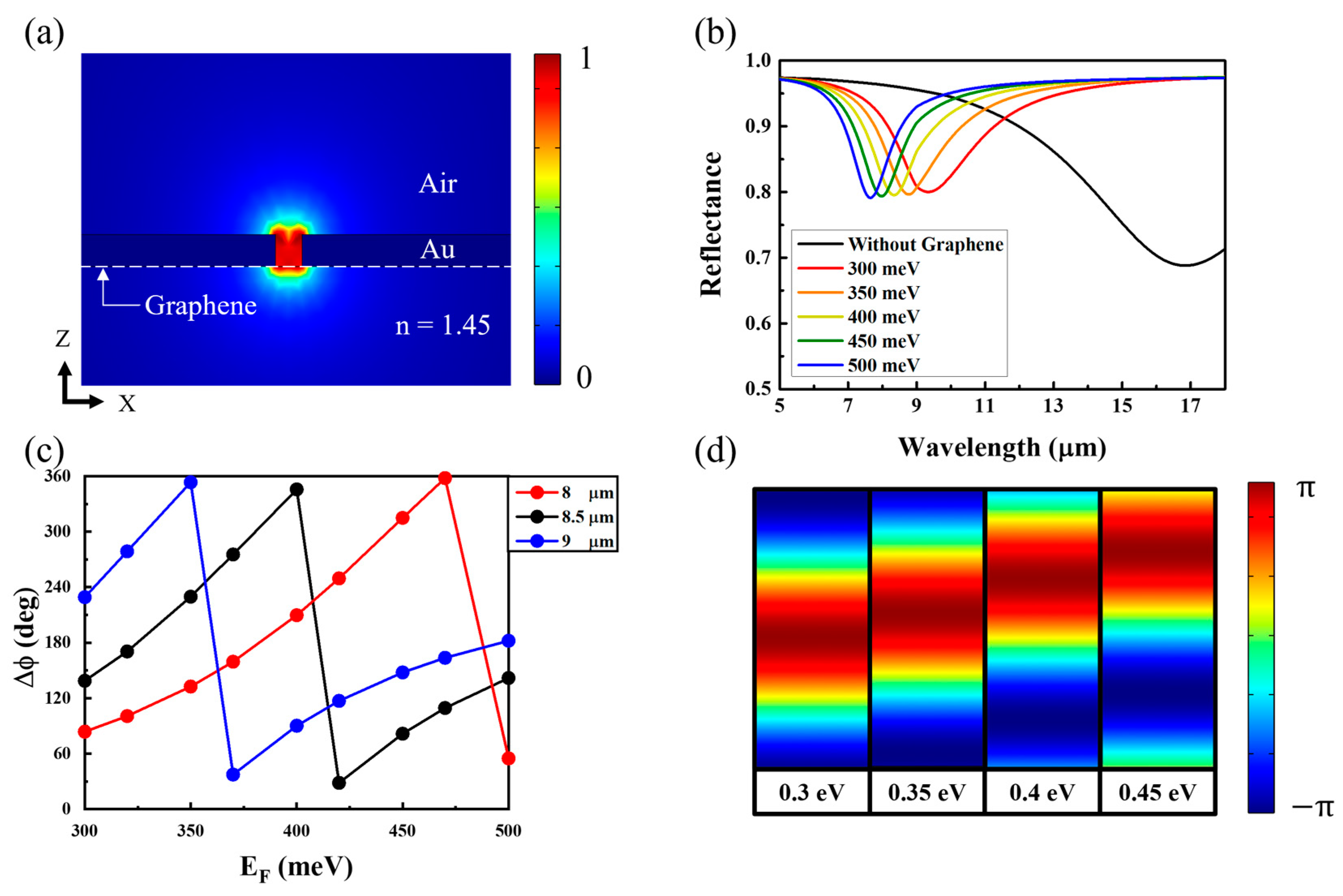
3.1. Reflectance and Phase Shifting in a Unit Cell of the Proposed Metasurface
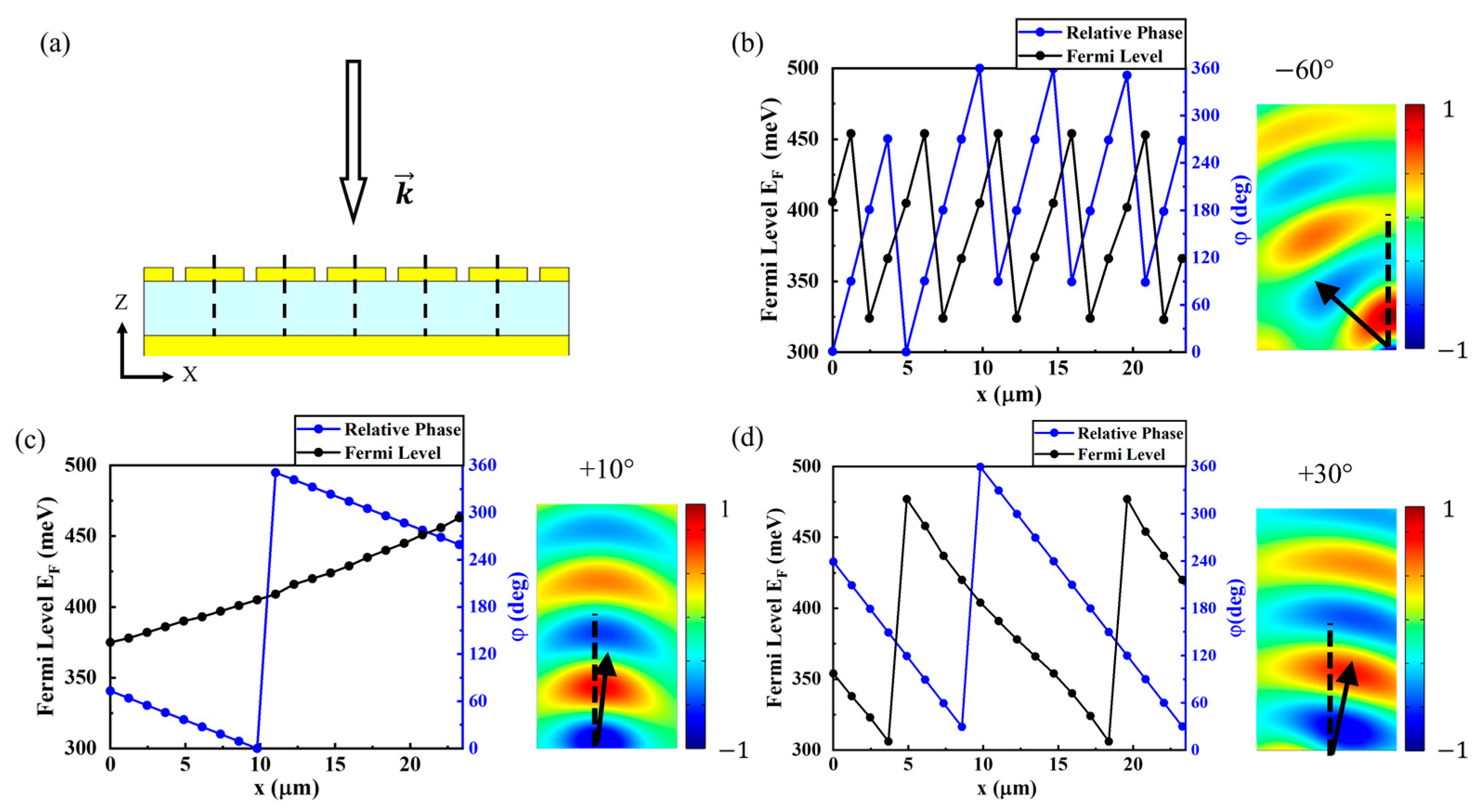
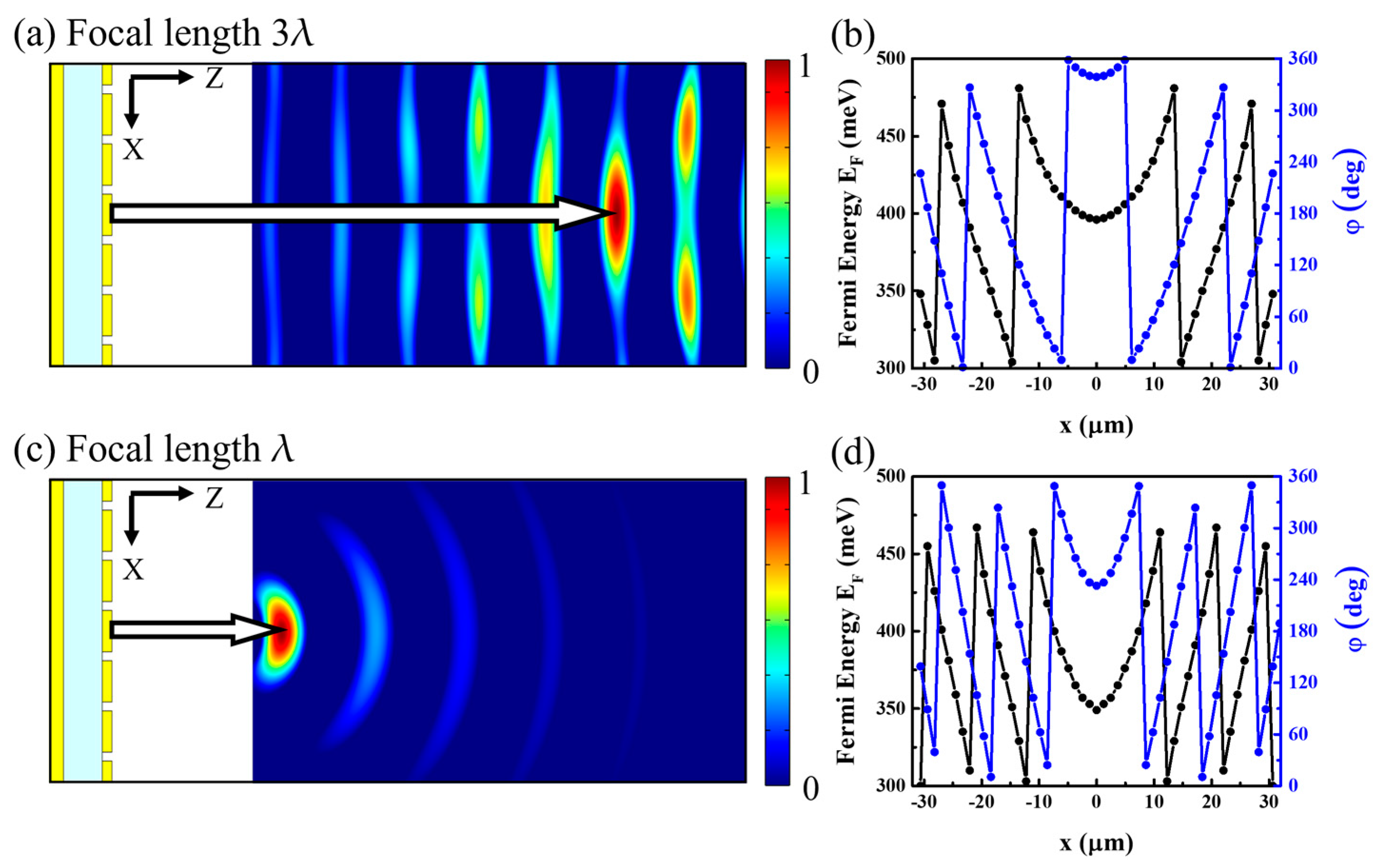
3.2. Constructing a Metasurface Mirror with a Finite Unit Cell Array
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katare, K.K.; Biswas, A.; Akhtar, M.J. Near-Field Phase Modulation Using a Semicircular Radially Gradient Metasurface for Beam Steering of an RF Antenna. J. Comput. Electron. 2019, 18, 671–679. [Google Scholar] [CrossRef]
- Sun, J.; Timurdogan, E.; Yaacobi, A.; Hosseini, E.S.; Watts, M.R. Large-Scale Nanophotonic Phased Array. Nature 2013, 493, 195–199. [Google Scholar] [CrossRef]
- Yu, B.; Yang, K.; Sim, C.; Yang, G. Communication With Metallic Casing Application. IEEE Trans. Antennas Propag. 2018, 66, 462–466. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless Communications and Applications above 100 GHz: Opportunities and Challenges for 6g and Beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Vasic, B.; Isic, G.; Gajic, R.; Hingerl, K. Controlling Electromagnetic Fields with Graded Photonic Crystals in Metamaterial Regime. Opt. Express 2010, 18, 20321. [Google Scholar] [CrossRef]
- Smith, N.R.; Abeysinghe, D.C.; Haus, J.W.; Heikenfeld, J. Agile Wide-Angle Beam Steering with Electrowetting Microprisms. Opt. Express 2006, 14, 6557. [Google Scholar] [CrossRef] [Green Version]
- Doylend, J.K.; Heck, M.J.R.; Bovington, J.T.; Peters, J.D.; Coldren, L.A.; Bowers, J.E. Two-Dimensional Free-Space Beam Steering with an Optical Phased Array on Silicon-on-Insulator. Opt. Express 2011, 19, 21595. [Google Scholar] [CrossRef] [Green Version]
- Kosaka, H.; Kawashima, T.; Tomita, A.; Notomi, M.; Tamamura, T.; Sato, T.; Kawakami, S. Photonic Crystals for Micro Lightwave Circuits Using Wavelength-Dependent Angular Beam Steering. Appl. Phys. Lett. 1999, 74, 1370–1372. [Google Scholar] [CrossRef]
- Chang, H.; Koschan, A.; Abidi, M.; Kong, S.G.; Won, C.H. Multispectral Visible and Infrared Imaging for Face Recognition. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar] [CrossRef]
- Liu, N.; Mesch, M.; Weiss, T.; Hentschel, M.; Giessen, H. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Hong, G.; Antaris, A.L.; Dai, H. Near-Infrared Fluorophores for Biomedical Imaging. Nat. Biomed. Eng. 2017, 1, 10. [Google Scholar] [CrossRef]
- Solgaard, O.; Godil, A.A.; Howe, R.T.; Lee, L.P.; Peter, Y.A.; Zappe, H. Optical MEMS: From Micromirrors to Complex Systems. J. Microelectromech. Syst. 2014, 23, 517–538. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, M.C. Micromirror Based Optical Phased Array for Wide-Angle Beamsteering. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 897–900. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, G.; Yu, K.; Wu, M.C. Large-Scale MEMS-Actuated 2-D Optical Phased Arrays. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; Volume 1, pp. 21–24. [Google Scholar]
- Wang, Y.; Zhou, G.; Zhang, X.; Kwon, K.; Blanche, P.-A.; Triesault, N.; Yu, K.; Wu, M.C. 2D Broadband Beamsteering with Large-Scale MEMS Optical Phased Array. Optica 2019, 6, 557. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-Tunable Conducting Oxide Metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tang, S.; Ding, F.; Zhong, S.; Yang, Y.; Jiang, T.; Zhou, J. Switchable Multifunctional Terahertz Metasurfaces Employing Vanadium Dioxide. Sci. Rep. 2019, 9, 5454. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1535. [Google Scholar]
- Han, S.A.; Bhatia, R.; Kim, S.W. Synthesis, Properties and Potential Applications of Two-Dimensional Transition Metal Dichalcogenides. Nano Converg. 2015, 2, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Zhang, Y.; Tian, C.; Girit, C.; Zettl, A.; Crommie, M.; Shen, Y.R. Gate-Variable Optical Transitions in Graphene. Science 2008, 320, 206–209. [Google Scholar] [CrossRef]
- He, Z.; Li, L.; Ma, H.; Pu, L.; Xu, H.; Yi, Z.; Cao, X.; Cui, W. Graphene-Based Metasurface Sensing Applications in Terahertz Band. Results Phys. 2021, 21, 103795. [Google Scholar] [CrossRef]
- Orazbayev, B.; Beruete, M.; Khromova, I. Tunable Beam Steering Enabled by Graphene Metamaterials. Opt. Express 2016, 24, 8848. [Google Scholar] [CrossRef] [Green Version]
- Maier, S.A. PLASMONICS_Fundamentals and Applications_Maier_Springer 2006; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-0387-33150-8. [Google Scholar]
- Maier, S.A. Plasmonic Field Enhancement and SERS in the Effective Mode Volume Picture. Opt. Express 2006, 14, 1957. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Helicity Dependent Directional Surface Plasmon Polariton Excitation Using a Metasurface with Interfacial Phase Discontinuity. Light Sci. Appl. 2013, 2, e70. [Google Scholar] [CrossRef] [Green Version]
- Bilotti, F.; Sevgi, L. Metamaterials: Definitions, Properties, Applications, and FDTD-Based Modeling and Simulation (Invited Paper). Int. J. RF Microw. Comput. Eng. 2012, 22, 422–438. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-Dimensional Optical Metamaterial with a Negative Refractive Index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Shankhwar, N.; Kalra, Y.; Li, Q.; Sinha, R.K. Zero-Index Metamaterial Based All-Dielectric Nanoantenna. AIP Adv. 2019, 9, 035115. [Google Scholar] [CrossRef] [Green Version]
- Lalbakhsh, A.; Afzal, M.U.; Hayat, T.; Esselle, K.P.; Mandal, K. All-Metal Wideband Metasurface for near-Field Transformation of Medium-to-High Gain Electromagnetic Sources. Sci. Rep. 2021, 11, 9421. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; Von Freymann, G.; Linden, S.; Wegener, M. Gold Helix Photonic Metamaterial as Broadband Circular Polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Chong, K.E.; Staude, I.; James, A.; Dominguez, J.; Liu, S.; Campione, S.; Subramania, G.S.; Luk, T.S.; Decker, M.; Neshev, D.N.; et al. Polarization-Independent Silicon Metadevices for Efficient Optical Wavefront Control. Nano Lett. 2015, 15, 5369–5374. [Google Scholar] [CrossRef]
- Vashistha, V.; Vaidya, G.; Hegde, R.S.; Serebryannikov, A.E.; Bonod, N.; Krawczyk, M. All-Dielectric Metasurfaces Based on Cross-Shaped Resonators for Color Pixels with Extended Gamut. ACS Photonics 2017, 4, 1076–1082. [Google Scholar] [CrossRef]
- Esfandiyari, M.; Lalbakhsh, A.; Jarchi, S.; Ghaffari-Miab, M.; Mahtaj, H.N.; Simorangkir, R.B.V.B. Tunable Terahertz Filter/Antenna-Sensor Using Graphene-Based Metamaterials. Mater. Des. 2022, 220, 110855. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. All-Metal Wideband Frequency-Selective Surface Bandpass Filter for TE and TM Polarizations. IEEE Trans. Antennas Propag. 2022, 70, 2790–2800. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Simorangkir, R.B.V.B.; Bayat-Makou, N.; Kishk, A.A.; Esselle, K.P. Advancements and Artificial Intelligence Approaches in Antennas for Environmental Sensing. Artif. Intell. Data Sci. Environ. Sens. 2022, 19–38. [Google Scholar] [CrossRef]
- Adibi, S.; Honarvar, M.A.; Lalbakhsh, A. Gain Enhancement of Wideband Circularly Polarized UWB Antenna Using FSS. Radio Sci. 2021, 56, 1–8. [Google Scholar] [CrossRef]
- Emani, N.K.; Chung, T.F.; Ni, X.; Kildishev, A.; Chen, Y.P.; Boltasseva, A. Electrically Tunable Plasmonic Resonances with Graphene. In Proceedings of the CLEO: Applications and Technology 2012, San Jose, CA, USA, 6–11 May 2012. [Google Scholar]
- Gahoi, A.; Wagner, S.; Bablich, A.; Kataria, S.; Passi, V.; Lemme, M.C. Contact Resistance Study of Various Metal Electrodes with CVD Graphene. Solid. State. Electron. 2016, 125, 234–239. [Google Scholar] [CrossRef]
- Guo, X.; Xue, L.; Yang, Z.; Xu, M.; Zhu, Y.; Shao, D.; Fu, Z.; Tan, Z.; Wang, C.; Cao, J.; et al. Strong Terahertz Absorption of Monolayer Graphene Embedded into a Microcavity. Nanomaterials 2021, 11, 421. [Google Scholar] [CrossRef]
- Katayama, I.; Inoue, K.I.; Arashida, Y.; Wu, Y.; Yang, H.; Inoue, T.; Chiashi, S.; Maruyama, S.; Nagao, T.; Kitajima, M.; et al. Ultrafast Optical Modulation of Dirac Electrons in Gated Single-Layer Graphene. Phys. Rev. B 2020, 101, 245408. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, Q.; Yao, J.; Sun, Z.; Kaneko, R.; Yan, Z.; Nanot, S.; Jin, Z.; Kawayama, I.; Tonouchi, M.; et al. Terahertz and Infrared Spectroscopy of Gated Large-Area Graphene. Nano Lett. 2012, 12, 3711–3715. [Google Scholar] [CrossRef] [Green Version]
- Das, P.; Mandal, K.; Lalbakhsh, A. Beam-Steering of Microstrip Antenna Using Single-Layer FSS Based Phase-Shifting Surface. Int. J. RF Microw. Comput. Eng. 2022, 32, e23033. [Google Scholar] [CrossRef]
- Torabi, Y.; Dadashzadeh, G.; Lalbakhsh, A.; Oraizi, H. High-Gain and Low-Profile Dielectric-Image-Line Leaky-Wave-Antenna for Wide-Angle Beam Scanning at Sub-THz Frequencies. Opt. Laser Technol. 2022, 150, 107968. [Google Scholar] [CrossRef]
- Hill, M.T.; Marell, M.; Leong, E.S.P.; Smalbrugge, B.; Zhu, Y.; Sun, M.; van Veldhoven, P.J.; Geluk, E.J.; Karouta, F.; Oei, Y.-S.; et al. Lasing in Metal-Insulator-Metal Sub-Wavelength Plasmonic Waveguides. Opt. Express 2009, 17, 11107. [Google Scholar] [CrossRef] [Green Version]
- Falkovsky, L.A. Optical Properties of Graphene. J. Phys. Conf. Ser. 2008, 129, 012004. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of Plasmonic Waves in Graphene by Guided-Mode Resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef] [PubMed]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geim, A.K.; Novoselov, K.S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The Electronic Properties of Graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.Q.; Henriksen, E.A.; Jiang, Z.; Hao, Z.; Martin, M.C.; Kim, P.; Stormer, H.L.; Basov, D.N. Dirac Charge Dynamics in Graphene by Infrared Spectroscopy. Nat. Phys. 2008, 4, 532–535. [Google Scholar] [CrossRef] [Green Version]
- Khavasi, A.; Rejaei, B. Analytical Modeling of Graphene Ribbons as Optical Circuit Elements. IEEE J. Quantum Electron. 2014, 50, 397–403. [Google Scholar] [CrossRef]
- Naghdehforushha, S.A.; Moradi, G. Design of Plasmonic Rectangular Ribbon Antenna Based on Graphene for Terahertz Band Communication. IET Microw. Antennas Propag. 2018, 12, 804–807. [Google Scholar] [CrossRef]
- Kats, M.A.; Capasso, F. Optical Absorbers Based on Strong Interference in Ultra-Thin Films. Laser Photon. Rev. 2016, 10, 735–749. [Google Scholar] [CrossRef]
- Salary, M.M.; Mosallaei, H. Electrically Tunable Metamaterials Based on Multimaterial Nanowires Incorporating Transparent Conductive Oxides. Sci. Rep. 2017, 7, 10055. [Google Scholar] [CrossRef] [Green Version]
- Lesina, A.C.; Lesina, A.C.; Lesina, A.C.; Lesina, A.C.; Lesina, A.C.; Lesina, A.C.; Goodwill, D.; Bernier, E.; Ramunno, L.; Ramunno, L.; et al. On the Performance of Optical Phased Array Technology for Beam Steering: Effect of Pixel Limitations. Opt. Express 2020, 28, 31637–31657. [Google Scholar] [CrossRef]
- Cala Lesina, A.; Goodwill, D.; Bernier, E.; Ramunno, L.; Berini, P. Tunable Plasmonic Metasurfaces for Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2021, 27. [Google Scholar] [CrossRef]
- Lin, S.; Chen, Y.; Wong, Z.J. High-Performance Optical Beam Steering with Nanophotonics. Nanophotonics 2022, 11, 2617–2638. [Google Scholar] [CrossRef]
- Shi, L.; Andrade, J.R.C.; Tajalli, A.; Geng, J.; Yi, J.; Heidenblut, T.; Segerink, F.B.; Babushkin, I.; Kholodtsova, M.; Merdji, H.; et al. Generating Ultrabroadband Deep-UV Radiation and Sub-10 Nm Gap by Hybrid-Morphology Gold Antennas. Nano Lett. 2019, 19, 4779–4786. [Google Scholar] [CrossRef] [PubMed]
- Sarriugarte, P.; Schnell, M.; Chuvilin, A.; Hillenbrand, R. Polarization-Resolved Near-Field Characterization of Nanoscale Infrared Modes in Transmission Lines Fabricated by Gallium and Helium Ion Beam Milling. ACS Photonics 2014, 1, 604–611. [Google Scholar] [CrossRef]
- Siegfried, T.; Ekinci, Y.; Martin, O.J.F.; Sigg, H. Gap Plasmons and Near-Field Enhancement in Closely Packed Sub-10 Nm Gap Resonators. Nano Lett. 2013, 13, 5449–5453. [Google Scholar] [CrossRef] [Green Version]
- Huang, I.C.; Holzgrafe, J.; Jensen, R.A.; Choy, J.T.; Bawendi, M.G.; Lončar, M. 10 Nm Gap Bowtie Plasmonic Apertures Fabricated By Modified Lift-Off Process. Appl. Phys. Lett. 2016, 109, 133105. [Google Scholar] [CrossRef] [Green Version]
- Yoo, D.; Gurunatha, K.L.; Choi, H.K.; Mohr, D.A.; Ertsgaard, C.T.; Gordon, R.; Oh, S.H. Low-Power Optical Trapping of Nanoparticles and Proteins with Resonant Coaxial Nanoaperture Using 10 Nm Gap. Nano Lett. 2018, 18, 3637–3642. [Google Scholar] [CrossRef]
- Im, H.; Bantz, K.C.; Lindquist, N.C.; Haynes, C.L.; Oh, S.H. Vertically Oriented Sub-10-Nm Plasmonic Nanogap Arrays. Nano Lett. 2010, 10, 2231–2236. [Google Scholar] [CrossRef]
- Yazdi, G.R.; Vasiliauskas, R.; Iakimov, T.; Zakharov, A.; Syväjärvi, M.; Yakimova, R. Growth of Large Area Monolayer Graphene on 3C-SiC and a Comparison with Other SiC Polytypes. Carbon 2013, 57, 477–484. [Google Scholar] [CrossRef]
- Wang, M.; Huang, M.; Luo, D.; Li, Y.; Choe, M.; Seong, W.K.; Kim, M.; Jin, S.; Wang, M.; Chatterjee, S.; et al. Single-Crystal, Large-Area, Fold-Free Monolayer Graphene. Nature 2021, 596, 519–524. [Google Scholar] [CrossRef]
- Sherrott, M.C.; Hon, P.W.C.; Fountaine, K.T.; Garcia, J.C.; Ponti, S.M.; Brar, V.W.; Sweatlock, L.A.; Atwater, H.A. Experimental Demonstration of >230° Phase Modulation in Gate-Tunable Graphene-Gold Reconfigurable Mid-Infrared Metasurfaces. Nano Lett. 2017, 17, 3027–3034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically Tunable Metasurface Perfect Absorbers for Ultrathin Mid-Infrared Optical Modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.T.; Kim, H.D.; Zhao, R.; Oh, S.S.; Ha, T.; Chung, D.S.; Lee, Y.H.; Min, B.; Zhang, S. Electrically Tunable Slow Light Using Graphene Metamaterials. ACS Photonics 2018, 5, 1800–1807. [Google Scholar] [CrossRef] [Green Version]

| Structure | Mechanism | Wavelength | Material | Function |
|---|---|---|---|---|
| Our Structure | Electrical Tuning | 8.5 μm | Metal/Graphene | Beam Steering |
| Atwater et al. (2016) [16] | Electrical Tuning | 1550 nm | Metal/Dielectric | Beam Steering |
| Zhou et al. (2019) [17] | Temperature Tuning | 25–60 μm | Metal/Dielectric | Reflectance Tuning |
| Lalbakhsh et al. (2021) [29] | Mechanical Tuning | 60 mm | All Metal | Gain Enhancement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Kim, Y.; Shin, E.; Kwon, S.-H. Dynamic Beam Steering and Focusing Graphene Metasurface Mirror Based on Fermi Energy Control. Micromachines 2023, 14, 715. https://doi.org/10.3390/mi14040715
Yu S, Kim Y, Shin E, Kwon S-H. Dynamic Beam Steering and Focusing Graphene Metasurface Mirror Based on Fermi Energy Control. Micromachines. 2023; 14(4):715. https://doi.org/10.3390/mi14040715
Chicago/Turabian StyleYu, Sanghyeok, Youngsoo Kim, Eunso Shin, and Soon-Hong Kwon. 2023. "Dynamic Beam Steering and Focusing Graphene Metasurface Mirror Based on Fermi Energy Control" Micromachines 14, no. 4: 715. https://doi.org/10.3390/mi14040715
APA StyleYu, S., Kim, Y., Shin, E., & Kwon, S.-H. (2023). Dynamic Beam Steering and Focusing Graphene Metasurface Mirror Based on Fermi Energy Control. Micromachines, 14(4), 715. https://doi.org/10.3390/mi14040715







