A New Inner Fabrication Method of Internal Cavity in Metal under Compound Acoustic Fields
Abstract
1. Introduction
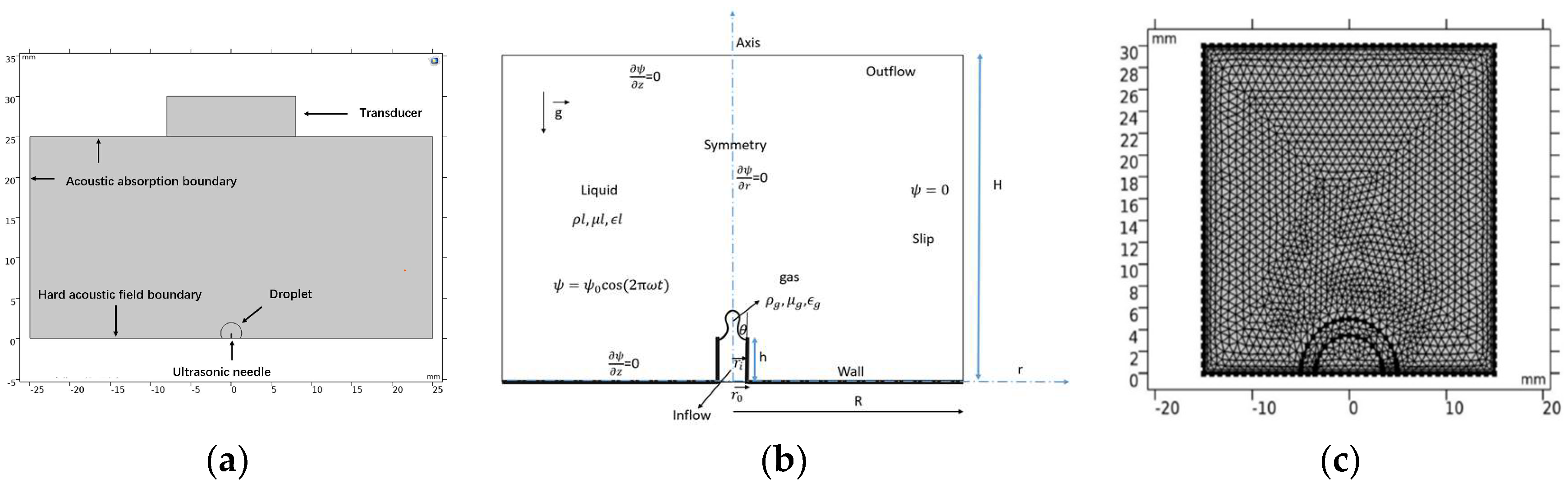
2. Models and Methods
2.1. Single Acoustic Cavitations’ Model in Droplet
2.2. Compound Acoustic Fields Model of Cavitations and Levitation
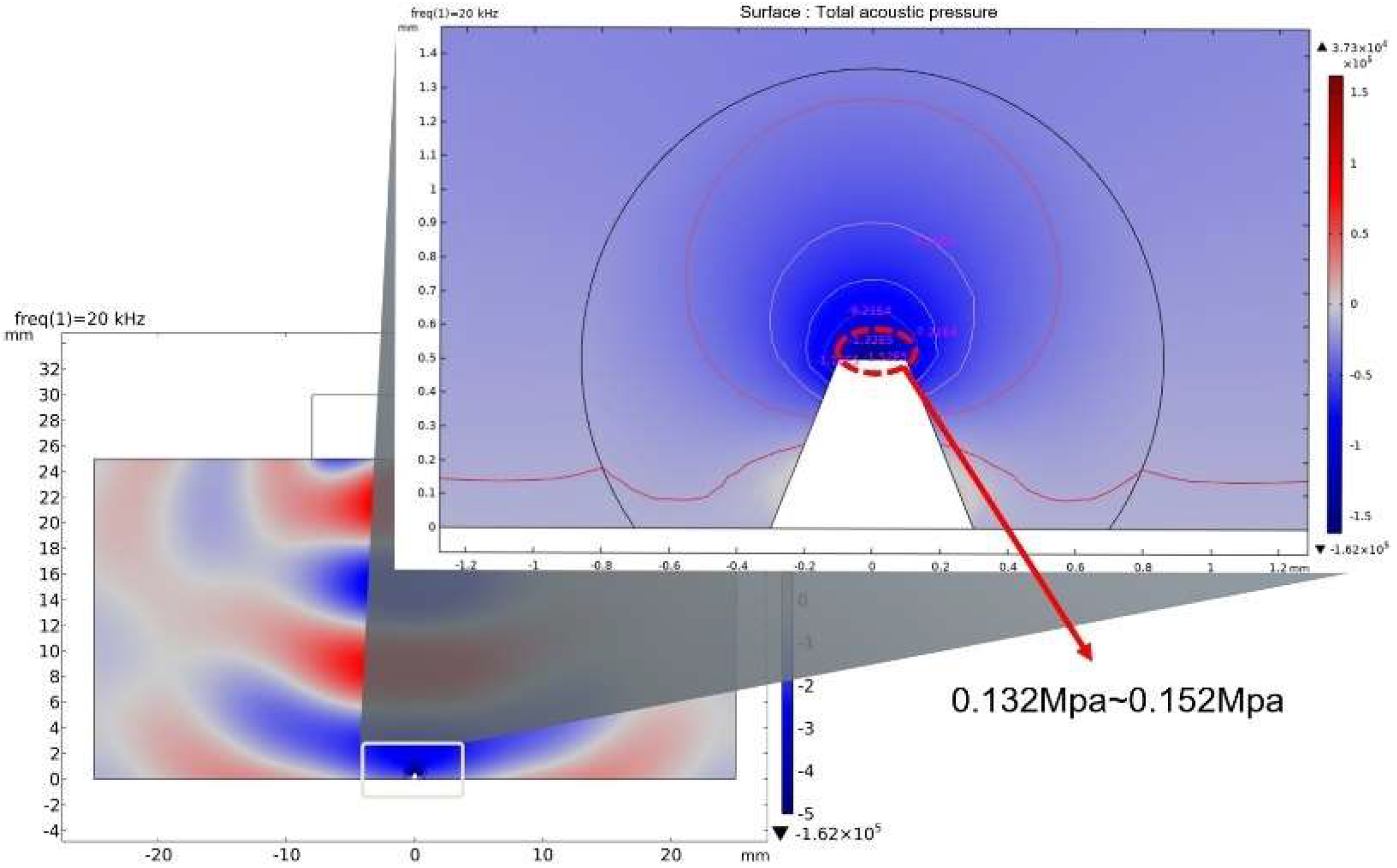
3. COMSOL Simulation Results and Discussion
- (1)
- The acoustic cavitations are composed of the needle tip ultrasonic emitter 1, ultrasonic needle tip 3, and annular ceramic plate 5;
- (2)
- The acoustic standing wave field in Z direction is formed by wave emission end 8 and reflection end 7;
- (3)
- The reflection end 7 is fixed with the ultrasonic needle-tip 1, and the isolation pad 4 is used in the middle;
- (4)
- Ga-In alloy droplet 9 was placed on annular ceramic plate 5, and the middle is isolated by a hydrophobic membrane 6. The radius of the solid–liquid interface is set as rg, and the wetting angle of the solid–liquid interface was set as θ. The measured droplet volume is about 1 mL;
- (5)
- The pointer ultrasonic emitter 3 emits ultrasonic waves to the metal droplet 9 to form a focused acoustic field, which transforms cavitations into a cavity;
- (6)
- Under the coupling effect of standing wave acoustic field and acoustic flow, the liquid surface of droplet 9 shrinks, the boundary is separated, then it is stably suspended at the standing wave node;
- (7)
- The relationship between the length and radius of the ultrasonic needle tip in the acoustic-solid coupling fields, and the initial radius, frequency, and amplitude of the acoustic cavitation droplets were studied;
3.1. Local Acoustic Cavitations at the Tip Point inside Droplet
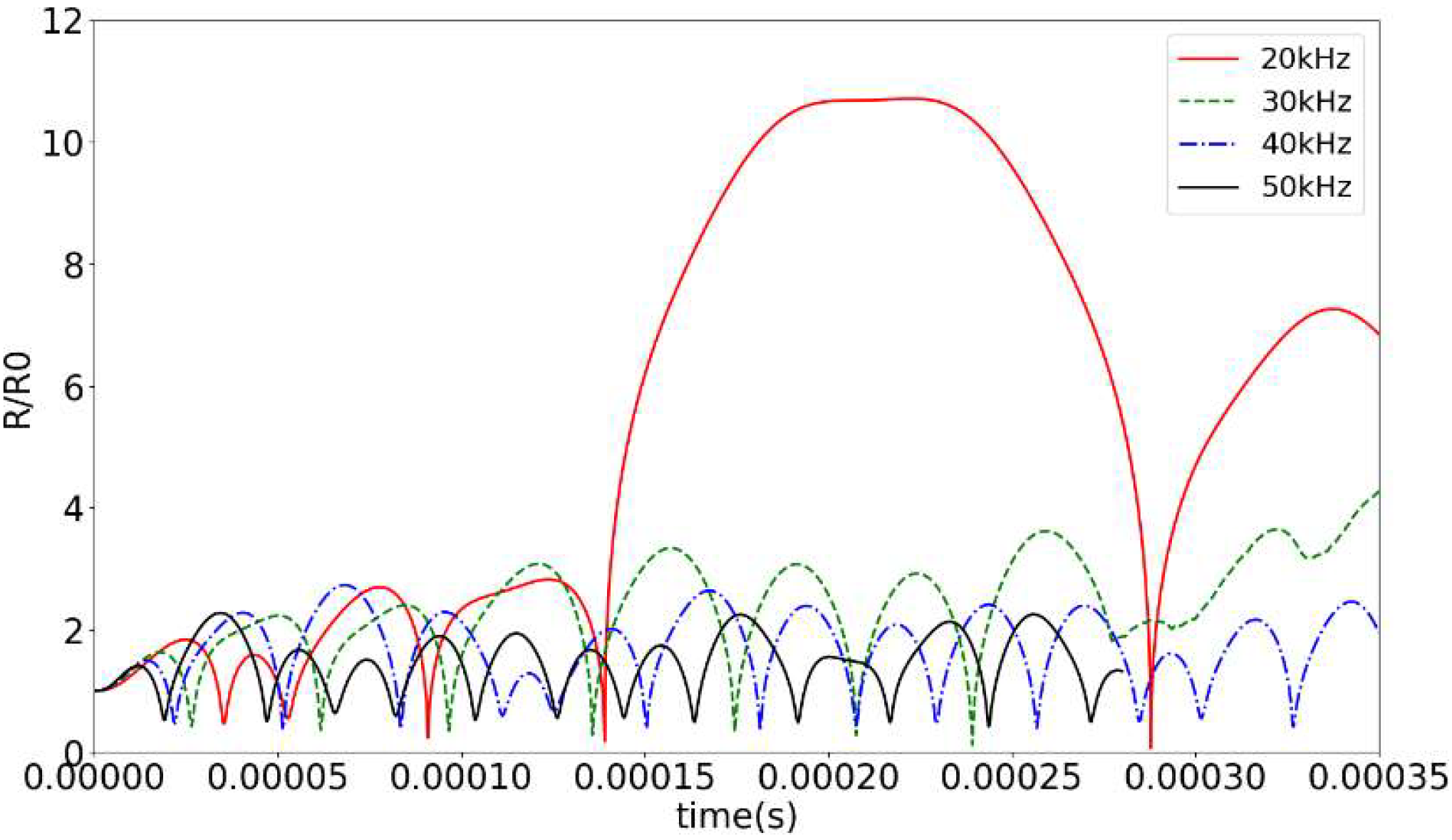
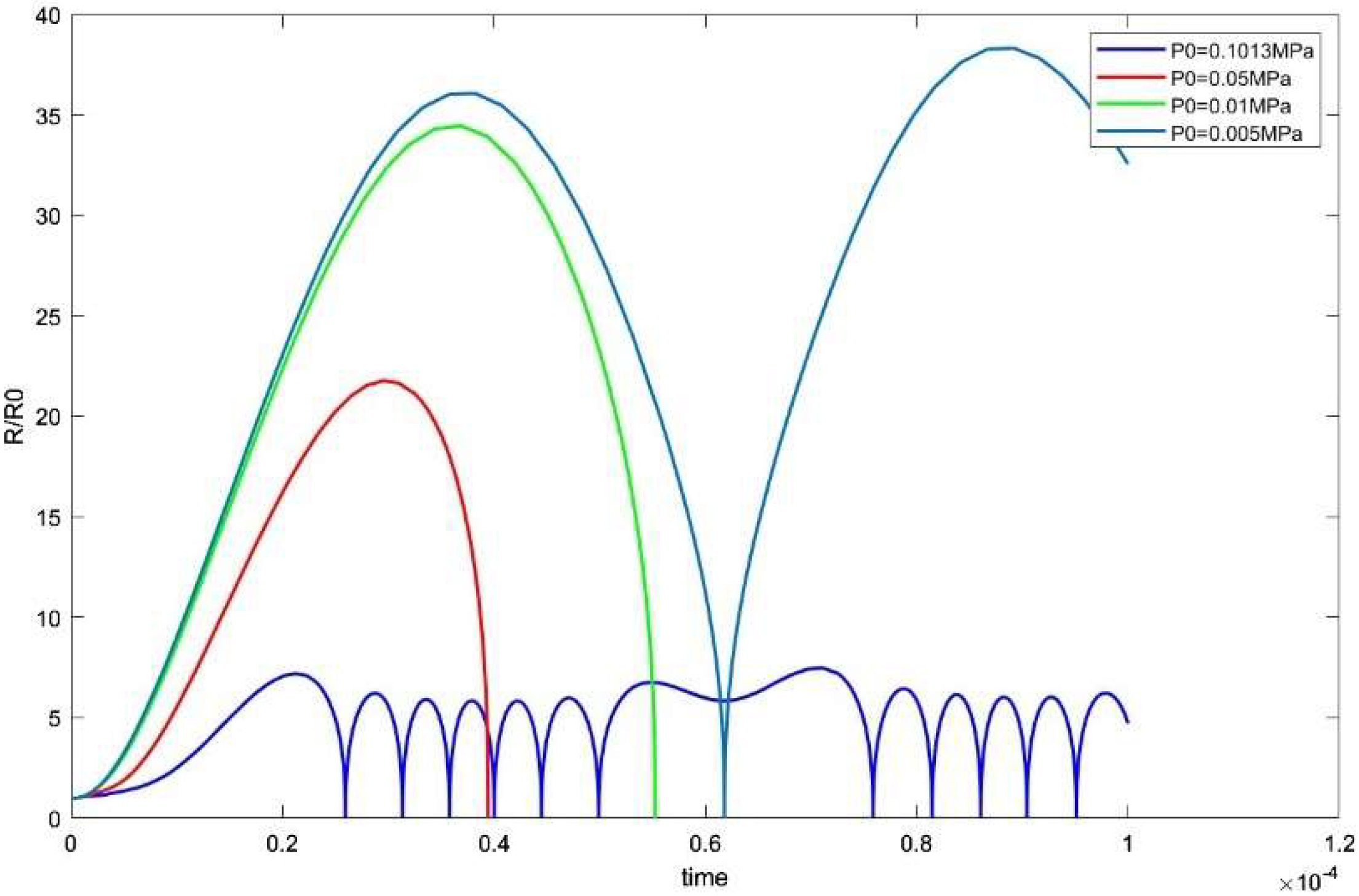
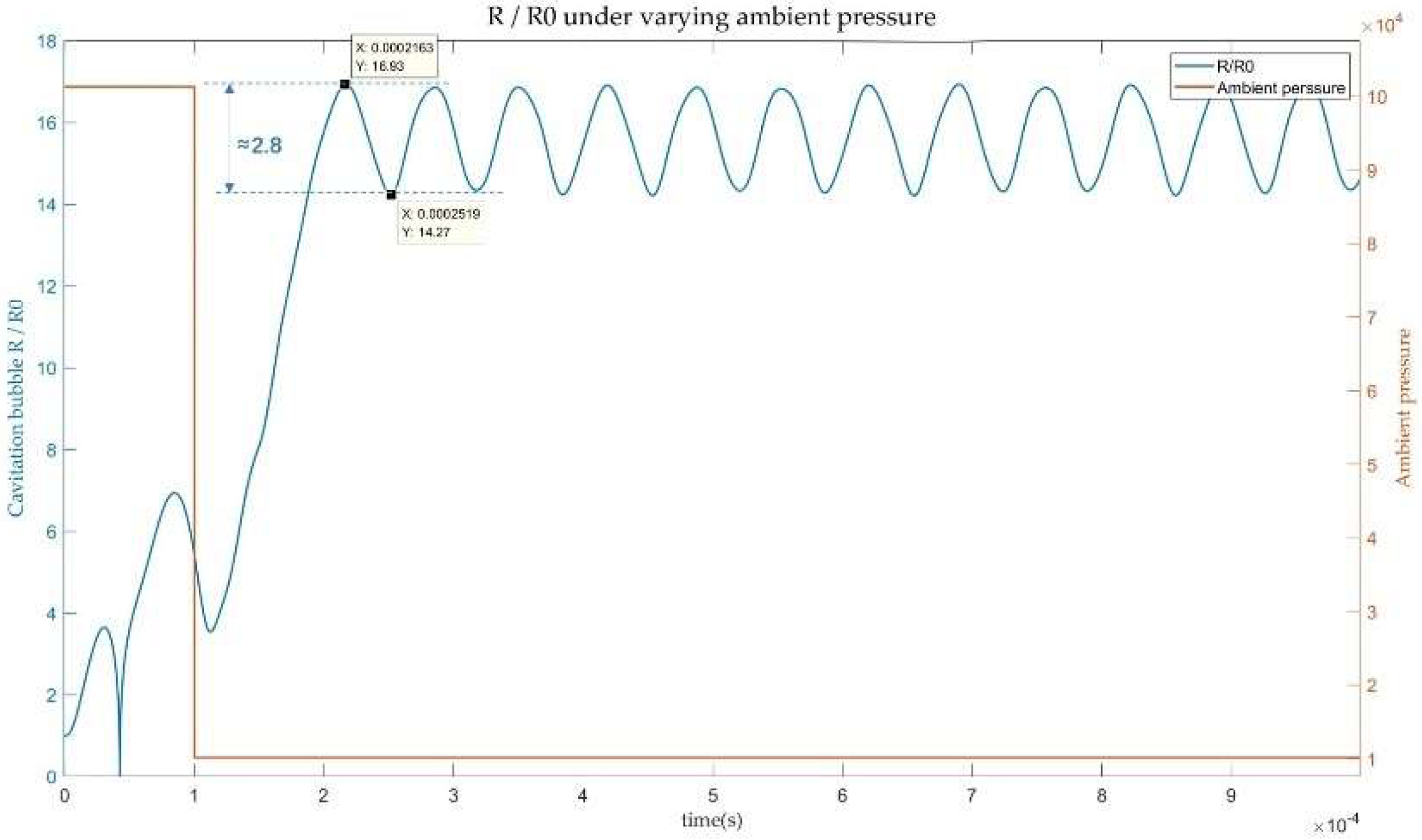
3.2. Scale Controllability of Acoustic Cavitations’ Bubble
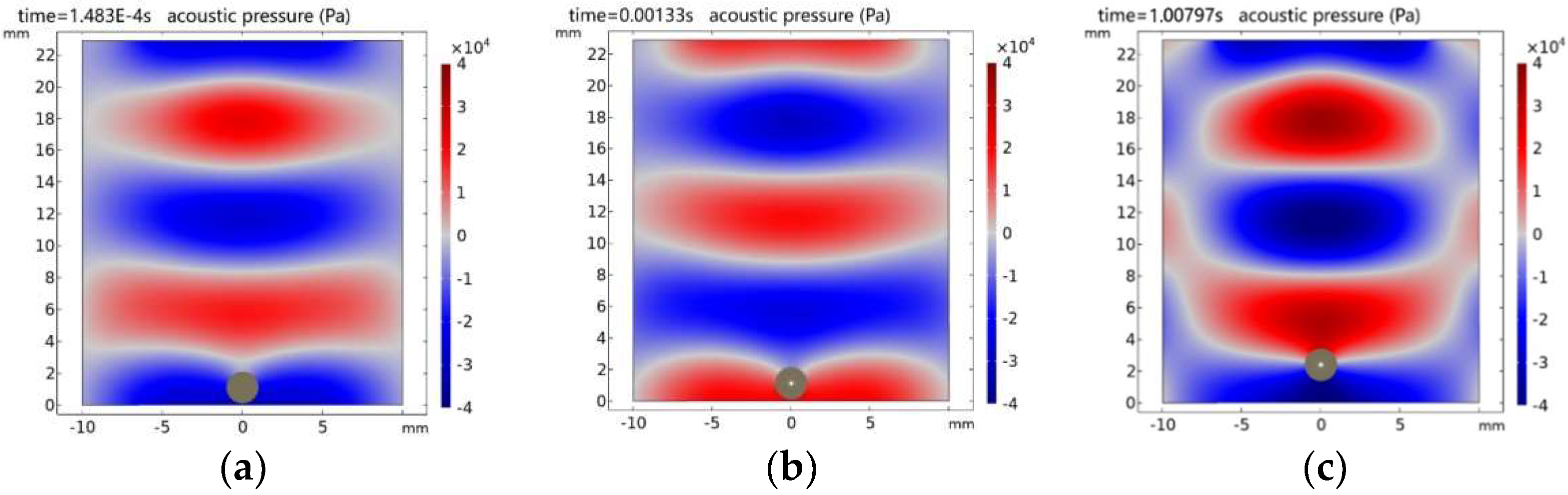
3.3. COMSOL Simulation of Acoustic Cavitation-Levitation Process
3.4. Mechanism Analysis
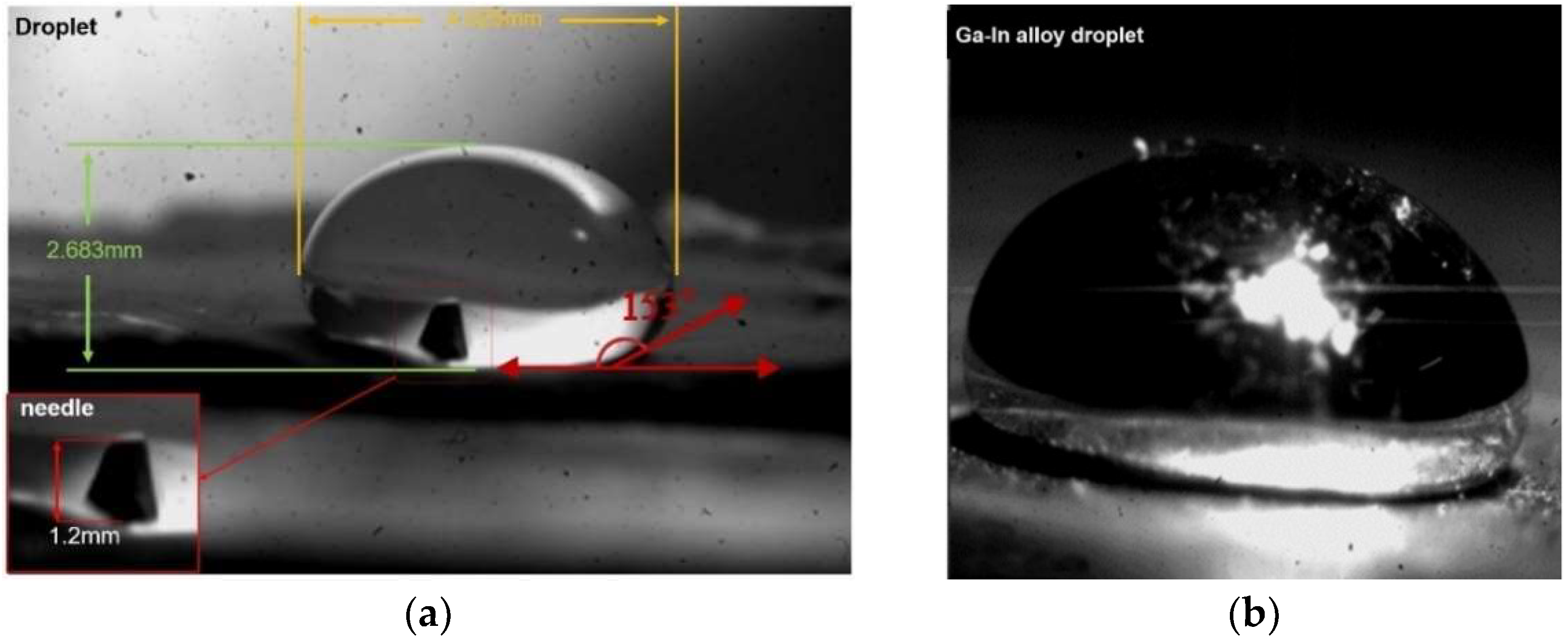
4. Test Results
- (1)
- The relationship between the acoustic pressure and frequency of compound fields with the initial radius of cavitation nuclei, and the formation behaviors of acoustic cavitation bubbles are studied using Formulas (1)~(3).
- (2)
- Cavitations are divided into transient and steady-state cavitations. The control method for the scale of acoustic cavitation cavities should be simulated and designed. The theoretical calculations and experimental conditions for controlling the scale of cavitation and critical stable suspension without bubble explosion are studied.
- (3)
- In the acoustic compound fields, the radiation force is added to the metal droplet as a volume force to simulate its movement in the moving grids, and the displacement generated is fed back to the metal droplet with dynamic radius R of cavitation bubbles as the corresponding independent variable.
- (4)
- Pure water droplets and low melting point Ga-In alloy are used in the tests.
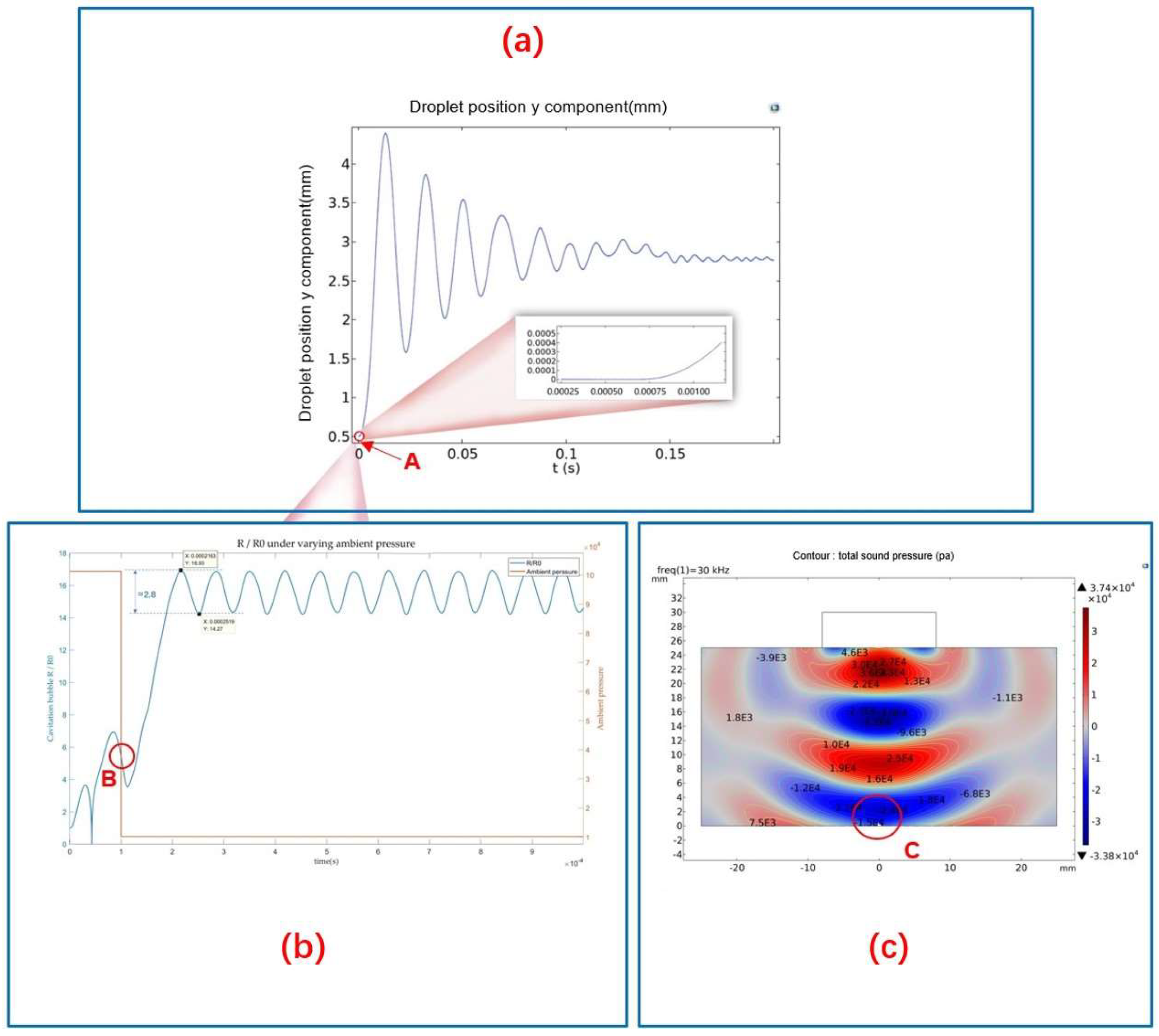
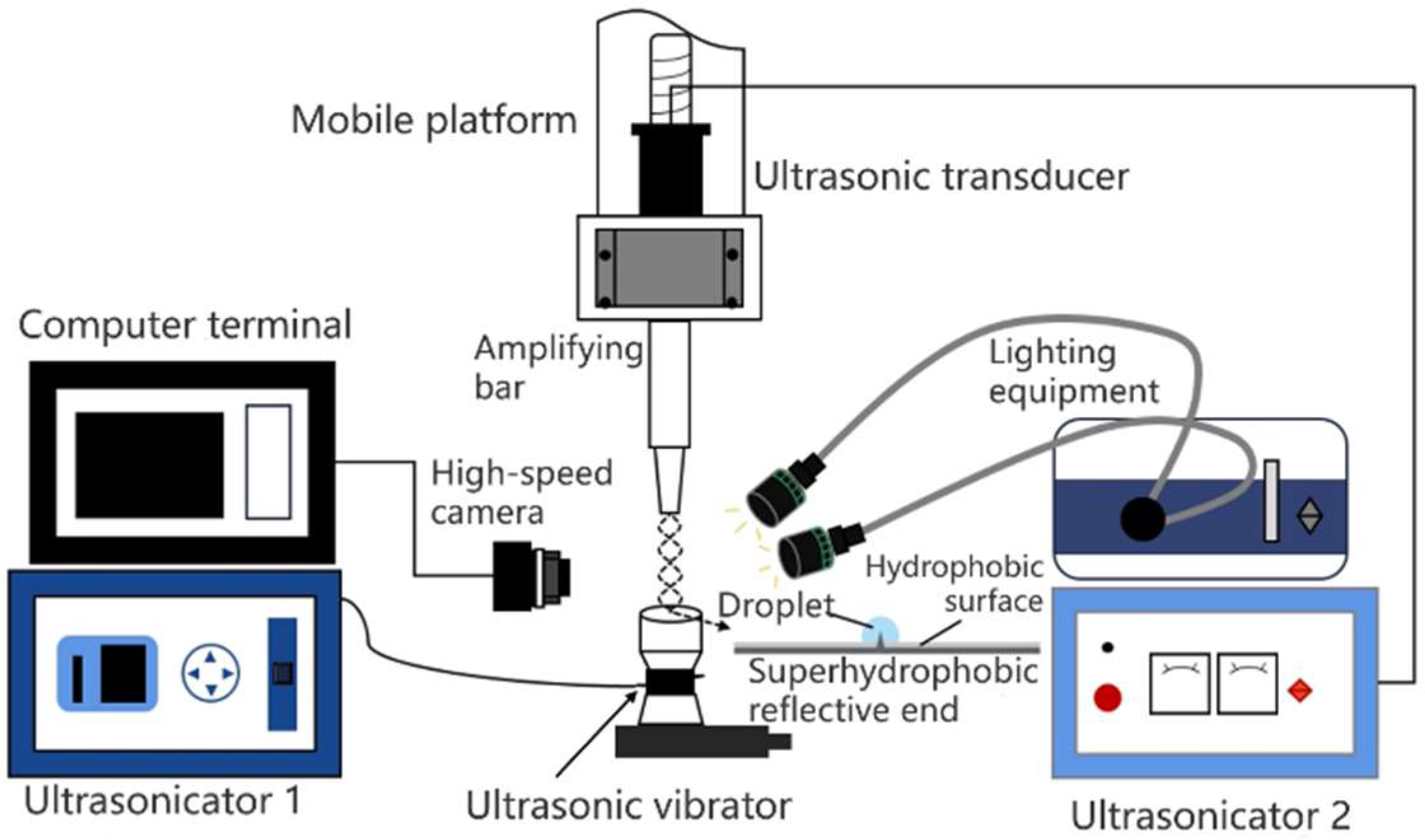
4.1. Experimental Results of Acoustic Cavitation-Levitation
4.2. Experimental Results Analysis
5. Conclusions
- (1)
- The acoustic levitation of droplets includes the processes of central contraction deformation, separation, and suspension, which typically takes milliseconds to seconds. However, the acoustic cavitation process of metal droplets only takes microseconds. This study constructs compound ultrasound fields to coordinate the cavitation-levitation process, ensuring the orderly progression of cavitation and levitation processes at specific time points to generate and maintain internal cavities.
- (2)
- Through simulation analysis, this study investigates the effects of ultrasonic frequency and ambient pressure on cavitation time and finds that reducing the frequency and negative pressure environment can prolong cavitation time. By selecting a parameter combination and coupling with the ultrasonic composite fields, the growth and stability of cavitation bubbles are successfully achieved.
- (3)
- This study establishes an ultrasonic composite fields and clarifies the manufacturing mechanism of controllable size and position of internal cavities, which is verified by simulation and experimental analysis. The mechanism demonstrates the feasibility of internal processing within metal droplets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ug | Vibration amplitude of the needle tip |
| D1 | Emission end diameter (mm) |
| D2 | Reflector diameter (mm) |
| H | Height (mm) |
| P | Local acoustic pressure on the cavitation bubble |
| R0 | Input terminal radius (mm) |
| R1 | Output end radius (mm) |
| Rg | Needle tip radius (mm) |
| L | Length of metal needle (mm) |
| Rμ | Needle tip air groove (μm) |
| R | Transient radius of cavitation bubble (mm) |
| RS | Radius of suspension droplet |
| Pc | Cavitation threshold acoustic pressure |
| Pu | Pressure amplitude |
| ρm | Droplet and air mixing density |
| ρg | Droplet mixing density (g/cm3) |
| ea | Mass coefficient |
| da | Damping coefficient |
| c | Diffusion coefficient |
| β | Convection coefficient |
| cS | Acoustic velocity of suspension droplet |
| λρ | Volume ratio of cavity to suspension droplet |
| υg | Viscosity (Ns/m2) |
| σg | Surface tension (N/m) |
| cg | Acoustic velocity (m/s) |
| rg | droplet radius (mm) |
| ρl | Density (g/cm3) |
| υl | Viscosity (Pa/s) |
| σl | Surface tension (N/m) |
| cl | Acoustic velocity (m/s) |
| ρ0 | Density (g/cm3) |
| υ0 | Viscosity (Pa/s) |
| c0 | Acoustic velocity (m/s) |
| g0 | Gravity acceleration (m/s) |
| ωg | working frequency (kHz) |
| f | Ultrasonic frequency (kHz) |
| A | Ultrasonic amplitude |
References
- Shi, H. From external processing to internal processing—A new development trend of fabyication fabricating technology. Chin. J. Mech. Eng. 2003, 39, 17–22. [Google Scholar] [CrossRef]
- Sugimoto, K.; Matsuo, S.; Naoi, Y. Inscribing Diffraction Grating inside Silicon Substrate Using a Subnanosecond Laser in One Photon Absorption Wavelength. Sci. Rep. 2020, 10, 21451. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Das, A.; Grojo, D. Ultrafast Laser Writing Deep inside Silicon with THz-Repetition-Rate Trains of Pulses. Research 2020, 2020, 8149764. [Google Scholar] [CrossRef] [PubMed]
- Farson, D.F.; Choi, H.W.; Lu, C.; Lee, L.J. Femtosecond Laser Bulk Micromachining of Microfluid Channels in Poly (Methylmethacrylate). J. Laser Appl. 2006, 18, 210–215. [Google Scholar] [CrossRef]
- Kuna, L.; Sommer, C.; Reil, F.; Krenn, J.R.; Hartmann, P.; Pachler, P.; Hoschopf, H.; Wenzl, F.P. Femtosecond Laser Processing as a Versatile Tool for Advanced Solid State Lighting Sources: From Efficacy Enhancement to Colour Temperature Control. Appl. Surf. Sci. 2012, 258, 9213–9217. [Google Scholar] [CrossRef]
- Plesset, M.W. The dynamics of cavitation bubbles. J. Appl. Mech. Sep. 1949, 16, 277–282. [Google Scholar] [CrossRef]
- Poritsky, H. The collapse or growth of a shperical bubble or cavity in a viscous fluid. In Proceedings of the First U.S. National Congress on Applied Mechanics, Chicago, IL, USA, 11–16 June 1951; Sternberg, E., Ed.; American Society of Mechanical Engineers: New York, NY, USA, 1952; pp. 813–821. [Google Scholar]
- Abe, Y.; Kawaji, M.; Watanabe, T. Study on the bubble motion control by ultrasonic wave. Exp. Therm. Fluid Sci. 2002, 26, 817–826. [Google Scholar] [CrossRef]
- Shen, Z.-Z. Dynamical behaviors of cavitation bubble under acoustic standing wave field. Acta Phys. Sin. 2015, 64, 124702. [Google Scholar] [CrossRef]
- Zang, D.; Li, L.; Di, W.; Zhang, Z.; Ding, C.; Chen, Z.; Shen, W.; Binks, B.P.; Geng, X. Inducing Drop to Bubble Transformation via Resonance in Ultrasound. Nat. Commun. 2018, 9, 3546. [Google Scholar] [CrossRef] [PubMed]
- Zang, D.; Li, J.; Chen, Z.; Zhai, Z.; Geng, X.; Binks, B.P. Switchable Opening and Closing of a Liquid Marble via Ultrasonic Levitation. Langmuir 2015, 31, 11502–11507. [Google Scholar] [CrossRef] [PubMed]
- Xie, W. Optimization Theory of Acoustic and Its Experimental Application; Xibei Gongye University: Xi’an, China, 2002. [Google Scholar]
- Wang, Y.; Wu, L.; Wang, Y.; Fan, Y. Mathematical Modeling and Experimental Study on Solid–Liquid Suspension Separation in Ultrasonic Standing Wave Field. J. Low Freq. Noise Vib. Act. Control 2021, 40, 2028–2036. [Google Scholar] [CrossRef]
- Lee, J.H.; Tey, W.Y.; Lee, K.M.; Kang, H.-S.; Lee, K.Q. Numerical Simulation on Ultrasonic Cavitation Due to Superposition of Acoustic Waves. Mater. Sci. Energy Technol. 2020, 3, 593–600. [Google Scholar] [CrossRef]
- Glynne-Jones, P.; Mishra, P.P.; Boltryk, R.J.; Hill, M. Efficient Finite Element Modeling of Radiation Forces on Elastic Particles of Arbitrary Size and Geometry. J. Acoust. Soc. Am. 2013, 133, 1885–1893. [Google Scholar] [CrossRef] [PubMed]
- Marzo, A.; Seah, S.A.; Drinkwater, B.W.; Sahoo, D.R.; Long, B.; Subramanian, S. Holographic Acoustic Elements for Manipulation of Levitated Objects. Nat. Commun. 2015, 6, 8661. [Google Scholar] [CrossRef] [PubMed]
- Andrade, M.A.; Ramos, T.S.; Adamowski, J.C.; Marzo, A. Contactless Pick-and-Place of Millimetric Objects Using Inverted near-Field Acoustic Levitation. Appl. Phys. Lett. 2020, 116, 054104. [Google Scholar] [CrossRef]
- Contreras, V.; Marzo, A. Adjusting Single-Axis Acoustic Levitators in Real Time Using Rainbow Schlieren Deflectometry. Rev. Sci. Instrum. 2021, 92, 015107. [Google Scholar] [CrossRef] [PubMed]
- Chen, S. Study on the Dynamic Behavior and Effect of Acoustic Cavitation Bubbles in Liquid Metal in Narrow Gap; Harbin Institute of Technology: Harbin, China, 2020. [Google Scholar]
- Wang, X.; Huang, H.; Zhou, Y. Research progress on ultrasonic acoustic characteristics in metal melts. China Foundry Equip. Technol. 2019, 53, 25–31. [Google Scholar] [CrossRef]
- Liu, R. Acoustic Field Distribution and Cavitation Effect of Ultrasonic Wave in Aluminum Melt and Its Influence on Solidification Process; Central South University: Guangzhou, China, 2007. [Google Scholar]
- Tang, Q. Study on Acoustic Flow Field in Ultrasonic Micro-Nano Manipulation Technology; Nanjing University of Aernautics and Astronautics: Nanjiang, China, 2018. [Google Scholar]
- Li, N. Optimization Design of Ultrasonic Needle and Its Application in Material Micromanipulation; Nanjing University of Aeronautics and Astronautics: Nanjiang, China, 2012. [Google Scholar]
- Liu, W. Dynamics of Ultrasonic Cavitation Bubbles in Anomalous Fluid; South China University of Technology: Guangzhou, China, 2020. [Google Scholar]




| Name | Parameter | Symbol | Quantity |
|---|---|---|---|
| Ultrasonic transducer | Emission end diameter Ultrasonic frequency | D1 f | 58.0 mm 30 kHz |
| Ultrasonic amplitude | A | 15.0 μm | |
| Acoustic compound fields | Reflector diameter | D2 | 300.0 mm |
| Height | H | 28.82 mm | |
| Ga-In alloy | Melting point | 289 K | |
| Density | ρg | 6.39 g/cm3 | |
| Viscosity | υg | 0.0013 Ns/m2 | |
| Surface tension | σg | 0.63 N/m | |
| Acoustic velocity | cg | 2771 m/s | |
| droplet radius | rg | 3.5 mm | |
| Water | melting point | 273 K | |
| Density | ρl | 1.0 g/cm3 | |
| Viscosity | υl | 0.001 Pa/s | |
| Surface tension | σl | 0.076 N/m | |
| Acoustic velocity | cl | 1481 m/s | |
| Air | Density | ρ0 | 1.21 g/cm3 |
| Viscosity | υ0 | 0.0008937 Pa/s | |
| Acoustic velocity | c0 | 340 m/s | |
| Gravity acceleration | g0 | 9.8 m/s2 | |
| PZT-8 ring | d33 | 325 × 10−12 C/N | |
| Qm | 2000 | ||
| k33 | 0.63 | ||
| tanδ | 0.60% | ||
| Needle’s Tip | Materials | steel | |
| working frequency | ωg | 15~70 kHz | |
| Input terminal radius | R0 | 4.0 mm | |
| Output end radius | R1 | 0.5 mm | |
| Ultrasonic amplitude | 3.0 μm | ||
| Needle tip radius | Rg | 0.16 mm | |
| Length of metal needle | L | 1.2 mm | |
| Needle tip air groove | Rμ | 3~12.6 μm | |
| (Radius of cavitations’ core) Natural frequency | 25 kHz | ||
| Weber number of acoustics | We | ||
| Bond number of droplet | Bo |
| Equipment | Manufacturer | Model | Parameter Configuration |
|---|---|---|---|
| Local ultrasonic source 1 Ultrasonic generator 2 | KMD-K3-II | XT2020 | Frequency: 25~45 kHz Frequency: 30 kHz |
| CCD | American VRI Company | MIROM310 | Frequency: 10,000 frame/s Resolution: 1024 × 512 |
| Light source Piezoelectric needle | Nanjing Yanan Special lighting | XD-300xenon | Frequency: 15~70 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wu, L.; Wang, Y.; Wang, Z.; Wu, G.; Wang, Y.; Wang, H. A New Inner Fabrication Method of Internal Cavity in Metal under Compound Acoustic Fields. Micromachines 2023, 14, 719. https://doi.org/10.3390/mi14040719
Zhang Z, Wu L, Wang Y, Wang Z, Wu G, Wang Y, Wang H. A New Inner Fabrication Method of Internal Cavity in Metal under Compound Acoustic Fields. Micromachines. 2023; 14(4):719. https://doi.org/10.3390/mi14040719
Chicago/Turabian StyleZhang, Zheng, Liqun Wu, Yaxing Wang, Ze’en Wang, Guanwu Wu, Yajing Wang, and Hongcheng Wang. 2023. "A New Inner Fabrication Method of Internal Cavity in Metal under Compound Acoustic Fields" Micromachines 14, no. 4: 719. https://doi.org/10.3390/mi14040719
APA StyleZhang, Z., Wu, L., Wang, Y., Wang, Z., Wu, G., Wang, Y., & Wang, H. (2023). A New Inner Fabrication Method of Internal Cavity in Metal under Compound Acoustic Fields. Micromachines, 14(4), 719. https://doi.org/10.3390/mi14040719





