Identification of the Position of a Tethered Delivery Catheter to Retrieve an Untethered Magnetic Robot in a Vascular Environment
Abstract
:1. Introduction
2. Position Identification and Control of an SRMR
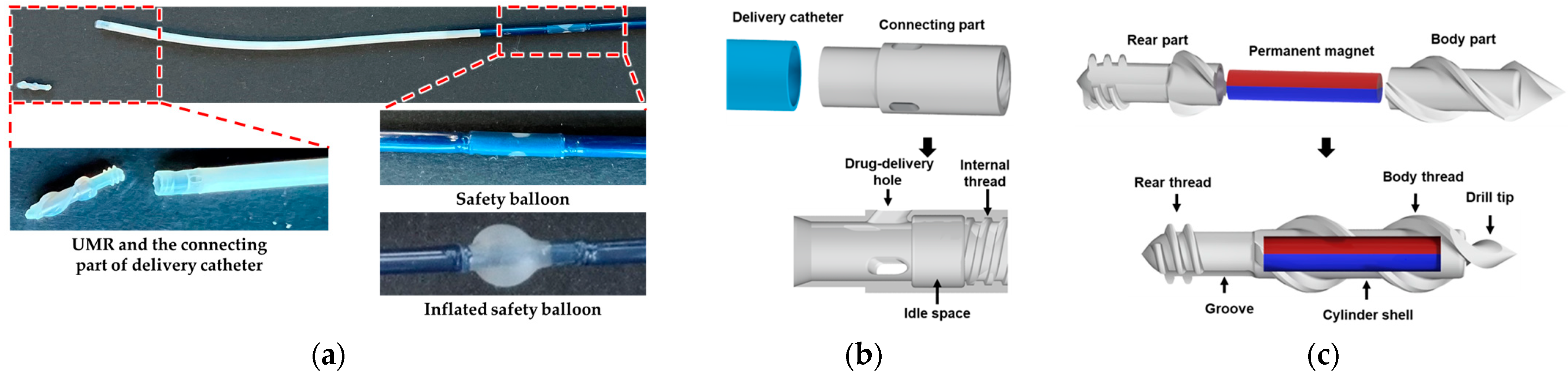
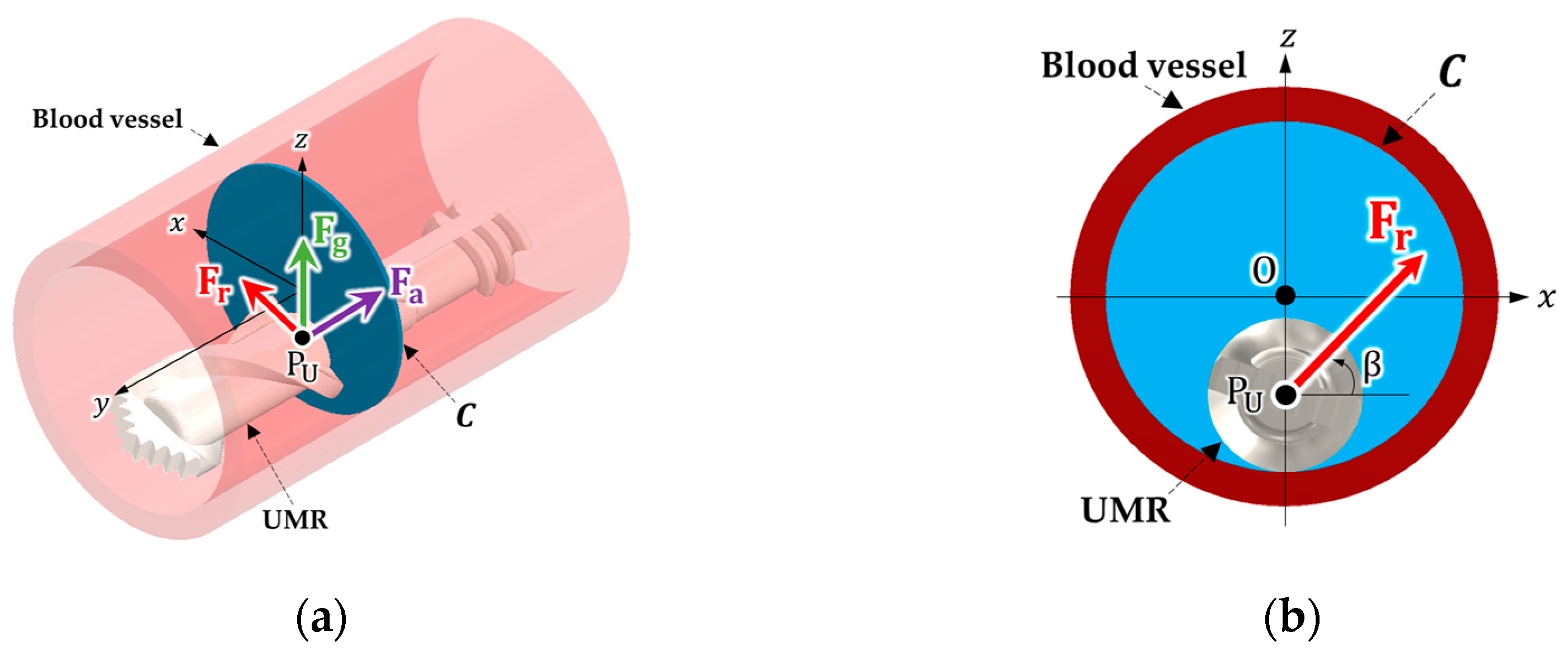
2.1. The Structure of the SRMR and the Manipulation Method
2.1.1. The Structure of the SRMR
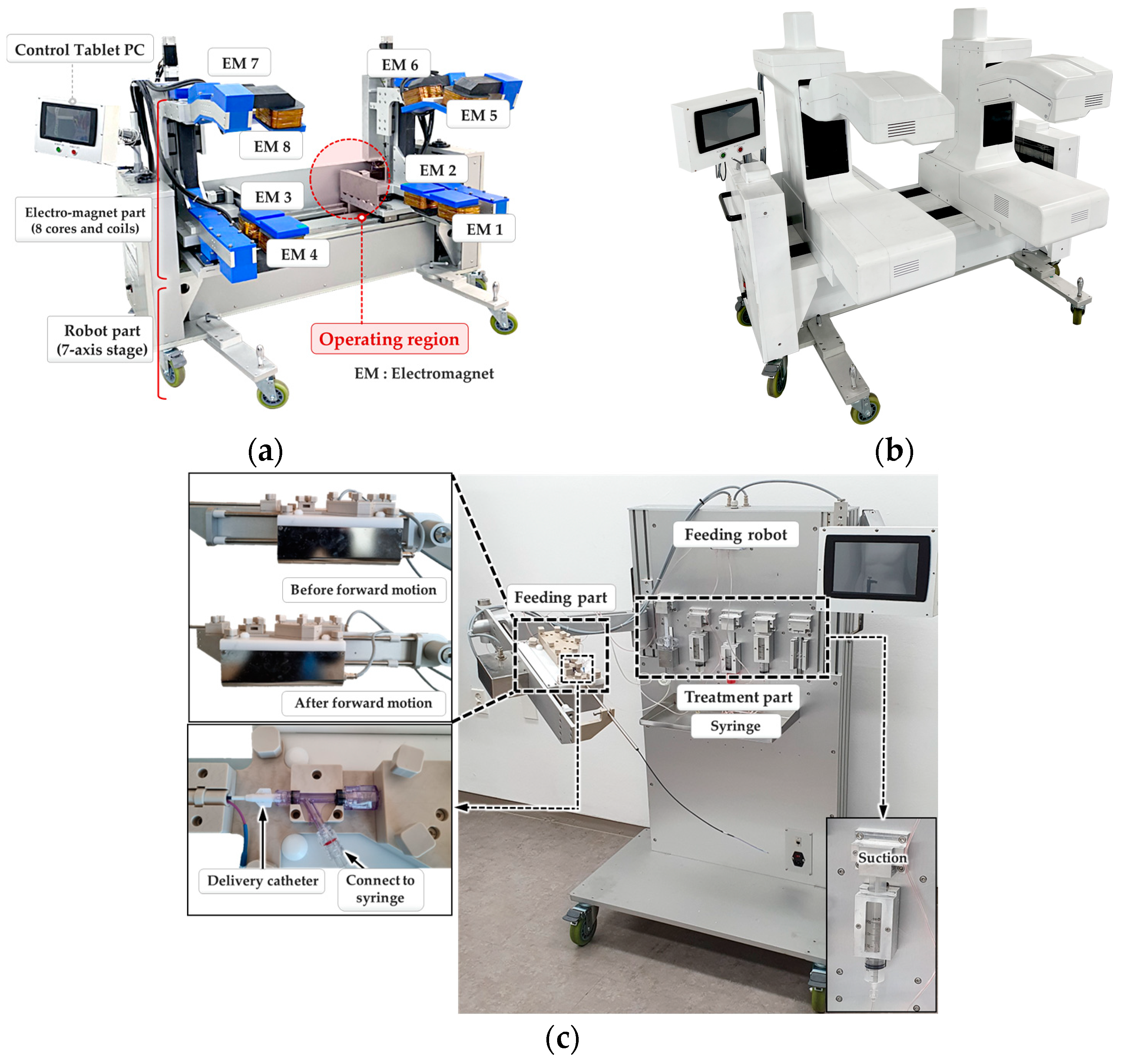
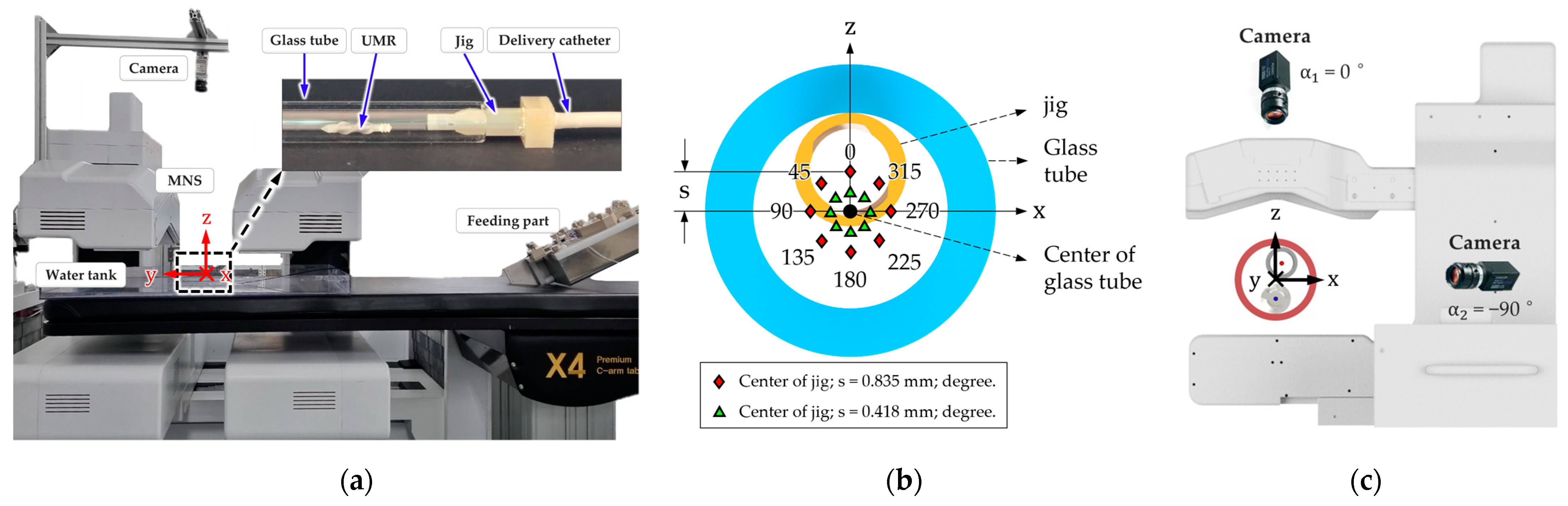
2.1.2. A Robotically Adjustable Magnetic Navigation System for Endovascular Interventions (I-RAMAN System)
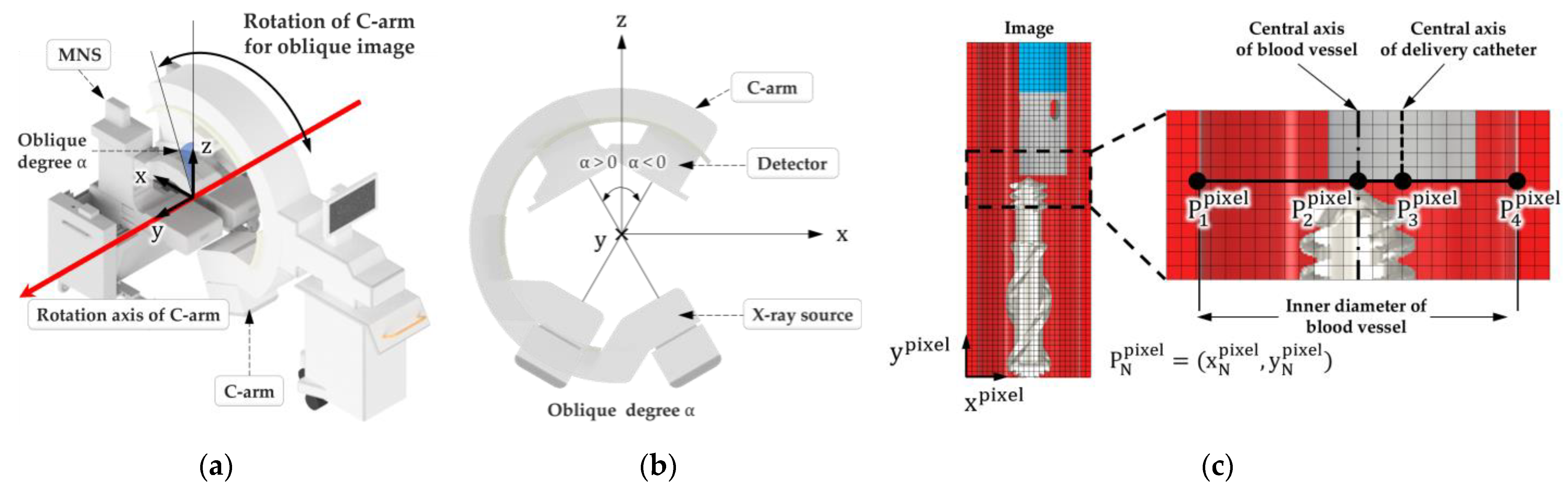
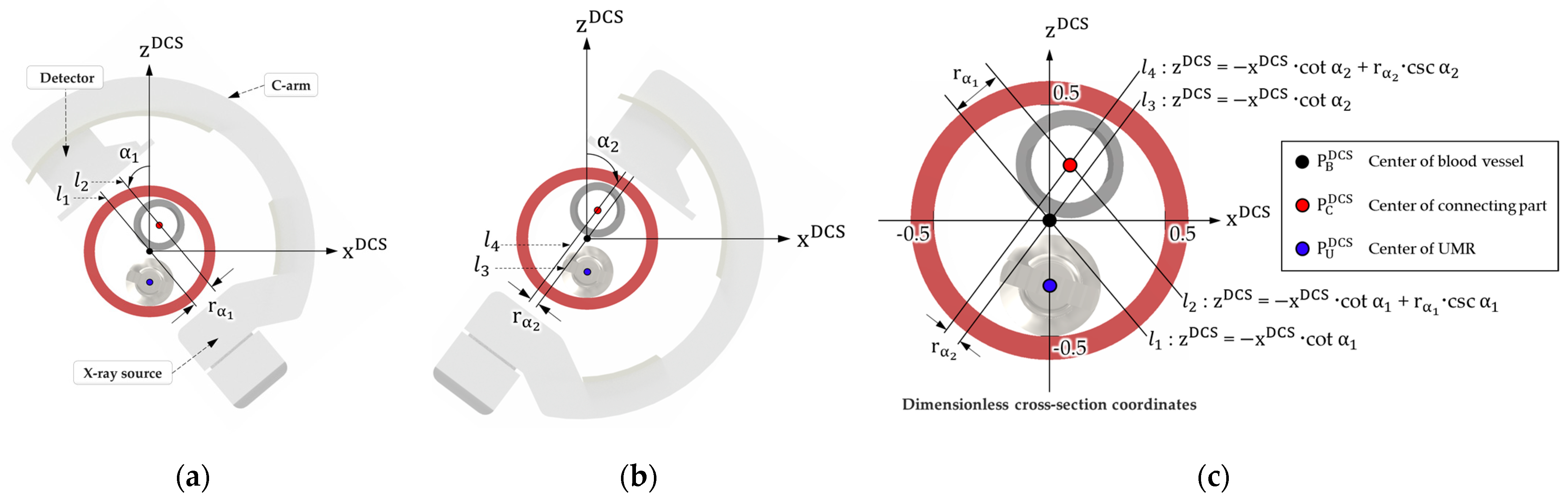
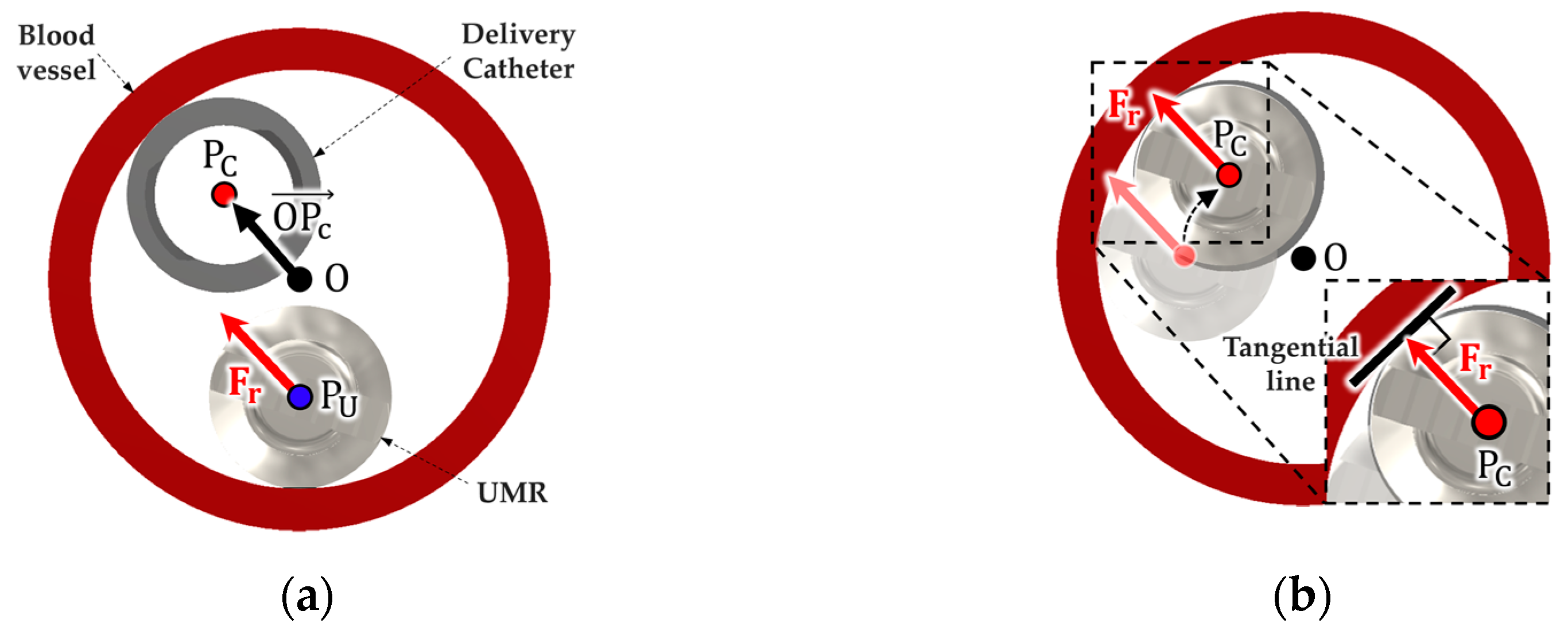
2.2. Algorithm for Identifying the Position of the Delivery Catheter in a Vascular Environment
2.3. Magnetic Field Control for Recombining the UMR with the Delivery Catheter
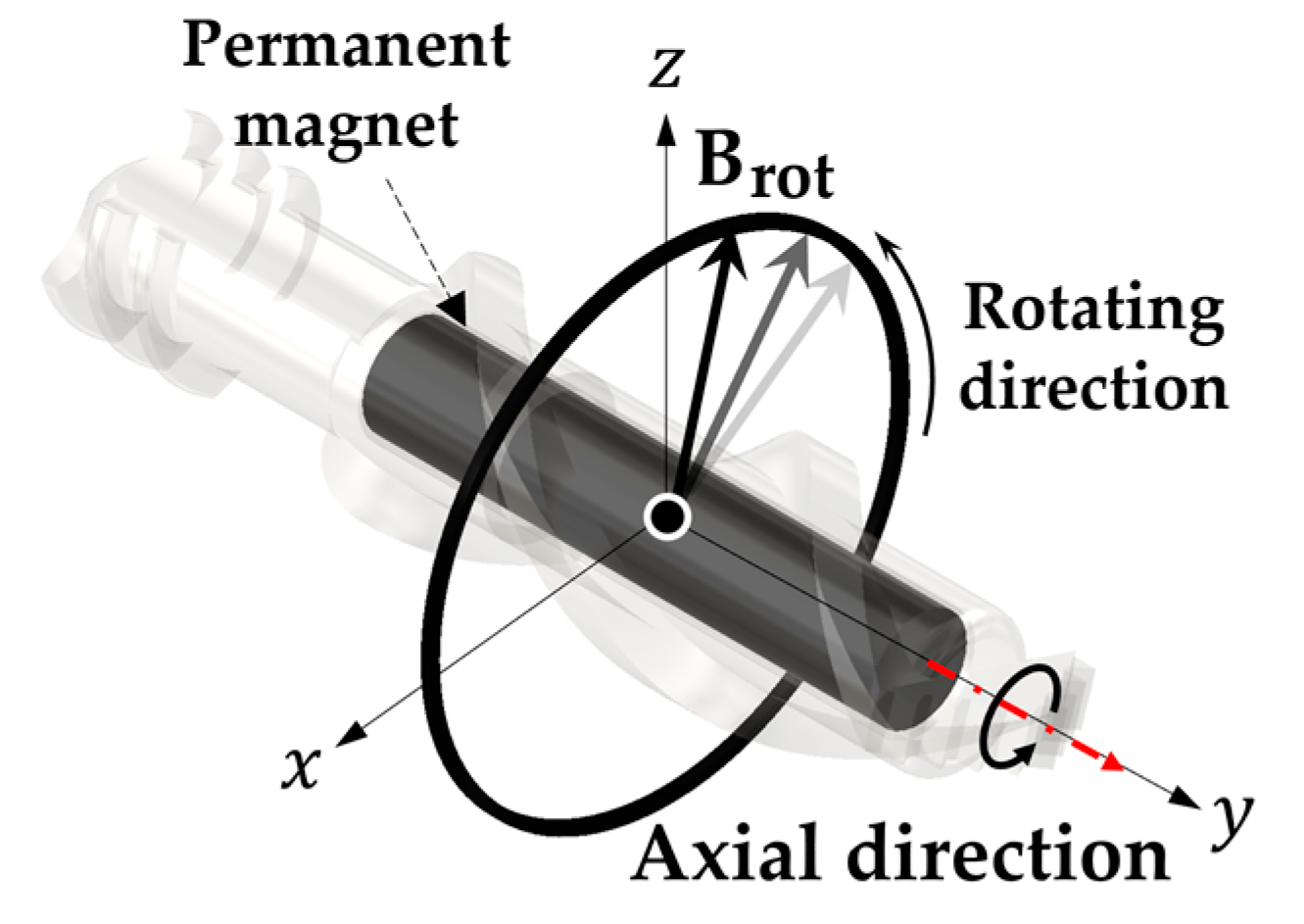
2.3.1. Magnetic Force and Rotating Magnetic Field Applied to the UMR
2.3.2. Procedure for Recombining the UMR with the Delivery Catheter
- (1)
- Two images of the delivery catheter in the blood vessel with different oblique angles are obtained from the X-ray image device. The central position of the connecting part of the delivery catheter is determined with the algorithm proposed in Section 2.2.
- (2)
- Fm is applied during t1 to align the UMR with the delivery catheter. Simultaneously, the feeding robot performs suction through the delivery catheter to assist with Fm. Fm and suction force are used to align the UMR with the connecting part of the delivery catheter. The application of Fm and the suction force starts simultaneously, and the application of Fm is completed before completing the suction force.
- (3)
- Brot is applied from t1, and it causes the rotational motion of the UMR in order to combine the UMR with the delivery catheter. The suction force finishes at t2. Brot is applied until recombination is complete at t3.
- (4)
- Fluid of the delivery catheter is injected into the inner hole to check if the delivery catheter and UMR are separated.
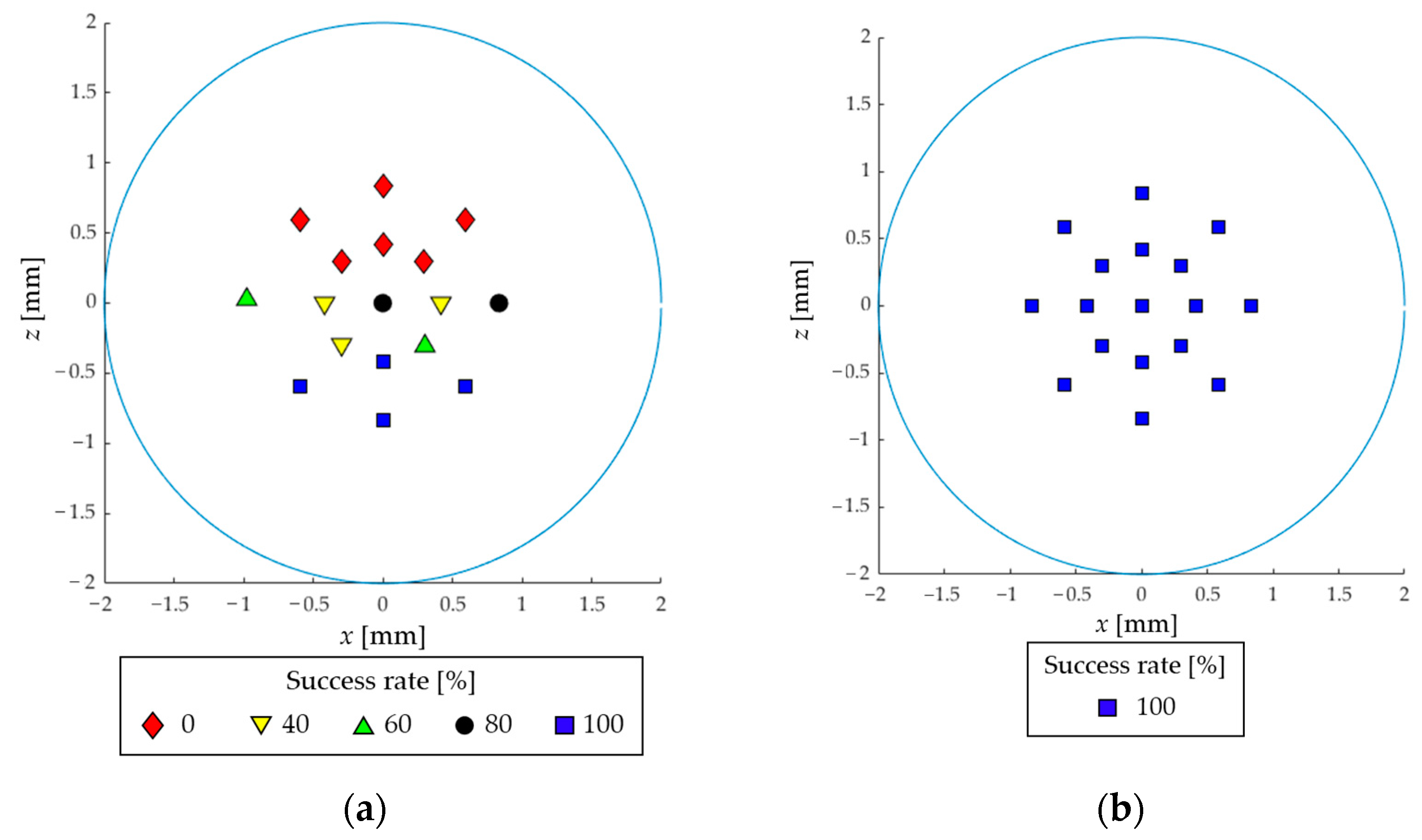
3. Experiment and Verification
3.1. In Vitro Experiment
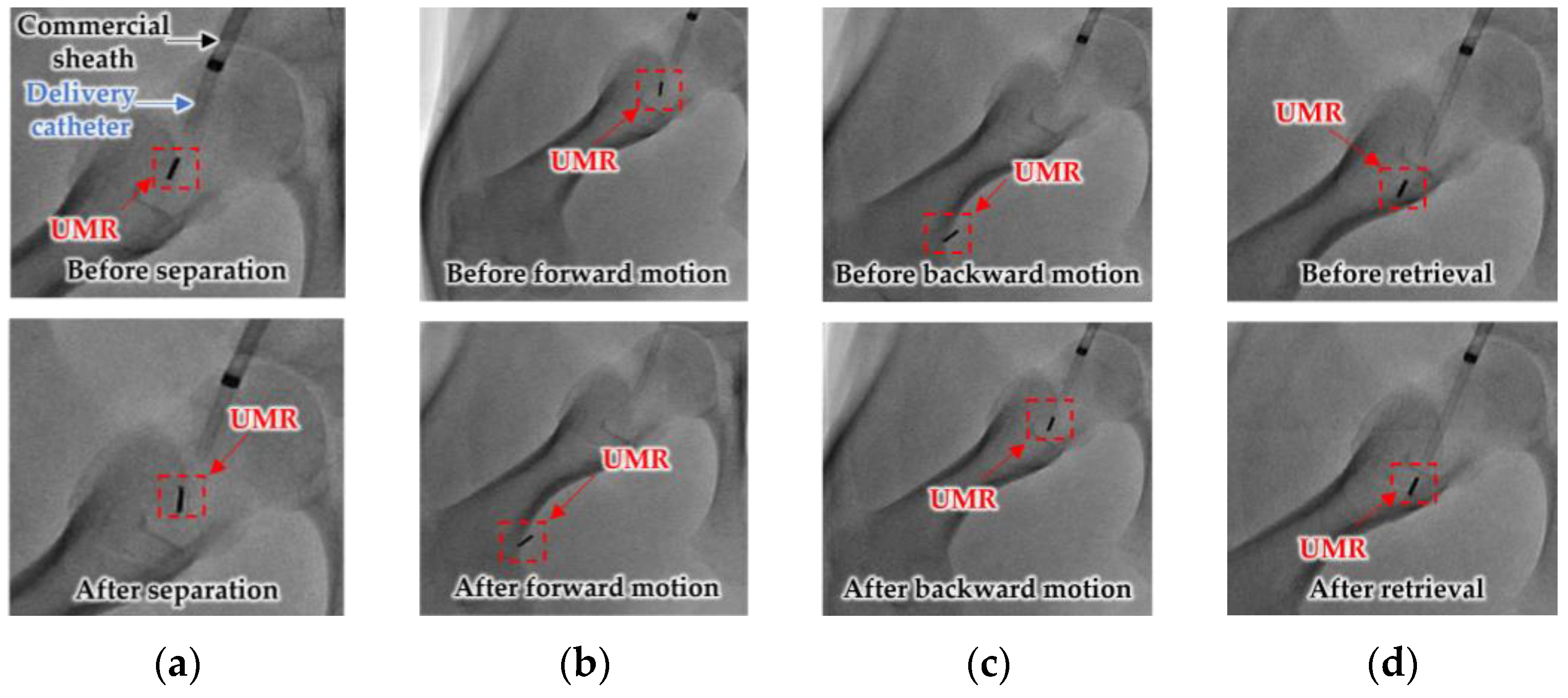
3.2. In Vivo Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gnatiuc, L.; Herrington, W.G. Sex-specific relevance of diabetes to occlusive vascular and other mortality: A collaborative meta-analysis of individual data from 980 793 adults from 68 prospective studies. Lancet Diabetes Endocrinol. 2018, 6, 538–546. [Google Scholar] [CrossRef]
- Pan, C.; Han, Y.; Lu, J. Structural design of vascular stents: A review. Micromachines 2021, 12, 770. [Google Scholar] [CrossRef] [PubMed]
- Ali, K.; Kruse, M.J. Guidewires, catheters, and sheaths used for thoracic endografting procedures. J. Card. Surg. 2009, 24, 113–119. [Google Scholar]
- Hwang, J.; Kim, J.Y.; Choi, H. A review of magnetic actuation systems and magnetically actuated guidewire-and catheter-based microrobots for vascular interventions. Intell. Serv. Robot. 2020, 13, 1–14. [Google Scholar] [CrossRef]
- Ali, A.; Plettenburg, D.H.; Breedveld, P. Steerable catheters in cardiology: Classifying steerability and assessing future challenges. IEEE Trans. Biomed. Eng. 2016, 63, 679–693. [Google Scholar] [CrossRef]
- Hu, X.; Chen, A.; Luo, Y.; Zhang, C.; Zhang, E. Steerable catheters for minimally invasive surgery: A review and future directions. Comput. Assist. Surg. 2018, 23, 21–41. [Google Scholar] [CrossRef]
- Schneider, P. Guidewire and catheter skills for endovascular surgery. In Endovascular Skills, 4th ed.; CRC Press: Boca Raton, FL, USA, 2019; pp. 53–58. [Google Scholar]
- Picano, E.; Vano, E.; Domenici, L.; Bottai, M.; Thierry-Chef, I. Cancer and non-cancer brain and eye effects of chronic low-dose ionizing radiation exposure. BMC Cancer 2012, 12, 157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, K.; Miller, D.L.; Balter, S.; Kleinerman, R.A.; Linet, M.S.; Kwon, D.; Simon, S.L. Occupational radiation doses to operators performing cardiac catheterization procedures. Health Phys. 2008, 94, 211–227. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, L. Magnetic actuation systems for miniature robots: A review. Adv. Intell. Syst. 2020, 2, 2000082. [Google Scholar] [CrossRef]
- Lee, H.; Lee, D.; Jeon, S. A Two-dimensional manipulation method for a magnetic microrobot with a large region of interest using a triad of electromagnetic coils. Micromachines 2022, 13, 416. [Google Scholar] [CrossRef]
- Nelson, B.J.; Gervasoni, S.; Chiu, P.W.Y.; Zhang, L.; Zemmar, A. Magnetically actuated medical robots: An in vivo perspective. Proc. IEEE 2022, 110, 1028–1037. [Google Scholar] [CrossRef]
- Lee, W.S.; Nam, J.W.; Kim, J.Y.; Jung, E.S.; Kim, N.H.; Jang, G.H. Steering, tunneling, and stent delivery of a multifunctional magnetic catheter robot to treat occlusive vascular disease. IEEE Trans. Ind. Electron. 2021, 68, 391–400. [Google Scholar] [CrossRef]
- Jeon, S.; Hoshiar, A.K.; Kim, K.; Lee, S.; Kim, E.; Lee, S.; Choi, H. A magnetically controlled soft microrobot steering a guidewire in a three-dimensional phantom vascular network. Soft Robot. 2019, 6, 54–68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nam, J.; Lee, W.; Kim, J.; Jang, G. Magnetic helical robot for targeted drug-delivery in tubular environments. IEEE/ASME Trans. Mechatron. 2017, 22, 2461–2468. [Google Scholar] [CrossRef]
- Ye, C.; Liu, J.; Wu, X.; Wang, B.; Zhang, L.; Zheng, Y.; Xu, T. Hydrophobicity influence on swimming performance of magnetically driven miniature helical swimmers. Micromachines 2019, 10, 175. [Google Scholar] [CrossRef] [Green Version]
- Park, J.; Lee, W.; Kim, J.; Jung, E.; Kim, N.; Jang, G. Selective separating and assembling motion control for delivery and retrieval of an untethered magnetic robot in human blood vessels. AIP Adv. 2019, 9, 125136. [Google Scholar] [CrossRef] [Green Version]
- Sa, J.; Park, J.; Jung, E.; Kim, N.; Lee, D.; Bae, S.; Lee, Y.; Jang, G. Separable and recombinable magnetic robot for robotic endovascular intervention. IEEE Robot. Autom. Lett. 2023, 8, 1881–1888. [Google Scholar] [CrossRef]
- Lee, W. Robotically Adjustable Magnetic Navigation System and Magnetic Catheter Robot for Vascular Intervention. Ph.D. Thesis, Hanyang University, Seoul, Republic of Korea, 2021. [Google Scholar]
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, B.; Sengul, A.; Nelson, B.J. OctoMag: An electromagnetic system for 5-DOF wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Lu, Q.; Sun, Z.; Zhang, J.; Zhang, J.; Zheng, J.; Qian, F. A novel remote-controlled vascular interventional robotic system based on hollow ultrasonic motor. Micromachines 2022, 13, 410. [Google Scholar] [CrossRef]
- Lee, K.H.; Fu, K.C.D.; Guo, Z.; Dong, Z.; Leong, M.C.W.; Cheung, C.-L.; Lee, A.P.-W.; Luk, W.; Kwok, K.-W. MR safe robotic manipulator for MRI-guided intracardiac catheterization. IEEE/ASME Trans. Mechatron. 2018, 23, 586–595. [Google Scholar] [CrossRef]
- M’hiri, F.; Duong, L.; Desrosiers, C.; Dahdah, N.; Miró, J.; Cheriet, M. Automatic evaluation of vessel diameter variation from 2D X-ray angiography. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 1867–1876. [Google Scholar] [CrossRef] [PubMed]
- Çimen, S.; Gooya, A.; Grass, M.; Frangi, A.F. Reconstruction of coronary arteries from X-ray angiography: A review. Med. Image Anal. 2016, 32, 46–68. [Google Scholar] [CrossRef] [PubMed] [Green Version]


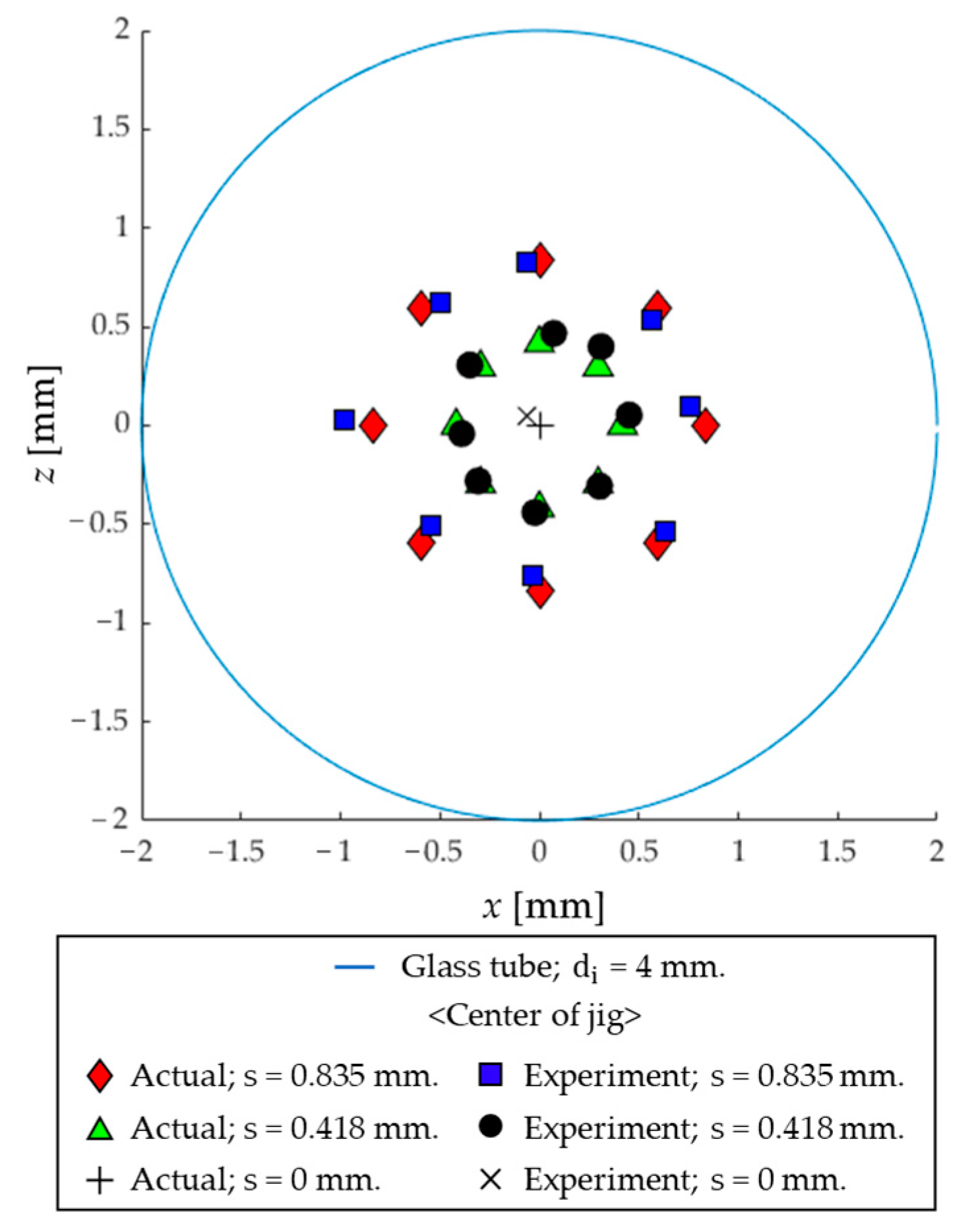

| S [mm] | Position 1 [°] | X (Cal.) 2 [mm] | Z (Cal.) 2 [mm] | X (Actual) [mm] | Z (Actual) [mm] | Error (X) [mm] | Error (Z) [mm] |
|---|---|---|---|---|---|---|---|
| 0.835 | 0 | −0.06 | 0.83 | 0.00 | 0.84 | 0.06 | 0.01 |
| 45 | −0.50 | 0.63 | −0.59 | 0.59 | 0.09 | 0.04 | |
| 90 | −0.98 | 0.03 | −0.84 | 0.00 | 0.14 | 0.03 | |
| 135 | −0.55 | −0.51 | −0.59 | −0.59 | 0.04 | 0.08 | |
| 180 | −0.03 | −0.76 | 0.00 | −0.84 | 0.03 | 0.08 | |
| 225 | 0.63 | −0.53 | 0.59 | −0.59 | 0.04 | 0.06 | |
| 270 | 0.76 | 0.09 | 0.84 | 0.00 | 0.08 | 0.09 | |
| 315 | 0.57 | 0.53 | 0.59 | 0.59 | 0.02 | 0.06 | |
| 0 | 0.07 | 0.47 | 0.00 | 0.42 | 0.07 | 0.05 | |
| 0.418 | 45 | −0.35 | 0.31 | −0.30 | 0.30 | 0.05 | 0.01 |
| 90 | −0.39 | −0.04 | −0.42 | 0.00 | 0.03 | 0.04 | |
| 135 | −0.31 | −0.28 | −0.30 | −0.30 | 0.01 | 0.02 | |
| 180 | −0.02 | −0.44 | 0.00 | −0.42 | 0.02 | 0.02 | |
| 225 | 0.30 | −0.31 | 0.30 | −0.30 | 0.01 | 0.01 | |
| 270 | 0.45 | 0.05 | 0.42 | 0.00 | 0.03 | 0.05 | |
| 315 | 0.31 | 0.40 | 0.30 | 0.30 | 0.01 | 0.10 | |
| 0 | center | −0.06 | 0.05 | 0.00 | 0.00 | 0.06 | 0.05 |
| Average error [mm] | 0.05 | 0.05 | |||||
| Pig * | Leg | Oblique Degree | PC (x, z) [mm] | Retrieval Result | |
|---|---|---|---|---|---|
| α1 [°] | α2 [°] | ||||
| 1 * | Right | 0 | −15 | (0.11, −1.29) | Success |
| Left | 0 | +15 | (−0.25, −0.35) | Success | |
| 2 * | Right | 0 | −15 | (−0.6, 1.13) | Success |
| Left | 0 | +15 | (0.6, 0.16) | Success | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, N.; Kwon, J.; Jang, G. Identification of the Position of a Tethered Delivery Catheter to Retrieve an Untethered Magnetic Robot in a Vascular Environment. Micromachines 2023, 14, 724. https://doi.org/10.3390/mi14040724
Lee S, Kim N, Kwon J, Jang G. Identification of the Position of a Tethered Delivery Catheter to Retrieve an Untethered Magnetic Robot in a Vascular Environment. Micromachines. 2023; 14(4):724. https://doi.org/10.3390/mi14040724
Chicago/Turabian StyleLee, Serim, Nahyun Kim, Junhyoung Kwon, and Gunhee Jang. 2023. "Identification of the Position of a Tethered Delivery Catheter to Retrieve an Untethered Magnetic Robot in a Vascular Environment" Micromachines 14, no. 4: 724. https://doi.org/10.3390/mi14040724
APA StyleLee, S., Kim, N., Kwon, J., & Jang, G. (2023). Identification of the Position of a Tethered Delivery Catheter to Retrieve an Untethered Magnetic Robot in a Vascular Environment. Micromachines, 14(4), 724. https://doi.org/10.3390/mi14040724







