2. Materials and Methods
An NV color center in the diamond is a combination of a nitrogen atom, which replaces a carbon atom, with its adjacent vacancy. Additionally, it is a stable luminous point defect with a
type symmetry; its crystal structure is shown in
Figure 1a [
12]. NV color center is considered to be a solid-state quantum sensor with a great performance. Its fluorescence property and electron spin property are the subject of research. Its energy level structure is shown in
Figure 1b [
13]. Electrons in an NV color center have spin triplet states in both the ground state
and excited state
(i.e.,
state), a magnetic dipole transition of a magnetically tunable spin level, and a zero field splitting D = 2.87 GHz between the
and
states. The electrons in the NV color center are in a degenerate
state without the magnetic field; when the magnetic field acts, its
state has zero field splitting [
14]. When the microwave acts on the electron in the NV color center and resonates with the energy level from the
state to
state, its quantum state is reversed. Due to the metastable state of the non-radiative transition
, the excited fluorescence intensity of the diamond decreases and shows a trough in the ODMR signal [
15].
The structure diagram of the space microwave field detection system designed in this paper in shown in
Figure 2a. In this paper, a type
diamond synthesized at high temperature and high pressure was used. Its volume was
. After 4 h of electron irradiation and 2.5 h of high-temperature annealing, its nitrogen content was less than 200 ppm. A laser (CRYSTALASER, Reno, Nevada, USA| CL532-100-SO|50 mW 532 nm) was used to irradiate the diamond, and an electromagnetic coil was used to apply a magnetic field along the axis of diamond <111> crystals. A continuous microwave was applied to the diamond using a microwave source (KEYSIGHT, Santa Rosa, CA, USA| N5183B) to make the NV color center in the diamond transition to the state of
. At the same time, an Olympus flat-field achromatic objective (THORLABS, Newton, NJ, USA| RMS10X) was used 10 times to measure the fluorescence excited from the diamond, and then a photoelectric detector (THORLABS, Newton, NJ, USA| PDA100A2) was used to collect the fluorescence, which is filtered by the 600~800 nm lens group (THORLABS, Newton, NJ, USA| FELH0600&FESH0800) and converged by a convex focusing lens. In this paper, an array antenna was used as the analog measurement microwave emission equipment, and its structure and simulation radiation field diagram are shown in
Figure 2b,c. The array antenna is composed of eight subunit antennas. The main radiation direction Z is the physical centerline perpendicular to the surface of the microwave antenna; the X direction represents the short side of the array microwave antenna, and the Y direction represents the long side of the array microwave antenna. From the simulation radiation diagram, it can be seen that the microwave power gain of this antenna in the main radiation direction is 18.15 dB. At the same time, the port reflection coefficient of the antenna is shown in
Figure 2d. It can be seen that the main radiation frequency of the array microwave antenna is approximately 2.9 GHz. Therefore, this article only needs to provide a magnetic field of
magnitude for the diamond NV color center to cause a decrease in the resonant microwave frequency within the range of the ODMR spectral peak. At the same time, the ODMR spectral peak contrast of the diamond NV color center is conveniently kept within an ideal range.
Based on the two-channel microwave coherent population oscillation (CPO) effect of a diamond NV color center, this paper designs an intensity detection scheme for an unknown microwave. When the pump source with an angular frequency of
and the detection source with an angular frequency of
are emitted into an active medium at the same time, and
of them is less than or equal to the particle lifetime, the pump source can effectively scatter the transient modulated ground-state particles onto the detection light, thus limiting the absorption of the detection source energy and causing its spectrum to change [
16]. We set the microwave frequency to be measured as 2.9063 GHz, which is transmitted by the array antenna described above. Based on the Zeeman splitting effect of diamond NV color center, the position of its ODMR spectral peak is regulated. The electromagnetic coil is used to apply a magnetic field along the <111> crystal axis direction of the diamond NV color center. The ODMR spectrum of the diamond NV color center is shown in
Figure 3a. In order to obtain the best test results, a 1.5 mT magnetic field is applied. At the same time, in order to use a single peak in the ODMR spectrum and make the contrast of this peak as high as possible, a frequency modulation (FM) microwave is used as a detection source microwave [
17] with a frequency of:
In this formula,
is the FM-modulated carrier frequency, which is same as the microwave to be measured (2.9063 GHz);
is the FM modulation depth, which is 3 MHz; and
is the FM modulation frequency, which is 100 kHz. When the dual-channel microwave frequency resonates with the diamond NV energy level, the population of the NV color center changes, i.e., the corresponding position in the ODMR spectrum changes in intensity, which is called the spectral hole-burning phenomenon. The results are shown in
Figure 3b. Under the same power of FM microwave emission intensity, the ODMR spectrum under the influence of different pump source microwave intensities also has different spectral hole-burning phenomena. That is, as the microwave emission intensity of the resonance source increases, the ODMR spectral signal amplitude of the diamond NV color center decreases, and the height of the peak formed by the resonance “hole burning” in the spectrum increases.
The ODMR spectral curve under the influence of the two-channel coherent population oscillation of the diamond NV color center is processed using a first-order differential operation, the results of which are shown in
Figure 3c. The first-order differential operation used in this article is located in the field programmable gate array (FPGA) control system, where the upper and lower limits of the output amplitude of the first-order differential system were set, with the output amplitude limit of 7.28 V (−3.64–3.64 V). The horizontal line existing in Image A is the cutoff amplitude. This processing method transforms the change in the overall intensity and waveform of the ODMR spectral curve caused by the dual-channel coherent population oscillation into the change in the zero position on its first-order differential curve [
18]. At the same time, the method of microwave closed-loop frequency PID locking is used to lock the zero position on the first-order differential curve. The drift amount
of the zero position is input to the FPGA control board. When the microwave intensity of the resonance source changes, the spectral morphology of CPO also changes, affecting the morphology of its first-order differential curve. When the microwave intensity increases, the depth of the “hole burning” on the CPO spectral curve increases, and the corresponding zero point on the first-order differential curve shifts to the left. This shift corresponds to a change in the microwave frequency of
. After calculation and processing, the feedback amount is input to the detection microwave source, which is used to control the FM microwave carrier frequency and realize the correction of the zero position on the first-order guide curve [
19]. At the same time, the feedback output from FPGA to the microwave source is taken as the result of the microwave intensity to be measured. The changes in the detection of the curve are shown in
Figure 3d. The final output
is used as the microwave intensity to be measured. Additionally, the structure diagram of the FPGA information solution system is shown in
Figure 4a. This system includes a band-pass filter, a low-pass filter, a multiplier, an amplifier, a linear region amplification module, an information solving module, and a PID locking module. Through an interconnection with a computer, the microwave signal parameters and the execution of the PID locking program can be directly controlled using a host computer control system. The transfer function of the locking system is:
In this formula,
is the transfer function of the PID frequency closed-loop locking system, where
is the system scale coefficient,
is the integral coefficient,
is the differential coefficient, and
is the transfer function of an open-loop linear system:
In this formula, C is the used NV color center ODMR spectral contrast, which is 6.2%; is the fluorescence intensity, which is 155 mV; is the full width at half height of the ODMR spectrum, which is 2 MHz; is the transfer function of the first-order low-pass filter, which is ; , is the cut-off frequency of the low-pass filter; and is the sampling frequency of the low-pass filter. By adjusting the PID parameters, the system is in the optimal state. The parameter regulates the error parameter multiple, which can improve the system’s error correction rate; parameter control error time integration can improve system time sensitivity; and the first-order differential component of the parameter adjustment error can shorten the system regression stability time. Through actual testing and alignment, the optimal PID parameters of the system are determined as: , .
The dynamic measurement of the microwave intensity can be carried out. With this scheme, the microwave intensity–feedback curve relationship can be established by setting the microwave intensity to be measured as the scanning mode. Because the variation of the ODMR spectral hole-burning position in the NV color center under the microwave coherent population oscillation effect is proportional to the microwave intensity measured in
, during data collection, the resonant microwave source used the microwave intensity measured in
, which has an exponential relationship with the microwave intensity measured in
. Therefore, an exponential form was used to fit the microwave intensity curve. We used exponential fitting to fit the curve. The results are shown in
Figure 4b, and the microwave intensity sensitivity in this article is
. Moreover, in the detection method described herein, the minimum detectable microwave intensity is −20 dBm:
Here, , , , , , , .
3. Results
The array antenna described above was used as an analog measurement antenna. The microwave intensity
in the area was obtained by measuring the microwave field emitted by the antenna in the space range [
20]:
In this formula,
is the included angle between the measurement position and the vertical line of the microwave transmitting antenna surface, which is set as (−15°~15°) in this paper.
is the linear distance between the measuring position and the central position of the microwave antenna, which is set as (100~150 cm).
is the output power of the microwave source used at the transmitter, which is set as (12~26 dBm) and packeted with an interval of 2 dBm. By using the above microwave intensity detection method, the microwave intensity field distribution is measured in the two-dimensional plane area in the main lobe direction of the antenna transmitting a microwave field (its horizontal height is the same as the horizontal height of the antenna physical center). The spatial distribution of the antenna microwave field is obtained by sampling the data in the spatial range, and the spatial position information of the dataset is improved via the third-order spline interpolation method [
21]. The results are shown in
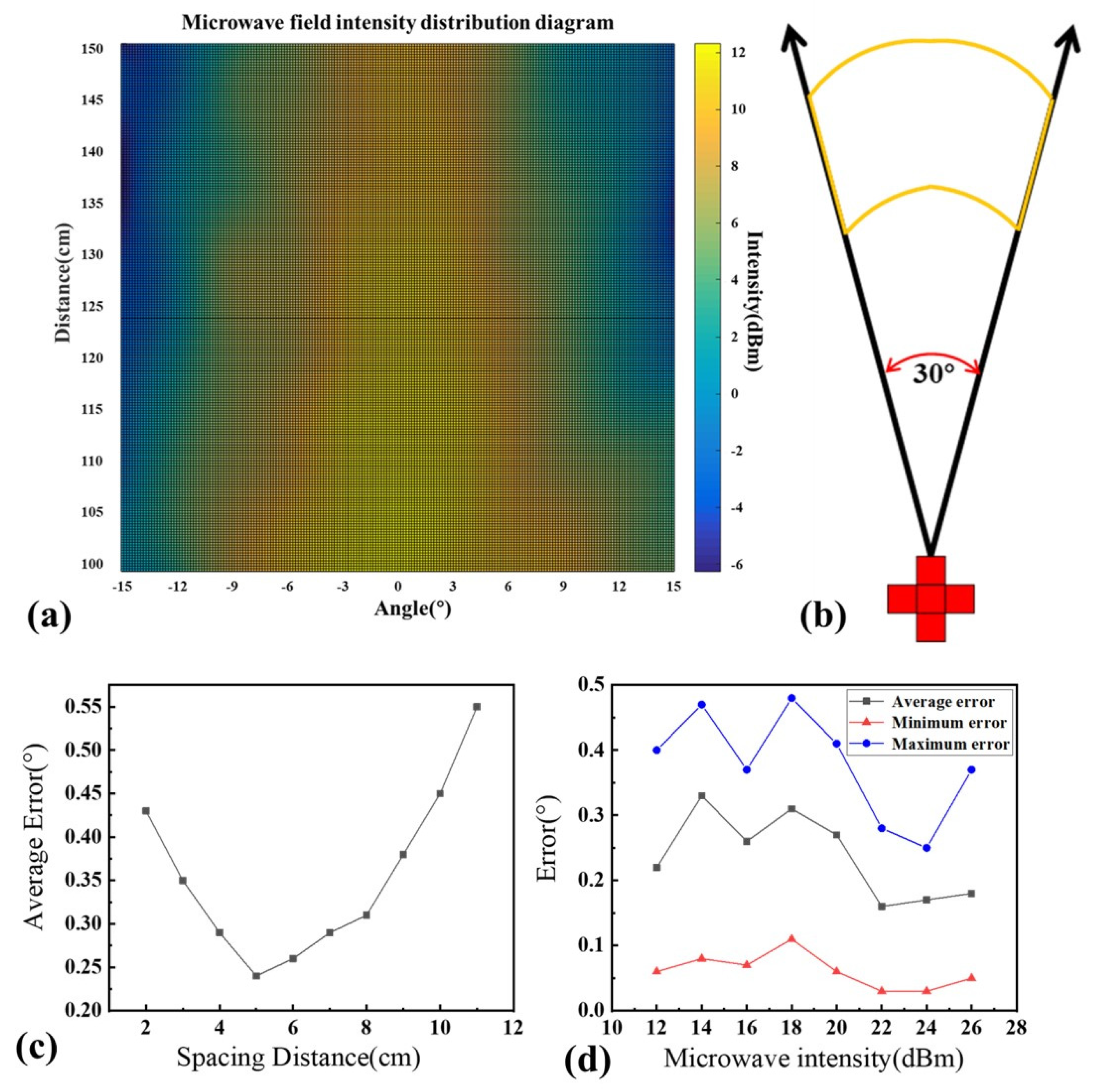
Figure 5a, and the input intensity of this microwave data is 26 dBm.
Based on the collected and constructed microwave field spatial distribution data, by measuring the microwave intensity at the cross position of five points in space, and by combining the data of these points, the weighted global least squares method of field distribution is used to restore the microwave source direction [
22]; the schematic diagram for this is shown in
Figure 5b. In the case of known microwave antenna radiation, for a microwave field formed by the radiation of a microwave source in an unknown direction, any position can be selected as the center point, and one point can be measured every 90° around the center. A total of five positions of microwave field intensity were measured, and the measurement structure formed an observation matrix [
23]. We used a microwave field intensity distribution matching method based on weighted global least squares to calculate the relationship between the measurement position and the relative angle of the microwave source.
Based on Gauss–Markov model, due to the unequal accuracy of the observation matrix and the coefficient matrix, the weighting method proposed by Schaffrin et al. [
24] was used to modify its weighted estimation constraint criteria as follows:
In this formula,
is the observation matrix;
is the weight matrix based on the field intensity distribution matrix;
and
are random errors; and
is a matrix vectorization operator. At the same time, the construction objective function is:
In this formula,
is the cofactor matrix of the matrix vector;
is Kronecker product;
is
Lagrange multiplier vector;
is
Identity matrix; and
is a full rank coefficient matrix based on
. The iterative expression of the Lagrange multiplier method used to solve its estimated quantity
is:
The relative relationship between the direction of the microwave source and the measured center point can be calculated. When selecting a five-point cross coordinate, the difference between the final angle determination result and the actual result is caused by the different distance interval between the five points. By setting the interval distance between different five points, many random actual measurements and calculations, as well as the calculation of the average angle error result, are carried out. The distance interval is set as 2–11 cm (the interval is 1 cm), and the average angle error result is shown in
Figure 5c. When the distance between the five points is 5 cm, the average angle error reaches the minimum value of 0.24°. Because the method for selecting test points in this paper is to sample the location of points within the microwave radiation field area, the excessively long sampling distance interval will lead to the loss of correlation between the obtained microwave field intensity distribution matrix, resulting in difficulties in determining the relative location of microwave sources. At the same time, when the sampling interval distance is too short, the microwave intensity distribution matrix will contain less information, and it may appear that the microwave intensity data within the same group are very close or even the same (depending on the minimum resolution of microwave intensity), causing difficulties in ultimately calculating the direction of the microwave source. Additionally, due to the power of different microwave emissions, there are differences in the intensity of the microwave field formed in the region, which also lead to different results of angle determination. Based on different microwave emission powers, the microwave source angle in this area is randomly measured and determined, and the final result is calculated, as shown in
Figure 5d. The result was measured at a distance of 5 cm. The maximum angle recognition error is 0.48° and the minimum angle recognition error is 0.03° under different microwave transmission power. For the same microwave antenna, although there are differences in input microwave intensity, the microwave radiation field distribution results are similar (there are differences in intensity). For different input intensities, an important reason for the difference in angle calculation error is the system’s minimum microwave intensity resolution limit. When the input microwave intensity is low in the microwave radiation field formed within the region, the number of indistinguishable regions of microwave intensity for the system will increase. These regions, in which it is difficult to distinguish between intensity differences, directly affect the final measurement results. As shown in
Figure 5d, the highest, average, and minimum angular error results for experimental groups with higher-input microwave intensity are better than those for groups with lower-input microwave intensity.