Dynamic Characteristics of a Small-Size Beam Mounted on an Accelerating Structure
Abstract
:1. Introduction
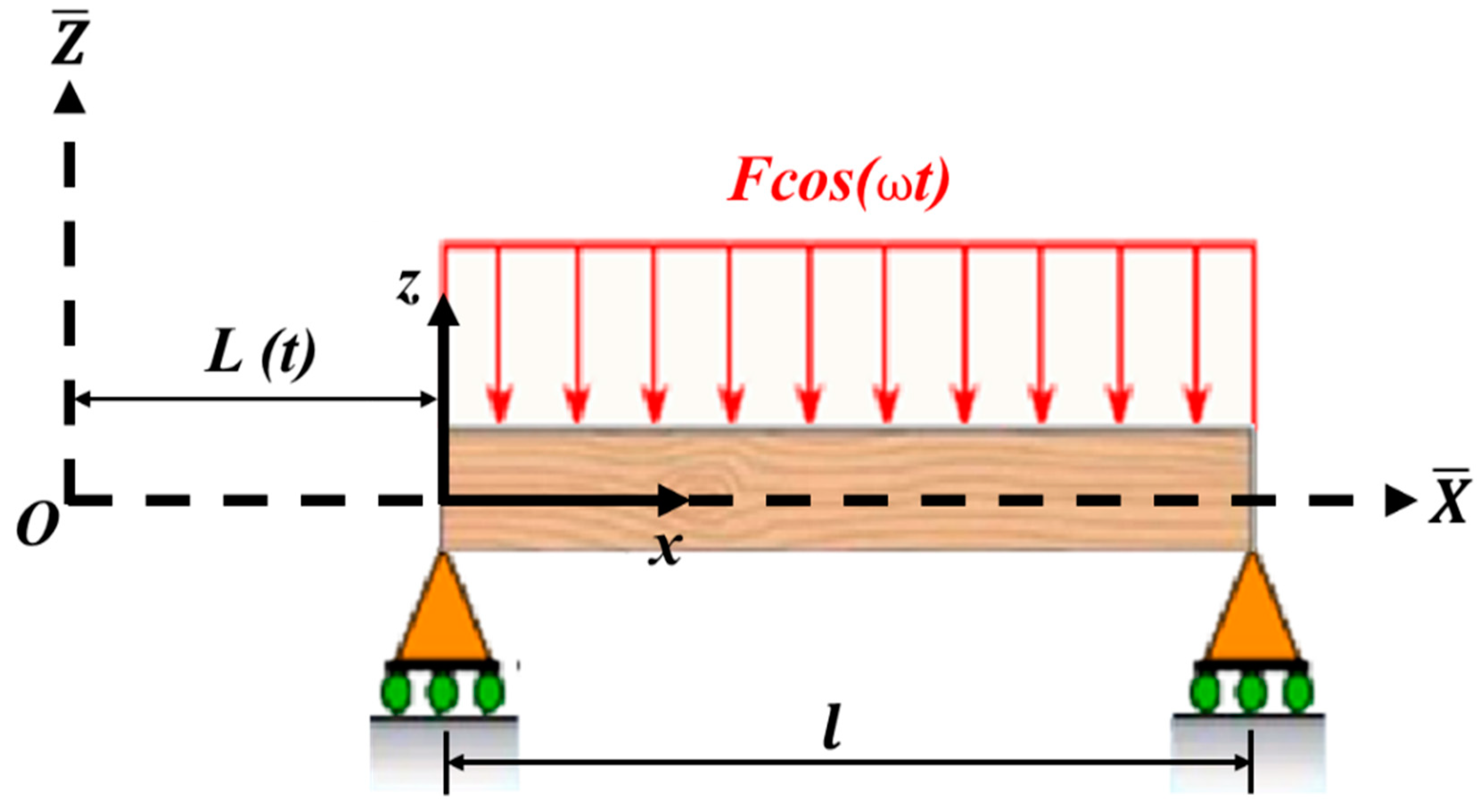
2. Mathematical Formulation
| (8) | |
| (17) | |
| (18) | |
| (19) | |
| (20) | |
| (21) | |
| (22) | |
| (23) | |
| (24) | |
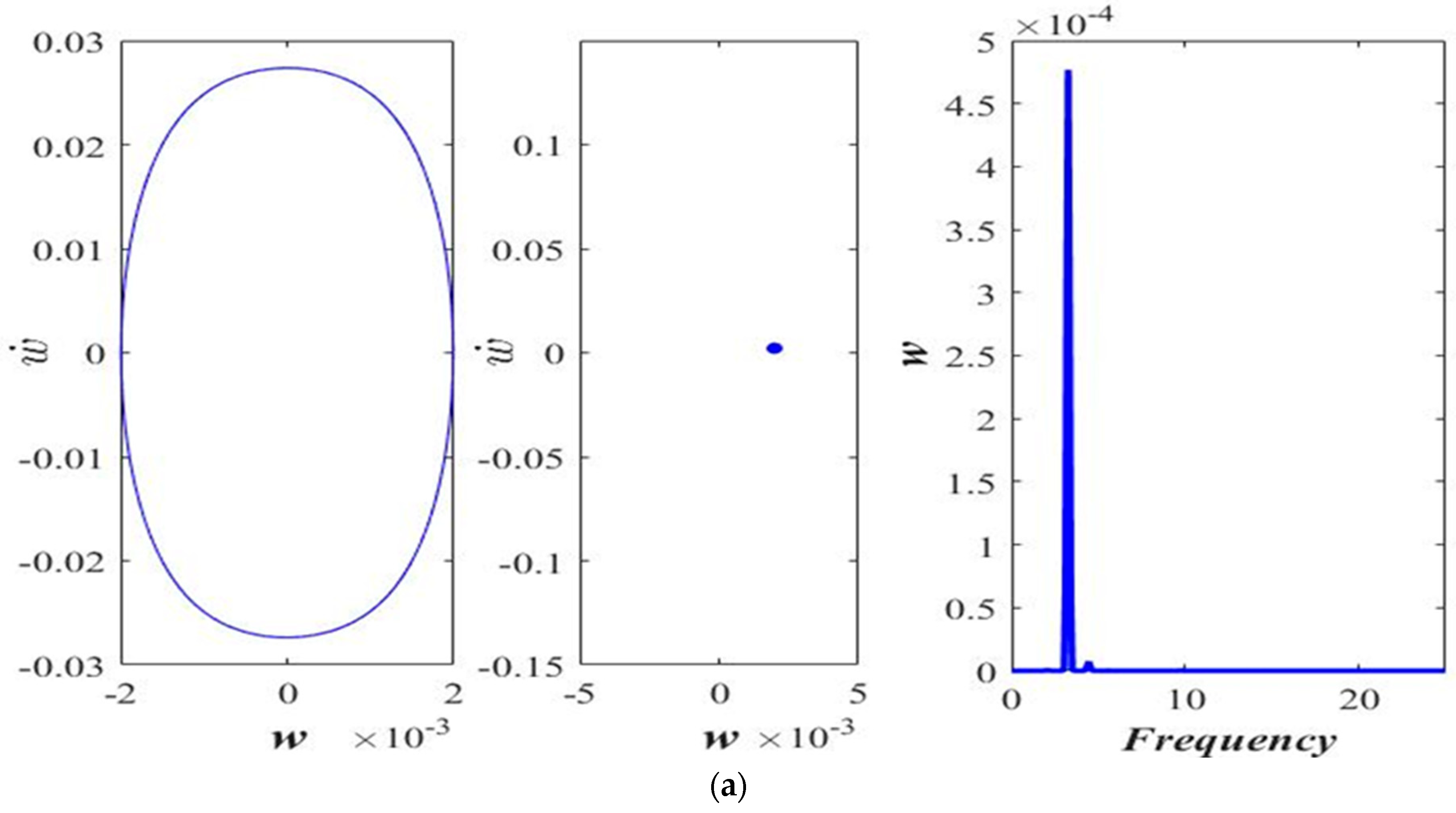
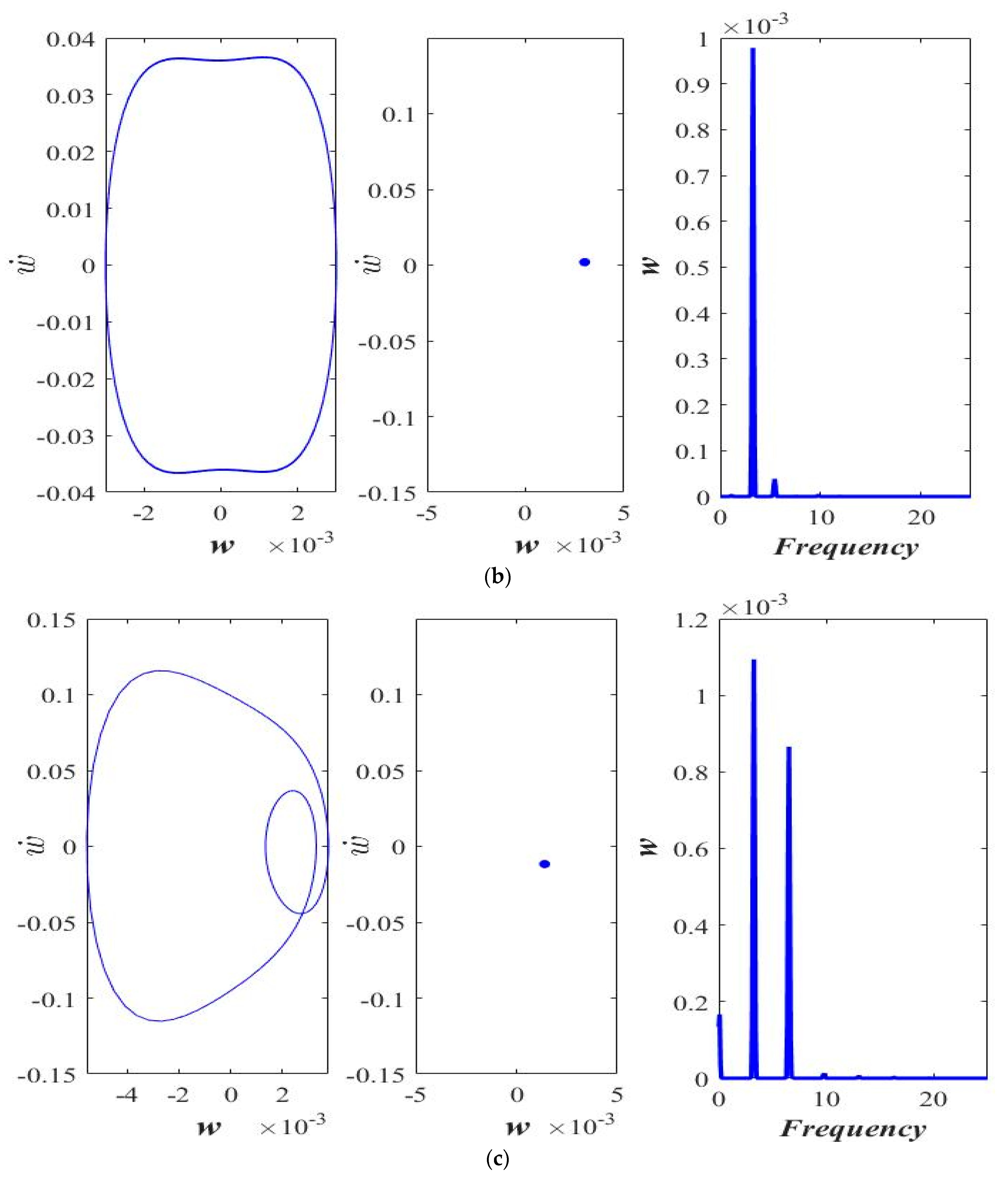
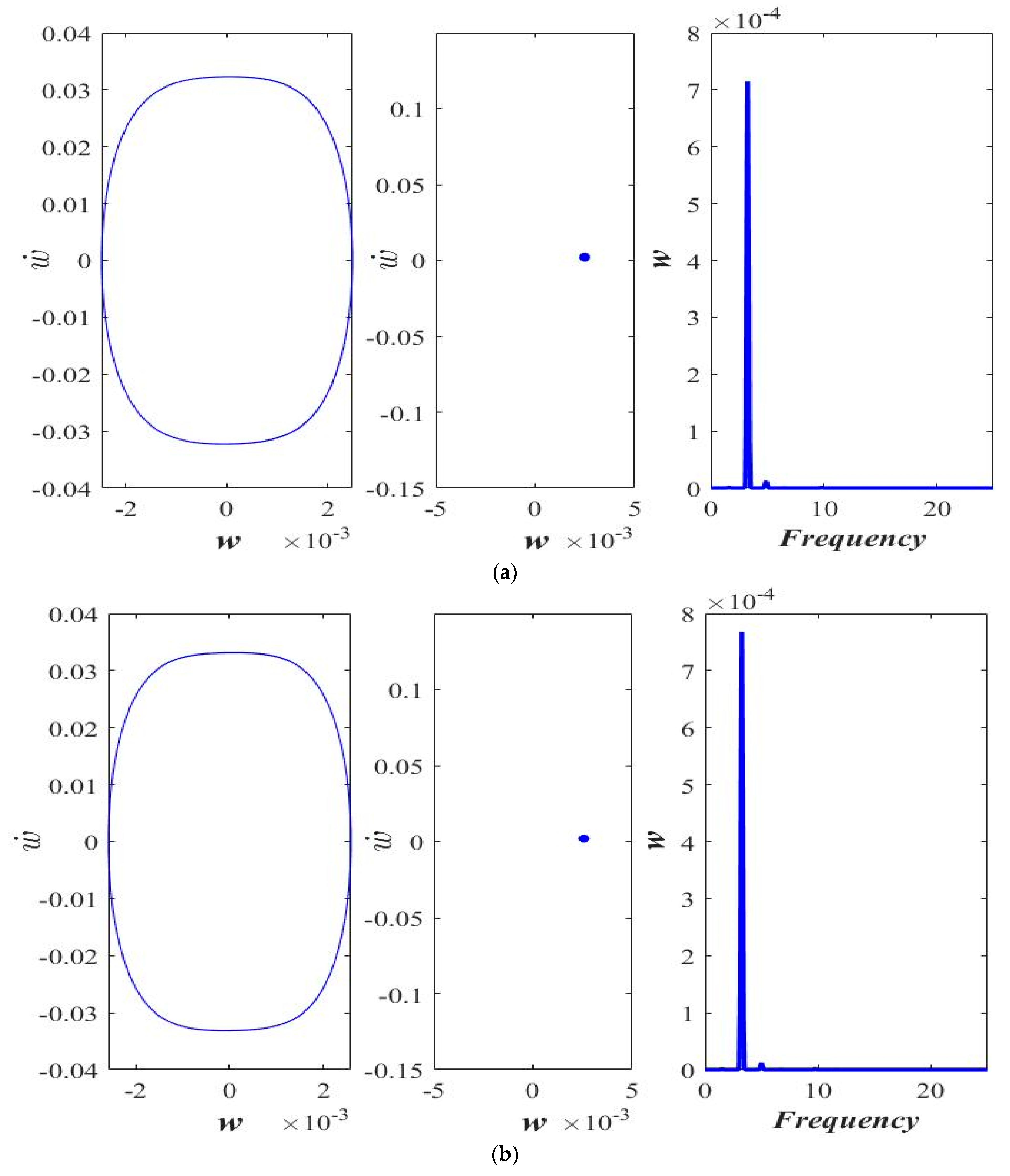
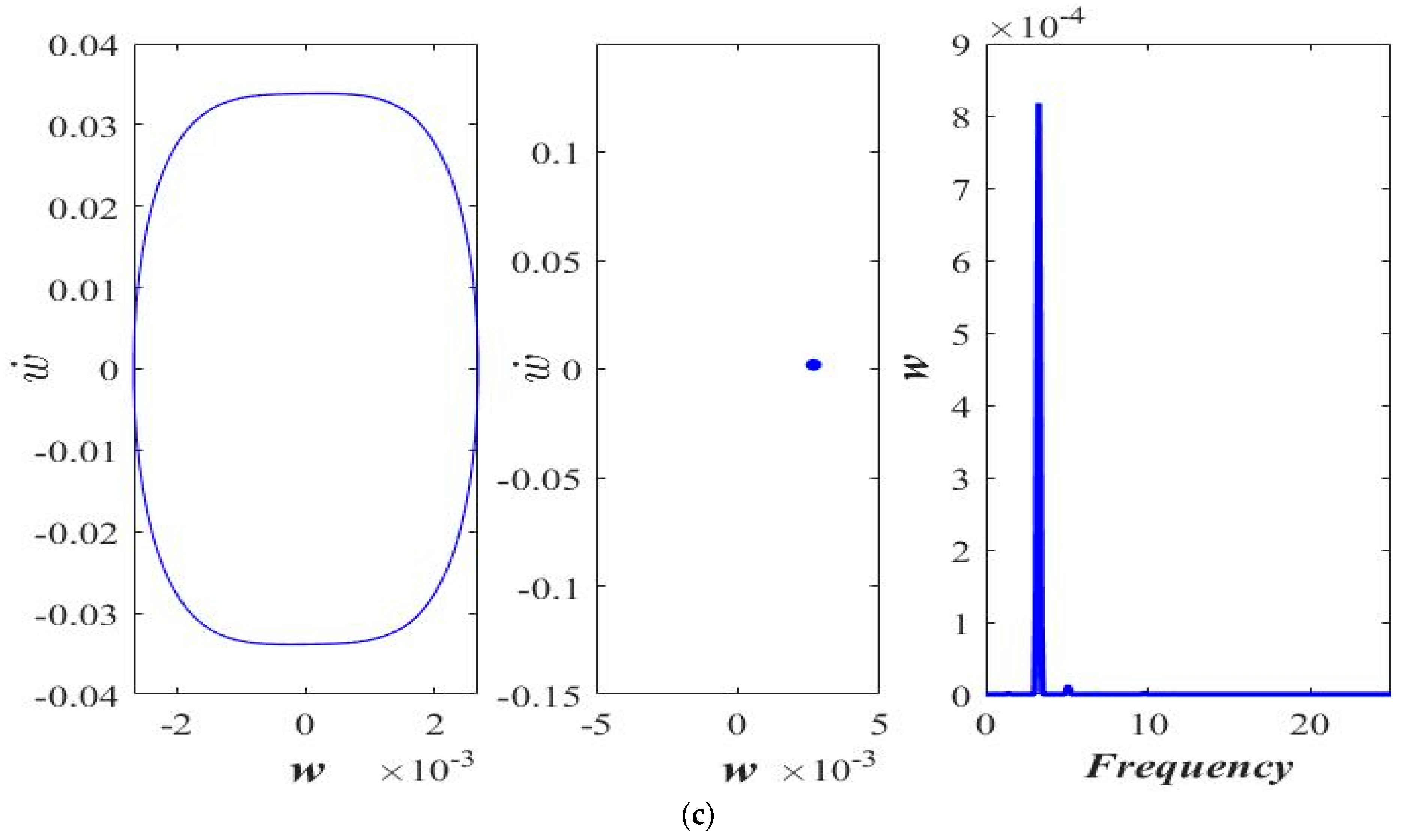
3. Results and Discussion
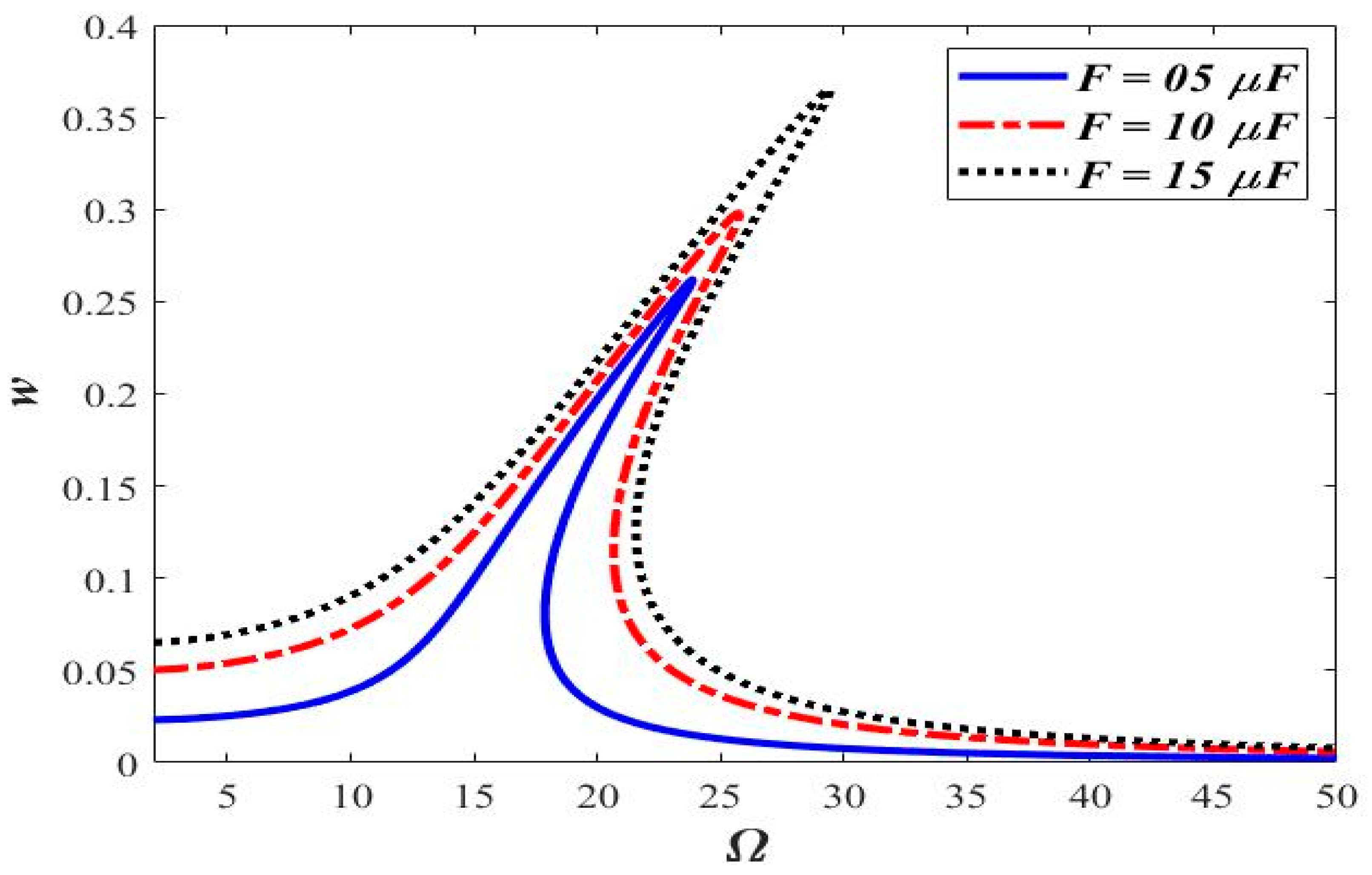
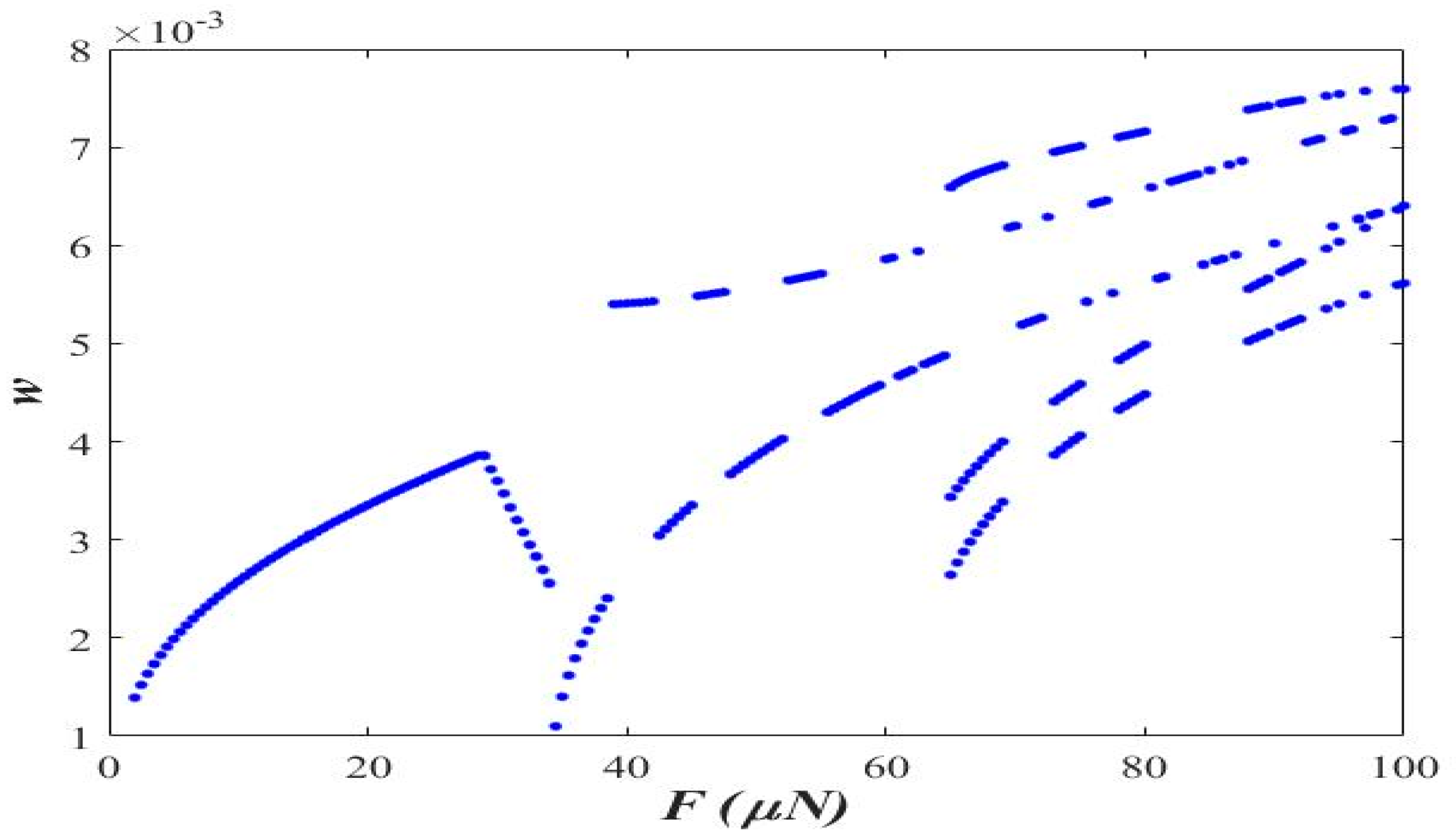
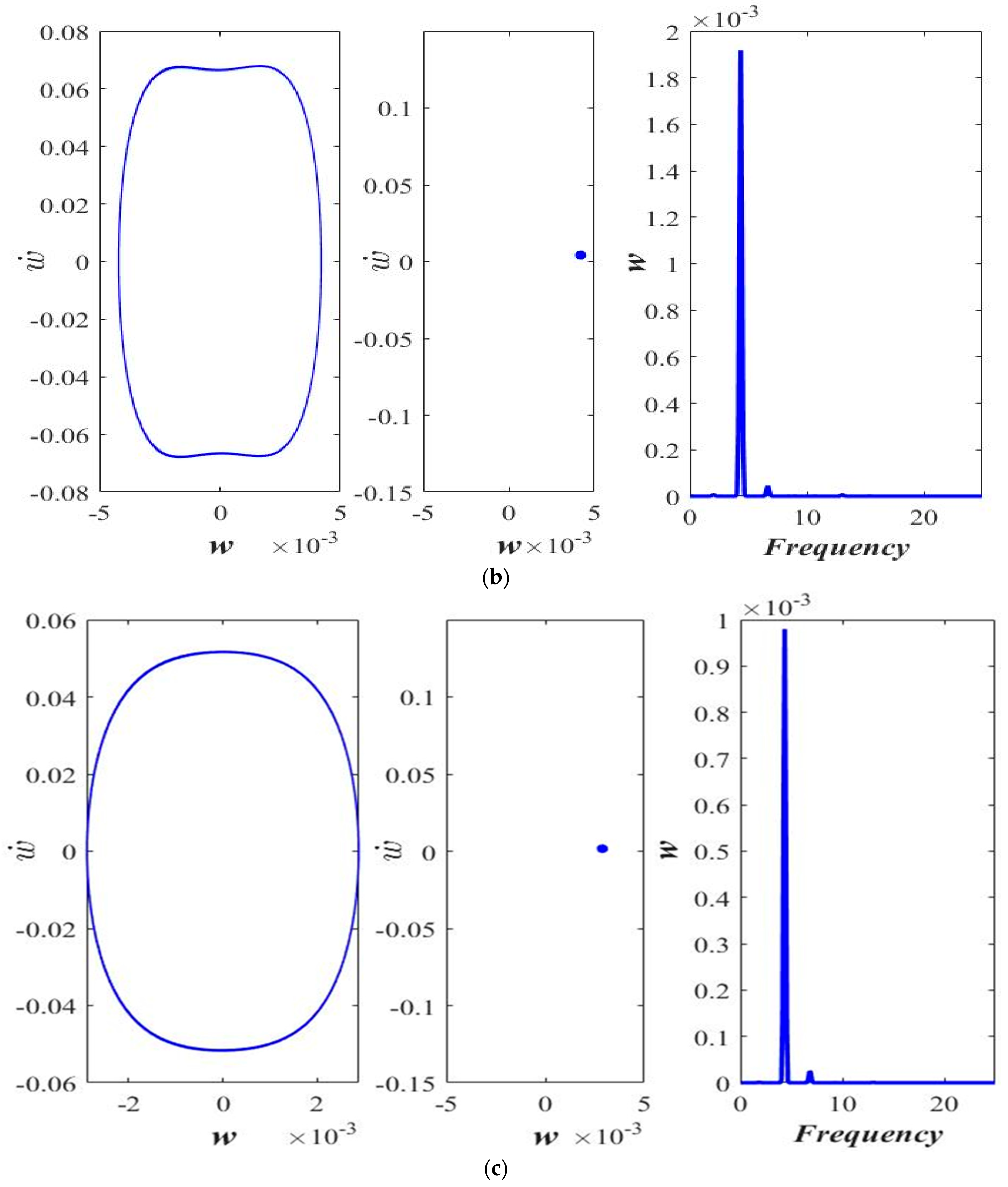
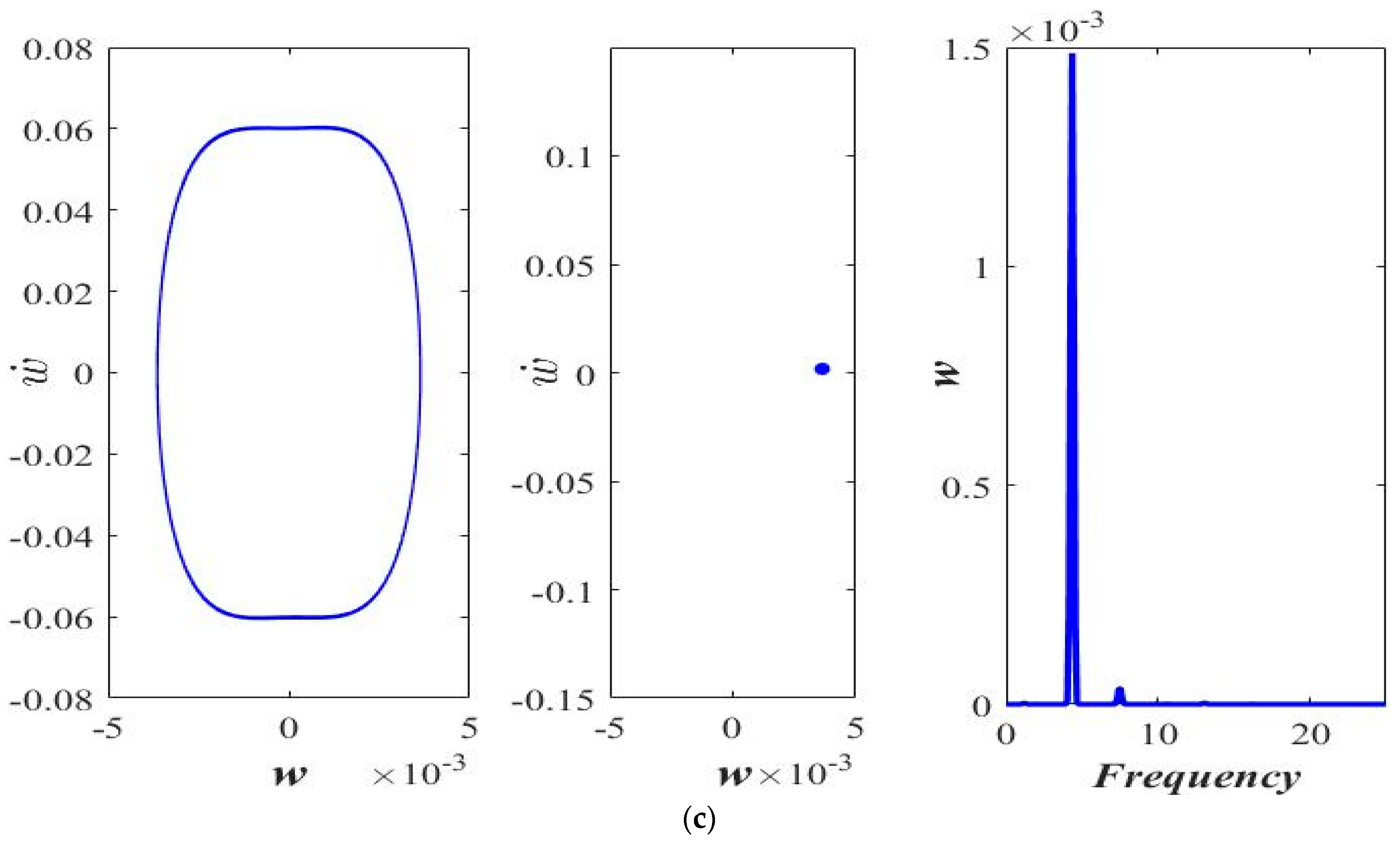
3.1. Varying the Magnitude of Applied Force (F)
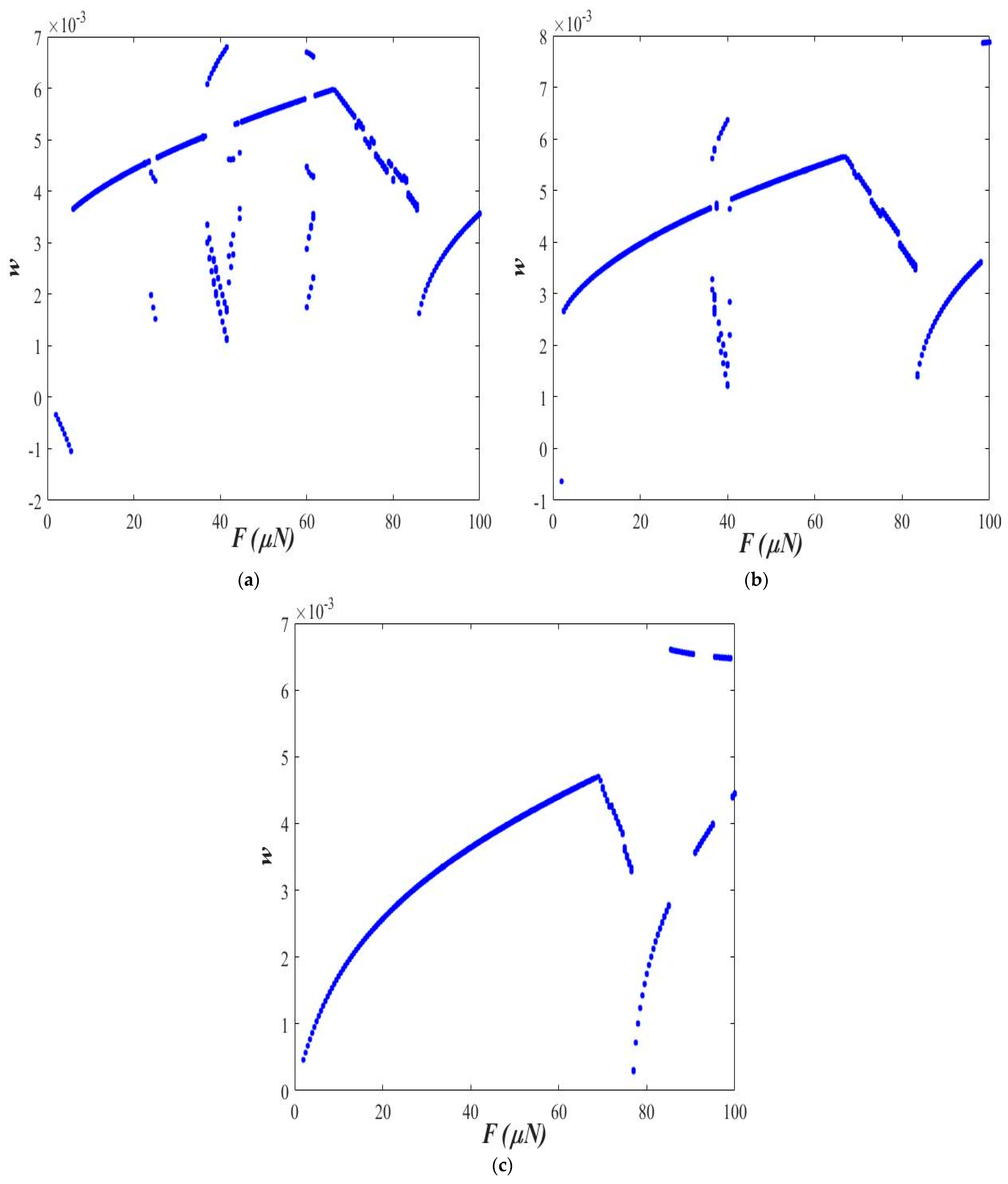
3.2. Varying Length Scale Parameter ()
3.3. Varying Acceleration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wicker, J.A.; Mote, C.D., Jr. Current Research on the Vibration and Stability of Axially-Moving Materials. Shock. Vib. Dig. 1988, 20, 3–13. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow; Academic Press: Cambridge, MA, USA, 1998; Volume 1, ISBN 008053175X. [Google Scholar]
- Gao, H.; Yang, B. Dynamic Response of a Beam Structure Excited by Sequentially Moving Rigid Bodies. Int. J. Struct. Stab. Dyn. 2020, 20, 2050093. [Google Scholar] [CrossRef]
- Xu, C.; Wang, Z.; Li, B. Dynamic Stability of Simply Supported Beams With Multi-Harmonic Parametric Excitation. Int. J. Struct. Stab. Dyn. 2021, 21, 2150027. [Google Scholar] [CrossRef]
- Hawwa, M.A.; Ali, S.; Hardt, D.E. Influence of Roll-to-Roll System’s Dynamics on Axially Moving Web Vibration. J. Vibroeng. 2019, 21, 556–569. [Google Scholar] [CrossRef] [Green Version]
- Ulsoy, A.G. Coupling between Spans in the Vibration of Axially Moving Materials. J. Vib. Acoust. Stress Reliab. 1986, 108, 207–212. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Ma, Z.-G. Nonlinear Vibration of Axially Moving Beams with Internal Resonance, Speed-Dependent Tension, and Tension-Dependent Speed. Nonlinear Dyn. 2019, 98, 2475–2490. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Ma, Z.-G.; Liu, S.; Zhang, L.-Y. Parametric Vibration and Numerical Validation of Axially Moving Viscoelastic Beams with Internal Resonance, Time and Spatial Dependent Tension, and Tension Dependent Speed. J. Vib. Acoust. 2019, 141, 61011. [Google Scholar] [CrossRef]
- Chen, L.-Q.; Yang, X.-D. Steady-State Response of Axially Moving Viscoelastic Beams with Pulsating Speed: Comparison of Two Nonlinear Models. Int. J. Solids Struct. 2005, 42, 37–50. [Google Scholar] [CrossRef]
- Ali, S.; Khan, S.; Jamal, A.; Horoub, M.M.; Iqbal, M.; Onyelowe, K.C. Transverse Response of an Axially Moving Beam with Intermediate Viscoelastic Support. Math Probl. Eng. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Guo, Z.; Zhu, L.; Liu, W. Nonlinear Vibrations of an Axially Moving Beam with Fractional Viscoelastic Damping. Adv. Civ. Eng. 2022, 2022, 4637716. [Google Scholar] [CrossRef]
- Ali, S.; Hawwa, M.A. Dynamics of Axially Moving Beams: A Finite Difference Approach. Ain Shams Eng. J. 2023, 14, 101817. [Google Scholar] [CrossRef]
- Bichay, N.A.; Elaikh, T.E. Transverse Vibration of Cracked Graded Shear Beam with Axial Motion. Int. J. Energy Environ. 2021, 12, 31–44. [Google Scholar]
- Cao, T.; Hu, Y. Magnetoelastic Primary Resonance and Bifurcation of an Axially Moving Ferromagnetic under Harmonic Magnetic Force. Commun. Nonlinear Sci. Numer. Simul. 2023, 117, 106974. [Google Scholar] [CrossRef]
- Hua, H. Transient Dynamics of an Axially Moving Beam Subject to Continuously Distributed Moving Mass. J. Vib. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Öz, H.R. On the Vibrations of an Axially Travelling Beam on Fixed Supports with Variable Velocity. J. Sound Vib. 2001, 239, 556–564. [Google Scholar] [CrossRef]
- Öz, H.R. Natural Frequencies of Axially Travelling Tensioned Beams in Contact with a Stationary Mass. J. Sound Vib. 2003, 259, 445–456. [Google Scholar] [CrossRef]
- Lim, C.W.; Li, C.; Yu, J.-L. Dynamic Behaviour of Axially Moving Nanobeams Based on Nonlocal Elasticity Approach. Acta Mech. Sin. 2010, 26, 755–765. [Google Scholar] [CrossRef]
- Li, C. Size-Dependent Thermal Behaviors of Axially Traveling Nanobeams Based on a Strain Gradient Theory. Struct. Eng. Mech. Int. J. 2013, 48, 415–434. [Google Scholar] [CrossRef]
- Kiani, K. Longitudinal and Transverse Instabilities of Moving Nanoscale Beam-like Structures Made of Functionally Graded Materials. Compos. Struct. 2014, 107, 610–619. [Google Scholar] [CrossRef]
- Sheykhi, M.; Eskandari, A.; Ghafari, D.; Ahmadi Arpanahi, R.; Mohammadi, B.; Hosseini Hashemi, S. Investigation of Fluid Viscosity and Density on Vibration of Nano Beam Submerged in Fluid Considering Nonlocal Elasticity Theory. Alex. Eng. J. 2023, 65, 607–614. [Google Scholar] [CrossRef]
- Ali, S.; Hawwa, M.A. A Parametric Study on the Dynamics of Two-Span Roll-to-Roll Microcontact Printing System. Sādhanā 2019, 44, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.; Hawwa, M.A.; Hardt, D.E. Vibration Suppression of an Axially Moving Web in a Multi-Span Roll-to-Roll Microcontact Printing System. J. Vib. Eng. Technol. 2020, 8, 35–46. [Google Scholar] [CrossRef]
- Ali, S.; Hawwa, M.A.; Hardt, D.E. Dynamic Behavior of Axially Moving Web in Multi-Span Roll-to-Roll Microcontact Printing System. Proc. Inst. Mech. Engineers. Part I J. Syst. Control Eng. 2022, 237, 348–358. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, Y.; Chen, L. Nonlinear Vibrations of Axially Moving Beams with Nonhomogeneous Boundary Conditions. Lixue Xuebao Chin. J. Theor. Appl. Mech. 2019, 51, 218–227. [Google Scholar] [CrossRef]
- Li, C. Nonlocal Thermo-Electro-Mechanical Coupling Vibrations of Axially Moving Piezoelectric Nanobeams. Mech. Based Des. Struct. Mach. 2017, 45, 463–478. [Google Scholar] [CrossRef]
- Marynowski, K. Axially Moving Microscale Panel Model Based on Modified Couple Stress Theory. J. Nanomech. Micromech. 2015, 5, A4014002. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Dehrouyeh, M.; Zafari-Koloukhi, H.; Ghamami, M. Size-Dependent Frequency and Stability Characteristics of Axially Moving Microbeams Based on Modified Couple Stress Theory. Int. J. Eng. Sci. 2015, 97, 98–112. [Google Scholar] [CrossRef]
- Damghanian, R.; Asemi, K.; Babaei, M. A New Beam Element for Static, Free and Forced Vibration Responses of Microbeams Resting on Viscoelastic Foundation Based on Modified Couple Stress and Third-Order Beam Theories. Iran. J. Sci. Technol. Trans. Mech. Eng. 2022, 46, 131–147. [Google Scholar] [CrossRef]
- Nazari, H.; Babaei, M.; Kiarasi, F.; Asemi, K. Geometrically Nonlinear Dynamic Analysis of Functionally Graded Material Plate Excited by a Moving Load Applying First-Order Shear Deformation Theory via Generalized Differential Quadrature Method. SN Appl. Sci. 2021, 3, 1–32. [Google Scholar] [CrossRef]
- Liu, J.J.; Li, C.; Fan, X.L.; Tong, L.H. Transverse Free Vibration and Stability of Axially Moving Nanoplates Based on Nonlocal Elasticity Theory. Appl. Math. Model. 2017, 45, 65–84. [Google Scholar] [CrossRef]
- Rezaee, M.; Lotfan, S. Non-Linear Nonlocal Vibration and Stability Analysis of Axially Moving Nanoscale Beams with Time-Dependent Velocity. Int. J. Mech. Sci. 2015, 96, 36–46. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Yang, C.; Shen, J.; Xie, F. Dynamical Responses and Stabilities of Axially Moving Nanoscale Beams with Time-Dependent Velocity Using a Nonlocal Stress Gradient Theory. J. Vib. Control 2017, 23, 3327–3344. [Google Scholar] [CrossRef]
- Li, C.; Yu, Y.M.; Fan, X.L.; Li, S. Dynamical Characteristics of Axially Accelerating Weak Visco-Elastic Nanoscale Beams Based on a Modified Nonlocal Continuum Theory. J. Vib. Eng. Technol. 2015, 3, 565–574. [Google Scholar]
- Ali, S. Nonlinear Dynamic and Stability of a Small Size Moving Beam under Thermal Conditions. Math. Methods Appl. Sci. 2023, 46, 7201–7214. [Google Scholar] [CrossRef]
- Moaaz, O.; Abouelregal, A.E.; Alsharari, F. Lateral Vibration of an Axially Moving Thermoelastic Nanobeam Subjected to an External Transverse Excitation. AIMS Math. 2023, 8, 2272–2295. [Google Scholar] [CrossRef]
- Ji, C.; Yao, L.; Li, C. Transverse Vibration and Wave Propagation of Functionally Graded Nanobeams with Axial Motion. J. Vib. Eng. Technol. 2020, 8, 257–266. [Google Scholar] [CrossRef]
- Michaltsos, G.T. Bouncing of a Vehicle on an Irregularity: A Mathematical Model. J. Vib. Control 2010, 16, 181–206. [Google Scholar] [CrossRef]
- Shi, X.M.; Cai, C.S. Simulation of Dynamic Effects of Vehicles on Pavement Using a 3D Interaction Model. J. Transp. Eng. 2009, 135, 736–744. [Google Scholar] [CrossRef]
- Lak, M.A.; Degrande, G.; Lombaert, G. The Effect of Road Unevenness on the Dynamic Vehicle Response and Ground-Borne Vibrations Due to Road Traffic. Soil Dyn. Earthq. Eng. 2011, 31, 1357–1377. [Google Scholar] [CrossRef]
- Barbosa, R.S. Vehicle Vibration Response Subjected to Longwave Measured Pavement Irregularity. J. Mech. Eng. Autom. 2012, 2, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Ghaith, F.A. Nonlinear Dynamic Modeling of Elastic Beam Fixed on a Moving Cart and Carrying Lumped Tip Mass Subjected to External Periodic Force. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; Volume 48982, pp. 935–941. [Google Scholar]
- Ragulskis, K.; Gegeckienė, L.; Kibirkštis, E.; Miliūnas, V.; Zubrickaitė, L.; Pauliukas, A.; Ragulskis, L.M. Dynamic Study of Transportation Containers with Packages. J. Vibroeng. 2012, 14, 1876–1884. [Google Scholar]
- Gim, G. Vehicle Dynamic Simulation with a Comprehensive Model for Pneumatic Tires; UC Berkeley Transportation Library: Berkeley, CA, USA, 1988. [Google Scholar]
- Lyasko, M.I. The Determination of Deflection and Contact Characteristics of a Pneumatic Tire on a Rigid Surface. J. Terramech. 1994, 31, 239–246. [Google Scholar] [CrossRef]
- An, C.; Su, J. Dynamic Response of Axially Moving Timoshenko Beams: Integral Transform Solution. Appl. Math. Mech. 2014, 35, 1421–1436. [Google Scholar] [CrossRef]





| Parameter | Definition |
|---|---|
| Small-size parameter | |
| Stretching parameter | |
| Nondimensional axial acceleration | |
| Nondimensional axial force | |
| Nondimensional time parameter | |
| Nondimensional frequency |
| Parameter | Values |
|---|---|
| (0.0, 0.1, 0.3) | |
| (0–100) μN | |
| (0–50) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, S.; Hawwa, M.A. Dynamic Characteristics of a Small-Size Beam Mounted on an Accelerating Structure. Micromachines 2023, 14, 780. https://doi.org/10.3390/mi14040780
Ali S, Hawwa MA. Dynamic Characteristics of a Small-Size Beam Mounted on an Accelerating Structure. Micromachines. 2023; 14(4):780. https://doi.org/10.3390/mi14040780
Chicago/Turabian StyleAli, Sajid, and Muhammad A. Hawwa. 2023. "Dynamic Characteristics of a Small-Size Beam Mounted on an Accelerating Structure" Micromachines 14, no. 4: 780. https://doi.org/10.3390/mi14040780





