Investigating the Performance of the Multi-Lobed Leaf-Shaped Oscillatory Obstacles in Micromixers Using Bulk Acoustic Waves (BAW): Mixing and Chemical Reaction
Abstract
:1. Introduction
2. Numerical Procedure
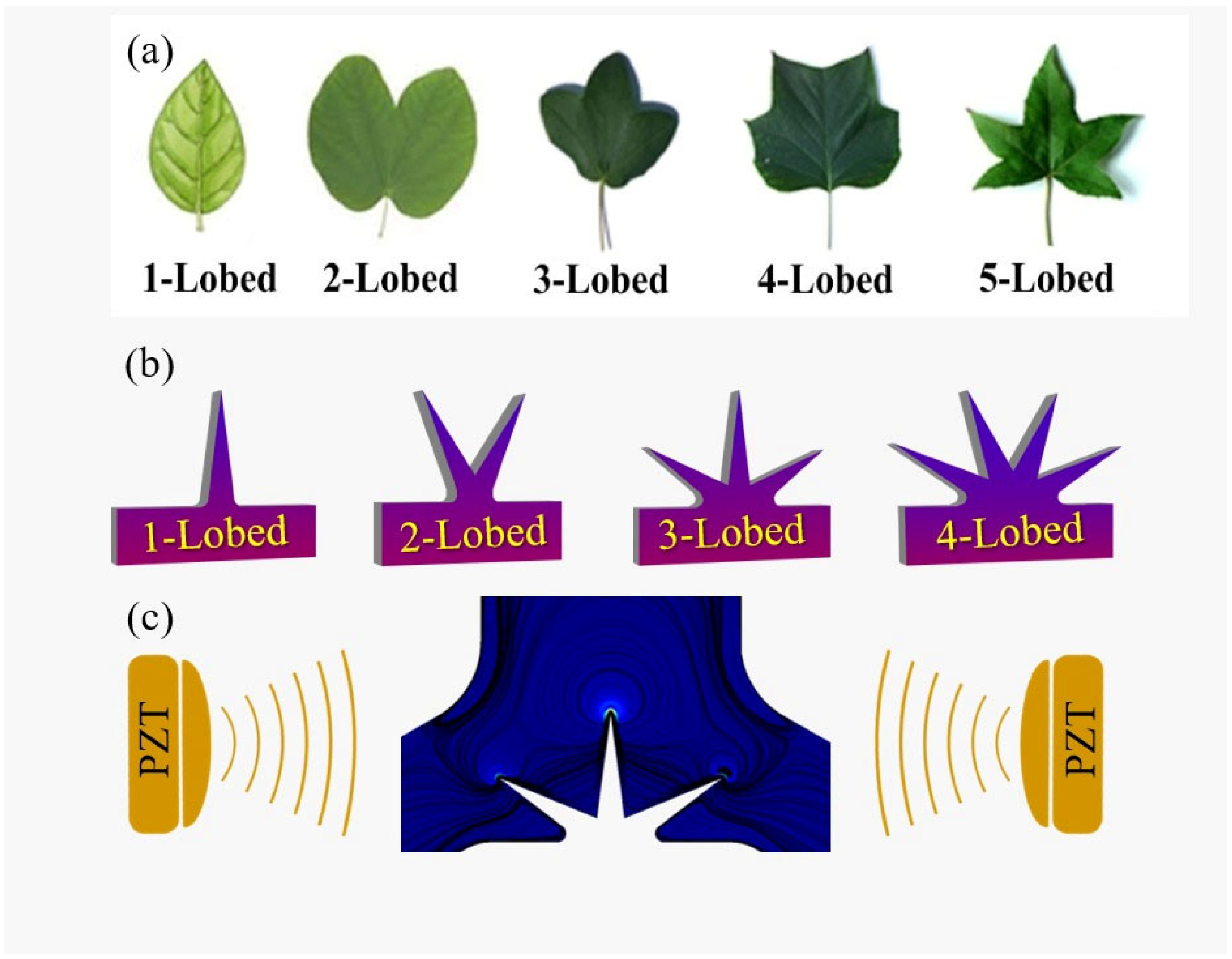
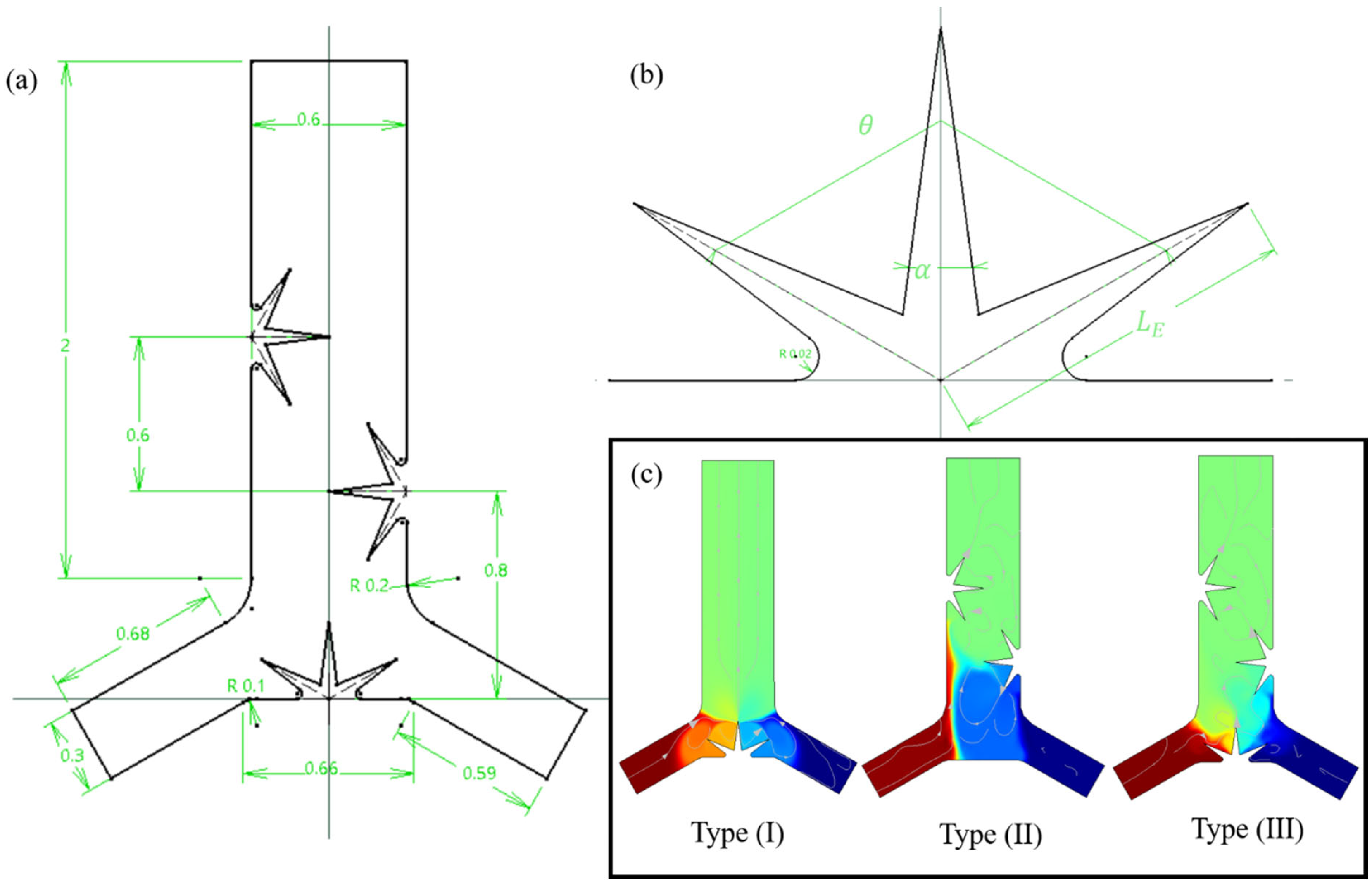
2.1. Defining the System’s Geometry and Scheme
2.2. Theory
3. Simulation Methodology
3.1. System’s Boundary Conditions
3.2. Numerical Implementation
- i.
- The first-order equations were solved using the “Thermoviscous acoustic” module by considering boundary conditions.
- ii.
- The zeroth-order and second-order equations were solved using the “Laminar flow” module by applying weak contribution modification for some equations.
- iii.
- The equations for concentration were solved using the module for “Transport of Diluted Species”.
| Parameter | Description | Value(s) | |
|---|---|---|---|
| Physical characteristics of the system | Density of fluid | 997 kg/m3 | |
| Speed of sound in water | 1497 m/s | ||
| Viscosity of fluid (Bulk) | 2.47 mPa s | ||
| Shear viscosity | 0.890 mPa s | ||
| Compressibility | 4.48 × 10−10 Pa−1 | ||
| Specific heat capacity | 4180 J/kg.K | ||
| Thermal diffusivity | 1.464 × 10−7 m2/s | ||
| Thermal conductivity | 0.61 w/(m.K) | ||
| Thermal expansion coefficient | 2.74 × 10−4 1/K | ||
| Specific heat capacity ratio | 1.012 | ||
| Absolute temperature | 298.15 K | ||
| Mass diffusion coefficient of solute | 4 × 10−10 m2/s | ||
| Operational parameters | Oscillation amplitude (displacement) | 1.4 to 3 µm | |
| Kinetic constant of the chemical reaction | −2 to 1 | ||
| Lobe’s length | 200 to 350 µm | ||
| Inlet velocities (background velocity) | 50 to 400 µm/s | ||
| lobes’ side inside angel | 15° to 45° | ||
| lobes’ pitch angle | 60° to 120° | ||
| Actuation frequency | 4 to 10 kHz |
3.3. Model Verification and Setting up the Numerical Procedure
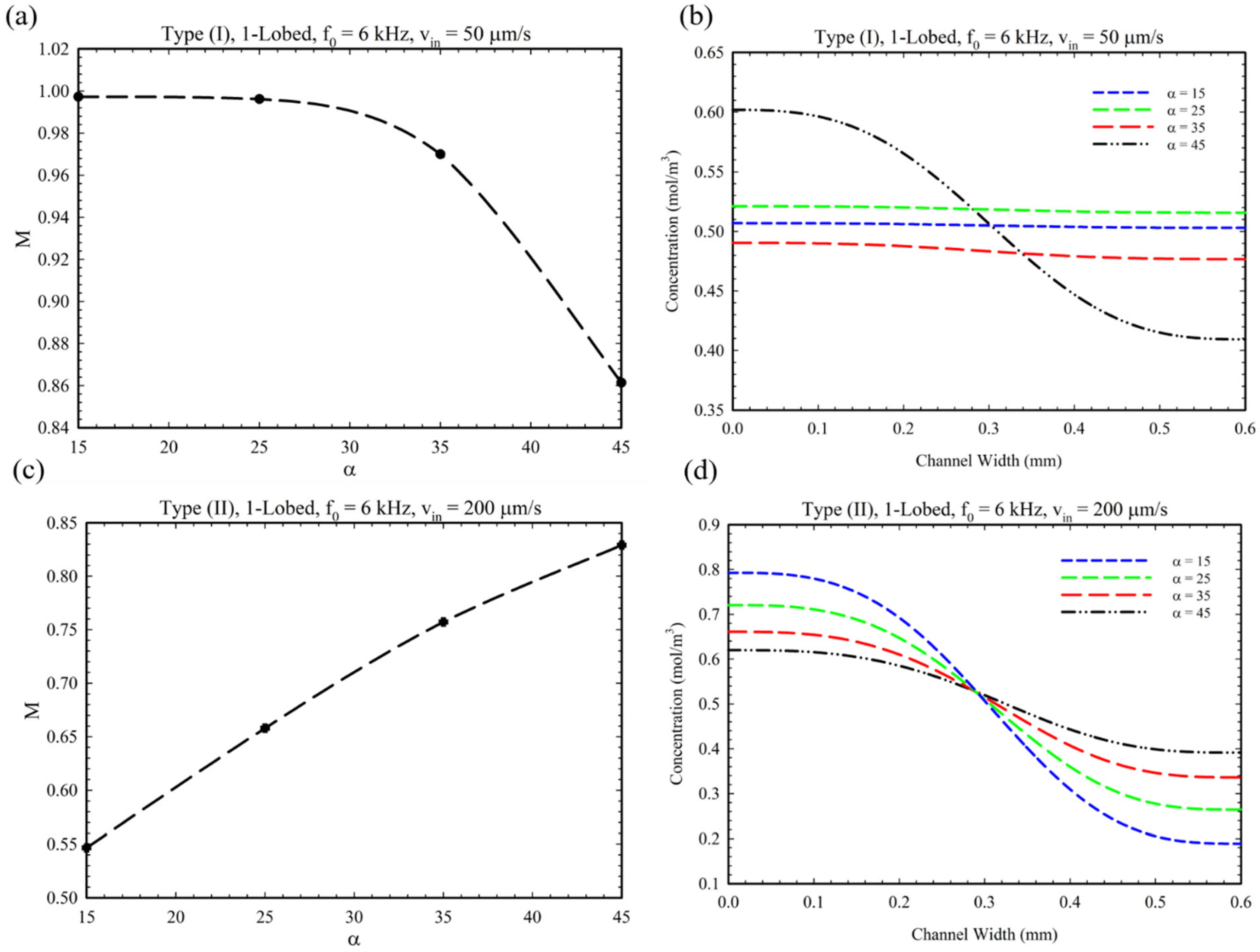
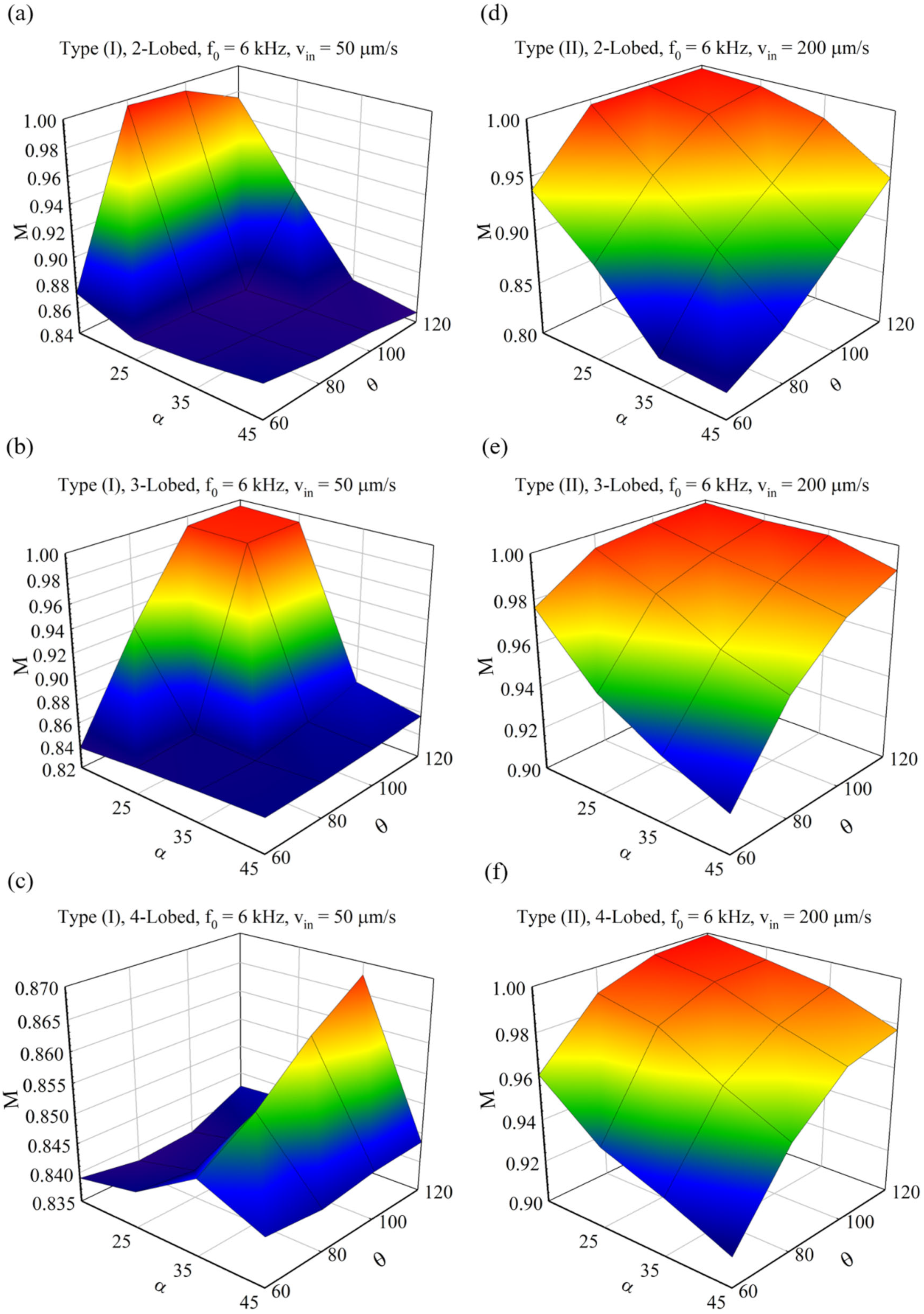
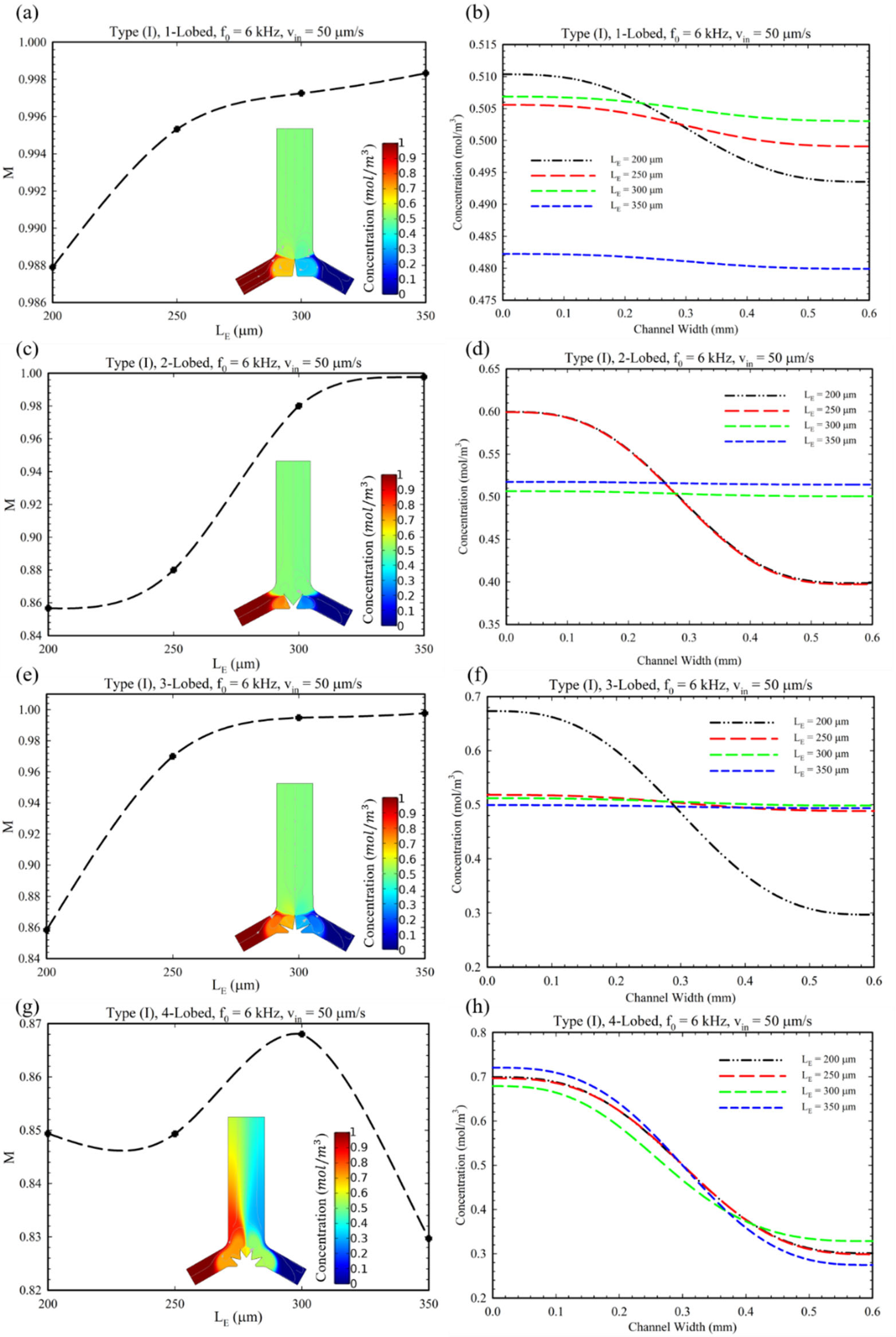
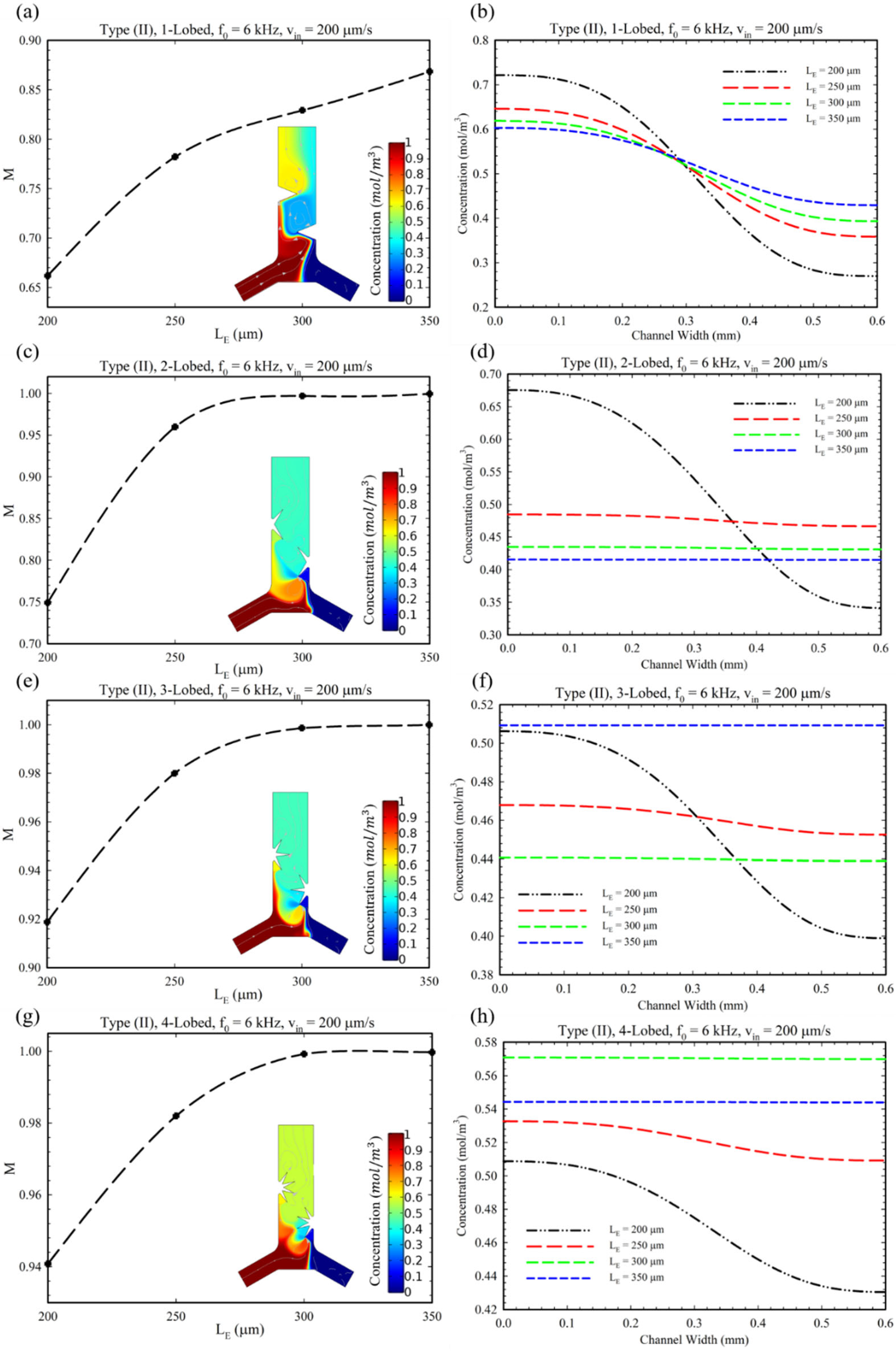
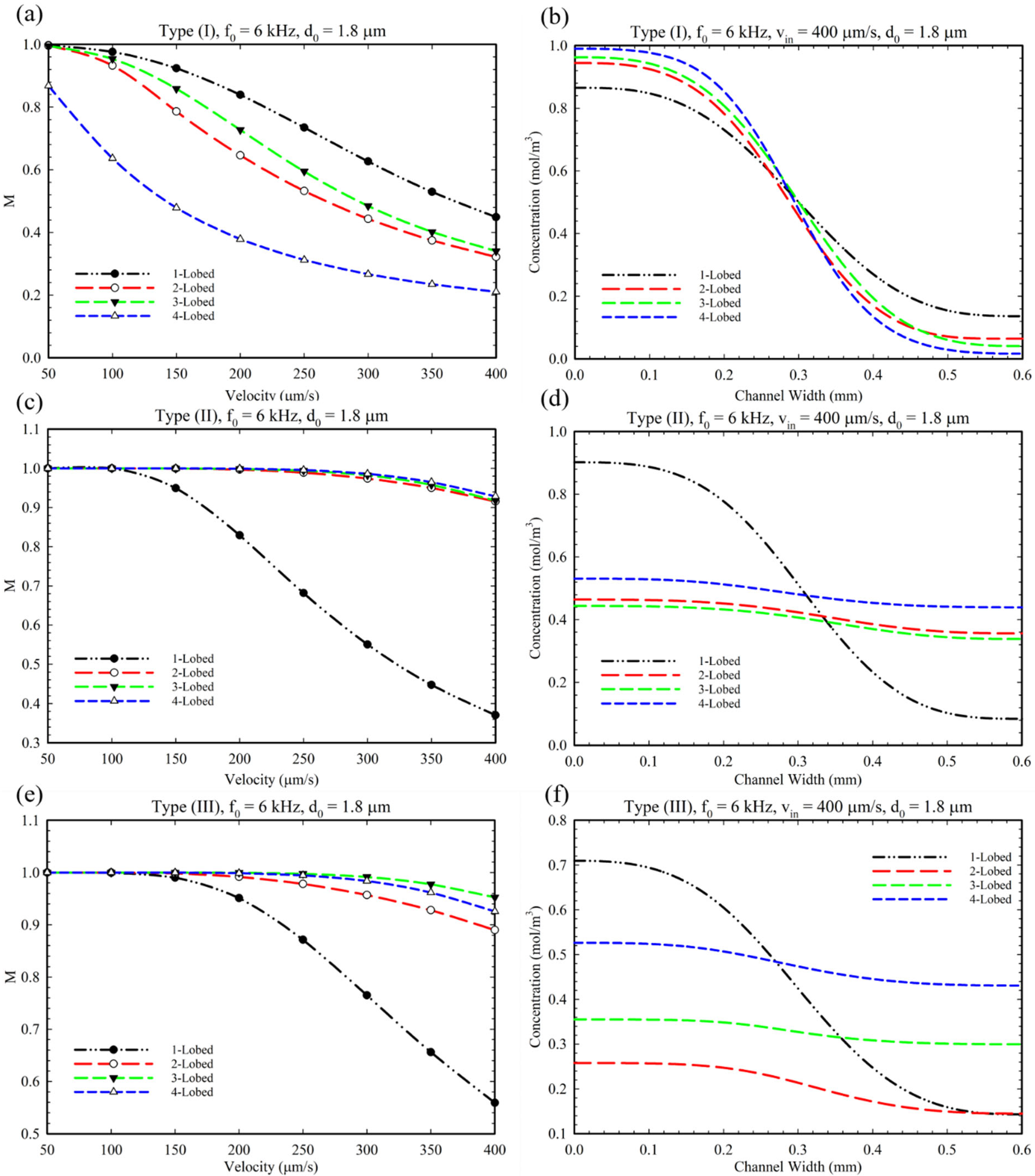
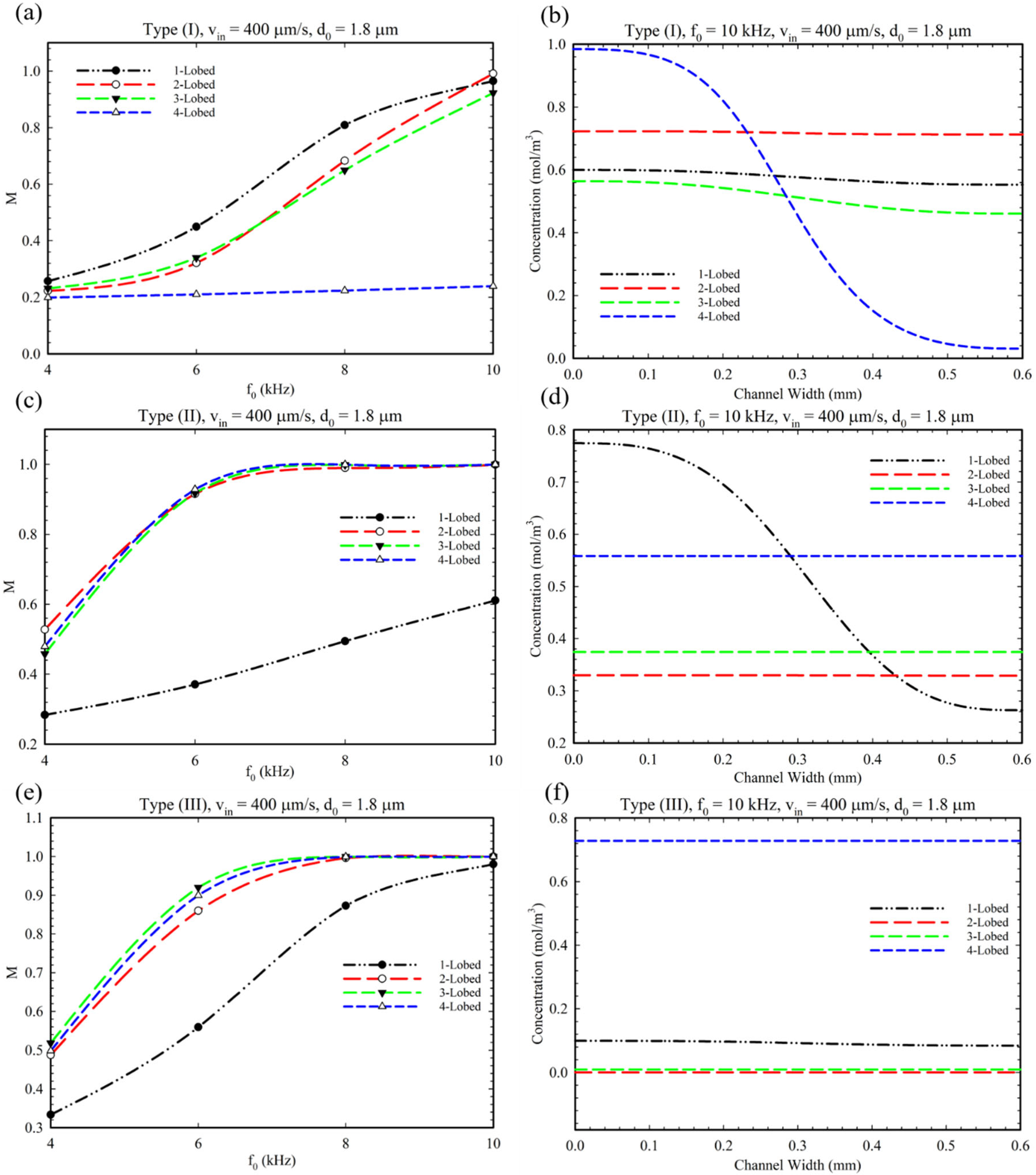
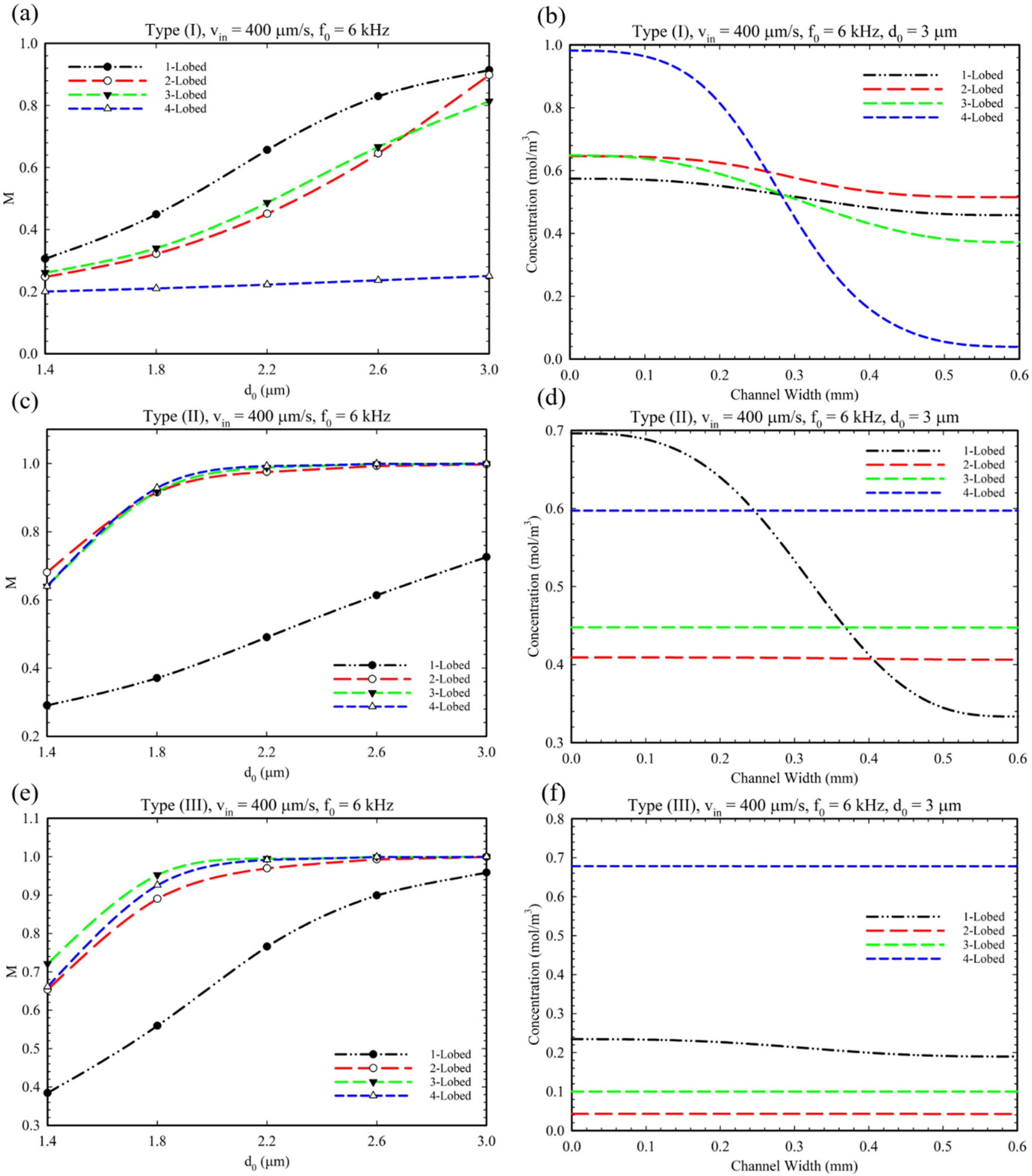
4. Results and Discussions
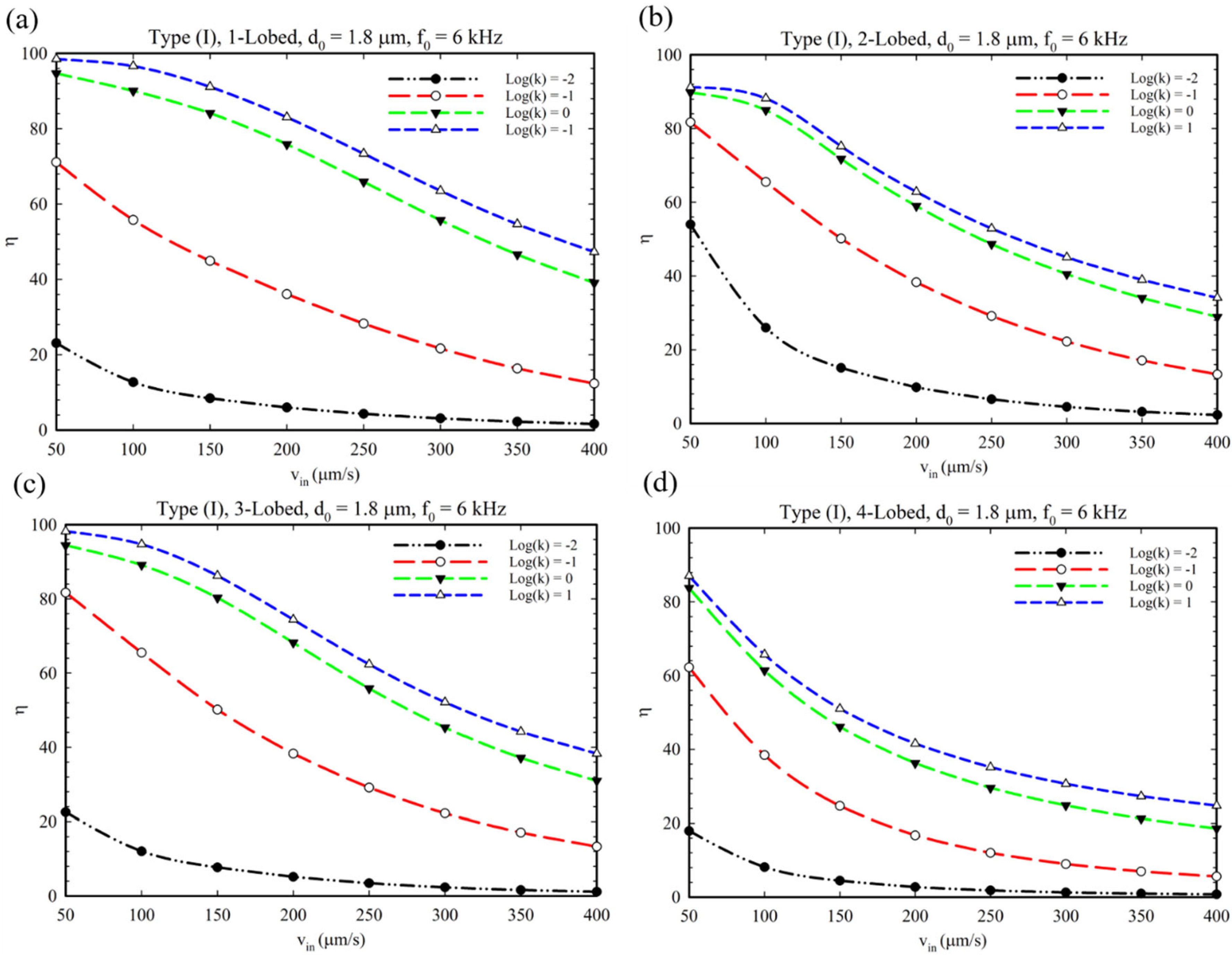
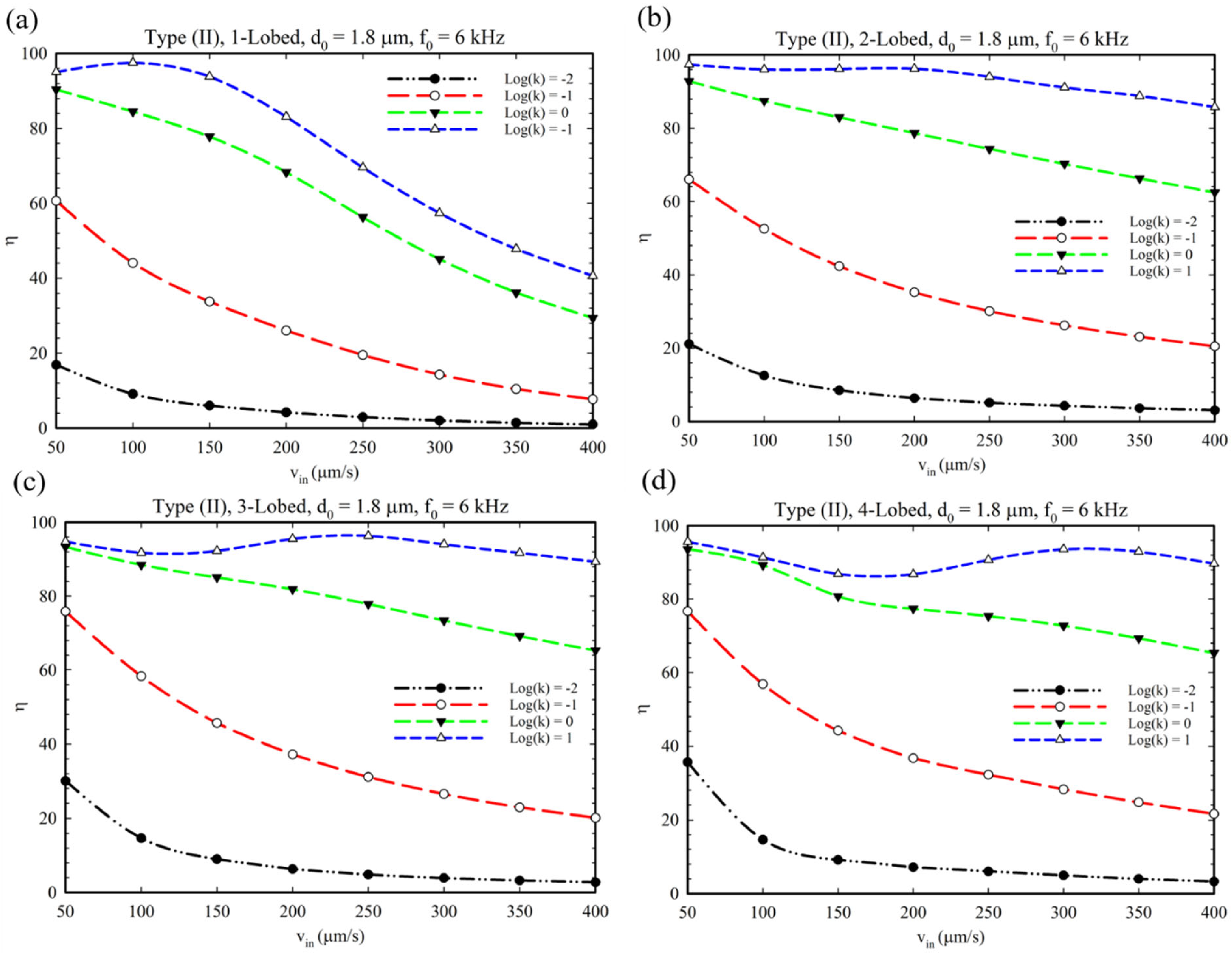
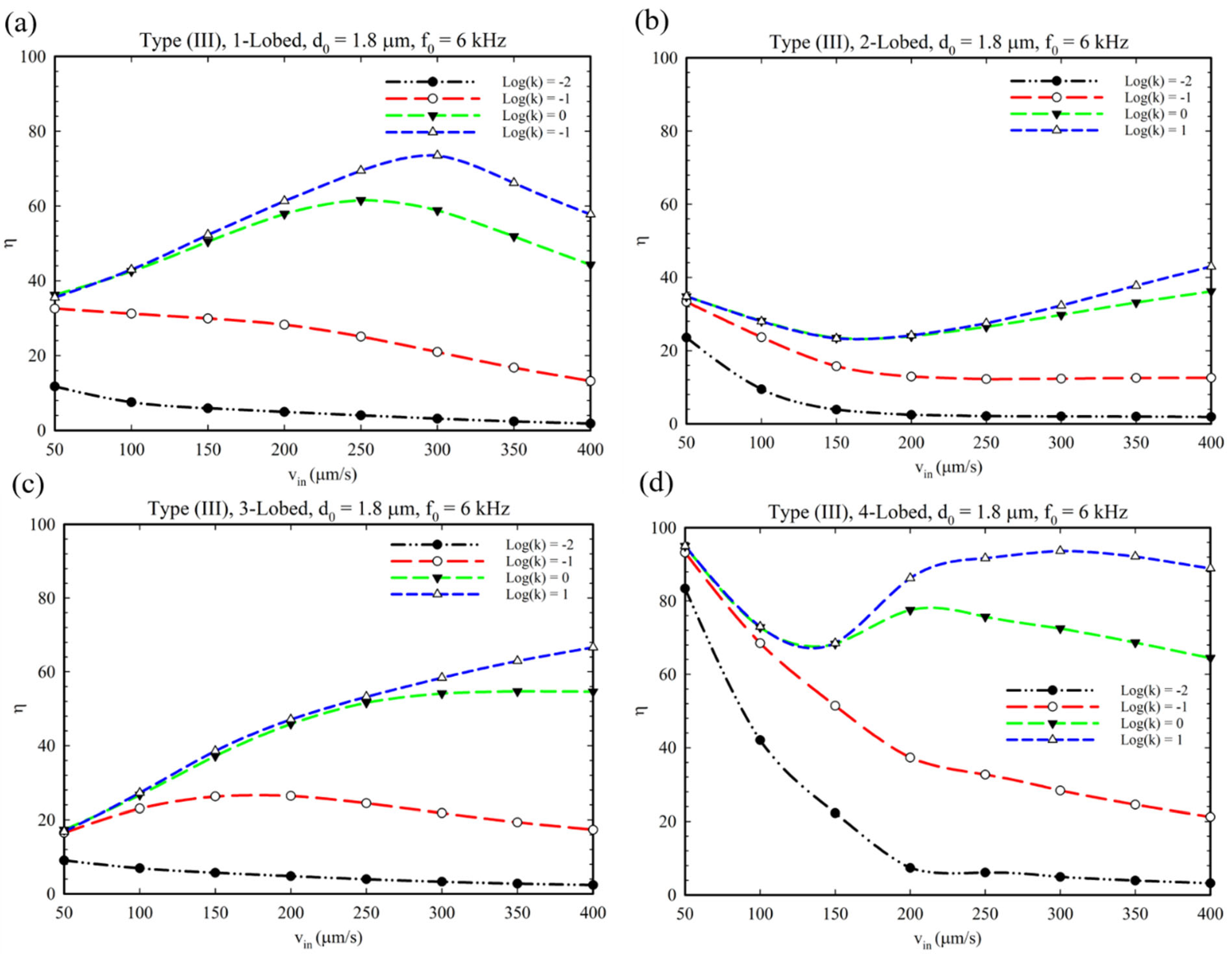
5. Chemical Reaction Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Zhang, B.; Dang, D.; Yang, X.; Yang, W.; Liang, W. A review of microfluidic-based mixing methods. Sens. Actuators A Phys. 2022, 344, 113757. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Hejazian, M.; Ooi, C.H.; Kashaninejad, N. Recent Advances and Future Perspectives on Microfluidic Liquid Handling. Micromachines 2017, 8, 186. [Google Scholar] [CrossRef] [Green Version]
- Kordzadeh-Kermani, V.; Madadelahi, M.; Ashrafizadeh, S.N.; Kulinsky, L.; Martinez-Chapa, S.O.; Madou, M.J. Electrified lab on disc systems: A comprehensive review on electrokinetic applications. Biosens. Bioelectron. 2022, 214, 114381. [Google Scholar] [CrossRef] [PubMed]
- Verlinden, E.J.; Madadelahi, M.; Sarajlic, E.; Shamloo, A.; Engel, A.H.; Staufer, U.; Ghatkesar, M.K. Volume and concentration dosing in picolitres using a two-channel microfluidic AFM cantilever. Nanoscale 2020, 12, 10292–10305. [Google Scholar] [CrossRef] [PubMed]
- Madadelahi, M.; Azimi-Boulali, J.; Madou, M.; Martinez-Chapa, S. Characterization of Fluidic-Barrier-Based Particle Generation in Centrifugal Microfluidics. Micromachines 2022, 13, 881. [Google Scholar] [CrossRef]
- Chen, Z.; Pei, Z.; Zhao, X.; Zhang, J.; Wei, J.; Hao, N. Acoustic microreactors for chemical engineering. Chem. Eng. J. 2022, 433, 133258. [Google Scholar] [CrossRef]
- Destgeer, G.; Sung, H.J. Recent advances in microfluidic actuation and micro-object manipulation via surface acoustic waves. Lab Chip 2015, 15, 2722–2738. [Google Scholar] [CrossRef]
- Ward, K.; Fan, Z.H. Mixing in microfluidic devices and enhancement methods. J. Micromech. Microeng. 2015, 25, 94001. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.Y.; Chang, C.L.; Wang, Y.N.; Fu, L.M. Microfluidic Mixing: A Review. Int. J. Mol. Sci. 2011, 12, 3263–3287. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Guo, F.; Yao, L.; Zhu, H.W.; Zheng, L.; Guo, Z.X.; Liu, W.; Chen, Y.; Guo, S.S.; Zhao, X.Z. Milliseconds mixing in microfluidic channel using focused surface acoustic wave. Sens. Actuators B Chem. 2011, 160, 1552–1556. [Google Scholar] [CrossRef]
- Chang, C.-C.; Yang, R.-J. Electrokinetic mixing in microfluidic systems. Microfluid. Nanofluidics 2007, 3, 501–525. [Google Scholar] [CrossRef]
- Chen, Z.; Shen, L.; Zhao, X.; Chen, H.; Xiao, Y.; Zhang, Y.; Yang, X.; Zhang, J.; Wei, J.; Hao, N. Acoustofluidic micromixers: From rational design to lab-on-a-chip applications. Appl. Mater. Today 2022, 26, 101356. [Google Scholar] [CrossRef]
- Go, D.B.; Atashbar, M.Z.; Ramshani, Z.; Chang, H.C. Surface acoustic wave devices for chemical sensing and microfluidics: A review and perspective. Anal. Methods 2017, 9, 4112–4134. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, M.; Lin, Y.; Xu, J. Acoustic Microfluidic Separation Techniques and Bioapplications: A Review. Micromachines 2020, 11, 921. [Google Scholar] [CrossRef]
- Li, Y.; Cai, S.; Shen, H.; Chen, Y.; Ge, Z.; Yang, W. Recent advances in acoustic microfluidics and its exemplary applications. Biomicrofluidics 2022, 16, 031502. [Google Scholar] [CrossRef]
- Strutt, J.W. Rayleigh, Lord on the Circulation of Air Observed in Kundt’s Tubes, and on Some Allied Acoustical Problems. Philos. Trans. R. Soc. Lond. 1884, 175, 1–21. [Google Scholar]
- Hutchisson, E.; Morgan, F.B. An experimental study of Kundt’s tube dust figures. Phys. Rev. 1931, 37, 1155–1163. [Google Scholar] [CrossRef]
- Huang, P.H.; Xie, Y.; Ahmed, D.; Rufo, J.; Nama, N.; Chen, Y.; Chan, C.Y.; Huang, T.J. An acoustofluidic micromixer based on oscillating sidewall sharp-edges. Lab Chip 2013, 13, 3847–3852. [Google Scholar] [CrossRef]
- Nama, N.; Huang, P.H.; Huang, T.J.; Costanzo, F. Investigation of acoustic streaming patterns around oscillating sharp edges. Lab Chip 2014, 14, 2824–2836. [Google Scholar] [CrossRef] [Green Version]
- Ozcelik, A.; Aslan, Z. A practical microfluidic pump enabled by acoustofluidics and 3D printing. Microfluid. Nanofluidics 2021, 25, 5. [Google Scholar] [CrossRef]
- Hao, N.; Pei, Z.; Liu, P.; Bachman, H.; Naquin, T.D.; Zhang, P.; Zhang, J.; Shen, L.; Yang, S.; Yang, K.; et al. Acoustofluidics-Assisted Fluorescence-SERS Bimodal Biosensors. Small 2020, 16, 2005179. [Google Scholar] [CrossRef] [PubMed]
- Gelin, P.; Sardan Sukas, Ö.; Hellemans, K.; Maes, D.; De Malsche, W. Study on the mixing and migration behavior of micron-size particles in acoustofluidics. Chem. Eng. J. 2019, 369, 370–375. [Google Scholar] [CrossRef]
- Doinikov, A.A.; Gerlt, M.S.; Dual, J. Acoustic Radiation Forces Produced by Sharp-Edge Structures in Microfluidic Systems. Phys. Rev. Lett. 2020, 124, 154501. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Guo, X.; Royon, L.; Brunet, P. Unveiling of the mechanisms of acoustic streaming induced by sharp edges. Phys. Rev. E 2020, 102, 43110. [Google Scholar] [CrossRef]
- Faradonbeh, V.R.; Rabiei, S.; Rabiei, H.; Goodarzi, M.; Safaei, M.R.; Lin, C.X. Power-law fluid micromixing enhancement using surface acoustic waves. J. Mol. Liq. 2022, 347, 117978. [Google Scholar] [CrossRef]
- Frampton, K.D.; Martin, S.E.; Minor, K. The scaling of acoustic streaming for application in micro-fluidic devices. Appl. Acoust. 2003, 64, 681–692. [Google Scholar] [CrossRef]
- Nama, N.; Huang, P.H.; Huang, T.J.; Costanzo, F. Investigation of micromixing by acoustically oscillated sharp-edges. Biomicrofluidics 2016, 10, 24124. [Google Scholar] [CrossRef] [Green Version]
- Ghorbani Kharaji, Z.; Kalantar, V.; Bayareh, M. Acoustic sharp-edge-based micromixer: A numerical study. Chem. Pap. 2022, 76, 1721–1738. [Google Scholar] [CrossRef]
- Zhang, C.; Brunet, P.; Royon, L.; Guo, X. Mixing intensification using sound-driven micromixer with sharp edges. Chem. Eng. J. 2021, 410, 128252. [Google Scholar] [CrossRef]
- Bachman, H.; Chen, C.; Rufo, J.; Zhao, S.; Yang, S.; Tian, Z.; Nama, N.; Huang, P.H.; Huang, T.J. An acoustofluidic device for efficient mixing over a wide range of flow rates. Lab Chip 2020, 20, 1238–1248. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, H.; Xiao, Y.; Zhang, J.; Qiu, Y.; Wei, J.; Hao, N. Rational design of robust flower-like sharp-edge acoustic micromixers towards efficient engineering of functional 3D ZnO nanorod array. Chem. Eng. J. 2022, 447, 137547. [Google Scholar] [CrossRef]
- Pourabed, A.; Brenker, J.; Younas, T.; He, L.; Alan, T. A Lotus shaped acoustofluidic mixer: High throughput homogenisation of liquids in 2 ms using hydrodynamically coupled resonators. Ultrason. Sonochem. 2022, 83, 105936. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, X.; Brunet, P.; Costalonga, M.; Royon, L. Acoustic streaming near a sharp structure and its mixing performance characterization. Microfluid. Nanofluidics 2019, 23, 104. [Google Scholar] [CrossRef]
- Endaylalu, S.A.; Tien, W.H. Mixing enhancement in T-junction microchannel with acoustic streaming induced by triangular structure. Biomicrofluidics 2021, 15, 34102. [Google Scholar] [CrossRef]
- Endaylalu, S.A.; Tien, W.H. A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines 2022, 13, 338. [Google Scholar] [CrossRef]
- Hamilton, M.F.; Blackstock, D.T. Nonlinear Acoustics; Academic Press: San Diego, CA, USA, 1998; Volume 237. [Google Scholar]
- Kharaji, Z.G.; Bayareh, M.; Kalantar, V. A review on acoustic field-driven micromixers. Int. J. Chem. React. Eng. 2021, 19, 553–569. [Google Scholar] [CrossRef]
- Madadelahi, M.; Shamloo, A. Droplet-based flows in serpentine microchannels: Chemical reactions and secondary flows. Int. J. Multiph. Flow 2017, 97, 186–196. [Google Scholar] [CrossRef]
- Tian, C.; Liu, W.; Zhao, R.; Li, T.; Xu, J.; Chen, S.W.; Wang, J. Acoustofluidics-based enzymatic constant determination by rapid and stable in situ mixing. Sens. Actuators B Chem. 2018, 272, 494–501. [Google Scholar] [CrossRef]
- Roberson, J.A.; Elger, D.F.; Crowe, C.T. Engineering Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef] [Green Version]
| Type | Condition | Description |
|---|---|---|
| Fluid | = | The velocity of fluid at inlets (zeroth order or background velocity) |
| = 0 | No-slip conditions on the channel’s walls | |
| = 0 | First-order acoustic velocity (on the walls) | |
| = | On the oscillatory walls (Sharp-edges) | |
| = 0 | On the walls | |
| Thermal | = | On the walls |
| Concentration | = 0 | Concentration of solute at inlet 1 |
| = 1 mol/m3 | Concentration of solute at inlet 2 | |
| = 0 | No flux on the walls | |
| Outflow condition at outlet |
| Structure of Lobes | Type | ||
|---|---|---|---|
| N/A | 15 | 1-Lobed | Type (I) |
| 80 | 15 | 2-Lobed | |
| 120 | 15 | 3-Lobed | |
| 120 | 35 | 4-Lobed | |
| N/A | 45 | 1-Lobed | Type (II) |
| 120 | 15 | 2-Lobed | |
| 120 | 15 | 3-Lobed | |
| 120 | 15 | 4-Lobed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kordzadeh-Kermani, V.; Dartoomi, H.; Azizi, M.; Ashrafizadeh, S.N.; Madadelahi, M. Investigating the Performance of the Multi-Lobed Leaf-Shaped Oscillatory Obstacles in Micromixers Using Bulk Acoustic Waves (BAW): Mixing and Chemical Reaction. Micromachines 2023, 14, 795. https://doi.org/10.3390/mi14040795
Kordzadeh-Kermani V, Dartoomi H, Azizi M, Ashrafizadeh SN, Madadelahi M. Investigating the Performance of the Multi-Lobed Leaf-Shaped Oscillatory Obstacles in Micromixers Using Bulk Acoustic Waves (BAW): Mixing and Chemical Reaction. Micromachines. 2023; 14(4):795. https://doi.org/10.3390/mi14040795
Chicago/Turabian StyleKordzadeh-Kermani, Vahid, Hossein Dartoomi, Mina Azizi, Seyed Nezameddin Ashrafizadeh, and Masoud Madadelahi. 2023. "Investigating the Performance of the Multi-Lobed Leaf-Shaped Oscillatory Obstacles in Micromixers Using Bulk Acoustic Waves (BAW): Mixing and Chemical Reaction" Micromachines 14, no. 4: 795. https://doi.org/10.3390/mi14040795
APA StyleKordzadeh-Kermani, V., Dartoomi, H., Azizi, M., Ashrafizadeh, S. N., & Madadelahi, M. (2023). Investigating the Performance of the Multi-Lobed Leaf-Shaped Oscillatory Obstacles in Micromixers Using Bulk Acoustic Waves (BAW): Mixing and Chemical Reaction. Micromachines, 14(4), 795. https://doi.org/10.3390/mi14040795







