Design and Fabrication of a High-Temperature SOI Pressure Sensor with Optimized Crossbeam Membrane
Abstract
:1. Introduction
2. Structure Design and Optimization
2.1. Structure Design
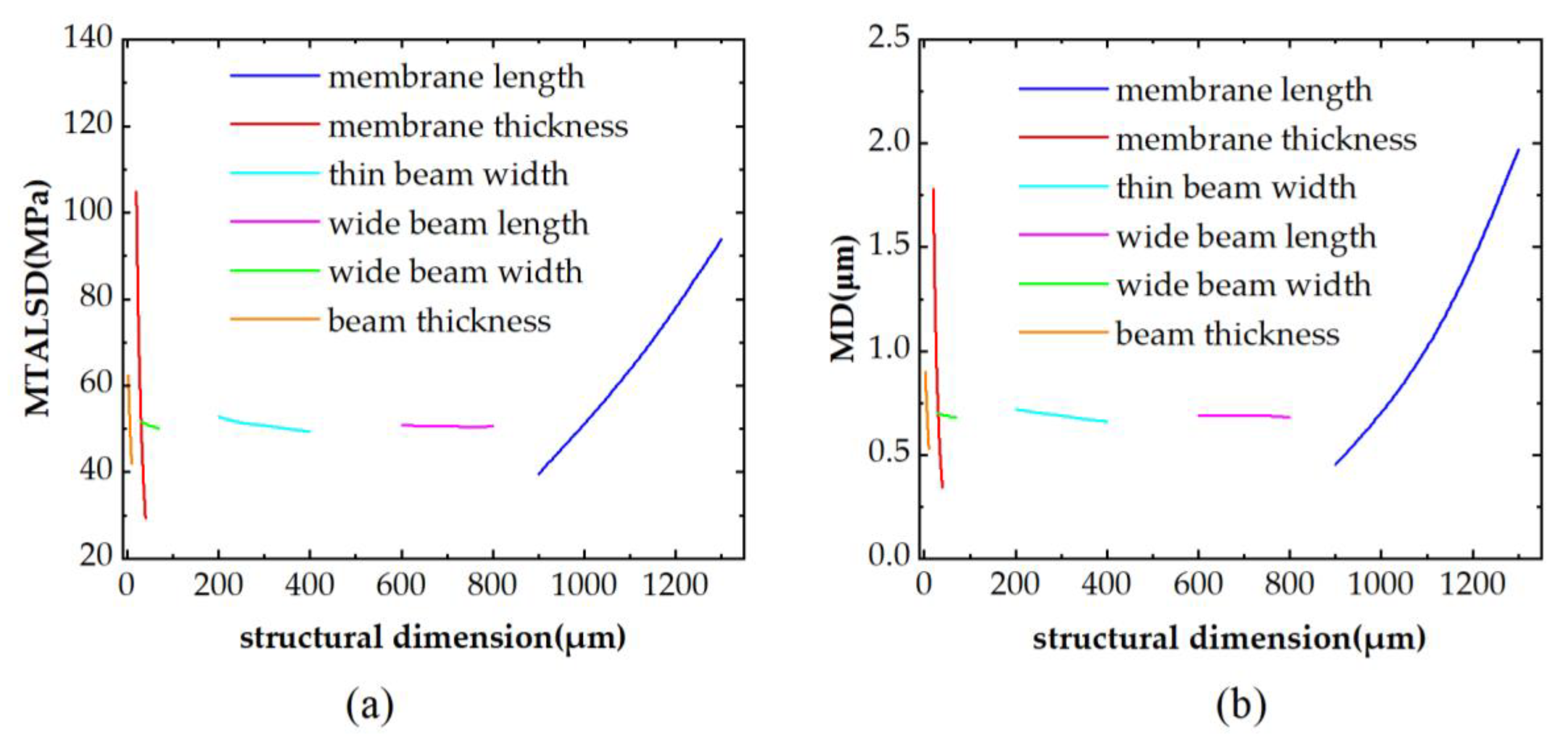
2.2. Geometry Optimization
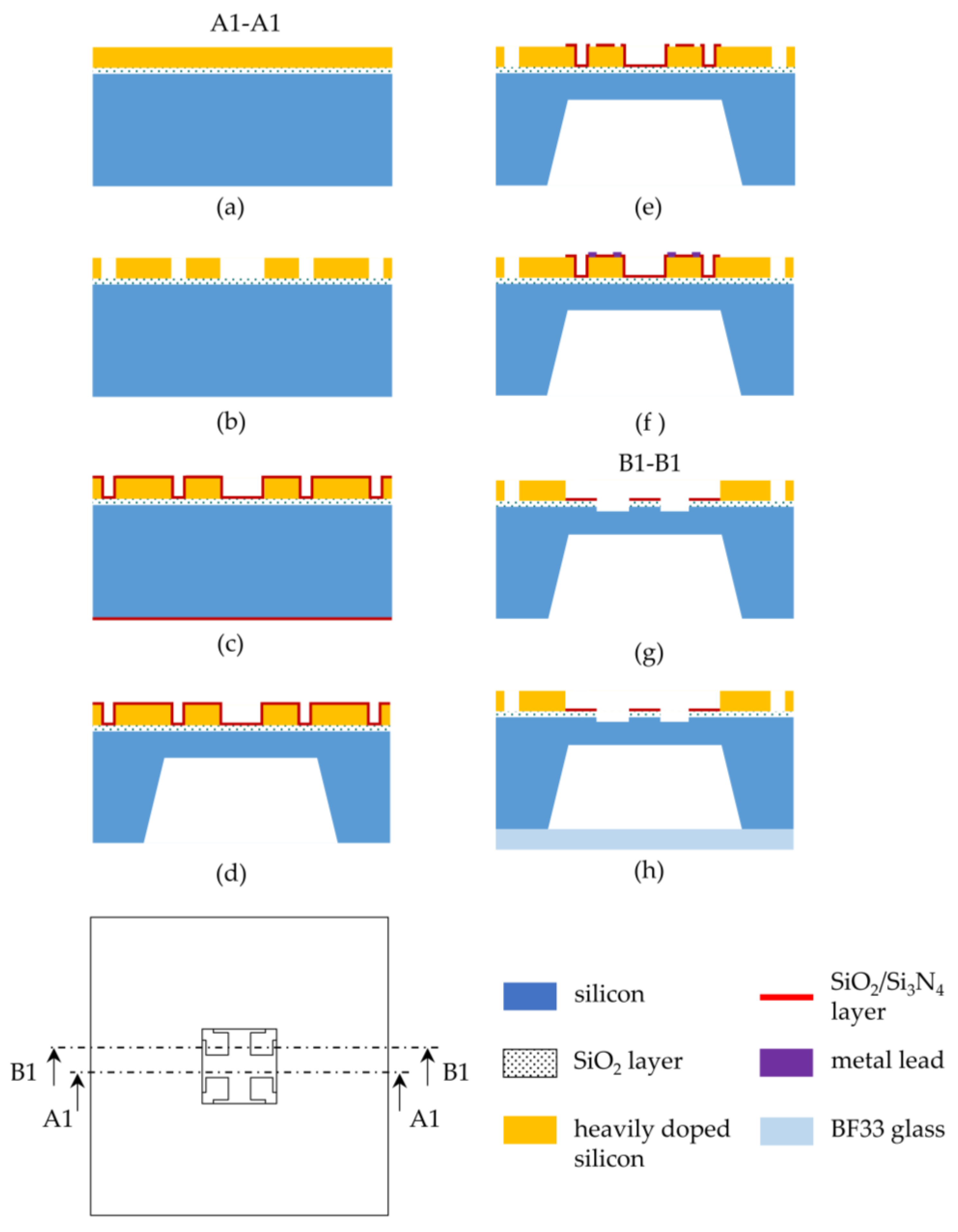
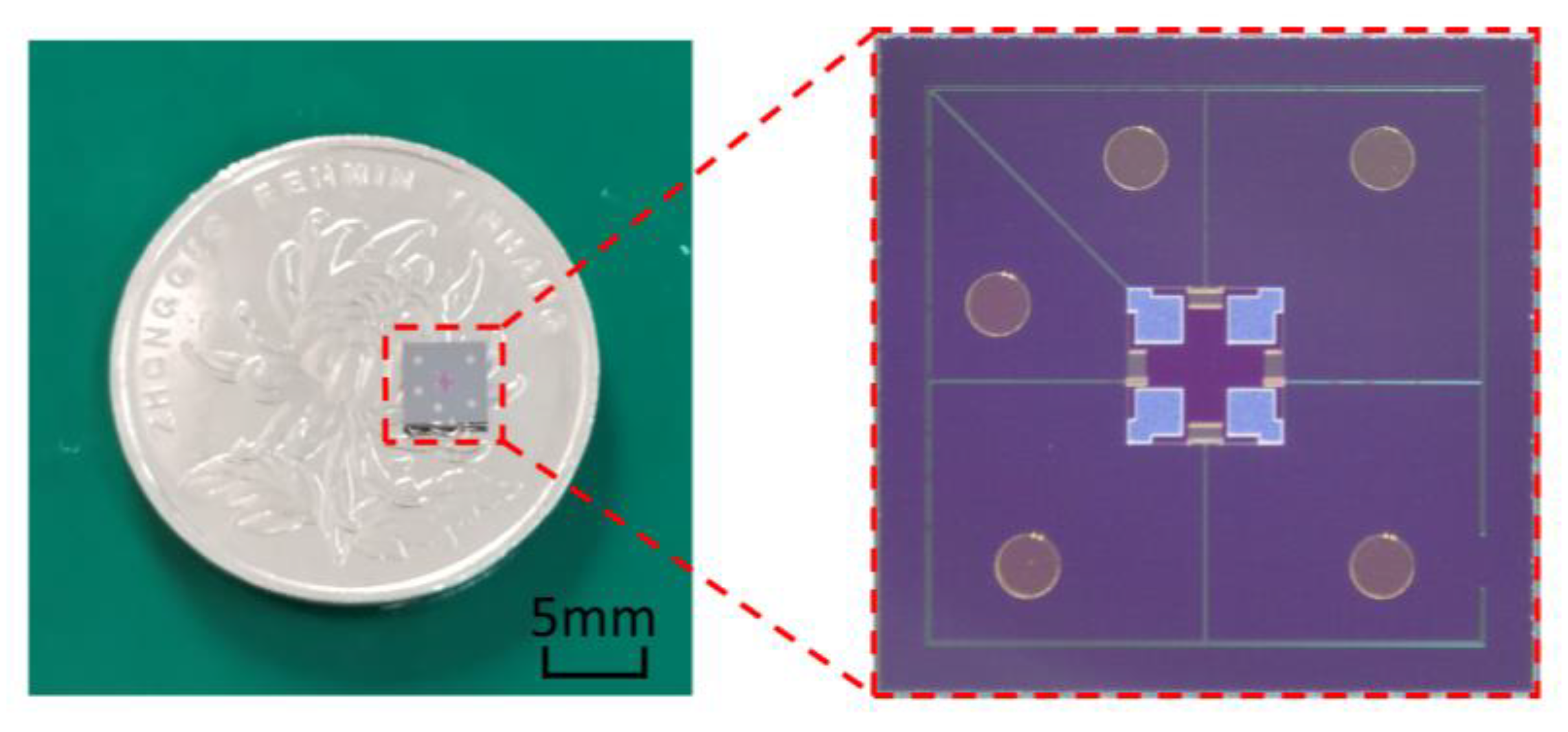
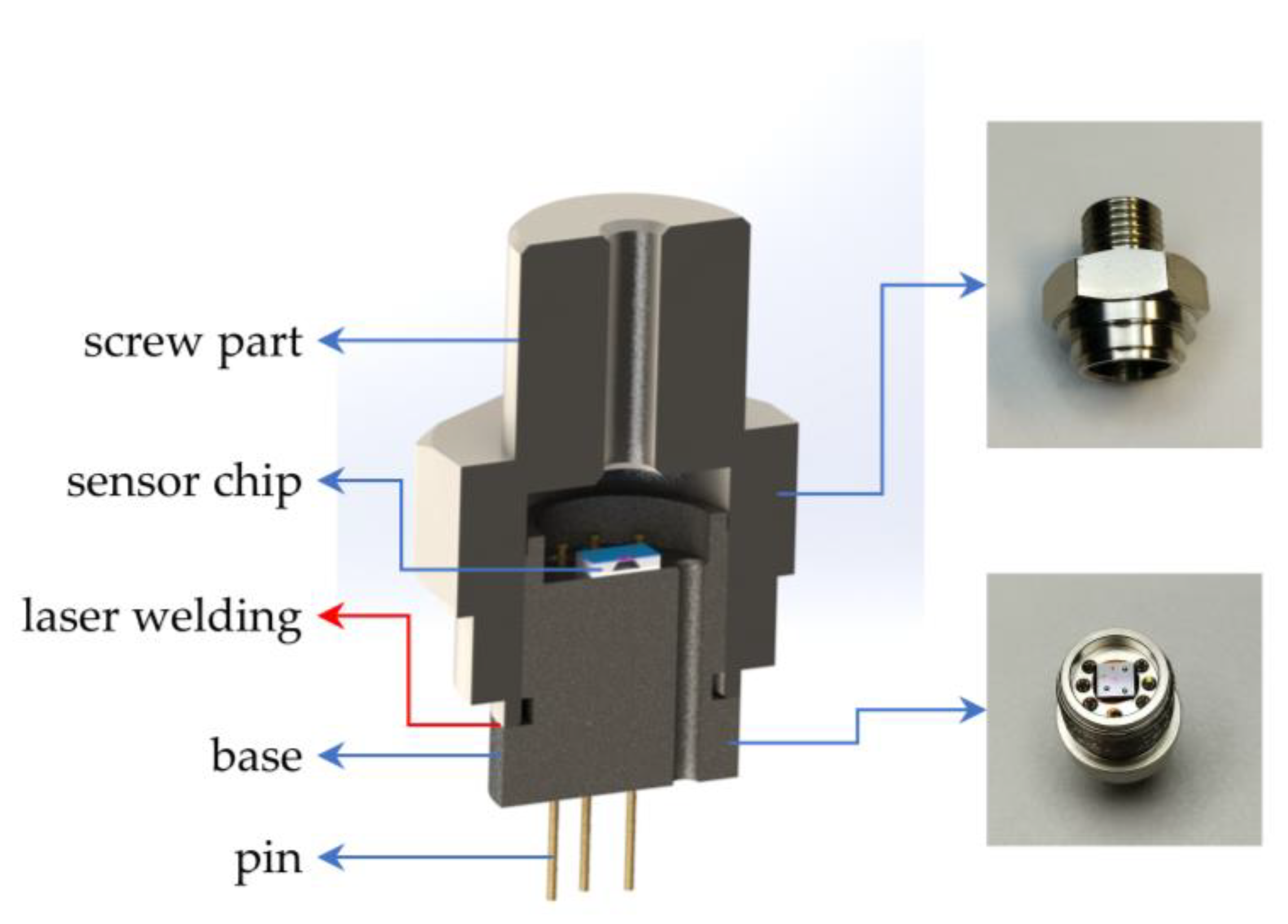
3. Fabrication and Package
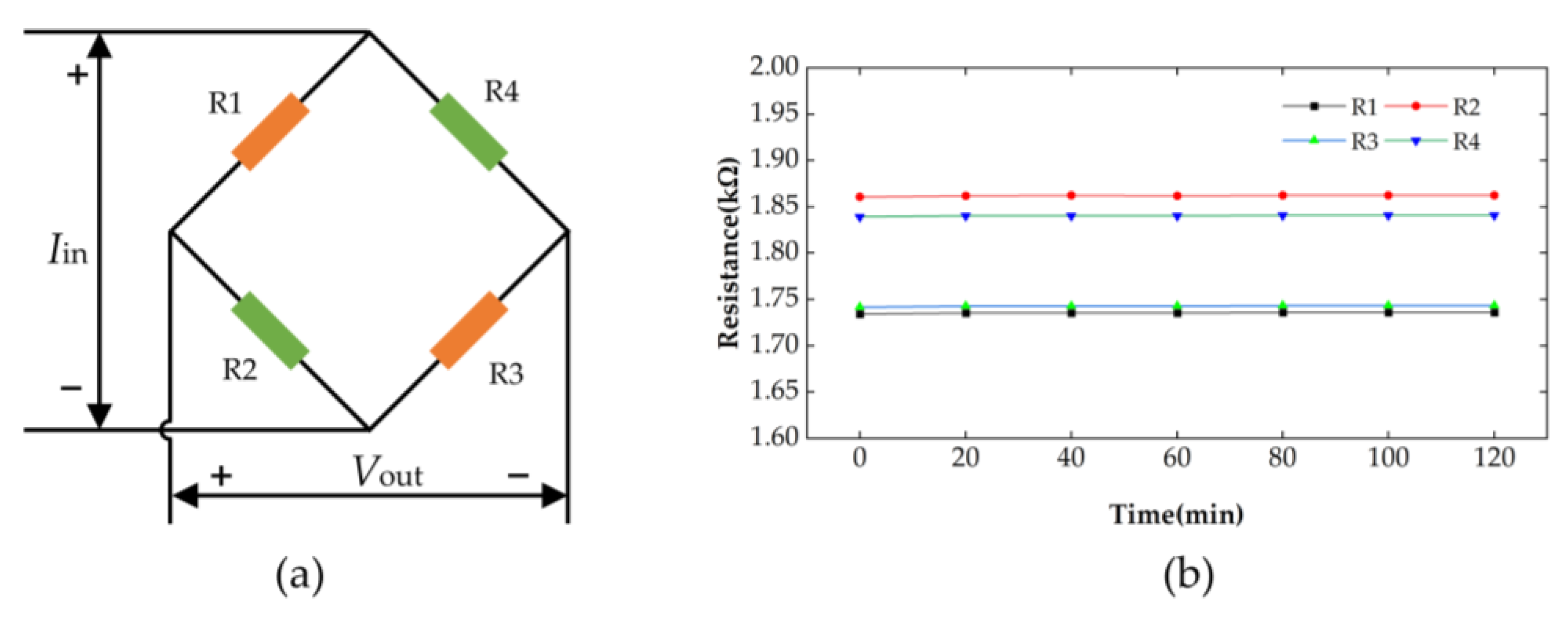
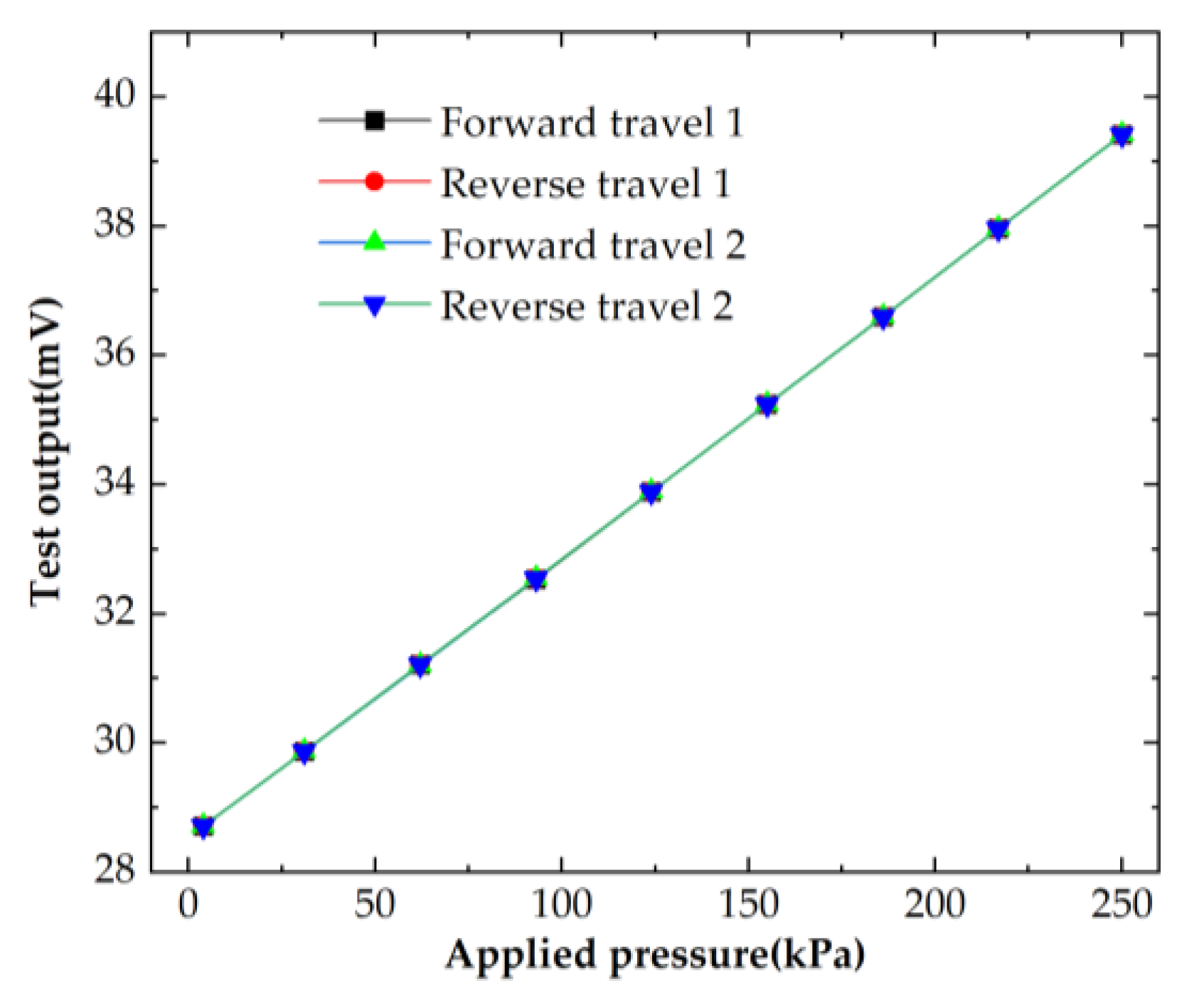
4. Testing and Analyzing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khodasevych, I.; Parmar, S.; Troynikov, O. Flexible Sensors for Pressure Therapy: Effect of Substrate Curvature and Stiffness on Sensor Performance. Sensors 2017, 17, 2399. [Google Scholar] [CrossRef] [PubMed]
- Barlian, A.A.; Park, W.T.; Mallon, J.R.; Rastegar, A.J.; Pruitt, B.L. Review: Semiconductor Piezoresistance for Microsystems. Proc. IEEE 2009, 97, 513–552. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.L.; Zhao, L.B.; Jiang, Z.D. High temperature and frequency pressure sensor based on silicon-on-insulator layers. Meas. Sci. Technol. 2006, 17, 519–523. [Google Scholar] [CrossRef]
- Li, X.; Liu, Q.; Pang, S.; Xu, K.; Tang, H.; Sun, C. High-temperature piezoresistive pressure sensor based on implantation of oxygen into silicon wafer. Sens. Actuators A Phys. 2012, 179, 277–282. [Google Scholar] [CrossRef]
- Phan, H.; Dao, D.V.; Nakamura, K.; Dimitrijev, S.; Nguyen, N. The Piezoresistive Effect of SiC for MEMS Sensors at High Temperatures: A Review. J. Microelectromech. Syst. 2015, 24, 1663–1677. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Zhao, Y.; Yang, Y.; Gong, T.; Hao, L.; Ren, W. Design and Fabrication of Bulk Micromachined 4H-SiC Piezoresistive Pressure Chips Based on Femtosecond Laser Technology. Micromachines 2021, 12, 56. [Google Scholar] [CrossRef]
- Belwanshi, V.; Philip, S.; Topkar, A. Performance Study of MEMS Piezoresistive Pressure Sensors at Elevated Temperatures. IEEE Sens. J. 2022, 22, 9313–9320. [Google Scholar] [CrossRef]
- Balavalad, K.B.; Sheeparamatti, B.G. Design, simulation analysis of SOI based micro piezoresistive pressure sensor for high temperature applications. In Proceedings of the 3rd IEEE International Conference on Recent Trends in Electronics, Information and Communication Technology, RTEICT 2018, Bangalore, India, 18–19 May 2018; Institute of Electrical and Electronics Engineers Inc.: Bangalore, India, 2018; pp. 2163–2167. [Google Scholar]
- Gradolph, C.; Friedberger, A.; Müller, G.; Wilde, J. Impact of high-g and high vibration environments on piezoresistive pressure sensor performance. Sens. Actuators A Phys. 2009, 150, 69–77. [Google Scholar] [CrossRef]
- Guo, Y.; Schutz, S.; Vaghi, A.; Li, Y.; Guo, Z.; Chang, F.; Barrettino, D.; Wang, S.X. Stand-Alone Stretchable Absolute Pressure Sensing System for Industrial Applications. IEEE Trans. Ind. Electron. 2017, 64, 8739–8746. [Google Scholar] [CrossRef]
- Niu, Z.; Zhao, Y.; Tian, B. Design optimization of high pressure and high temperature piezoresistive pressure sensor for high sensitivity. Rev. Sci. Instrum. 2014, 85, 15001. [Google Scholar] [CrossRef]
- Xu, Z.; Yan, J.; Ji, M.; Zhou, Y.; Wang, D.; Wang, Y.; Mai, Z.; Zhao, X.; Nan, T.; Xing, G.; et al. An SOI-Structured Piezoresistive Differential Pressure Sensor with High Performance. Micromachines 2022, 13, 2250. [Google Scholar] [CrossRef] [PubMed]
- Song, P.; Si, C.; Zhang, M.; Zhao, Y.; He, Y.; Liu, W.; Wang, X. A Novel Piezoresistive MEMS Pressure Sensors Based on Temporary Bonding Technology. Sensors 2020, 20, 337. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Li, D.; Yu, Y.; Wen, D. Temperature characteristics research of SOI pressure sensor based on asymmetric base region transistor. J. Semicond. 2017, 38, 074008. [Google Scholar] [CrossRef]
- Hase, Y.; Bessho, M.; Ipposhi, T. SOI type pressure sensor for high temperature pressure measurement. In Proceedings of the 1994 SAE International Congress and Exposition, Detroit, MI, USA, 28 February–3 March 1994; SAE International: Detroit, MI, USA, 1994. [Google Scholar]
- Chung, G.S. Thin Soi Structures for Sensing and Integrated-Circuit Applications. Sens. Actuators A Phys. 1993, 39, 241–251. [Google Scholar] [CrossRef]
- Li, C.; Cordovilla, F.; Jagdheesh, R.; Ocana, J.L. Design Optimization and Fabrication of a Novel Structural SOI Piezoresistive Pressure Sensor with High Accuracy. Sensors 2018, 18, 439. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, L.; Jiang, Z.; Guo, X.; Ding, J.; Xiang, W.; Zhao, Y. A high sensitive pressure sensor with the novel bossed diaphragm combined with peninsula-island structure. Sens. Actuators A Phys. 2016, 244, 66–76. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, Y. The Design and Optimization of a Highly Sensitive and Overload-Resistant Piezoresistive Pressure Sensor. Sensors 2016, 16, 348. [Google Scholar] [CrossRef]
- Tang, X.; Tian, J.; Zhao, J.; Jin, Z.; Liu, Y.; Liu, J.; Chen, T.; Li, J. Structure design and optimization of SOI high-temperature pressure sensor chip. Microelectron. J. 2021, 118, 105245. [Google Scholar] [CrossRef]
- Wang, Q.; Ding, J.N.; Wang, W.X. Fabrication and temperature coefficient compensation technology of low cost high temperature pressure sensor. Sens. Actuators A Phys. 2005, 120, 468–473. [Google Scholar] [CrossRef]
- Meng, Q.; Lu, Y.; Wang, J.; Chen, D.; Chen, J. A Piezoresistive Pressure Sensor with Optimized Positions and Thickness of Piezoresistors. Micromachines 2021, 12, 1095. [Google Scholar] [CrossRef]
- Wu, J.; Zhao, X.; Liu, Y.; Wen, D. The simulation, fabrication technology and characteristic research of micro-pressure sensor with isosceles trapezoidal beam-membrane. Mod. Phys. Lett. B 2020, 34, 2050328. [Google Scholar] [CrossRef]
- Tian, B.; Zhao, Y.; Jiang, Z.; Hu, B. The design and analysis of beam-membrane structure sensors for micro-pressure measurement. Rev. Sci. Instrum. 2012, 83, 045003. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.; Liu, X.; Su, X.; Jiang, X. Design and Optimization of a Pressure Sensor Based on Serpentine-Shaped Graphene Piezoresistors for Measuring Low Pressure. Sensors 2022, 22, 4937. [Google Scholar] [CrossRef]
- Anh, V.T.; Zhang, X.; Zhu, B. Mechanical Structural Design of a Piezoresistive Pressure Sensor for Low-Pressure Measurement: A Computational Analysis by Increases in the Sensor Sensitivity. Sensors 2018, 18, 2023. [Google Scholar]
- Shang, H.; Tian, B.; Wang, D.; Liu, Y.; Wang, W. Development of All-SiC Absolute Pressure Sensor Based on Sealed Cavity Structure. IEEE Sens. J. 2021, 21, 27308–27314. [Google Scholar] [CrossRef]


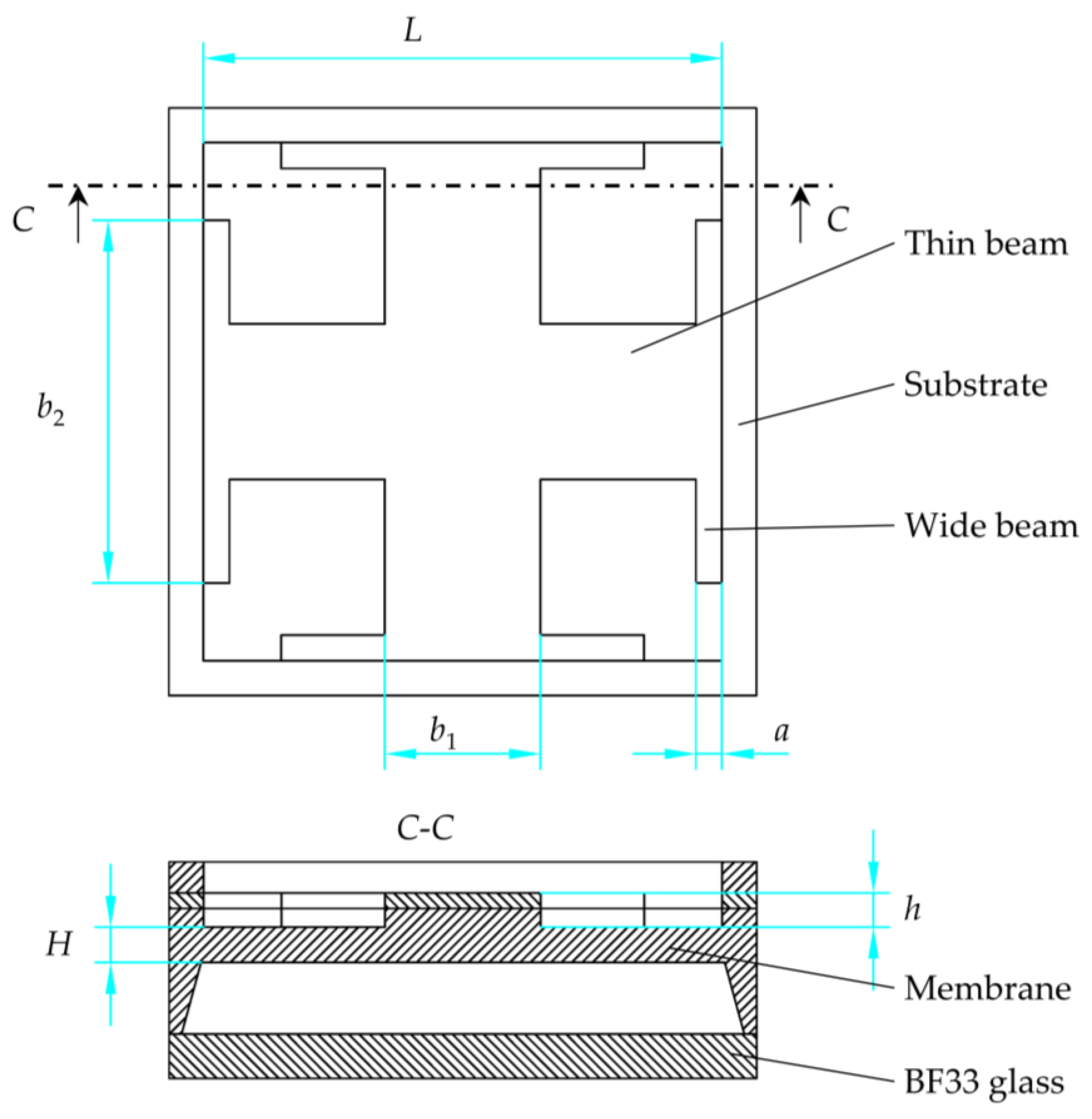



| Parameters | L | H | b1 | b2 | a | h |
|---|---|---|---|---|---|---|
| Dimension (μm) | 1100 | 25 | 280 | 700 | 40 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, L.; Li, C.; Wang, L.; Bai, B.; Zhao, Y.; Luo, C. Design and Fabrication of a High-Temperature SOI Pressure Sensor with Optimized Crossbeam Membrane. Micromachines 2023, 14, 1045. https://doi.org/10.3390/mi14051045
Hao L, Li C, Wang L, Bai B, Zhao Y, Luo C. Design and Fabrication of a High-Temperature SOI Pressure Sensor with Optimized Crossbeam Membrane. Micromachines. 2023; 14(5):1045. https://doi.org/10.3390/mi14051045
Chicago/Turabian StyleHao, Le, Cun Li, Lukang Wang, Bing Bai, Yulong Zhao, and Chao Luo. 2023. "Design and Fabrication of a High-Temperature SOI Pressure Sensor with Optimized Crossbeam Membrane" Micromachines 14, no. 5: 1045. https://doi.org/10.3390/mi14051045
APA StyleHao, L., Li, C., Wang, L., Bai, B., Zhao, Y., & Luo, C. (2023). Design and Fabrication of a High-Temperature SOI Pressure Sensor with Optimized Crossbeam Membrane. Micromachines, 14(5), 1045. https://doi.org/10.3390/mi14051045






