Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate
Abstract
:1. Introduction
2. The Governing Equations
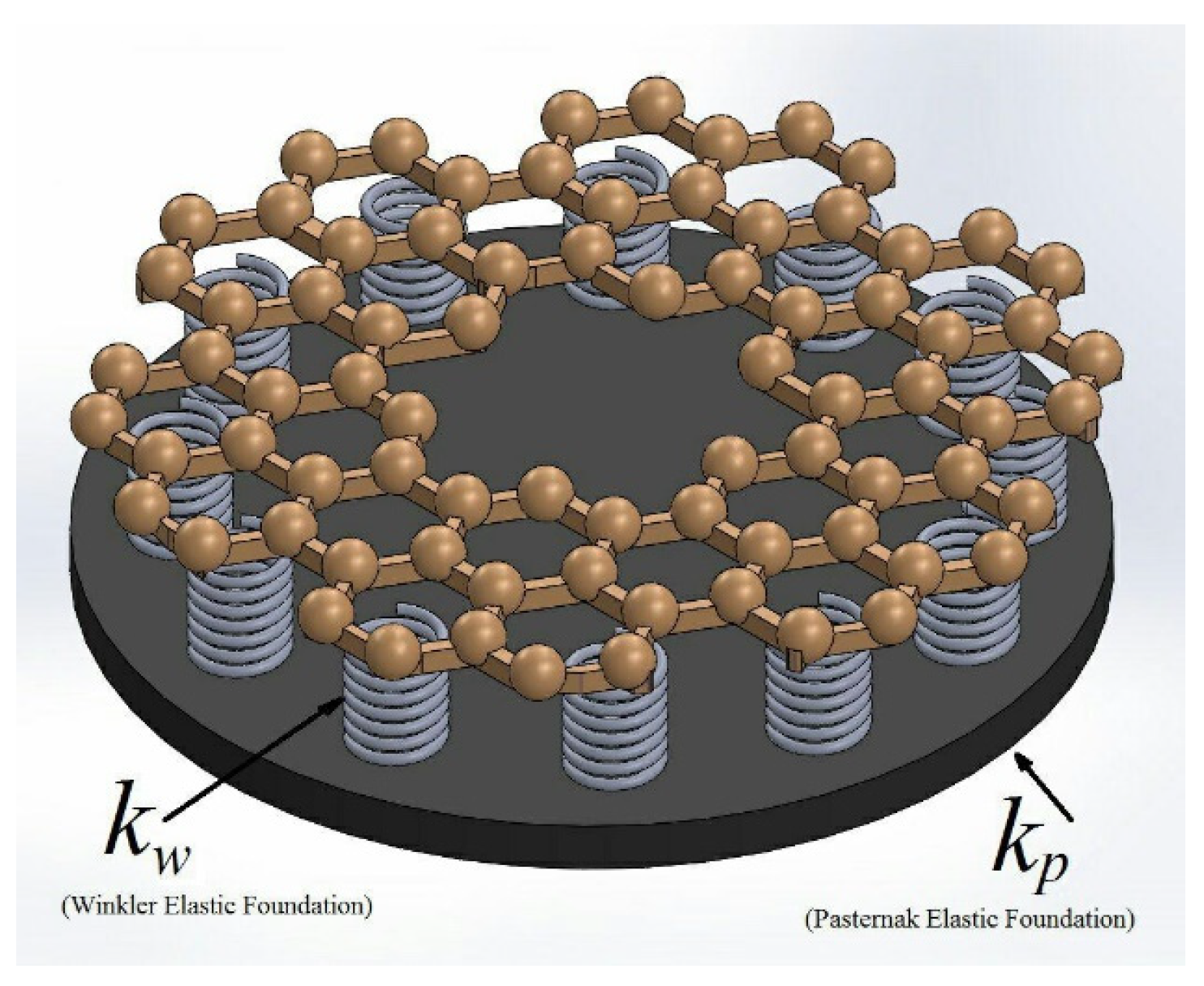
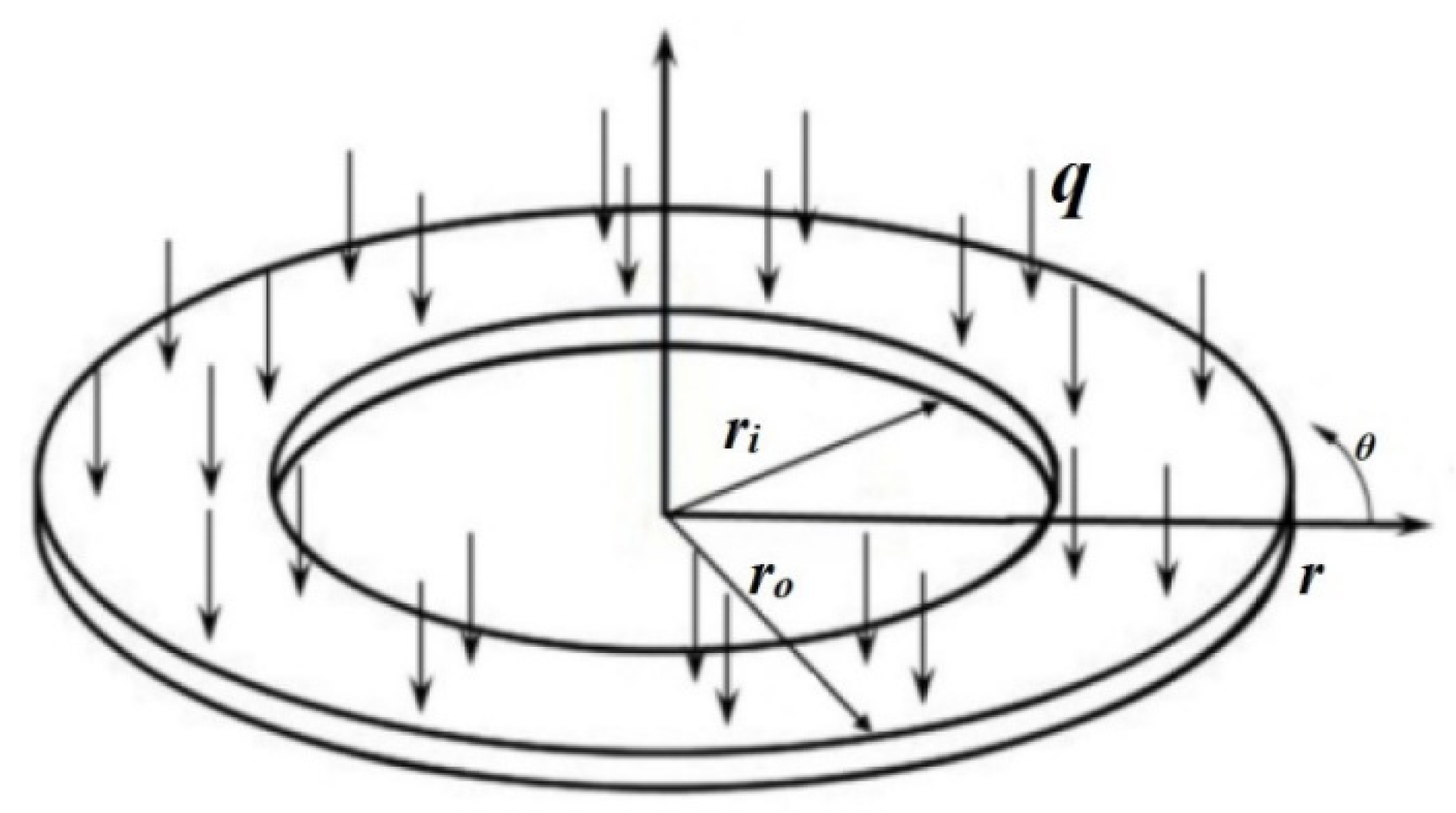
2.1. The Governing Equations for the Axisymmetric Single-Layer Circular/Annular Nanoplate
2.2. Derivation of Equilibrium Equations Based on the Energy Method
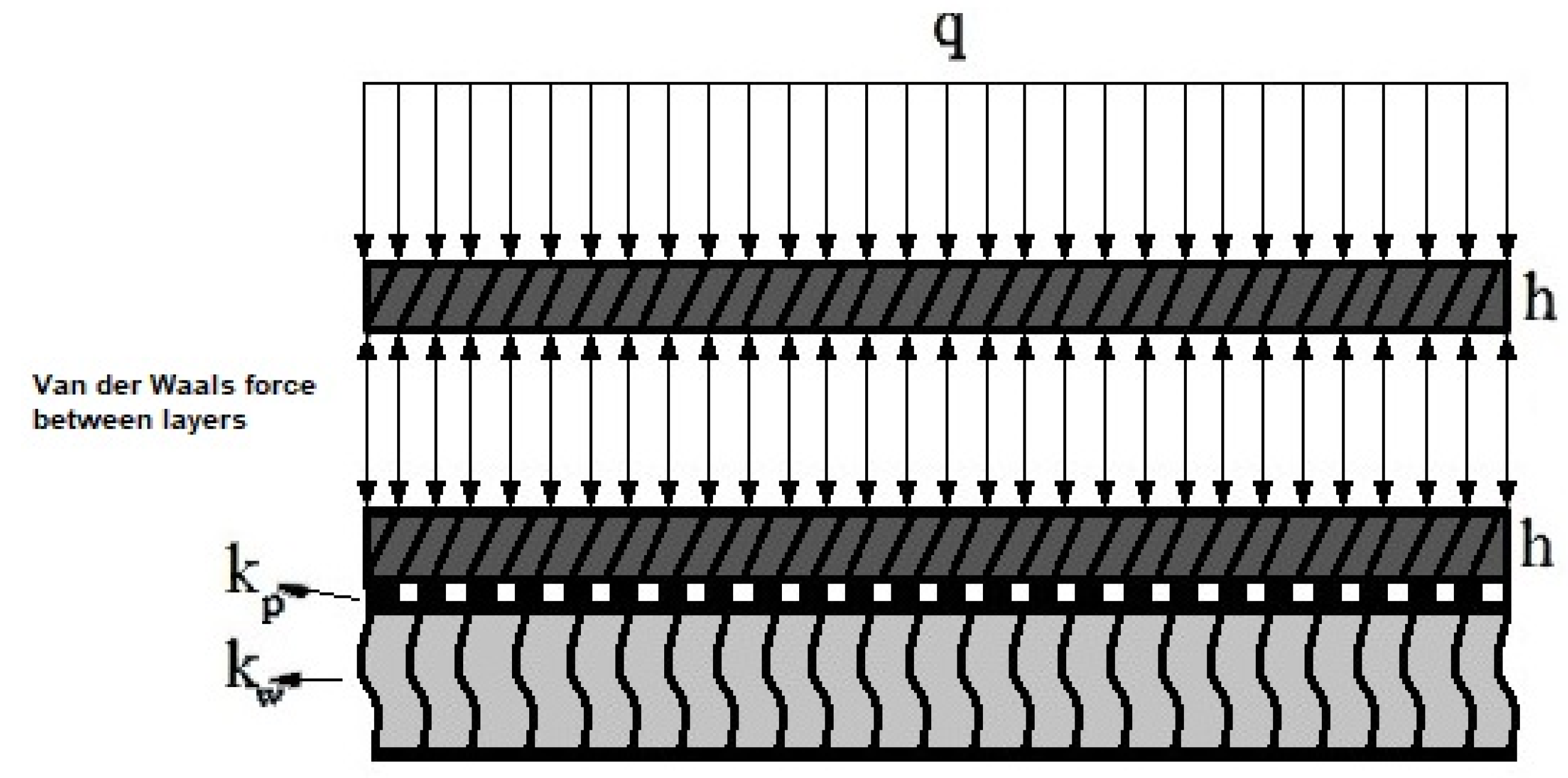
2.3. Equilibrium Equations of the Bilayer Axisymmetric Circular/Annular Nanoplate
2.4. Boundary Conditions
2.5. Dimensionless Assumptions
3. Numerical Solution Method
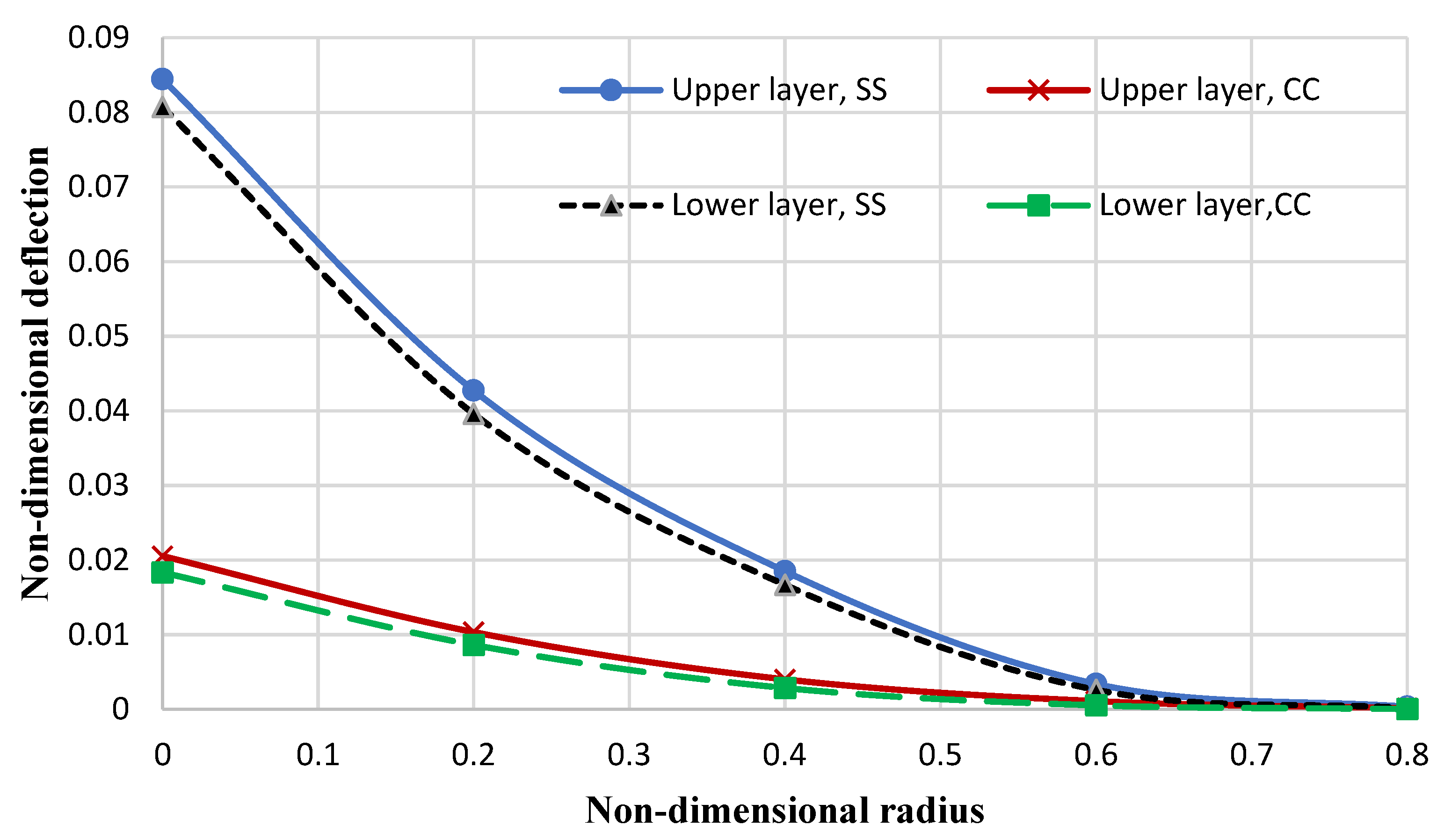
4. Results and Discussion
5. Conclusions
- ∗
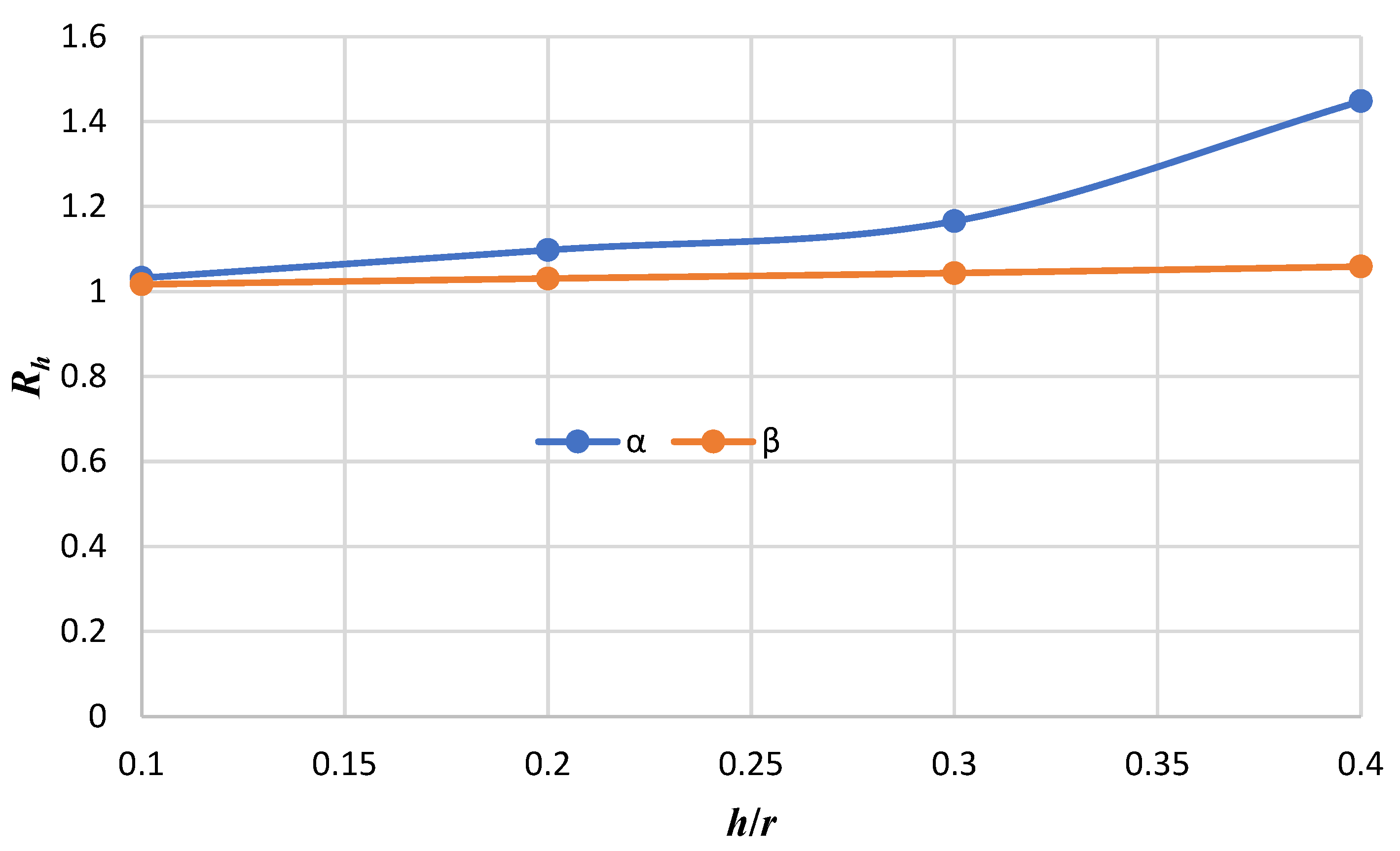
- Deflection decreases with the increasing order of the theory. In other words, FSDT overestimates the deflection results, especially at higher thickness-to-radius ratios, so it is better to use HSDT models in those cases.
- ∗
- The ratio of the maximum dimensionless deflection obtained from FSDT to HSDT is enhanced as the ratio of the thickness-to-radius increases.
- ∗
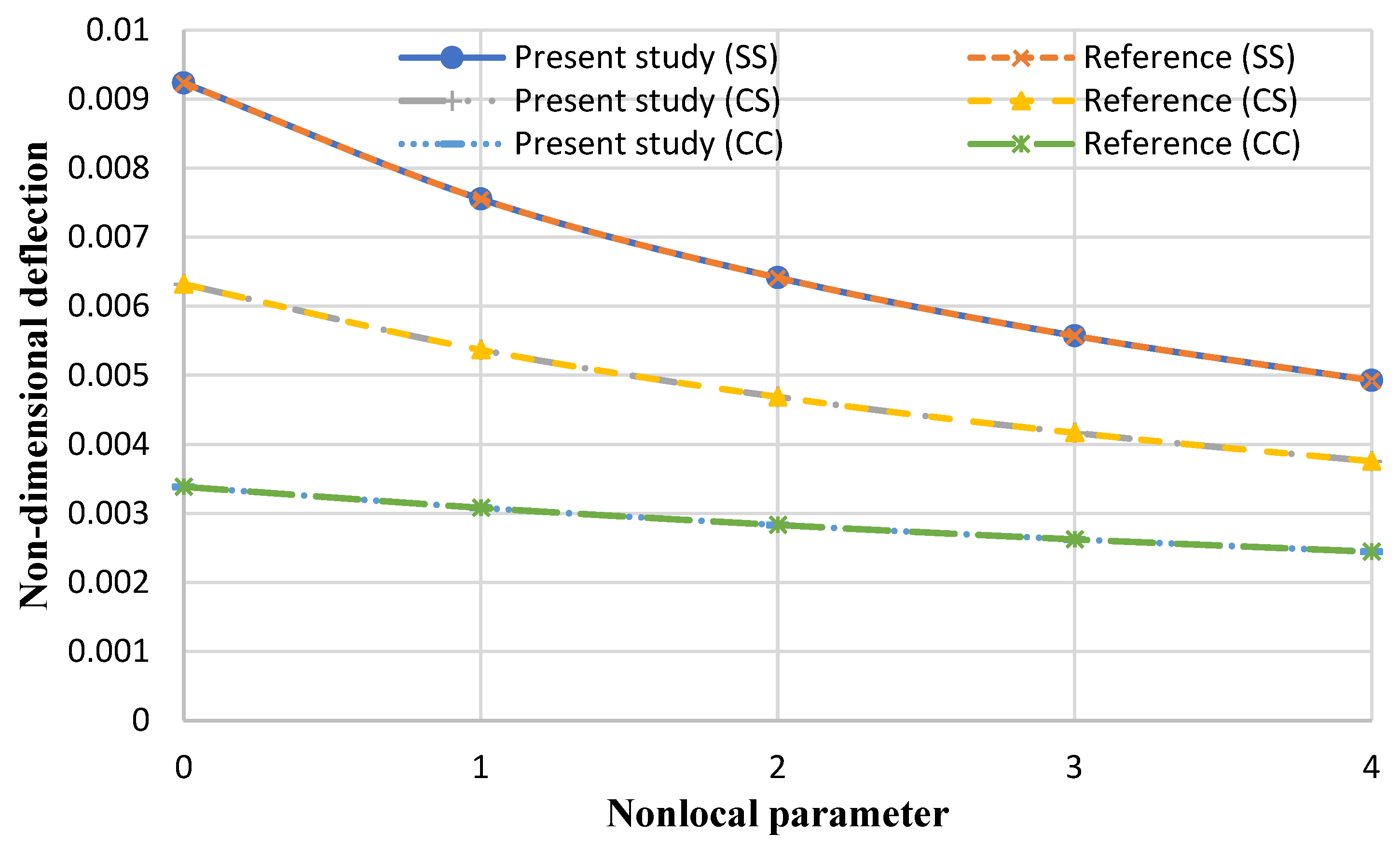
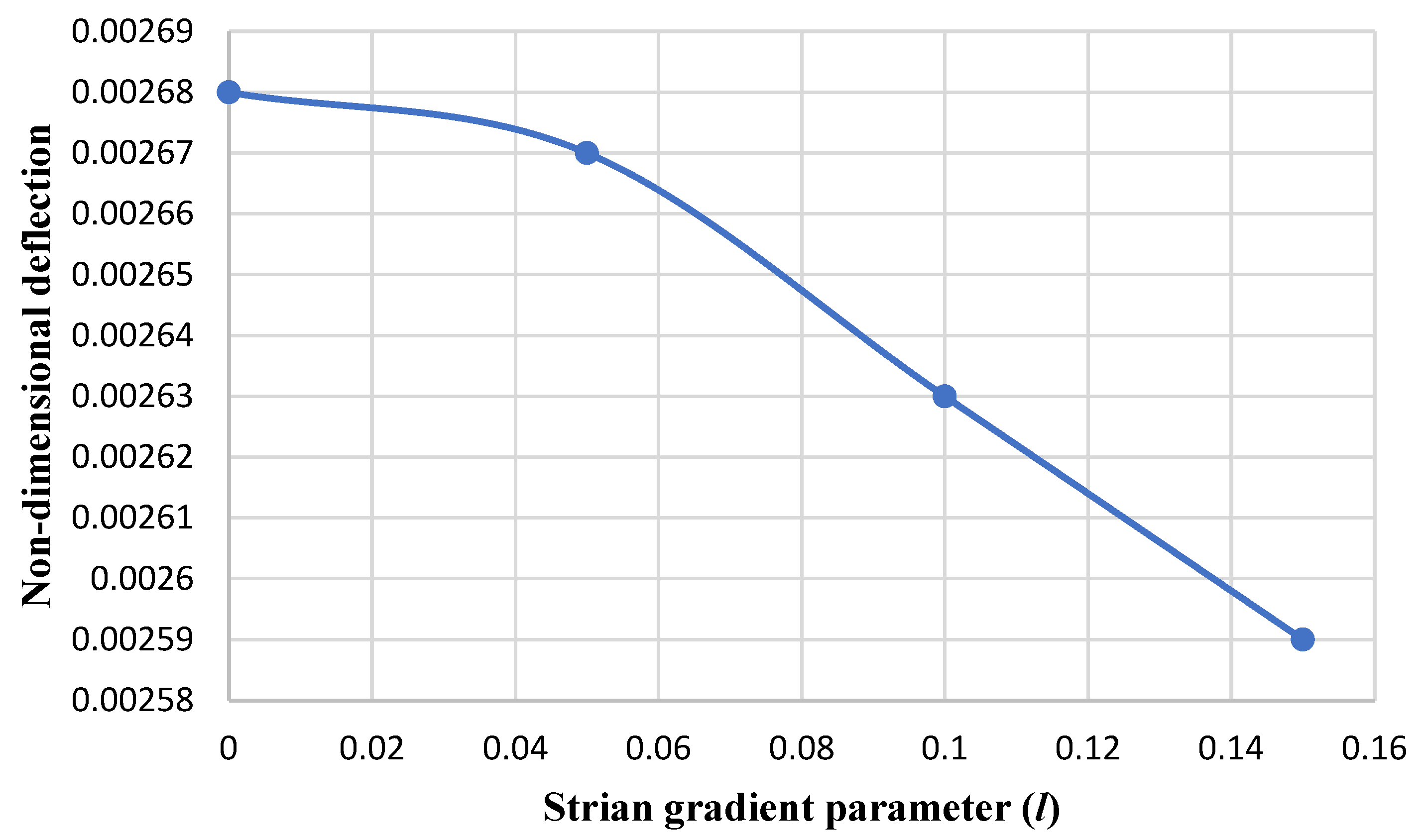
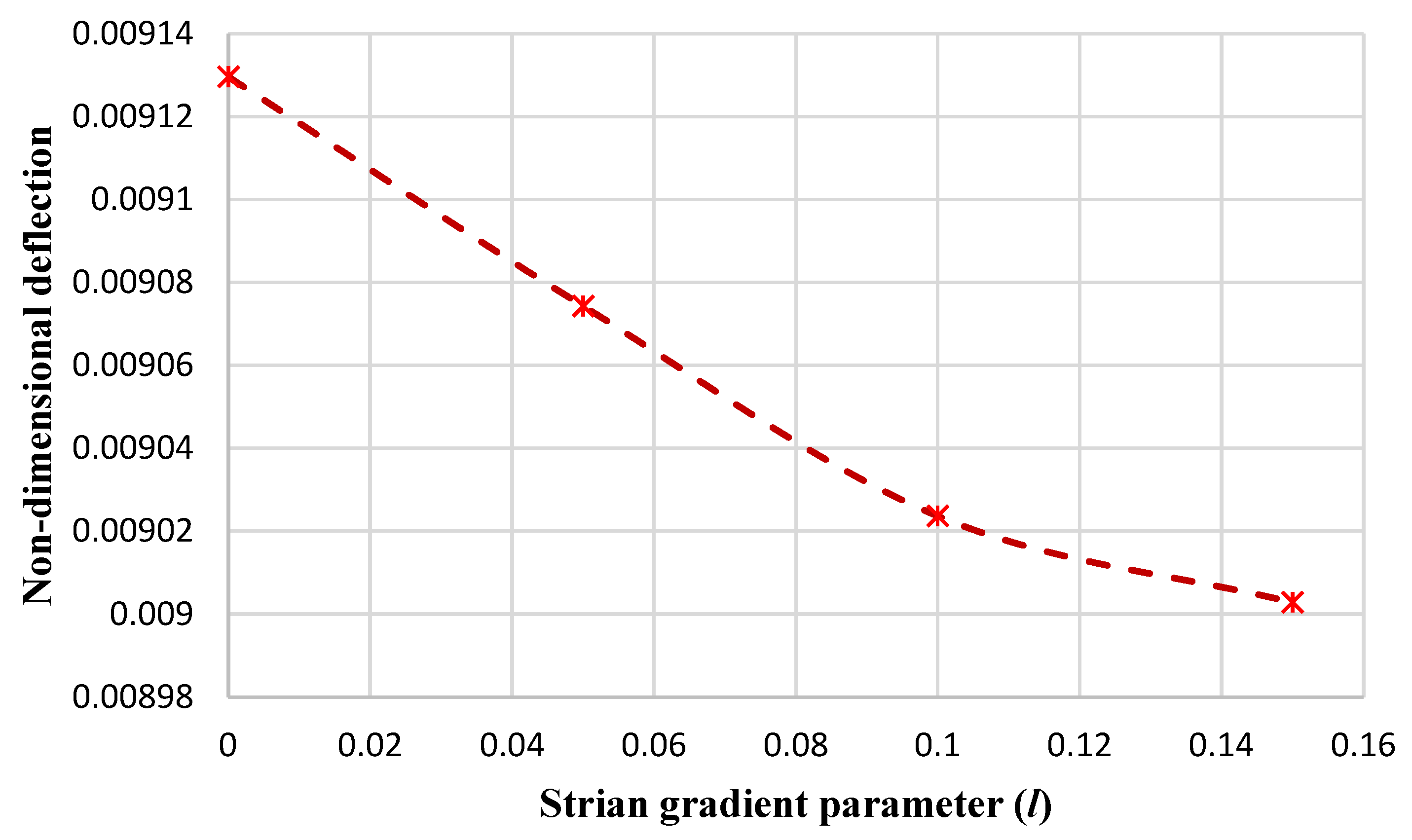
- With the increase in the strain gradient parameter, the nondimensional maximum deflection of the nanoplate decreases.
- ∗
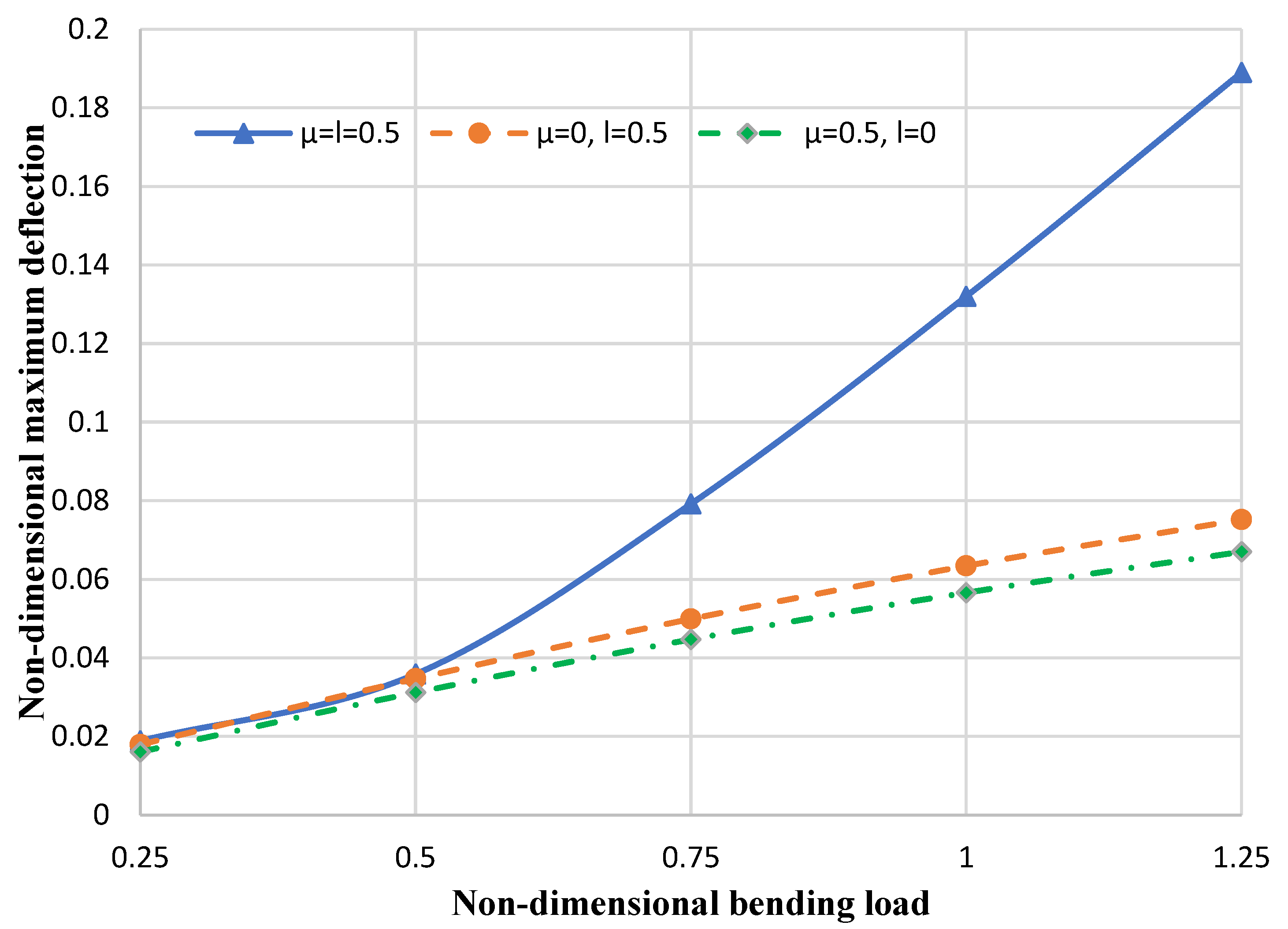
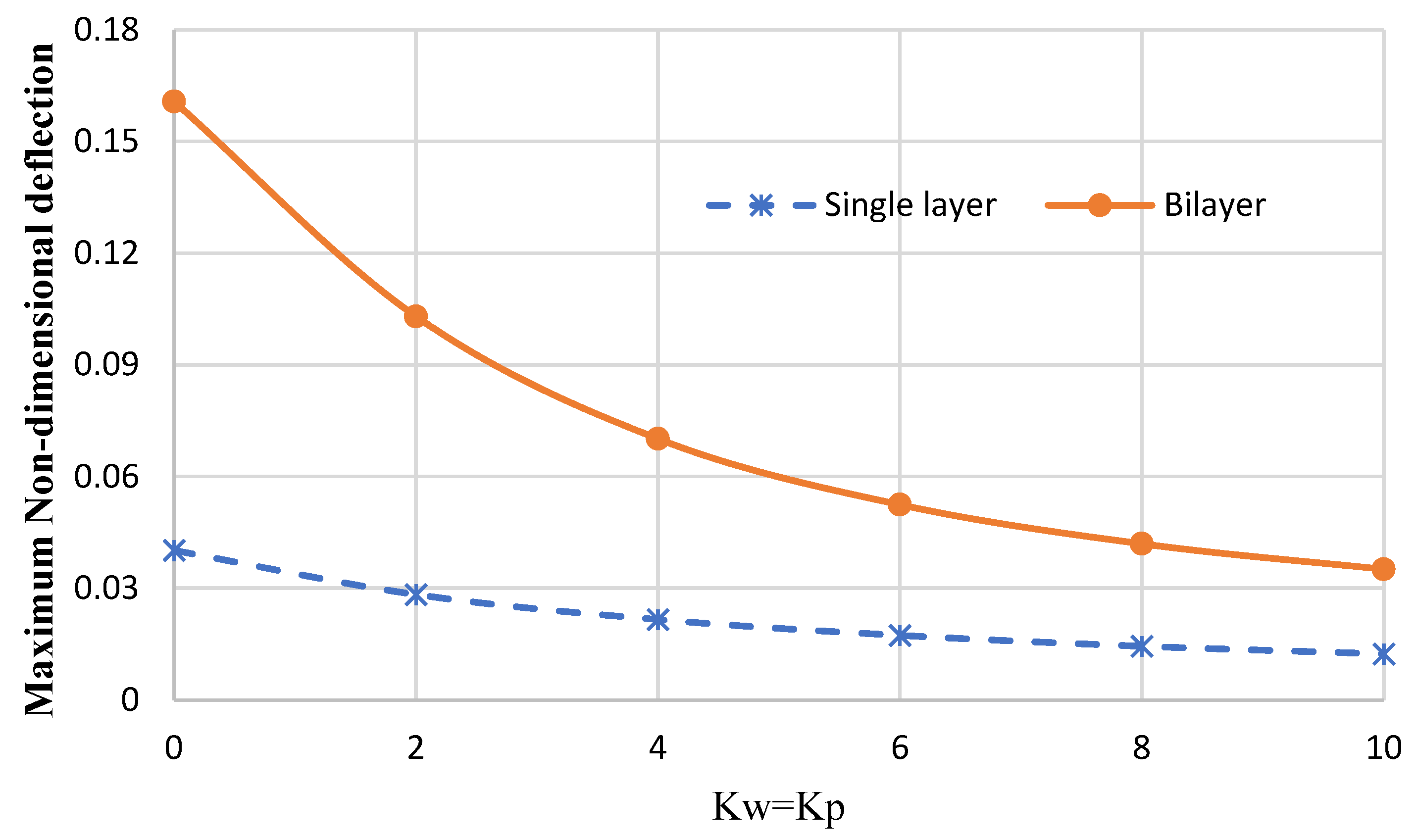
- Replacing a bilayer nanoplate (considering van der Waals forces between layers) with a single-layer nanoplate (which has the same equivalent thickness as the bilayer plate) is not possible when obtaining exact deflection results, especially when reducing the stiffness of the elastic foundations (or in higher bending loads). In addition, the single-layer nanoplate underestimates the deflection results of the bilayer nanoplate (with the same equivalent thickness as the single-layer nanoplate).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Xiao, Y.; Luo, F.; Zhang, Y.; Hu, F.; Zhu, M.; Qin, S. A Review on Graphene-Based Nano-Electromechanical Resonators: Fabrication, Performance, and Applications. Micromachines 2022, 13, 215. [Google Scholar] [CrossRef] [PubMed]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Thai, H.-T.; Vo, T.P.; Nguyen, T.-K.; Kim, S.-E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Su, Y.; Zhou, Z. Electromechanical Analysis of Flexoelectric Nanosensors Based on Nonlocal Elasticity Theory. Micromachines 2020, 11, 1077. [Google Scholar] [CrossRef]
- Gui, Y.; Wu, R. Buckling analysis of embedded thermo-magneto-electro-elastic nano cylindrical shell subjected to axial load with nonlocal strain gradient theory. Mech. Res. Commun. 2023, 128, 104043. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Gao, W.; Hui, D. Nonlinear dynamic stability analysis of axial impact loaded structures via the nonlocal strain gradient theory. Appl. Math. Model. 2023, 115, 259–278. [Google Scholar] [CrossRef]
- Mohammadian, M.; Hosseini, S.M. A size-dependent differential quadrature element model for vibration analysis of FG CNT reinforced composite microrods based on the higher order Love-Bishop rod model and the nonlocal strain gradient theory. Eng. Anal. Bound. Elem. 2022, 138, 235–252. [Google Scholar] [CrossRef]
- Penna, R.; Feo, L.; Lovisi, G. Hygro-thermal bending behavior of porous FG nano-beams via local/nonlocal strain and stress gradient theories of elasticity. Compos. Struct. 2021, 263, 113627. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Hoang-Le, M.; Sang-To, T.; Phan-Vu, P.; Wahab, M.A. Nonlocal strain gradient IGA numerical solution for static bending, free vibration and buckling of sigmoid FG sandwich nanoplate. Phys. B Condens. Matter 2022, 631, 413726. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Rabczuk, T. Static analysis of functionally graded anisotropic nanoplates using nonlocal strain gradient theory. Compos. Struct. 2019, 227, 111249. [Google Scholar] [CrossRef]
- Alghanmi, R.A. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials 2022, 15, 8601. [Google Scholar] [CrossRef] [PubMed]
- Arefi, M.; Kiani, M.; Rabczuk, T. Application of nonlocal strain gradient theory to size dependent bending analysis of a sandwich porous nanoplate integrated with piezomagnetic face-sheets. Compos. Part B Eng. 2019, 168, 320–333. [Google Scholar] [CrossRef]
- Bera, P.; Varun, J.P.; Mahato, P.K. Buckling analysis of isotropic and orthotropic square/rectangular plate using CLPT and different HSDT models. Mater. Today Proc. 2022, 56, 237–244. [Google Scholar] [CrossRef]
- Zhong, R.; Hu, S.; Wang, Q.; Qin, B.; Shuai, C. Legendre-meshfree vibration analysis of cross-ply laminated elliptical shell of revolution considering the effect of drop-off ply. Thin-Walled Struct. 2023, 182, 110293. [Google Scholar] [CrossRef]
- Sobhani, E.; Koohestani, M.; Civalek, Ö.; Avcar, M. Natural frequency investigation of graphene oxide powder nanocomposite cylindrical shells surrounded by Winkler/Pasternak/Kerr elastic foundations with a focus on various boundary conditions. Eng. Anal. Bound. Elem. 2023, 149, 38–51. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Phung, V.B. Static bending, free vibration, and buckling analyses of two-layer FGM plates with shear connectors resting on elastic foundations. Alex. Eng. J. 2023, 62, 369–390. [Google Scholar] [CrossRef]
- Padawale, N.; Patil, S.; Datar, G. Nonlinear vibration of annular radially graded plate subjected to temperature at one edge. Mater. Today Proc. 2023, 77, 991–1006. [Google Scholar] [CrossRef]
- Qin, X.; Shen, Y.; Chen, W.; Yang, J.; Peng, L.X. Bending and free vibration analyses of circular stiffened plates using the FSDT mesh-free method. Int. J. Mech. Sci. 2021, 202–203, 106498. [Google Scholar] [CrossRef]
- He, X.C.; Yang, J.S.; Mei, G.X.; Peng, L.X. Bending and free vibration analyses of ribbed plates with a hole based on the FSDT meshless method. Eng. Struct. 2022, 272, 114914. [Google Scholar] [CrossRef]
- Xu, L.-L.; Chen, C.-P.; Zheng, Y.-F. Two-degrees-of-freedom nonlinear free vibration analysis of magneto-electro-elastic plate based on high order shear deformation theory. Commun. Nonlinear Sci. Numer. Simul. 2022, 114, 106662. [Google Scholar] [CrossRef]
- Kharghani, N.; Guedes Soares, C. Application of layerwise HSDT and fracture analysis in the ultimate strength of composite plates with delamination in bending. Int. J. Solids Struct. 2022, 234–235, 111263. [Google Scholar] [CrossRef]
- Pavan, G.S.; Muppidi, H.; Dixit, J. Static, free vibrational and buckling analysis of laminated composite beams using isogeometric collocation method. Eur. J. Mech. A/Solids 2022, 96, 104758. [Google Scholar] [CrossRef]
- Rodrigues, D.E.S.; Belinha, J.; Dinis, L.M.J.S.; Natal Jorge, R.M. The bending behaviour of antisymmetric cross-ply laminates using high-order shear deformation theories and a Radial Point Interpolation Method. Structures 2021, 32, 1589–1603. [Google Scholar] [CrossRef]
- Zghal, S.; Dammak, F. Vibration characteristics of plates and shells with functionally graded pores imperfections using an enhanced finite shell element. Comput. Math. Appl. 2021, 99, 52–72. [Google Scholar] [CrossRef]
- Trabelsi, S.; Frikha, A.; Zghal, S.; Dammak, F. Thermal post-buckling analysis of functionally graded material structures using a modified FSDT. Int. J. Mech. Sci. 2018, 144, 74–89. [Google Scholar] [CrossRef]
- Zghal, S.; Trabelsi, S.; Frikha, A.; Dammak, F. Thermal free vibration analysis of functionally graded plates and panels with an improved finite shell element. J. Therm. Stress. 2021, 44, 315–341. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Large deflection response-based geometrical nonlinearity of nanocomposite structures reinforced with carbon nanotubes. Appl. Math. Mech. 2020, 41, 1227–1250. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Non-linear bending analysis of nanocomposites reinforced by graphene-nanotubes with finite shell element and membrane enhancement. Eng. Struct. 2018, 158, 95–109. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Zghal, S.; Joueid, N.; Tornabene, F.; Dimitri, R.; Chrigui, M.; Dammak, F. Time-Dependent Deflection Responses of FG Porous Structures Subjected to Different External Pulse Loads. J. Vib. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Frikha, A.; Zghal, S.; Dammak, F. Dynamic analysis of functionally graded carbon nanotubes-reinforced plate and shell structures using a double directors finite shell element. Aerosp. Sci. Technol. 2018, 78, 438–451. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Free vibration analysis of carbon nanotube-reinforced functionally graded composite shell structures. Appl. Math. Model. 2018, 53, 132–155. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Static analysis of functionally graded carbon nanotube-reinforced plate and shell structures. Compos. Struct. 2017, 176, 1107–1123. [Google Scholar] [CrossRef]
- Frikha, A.; Zghal, S.; Dammak, F. Finite rotation three and four nodes shell elements for functionally graded carbon nanotubes-reinforced thin composite shells analysis. Comput. Methods Appl. Mech. Eng. 2018, 329, 289–311. [Google Scholar] [CrossRef]
- Zghal, S.; Trabelsi, S.; Dammak, F. Post-buckling behavior of functionally graded and carbon-nanotubes based structures with different mechanical loadings. Mech. Based Des. Struct. Mach. 2022, 50, 2997–3039. [Google Scholar] [CrossRef]
- Zghal, S.; Frikha, A.; Dammak, F. Mechanical buckling analysis of functionally graded power-based and carbon nanotubes-reinforced composite plates and curved panels. Compos. Part B Eng. 2018, 150, 165–183. [Google Scholar] [CrossRef]
- Qaderi, S.; Ghadiri, M.; Najafi, M.; Imam, A.; Soleimanimehr, H. Size-dependent nonlinear vibration analysis of cracked graphene-platelets-reinforced-composites (GPLRC) plate under parametric excitation. Commun. Nonlinear Sci. Numer. Simul. 2023, 121, 107232. [Google Scholar] [CrossRef]
- Mahinzare, M.; Akhavan, H.; Ghadiri, M. A nonlocal strain gradient theory for rotating thermo-mechanical characteristics on magnetically actuated viscoelastic functionally graded nanoshell. J. Intell. Mater. Syst. Struct. 2020, 31, 1511–1523. [Google Scholar] [CrossRef]
- Rashidpour, P.; Ghadiri, M.; Zajkani, A. Low-velocity impact analysis of viscoelastic composite laminated nanoplate based on nonlocal strain gradient theory for different boundary conditions. J. Sandw. Struct. Mater. 2020, 23, 3194–3233. [Google Scholar] [CrossRef]
- Ghorbani, K.; Rajabpour, A.; Ghadiri, M.; Keshtkar, Z. Investigation of surface effects on the natural frequency of a functionally graded cylindrical nanoshell based on nonlocal strain gradient theory. Eur. Phys. J. Plus 2020, 135, 701. [Google Scholar] [CrossRef]
- Szekrényes, A. Application of differential quadrature method to delaminated first-order shear deformable composite plates. Thin-Walled Struct. 2021, 166, 108028. [Google Scholar] [CrossRef]
- Duryodhana, D.; Waddar, S.; Bonthu, D.; Pitchaimani, J.; Powar, S.; Doddamani, M. Buckling and free vibrations behaviour through differential quadrature method for foamed composites. Results Eng. 2023, 17, 100894. [Google Scholar] [CrossRef]
- Han, J.; Li, L.; Jin, G.; Ma, W.; Feng, J.; Jia, H.; Chang, D. Qualitative Identification of the Static Pull-In and Fundamental Frequency of One-Electrode MEMS Resonators. Micromachines 2018, 9, 614. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.L.; Li, S.; Li, Y.S. Bending of FGM sandwich plates with tunable auxetic core using DQM. Eur. J. Mech. A/Solids 2023, 97, 104838. [Google Scholar] [CrossRef]
- Ambartsumian, S. On the theory of bending plates. Izv. Otd. Tech. Nauk. AN SSSR 1958, 5, 69–77. [Google Scholar]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. Dec. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Reissner, E. On tranverse bending of plates, including the effect of transverse shear deformation. Int. J. Solids Struct. 1974, 11, 569–673. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Mantari, J.; Oktem, A.; Soares, C.G. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B Eng. 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.; Chen, X.; Liu, L.; Yu, Y.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Bellman, R.; Casti, J. Differential quadrature and long-term integration. J. Math. Anal. Appl. 1971, 34, 235–238. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Jabbarzadeh, M.; Aliabadi, S. Nonlinear static analysis of single layer annular/circular graphene sheets embedded in Winkler–Pasternak elastic matrix based on non-local theory of Eringen. Ain Shams Eng. J. 2016, 7, 873–884. [Google Scholar] [CrossRef]
- Altekin, M.; Yükseler, R.F. Large Deflection Analysis of Clamped Circular Plates. In Proceedings of the World Congress on Engineering, London, UK, 6–8 July 2011. [Google Scholar]
- Szilard, R. Theory and Analysis of Plates: Classical and Numerical Methods (Book); Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1974; p. 728. [Google Scholar]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959; Volume 2. [Google Scholar]


| Model | |
|---|---|
| Ambartsumian [47] | |
| Reddy [48] | |
| Reissner [49] | |
| Touratier [50] | |
| Soldatos [51] | |
| Aydogdu [52] | |
| Mantari [53] |
| q* | Ref. [58] | Ref. [60] | Ref. [59] | DQM Ref. [57] | SAPM Ref. [57] | Present (FSDT) | Present (g1) | Present (g2) | Present (g3) | Present (g4) | Present (g5) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0001 | 0.1678 | 0.1687 | 0.1706 | 0.168 | 0.1685 | 0.1685 | 0.1732 | 0.1801 | 0.1793 | 0.1789 | 0.1801 |
| 0.0003 | 0.4583 | 0.4655 | 0.5119 | 0.4588 | 0.4642 | 0.4642 | 0.471 | 0.4863 | 0.4843 | 0.4835 | 0.4863 |
| 0.001 | 1.0509 | 1.0937 | 1.7069 | 1.0514 | 1.0557 | 1.0557 | 1.0708 | 1.0929 | 1.0899 | 1.0887 | 1.0929 |
| α = h/ro | Theory | μ = 0 | μ = 1 | μ = 2 | μ = 3 | μ = 4 |
|---|---|---|---|---|---|---|
| 0.05 | FSDT | 0.09482 | 0.08832 | 0.08238 | 0.07706 | 0.07231 |
| HSDT-g1(z) | 0.09413 | 0.08754 | 0.08145 | 0.07603 | 0.07125 | |
| HSDT-g2(z) | 0.09413 | 0.08753 | 0.08145 | 0.07603 | 0.07126 | |
| HSDT-g3(z) | 0.09412 | 0.08752 | 0.08144 | 0.07604 | 0.0713 | |
| HSDT-g4(z) | 0.09413 | 0.08754 | 0.08145 | 0.07604 | 0.07128 | |
| HSDT-g5(z) | 0.09413 | 0.08754 | 0.08145 | 0.076 | 0.07126 | |
| 0.1 | FSDT | 0.06384 | 0.05277 | 0.04528 | 0.03973 | 0.03541 |
| HSDT-g1(z) | 0.06310 | 0.05157 | 0.04403 | 0.03855 | 0.03433 | |
| HSDT-g2(z) | 0.06311 | 0.05156 | 0.04402 | 0.03855 | 0.03432 | |
| HSDT-g3(z) | 0.06312 | 0.05157 | 0.04403 | 0.03854 | 0.03433 | |
| HSDT-g4(z) | 0.06310 | 0.05156 | 0.04401 | 0.03855 | 0.03432 | |
| HSDT-g5(z) | 0.06311 | 0.05155 | 0.044 | 0.03854 | 0.03433 | |
| 0.3 | FSDT | 0.00515 | 0.00429 | 0.00368 | 0.00323 | 0.00287 |
| HSDT-g1(z) | 0.00494 | 0.00386 | 0.00316 | 0.00268 | 0.00232 | |
| HSDT-g2(z) | 0.00494 | 0.00385 | 0.00316 | 0.00268 | 0.00233 | |
| HSDT-g3(z) | 0.00495 | 0.00386 | 0.00317 | 0.00267 | 0.00231 | |
| HSDT-g4(z) | 0.00493 | 0.00385 | 0.00315 | 0.00266 | 0.00234 | |
| HSDT-g5(z) | 0.00495 | 0.00386 | 0.00317 | 0.00268 | 0.00233 |
| α = h/ro | Theory | μ = 0 | μ = 1 | μ = 2 | μ = 3 | μ = 4 |
|---|---|---|---|---|---|---|
| 0.05 | FSDT | 0.09956 | 0.09710 | 0.09365 | 0.08989 | 0.08610 |
| HSDT-g1(z) | 0.09960 | 0.09703 | 0.09338 | 0.08945 | 0.08557 | |
| HSDT-g2(z) | 0.09959 | 0.09703 | 0.09337 | 0.08941 | 0.08556 | |
| HSDT-g3(z) | 0.09961 | 0.09702 | 0.09338 | 0.08944 | 0.08565 | |
| HSDT-g4(z) | 0.09960 | 0.09703 | 0.09337 | 0.08945 | 0.08556 | |
| HSDT-g5(z) | 0.09961 | 0.097 | 0.09336 | 0.08556 | 0.08945 | |
| 0.1 | FSDT | 0.09391 | 0.08401 | 0.07546 | 0.06814 | 0.06190 |
| HSDT-g1(z) | 0.09389 | 0.08352 | 0.07493 | 0.0677 | 0.06176 | |
| HSDT-g2(z) | 0.0939 | 0.08353 | 0.07492 | 0.06778 | 0.06177 | |
| HSDT-g3(z) | 0.09389 | 0.0835 | 0.07493 | 0.06778 | 0.06177 | |
| HSDT-g4(z) | 0.0938 | 0.08352 | 0.07494 | 0.06824 | 0.06178 | |
| HSDT-g5(z) | 0.09389 | 0.08351 | 0.07493 | 0.06778 | 0.06177 | |
| 0.3 | FSDT | 0.01623 | 0.01309 | 0.01079 | 0.00918 | 0.00806 |
| HSDT-g1(z) | 0.01597 | 0.01274 | 0.0106 | 0.00912 | 0.00801 | |
| HSDT-g2(z) | 0.01598 | 0.01274 | 0.01063 | 0.0091 | 0.008 | |
| HSDT-g3(z) | 0.01599 | 0.01273 | 0.01064 | 0.00913 | 0.00801 | |
| HSDT-g4(z) | 0.01596 | 0.01272 | 0.01062 | 0.00912 | 0.00799 | |
| HSDT-g5(z) | 0.01598 | 0.01274 | 0.01063 | 0.00913 | 0.008 |
| μ | g1 (HSDT) | g2 (HSDT) | g3 (HSDT) | g4 (HSDT) | g5 (HSDT) |
|---|---|---|---|---|---|
| 0 | 0.00488 | 0.00488 | 0.00487 | 0.00487 | 0.00488 |
| 1 | 0.00379 | 0.0038 | 0.0038 | 0.00378 | 0.00379 |
| 2 | 0.00311 | 0.00311 | 0.0031 | 0.0031 | 0.00309 |
| 3 | 0.00263 | 0.00263 | 0.0026 | 0.00262 | 0.00263 |
| 4 | 0.00227 | 0.00228 | 0.00228 | 0.00229 | 0.00228 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghian, M.; Palevicius, A.; Janusas, G. Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate. Micromachines 2023, 14, 1052. https://doi.org/10.3390/mi14051052
Sadeghian M, Palevicius A, Janusas G. Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate. Micromachines. 2023; 14(5):1052. https://doi.org/10.3390/mi14051052
Chicago/Turabian StyleSadeghian, Mostafa, Arvydas Palevicius, and Giedrius Janusas. 2023. "Nonlocal Strain Gradient Model for the Nonlinear Static Analysis of a Circular/Annular Nanoplate" Micromachines 14, no. 5: 1052. https://doi.org/10.3390/mi14051052





