Next Article in Journal
A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism
Next Article in Special Issue
Design of Wideband FMCW Radar Transceiver System Using Photonic Elements
Previous Article in Journal
Study of Rotation Speed Curve Optimization under the Three-Body Coupling Grinding Mode
Previous Article in Special Issue
A Review of Photonic Sensors Based on Ring Resonator Structures: Three Widely Used Platforms and Implications of Sensing Applications
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Micromachines
Volume 14
Issue 6
10.3390/mi14061116
micromachines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Three-Dimensional Modeling of the Optical Switch Based on Guided-Mode Resonances in Photonic Crystals

by
Atiq Ur Rehman
1,
Yousuf Khan
1,*,
Muhammad Irfan
1,
Shahzaib Choudri
1,
Svetlana N. Khonina
2,3,
Nikolay L. Kazanskiy
2,3 and
Muhammad A. Butt
2
1
Nanophotonics Research Group, Department of Electronic Engineering, Balochistan University of Information Technology, Engineering and Management Sciences, Quetta 87300, Pakistan
2
Department of Technical Cybernetics, Samara National Research University, 443086 Samara, Russia
3
IPSI RAS-Branch of the FSRC “Crystallography and Photonics” RAS, 443001 Samara, Russia
*
Author to whom correspondence should be addressed.
Micromachines 2023, 14(6), 1116; https://doi.org/10.3390/mi14061116
Submission received: 16 April 2023 / Revised: 19 May 2023 / Accepted: 24 May 2023 / Published: 26 May 2023
(This article belongs to the Special Issue Photonic and Optoelectronic Devices and Systems)
Browse Figures
Versions Notes

Abstract

:
Optical switching is an essential part of photonic integrated circuits and the focus of research at the moment. In this research, an optical switch design working on the phenomenon of guided-mode resonances in a 3D photonic-crystal-based structure is reported. The optical-switching mechanism is studied in a dielectric slab-waveguide-based structure operating in the near-infrared range in a telecom window of 1.55 µm. The mechanism is investigated via the interference of two signals, i.e., the data signal and the control signal. The data signal is coupled into the optical structure and filtered utilizing guided-mode resonance, whereas the control signal is index-guided in the optical structure. The amplification or de-amplification of the data signal is controlled by tuning the spectral properties of the optical sources and structural parameters of the device. The parameters are optimized first using a single-cell model with periodic boundary conditions and later in a finite 3D-FDTD model of the device. The numerical design is computed in an open-source Finite Difference Time Domain simulation platform. Optical amplification in the range of 13.75% is achieved in the data signal with a decrease in the linewidth up to 0.0079 µm, achieving a quality factor of 114.58. The proposed device presents great potential in the field of photonic integrated circuits, biomedical technology, and programmable photonics.

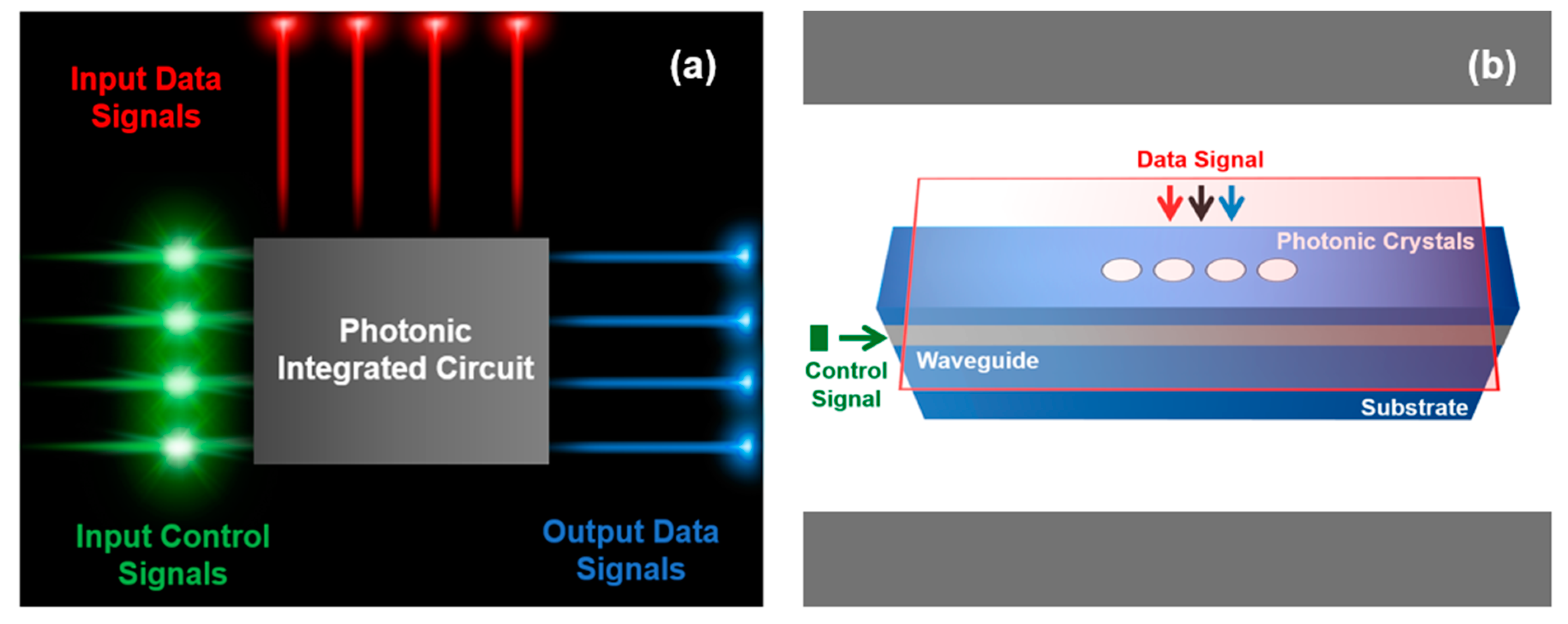
1. Introduction

Photonic technology has undergone a boost in the last couple of decades and has come forward to replace electronic technology in various applications due to its power efficiency and ability to operate in Terahertz (THz) frequency ranges. Specifically, the optical integrated components such as switches [1], modulators [2], multiplexers [3], logic gates [4,5], and filters [6], which play an essential role in an optical integrated circuit, have become the center of research nowadays. Researchers are busy digging down the architecture and topology of photonic integrated circuits (PICs), keeping in view the process-related complexity, performance, and fabrication as a whole. Considering optical technology as the best alternative to electronic technology [7], the optical fields are brought together to use different phenomena such as interference [8], guided-mode resonances (GMR) [9], the Kerr effect [10], and many more [11]. Moreover, the proper choice of materials is a key factor in designing these optical devices. Therefore, among periodic nanostructures, photonic crystals (PhCs) have recently brought us a step closer to the achievement of optical integrated circuits. These PhCs are periodic dielectric nanostructures that are capable of controlling light at the wavelength scale [12]. The concept of the PhCs is derived from nature, presenting themselves on the bodies of different living organisms, i.e., insects, parrots, peacocks, and stones [13]. They exhibit different phenomena of light in terms of reflection, refraction, diffraction, and total internal reflection [14]. PhCs can be created artificially to design, produce, and achieve what is required of a certain component or a device in the real world [15].
Considering the components of a PIC, an optical switch is an important element that can work analogous to the electronic transistor in electronic integrated circuits. Therefore, utmost efforts are made to achieve the functions of optical switching elements using the time domain [16] or frequency domain [17], with different topologies in the form of cross waveguide geometries [18], quantum dots [19], optoelectronic hybrid devices [20], ring resonators [21], combined configurations of thermodynamics and optical components [22], and the utilization of transparent and active materials [23,24], with its desired function and implementation in optical circuits. Therefore, a 2D-FDTD design of an optical switch is investigated in [25], utilizing the phenomenon of GMR with varying radius cavities implemented at the start of the PhC-mesh. Another approach uses GMR modes to achieve optical switching using the changeable radius cavity within the middle of the PhC-mesh [26,27]. An optical switch using two linear waveguides and a circular geometry of the PhCs is studied in [28], using temperature as the variable quantity for the switching mechanism in terms of a shift in the resonance wavelength. The use of broken mirror symmetry to obtain asymmetric Fano-shapes is described in [29], utilizing partially transmitting material within the waveguide to propose an optical switching device and its prospects [30]. A four-port optical switch is investigated in [31], using the square lattice of the PhCs and rods of gallium phosphide with a medium composed of air; metallic embedding nanowires [32], the use of the Finite Difference Time Domain (FDTD) approach, and a thermo-optic effect with a super-ellipse shape [33] have also been studied. A similar idea is perceived in [34], using the plane-wave expansion (PWE) approach to estimate the bandgap of an optical switching device with a discussion of its applications in optical comparators [35]. Based on the design of the 2D PhC-cavity structure and its transmission spectra, an optical switching device is investigated by using the Kerr effects to produce a shift in its resonant wavelength given in [36]; the use of III-V nanowires on a silicon (Si) platform for the purpose [37], strong carrier-induced nonlinearity [38], defect rods made of doped glass [39], linear PhCs [40], and a non-linear cavity coupled to input and output of the waveguide [41] have also been studied.
Similarly, using quantum dots (QDs) to observe the mechanisms of optical switching and achieve higher rates of transmittance and flat bandwidth using latch function is premediated in [42], and are utilized through a Symmetric Mach Zehnder (SMZ) for the purpose in [43]. Plasmonics effects are exploited for optical switching by applying a strip of a graphene layer onto a structure of PhCs in [44], and the mechanism is investigated using graphene rods in [45]. An approach of using concepts of mott phase change material in PhC-based structures responsible for the shifting of the optical bandgap is investigated in [46], and polymer waveguides with high thermos-optic and electro-optic properties are used in in [47]. Similarly, a 3D Si-opal composite is reported in [48], with a pump-probe technique in [49], and 1D graphene-based plasmonics crystals are used in [50] to efficiently determine the effects of optical switching. In addition, using two PhC cavities within one arrangement is reported in [51], using a waveguide between them. Thus, coupling a probe signal in the waveguide affects the field distribution and quality factor of both of the PhC-cavities, enabling the structure to be comprehended as an optical switch. Soft PhCs in the form of chiral liquid crystals are also used to obtain certain properties of the optical switch, as described in [52], while are obtained through effects of physics in terms of parity–time symmetry and topological insulators in [53], and by using phase change nanomaterials [54], air-trench [55] and carrier diffusion and recombination processes in PhCs [56], with the design based on 3D Micro-Electro-Mechanical-Systems (MEMS) reported in [57].
This research investigates the design of a 3D-optical switch working in the near-infrared region (NIR), suitable for communication systems. Moreover, the design is implemented using the 3D-FDTD domain and the interference phenomenon between the GMR modes and index-guided modes inside a slab-waveguide PhC structure. For this purpose, the proposed device uses two optical signals, i.e., data and control. The data signal is integrated into the optical structure utilizing the out-of-plane method, i.e., GMR, and is amplified or de-amplified using a control signal, which is index-guided into the slab-waveguide structure. Figure 1a imitates the theoretic 3D structure of the optical switch, presenting an innovative, compact, easy-to-fabricate, and implementable device. Likewise, due to the lower absorption of dielectric materials, they are suitable for broad spectral ranges; in contrast, semiconductors have higher material costs and absorption levels, making their use and fabrication difficult in densely populated optical integrated circuits, as investigated in previous studies. Figure 1b illustrates the use of the proposed optical switch in an optical integrated circuit. Therefore, it can find applications in the field of optical integrated components, filters, sensors, quantum computing, and communication systems.

2. Simulation Approach

The 3D-FDTD simulation of the proposed structure is performed using the MIT Electromagnetic Equation Propagation (MEEP) software [58], an open-source platform, based on the FDTD domain [59]. Therefore, during execution, the desired arrangement is initially transformed into a finite-arrangement of grids, known as YEE grids [60], to compute the Electric ‘E’ field and Magnetic ‘B’ field based on Maxwell’s equations. Moreover, FDTD is advantageous in terms of computing the response of the system in a single run (using a short Gaussian pulse), providing the user with the propagation of the wave both in the near-field and far-field, especially inside complex structures such as PhCs [61]. Apart from these advantages, it requires fewer computational resources, less memory, and less time as compared to frequency-domain-based simulations [62].

3. Designing Parameters

The optimized designing parameters of the proposed 3D-optical switch are given in Table 1 in terms of lattice-constant ‘a’ chosen as (a = 1 µm), serving two purposes, i.e., to enable the design of the device scalable to any range of wavelength and enable its operation in the telecommunication window around 1.55 µm, using cylindrical-shaped-based PhC elements filled with air having a refractive index of nair = 1.
Figure 2 imitates the design of the proposed 3D-optical switch using niobium pentaoxide (Nb2O5) as the waveguiding material, with a refractive index of nwav = 2.2 [25], which is deposited on a substrate made up of silicon dioxide (SiO2) with a refractive index of nsub = 1.5 [27], along a cladding layer of the SiO2 placed on the topmost side of the waveguiding layer. Moreover, it represents the strip model of the 3D-optical switch, based on which, the investigations are performed and two finite models are computed in the end.
For the data signal, a Gaussian time profile source is used, located at a range of 2.7a above the waveguide, with a similar profile source for the control signal index guided in the optical structure from the lateral side using a user definite sum of frequencies ‘nf’ as (nf = 550) for both of the sources. Similarly, the transmission and reflection monitoring layers are positioned at a range of 1.0a below and above the waveguide, respectively, to compute the electromagnetic (EM) fields. For the purpose of terminating the simulation process, a field decay monitoring point is positioned at a user-definite distance of 1.5a. To observe the behavior and prevent back-and-forth of the EM fields at the boundaries of the structure, the Perfectly Matched Layers (PML) are implemented along the x-z axes. Moreover, to save time and computational resources, the periodic boundary condition (PBC) is used on the y-axis. However, the condition of the PBC is removed and is replaced by PML during the simulation of the finite structures of the 3D-optical switch.

4. Results

The 3D-FDTD simulation of the optical switch is performed in this research using the stripe model criterion. For this purpose, the first step is determining the number of PhC elements using a single source, i.e., the data signal only, to tune the GMR modes around the resonant wavelength, i.e., 1.55 µm. For this purpose, Figure 3a imitates the output reflection spectra of the structure comprising two and four PhC elements. Therefore, it can be seen that the structure based on two PhC elements has a higher intensity of reflection peaks, as compared to the four-PhC-element-based structure. However, it is worth noting from the output spectra that the resonant wavelength of the two-PhC-element-based arrangement is around 1.528 µm, while is at 1.547 µm in the four-PhC-element-based structure. Similarly, Figure 3b,c and Figure 3d,e show the Electric ‘E’ and Magnetic ‘B’ fields’ confinement in the structures comprising two and four PhC elements, respectively.
Therefore, comparing the arrangements based on the number of PhCs, the two-PhC-based structure has the advantage of coupling the GMR modes more efficiently, which is due to the lesser change in the effective refractive index of the waveguide. However, the modes are not confined to the required resonant wavelength of the device. In contrast, the four-PhC-based arrangement having a higher number of PhCs elements produces lower values of reflection peaks due to changes in the refractive index of the waveguide and an increased fill factor (air) inside the optical structure, resulting in lower intensities. However, the increase in the number of PhC elements does produce confined GMR modes near the resonant wavelength of the device. This can be attributed to the increased phenomenon of interference between the incident modes and the leaky modes inside the optical device. Table 2 presents detailed comparisons between the two- and four-PhC-based structures in terms of resonant wavelength, the percentage of reflection peak, linewidth, and quality factor, i.e., calculated by using Equation (1):
Q u a l i t y   f a c t o r = r e f l e c t i o n   p e a k / l i n e w i d t h
Apart from the change in reflection peaks and resonant wavelength, there is a visible difference in the linewidth and the quality factor between these two structures. Corresponding to the linewidth, it remains low in the two-PhC-element-based arrangement and is a bit on the higher side in the four-PhC-element-based structure. Similarly, the quality factor is higher in the former structure, and vice versa. However, each arrangement possesses its pros and cons, which can be entangled during the design of the 3D-optical switch. As an acknowledgeable fact, the number of PhC elements can be increased, as it may create more confined GMR modes using data signal only, but it is limited to four PhC elements only, due to the fact that it will in turn reduce the outcomes of the control signal on the output of the data signal. In other words, it will reduce the switching properties of the device equivalent to the depletion region of the electronic transistor. Apart from these, further structuring in the 3D domain relating to an increase in the number of PhC elements is also limited by the computational resources in terms of speed and memory. As a result, achieving the unity factor in the output spectra is hindered. Similarly, the propagation losses incurred by the control signal due to gratings also contribute to this and are added to the absorption losses of the materials. Henceforth, both of the arrangements are investigated in relation to the operations of optical switching, resulting in two 3D finite structures of the device i.e., based on two and four PhC elements in the end.

4.1. Study of Optical Switching Phenomenon by Changing the Number of PhC Elements Using Data and Control Signals Simultaneously

To investigate the phenomena of the optical switching in 3D PhC-element-based structures, i.e., two and four PhC elements, the control signal is executed along with the data signal. Moreover, the wavelength of the control signal is also varied to investigate its detailed response on the output of the data signal. Table 3 shows the criterion used in changing the wavelength of the control signal with regard to the data signal.
The effects of the control signal are given in the reflection spectra of the two-PhC-element-based structure in Figure 4a. It investigates the increase in the percentage of the reflection peaks as the wavelength of the control source is varied from 1.67 µm to 1.55 µm and vice versa. Therefore, it studies a prominent change in the control source at a wavelength of 1.55 µm. Figure 4b illustrates the alteration in the linewidth of the structure as the wavelength of the control signal is varied, reporting the lowest value of 0.0079 µm at a wavelength of 1.60 µm. Figure 4c probes the quality factor of the structure, achieving a maximum value of 112 at a wavelength of 1.60 µm of the control signal. Thus, the GMR modes are confined and offer higher selectivity for the two-PhC-element-based structure.
Similarly, Figure 5a investigates the four-PhC-element-based structure for optical switching action. Therefore, it can be seen that implementing the control signal along the data signal increases the coupling of the GMR modes and energy further into the optical structure, and as a result, reaches nearer to the desired resonant wavelength of the structure, i.e., 1.55 µm. Moreover, it achieves higher percentages of reflection spectra when the wavelength of the control signal is varied from 1.67 µm to 1.55 µm and is maximum when this wavelength is equivalent to the wavelength of the data signal, i.e., 1.55 µm. Figure 5b imitates the variation in the linewidth of the structure based on four PhC elements, achieving a minimum value of around 0.0149 µm at a wavelength of 1.67 µm of the control signal. Figure 5c reports the variation in the quality factor with regard to change in the wavelength of the control signal. Therefore, it can be concluded that the structure achieves the maximum value of quality factor, i.e., 49.28, at a 1.67 µm wavelength of the control signal. Therefore, the optimum figure of the wavelength of the control signal is 1.60 µm and 1.67 µm for the two- and four-PhC-element-based structures, respectively. Table 4 shows the detailed responses of both of the topologies in terms of resonant wavelength, reflection, linewidth, and quality factor.
Correspondingly, the phenomenon which is responsible for the change in the output of the data signal is due to non-linear optical effects. Elaborating upon the non-linear effects, when a data signal and the control signal are coupled into the optical structure comprising the PhC elements, the frequency of the output signal is doubled, which in turn helps in the amplification of the data signal of the optical device and occurs when there are higher-order modes in the E field. Apart from these, the effects depend on other factors as well, i.e., the propagation of the wave in the medium, second harmonic generations, and conservation laws for photons. Therefore, the non-linearity factor of the device leads to the generation of the new frequency components and, as a result, leads to the amplification of the data signal. Moreover, it is worth noting here that as the frequency of the control signal is increased, it results in the amplification of the data signal in an ascending order. However, the applied frequency of the control signal, i.e., 1.60 µm, produces a narrower linewidth and highest quality factor in both of the cases of the PhC-based structures. This can be attributed to the resonance factor of all the frequencies in the structure inducing the GMR modes and coupling of energy further into the optical structure. Considering the highest percentage of amplification achieved, with an applied frequency of the control signal of 1.55 µm, the linewidth is wider and the quality factor is lower for this case. Although the frequency of both sources, i.e., data and control, are the same, due to the non-linear nature of the device, this leads to a degrading linewidth and quality factor of the device. Henceforth, by applying the control signal, the linewidth of the device is narrowed and the quality factor is increased, helping in the enhancement of the GMR modes, the coupling of energy, and the selectivity of the device.

4.2. Finite Structures of the 3D-Optical Switch Based on Two and Four PhC Elements

The next step is to investigate and draw finite structures of the 3D-optical switch by removing the PBC, previously implemented on the y-axis, in the case of the striped model. Moreover, instead, the PML is executed on all of the three axes for the finite realization of the device. For this purpose, the two-PhC-element-based structure is realized first, as shown in Figure 6a–c, depicting the length, width, and height of the device.
Therefore, for the optical switching mechanism, the structure is simulated using data and control signals simultaneously, with reflection and transmission spectra imitated in Figure 6d. So, it can be shown from the spectra that by implementing the control signal and varying its wavelength from 1.67 µm to 1.55 µm, the output of the data signal tends to increase and vice versa, thus, helping in the confinement of GMR modes and energy. However, it is worth noting here that the intensity and coupling of energy of the resonant modes is lower to a certain degree in comparison to the infinite striped model of the two-PhC-element-based structure. Henceforth, it can be increased and the desired level can be achieved by increasing the number of PhC elements along the y-axis, which is limited by the computational resources at present. Figure 6e,f, show the field confinement of the structure along the x and y directions, and Figure 6g depicts the intensity and confinement of the data signal only on the surface of the structure.
Similarly, the structure of the 3D-optical switch based on the arrangement of the four PhC elements is imitated in Figure 7a–c, reporting the length, width, and height of the finite model, respectively. Moreover, the optical switching action is shown in Figure 7d using the reflection and transmission spectra of the structure, executing the control signal with a varying wavelength in the range, i.e., 1.67–1.55 µm along the data signal simultaneously. Therefore, it can be seen that increasing the units of PhC elements increases the confinement of the GMR modes and coupling of energy further into the optical device. However, the increase in the number of the PhC elements (x-axis) has been reported to have adverse effects on the optical switching properties of the device. Therefore, the number of PhC elements is limited to four only, according to this research. Moreover, to increase the coupling and confinement of the GMR modes, the number of PhC elements can be increased along the y-axis, which will result in the reduction in the compactness of the device as a whole. Similarly, the field confinement by the structure along the x and y directions is shown in Figure 7e,f, with Figure 7g depicting the intensity of the data signal only on the surface of the optical structure.
The designed optical switching device can be used in a number of applications relating to the control and utilization of light. One specific application of the device is in the field of biotechnology, i.e., testing the numerous components in the blood. This can be achieved as the device will produce spectra of different intensities and values, beneficial in determining its composition. In this case, if the intensity of a specific component is lower than the threshold value, it can be enhanced by the execution of the control signal for this purpose. Similarly, the same phenomena of testing can be utilized to investigate the different components of water as well, as safe for drinking and as recommended by the World Health Organization (WHO). Moreover, considering communication systems, the designed device can be used as an amplification device, acting as a repeater and helping in the overall transmission of optical data over long-haul communications.

5. Discussion

The modeling of a 3D-optical switch is still an innovative idea, having qualities such as compactness, ease of fabrication, and being implementable in PICs. Therefore, an optical switching idea presented in [25] uses a control signal for the amplification of the data signal in numeral structures composed of a variable number of PhC elements. Moreover, another structure of the optical switch, as presented in [25,26], uses 11 PhC elements along with a variable PhC cavity realized at the start of the PhC mesh to modulate the GMR modes. Apart from these, a variable PhC cavity along the outcomes of the control signal on the output of the data signal and tunning of the GMR modes are modeled in [27]. To achieve efficient optical switching, different PhC-element-based structures are used. However, one common path is followed in all of these investigations, i.e., using the 2D simulation domain. Apart from these, optical switching is reported in [63], using the plasmonics characteristics of graphene having a Si-core-based waveguide. The refractive index of the graphene clad is varied with a low-intensity pulse, in contrast, which modifies the characteristics of the device, and as an outcome, the aspects of the optical switch are achieved. Table 5 reports the details of the previous studies in comparison with the current research.

6. Proposed Fabrication Process

The proposed optical switching device can be realized using the conventional fabrication techniques used for optical integrated components, as shown in Figure 8. In the first step, Plasma-Enhanced Chemical Vapor Deposition (PECVD) can be used for the deposition of SiO2 to form the base of the structure [64]. In the second step, the waveguiding layer, i.e., Nb2O5, can be deposited over the layer of SiO2 using the method of Ion Beam Sputtering Deposition (IBSD) [65]. In the last step, an array of PhC elements can be structured using the Focused Ion-Beam (FIB) platform [66].

7. Conclusions

In this study, a 3D-FDTD depiction of an optical switch is investigated. The switching action is studied by utilizing two sources, namely the data signal and the control signal in a dielectric slab-waveguide structure having an array of PhC elements. The data signal is coupled into the device using GMR, which filters the data signal at the same time, while the control signal is index-guided into the optical structure, which is responsible for the optical switching and amplification of the data signal. The switching and amplification operation is fine-tuned by varying the central wavelength of the control and structural parameters of the device. The structural specifications of the device are optimized in terms of the radius and number of periods of the PhCs, i.e., two PhC elements and four PhC elements (along the x-axis). Likewise, two topologies are used, i.e., structuring of the device using an infinite modeling mechanism, where a specific chunk of the device (along the y-axis in this research) is repeated using the condition of PBC, to save time and computational resources. Secondly, a finite modeling mechanism is used, where a finite structure is concluded based on the results of the infinite structuring mechanism. Therefore, in the case of the arrangement composed of two PhC elements, it produces pronounced effects of optical switching with high peaks in reflection spectra, narrow linewidth, and high-quality factor. However, it is not very effective in achieving the required resonant wavelength of the device. Similarly, implementing the four-PhC-element-based structure achieved the lower coupling of energy having a wider linewidth and decreased quality factor as compared to the two-PhC-element-based structure. However, the device can efficiently achieve optical switching at the desired wavelength range of the device, i.e., 1.55 µm. As a result, an amplification of about 13.75% with a linewidth of 0.0079 µm and a quality factor of 114.58 is attained. Considering the cases of finite modeling, i.e., two PhC elements and four PhC elements (along the x-axis), the expected results of the infinite structuring mechanism have been reported. The design can be improved further by increasing the units of the PhC elements (along the y-axis), which is currently limited by the computational resources. Henceforth, the proposed design can be efficiently used in the fields of PICs, communications systems, biomedical sensors, and programmable photonics.

Author Contributions

Conceptualization, A.U.R., Y.K., M.I., S.C., S.N.K., N.L.K. and M.A.B.; methodology, A.U.R., Y.K., S.C. and M.A.B.; software, A.U.R., Y.K., S.C. and M.I.; validation, A.U.R., Y.K., M.I., S.N.K., N.L.K. and M.A.B.; formal analysis, A.U.R., Y.K., M.I., S.C. and M.A.B.; investigation, A.U.R., Y.K., M.I., S.C. and M.A.B.; resources, A.U.R., Y.K. and M.A.B.; data curation, A.U.R., N.L.K., Y.K., S.C. and M.A.B.; writing—original draft preparation, A.U.R., Y.K. and M.I.; writing—review and editing, A.U.R., Y.K., M.I., S.C., S.N.K., N.L.K. and M.A.B.; visualization, A.U.R., Y.K. and M.A.B.; supervision, Y.K., S.N.K., N.L.K. and M.A.B.; project administration, A.U.R., Y.K., S.N.K. and M.A.B.; funding acquisition, Y.K. and M.A.B. All authors have read and agreed to the published version of the manuscript.

Funding

This work was performed within the State assignment of the Federal Scientific Research Center “Crystallography and Photonics” of the Russian Academy of Sciences.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors would like to express gratitude to the Nanophotonics Research Group (BUITEMS), Quetta, for their support and appreciation.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef]
  2. Sinatkas, G.; Christopoulos, T.; Tsilipakos, O.; Kriezis, E.E. Electro-optic modulation in integrated photonics. J. Appl. Phys. 2021, 130, 010901. [Google Scholar] [CrossRef]
  3. Rao, D.G.; Swarnakar, S.; Kumar, S. Design of photonic crystal based compact all-optical 2 × 1 multiplexer for optical processing devices. Microelectron. J. 2021, 112, 105046. [Google Scholar] [CrossRef]
  4. Jiao, S.; Liu, J.; Zhang, L.; Yu, F.; Zuo, G.; Zhang, J.; Zhao, F.; Lin, W.; Shao, L. All-optical logic gate computing for high-speed parallel information processing. Opto-Electron. Sci. 2022, 1, 220010. [Google Scholar] [CrossRef]
  5. Rao, D.G.; Swarnakar, S.; Palacharla, V.; Raju, K.S.; Kumar, S. Design of all-optical AND, OR, and XOR logic gates using photonic crystals for switching applications. Photonic Netw. Commun. 2021, 41, 109–118. [Google Scholar] [CrossRef]
  6. Foroughifar, A.; Saghaei, H.; Veisi, E. Design and analysis of a novel four-channel optical filter using ring resonators and line defects in photonic crystal microstructure. Opt. Quantum Electron. 2021, 53, 101. [Google Scholar] [CrossRef]
  7. Miller, D.A.B. Are optical transistors the logical next step? Nat. Photonics 2010, 4, 3–5. [Google Scholar] [CrossRef]
  8. Safinezhad, A.; Babaei Ghoushji, H.; Shiri, M.; Rezaei, M.H. High-performance and ultrafast configurable all-optical photonic crystal logic gates based on interference effects. Opt. Quantum Electron. 2021, 53, 259. [Google Scholar] [CrossRef]
  9. Liu, C.; Bai, Y.; Zhou, J.; Chen, J.; Qiao, L. Refractive index sensing by asymmetric dielectric gratings with both bound states in the continuum and guided mode resonances. Opt. Express 2021, 29, 42978–42988. [Google Scholar] [CrossRef]
  10. Royer, F.; Varghese, B.; Gamet, E.; Neveu, S.; Jourlin, Y.; Jamon, D. Enhancement of both Faraday and Kerr effects with an all-dielectric grating based on a magneto-optical nanocomposite material. ACS Omega 2020, 5, 2886–2892. [Google Scholar] [CrossRef]
  11. Mitrofanov, A.V.; Sidorov-Biryukov, D.A.; Rozhko, M.V.; Voronin, A.A.; Glek, P.B.; Ryabchuk, S.V.; Serebryannikov, E.E.; Fedotov, A.B.; Zheltikov, A.M. Relativistic nonlinear optical phenomena in the field of sub terawatt laser pulses. JETP Lett. 2020, 112, 17–23. [Google Scholar] [CrossRef]
  12. Raja-Mogan, T.; Ohtani, B.; Kowalska, E. Photonic crystals for plasmonic photocatalysis. Catalysts 2020, 10, 827. [Google Scholar] [CrossRef]
  13. Vigneron, J.P.; Simonis, P. Natural photonic crystals. Phys. B Condens. Matter 2012, 407, 4032–4036. [Google Scholar] [CrossRef]
  14. Yablonovitch, E. Photonic crystals. J. Mod. Opt. 1994, 41, 173–194. [Google Scholar] [CrossRef]
  15. Ahmed, U.; Khan, Y.; Ehsan, M.K.; Amirzada, M.R.; Ullah, N.; Khatri, A.R.; Ur Rehman, A.; Butt, M.A. Investigation of spectral properties of dbr-based photonic crystal structure for optical filter application. Crystals 2022, 12, 409. [Google Scholar] [CrossRef]
  16. Decleer, P.; Van Londersele, A.; Rogier, H.; Ginste, D.V. An alternating-direction hybrid implicit-explicit finite-difference time-domain method for the schrödinger equation. J. Comput. Appl. Math. 2022, 403, 113881. [Google Scholar] [CrossRef]
  17. Barabanova, E.A.; Vytovtov, K.A.; Nguyen, T.T. The control system elements of the new generation optical switching cell. J. Phys. Conf. Ser. 2019, 1368, 022002. [Google Scholar] [CrossRef]
  18. Yanik, M.F.; Fan, S.; Soljačić, M.; Joannopoulos, J.D. All-optical transistor action with bistable switching in a photonic crystal cross-waveguide geometry. Opt. Lett. 2003, 28, 2506–2508. [Google Scholar] [CrossRef]
  19. Nguyen, H.A.; Grange, T.; Malik, N.S.; Dupuy, E.; Tumanov, D.; de Assis, P.L.; Yeo, I.; Fratini, F.; Gregersen, N.; Auffèves, A.; et al. Ultra-low power optical transistor using a single quantum dot embedded in a photonic wire. In Quantum Information and Measurement; Optica Publishing Group: Washington, DC, USA, 2017; p. QT2B-2. [Google Scholar]
  20. Agranovich, V.M.; Gartstein, Y.N.; Litinskaya, M. Hybrid resonant organic–inorganic nanostructures for optoelectronic applications. Chem. Rev. 2011, 111, 5179–5214. [Google Scholar] [CrossRef]
  21. Parandin, F.; Sheykhian, A.; Bagheri, N. A novel design for an ultracompact optical majority gate based on a ring resonator on photonic crystal substrate. J. Comput. Electron. 2023, 22, 716–722. [Google Scholar] [CrossRef]
  22. Brunetti, G.; Marocco, G.; Di Benedetto, A.; Giorgio, A.; Armenise, M.N.; Ciminelli, C. Design of a large bandwidth 2 × 2 interferometric switching cells based on a sub-wavelength grating. J. Opt. 2021, 23, 085801. [Google Scholar] [CrossRef]
  23. Huang, Y.; Ho, S.T. Photonic Transistors based on Gain and Absorption Manipulation of Optical Interference. In Proceedings of the 2007 Photonics in Switching, San Francisco, CA, USA, 19–22 August 2007; pp. 137–138. [Google Scholar]
  24. Ju, S.; Facchetti, A.; Xuan, Y.; Liu, J.; Ishikawa, F.; Ye, P.; Zhou, C.; Marks, T.J.; Janes, D.B. Fabrication of fully transparent nanowire transistors for transparent and flexible electronics. Nat. Nanotechnol. 2007, 2, 378–384. [Google Scholar] [CrossRef] [PubMed]
  25. Rehman, A.U.; Khan, Y.; Irfan, M.; Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. A novel design of optical switch based on guided mode resonances in dielectric photonic crystal structures. Photonics 2022, 9, 580. [Google Scholar] [CrossRef]
  26. Rehman, A.U.; Khan, Y.; Fomchenkov, S.; Butt, M.A. Investigation of Optical Amplification Action in Dielectric Photonic Crystals Cavity Based Structure. In Proceedings of the 2022 VIII International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 23–27 May 2022; pp. 1–5. [Google Scholar]
  27. Rehman, A.U.; Khan, Y.; Irfan, M.; Butt, M.A. Investigation of Optical-Switching Mechanism Using Guided Mode Resonances. Photonics 2022, 10, 13. [Google Scholar] [CrossRef]
  28. Chhipa, M.K.; Madhav, B.T.; Suthar, B. An all-optical ultracompact microring-resonator-based optical switch. J. Comput. Electron. 2021, 20, 419–425. [Google Scholar] [CrossRef]
  29. Yu, Y.; Xue, W.; Hu, H.; Oxenløwe, L.K.; Yvind, K.; Mork, J. All-optical switching improvement using photonic-crystal Fano structures. IEEE Photonics J. 2016, 8, 1–8. [Google Scholar] [CrossRef]
  30. Bekele, D.; Yu, Y.; Yvind, K.; Mork, J. In-Plane Photonic Crystal Devices Using Fano Resonances. Laser Photonics Rev. 2019, 13, 1900054. [Google Scholar] [CrossRef]
  31. Rajasekar, R.; Parameshwari, K.; Robinson, S. Nano-optical switch based on photonic crystal ring resonator. Plasmonics 2019, 14, 1687–1697. [Google Scholar] [CrossRef]
  32. Ghadrdan, M.; Mansouri-Birjandi, M.A. Implementation of all-optical switch based on nonlinear photonic crystal ring resonator with embedding metallic nanowires in the ring resonators. Opt. Quantum Electron. 2016, 48, 299. [Google Scholar] [CrossRef]
  33. Radhouene, M.; Najjar, M.; Chhipa, M.K.; Robinson, S.; Suthar, B. Design and analysis a thermo-optic switch based on photonic crystal ring resonator. Optik 2018, 172, 924–929. [Google Scholar] [CrossRef]
  34. Rajasekar, R.; Kumar, K.V.; Ayyanar, N.; Raja, G.T. High Speed Optical Switch Based on Photonic Crystal Resonator. In Proceedings of the 2020 IEEE 20th International Conference on Nanotechnology (IEEE-NANO), Montreal, QC, Canada, 29–31 July 2020; pp. 295–298. [Google Scholar]
  35. Askarian, A.; Parandin, F. Numerical analysis of all optical 1-bit comparator based on PhC structure for optical integrated circuits. Opt. Quantum Electron. 2023, 55, 419. [Google Scholar] [CrossRef]
  36. Rebhi, S.; Najjar, M. Hourglass nonlinear photonic crystal cavity for ultra-fast all-optical switching. Optik 2019, 180, 858–865. [Google Scholar] [CrossRef]
  37. Takiguchi, M.; Takemura, N.; Tateno, K.; Nozaki, K.; Sasaki, S.; Sergent, S.; Kuramochi, E.; Wasawo, T.; Yokoo, A.; Shinya, A.; et al. All-optical switching using a III–V nanowire integrated Si photonic crystal nanocavity. In Proceedings of the 2019 IEEE Photonics Conference (IPC), San Antonio, TX, USA, 29 September–3 October 2019; pp. 1–2. [Google Scholar]
  38. Nozaki, K.; Tanabe, T.; Shinya, A.; Matsuo, S.; Sato, T.; Taniyama, H.; Notomi, M. Sub-femtojoule all-optical switching using a photonic-crystal nanocavity. Nat. Photonics 2010, 4, 477–483. [Google Scholar] [CrossRef]
  39. Mehdizadeh, F.; Alipour-Banaei, H.; Serajmohammadi, S. Study the role of non-linear resonant cavities in photonic crystal-based decoder switches. J. Mod. Opt. 2017, 64, 1233–1239. [Google Scholar] [CrossRef]
  40. Askarian, A.; Parandin, F. A novel proposal for all optical 1-bit comparator based on 2D linear photonic crystal. J. Comput. Electron. 2023, 22, 288–295. [Google Scholar] [CrossRef]
  41. Shirdel, M.; Mansouri-Birjandi, M.A. Photonic crystal all-optical switch based on a nonlinear cavity. Optik 2016, 127, 3955–3958. [Google Scholar] [CrossRef]
  42. Asakawa, K.; Sugimoto, Y.; Watanabe, Y.; Ozaki, N.; Mizutani, A.; Takata, Y.; Kitagawa, Y.; Ishikawa, H.; Ikeda, N.; Awazu, K.; et al. Photonic crystal and quantum dot technologies for all-optical switch and logic device. New J. Phys. 2006, 8, 208. [Google Scholar] [CrossRef]
  43. Nakamura, H.; Sugimoto, Y.; Kanamoto, K.; Ikeda, N.; Tanaka, Y.; Nakamura, Y.; Ohkouchi, S.; Watanabe, Y.; Inoue, K.; Ishikawa, H.; et al. Ultra-fast photonic crystal/quantum dot all-optical switch for future photonic networks. Opt. Express 2004, 12, 6606–6614. [Google Scholar] [CrossRef]
  44. Chen, F. A tunable high-efficiency optical switch based on graphene coupled photonic crystal’s structure. J. Mod. Opt. 2017, 64, 1531–1537. [Google Scholar] [CrossRef]
  45. Jalali Azizpour, M.R.; Soroosh, M.; Dalvand, N.; Seifi-Kavian, Y. All-optical ultra-fast graphene-photonic crystal switch. Crystals 2019, 9, 461. [Google Scholar] [CrossRef]
  46. Zhang, L.; Sun, Y.; Li, Z.; Wang, L.; Cao, S.; Yang, S.; Wu, Y.; Tai, R. Photonic crystal based on mott phase change material as all-optical bandgap switch and composite logic gate. Opt. Mater. 2021, 113, 110855. [Google Scholar] [CrossRef]
  47. Jiang, M.; Zhang, D.; Lian, T.; Wang, L.; Niu, D.; Chen, C.; Li, Z.; Wang, X. On-chip integrated optical switch based on polymer waveguides. Opt. Mater. 2019, 97, 109386. [Google Scholar] [CrossRef]
  48. Mazurenko, D.A.; Kerst, R.; Dijkhuis, J.I.; Akimov, A.V.; Golubev, V.G.; Kurdyukov, D.A.; Pevtsov, A.B.; Sel’Kin, A.V. Ultrafast optical switching in three-dimensional photonic crystals. Phys. Rev. Lett. 2003, 91, 213903. [Google Scholar] [CrossRef] [PubMed]
  49. Meng, Z.M.; Chen, C.B.; Qin, F. Theoretical investigation of integratable photonic crystal nanobeam all-optical switching with ultrafast response and ultralow switching energy. J. Phys. D Appl. Phys. 2020, 53, 205105. [Google Scholar] [CrossRef]
  50. Monfared, S.A.; Seifouri, M.; Hamidi, S.M.; Mohseni, S.M. Electro-optical switch based on one-dimensional graphene-plasmonic crystals. Opt. Mater. 2021, 115, 111051. [Google Scholar] [CrossRef]
  51. Zhao, Y.; Qian, C.; Qiu, K.; Gao, Y.; Xu, X. Ultrafast optical switching using photonic molecules in photonic crystal waveguides. Opt. Express 2015, 23, 9211–9220. [Google Scholar] [CrossRef] [PubMed]
  52. Ma, L.; Li, C.; Sun, L.; Song, Z.; Lu, Y.; Li, B. Submicrosecond electro-optical switching of one-dimensional soft photonic crystals. Photonics Res. 2022, 10, 786–792. [Google Scholar] [CrossRef]
  53. Qi, H.; Wang, X.; Hu, X.; Du, Z.; Yang, J.; Yu, Z.; Ding, S.; Chu, S.; Gong, Q. All-optical switch based on novel physics effects. J. Appl. Phys. 2021, 129, 210906. [Google Scholar] [CrossRef]
  54. Rajasekar, R.; Raja, G.T.; Robinson, S. Numerical investigation of reconfigurable photonic crystal switch based on phase change nanomaterial. IEEE Trans. Nanotechnol. 2020, 19, 545–552. [Google Scholar] [CrossRef]
  55. Takiguchi, M.; Takemura, N.; Tateno, K.; Nozaki, K.; Sasaki, S.; Sergent, S.; Kuramochi, E.; Wasawo, T.; Yokoo, A.; Shinya, A.; et al. All-optical InAsP/InP nanowire switches integrated in a Si photonic crystal. ACS Photonics 2020, 7, 1016–1021. [Google Scholar] [CrossRef]
  56. Tanabe, T.; Taniyama, H.; Notomi, M. Carrier diffusion and recombination in photonic crystal nanocavity optical switches. J. Light. Technol. 2008, 26, 1396–1403. [Google Scholar] [CrossRef]
  57. Plander, I.; Stepanovsky, M. MEMS optical switch: Switching time reduction. Open Comput. Sci. 2016, 6, 116–125. [Google Scholar] [CrossRef]
  58. MEEP Documentation MkDocs. Available online: https://meep.readthedocs.io/en/latest/ (accessed on 14 April 2022).
  59. Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. A flexible free-software package for electromagnetic simulations by the fdtd method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
  60. Yee, K.S. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar]
  61. Khan, Y.; Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N. numerical study of fabrication-related effects of the structural-profile on the performance of a dielectric photonic crystal-based fluid sensor. Materials 2022, 15, 3277. [Google Scholar] [CrossRef]
  62. Khan, Y. Design and Numerical Simulation of Dielectric Photonic Crystal Devices and Investigation of an Optical Characterization Method. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2017. [Google Scholar]
  63. Sahu, P.P. Optical switch based on graphene clad two surface plasmonic polariton mode coupler. Optik 2021, 227, 166026. [Google Scholar] [CrossRef]
  64. Okada, H.; Baba, M.; Furukawa, M.; Yamane, K.; Sekiguchi, H.; Wakahara, A. Formation of SiO2 film by chemical vapor deposition enhanced by atomic species extracted from a surface-wave generated plasma. AIP Conf. Proc. 2017, 1807, 020006. [Google Scholar]
  65. Becker, M.; Benz, S.L.; Chen, L.; Polity, A.; Klar, P.J.; Chatterjee, S. Controlled thin-film deposition of α or β Ga2O3 by ion-beam sputtering. J. Vac. Sci. Technol. A Vac. Surf. Films 2020, 38, 063412. [Google Scholar] [CrossRef]
  66. Li, W.; van Baren, J.; Berges, A.; Bekyarova, E.; Lui, C.H.; Bardeen, C.J. Shaping organic microcrystals using focused ion beam milling. Cryst. Growth Des. 2020, 20, 1583–1589. [Google Scholar] [CrossRef]
Micromachines 14 01116 g001 550
Figure 1. (a) Photonic integrated circuit. (b) conceptual diagram of the 3D-optical switch.
Figure 1. (a) Photonic integrated circuit. (b) conceptual diagram of the 3D-optical switch.
Micromachines 14 01116 g001
Micromachines 14 01116 g002 550
Figure 2. Infinite structures of the 3D-optical switch. (a) The view of the 3D-optical switch along x-axis showing the data signal, reflection, and transmission monitoring layers, and field decay monitor point. (b) Cross-section view along y-axis. (c) Top view along x-axis. (d) A unit cell of the device showing the direction of the control signal.
Figure 2. Infinite structures of the 3D-optical switch. (a) The view of the 3D-optical switch along x-axis showing the data signal, reflection, and transmission monitoring layers, and field decay monitor point. (b) Cross-section view along y-axis. (c) Top view along x-axis. (d) A unit cell of the device showing the direction of the control signal.
Micromachines 14 01116 g002
Micromachines 14 01116 g003 550
Figure 3. (a) The output reflection spectra of the infinite models of the 3D-optical switch comprising 2 and 4 PhC elements (along the x-axis). (b) Electric field confinement by the 2-PhC-element-based structure. (c) Electric field confinement by the 4-PhC-element-based structure. (d) Magnetic field confinement by the 2-PhC-element-based structure. (e) Magnetic field confinement by the 4-PhC-element-based structure.
Figure 3. (a) The output reflection spectra of the infinite models of the 3D-optical switch comprising 2 and 4 PhC elements (along the x-axis). (b) Electric field confinement by the 2-PhC-element-based structure. (c) Electric field confinement by the 4-PhC-element-based structure. (d) Magnetic field confinement by the 2-PhC-element-based structure. (e) Magnetic field confinement by the 4-PhC-element-based structure.
Micromachines 14 01116 g003
Micromachines 14 01116 g004 550
Figure 4. (a) Output reflection spectra of the data signal relating to infinite model of the 2-PhC-element-based structure, investigating the phenomenon of optical switching relating to varying wavelength of the control signal. (b) Linewidth. (c) Quality factor.
Figure 4. (a) Output reflection spectra of the data signal relating to infinite model of the 2-PhC-element-based structure, investigating the phenomenon of optical switching relating to varying wavelength of the control signal. (b) Linewidth. (c) Quality factor.
Micromachines 14 01116 g004
Micromachines 14 01116 g005 550
Figure 5. (a) Output reflection spectra of the data signal relating to infinite model of the 4-PhC-element-based structure, investigating the phenomenon of optical switching with regard to varying wavelength of the control signal. (b) Linewidth. (c) Quality factor.
Figure 5. (a) Output reflection spectra of the data signal relating to infinite model of the 4-PhC-element-based structure, investigating the phenomenon of optical switching with regard to varying wavelength of the control signal. (b) Linewidth. (c) Quality factor.
Micromachines 14 01116 g005
Micromachines 14 01116 g006a 550Micromachines 14 01116 g006b 550
Figure 6. Finite model of the 3D-optical switch comprising the 2 PhC elements along x-axis. (a) Lateral view of the optical switch along y-axis. (b) Cross-sectional view along x-axis. (c) Finite model representation along x, y, and z directions. (d) Output reflection and transmission spectra of the finite model signifying the properties of the optical switching. (e) Field confinement (x-axis). (f) Field confinement (y-axis). (g) Intensity of data signal on the surface of the optical switch (z-axis).
Figure 6. Finite model of the 3D-optical switch comprising the 2 PhC elements along x-axis. (a) Lateral view of the optical switch along y-axis. (b) Cross-sectional view along x-axis. (c) Finite model representation along x, y, and z directions. (d) Output reflection and transmission spectra of the finite model signifying the properties of the optical switching. (e) Field confinement (x-axis). (f) Field confinement (y-axis). (g) Intensity of data signal on the surface of the optical switch (z-axis).
Micromachines 14 01116 g006aMicromachines 14 01116 g006b
Micromachines 14 01116 g007 550
Figure 7. Finite model of the 3D-optical switch comprising the 4 PhC elements along x-axis. (a) Lateral view of the optical switch along y-axis. (b) Cross-sectional view along x-axis. (c) Finite model representation along x, y, and z directions. (d) Output reflection and transmission spectra of the finite model signifying the properties of optical switching. (e) Field confinement (x-axis). (f) Field confinement (y-axis). (g) Intensity of data signal on the surface of the optical switch (z-axis).
Figure 7. Finite model of the 3D-optical switch comprising the 4 PhC elements along x-axis. (a) Lateral view of the optical switch along y-axis. (b) Cross-sectional view along x-axis. (c) Finite model representation along x, y, and z directions. (d) Output reflection and transmission spectra of the finite model signifying the properties of optical switching. (e) Field confinement (x-axis). (f) Field confinement (y-axis). (g) Intensity of data signal on the surface of the optical switch (z-axis).
Micromachines 14 01116 g007
Micromachines 14 01116 g008 550
Figure 8. The stepwise fabrication process of the reported optical switching device.
Figure 8. The stepwise fabrication process of the reported optical switching device.
Micromachines 14 01116 g008
Table
Table 1. Augmented parameters of the 3D-optical switch.
Table 1. Augmented parameters of the 3D-optical switch.
ParametersSymbolValue
Lattice constanta1 µm
Radius of PhC elementsr0.300a
Thickness of waveguidewthick0.330a
Thickness of cladding-0.300a
Thickness of Perfectly Matched Layer PML3.0a, (along x and z) axes
Refractive index of the substratensub1.5
Refractive index of the waveguidenwav2.2
Field decay monitoring point-1 × 10−3
PaddingPadd2.0a
Periodic boundary conditionPBCAlong y-axis
Resolution -20
Smoothing factor-0.05
Grid size-0.52
Table
Table 2. Properties achieved by the infinite models of the 3D-optical switch comprising of 2 and 4 PhC elements.
Table 2. Properties achieved by the infinite models of the 3D-optical switch comprising of 2 and 4 PhC elements.
Number of PhC ElementsResonant Wavelength (µm)Reflection Peak
(%)		Linewidth
(µm)		Quality Factor
-
2 PhC elements1.52881.130.020439.76
4 PhC elements1.54771.430.026626.85
Table
Table 3. Names and differences in wavelengths of the data and control signal.
Table 3. Names and differences in wavelengths of the data and control signal.
Type of SourceName of Source
d1c1c2c3
Data signal1.55 µm---
Control signal-1.67 µm1.60 µm1.55 µm
Table
Table 4. A detailed comparison between the infinite models of the 3D-optical switch based on 2 and 4 PhC elements.
Table 4. A detailed comparison between the infinite models of the 3D-optical switch based on 2 and 4 PhC elements.
2 PhC Elements
Sourcesd1c1c2c3
Resonant wavelength (µm)1.5281.5281.5281.528
Reflection (×100%)0.81130.84340.90520.9488
Linewidth (µm)0.02040.01500.00790.0214
Quality Factor39.7756.23114.5844.34
4 PhC Elements
Sourcesd1c1c2c3
Resonant wavelength (µm)1.5471.5471.5471.547
Reflection (×100%)0.71430.73430.76230.7741
Linewidth (µm)0.02660.01490.02760.0269
Quality Factor26.8549.2827.6228.78
Table
Table 5. Comparison of the previous research studies with the current investigation for the design of the 3D-optical switch.
Table 5. Comparison of the previous research studies with the current investigation for the design of the 3D-optical switch.
DesignResonant Wavelength (µm)Reflection (×100%)Simulation
Domain		Linewidth (µm)Quality FactorResearch Work
SiO2 + Nb2O5 + PhCs (air)1.5440.95922D0.069611.87[25]
SiO2 + Nb2O5 + PhCs (air)1.5340.86952D0.0727-[26]
SiO2 + Nb2O5 + PhCs (air)1.5420.95182D0.065212.96[27]
SiO2 + Nb2O5 + PhCs (air)1.5280.94883D0.0079114.58This work
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rehman, A.U.; Khan, Y.; Irfan, M.; Choudri, S.; Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Three-Dimensional Modeling of the Optical Switch Based on Guided-Mode Resonances in Photonic Crystals. Micromachines 2023, 14, 1116. https://doi.org/10.3390/mi14061116

AMA Style

Rehman AU, Khan Y, Irfan M, Choudri S, Khonina SN, Kazanskiy NL, Butt MA. Three-Dimensional Modeling of the Optical Switch Based on Guided-Mode Resonances in Photonic Crystals. Micromachines. 2023; 14(6):1116. https://doi.org/10.3390/mi14061116

Chicago/Turabian Style

Rehman, Atiq Ur, Yousuf Khan, Muhammad Irfan, Shahzaib Choudri, Svetlana N. Khonina, Nikolay L. Kazanskiy, and Muhammad A. Butt. 2023. "Three-Dimensional Modeling of the Optical Switch Based on Guided-Mode Resonances in Photonic Crystals" Micromachines 14, no. 6: 1116. https://doi.org/10.3390/mi14061116

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop