A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism
Abstract
1. Introduction
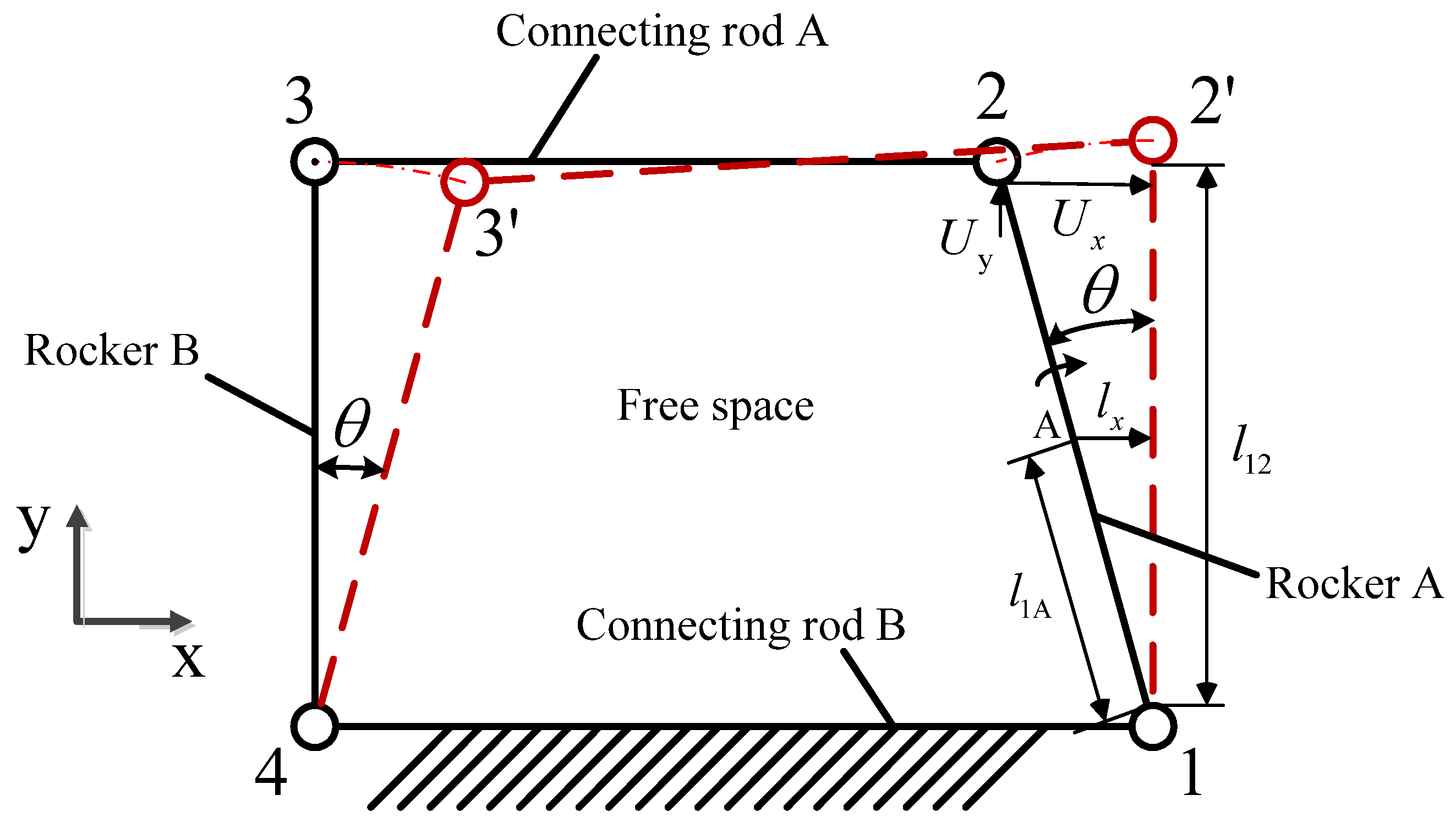
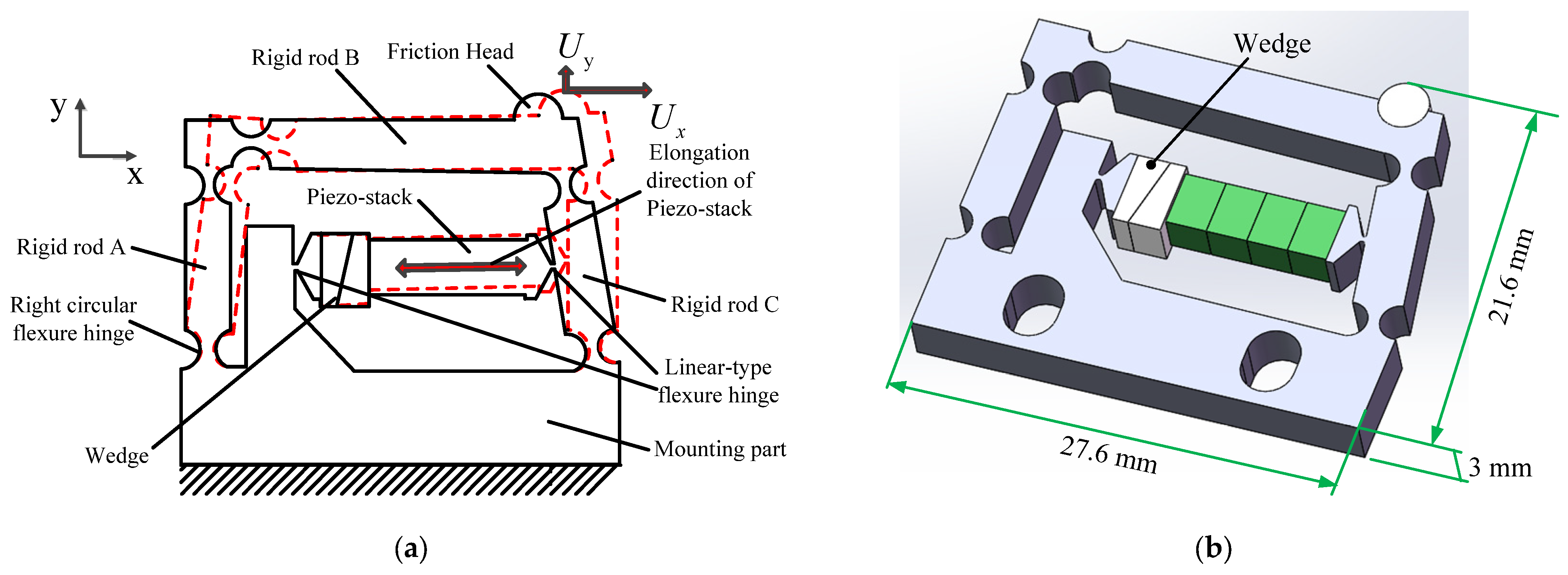
2. Design and Analysis
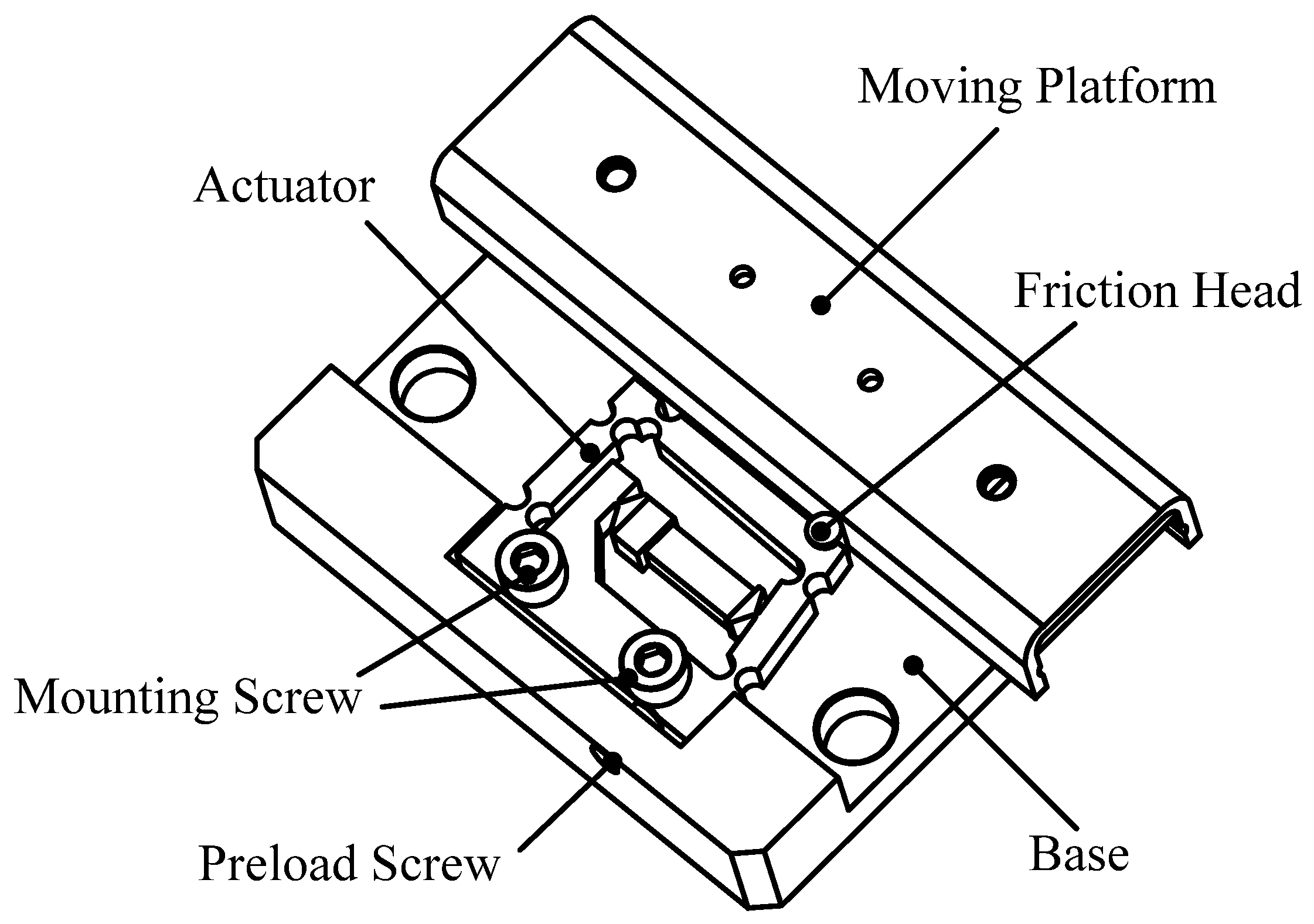
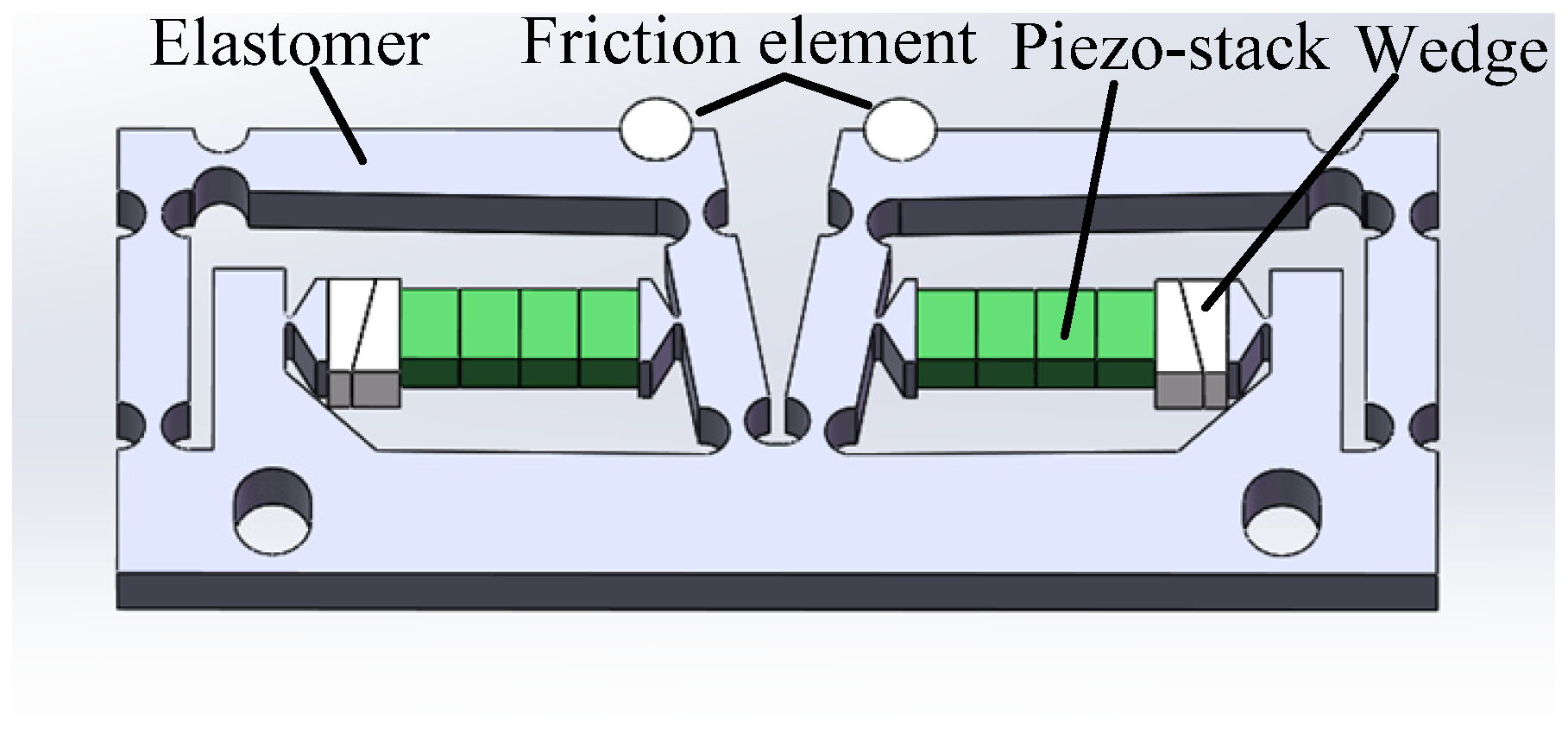
2.1. Structure of Actuator
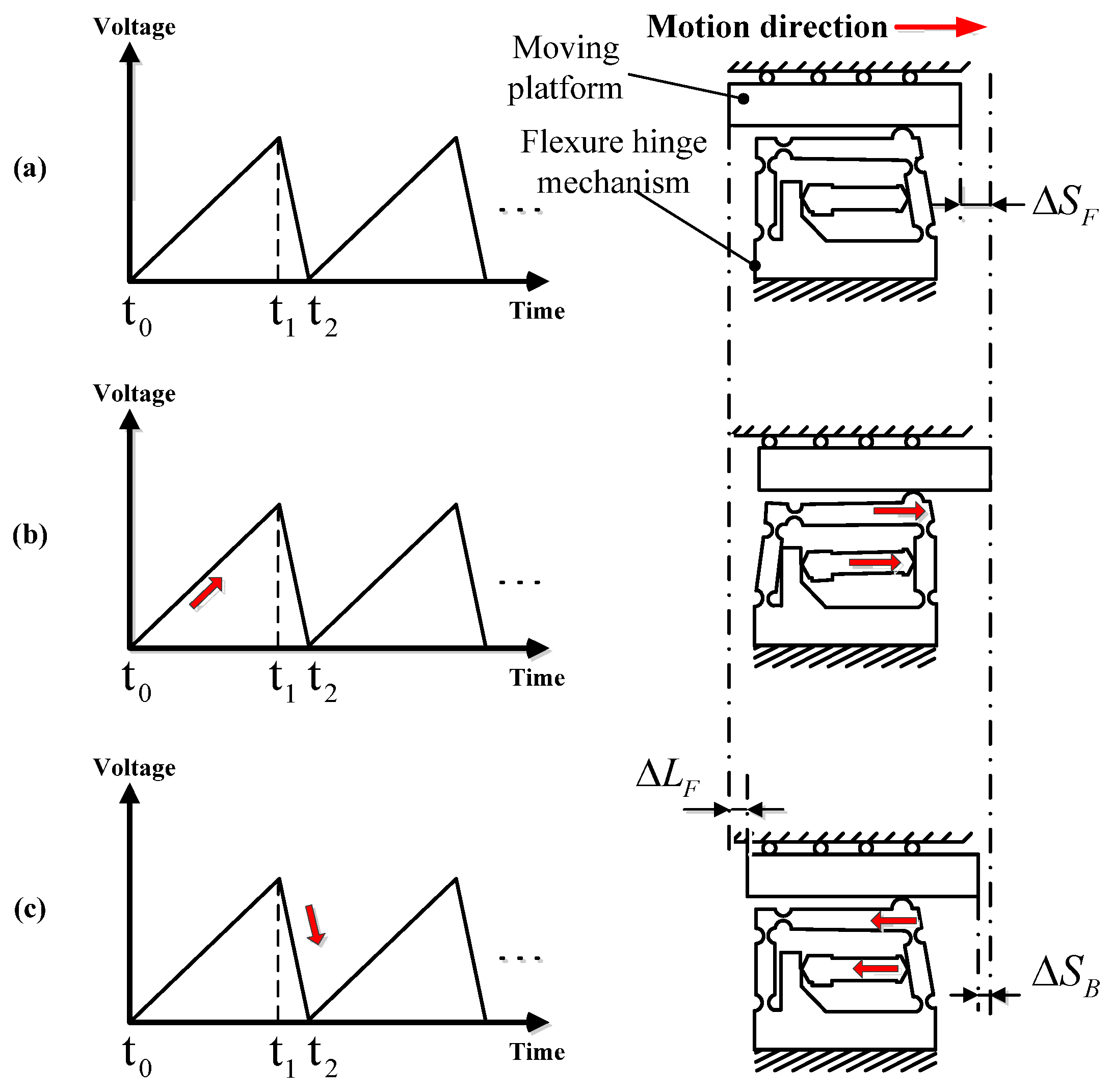
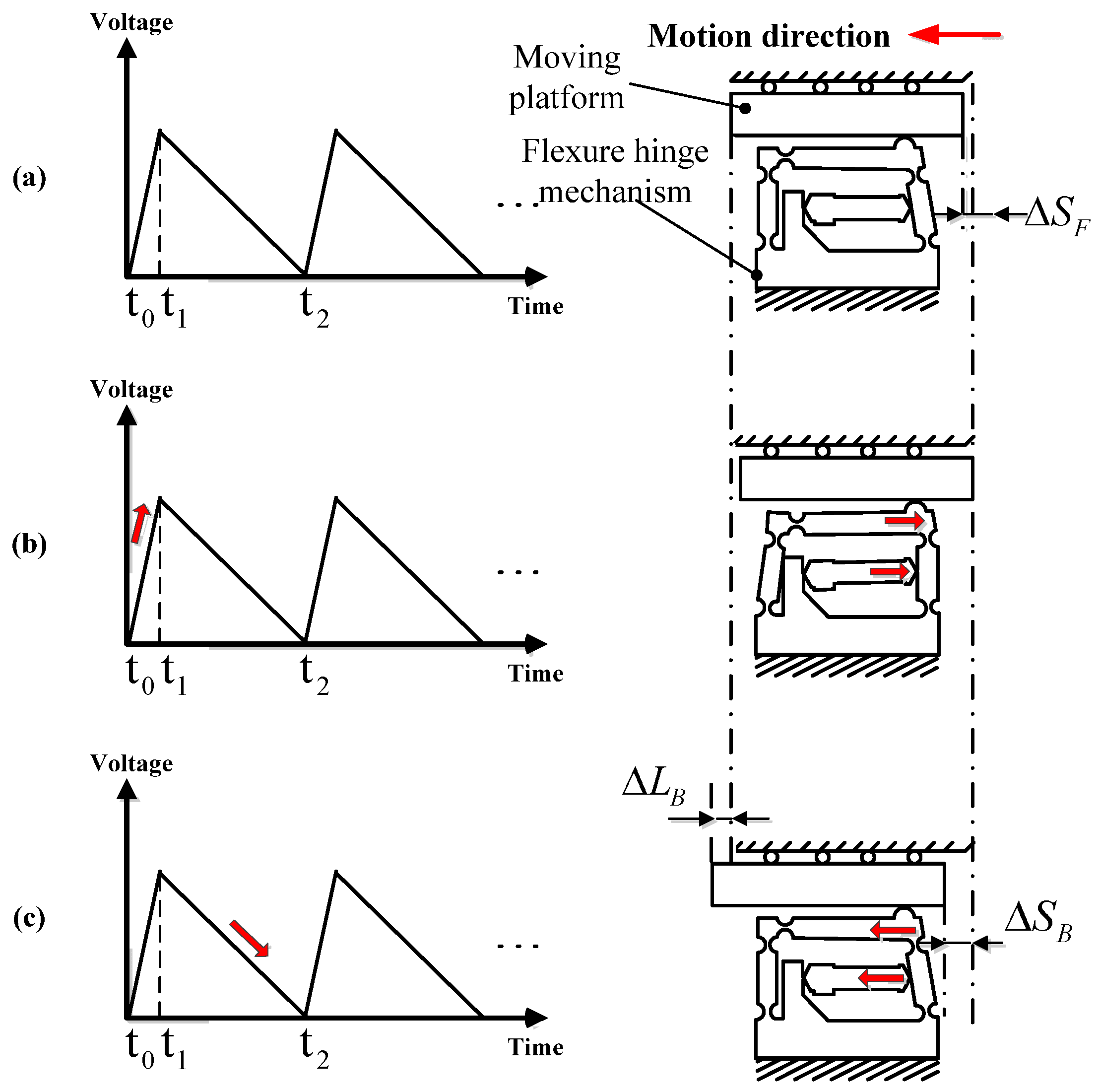
2.2. Operating Principle of Actuator
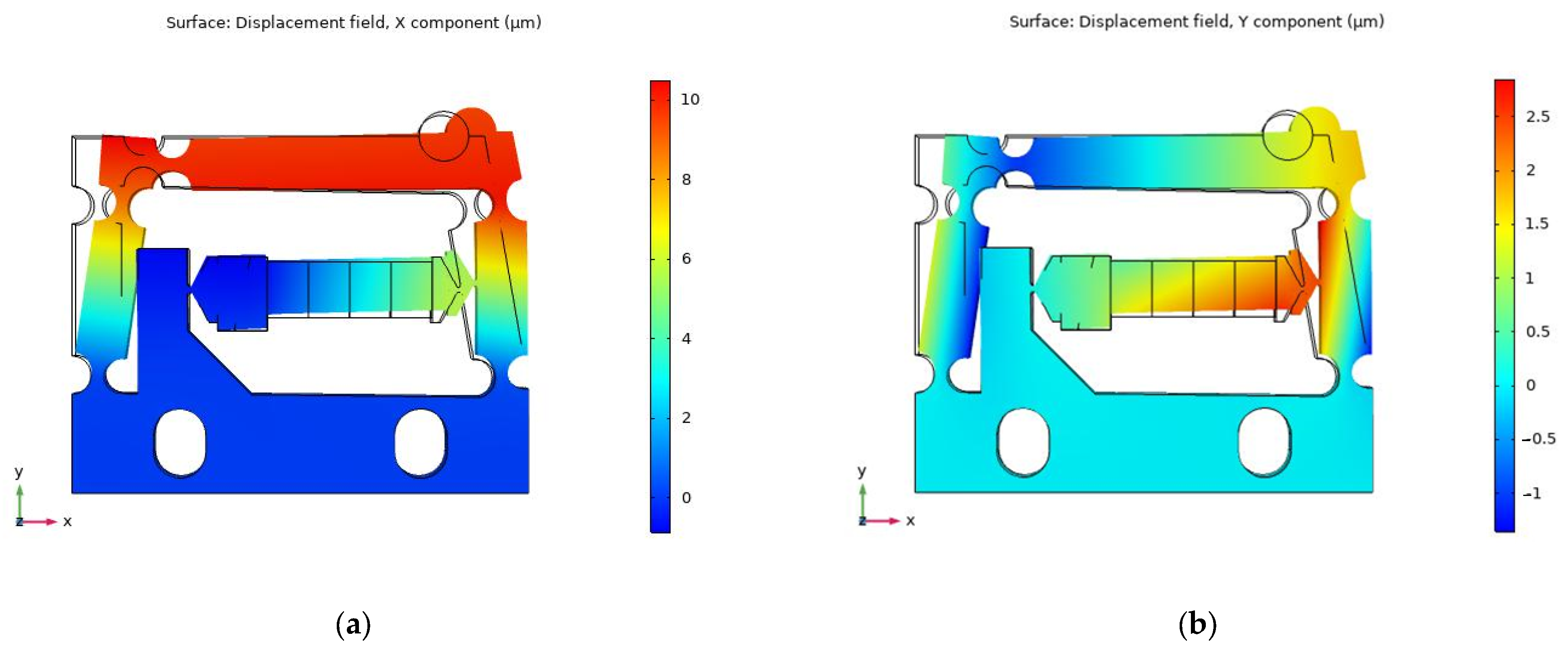
2.3. Simulation of Flexure Hinge Mechanism
3. Experiments and Results
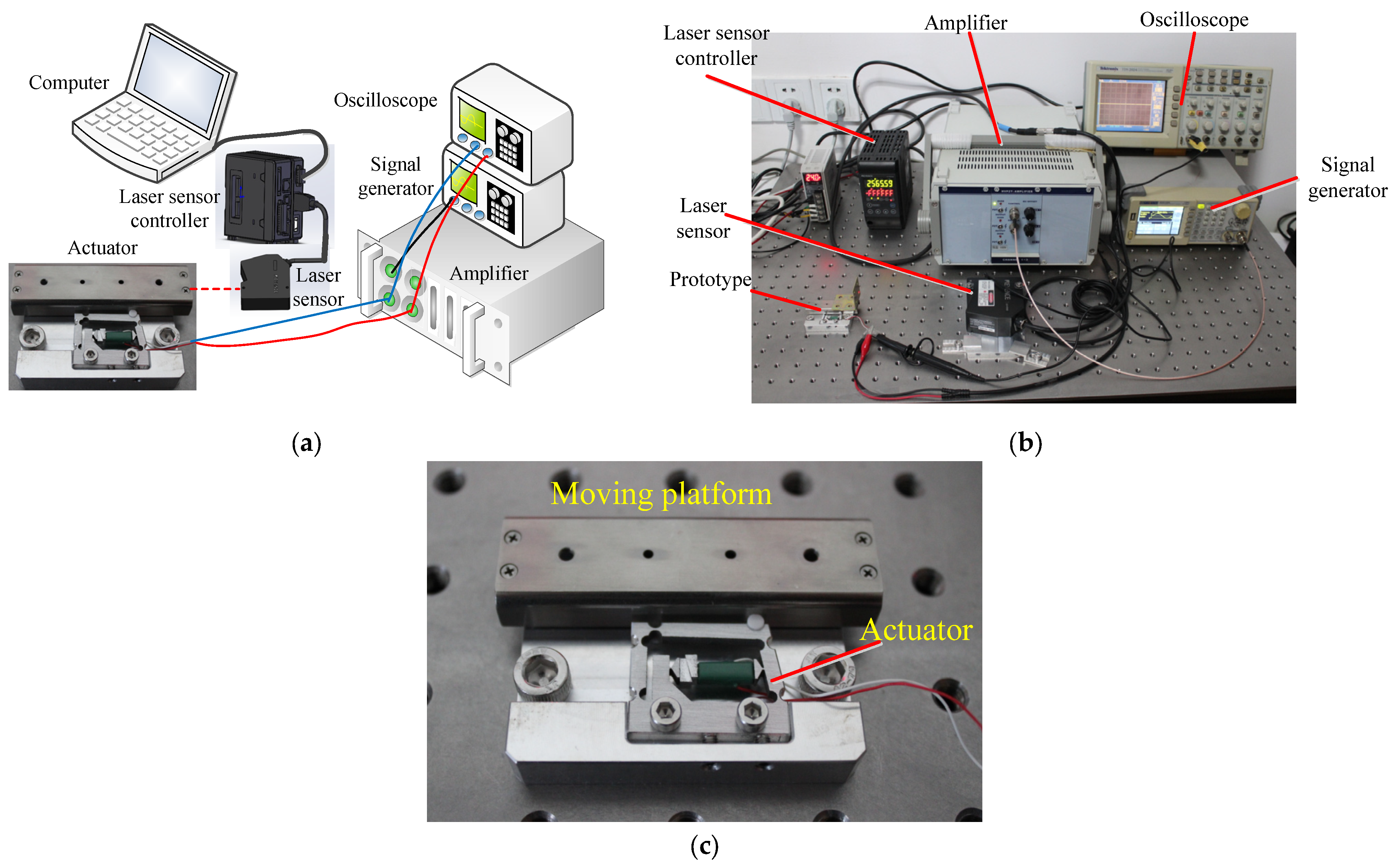
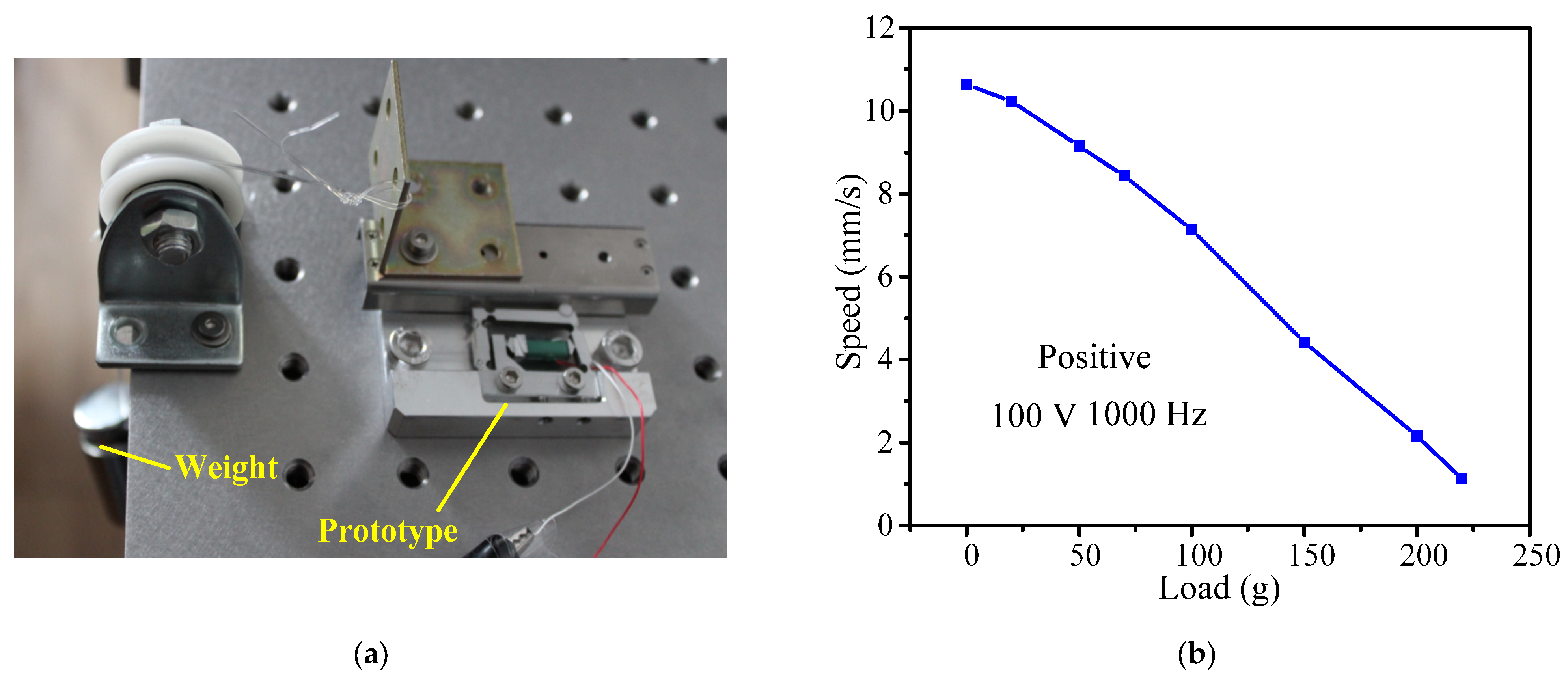
3.1. Experimental System
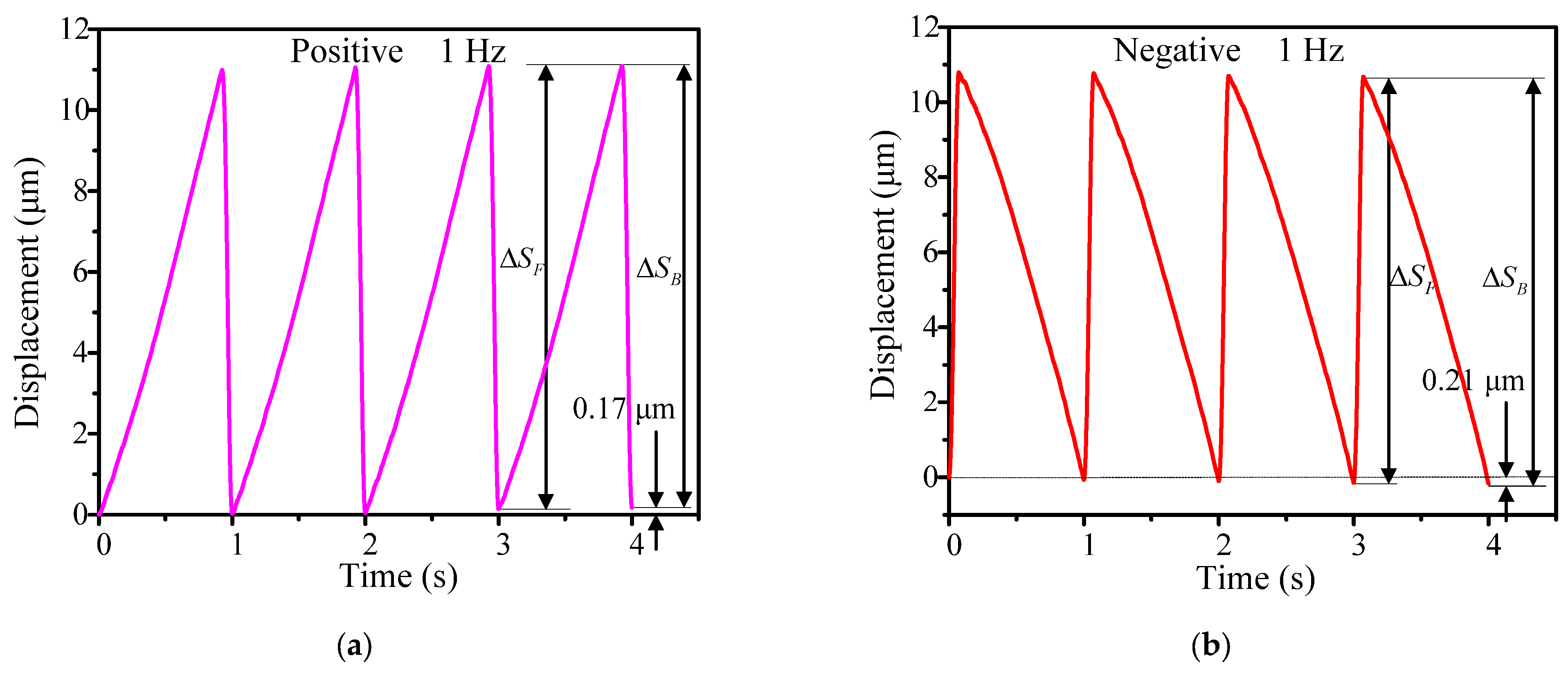
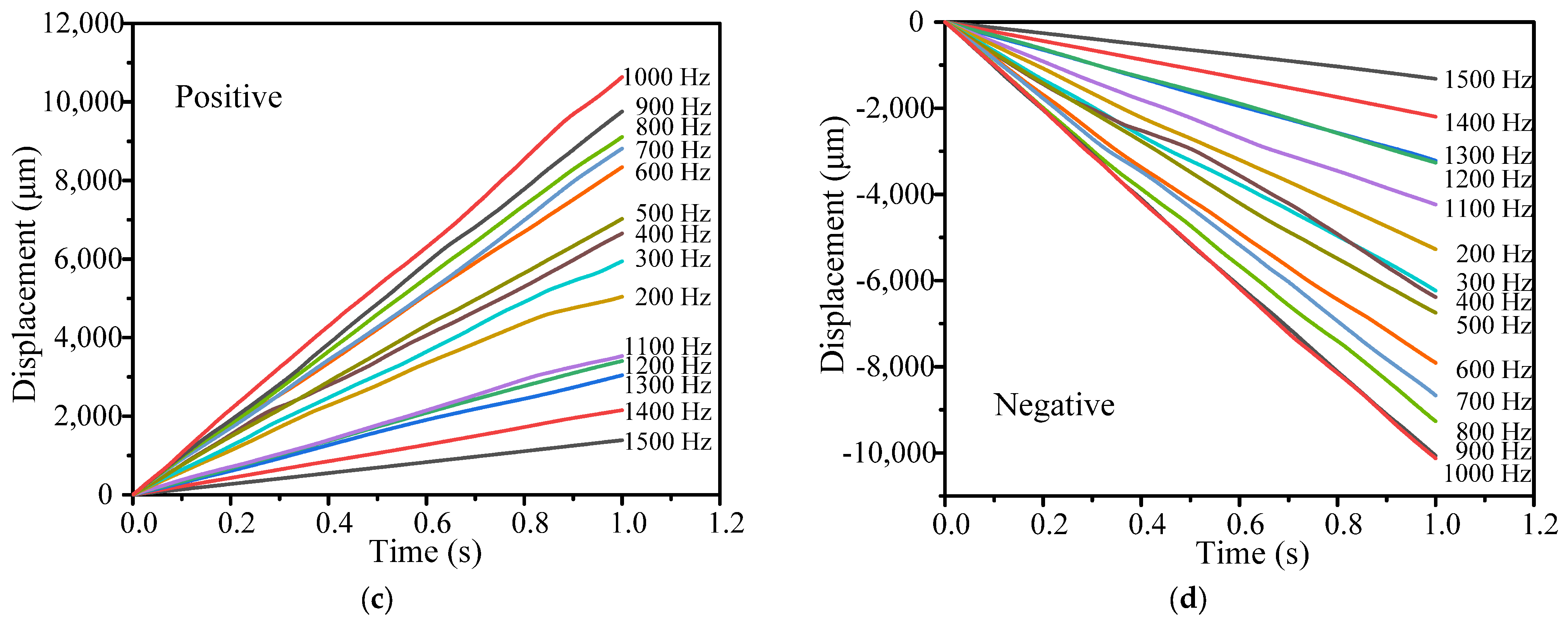
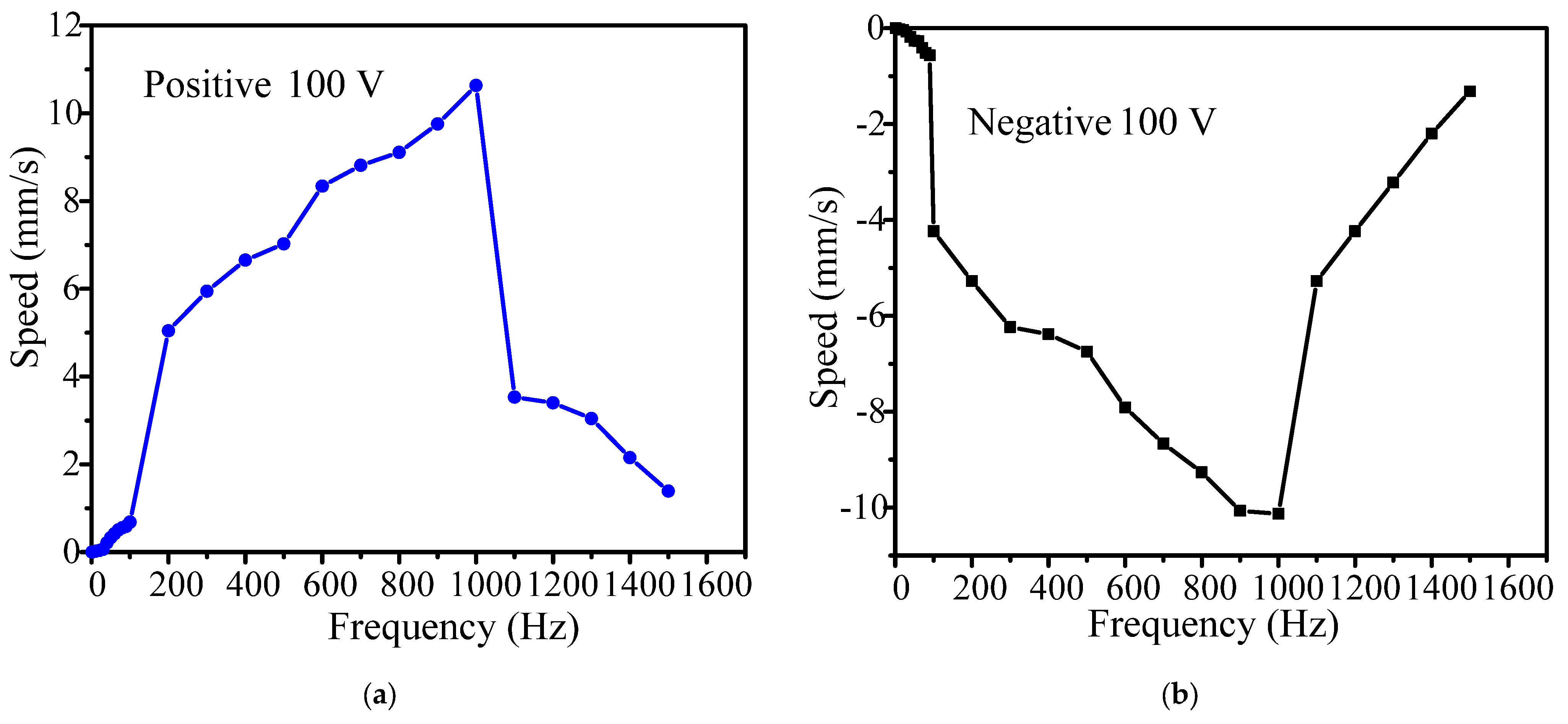
3.2. Output Characteristics under Various Driving Frequencies
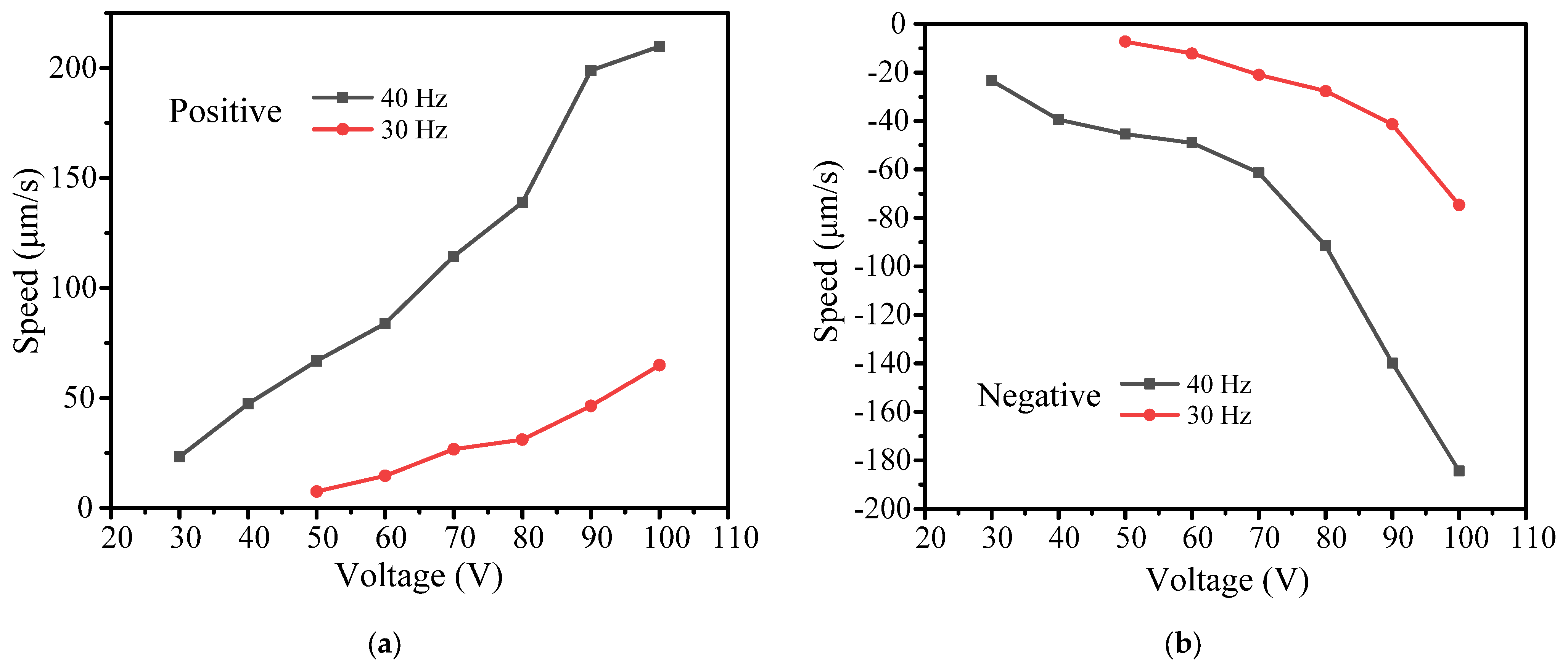
3.3. Output Characteristics at Various Driving Voltages
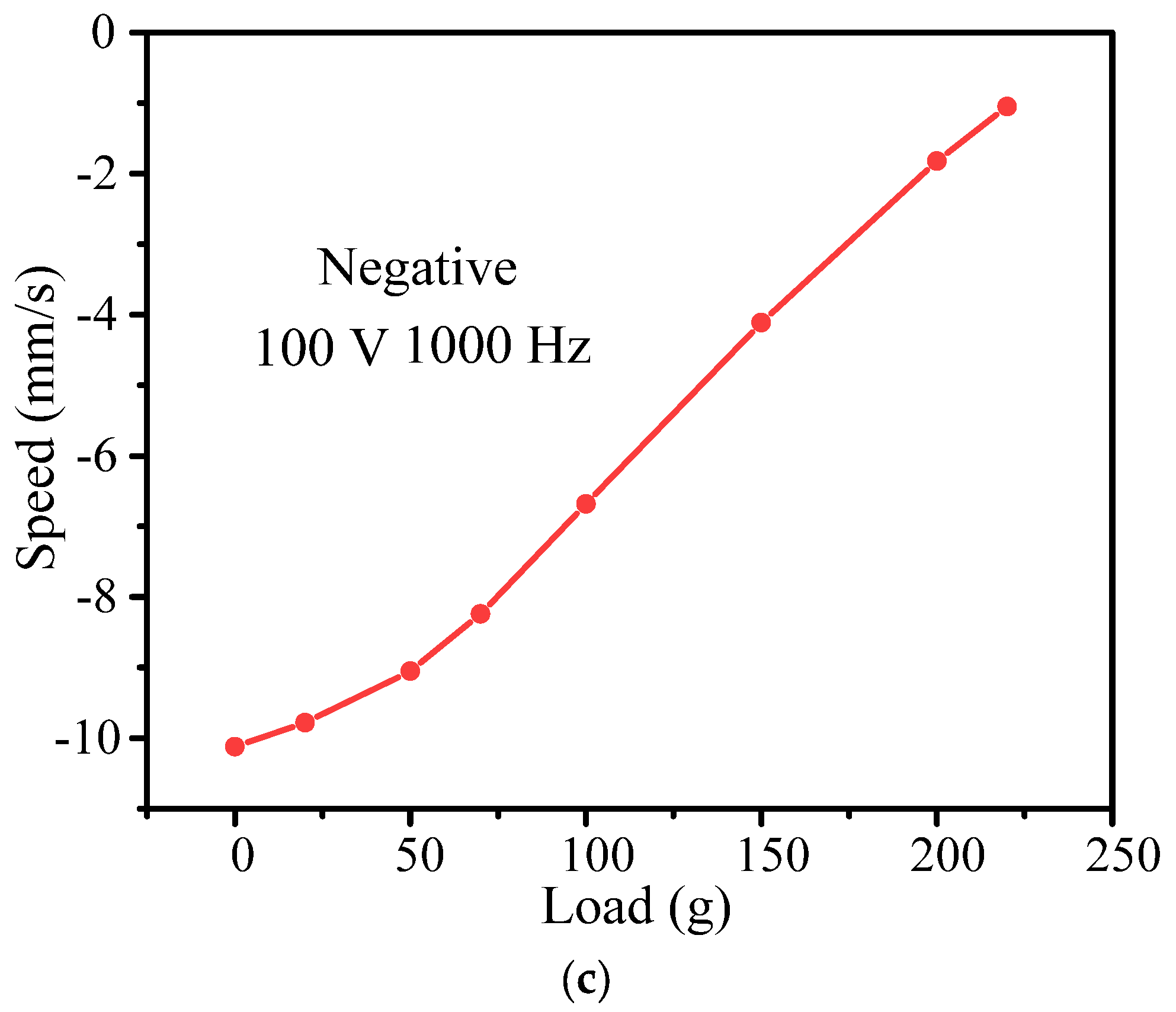
3.4. Load Characteristics
4. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lehmann, P.; Tereschenko, S.; Xie, W. Fundamental aspects of resolution and precision in vertical scanning white-light interferometry. Surf. Topogr. Metrol. Prop. 2016, 4, 024004. [Google Scholar] [CrossRef]
- Luo, S.; Suzuki, T.; Sasaki, O.; Choi, S.; Chen, Z.; Pu, J. Signal correction by detection of scanning position in a white-light interferometer for exact surface profile measurement. Appl. Opt. 2019, 58, 3548–3554. [Google Scholar] [CrossRef] [PubMed]
- Meggitt, B.T.; Hall, C.J.; Weir, K. An all fibre white light interferometric strain measurement system. Sens. Actuators 2000, 79, 1–7. [Google Scholar] [CrossRef]
- Alsteens, D.; Gaub, H.E.; Newton, R.; Pfreundschuh, M.; Gerber, C.; Müller, D.J. Atomic force microscopy-based characterization and design of biointerfaces. Nat. Rev. Mater. 2017, 2, 17008. [Google Scholar] [CrossRef]
- Giessibl, F.J. Advances in atomic force microscopy. Rev. Mod. Phys. 2003, 75, 949. [Google Scholar] [CrossRef]
- Huang, H.; Gao, X.; Teng, L. Fiber alignment and its effect on mechanical properties of UHPC: An overview. Constr. Build. Mater. 2021, 296, 123741. [Google Scholar] [CrossRef]
- Robinson, A.J.; Perez-Nava, A.; Ali, S.C.; Gonzalez-Campos, J.B.; Holloway, J.L.; Cosgriff-Hernandez, E.M. Comparative Analysis of Fiber Alignment Methods in Electrospinning. Matter 2021, 4, 821–844. [Google Scholar] [CrossRef]
- Tower, T.T.; Neidert, M.R.; Tranquillo, R.T. Fiber Alignment Imaging During Mechanical Testing of Soft Tissues. Ann. Biomed. Eng. 2002, 30, 1221–1233. [Google Scholar] [CrossRef]
- Huang, Z.; Shao, G.; Li, L. Micro/nano functional devices fabricated by additive manufacturing. Prog. Mater. Sci. 2023, 131, 101020. [Google Scholar] [CrossRef]
- Qin, Y.; Brockett, A.; Ma, Y.; Razali, A.; Zhao, J.; Harrison, C.; Pan, W.; Dai, X.; Loziak, D. Micro-manufacturing: Research, technology outcomes and development issues. Int. J. Adv. Manuf. Technol. 2009, 47, 821–837. [Google Scholar] [CrossRef]
- Zheng, B.; Wang, W.; Jiang, G.; Wang, K.; Mei, X. Research status and application prospects of manufacturing technology for micro–nano surface structures with low reflectivity. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 229, 1877–1892. [Google Scholar] [CrossRef]
- Delibas, B.; Koc, B. L1B2 Piezo Motor Using D33 Effect. In Proceedings of the ACTUATOR 2018: 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018. [Google Scholar]
- Ren, W.; Yang, M.; Chen, L.; Ma, C.; Yang, L. Mechanical optimization of a novel hollow traveling wave rotary ultrasonic motor. J. Intell. Mater. Syst. Struct. 2020, 31, 1091–1100. [Google Scholar] [CrossRef]
- Zhao, B.; Fang, R.; Shi, W. Modeling of Motion Characteristics and Performance Analysis of an Ultra-Precision Piezoelectric Inchworm Motor. Materials 2020, 13, 3976. [Google Scholar] [CrossRef] [PubMed]
- Merry, R.J.E.; de Kleijn, N.C.T.; van de Molengraft, M.J.G.; Steinbuch, M. Using a Walking Piezo Actuator to Drive and Control a High-Precision Stage. IEEE/ASME Trans. Mechatron. 2009, 14, 21–31. [Google Scholar] [CrossRef]
- Pohl, D.W. Dynamic piezoelectric translation devices. Rev. Sci. Instrum. 1987, 58, 54–57. [Google Scholar] [CrossRef]
- Pohl, D.W. Sawtooth Nanometer Slider: A Versatile Low Voltage Piezoelectric Translation Device. Surf. Sci. 1987, 181, 174–175. [Google Scholar] [CrossRef]
- Wang, J.; Huang, H.; Wang, Z.; Liang, T.; Zhao, H. Analysis and comparison of flexible mechanisms for parasitic motion principle piezoelectric actuator. Smart Mater. Struct. 2021, 30, 075021. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Sun, W.; Yang, Z.; Liang, T.; Huang, H. A novel piezoelectric linear actuator designed by imitating skateboarding movement. Smart Mater. Struct. 2020, 29, 115038. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Sun, W.; Wang, K.; Yang, Z.; Liang, T.; Huang, H. A compact 2-DOF piezo-driven positioning stage designed by using the parasitic motion of flexure hinge mechanism. Smart Mater. Struct. 2020, 29, 015022. [Google Scholar] [CrossRef]
- Shi, Y.; Lou, C.; Zhang, J. Investigation on a Linear Piezoelectric Actuator Based on Stick-Slip/Scan Excitation. Actuators 2021, 10, 39. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Koc, B.; Delibas, B. Impact Force Analysis in Inertia-Type Piezoelectric Motors. Actuators 2023, 12, 52. [Google Scholar] [CrossRef]



| Material | PZT-5H |
|---|---|
| Density (kg/m3) | 7500 |
| Poisson’s ratio | 0.3 |
| Elastic modulus (×1010 N/m2) | |
| Piezoelectric constant (C/m2) | |
| Dielectric constant |
| Literature | [19] | [20] | [21] | [23] | This Work |
|---|---|---|---|---|---|
| Driving voltage (V) | 100 | 100 | 60 | ±25 | 100 |
| Driving frequency (Hz) | 280 | 100 | 2200 | 20,000 | 1000 |
| Number of driving voltages | 1 | 1 | 1 | 2 | 1 |
| Maximum forward speed (mm/s) | 7.613 | 1.648 | 2.5 | 16 | 10.63 |
| Maximum reverse speed (mm/s) | 10.058 | 1.403 | 1.8 | / | 10.12 |
| Speed deviation | 27.67% | 16.06% | 32.56% | / | 4.9% |
| Forward displacement resolution (nm) | 47 | 17,900 | 4 | 800 | 42.5 |
| Reverse displacement resolution (nm) | 45 | 15,300 | / | 800 | 52.5 |
| Load (N) | 2 | 2 | / | 3.2 | 2.2 |
| Overall size of the actuator (mm3) | 62.3 × 32 × 38 | 55 × 55 × 29.75 | 17 × 5 × 6 | / | 27.6 × 21.6 × 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Lei, C.; Ge, C.; Guo, Y.; Zhu, X. A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism. Micromachines 2023, 14, 1117. https://doi.org/10.3390/mi14061117
Sun P, Lei C, Ge C, Guo Y, Zhu X. A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism. Micromachines. 2023; 14(6):1117. https://doi.org/10.3390/mi14061117
Chicago/Turabian StyleSun, Pingping, Chenglong Lei, Chuannan Ge, Yunjun Guo, and Xingxing Zhu. 2023. "A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism" Micromachines 14, no. 6: 1117. https://doi.org/10.3390/mi14061117
APA StyleSun, P., Lei, C., Ge, C., Guo, Y., & Zhu, X. (2023). A Compact Piezo-Inertia Actuator Utilizing the Double-Rocker Flexure Hinge Mechanism. Micromachines, 14(6), 1117. https://doi.org/10.3390/mi14061117






