Numerical and Experimental Investigation on a “Tai Chi”-Shaped Planar Passive Micromixer
Abstract
:1. Introduction
2. Materials and Methods
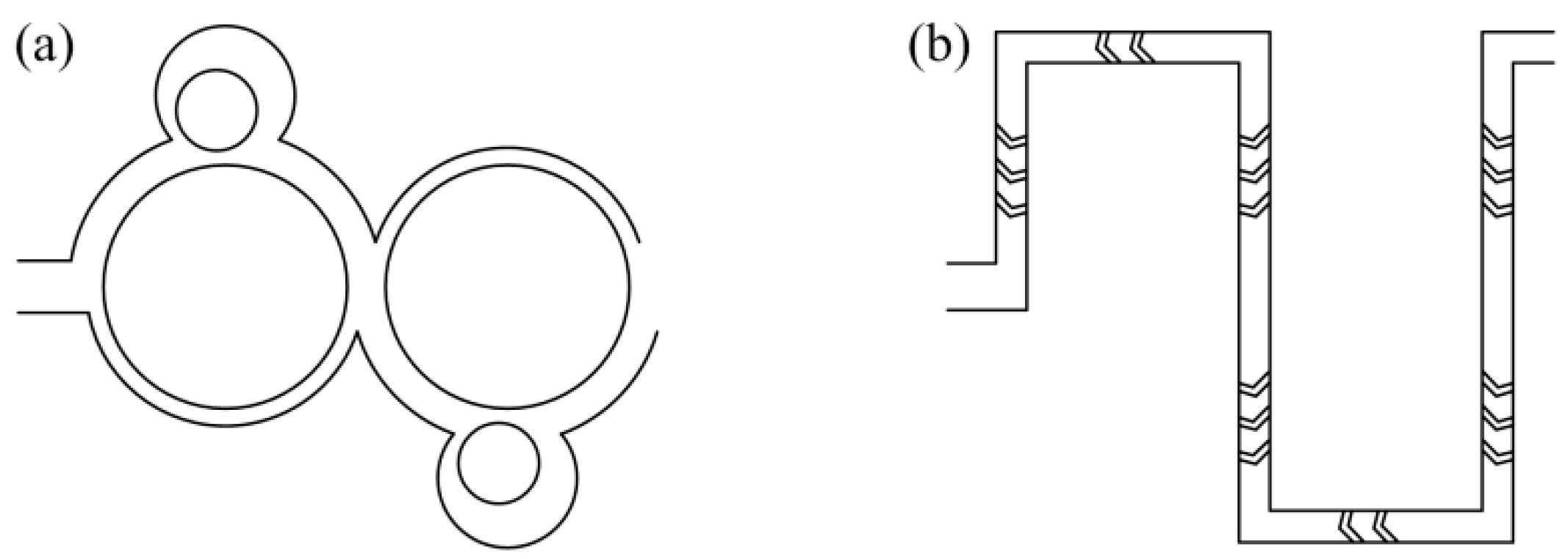
2.1. Micromixer Model
2.2. Governing Equations
2.3. Boundary Conditions
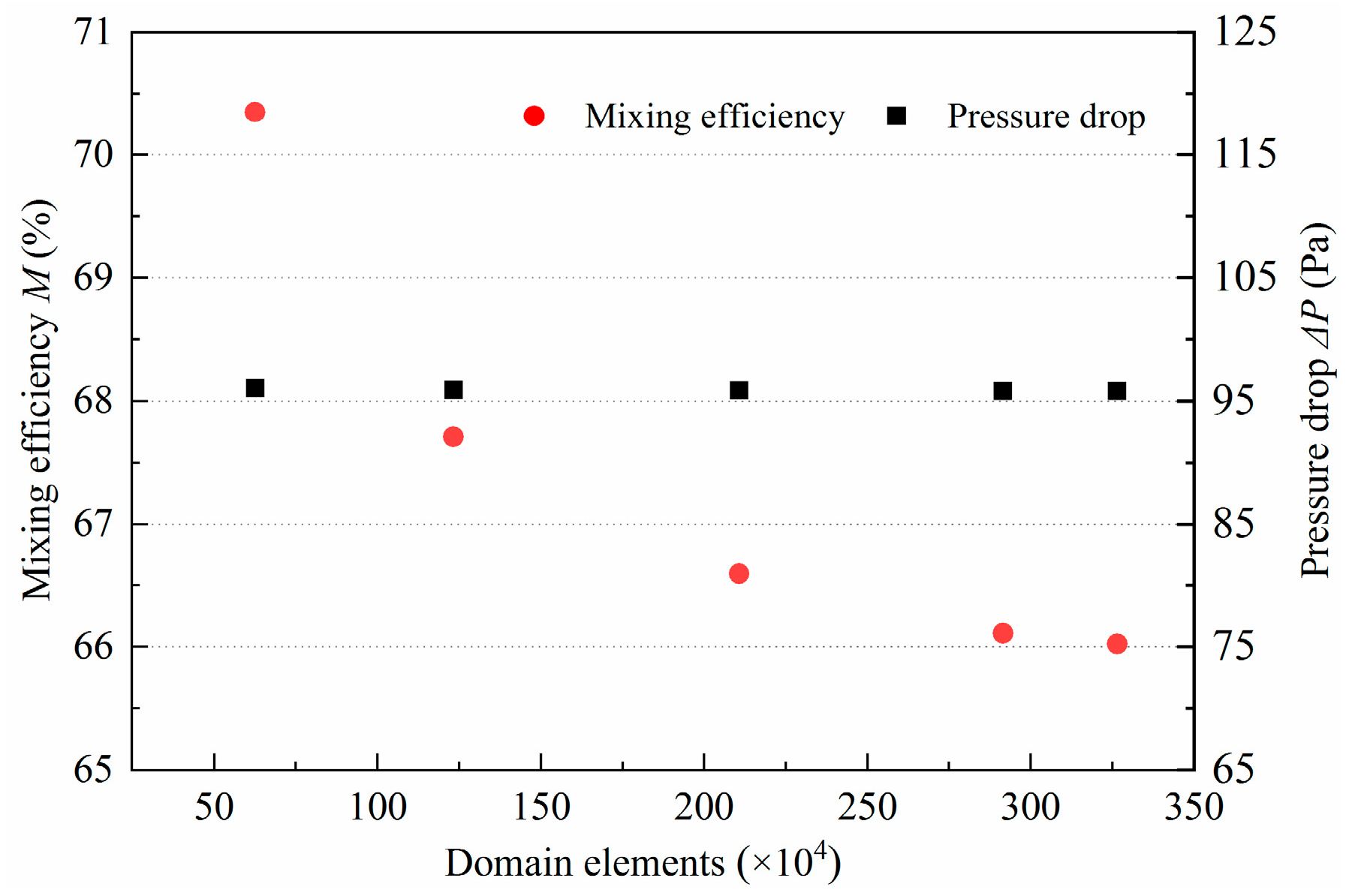
2.4. Mesh Independence Test
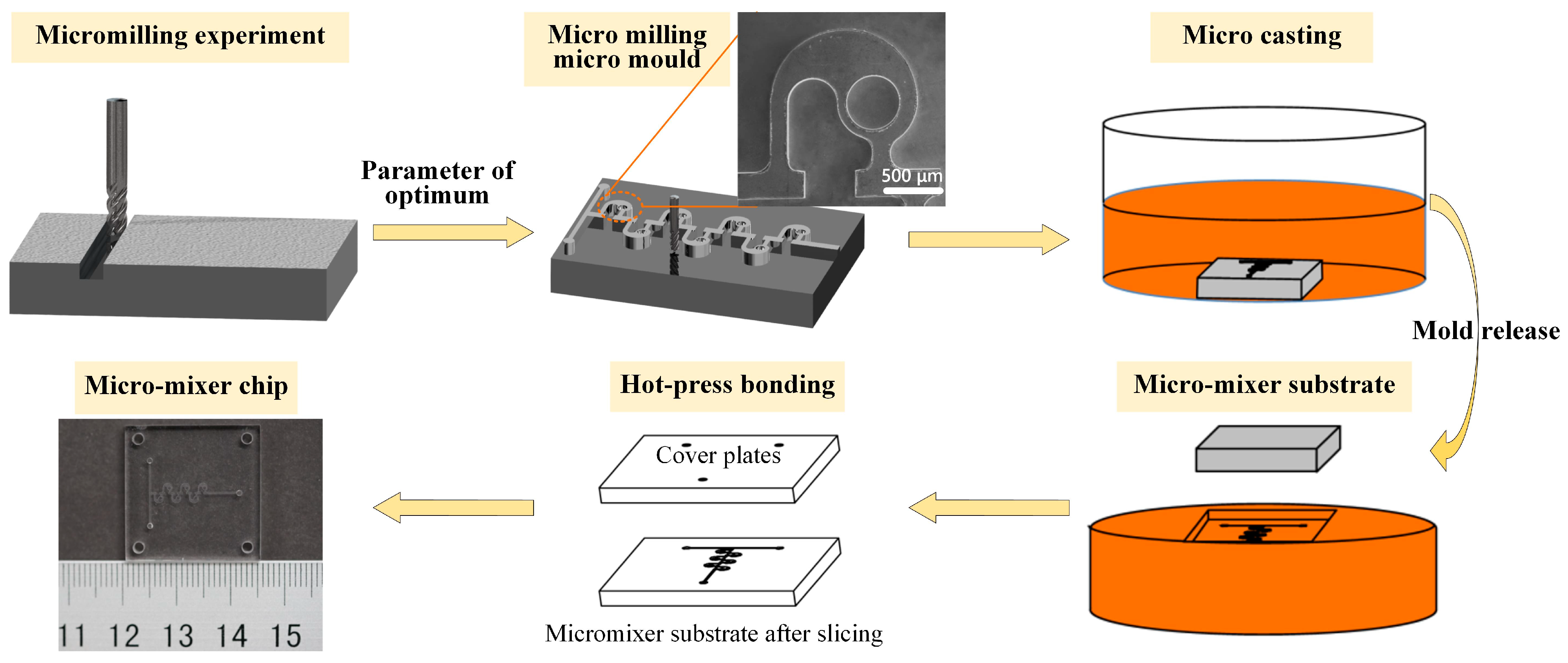
2.5. Preparation of Micromixer
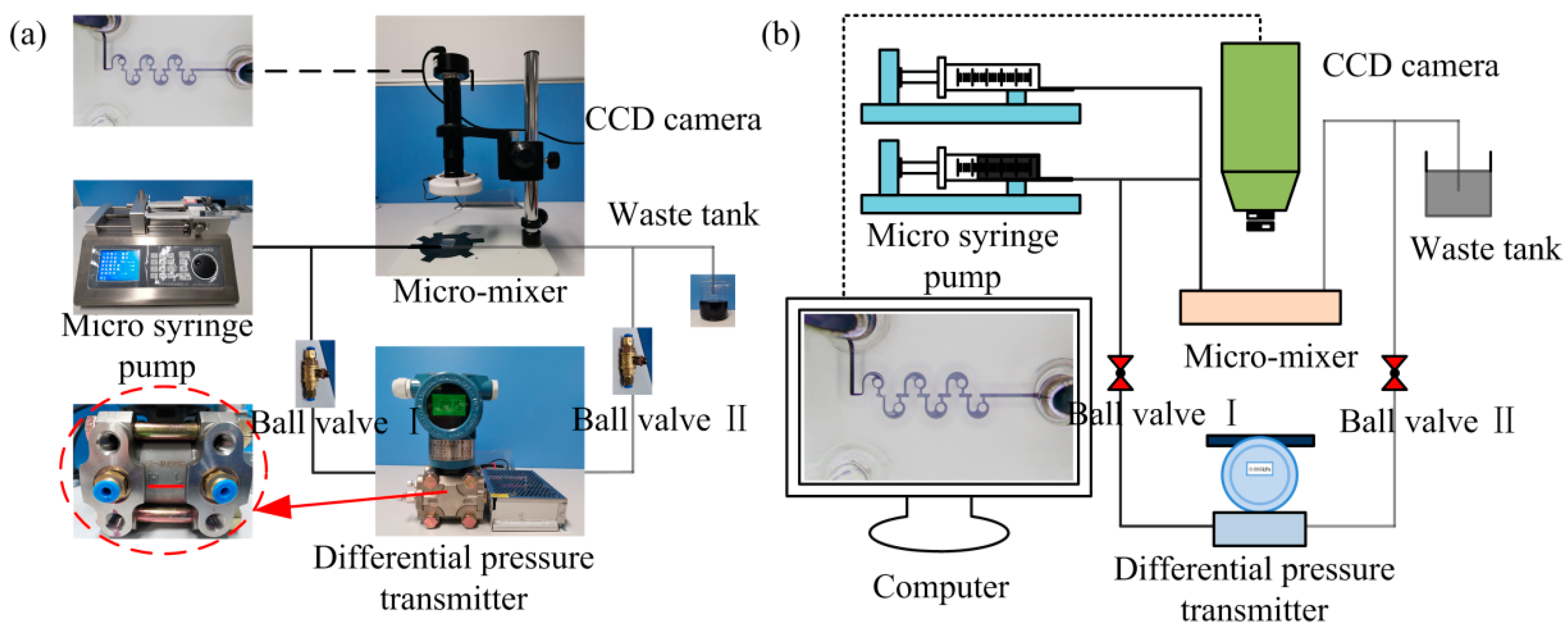
2.6. Experiment on Mixing Performance of Micromixer
3. Results and Discussion
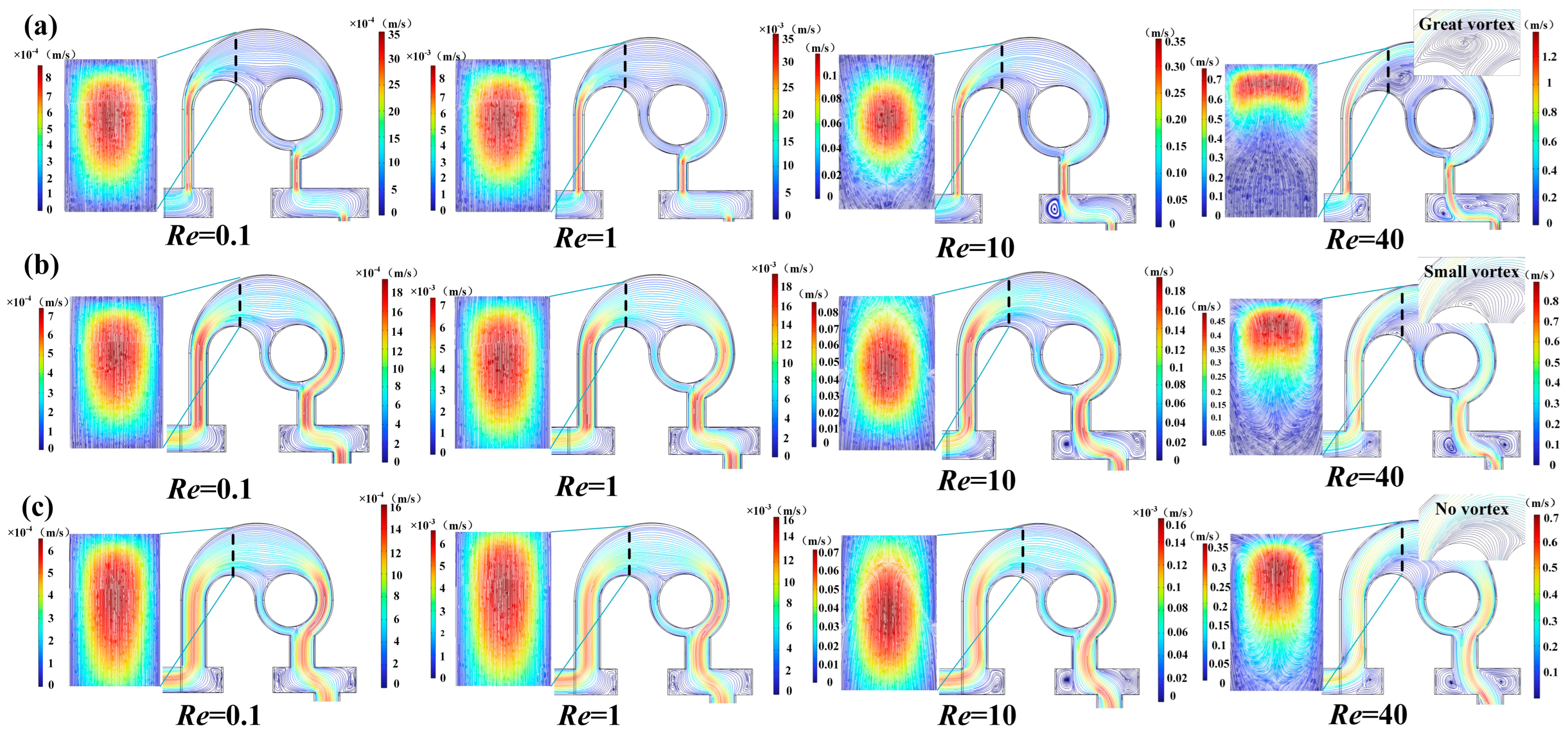
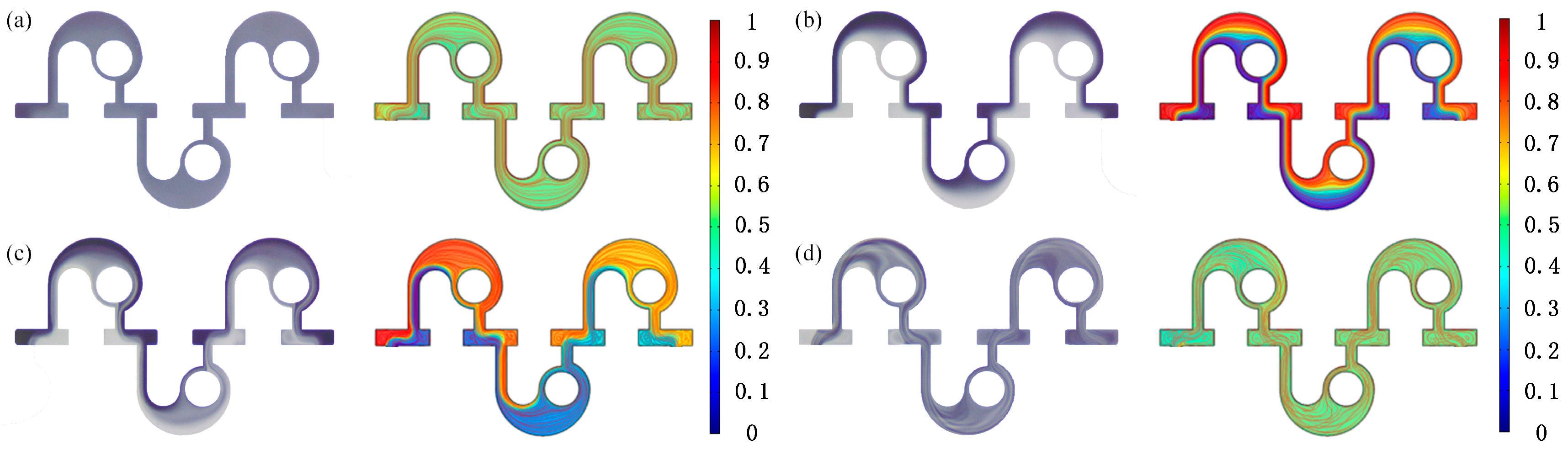
3.1. Effect of the Width of the Straight Channel on Mixing Performance
3.2. Effect of the Ratio of the Outer (r1) and Inner (r2) Walls on Mixing Performance
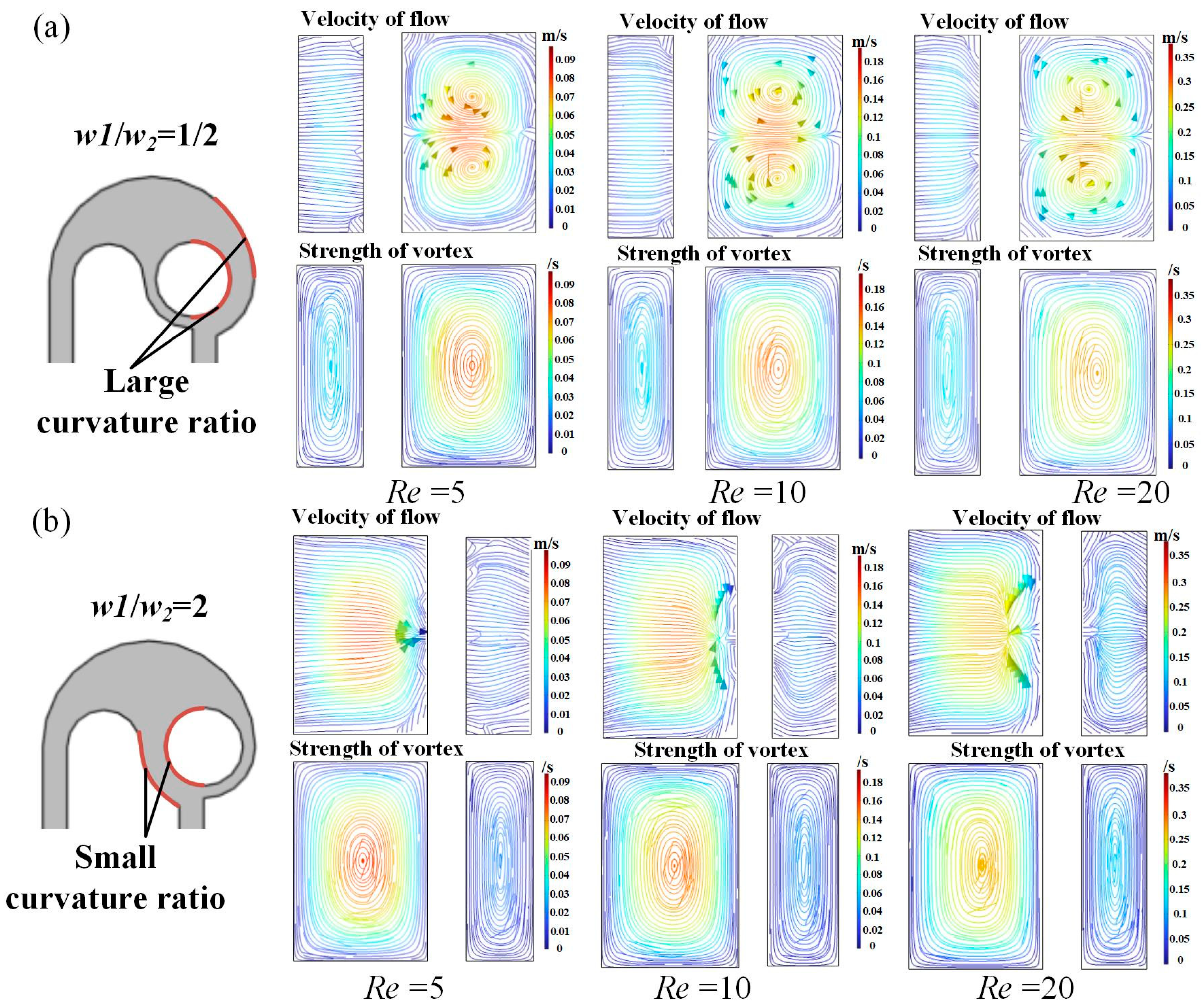
3.3. Effect of the Width Ratio (w1/w2) of the Arc Channel on Mixing Performance
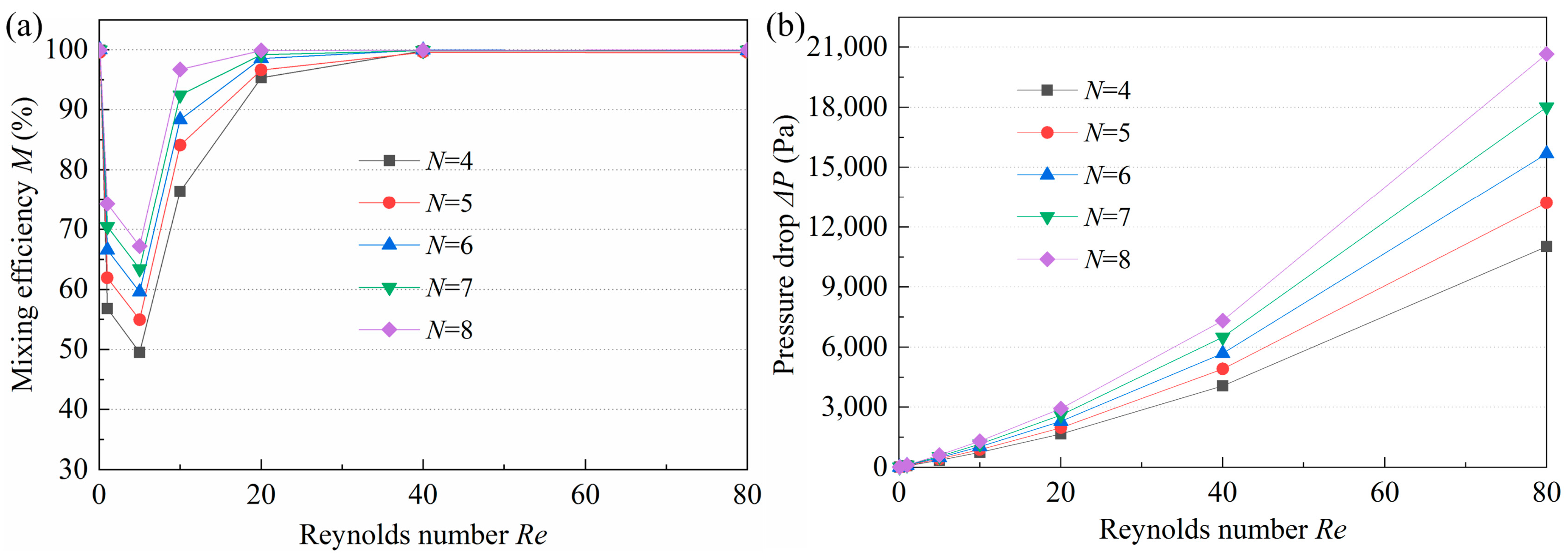
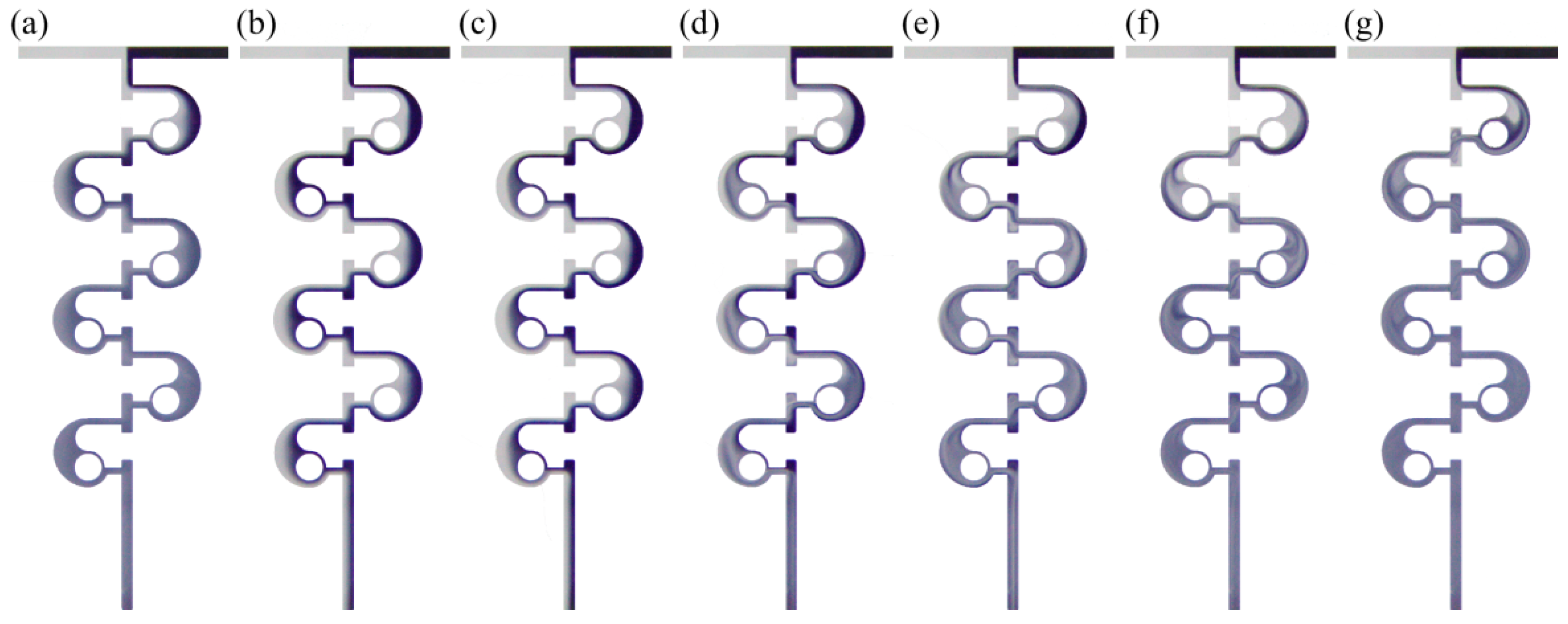
3.4. Effect of the Number of Mixing Units on Mixing Performance
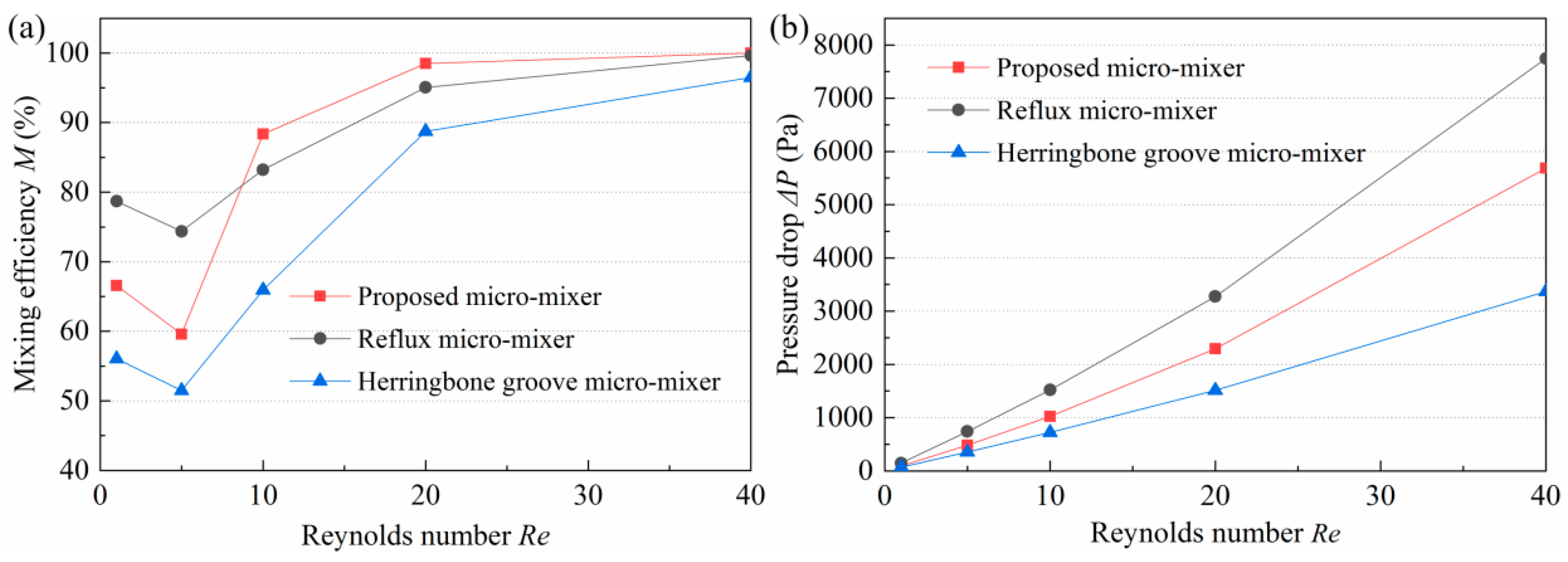
3.5. Comparison with Other Micromixers
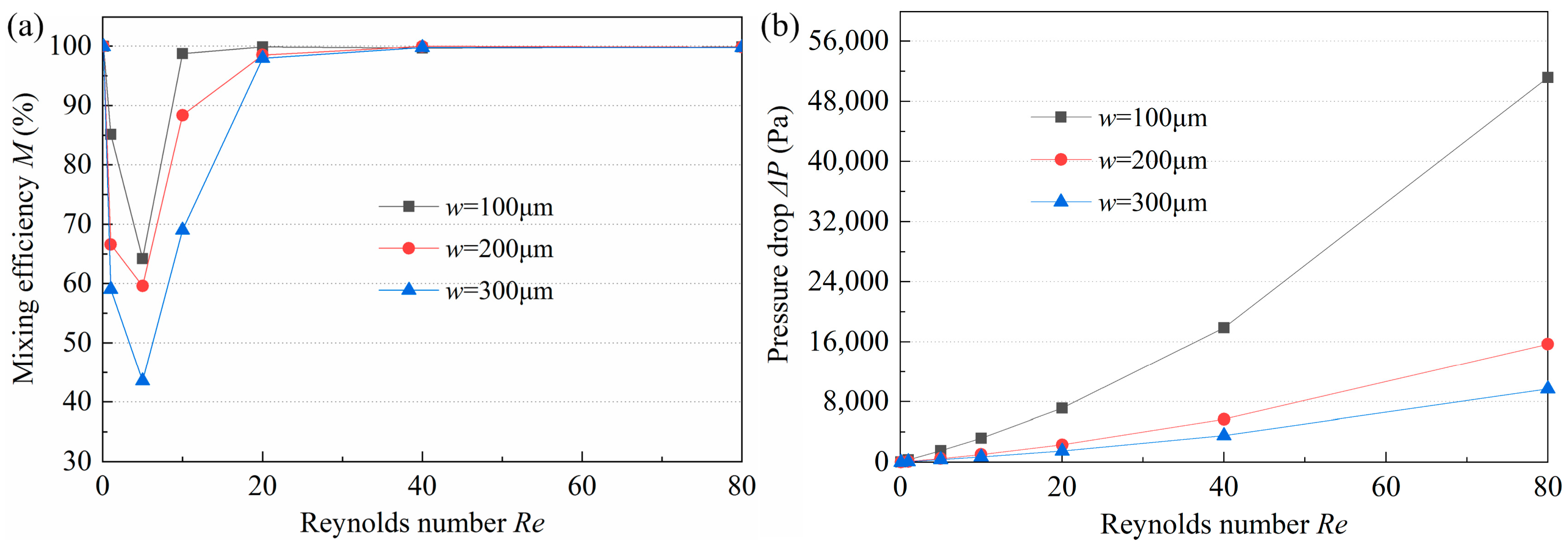
3.6. Experiment Analysis Using the Proposed Micromixer
4. Conclusions
- (1)
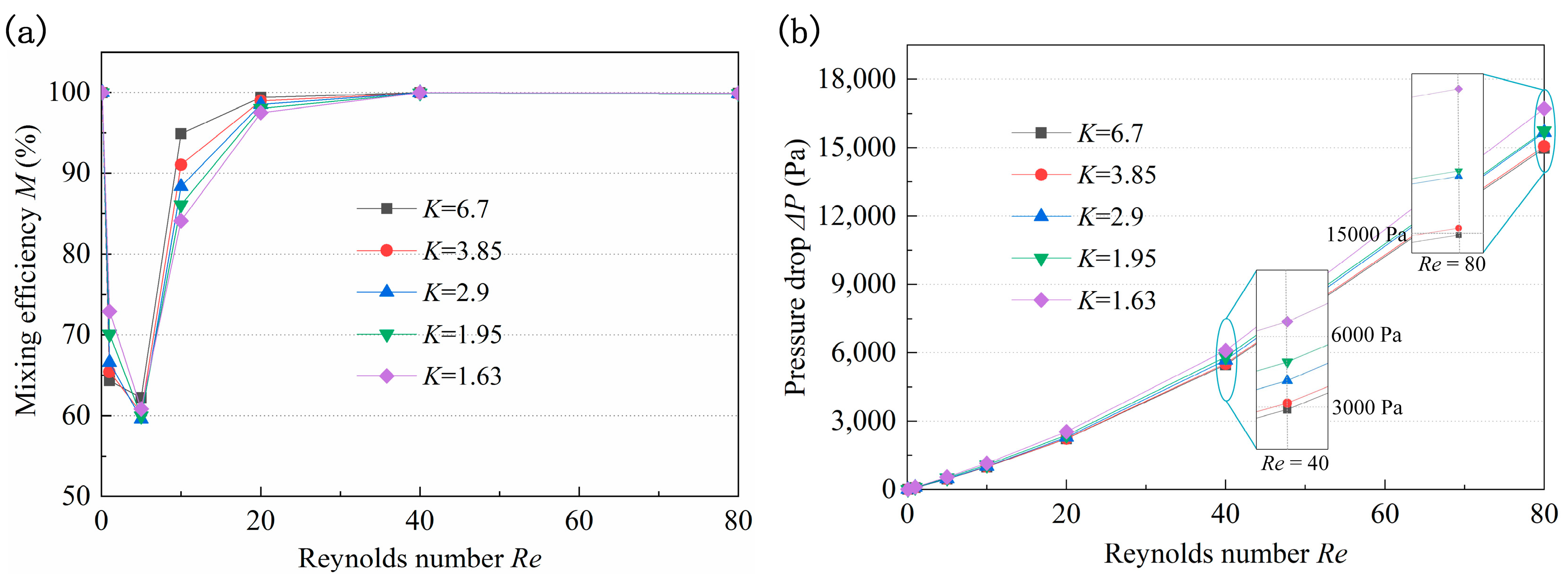
- The mixing state changes from molecular diffusion to chaotic convection with the increase of Re. At very low (Re < 1) and high (Re > 40) Re, the M is almost 100%. Nevertheless, in the case of medium Re, the intensity of the interaction of the two mechanisms is not high, leading to low M. In addition, the larger the Re, the higher the velocity, and the higher the pressure loss, especially at larger Re, the higher the increase of pressure drop.
- (2)
- Furthermore, the smaller the w, the larger the M and pressure drop. The effect of K on mixing performance is mainly reflected under medium Re, where the larger K results in a larger increase in the M and a smaller pressure drop. The w1/w2 has a significant effect on mixing performance, and the micromixer with w1/w2 = 1/2 was preferred. With the increase of N, the M and pressure drop tend to increase. Considering the M and pressure drop under different structural parameters at different Re ranging from 0.1 to 80, the structural parameters were optimized to be w = 200 μm, K = 2.9, w1/w2 = 1/2, and N = 6.
- (3)
- The experimental results demonstrated that the M at all Re studied was more than 50%, and at most Re, the M was nearly 100%. Moreover, the pressure drop was less than 18,000 Pa. The experimental and simulation results were in good agreement, which shows that numerical simulations have certain accuracy and can provide guidance for subsequent experimental research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Zhou, M.; Li, J.; Wang, Z.; Zhang, W.; Yue, C.; Ma, Y.; Peng, H.; Wei, Z.; Hu, Z. Identifying EGFR-expressed cells and detecting EGFR multi-mutations at single-cell level by microfluidic chip. Nano-Micro Lett. 2018, 10, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, X.-Y.; Deng, Z.-F.; Yan, Y.-Y.; Orel, V.E.; Shypko, A.; Orel, V.B.; Ivanova, D.; Pilarsky, C.; Tang, J.; Chen, Z.-S. Application of microfluidic chips in anticancer drug screening. Bosn. J. Basic Med. Sci. 2022, 22, 302. [Google Scholar] [CrossRef]
- Ho, N.R.; Lim, G.S.; Sundah, N.R.; Lim, D.; Loh, T.P.; Shao, H. Visual and modular detection of pathogen nucleic acids with enzyme–DNA molecular complexes. Nat. Commun. 2018, 9, 3238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dena, I.; Trieu, N.; Lisa, L. Complete Procedure for Fabrication of a Fused Silica Ultrarapid Microfluidic Mixer Used in Biophysical Measurements. Micromachines 2017, 8, 16. [Google Scholar]
- Phillips, R.H.; Jain, R.; Browning, Y.; Shah, R.; Kauffman, P.; Dinh, D.; Lutz, B.R. Flow control using audio tones in resonant microfluidic networks: Towards cell-phone controlled lab-on-a-chip devices. Lab Chip 2016, 16, 3260–3267. [Google Scholar] [CrossRef]
- Sollier, E.; Amini, H.; Go, D.E.; Sandoz, P.A.; Owsley, K.; Di Carlo, D. Inertial microfluidic programming of microparticle-laden flows for solution transfer around cells and particles. Microfluid. Nanofluidics 2015, 19, 53–65. [Google Scholar] [CrossRef]
- Adekanmbi, E.O.; Srivastava, S.K. Dielectrophoretic applications for disease diagnostics using lab-on-a-chip platforms. Lab Chip 2016, 16, 2148–2167. [Google Scholar] [CrossRef]
- Angelopoulou, M.; Petrou, P.S.; Makarona, E.; Haasnoot, W.; Moser, I.; Jobst, G.; Goustouridis, D.; Lees, M.; Kalatzi, K.; Raptis, I. Ultrafast multiplexed-allergen detection through advanced fluidic design and monolithic interferometric silicon chips. Anal. Chem. 2018, 90, 9559–9567. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, X.; Wu, Z.; Zhang, Q.; Gao, Q. Experimental study of fabricating a four-layers Cantor fractal microfluidic chip by CO2 laser system. Microsyst. Technol. 2019, 25, 1251–1256. [Google Scholar] [CrossRef]
- Hossain, S.; Kim, K.-Y. Mixing analysis in a three-dimensional serpentine split-and-recombine micromixer. Chem. Eng. Res. Des. 2015, 100, 95–103. [Google Scholar] [CrossRef]
- Ducrée, J. Ultrafast micromixing by coriolis-induced multi-lamination of centrifugal flow. In Proceedings of the Proc. of ACTUATOR 2004 9th International Conference on New Actuators, Bremen, Germany, 14–16 June 2004. [Google Scholar]
- Fallenius, B.E.; Sattari, A.; Fransson, J.H.; Sandberg, M. Experimental study on the effect of pulsating inflow to an enclosure for improved mixing. Int. J. Heat Fluid Flow 2013, 44, 108–119. [Google Scholar] [CrossRef]
- Nazari, M.; Chuang, P.-Y.A.; Esfahani, J.A.; Rashidi, S. A comprehensive geometrical study on an induced-charge electrokinetic micromixer equipped with electrically conductive plates. Int. J. Heat Mass Transf. 2020, 146, 118892. [Google Scholar] [CrossRef]
- Guan, Y.; Xu, F.; Sun, B.; Meng, X.; Liu, Y.; Bai, M. A hybrid electrically-and-piezoelectrically driven micromixer built on paper for microfluids mixing. Biomed. Microdevices 2020, 22, 47. [Google Scholar] [CrossRef] [PubMed]
- Azimi, N.; Rahimi, M.; Abdollahi, N. Using magnetically excited nanoparticles for liquid–liquid two-phase mass transfer enhancement in a Y-type micromixer. Chem. Eng. Process. Process Intensif. 2015, 97, 12–22. [Google Scholar] [CrossRef]
- Kamali, R.; Shekoohi, S.A.; Binesh, A. Effects of magnetic particles entrance arrangements on mixing efficiency of a magnetic bead micromixer. Nano-Micro Lett. 2014, 6, 30–37. [Google Scholar] [CrossRef]
- Zhang, C.; Brunet, P.; Royon, L.; Guo, X. Mixing intensification using sound-driven micromixer with sharp edges. Chem. Eng. J. 2021, 410, 128252. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, P.; Zhao, X.; Huang, L.; Xiao, Y.; Zhang, Y.; Zhang, J.; Hao, N. Sharp-edge acoustic microfluidics: Principles, structures, and applications. Appl. Mater. Today 2021, 25, 101239. [Google Scholar] [CrossRef]
- Mensing, G.A.; Pearce, T.M.; Graham, M.D.; Beebe, D.J. An externally driven magnetic microstirrer. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 1059–1068. [Google Scholar] [CrossRef]
- Santana, H.S.; Silva Jr, J.L.; Taranto, O.P. Numerical simulation of mixing and reaction of Jatropha curcas oil and ethanol for synthesis of biodiesel in micromixers. Chem. Eng. Sci. 2015, 132, 159–168. [Google Scholar] [CrossRef]
- Hedde, P.N.; Abram, T.J.; Jain, A.; Nakajima, R.; de Assis, R.R.; Pearce, T.; Jasinskas, A.; Toosky, M.N.; Khan, S.; Felgner, P.L. A modular microarray imaging system for highly specific COVID-19 antibody testing. Lab Chip 2020, 20, 3302–3309. [Google Scholar] [CrossRef]
- Hsieh, S.-S.; Lin, J.-W.; Chen, J.-H. Mixing efficiency of Y-type micromixers with different angles. Int. J. Heat Fluid Flow 2013, 44, 130–139. [Google Scholar] [CrossRef]
- Meunier, P. Geoinspired soft mixers. J. Fluid Mech. 2020, 903, A15. [Google Scholar] [CrossRef]
- Djenidi, L.; Moghtaderi, B. Numerical investigation of laminar mixing in a coaxial microreactor. J. Fluid Mech. 2006, 568, 223–242. [Google Scholar] [CrossRef] [Green Version]
- Kamholz, A.E.; Weigl, B.H.; Finlayson, B.A.; Yager, P. Quantitative analysis of molecular interaction in a microfluidic channel: The T-sensor. Anal. Chem. 1999, 71, 5340–5347. [Google Scholar] [CrossRef] [PubMed]
- Ismagilov, R.F.; Stroock, A.D.; Kenis, P.J.; Whitesides, G.; Stone, H.A. Experimental and theoretical scaling laws for transverse diffusive broadening in two-phase laminar flows in microchannels. Appl. Phys. Lett. 2000, 76, 2376–2378. [Google Scholar] [CrossRef] [Green Version]
- Veenstra, T.; Lammerink, T.S.; Elwenspoek, M.C.; van den Berg, A. Characterization method for a new diffusion mixer applicable in micro flow injection analysis systems. J. Micromech. Microeng. 1999, 9, 199. [Google Scholar] [CrossRef]
- Rahimi, M.; Akbari, M.; Parsamoghadam, M.A.; Alsairafi, A.A. CFD study on effect of channel confluence angle on fluid flow pattern in asymmetrical shaped microchannels. Comput. Chem. Eng. 2015, 73, 172–182. [Google Scholar] [CrossRef]
- Virginie, M.; Jacques, J.; Girault, H.H. Mixing processes in a zigzag microchannel: Finite element simulations and optical study. Anal. Chem. 2002, 74, 4279–4286. [Google Scholar]
- Zhang, K.; Guo, S.; Zhao, L.; Zhao, X.; Chan, H.L.; Wang, Y. Realization of planar mixing by chaotic velocity in microfluidics. Microelectron. Eng. 2011, 88, 959–963. [Google Scholar] [CrossRef]
- Solehati, N.; Bae, J.; Sasmito, A.P. Numerical investigation of mixing performance in microchannel T-junction with wavy structure. Comput. Fluids 2014, 96, 10–19. [Google Scholar] [CrossRef]
- Bessoth, F.G.; deMello, A.J.; Manz, A. Microstructure for efficient continuous flow mixing. Anal. Commun. 1999, 36, 213–215. [Google Scholar] [CrossRef]
- Ansari, M.A.; Kim, K.-Y.; Anwar, K.; Kim, S.M. A novel passive micromixer based on unbalanced splits and collisions of fluid streams. J. Micromech. Microeng. 2010, 20, 055007. [Google Scholar] [CrossRef] [Green Version]
- Stroock, A.D.; Dertinger, S.K.; Ajdari, A.; Mezic, I.; Stone, H.A.; Whitesides, G.M. Chaotic mixer for microchannels. Science 2002, 295, 647–651. [Google Scholar] [CrossRef] [Green Version]
- Wangikar, S.S.; Patowari, P.K.; Misra, R.D. Numerical and experimental investigations on the performance of a serpentine microchannel with semicircular obstacles. Microsyst. Technol. 2018, 24, 3307–3320. [Google Scholar] [CrossRef]
- Wang, L.; Ma, S.; Wang, X.; Bi, H.; Han, X. Mixing enhancement of a passive microfluidic mixer containing triangle baffles. Asia-Pac. J. Chem. Eng. 2014, 9, 877–885. [Google Scholar] [CrossRef]
- Miyake, R.; Lammerink, T.; Elwenspoek, M.; Fluitman, J. Micro mixer with fast diffusion. In Proceedings of the Micro Electro Mechanical Systems, Mems 93, An Investigation of Micro Structures, Sensors, Actuators, Machines & Systems IEEE, Fort Lauderdale, FL, USA, 10 February 1993; pp. 248–253. [Google Scholar]
- Song, H.; Bringer, M.R.; Tice, J.D.; Gerdts, C.J.; Ismagilov, R.F. Experimental test of scaling of mixing by chaotic advection in droplets moving through microfluidic channels. Appl. Phys. Lett. 2003, 83, 4664–4666. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Yang, Q.; Chen, F.; Zhao, Y.; Meng, X.; Shan, C.; Li, Y. Design and analysis of the cross-linked dual helical micromixer for rapid mixing at low Reynolds numbers. Microfluid. Nanofluidics 2015, 19, 169–180. [Google Scholar] [CrossRef]
- Vinogradova, O.I. Slippage of water over hydrophobic surfaces. Int. J. Miner. Process. 1999, 56, 31–60. [Google Scholar] [CrossRef]
- Eijkel, J. Liquid slip in micro-and nanofluidics: Recent research and its possible implications. Lab Chip 2007, 7, 299–301. [Google Scholar]
- Woldemariam, M.; Filimonov, R.; Purtonen, T.; Sorvari, J.; Koiranen, T.; Eskelinen, H. Mixing performance evaluation of additive manufactured milli-scale reactors. Chem. Eng. Sci. 2016, 152, 26–34. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; He, Y.; Wang, T.; Zhu, Z.; Xu, R.; Yu, Q.; Zhao, B.; Zhao, W.; Liu, P.; Wang, X. A review of the techniques for the mold manufacturing of micro/nano-structures for precision glass molding. Int. J. Extrem. Manuf. 2021, 3, 042002. [Google Scholar] [CrossRef]
- O’Hara, J.; Fang, F. Advances in micro cutting tool design and fabrication. Int. J. Extrem. Manuf. 2019, 1, 032003. [Google Scholar] [CrossRef]



| Reynolds number Re | 0.1 | 1 | 5 | 10 | 20 | 40 | 80 |
| Inlet velocity u (×10−2 m/s) | 0.032 | 0.32 | 1.62 | 3.23 | 6.47 | 12.93 | 25.87 |
| Cutter Diameter (mm) | Spindle Speed (r·min−1) | Feed per Tooth (μm/z) | The Axial Cutting Depth (μm) | The Radial Cutting Depth (μm) |
|---|---|---|---|---|
| 0.2 | 40,000 | 2.5 | 8 | 120 |
| 0.5 | 30,000 | 5.333 | 15 | 200 |
| Reynolds number Re | 0.1 | 1 | 5 | 10 | 20 | 40 | 80 |
| Flow rate q (μL/min) | 1.746 | 17.46 | 87.3 | 174.6 | 349.2 | 698.4 | 1396.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, A.; Shen, C.; Wei, C.; Meng, L.; Hu, Z.; Zhang, L.; Chen, M.; Li, L.; He, N.; Hao, X. Numerical and Experimental Investigation on a “Tai Chi”-Shaped Planar Passive Micromixer. Micromachines 2023, 14, 1414. https://doi.org/10.3390/mi14071414
Xia A, Shen C, Wei C, Meng L, Hu Z, Zhang L, Chen M, Li L, He N, Hao X. Numerical and Experimental Investigation on a “Tai Chi”-Shaped Planar Passive Micromixer. Micromachines. 2023; 14(7):1414. https://doi.org/10.3390/mi14071414
Chicago/Turabian StyleXia, Annan, Cheng Shen, Chengfeng Wei, Lingchen Meng, Zhiwen Hu, Luming Zhang, Mengyue Chen, Liang Li, Ning He, and Xiuqing Hao. 2023. "Numerical and Experimental Investigation on a “Tai Chi”-Shaped Planar Passive Micromixer" Micromachines 14, no. 7: 1414. https://doi.org/10.3390/mi14071414
APA StyleXia, A., Shen, C., Wei, C., Meng, L., Hu, Z., Zhang, L., Chen, M., Li, L., He, N., & Hao, X. (2023). Numerical and Experimental Investigation on a “Tai Chi”-Shaped Planar Passive Micromixer. Micromachines, 14(7), 1414. https://doi.org/10.3390/mi14071414








