Thermal Performance Optimization of Integrated Microchannel Cooling Plate for IGBT Power Module
Abstract
:1. Introduction
2. Computational Models and Methods
2.1. Geometric Modeling of IGBT Power Module
- (1)
- The size and quality are the same before and after equivalency;
- (2)
- The effect of the model before and after equivalency on-chip heat dissipation is the same. (This signifies that the thermal conductivity of the equivalent block is the same as the thermal conductivity of the actual model).
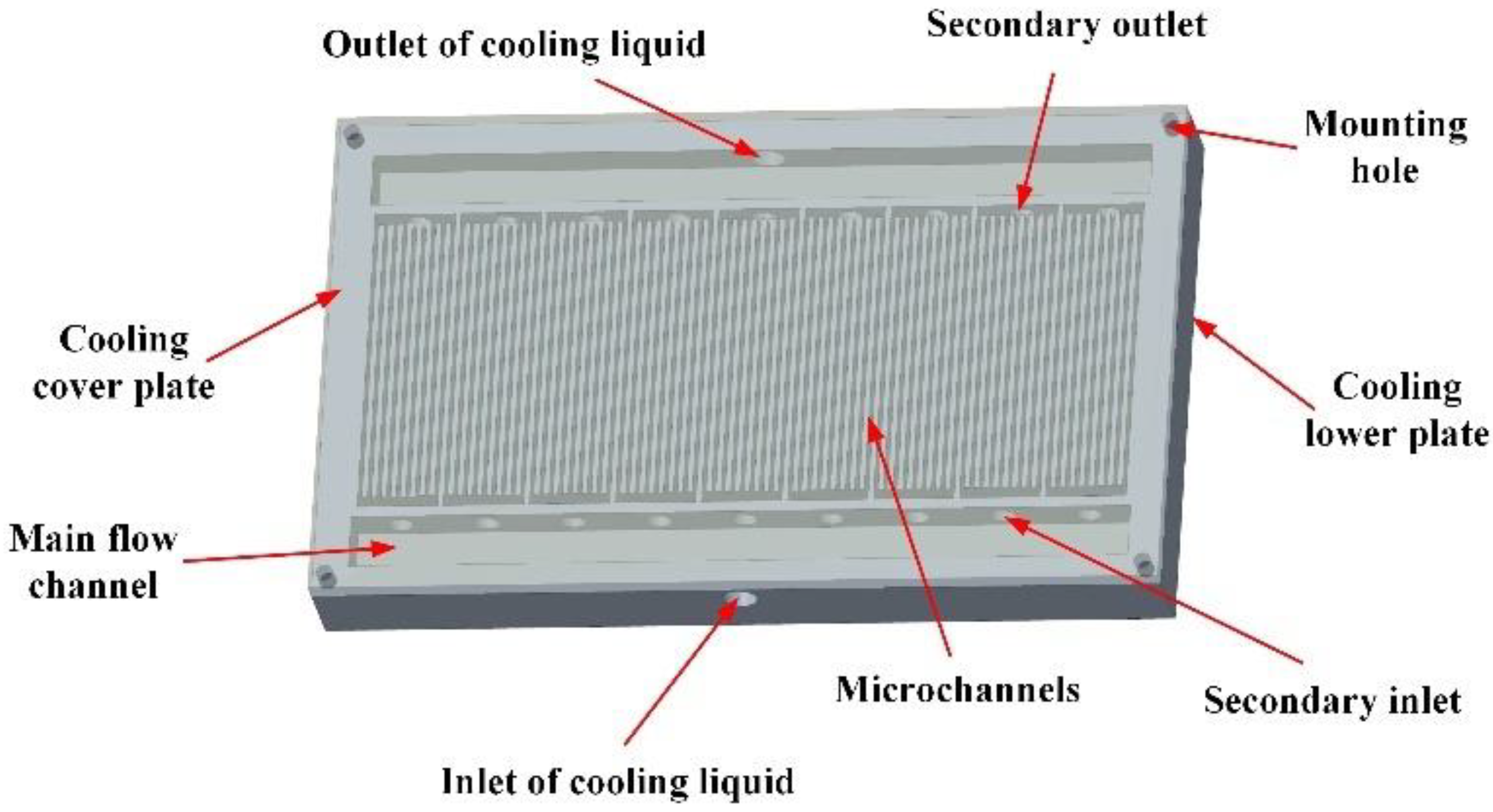
2.2. Geometric Modeling of Cooling Plate
2.3. Governing Equations
2.4. Computational Models and Boundary Conditions
- (1)
- For the module of incompressible laminar flow, the pressure at the inlet of the fluid is 200 Pa, the pressure at the outlet is 0 Pa, and the initial temperature of the cooling liquid is 20 °C;
- (2)
- For the module of heat transfer, the heat sources of 16 SiC chips are 3.87 × 109 W/m3;
- (3)
- The condition of the walls in incompressible laminar flow module is no slipping wall.
3. Result and Discussion
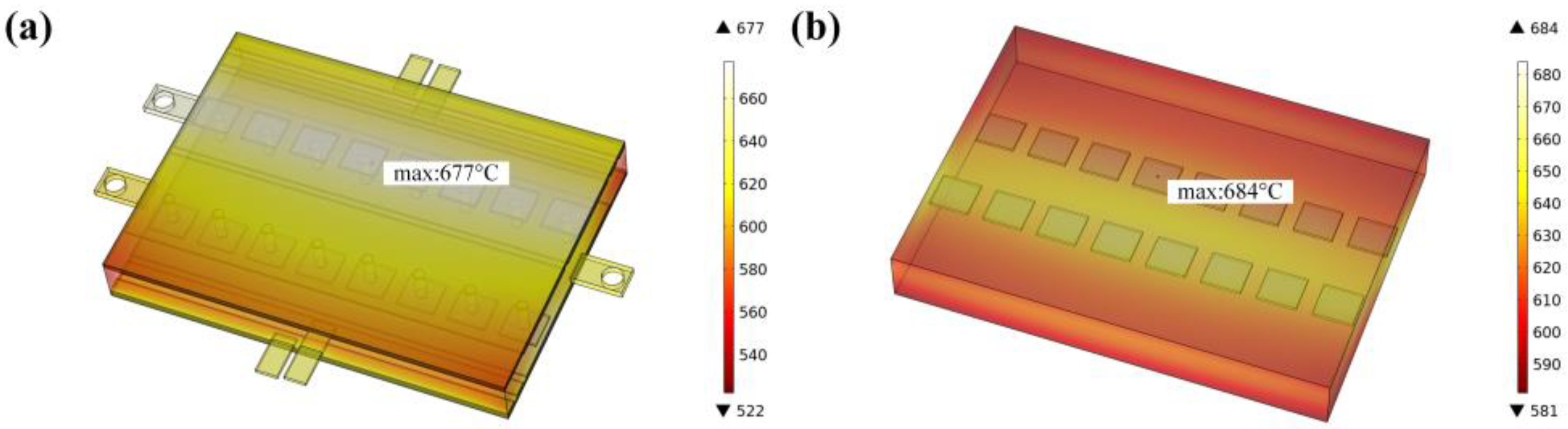
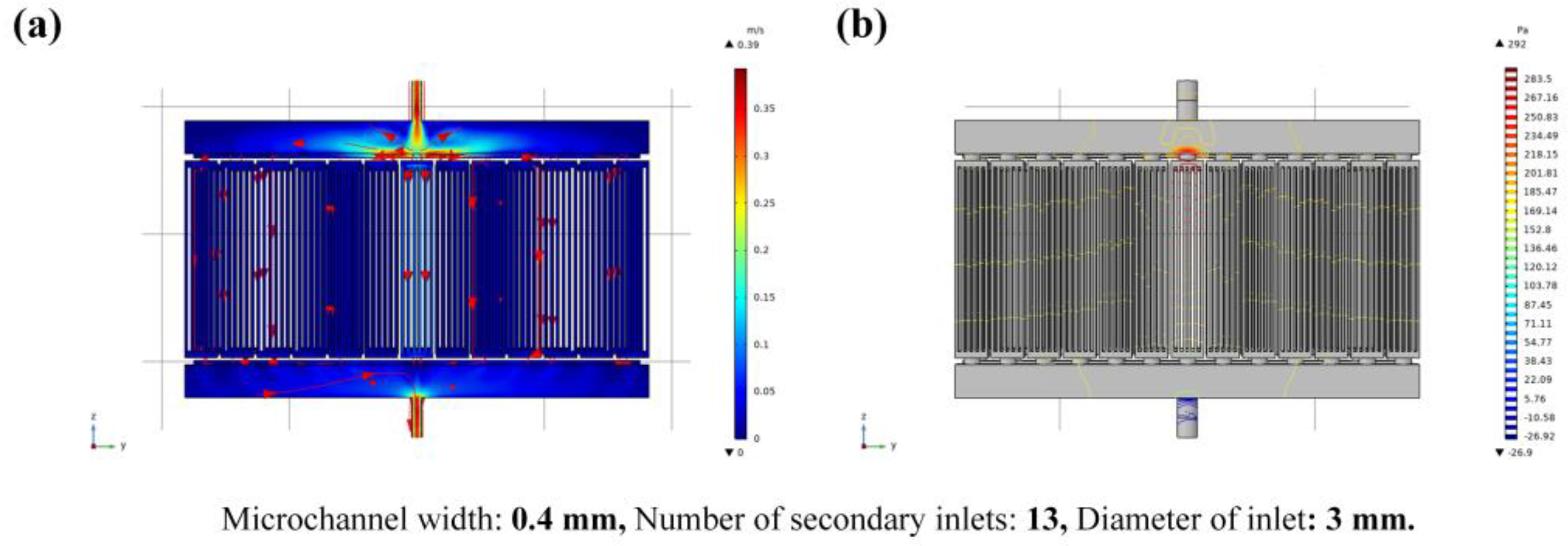
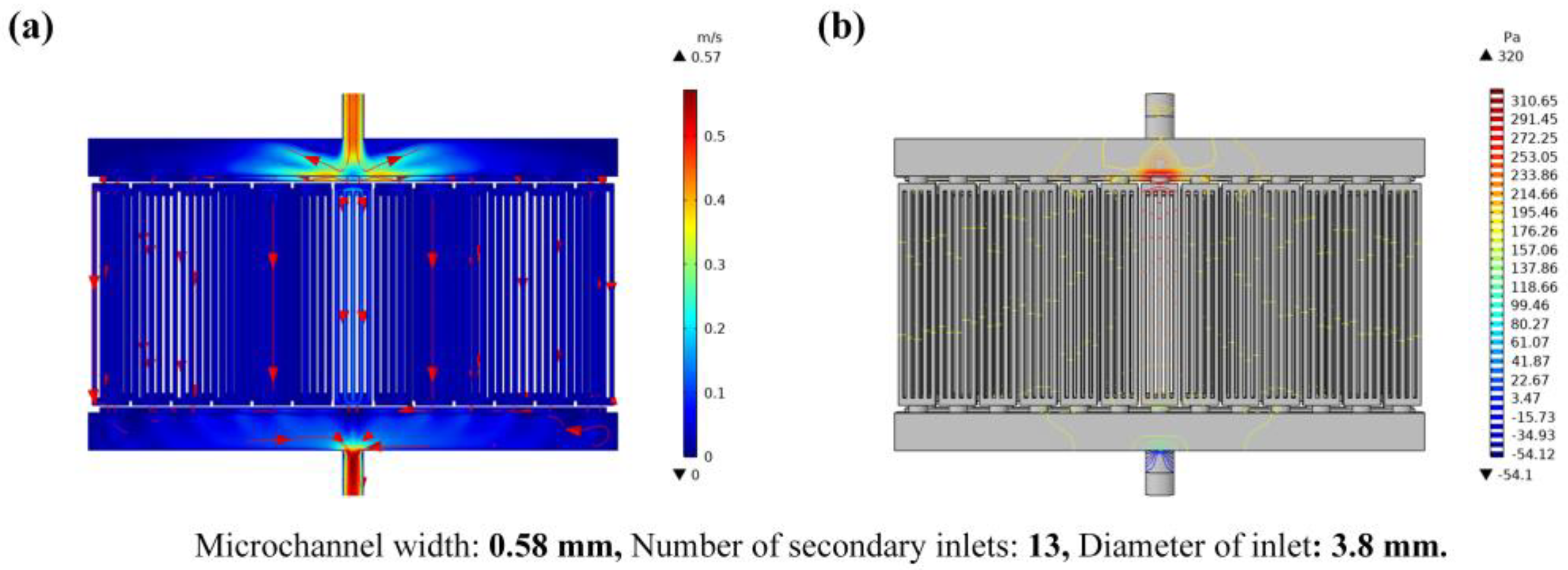
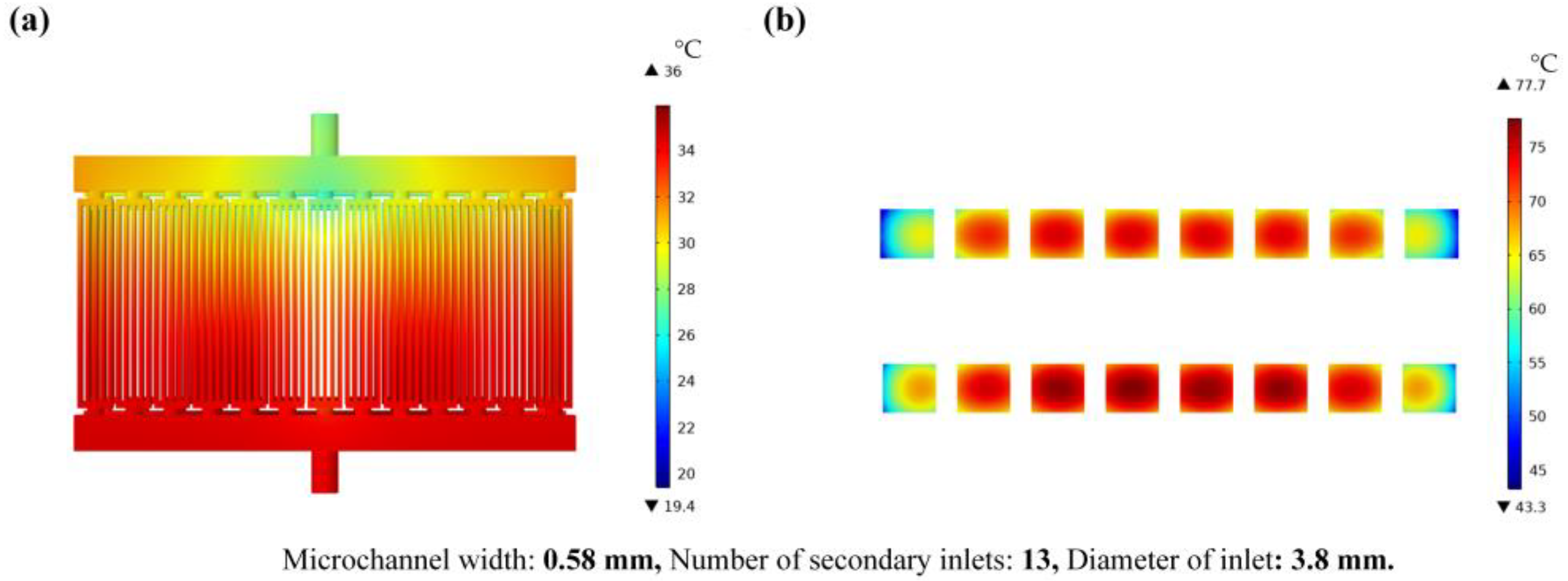
3.1. Thermal Performance of Microchannel Cooling Plate
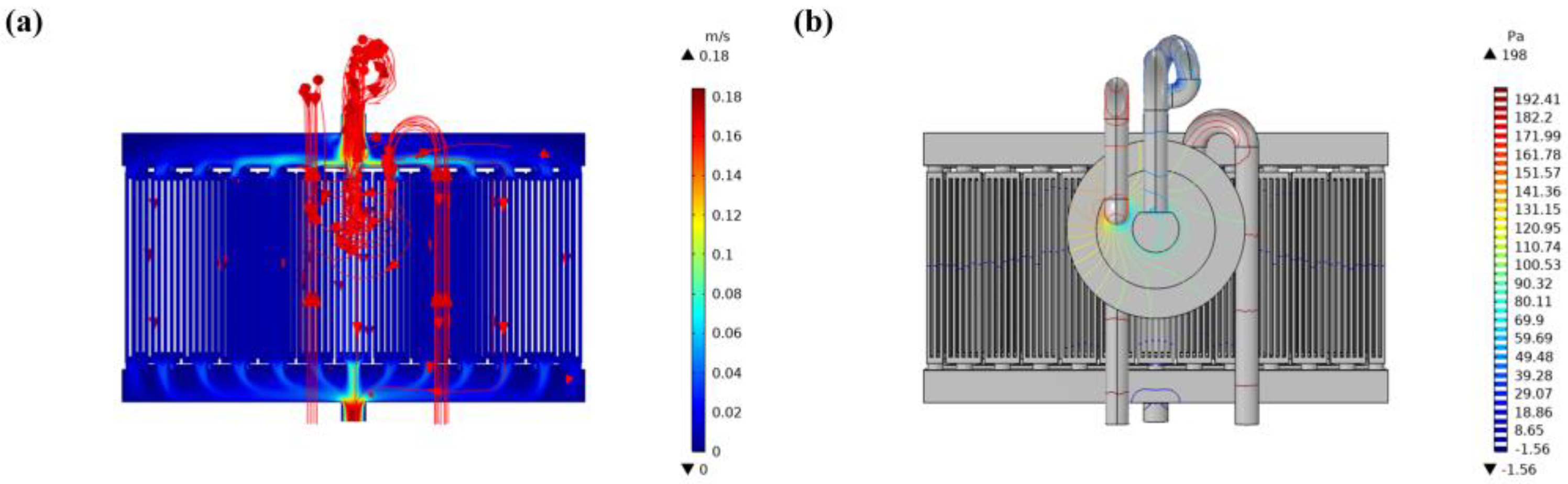
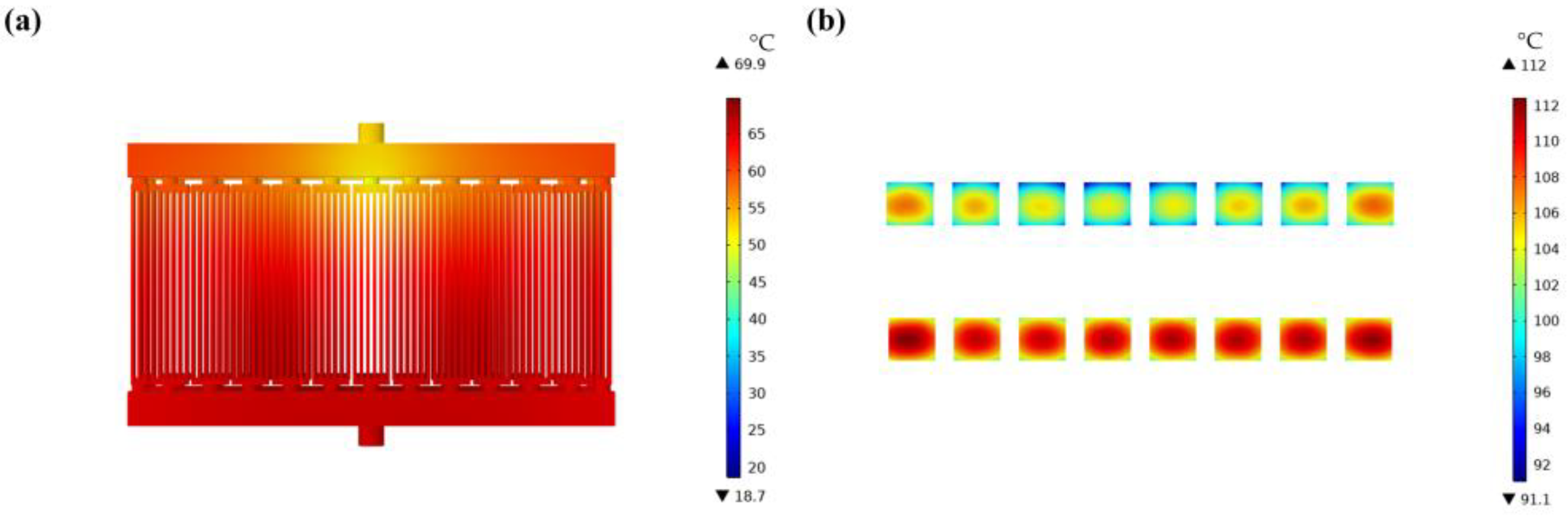
3.2. Effect of Micropumps on the Thermal Performance of Microchannel Cooling Plates
4. Conclusions
- (1)
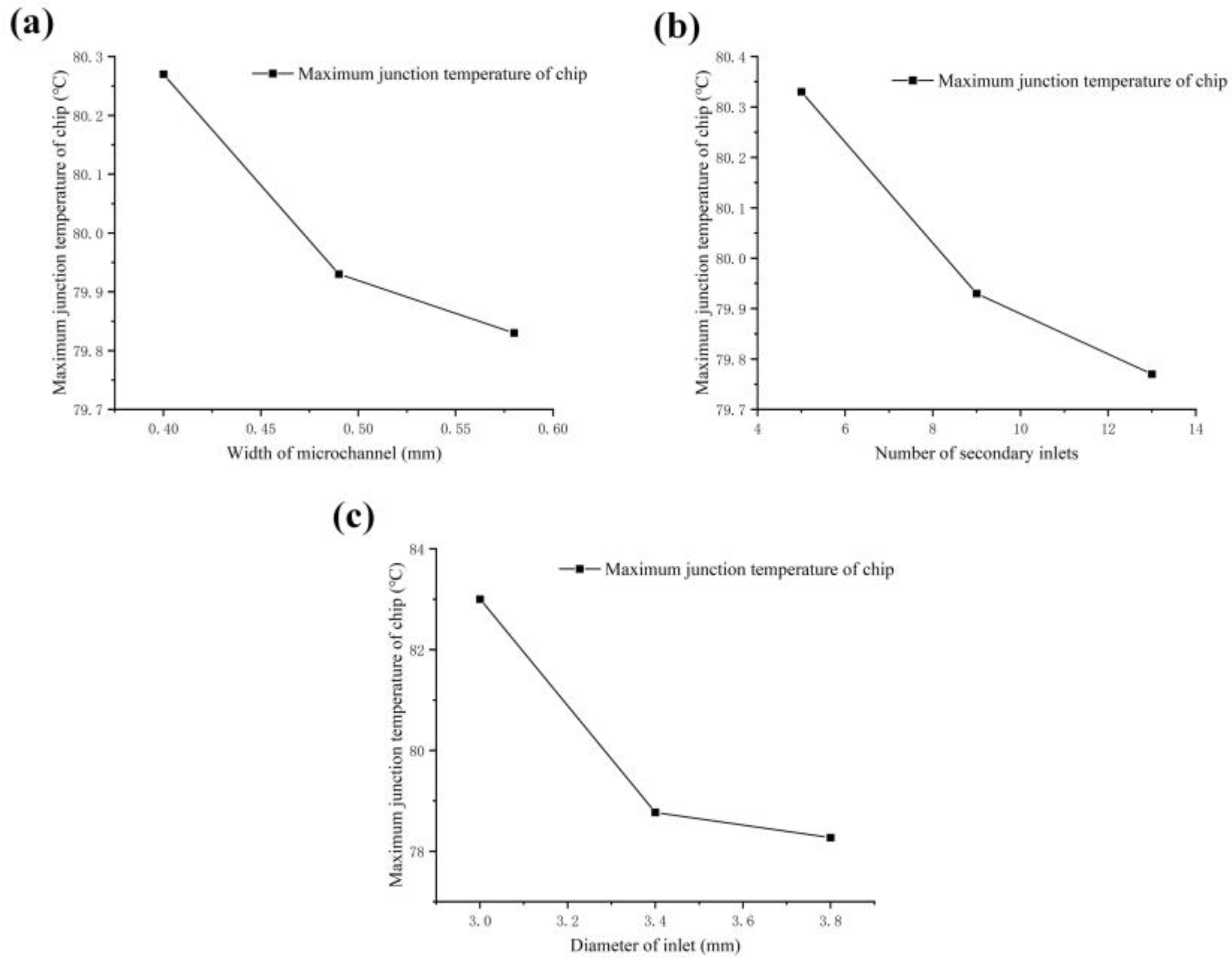
- The microchannel cooling plate can reduce the operating temperature of IGBT power modules. In addition, as the width of the microchannel, the number of secondary inlets, and the diameter of the inlet increase, the chip-junction temperature gradually decreases. The order of influence of the three factors is the diameter of the inlet > number of secondary inlets > width of the microchannel;
- (2)
- The optimal structure of the cooling plate theory obtained by orthogonal analysis is that the width of the microchannel is 0.58 mm, the number of secondary inlets is 13, the diameter of inlets is 3.8 mm, and the maximum junction temperature of chips decreased from 677 °C to 77.7 °C. Therefore, the temperature of the chip can be significantly reduced by optimizing the cooling plate structure reasonably;
- (3)
- The micropump increases the distance of fluid flow, the resistance of the fluid along the way increases, and the velocity of the cooling plate fluid input decreases. The maximum chip-junction temperature of the microchannel cooling plate after installing the micropump increased from 77.7 °C to 110 °C. Hence, in order to reduce the impact of micropumps on the cooling efficiency of the cooling plate, the length of the connecting pipe between the micropump and the cooling plate should be reduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandeya, R.; Chen, C.; Pickert, V.; Naayagi, R.T.; Ji, B. Gate–emitter pre-threshold voltage as a health-sensitive parameter for IGBT chip failure monitoring in high-voltage multichip IGBT power modules. IEEE Trans. Power Electron. 2019, 34, 9158–9169. [Google Scholar] [CrossRef] [Green Version]
- Shammas, N.; Rodriguez, M.; Plumpton, A.; Newcombe, D. Finite element modelling of thermal fatigue effects in IGBT modules. IEE Proc. Circuits Devices Syst. 2001, 148, 95–100. [Google Scholar] [CrossRef]
- Naqiuddin, N.H.; Saw, L.H.; Yew, M.C.; Yusof, F.; Ng, T.C.; Yew, M.K. Overview of micro-channel design for high heat flux application. Renew. Sustain. Energy Rev. 2018, 82, 901–914. [Google Scholar] [CrossRef]
- Tounsi, M.; Oukaour, A.; Tala-Ighil, B.; Gualous, H.; Boudart, B.; Aissani, D. Characterization of high-voltage IGBT module degradations under PWM power cycling test at high ambient temperature. Microelectron. Reliab. 2010, 50, 1810–1814. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, X.; Tolbert, L.M.; Wang, F.; Liang, Z.; Costinett, D. A high temperature silicon carbide mosfet power module with integrated silicon-On-insulator-based gate drive. IEEE Trans. Power Electron. 2014, 30, 1432–1445. [Google Scholar] [CrossRef]
- Arabi, F.; Gracia, A.; Delétage, J.Y.; Frémont, H. Sequential combined thermal cycling and vibration test and simulation of printed circuit board. Microelectron. Reliab. 2018, 88–90, 768–773. [Google Scholar] [CrossRef]
- Amalu, E.H.; Ekere, N.N. Damage of lead-free solder joints in flip chip assemblies subjected to high-temperature thermal cycling. Comput. Mater. Sci. 2012, 65, 470–484. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J.; Dong, F.; Yu, J. Power cycling failure analysis of double side cooled IGBT modules for automotive applications. Microelectron. Reliab. 2021, 124, 114282. [Google Scholar] [CrossRef]
- Ji, B.; Song, X.; Cao, W.; Pickert, V.; Hu, Y.; Mackersie, J.W.; Pierce, G. In situ diagnostics and prognostics of solder fatigue in IGBT modules for electric vehicle drives. IEEE Trans. Power Electron. 2015, 30, 1535–1543. [Google Scholar]
- Xu, Y.; Bao, J.; Ning, R.; Chen, Z.; Xu, W. Heat dissipation study of graphene-based film in single tube IGBT devices. AIP Adv. 2019, 9, 035103. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.-H.; Moon, C.-H. Comparison of the Thermal Performance of the Multichip LED Packages. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1832–1837. [Google Scholar]
- Lin, H.; Guo, X.; Chen, G. Comprehensive thermal resistance model of forced air cooling system for multiple power chips. Energy Rep. 2021, 7, 261–267. [Google Scholar] [CrossRef]
- Colgan, E.G.; Furman, B.; Gaynes, M.; Graham, W.S.; LaBianca, N.C.; Magerlein, J.H.; Polastre, R.J.; Rothwell, M.B.; Bezama, R.J.; Choudhary, R.; et al. A practical implementation of silicon microchannel coolers for high power chips. IEEE Trans. Compon. Packag. Technol. 2007, 30, 218–225. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X.; Zheng, S. Condition monitoring of IGBT module and forced air cooling system using time constants of heat sink temperature cooling curve. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 2554–2558. [Google Scholar]
- Maghrabie, H.M.; Olabi, A.G.; Sayed, E.T.; Wilberforce, T.; Elsaid, K.; Doranehgard, M.H.; Abdelkareem, M.A. Microchannel heat sinks with nanofluids for cooling electronic components: Performance enhancement, challenges, and limitations. Therm. Sci. Eng. Prog. 2023, 37, 101608. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, H.; Liu, C.; Chen, J.; Liu, C.; Zhang, T.; Gong, W. Transient Heat Transfer Characteristics in a Flat Plate Heat Sink with Mini-Channels for Cooling High Heat Flux IGBT. Micromachines 2022, 13, 1417. [Google Scholar] [CrossRef]
- Hung, T.C.; Yan, W.-M.; Li, W.-P. Analysis of heat transfer characteristics of double-layered microchannel heat sink. Int. J. Heat Mass Transf. 2012, 55, 3090–3099. [Google Scholar] [CrossRef]
- Alfellag, M.A.; Ahmed, H.E.; Kherbeet, A.S. Numerical simulation of hydrothermal performance of minichannel heat sink using inclined slotted plate-fins and triangular pins. Appl. Therm. Eng. 2020, 164, 114509. [Google Scholar] [CrossRef]
- Yin, L.; Wang, M.; Zhou, J.; Tang, L. Design and Numerical Simulation of a New Microchannel Heat Sink. In Proceedings of the Seventh Asia International Symposium on Mechatronics, Osaka, Japan, 24–26 April 2020. [Google Scholar]
- Zheng, X.; Hu, X.; Zhang, L.; Zhang, X.; Chen, F.; Mai, C. Study on the Effect of Spoiler Columns on the Heat Dissipation Performance of S-Type Runner Water-Cooling Plates. Energies 2022, 15, 3085. [Google Scholar] [CrossRef]
- Fu, J.; Xu, X.; Li, R. Battery module thermal management based on liquid cold plate with heat transfer enhanced fin. Int. J. Energy Res. 2019, 43, 4312–4321. [Google Scholar] [CrossRef]
- Li, J.; Xiao, W.; Ge, Y. Research on the shape and arrangement of heat sink fins of liquid-cooled cold plates. Fluid Mach. 2020, 48, 5. [Google Scholar]
- Tian, W.; Cui, H. A simplification method of TSV interposer for thermal analysis in 3D packages. In Proceedings of the 2016 17th International Conference on Electronic Packaging Technology (ICEPT), Wuhan, China, 16–19 August 2016. [Google Scholar]
- Liu, W.; Mei, Y.; Xie, Y.; Wang, M.; Li, X.; Lu, G.-Q. Design and characterizations of a planar multichip half-bridge power module by pressureless sintering of nanosilver paste. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1627–1636. [Google Scholar] [CrossRef]
- Ding, C.; Liu, H.; Ngo, K.D.T.; Burgos, R.; Lu, G.-Q. A double-side cooled SiC MOSFET power module with sintered-silver interposers: I-design simulation fabrication and performance characterization. IEEE Trans. Power Electron. 2021, 36, 11672–11680. [Google Scholar] [CrossRef]
- Tang, S.; Chen, H.; Che, W.; Xue, Q. Simulation and experimental study of flexible cooling system based on microchannel in PDMS. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 2027–2036. [Google Scholar] [CrossRef]
- Hu, L.; Fang, Y.; Yang, W.; Xu, D.; Sun, L.; Li, K. Experimental study on heat transfer characteristics of direct cooling plates in parallel small channels. Acta Refrig. 2021, 42, 6. [Google Scholar]
- Fathi, M.; Heyhat, M.M.; Targhi, M.Z.; Bigham, S. Porous-fin microchannel heat sinks for future micro-electronics cooling. Int. J. Heat Mass Transf. 2023, 202, 123662. [Google Scholar] [CrossRef]
- Lee, Y.J.; Lee, P.S.; Chou, S.K. Hotspot mitigating with obliquely finned microchannel heat sink—An experimental study. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 1332–1341. [Google Scholar] [CrossRef]




| Structure | Material | Length | Wide | Height | Diameter |
|---|---|---|---|---|---|
| SiC chips | SiC | 5 (mm) | 4.6 (mm) | 0.36 (mm) | / |
| Chip solder layer | Nanosilver | 5 (mm) | 4.6 (mm) | 0.10 (mm) | / |
| Mo column solder layer | Nanosilver | / | / | 0.10 (mm) | 1.5 (mm) |
| Mo column | Mo | / | / | 4 (mm) | 1.5 (mm) |
| DBC adhesive layer | AuGe | 55 (mm) | 40 (mm) | 0.20 (mm) | / |
| Upper layer of DBC | Copper | 55 (mm) | 40 (mm) | 0.3 (mm) | / |
| DBC ceramic | Si3N4 | 55 (mm) | 40 (mm) | 0.32 (mm) | / |
| Bottom layer of DBC | Copper | 55 (mm) | 34 (mm) | 0.3 (mm) | / |
| Density (g/cm3) | Specific Heat Capacity (J/(kg·K)) | Volume (cm3) | Mass (g) | |
|---|---|---|---|---|
| Si3N4 | 3.2 | 710 | 1.408 | 4.5056 |
| Copper | 8.9 | 385 | 2.47303 | 20.773452 |
| Mo column | 10.2 | 250 | 0.113097 | 1.1535894 |
| Nanosilver layer | 10.49 | 232 | 0.042455 | 0.44535295 |
| AuGe | 17.5 | 130 | 0.88 | 15.4 |
| Potting adhesive | 1.95 | 550 | 10.2241 | 19.936995 |
| SiC chip | 3.2 | 670 | 0.13248 | 0.423936 |
| Equivalent device | 4.10 | 512.53 | 15.27 | 62.64 |
| Material | Thermal Conductivity (W/(m·K)) | hvertical (mm) | Avertical (mm2) |
|---|---|---|---|
| Si3N4 | 80 | 0.64 | 2200 |
| Copper | 400 | 1.2 | 2200 |
| Mo | 137 | 4 | 28.27 |
| Nanosilver | 418 | 0.1 | 28.27 |
| AuGe | 44.4 | 0.4 | 2200 |
| Potting adhesive | 4 | 4.66 | 2171.73 |
| Materials | Density (kg/m3) | Thermal Conductivity (W/(m·K)) | Specific Heat Capacity (J/(kg·K)) | Dynamic Viscosity (Pa·s) |
|---|---|---|---|---|
| Copper | 8900 | 400 | 390 | / |
| SiC | 3200 | 400 | 670 | / |
| Aluminum | 2700 | 210 | 880 | / |
| Equivalent devices | 4100 | 8.33 (XY direction) 105.47 (Z direction) | 512.53 | / |
| Water | 1000 | 0.609 (25 °C) 0.648 (50) 0.671 (75 °C) 0.683 (100 °C) | 4200 | 9.028 × 10−4 (25 °C) 5.494 × 10−4 (50 °C) 3.806 × 10−4 (75 °C) 2.825 × 10−4 (100 °C) |
| Number | Microchannel Width (mm) | Number of Secondary Inlets | Diameter of Inlet (mm) | Maximum Junction Temperature of Chips (°C) |
|---|---|---|---|---|
| 1 | A1 0.40 | B1 13 | C1 3.0 | 83.1 °C |
| 2 | A1 0.40 | B2 9 | C2 3.4 | 78.8 °C |
| 3 | A1 0.40 | B3 5 | C3 3.8 | 78.9 °C |
| 4 | A2 0.49 | B1 13 | C2 3.4 | 78.5 °C |
| 5 | A2 0.49 | B2 9 | C3 3.8 | 78.2 °C |
| 6 | A2 0.49 | B3 5 | C1 3.0 | 83.1 °C |
| 7 | A3 0.58 | B1 13 | C3 3.8 | 77.7 °C |
| 8 | A3 0.58 | B2 9 | C1 3.0 | 82.8 °C |
| 9 | A3 0.58 | B3 5 | C2 3.4 | 79.0 °C |
| Factor A | Factor B | Factor C | |
|---|---|---|---|
| K1 | 240.8 | 239.3 | 249 |
| K2 | 239.8 | 239.8 | 236.3 |
| K3 | 239.5 | 241 | 234.8 |
| 80.27 | 79.77 | 83 | |
| 79.93 | 79.93 | 78.77 | |
| 79.83 | 80.33 | 78.27 | |
| Range | 0.44 | 0.56 | 4.73 |
| The order of influence of factors | C > B > A | ||
| Maximum Junction Temperature of Chips | |
|---|---|
| Original chips | 677 °C |
| Chips with optimized cooling plate | 77.7 °C |
| Chips with micropump | 110 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Huang, J.; Tian, W.; Li, Z. Thermal Performance Optimization of Integrated Microchannel Cooling Plate for IGBT Power Module. Micromachines 2023, 14, 1498. https://doi.org/10.3390/mi14081498
Xu H, Huang J, Tian W, Li Z. Thermal Performance Optimization of Integrated Microchannel Cooling Plate for IGBT Power Module. Micromachines. 2023; 14(8):1498. https://doi.org/10.3390/mi14081498
Chicago/Turabian StyleXu, Hanyang, Jiabo Huang, Wenchao Tian, and Zhao Li. 2023. "Thermal Performance Optimization of Integrated Microchannel Cooling Plate for IGBT Power Module" Micromachines 14, no. 8: 1498. https://doi.org/10.3390/mi14081498





