A Comprehensive Review of Surface Acoustic Wave-Enabled Acoustic Droplet Ejection Technology and Its Applications
Abstract
:1. Introduction
2. Fundamentals of ADE
2.1. Acoustic Streaming Theory
2.2. Jetting Induced by SAW
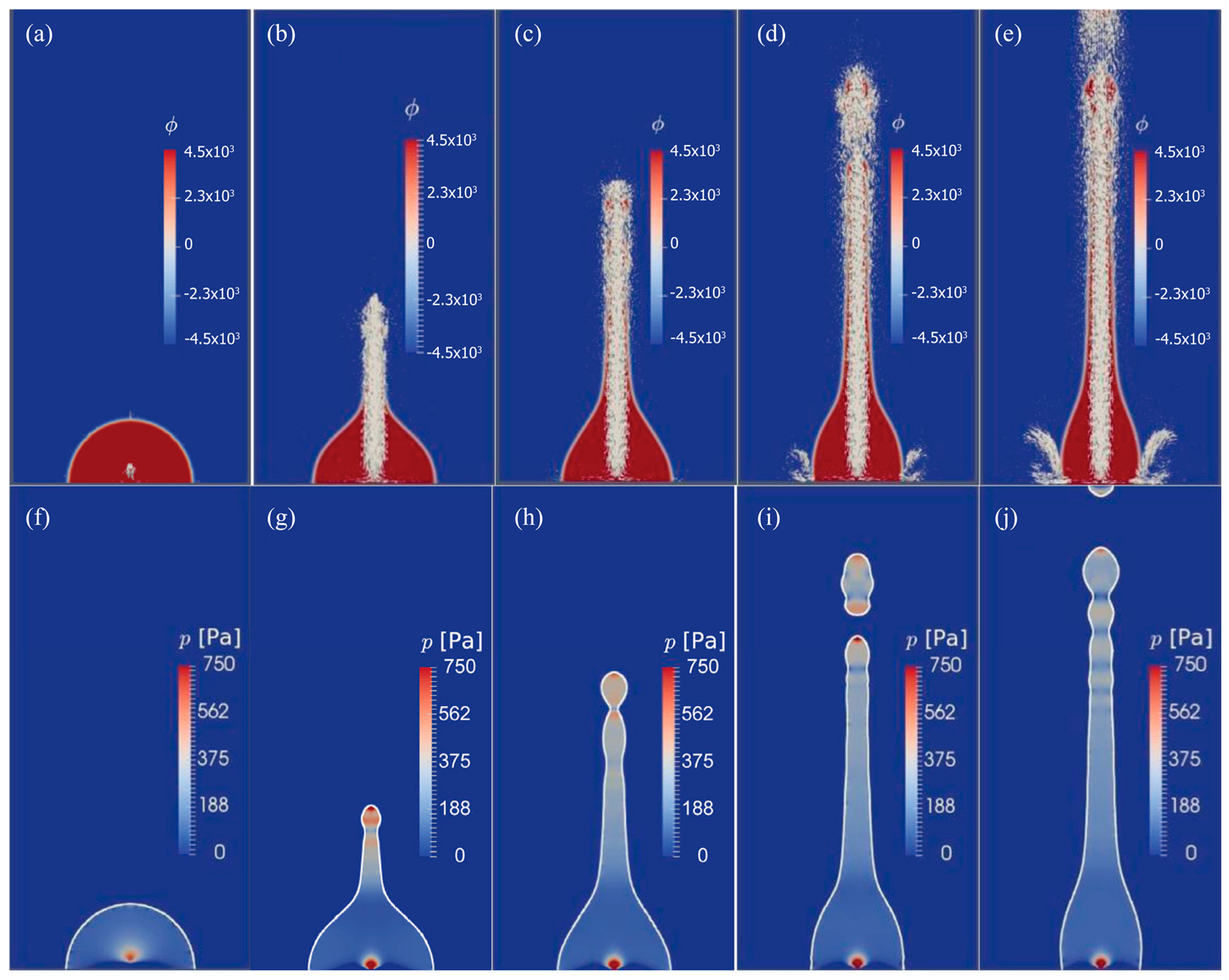
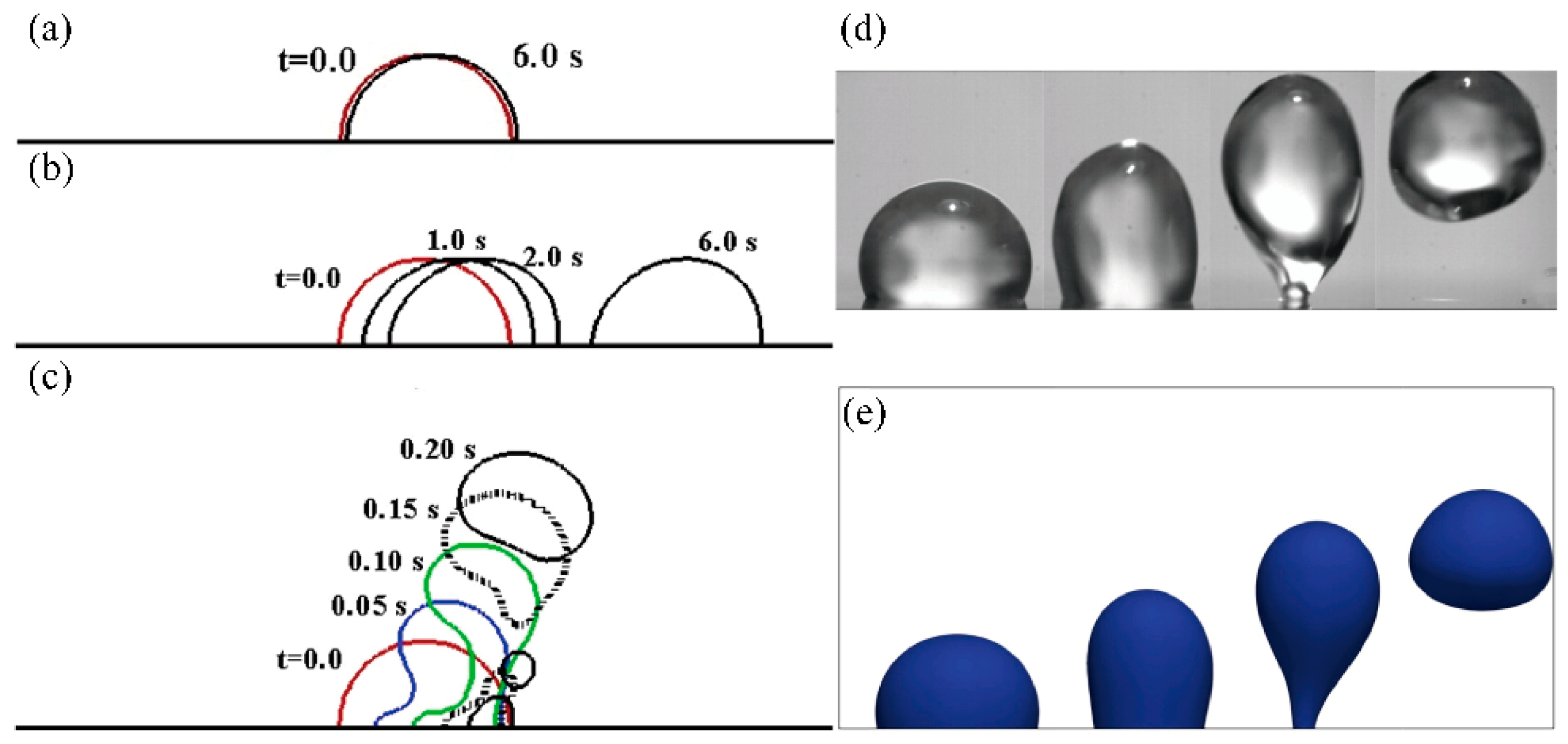
2.3. Simulation of Droplet Ejection Using SAW
2.3.1. Coupled Level Set with Volume of Fluid
2.3.2. Lattice Boltzmann Method
2.4. Other Types of ADE
3. Influencing Factors of Surface Acoustic Wave Ejection
3.1. Factors of Fluid
3.1.1. Volume
3.1.2. Viscosity
3.1.3. Surface Tension
3.2. Factors of Device
3.2.1. Material Properties
- piezoelectric single crystals
- piezoelectric thin films
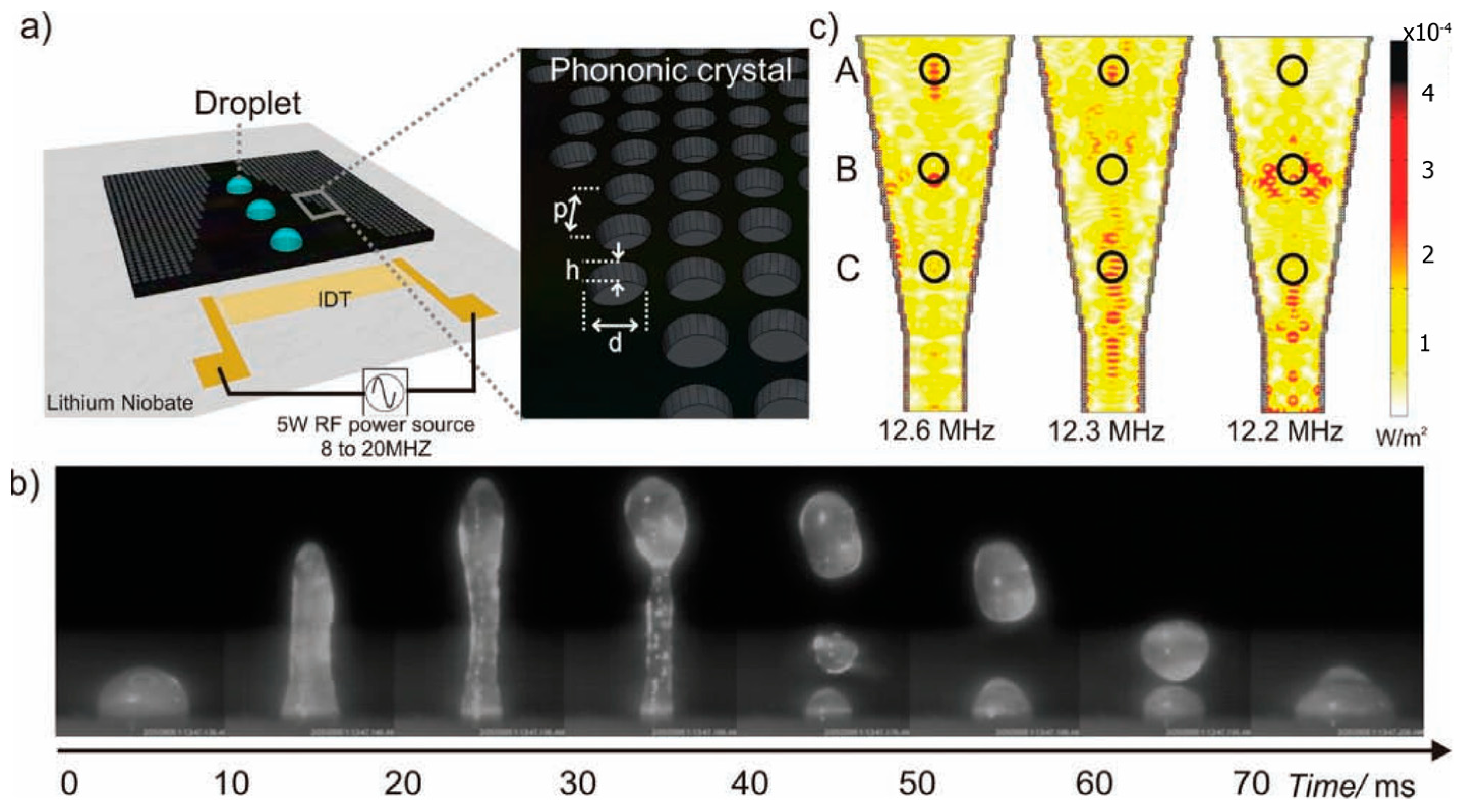
- Phononic crystals
- Hydrophobic treatment
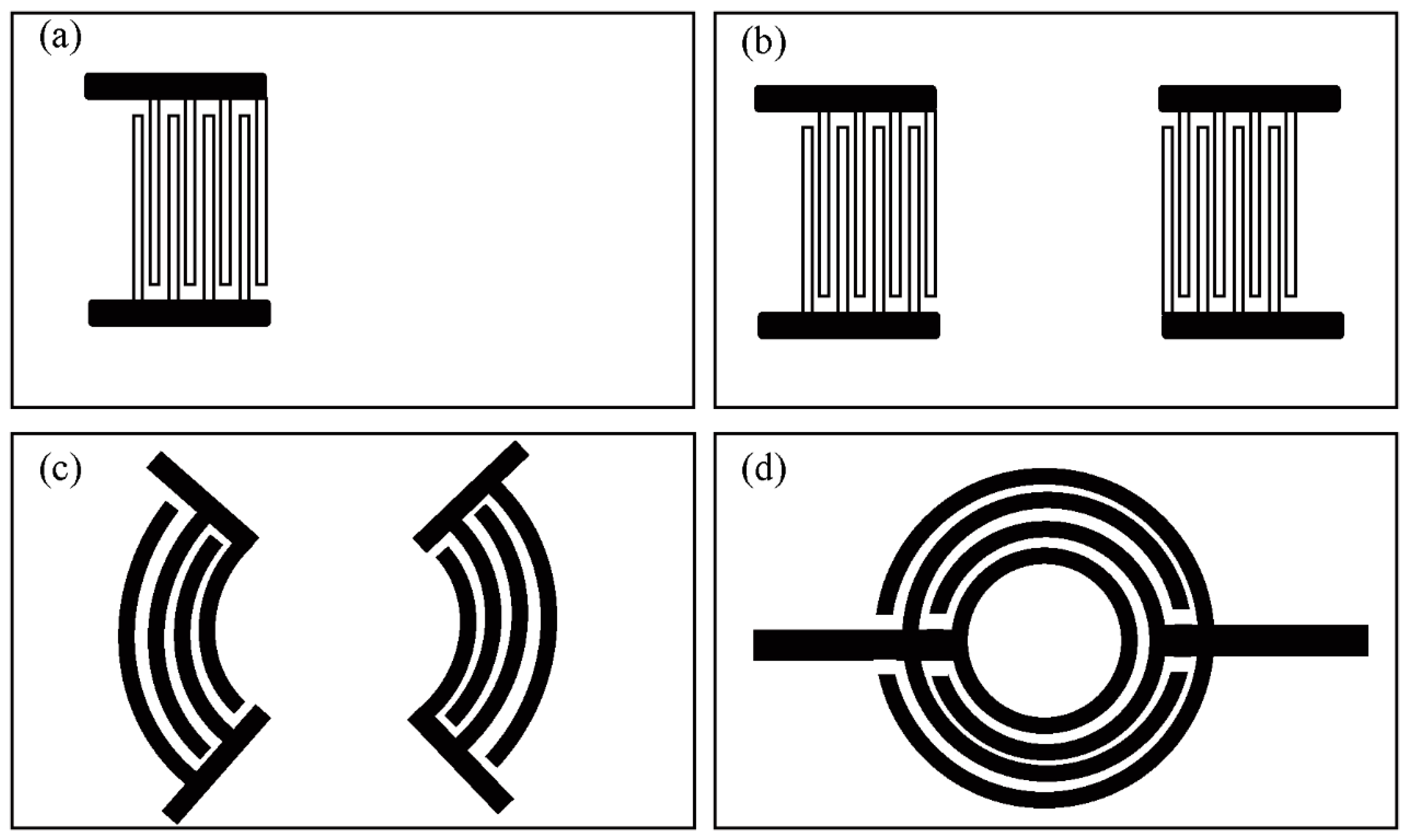
3.2.2. Type of Interdigitated Transducers
- Circular interdigital transducers
- Elliptical focusing interdigital transducers
- Double straight interdigital transducers
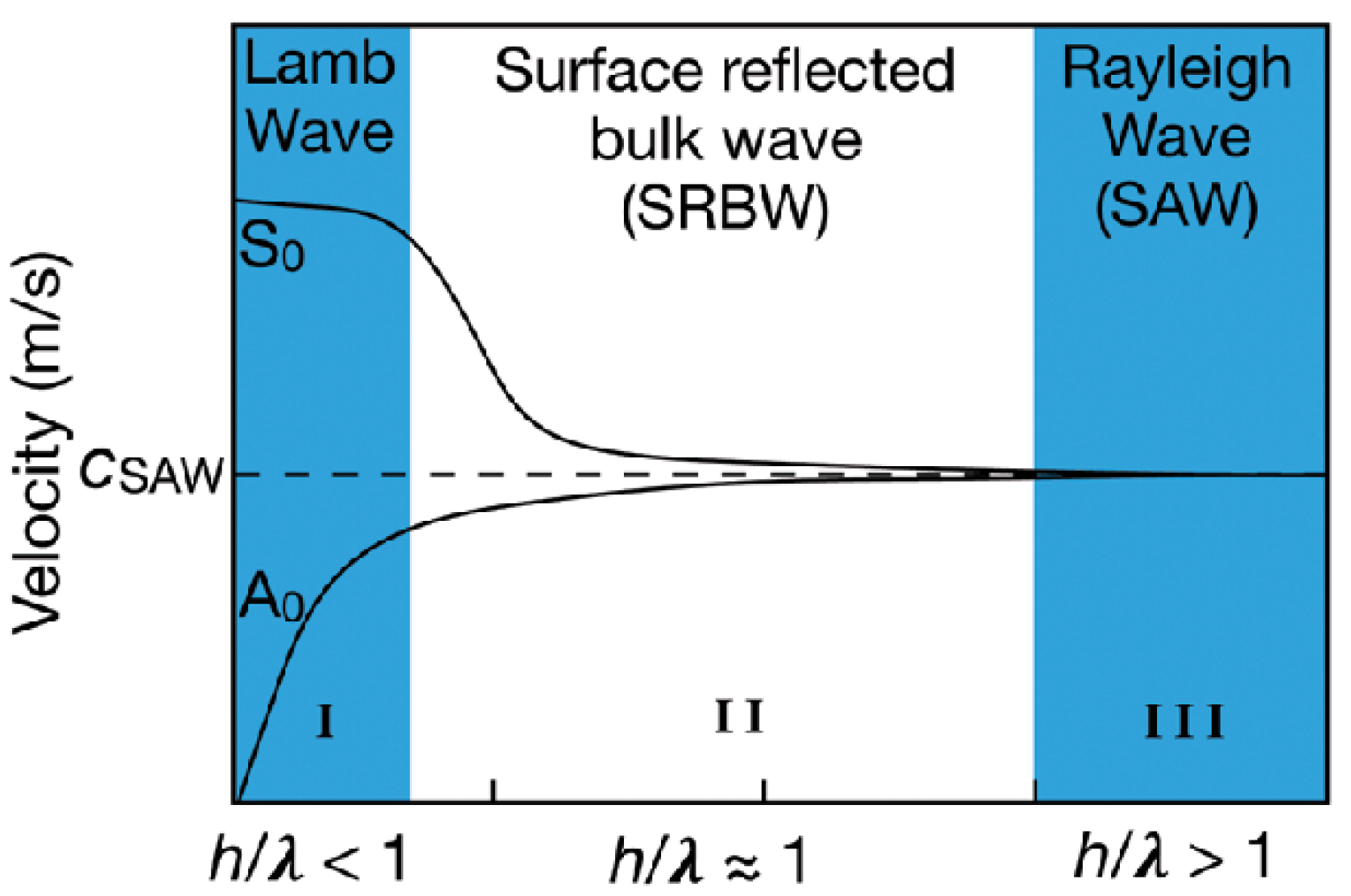
3.2.3. Types of Waves Excitation
- Lamb waves
- surface reflection body waves
- Rayleigh SAW
- High-order wave
- SH-SAW
3.3. Presence of Channel or Chamber
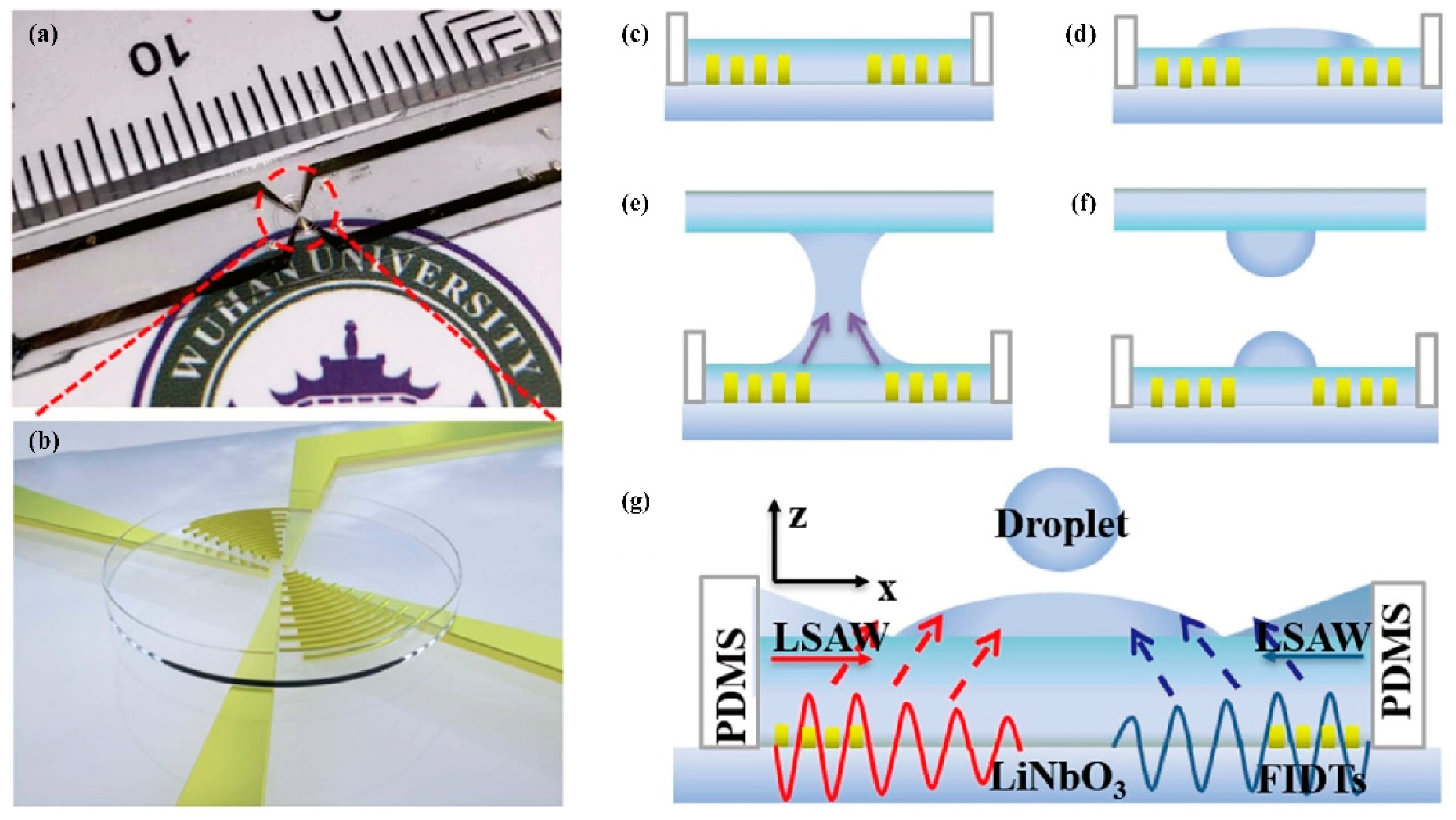
3.3.1. Sessile Droplet
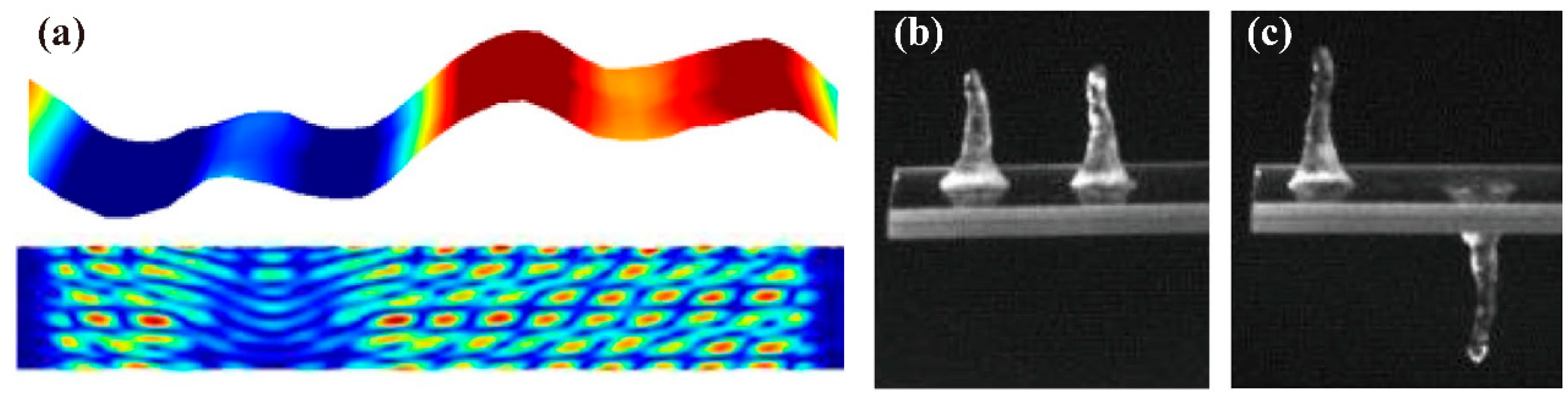
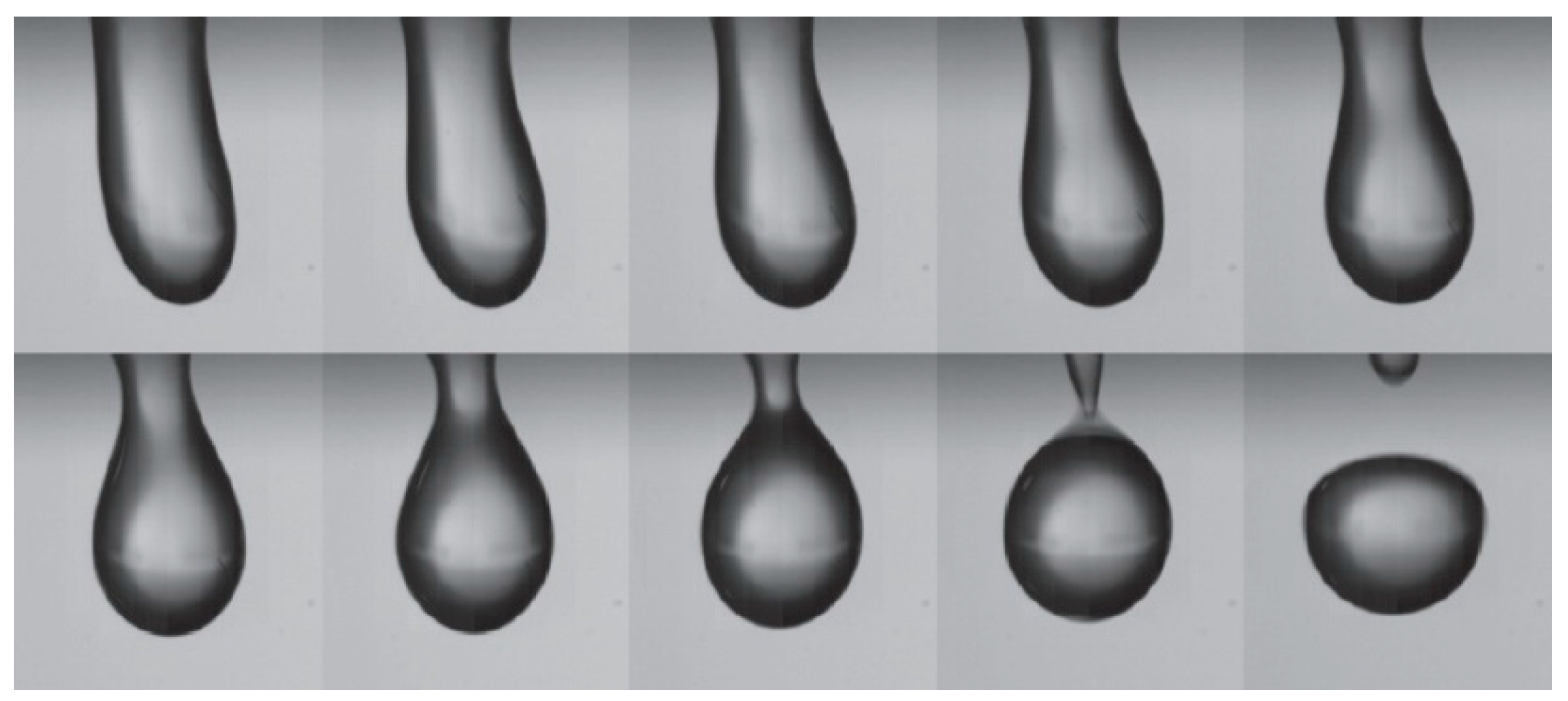
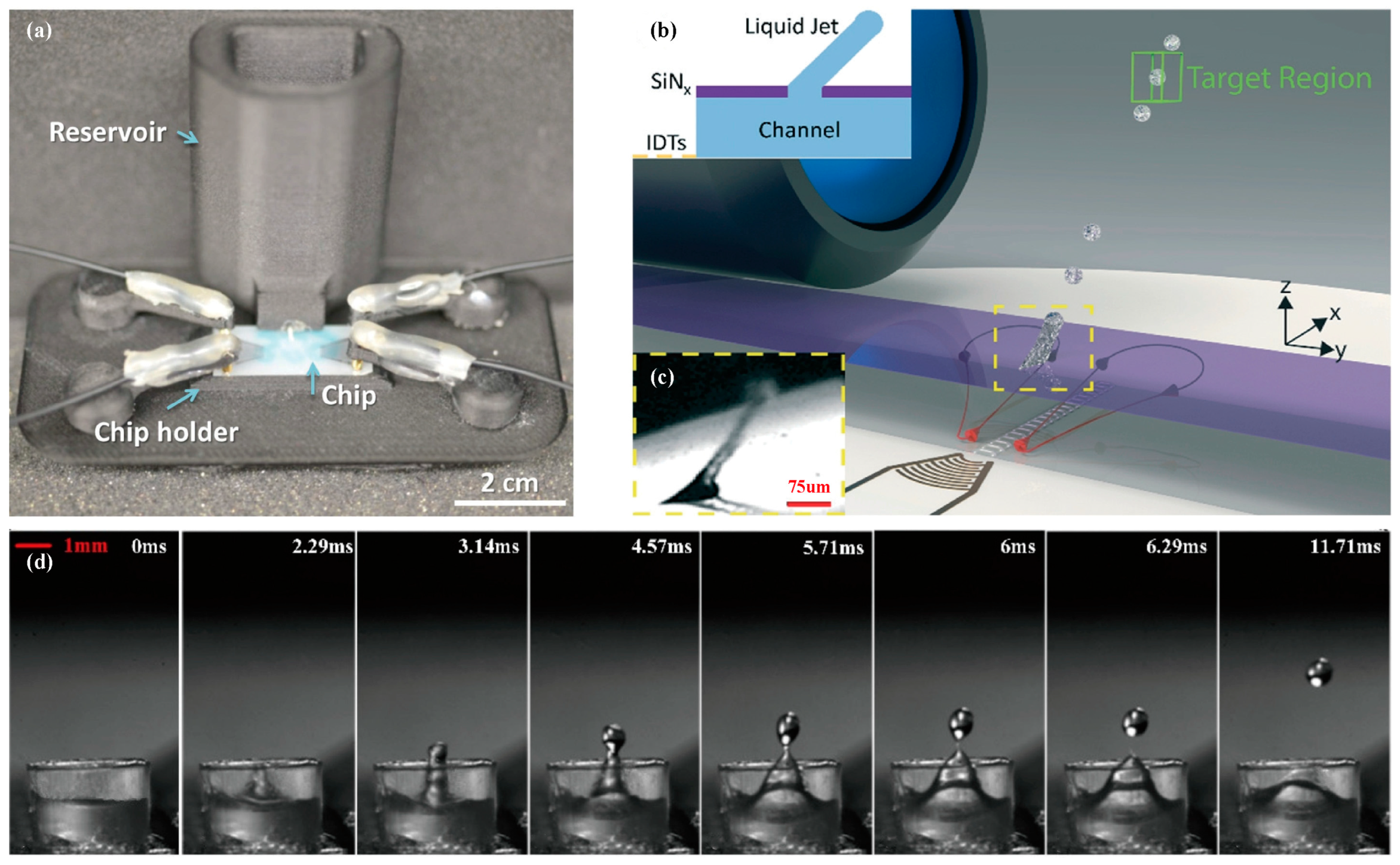
- Jetting
- Liquid Bridge
- Pendant
3.3.2. Channel
- Droplet production or splitting in the channel
- Jetting in the chamber
3.4. Factors of Driving Signal
3.4.1. Input Power
3.4.2. Frequency
3.4.3. Input Signal Modulation
3.5. Summary
4. Application in Bioprinters and Chemical Analysis
4.1. Encapsulation of Circulating Tumor Cell
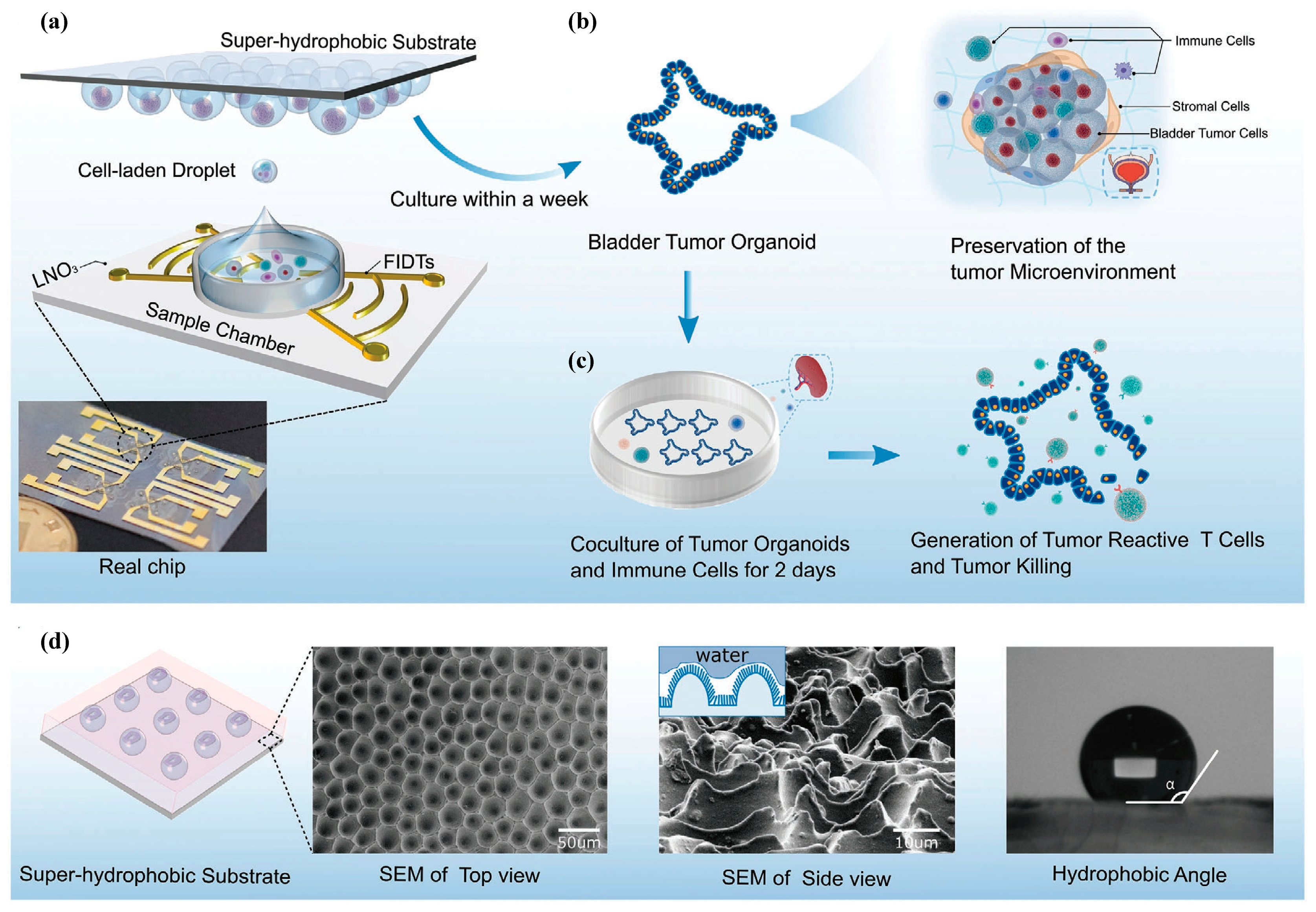
4.2. Construction of Tumor Microenvironment
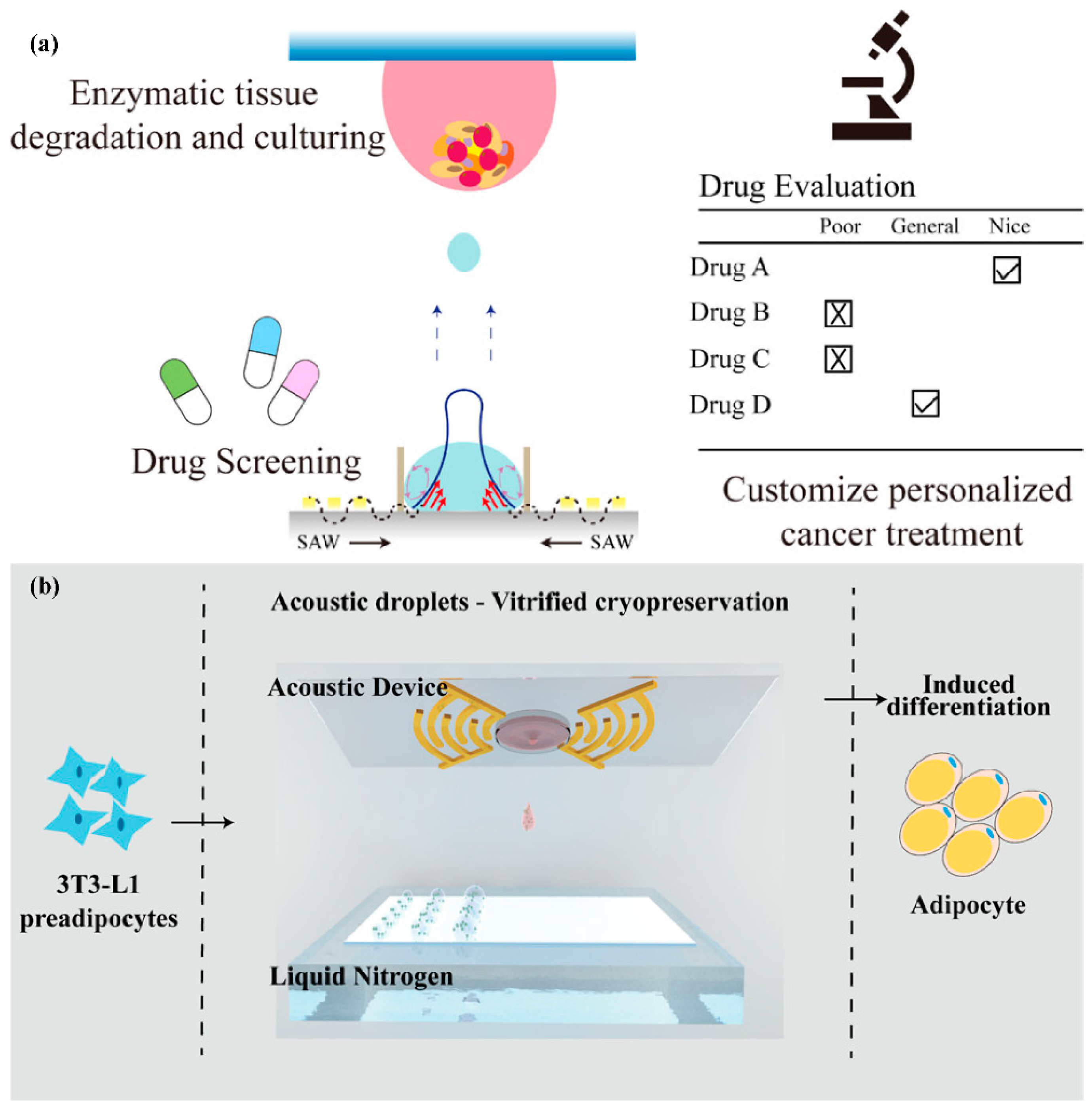
4.3. Drug Discovery and Cell Cryopreservation
4.4. Chemical Synthesis and Protein Crystallography
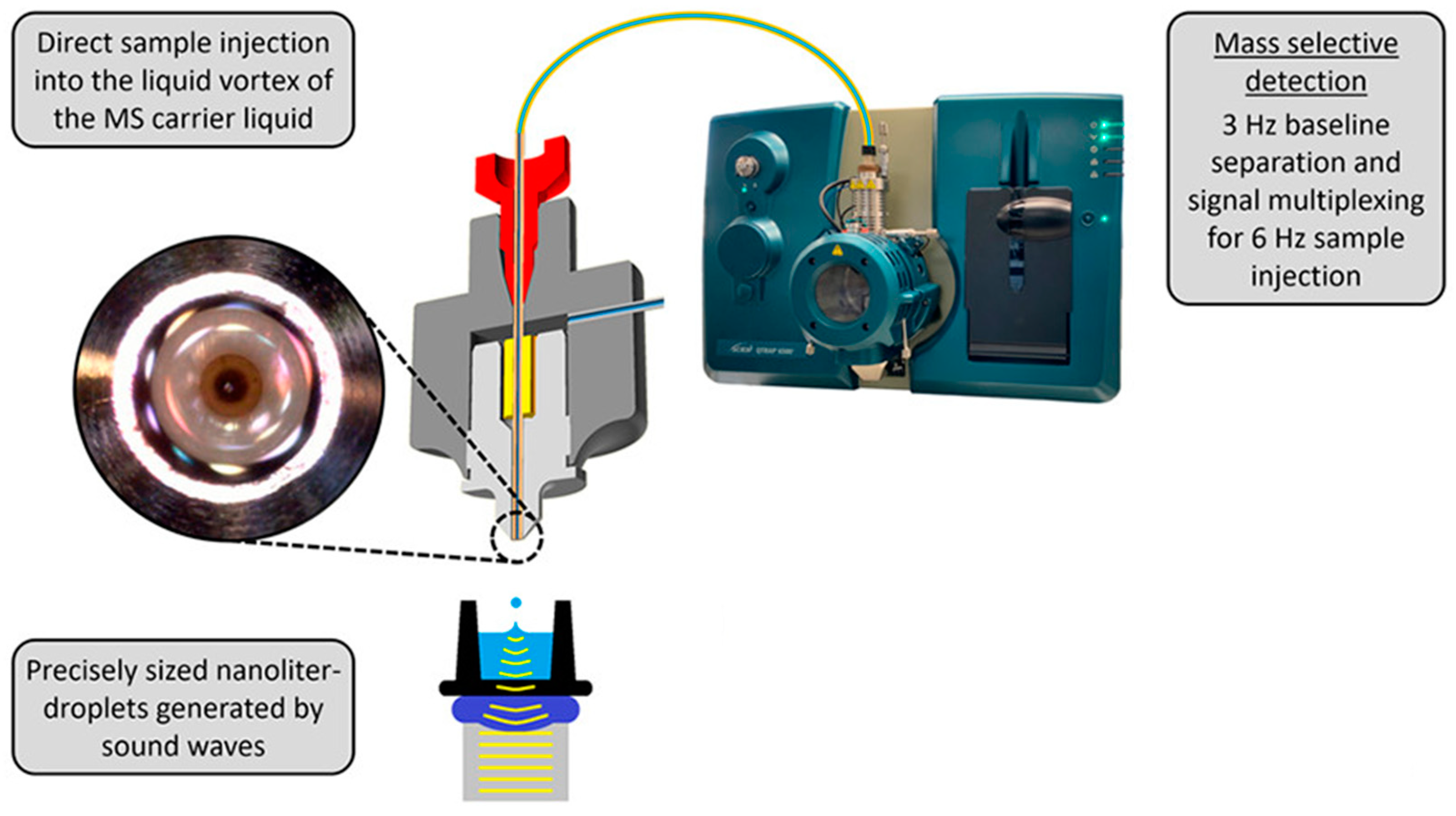
4.5. Acoustic Ejection Mass Spectrometry
5. Conclusions and Future Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vadodaria, S.; Mills, T. Jetting-based 3D printing of edible materials. Food Hydrocoll. 2020, 106, 105857. [Google Scholar] [CrossRef]
- Li, H.Y.; Liu, J.K.; Li, K.; Liu, Y.X. Piezoelectric micro-jet devices: A review. Sens. Actuators A-Phys. 2019, 297, 111552. [Google Scholar] [CrossRef]
- Mkhize, N.; Bhaskaran, H. Electrohydrodynamic Jet Printing: Introductory Concepts and Considerations. Small Sci. 2022, 2, 2100073. [Google Scholar] [CrossRef]
- Puerto, A.; Coppola, S.; Miccio, L.; Vespini, V.; García-Cabañes, Á.; Carrascosa, M.; Ferraro, P. Droplet Ejection and Liquid Jetting by Visible Laser Irradiation in Pyro-Photovoltaic Fe-Doped LiNbO3 Platforms. Adv. Mater. Interfaces 2021, 8, 2101164. [Google Scholar] [CrossRef]
- Guo, Q.; Su, X.; Zhang, X.; Shao, M.; Yu, H.; Li, D. A review on acoustic droplet ejection technology and system. Soft Matter 2021, 17, 3010–3021. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L. On waves propagated along the plane surface of an elastic solid. Proc. Lond. Math. Soc. 1885, 1, 4–11. [Google Scholar] [CrossRef]
- White, R.M.; Voltmer, F.W. Direct piezoelectric coupling to surface elastic waves. Appl. Phys. Lett. 1965, 7, 314–316. [Google Scholar] [CrossRef]
- Avramov, I.D.; Voigt, A.; Rapp, M. Rayleigh SAW resonators using gold electrode structure for gas sensor applications in chemically reactive environments. Electron. Lett. 2005, 41, 450–452. [Google Scholar] [CrossRef]
- Shiokawa, S.; Matsui, Y.; Ueda, T. Liquid streaming and droplet formation caused by leaky Rayleigh waves. In Proceedings of the Proceedings, IEEE Ultrasonics Symposium, Montreal, QC, Canada, 3–6 October 1989; pp. 643–646. [Google Scholar]
- Martin, F.; Newton, M.I.; McHale, G.; Melzak, K.A.; Gizeli, E. Pulse mode shear horizontal-surface acoustic wave (SH-SAW) system for liquid based sensing applications. Biosens. Bioelectron. 2004, 19, 627–632. [Google Scholar] [CrossRef]
- Lin, C.M.; Yen, T.T.; Lai, Y.J.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Temperature-compensated aluminum nitride lamb wave resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 524–532. [Google Scholar] [CrossRef]
- Lei, Y.; Hu, H. SAW-driven droplet jetting technology in microfluidic: A review. Biomicrofluidics 2020, 14, 061505. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.H.; Zhan, Z.J.; Zhuo, F.L.; Ji, Z.B.; Zheng, Y.J.; Fu, Y.Q.; Duan, H.G. Strategies for Giant Mass Sensitivity Using Super-High-Frequency Acoustic Waves. IEEE Sens. J. 2022, 22, 20336–20345. [Google Scholar] [CrossRef]
- Hashimoto, K.-y. Surface Acoustic Wave Devices in Telecommunications; Springer: Berlin/Heidelberg, Germany, 2000; Volume 116. [Google Scholar]
- Fu, Y.Q.; Luo, J.; Nguyen, N.-T.; Walton, A.; Flewitt, A.J.; Zu, X.-T.; Li, Y.; McHale, G.; Matthews, A.; Iborra, E. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef] [Green Version]
- Friend, J.; Yeo, L.Y. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 2011, 83, 647–704. [Google Scholar] [CrossRef] [Green Version]
- Rajapaksa, A.; Qi, A.; Yeo, L.Y.; Coppel, R.; Friend, J.R. Enabling practical surface acoustic wave nebulizer drug delivery via amplitude modulation. Lab Chip 2014, 14, 1858–1865. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R. Surface Acoustic Wave Microfluidics. Annu. Rev. Fluid Mech. 2014, 46, 379–406. [Google Scholar] [CrossRef] [Green Version]
- Rezk, A.R.; Ahmed, H.; Ramesan, S.; Yeo, L.Y. High Frequency Sonoprocessing: A New Field of Cavitation-Free Acoustic Materials Synthesis, Processing, and Manipulation. Adv. Sci. 2020, 8, 2001983. [Google Scholar] [CrossRef]
- Roudini, M.; Rosselló, J.M.; Manor, O.; Ohl, C.-D.; Winkler, A. Acoustic resonance effects and cavitation in SAW aerosol generation. Ultrason. Sonochemistry 2023, 98, 106530. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, Z.; Zhang, P.; Naquin, T.D.; Mai, J.; Wu, Y.; Yang, S.; Gu, Y.; Bachman, H.; Liang, Y.; et al. Generating multifunctional acoustic tweezers in Petri dishes for contactless, precise manipulation of bioparticles. Sci. Adv. 2020, 6, eabb0494. [Google Scholar] [CrossRef]
- Zhang, P.; Rufo, J.; Chen, C.; Xia, J.; Tian, Z.; Zhang, L.; Hao, N.; Zhong, Z.; Gu, Y.; Chakrabarty, K.; et al. Acoustoelectronic nanotweezers enable dynamic and large-scale control of nanomaterials. Nat. Commun. 2021, 12, 3844. [Google Scholar] [CrossRef]
- Nam, H.; Sung, H.J.; Park, J.; Jeon, J.S. Manipulation of cancer cells in a sessile droplet via travelling surface acoustic waves. Lab Chip 2021, 22, 47–56. [Google Scholar] [CrossRef]
- Nichols, M.K.; Kumar, R.K.; Bassindale, P.G.; Tian, L.; Barnes, A.C.; Drinkwater, B.W.; Patil, A.J.; Mann, S. Fabrication of Micropatterned Dipeptide Hydrogels by Acoustic Trapping of Stimulus-Responsive Coacervate Droplets. Small 2018, 14, e1800739. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Hartman, J.H.; Chen, C.; Yang, S.; Li, Q.; Tian, Z.; Huang, P.H.; Wang, L.; Meyer, J.N.; Huang, T.J. Fluorescence-based sorting of Caenorhabditis elegans via acoustofluidics. Lab Chip 2020, 20, 1729–1739. [Google Scholar] [CrossRef]
- Naseer, S.M.; Manbachi, A.; Samandari, M.; Walch, P.; Gao, Y.; Zhang, Y.S.; Davoudi, F.; Wang, W.; Abrinia, K.; Cooper, J.M.; et al. Surface acoustic waves induced micropatterning of cells in gelatin methacryloyl (GelMA) hydrogels. Biofabrication 2017, 9, 015020. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Zhu, J.; Zuo, Y.; Yang, D.; Zhang, J.; Cheng, Y.; Yang, Y. Versatile biomimetic array assembly by phase modulation of coherent acoustic waves. Lab Chip 2020, 20, 3515–3523. [Google Scholar] [CrossRef]
- Akther, A.; Marqus, S.; Rezk, A.R.; Yeo, L.Y. Submicron Particle and Cell Concentration in a Closed Chamber Surface Acoustic Wave Microcentrifuge. Anal. Chem. 2020, 92, 10024–10032. [Google Scholar] [CrossRef]
- Peng, T.; Fan, C.; Zhou, M.; Jiang, F.; Drummer, D.; Jiang, B. Rapid Enrichment of Submicron Particles within a Spinning Droplet Driven by a Unidirectional Acoustic Transducer. Anal. Chem. 2021, 93, 13293–13301. [Google Scholar] [CrossRef]
- Destgeer, G.; Jung, J.H.; Park, J.; Ahmed, H.; Sung, H.J. Particle Separation inside a Sessile Droplet with Variable Contact Angle Using Surface Acoustic Waves. Anal. Chem. 2017, 89, 736–744. [Google Scholar] [CrossRef]
- Zhang, N.; Zuniga-Hertz, J.P.; Zhang, E.Y.; Gopesh, T.; Fannon, M.J.; Wang, J.; Wen, Y.; Patel, H.H.; Friend, J. Microliter ultrafast centrifuge platform for size-based particle and cell separation and extraction using novel omnidirectional spiral surface acoustic waves. Lab Chip 2021, 21, 904–915. [Google Scholar] [CrossRef]
- Ayan, B.; Ozcelik, A.; Bachman, H.; Tang, S.Y.; Xie, Y.; Wu, M.; Li, P.; Huang, T.J. Acoustofluidic coating of particles and cells. Lab Chip 2016, 16, 4366–4372. [Google Scholar] [CrossRef] [Green Version]
- Nath, A.; Sudeepthi, A.; Sen, A.K. Trapping of Aqueous Droplets under Surface Acoustic Wave-Driven Streaming in Oil-Filled Microwells. Langmuir 2022, 38, 4763–4773. [Google Scholar] [CrossRef] [PubMed]
- Cheung, Y.N.; Qiu, H.H. Acoustic microstreaming for droplet breakup in a microflow-focusing device. Appl. Phys. Lett. 2010, 97, 133111. [Google Scholar] [CrossRef]
- Wixforth, A.; Strobl, C.; Gauer, C.; Toegl, A.; Scriba, J.; v Guttenberg, Z. Acoustic manipulation of small droplets. Anal. Bioanal. Chem. 2004, 379, 982–991. [Google Scholar] [CrossRef]
- Sui, M.; Dong, H.; Mu, G.; Xia, J.; Zhao, J.; Yang, Z.; Li, T.; Sun, T.; Grattan, K.T.V. Droplet transportation by adjusting the temporal phase shift of surface acoustic waves in the exciter-exciter mode. Lab Chip 2022, 22, 3402–3411. [Google Scholar] [CrossRef]
- Sudeepthi, A.; Nath, A.; Yeo, L.Y.; Sen, A.K. Coalescence of Droplets in a Microwell Driven by Surface Acoustic Waves. Langmuir 2021, 37, 1578–1587. [Google Scholar] [CrossRef]
- Du, X.; Fu, Y.Q.; Luo, J.; Flewitt, A.; Milne, W. Microfluidic pumps employing surface acoustic waves generated in ZnO thin films. J. Appl. Phys. 2009, 105, 024508. [Google Scholar] [CrossRef]
- Shilton, R.J.; Travagliati, M.; Beltram, F.; Cecchini, M. Microfluidic pumping through miniaturized channels driven by ultra-high frequency surface acoustic waves. Appl. Phys. Lett. 2014, 105, 074106. [Google Scholar] [CrossRef]
- Tan, M.K.; Yeo, L.Y.; Friend, J.R. Rapid fluid flow and mixing induced in microchannels using surface acoustic waves. Epl 2009, 87, 47003. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Li, J.; Huang, L.X.; Hua, B.; Guo, S.S. In Situ Microreaction Platform Based on Acoustic Droplet Manipulation for Ultra-High-Precision Multiplex Bioassay. Anal. Chem. 2022, 94, 6347–6354. [Google Scholar] [CrossRef]
- Bussiere, V.; Vigne, A.; Link, A.; McGrath, J.; Srivastav, A.; Baret, J.C.; Franke, T. High-Throughput Triggered Merging of Surfactant-Stabilized Droplet Pairs Using Traveling Surface Acoustic Waves. Anal. Chem. 2019, 91, 13978–13985. [Google Scholar] [CrossRef]
- Qi, A.; Yeo, L.Y.; Friend, J.R. Interfacial destabilization and atomization driven by surface acoustic waves. Phys. Fluids 2008, 20, 074103. [Google Scholar] [CrossRef] [Green Version]
- Friend, J.R.; Yeo, L.Y.; Arifin, D.R.; Mechler, A. Evaporative self-assembly assisted synthesis of polymeric nanoparticles by surface acoustic wave atomization. Nanotechnology 2008, 19, 145301. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.S.; Lim, W.T.H.; Ooi, C.W.; Yeo, L.Y.; Tan, M.K. In situ generation of plasma-activated aerosols via surface acoustic wave nebulization for portable spray-based surface bacterial inactivation. Lab Chip 2020, 20, 1856–1868. [Google Scholar] [CrossRef]
- Gai, C.; Hu, H.; Han, J.; Lei, Y.; Ning, J.; Ye, D. Combination of pulse signal modulation and hydrophilic treatment of a substrate for controlling the thermal distribution in surface acoustic wave atomization. Appl. Therm. Eng. 2023, 228, 120377. [Google Scholar] [CrossRef]
- Tan, M.K.; Friend, J.R.; Yeo, L.Y. Interfacial jetting phenomena induced by focused surface vibrations. Phys. Rev. Lett. 2009, 103, 024501. [Google Scholar] [CrossRef] [Green Version]
- Alghane, M.; Fu, Y.Q.; Chen, B.X.; Li, Y.; Desmulliez, M.P.Y.; Walton, A.J. Frequency effect on streaming phenomenon induced by Rayleigh surface acoustic wave in microdroplets. J. Appl. Phys. 2012, 112, 084902. [Google Scholar] [CrossRef] [Green Version]
- Dentry, M.B.; Yeo, L.Y.; Friend, J.R. Frequency effects on the scale and behavior of acoustic streaming. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014, 89, 013203. [Google Scholar] [CrossRef] [Green Version]
- Sankaranarayanan, S.K.; Bhethanabotla, V.R. Numerical analysis of wave generation and propagation in a focused surface acoustic wave device for potential microfluidics applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 631–643. [Google Scholar] [CrossRef]
- Marsnyborg, W.L. 11-Acoustic streaming. Phys. Acoust. 1965, 2, 265–331. [Google Scholar]
- Shiokawa, S.; Matsui, Y. The Dynamics of SAW Streaming and its Application to Fluid Devices. MRS Proc. 2011, 360, 53–64. [Google Scholar] [CrossRef]
- Campbell, J.J.; Jones, W.R. Propagation of surface waves at the boundary between a piezoelectric crystal and a fluid medium. IEEE Trans. Sonics Ultrason. 1970, 17, 71–76. [Google Scholar] [CrossRef]
- Biroun, M.H.; Rahmati, M.T.; Jangi, M.; Tao, R.; Chen, B.X.; Fu, Y.Q. Computational and experimental analysis of droplet transportation/jetting behaviours driven by thin film surface acoustic waves. Sens. Actuators A-Phys. 2019, 299, 111624. [Google Scholar] [CrossRef]
- Tan, M.K.; Friend, J.R.; Yeo, L.Y. Microparticle collection and concentration via a miniature surface acoustic wave device. Lab Chip 2007, 7, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (Vof) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Dianat, M.; Skarysz, M.; Garmory, A. A coupled level set and volume of fluid method for automotive exterior water management applications. Int. J. Multiphas Flow 2017, 91, 19–38. [Google Scholar] [CrossRef] [Green Version]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef] [Green Version]
- Jangi, M.; Luo, J.T.; Tao, R.; Reboud, J.; Wilson, R.; Cooper, J.M.; Gibson, D.; Fu, Y.Q. Concentrated vertical jetting mechanism for isotropically focused Zno/Si surface acoustic waves. Int. J. Multiphas Flow 2019, 114, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Biroun, M.H.; Rahmati, M.; Jangi, M.; Chen, B.X.; Fu, Y.Q. Numerical and experimental investigations of interdigital transducer configurations for efficient droplet streaming and jetting induced by surface acoustic waves. Int. J. Multiphas Flow 2021, 136, 103545. [Google Scholar] [CrossRef]
- Tan, M.K.; Yeo, L.Y. Hybrid finite-difference/lattice Boltzmann simulations of microchannel and nanochannel acoustic streaming driven by surface acoustic waves. Phys. Rev. Fluids 2018, 3, 044202. [Google Scholar] [CrossRef]
- Noori, M.S.; Rahni, M.T.; Taleghani, A.S. Effects of contact angle hysteresis on drop manipulation using surface acoustic waves. Theor. Comput. Fluid Dyn. 2020, 34, 145–162. [Google Scholar] [CrossRef]
- Noori, M.S.; Taleghani, A.S.; Rahni, M.T. Phenomenological Investigation of Drop Manipulation Using Surface Acoustic Waves. Microgravity Sci. Technol. 2020, 32, 1147–1158. [Google Scholar] [CrossRef]
- Noori, S.M.S.; Rahni, M.T.; Taleghani, S.A.S. Numerical Analysis of Droplet Motion over a Flat Plate Due to Surface Acoustic Waves. Microgravity Sci. Technol. 2020, 32, 647–660. [Google Scholar] [CrossRef]
- Noori, M.S.; Taleghani, A.S.; Rahni, M.T. Surface acoustic waves as control actuator for drop removal from solid surface. Fluid Dyn. Res. 2021, 53, 045503. [Google Scholar] [CrossRef]
- Taeibi Rahni, M.; Shams Taleghani, A.; Sheikholeslam, M.; Ahmadi, G. Computational simulation of water removal from a flat plate, using surface acoustic waves. Wave Motion 2022, 111, 102867. [Google Scholar] [CrossRef]
- Burnside, S.B.; Pasieczynski, K.; Zarareh, A.; Mehmood, M.; Fu, Y.Q.; Chen, B. Simulations of surface acoustic wave interactions on a sessile droplet using a three-dimensional multiphase lattice Boltzmann model. Phys. Rev. E 2021, 104, 045301. [Google Scholar] [CrossRef] [PubMed]
- Elrod, S.; Hadimioglu, B.; Khuri-Yakub, B.; Rawson, E.; Quate, C. Focused acoustic beams for nozzleless droplet formation. In Proceedings of the IEEE 1988 Ultrasonics Symposium Proceedings, Chicago, IL, USA, 2–5 October 1988; pp. 699–703. [Google Scholar]
- Elrod, S.A.; Hadimioglu, B.; Khuriyakub, B.T.; Rawson, E.G.; Richley, E.; Quate, C.F.; Mansour, N.N.; Lundgren, T.S. Nozzleless Droplet Formation with Focused Acoustic Beams. J. Appl. Phys. 1989, 65, 3441–3447. [Google Scholar] [CrossRef]
- Hadimioglu, B.; Elrod, S.; Steinmetz, D.; Lim, M.; Zesch, J.; Khuri-Yakub, B.; Rawson, E.; Quate, C. Acoustic ink printing. In Proceedings of the IEEE 1992 Ultrasonics Symposium Proceedings, Tucson, AZ, USA, 20–23 October 1992; pp. 929–935. [Google Scholar]
- Aerni, H.R.; Cornett, D.S.; Caprioli, R.M. Automated acoustic matrix deposition for MALDI sample preparation. Anal. Chem. 2006, 78, 827–834. [Google Scholar] [CrossRef]
- Fang, Y.; Frampton, J.P.; Raghavan, S.; Sabahi-Kaviani, R.; Luker, G.; Deng, C.X.; Takayama, S. Rapid generation of multiplexed cell cocultures using acoustic droplet ejection followed by aqueous two-phase exclusion patterning. Tissue Eng. Part C Methods 2012, 18, 647–657. [Google Scholar] [CrossRef] [Green Version]
- Tomita, Y. Jet atomization and cavitation induced by interactions between focused ultrasound and a water surface. Phys. Fluids 2014, 26, 097105. [Google Scholar] [CrossRef]
- Tanaka, H.; Mizuno, Y.; Nakamura, K. Ejection of small droplet from microplate using focused ultrasound. Jpn. J. Appl. Phys. 2017, 56, 087202. [Google Scholar] [CrossRef]
- Guo, Q.; Shao, M.; Su, X.; Zhang, X.; Yu, H.; Li, D. Controllable Droplet Ejection of Multiple Reagents through Focused Acoustic Beams. Langmuir 2021, 37, 14805–14812. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Shao, M.; Zhang, X.; Su, X.; Yu, H.; Li, D. A novel method to realize continuous input power control during acoustic droplet ejection. In Proceedings of the 2021 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 17–20 May 2021; pp. 1–5. [Google Scholar]
- Liang, S.; Zhang, Z.; Wang, X.; Su, M.; Qiu, W.; Zheng, H. Flexible Pico-Liter Acoustic Droplet Ejection Based on High-Frequency Ultrasound Transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 2212–2218. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, J.; Lyu, X.; Yang, T.; Liu, W.; Wang, B.; Luo, G. Hundred-micron droplet ejection by focused ultrasound for genomic applications. Sens. Actuators A-Phys. 2023, 354, 114271. [Google Scholar] [CrossRef]
- Jentsch, S.; Nasehi, R.; Kuckelkorn, C.; Gundert, B.; Aveic, S.; Fischer, H. Multiscale 3D Bioprinting by Nozzle-Free Acoustic Droplet Ejection. Small Methods 2021, 5, e2000971. [Google Scholar] [CrossRef]
- Huang, D.; Kim, E.S. Micromachined acoustic-wave liquid ejector. J. Microelectromechanical Syst. 2001, 10, 442–449. [Google Scholar] [CrossRef]
- Yu, H.; Kwon, J.W.; Kim, E.S. Chembio extraction on a chip by nanoliter droplet ejection. Lab Chip 2005, 5, 344–349. [Google Scholar] [CrossRef]
- Kwon, J.W.; Yu, H.Y.; Zou, Q.; Kim, E.S. Directional droplet ejection by nozzleless acoustic ejectors built on ZnO and PZT. J. Micromech. Microeng. 2006, 16, 2697–2704. [Google Scholar] [CrossRef]
- Tang, Y.K.; Kim, E.S. Nozzleless Acoustic Droplet Ejector With Electrically Tunable Droplet Size for Picking and Placing Semiconductor Chips. J. Microelectromechanical Syst. 2021, 30, 262–270. [Google Scholar] [CrossRef]
- Lee, C.Y.; Yu, H.Y.; Kim, E.S. Nanoliter droplet coalescence in air by directional acoustic ejection. Appl. Phys. Lett. 2006, 89, 223902. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.Y.; Pang, W.; Yu, H.Y.; Kim, E.S. Subpicoliter droplet generation based on a nozzle-free acoustic transducer. Appl. Phys. Lett. 2008, 93, 034104. [Google Scholar] [CrossRef] [Green Version]
- Foresti, D.; Kroll, K.T.; Amissah, R.; Sillani, F.; Homan, K.A.; Poulikakos, D.; Lewis, J.A. Acoustophoretic printing. Sci. Adv. 2018, 4, eaat1659. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Zhou, Y.; Cui, W.; Yang, Y.; Zhang, H.; Chen, X.; Pang, W.; Duan, X. An on-demand femtoliter droplet dispensing system based on a gigahertz acoustic resonator. Lab Chip 2018, 18, 2540–2546. [Google Scholar] [CrossRef]
- Alghane, M.; Fu, Y.Q.; Chen, B.X.; Li, Y.; Desmulliez, M.P.Y.; Walton, A.J. Streaming phenomena in microdroplets induced by Rayleigh surface acoustic wave. J. Appl. Phys. 2011, 109, 114901. [Google Scholar] [CrossRef]
- Du, X.Y.; Swanwick, M.E.; Fu, Y.Q.; Luo, J.K.; Flewitt, A.J.; Lee, D.S.; Maeng, S.; Milne, W.I. Surface acoustic wave induced streaming and pumping in 128° Y-cut LiNbO3for microfluidic applications. J. Micromech. Microeng. 2009, 19, 035016. [Google Scholar] [CrossRef]
- Wang, Y.; Tao, X.; Tao, R.; Zhou, J.; Zhang, Q.; Chen, D.Y.; Jin, H.; Dong, S.R.; Xie, J.; Fu, Y.Q. Acoustofluidics along inclined surfaces based on AlN/Si Rayleigh surface acoustic waves. Sens. Actuators A-Phys. 2020, 306, 111967. [Google Scholar] [CrossRef]
- Brunet, P.; Baudoin, M.; Matar, O.B.; Zoueshtiagh, F. Droplet displacements and oscillations induced by ultrasonic surface acoustic waves: A quantitative study. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 81, 036315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhattacharjee, P.K.; McDonnell, A.G.; Prabhakar, R.; Yeo, L.Y.; Friend, J. Extensional flow of low-viscosity fluids in capillary bridges formed by pulsed surface acoustic wave jetting. New J. Phys. 2011, 13, 023005. [Google Scholar] [CrossRef]
- Castro, J.O.; Ramesan, S.R.; Dang, H.D.; Rezk, A.R.; Yeo, L.Y. Acoustopipetting: Tunable Nanoliter Sample Dispensing Using Surface Acoustic Waves. Anal. Chem. 2019, 91, 5621–5628. [Google Scholar] [CrossRef]
- Li, J.; Biroun, M.H.; Tao, R.; Wang, Y.; Torun, H.; Xu, N.; Rahmati, M.; Li, Y.F.; Gibson, D.; Fu, C.; et al. Wide range of droplet jetting angles by thin-film based surface acoustic waves. J. Phys. D-Appl. Phys. 2020, 53, 355402. [Google Scholar] [CrossRef]
- Pang, H.F.; Fu, Y.Q.; Garcia-Gancedo, L.; Porro, S.; Luo, J.K.; Placido, F.; Wilson, J.I.B.; Flewitt, A.J.; Milne, W.I.; Zu, X.T. Enhancement of microfluidic efficiency with nanocrystalline diamond interlayer in the ZnO-based surface acoustic wave device. Microfluid. Nanofluidics 2013, 15, 377–386. [Google Scholar] [CrossRef]
- Chen, K.; Sui, C.; Wu, Y.; Ao, Z.; Guo, S.S.; Guo, F. A digital acoustofluidic device for on-demand and oil-free droplet generation. Nanotechnology 2019, 30, 084001. [Google Scholar] [CrossRef] [PubMed]
- Friend, J.; Tan, M.; Yeo, L. Unraveling interfacial jetting phenomena induced by focused surface acoustic waves. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Rome, Italy, 20–23 September 2009; pp. 811–814. [Google Scholar]
- Zahertar, S.; Torun, H.; Tao, R.; Canyelles-Pericas, P.; Luo, J.; Wu, Q.; Fu, Y.-Q. An integrated platform for metamaterial-based sensing and surface acoustic wave-based acoustofluidics utilising circular interdigital transducers. Sens. Diagn. 2022, 1, 270–279. [Google Scholar] [CrossRef]
- Fu, C.; Quan, A.J.; Luo, J.T.; Pang, H.F.; Guo, Y.J.; Wu, Q.; Ng, W.P.; Zu, X.T.; Fu, Y.Q. Vertical jetting induced by shear horizontal leaky surface acoustic wave on 36 degrees Y-X LiTaO3. Appl. Phys. Lett. 2017, 110, 173501. [Google Scholar] [CrossRef] [Green Version]
- Tao, R.; McHale, G.; Reboud, J.; Cooper, J.M.; Torun, H.; Luo, J.; Luo, J.; Yang, X.; Zhou, J.; Canyelles-Pericas, P.; et al. Hierarchical Nanotexturing Enables Acoustofluidics on Slippery yet Sticky, Flexible Surfaces. Nano Lett. 2020, 20, 3263–3270. [Google Scholar] [CrossRef]
- Du, X.Y.; Fu, Y.Q.; Tan, S.C.; Luo, J.K.; Flewitt, A.J.; Milne, W.I.; Lee, D.S.; Park, N.M.; Park, J.; Choi, Y.J.; et al. ZnO film thickness effect on surface acoustic wave modes and acoustic streaming. Appl. Phys. Lett. 2008, 93, 094105. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Garcia-Gancedo, L.; Pang, H.F.; Porro, S.; Gu, Y.W.; Luo, J.K.; Zu, X.T.; Placido, F.; Wilson, J.I.; Flewitt, A.J.; et al. Microfluidics based on ZnO/nanocrystalline diamond surface acoustic wave devices. Biomicrofluidics 2012, 6, 24105–2410511. [Google Scholar] [CrossRef]
- Ong, H.; Pang, H.F.; Zhou, J.; Tao, R.; Agrawal, P.; Torun, H.; Thummavichai, K.; Luo, J.T.; Tao, K.; Wu, Q.; et al. ZnO/glass thin film surface acoustic waves for efficient digital acoustofluidics and active surface cleaning. Mater. Chem. Phys. 2022, 287, 126290. [Google Scholar] [CrossRef]
- Zhou, J.; DeMiguel-Ramos, M.; Garcia-Gancedo, L.; Iborra, E.; Olivares, J.; Jin, H.; Luo, J.K.; Elhady, A.S.; Dong, S.R.; Wang, D.M.; et al. Characterisation of aluminium nitride films and surface acoustic wave devices for microfluidic applications. Sens. Actuators B-Chem. 2014, 202, 984–992. [Google Scholar] [CrossRef]
- Zhou, J.; Pang, H.F.; Garcia-Gancedo, L.; Iborra, E.; Clement, M.; De Miguel-Ramos, M.; Jin, H.; Luo, J.K.; Smith, S.; Dong, S.R.; et al. Discrete microfluidics based on aluminum nitride surface acoustic wave devices. Microfluid. Nanofluidics 2014, 18, 537–548. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R.; Reboud, J.; Bourquin, Y.; Neale, S.L.; Zhang, Y.; Cooper, J.M. Phononic crystal structures for acoustically driven microfluidic manipulations. Lab Chip 2011, 11, 323–328. [Google Scholar] [CrossRef]
- Bourquin, Y.; Wilson, R.; Zhang, Y.; Reboud, J.; Cooper, J.M. Phononic crystals for shaping fluids. Adv Mater 2011, 23, 1458–1462. [Google Scholar] [CrossRef] [PubMed]
- Beyssen, D.; Le Brizoual, L.; Elmazria, O.; Alnot, P. Microfluidic device based on surface acoustic wave. Sens. Actuators B-Chem. 2006, 118, 380–385. [Google Scholar] [CrossRef]
- Renaudin, A.; Tabourier, P.; Zhang, V.; Camart, J.C.; Druon, C. SAW nanopump for handling droplets in view of biological applications. Sens. Actuators B-Chem. 2006, 113, 389–397. [Google Scholar] [CrossRef]
- Bennès, J.; Ballandras, S.; Chérioux, F. Easy and versatile functionalization of lithium niobate wafers by hydrophobic trichlorosilanes. Appl. Surf. Sci. 2008, 255, 1796–1800. [Google Scholar] [CrossRef]
- Nihonyanagi, S.; Eftekhari-Bafrooei, A.; Hines, J.; Borguet, E. Self-assembled monolayer compatible with metal surface acoustic wave devices on lithium niobate. Langmuir 2008, 24, 5161–5165. [Google Scholar] [CrossRef] [PubMed]
- Glass, N.R.; Tjeung, R.; Chan, P.; Yeo, L.Y.; Friend, J.R. Organosilane deposition for microfluidic applications. Biomicrofluidics 2011, 5, 36501–365017. [Google Scholar] [CrossRef] [Green Version]
- Bennes, J.; Alzuaga, S.; Ballandras, S.; Cherioux, F.; Bastien, F.; Manceau, J.-F. Droplet ejector using surface acoustic waves. In Proceedings of the IEEE Ultrasonics Symposium, Rotterdam, The Netherlands, 18–21 September 2005; pp. 823–826. [Google Scholar]
- Bussonniere, A.; Baudoin, M.; Brunet, P.; Matar, O.B. Dynamics of sessile and pendant drops excited by surface acoustic waves: Gravity effects and correlation between oscillatory and translational motions. Phys. Rev. E 2016, 93, 053106. [Google Scholar] [CrossRef] [Green Version]
- Darmawan, M.; Byun, D. Focused surface acoustic wave induced jet formation on superhydrophobic surfaces. Microfluid. Nanofluidics 2014, 18, 1107–1114. [Google Scholar] [CrossRef]
- Lei, Y.L.; Hu, H.; Han, J.L.; Huang, Q.Y. High-order modal acoustic wave driving vertical jetting of droplets on 128 degrees Y-X LiNbO3. Exp. Fluids 2021, 62, 123. [Google Scholar] [CrossRef]
- Rezk, A.R.; Tan, J.K.; Yeo, L.Y. HYbriD Resonant Acoustics (HYDRA). Adv. Mater. 2016, 28, 1970–1975. [Google Scholar] [CrossRef]
- Fu, C.; Yang, Q.; Ke, Y.; Tao, R.; Luo, J.; Fan, X.; Zhang, B.; Li, H. Development of Lamb Wave-Based Unidirectional Transducers Toward Highly Efficient Microfluidic Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 1549–1555. [Google Scholar] [CrossRef] [PubMed]
- Demirci, U. Acoustic picoliter droplets for emerging applications in semiconductor industry and biotechnology. J. Microelectromechanical Syst. 2006, 15, 957–966. [Google Scholar] [CrossRef]
- Demirci, U. Droplet-based photoresist deposition. Appl. Phys. Lett. 2006, 88, 144104. [Google Scholar] [CrossRef] [Green Version]
- Demirci, U.; Montesano, G. Single cell epitaxy by acoustic picolitre droplets. Lab Chip 2007, 7, 1139–1145. [Google Scholar] [CrossRef]
- Ning, Y.; Zhang, M.; Zhang, H.; Duan, X.; Yuan, Y.; Liu, B.; Pang, W. Mechanism and stability investigation of a nozzle-free droplet-on-demand acoustic ejector. Analyst 2021, 146, 5650–5657. [Google Scholar] [CrossRef] [PubMed]
- Connacher, W.; Orosco, J.; Friend, J. Droplet Ejection at Controlled Angles via Acoustofluidic Jetting. Phys. Rev. Lett. 2020, 125, 184504. [Google Scholar] [CrossRef]
- Nguyen, E.P.; Lee, L.; Rezk, A.R.; Sabri, Y.M.; Bhargava, S.K.; Yeo, L.Y. Hybrid Surface and Bulk Resonant Acoustics for Concurrent Actuation and Sensing on a Single Microfluidic Device. Anal. Chem. 2018, 90, 5335–5342. [Google Scholar] [CrossRef]
- Tao, R.; Reboud, J.; Torun, H.; McHale, G.; Dodd, L.E.; Wu, Q.; Tao, K.; Yang, X.; Luo, J.T.; Todryk, S.; et al. Integrating microfluidics and biosensing on a single flexible acoustic device using hybrid modes. Lab Chip 2020, 20, 1002–1011. [Google Scholar] [CrossRef]
- Rezk, A.R.; Ramesan, S.; Yeo, L.Y. Plug-and-actuate on demand: Multimodal individual addressability of microarray plates using modular hybrid acoustic wave technology. Lab Chip 2018, 18, 406–411. [Google Scholar] [CrossRef]
- Montanero, J.M.; Ponce-Torres, A. Review on the Dynamics of Isothermal Liquid Bridges. Appl. Mech. Rev. 2020, 72, 010803. [Google Scholar] [CrossRef]
- Bertin, N.; Wunenburger, R.; Brasselet, E.; Delville, J.P. Liquid-column sustainment driven by acoustic wave guiding. Phys. Rev. Lett. 2010, 105, 164501. [Google Scholar] [CrossRef]
- Schmid, L.; Franke, T. SAW-controlled drop size for flow focusing. Lab Chip 2013, 13, 1691–1694. [Google Scholar] [CrossRef]
- Schmid, L.; Franke, T. Acoustic modulation of droplet size in a T-junction. Appl. Phys. Lett. 2014, 104, 133501. [Google Scholar] [CrossRef]
- Jung, J.H.; Destgeer, G.; Ha, B.; Park, J.; Sung, H.J. On-demand droplet splitting using surface acoustic waves. Lab Chip 2016, 16, 3235–3243. [Google Scholar] [CrossRef]
- Sesen, M.; Alan, T.; Neild, A. Microfluidic plug steering using surface acoustic waves. Lab Chip 2015, 15, 3030–3038. [Google Scholar] [CrossRef]
- Sesen, M.; Devendran, C.; Malikides, S.; Alan, T.; Neild, A. Surface acoustic wave enabled pipette on a chip. Lab Chip 2017, 17, 438–447. [Google Scholar] [CrossRef]
- Park, J.; Jung, J.H.; Park, K.; Destgeer, G.; Ahmed, H.; Ahmad, R.; Sung, H.J. On-demand acoustic droplet splitting and steering in a disposable microfluidic chip. Lab Chip 2018, 18, 422–432. [Google Scholar] [CrossRef]
- Mutafopulos, K.; Lu, P.J.; Garry, R.; Spink, P.; Weitz, D.A. Selective cell encapsulation, lysis, pico-injection and size-controlled droplet generation using traveling surface acoustic waves in a microfluidic device. Lab Chip 2020, 20, 3914–3921. [Google Scholar] [CrossRef]
- Park, J.; Destgeer, G.; Afzal, M.; Sung, H.J. Acoustofluidic generation of droplets with tunable chemical concentrations. Lab Chip 2020, 20, 3922–3929. [Google Scholar] [CrossRef]
- Collins, D.J.; Alan, T.; Helmerson, K.; Neild, A. Surface acoustic waves for on-demand production of picoliter droplets and particle encapsulation. Lab Chip 2013, 13, 3225–3231. [Google Scholar] [CrossRef]
- Brenker, J.C.; Collins, D.J.; Van Phan, H.; Alan, T.; Neild, A. On-chip droplet production regimes using surface acoustic waves. Lab Chip 2016, 16, 1675–1683. [Google Scholar] [CrossRef]
- Sesen, M.; Alan, T.; Neild, A. Microfluidic on-demand droplet merging using surface acoustic waves. Lab Chip 2014, 14, 3325–3333. [Google Scholar] [CrossRef]
- Castro, J.O.; Ramesan, S.; Rezk, A.R.; Yeo, L.Y. Continuous tuneable droplet ejection via pulsed surface acoustic wave jetting. Soft Matter 2018, 14, 5721–5727. [Google Scholar] [CrossRef]
- Brenker, J.C.; Devendran, C.; Neild, A.; Alan, T. On-demand sample injection: Combining acoustic actuation with a tear-drop shaped nozzle to generate droplets with precise spatial and temporal control. Lab Chip 2020, 20, 253–265. [Google Scholar] [CrossRef]
- Lei, Y.L.; Hu, H.; Chen, J.; Zhang, P. Microfluidic Jetting Deformation and Pinching-off Mechanism in Capillary Tubes by Using Traveling Surface Acoustic Waves. Actuators 2020, 9, 5. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Chen, K.; Cai, B.; Rao, L.; Wang, Z.; Sun, Y.; Yu, M.; Liu, W.; Guo, S.; Zhao, X.Z. An Acoustic Droplet-Induced Enzyme Responsive Platform for the Capture and On-Demand Release of Single Circulating Tumor Cells. ACS Appl. Mater. Interfaces 2019, 11, 41118–41126. [Google Scholar] [CrossRef]
- Li, R.; Gong, Z.Y.; Wu, Z.Z.; Chen, H.; Xia, Y.; Liu, Y.C.; Wang, F.B.; Guo, S.S. Nozzle-free droplet generation with focused acoustic beams for encapsulation of single circulating tumor cells. Nano Futures 2020, 4, 045001. [Google Scholar] [CrossRef]
- Li, R.; Gong, Z.; Yi, K.; Li, W.; Liu, Y.; Wang, F.; Guo, S.S. Efficient Detection and Single-Cell Extraction of Circulating Tumor Cells in Peripheral Blood. ACS Appl. Bio. Mater. 2020, 3, 6521–6528. [Google Scholar] [CrossRef]
- Chen, K.; Jiang, E.; Wei, X.; Xia, Y.; Wu, Z.; Gong, Z.; Shang, Z.; Guo, S. The acoustic droplet printing of functional tumor microenvironments. Lab Chip 2021, 21, 1604–1612. [Google Scholar] [CrossRef]
- Gong, Z.; Huang, L.; Tang, X.; Chen, K.; Wu, Z.; Zhang, L.; Sun, Y.; Xia, Y.; Chen, H.; Wei, Y.; et al. Acoustic Droplet Printing Tumor Organoids for Modeling Bladder Tumor Immune Microenvironment within a Week. Adv. Healthc. Mater. 2021, 10, e2101312. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, H.; Li, J.; Hu, H.; Qian, Q.; He, R.X.; Ding, Z.; Guo, S.S. Acoustic Droplet-Assisted Superhydrophilic-Superhydrophobic Microarray Platform for High-Throughput Screening of Patient-Derived Tumor Spheroids. ACS Appl. Mater. Interfaces 2021, 13, 23489–23501. [Google Scholar] [CrossRef]
- Xia, Y.; Huang, L.X.; Chen, H.; Li, J.; Chen, K.K.; Hu, H.; Wang, F.B.; Ding, Z.; Guo, S.S. Acoustic Droplet Vitrification Method for High-Efficiency Preservation of Rare Cells. ACS Appl. Mater. Interfaces 2021, 13, 12950–12959. [Google Scholar] [CrossRef]
- Chen, H.; Du, L.; Li, J.; Wu, Z.; Gong, Z.; Xia, Y.; Fan, Z.; Qian, Q.; Ding, Z.; Hu, H.; et al. Modeling cancer metastasis using acoustically bio-printed patient-derived 3D tumor microtissues. J. Mater. Chem. B 2022, 10, 1843–1852. [Google Scholar] [CrossRef]
- Chen, H.; Wu, Z.; Gong, Z.; Xia, Y.; Li, J.; Du, L.; Zhang, Y.; Gao, X.; Fan, Z.; Hu, H.; et al. Acoustic Bioprinting of Patient-Derived Organoids for Predicting Cancer Therapy Responses. Adv. Healthc. Mater. 2022, 11, e2102784. [Google Scholar] [CrossRef]
- Chono, K.; Shimizu, N.; Matsui, Y.; Kondoh, J.; Shiokawa, S. Development of novel atomization system based on SAW streaming. Jpn. J. Appl. Phys. Part 1-Regul. Pap. Brief Commun. Rev. Pap. 2004, 43, 2987–2991. [Google Scholar] [CrossRef]
- Guo, Y.J.; Lv, H.B.; Li, Y.F.; He, X.L.; Zhou, J.; Luo, J.K.; Zu, X.T.; Walton, A.J.; Fu, Y.Q. High frequency microfluidic performance of LiNbO3 and ZnO surface acoustic wave devices. J. Appl. Phys. 2014, 116, 024501. [Google Scholar] [CrossRef]
- Baudoin, M.; Brunet, P.; Matar, O.B.; Herth, E. Low power sessile droplets actuation via modulated surface acoustic waves. Appl. Phys. Lett. 2012, 100, 154102. [Google Scholar] [CrossRef] [Green Version]
- Shaabani, S.; Xu, R.; Ahmadianmoghaddam, M.; Gao, L.; Stahorsky, M.; Olechno, J.; Ellson, R.; Kossenjans, M.; Helan, V.; Domling, A. Automated and Accelerated Synthesis of Indole Derivatives on a Nano-Scale. Green Chem. 2019, 21, 225–232. [Google Scholar] [CrossRef]
- Wang, Y.; Shaabani, S.; Ahmadianmoghaddam, M.; Gao, L.; Xu, R.; Kurpiewska, K.; Kalinowska-Tluscik, J.; Olechno, J.; Ellson, R.; Kossenjans, M.; et al. Acoustic Droplet Ejection Enabled Automated Reaction Scouting. ACS Cent. Sci. 2019, 5, 451–457. [Google Scholar] [CrossRef] [Green Version]
- Sangouard, G.; Zorzi, A.; Wu, Y.; Ehret, E.; Schuttel, M.; Kale, S.; Diaz-Perlas, C.; Vesin, J.; Bortoli Chapalay, J.; Turcatti, G.; et al. Picomole-Scale Synthesis and Screening of Macrocyclic Compound Libraries by Acoustic Liquid Transfer. Angew. Chem. Int. Ed. Engl. 2021, 60, 21702–21707. [Google Scholar] [CrossRef]
- Wu, P.; Noland, C.; Ultsch, M.; Edwards, B.; Harris, D.; Mayer, R.; Harris, S.F. Developments in the Implementation of Acoustic Droplet Ejection for Protein Crystallography. J. Lab Autom. 2016, 21, 97–106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DiRico, K.J.; Hua, W.; Liu, C.; Tucker, J.W.; Ratnayake, A.S.; Flanagan, M.E.; Troutman, M.D.; Noe, M.C.; Zhang, H. Ultra-High-Throughput Acoustic Droplet Ejection-Open Port Interface-Mass Spectrometry for Parallel Medicinal Chemistry. ACS Med. Chem. Lett. 2020, 11, 1101–1110. [Google Scholar] [CrossRef] [PubMed]
- Habe, T.T.; Liu, C.; Covey, T.R.; Simon, R.P.; Reindl, W.; Buttner, F.H.; Winter, M.; Bischoff, D.; Luippold, A.H.; Runge, F. Ultrahigh-Throughput ESI-MS: Sampling Pushed to Six Samples per Second by Acoustic Ejection Mass Spectrometry. Anal. Chem. 2020, 92, 12242–12249. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Van Berkel, G.J.; Cox, D.M.; Covey, T.R. Operational Modes and Speed Considerations of an Acoustic Droplet Dispenser for Mass Spectrometry. Anal. Chem. 2020, 92, 15818–15826. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, J.; Lei, Y.; Hu, H.; Gai, C. A Comprehensive Review of Surface Acoustic Wave-Enabled Acoustic Droplet Ejection Technology and Its Applications. Micromachines 2023, 14, 1543. https://doi.org/10.3390/mi14081543
Ning J, Lei Y, Hu H, Gai C. A Comprehensive Review of Surface Acoustic Wave-Enabled Acoustic Droplet Ejection Technology and Its Applications. Micromachines. 2023; 14(8):1543. https://doi.org/10.3390/mi14081543
Chicago/Turabian StyleNing, Jia, Yulin Lei, Hong Hu, and Chenhui Gai. 2023. "A Comprehensive Review of Surface Acoustic Wave-Enabled Acoustic Droplet Ejection Technology and Its Applications" Micromachines 14, no. 8: 1543. https://doi.org/10.3390/mi14081543
APA StyleNing, J., Lei, Y., Hu, H., & Gai, C. (2023). A Comprehensive Review of Surface Acoustic Wave-Enabled Acoustic Droplet Ejection Technology and Its Applications. Micromachines, 14(8), 1543. https://doi.org/10.3390/mi14081543





