Microfluidic Droplet-Generation Device with Flexible Walls
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
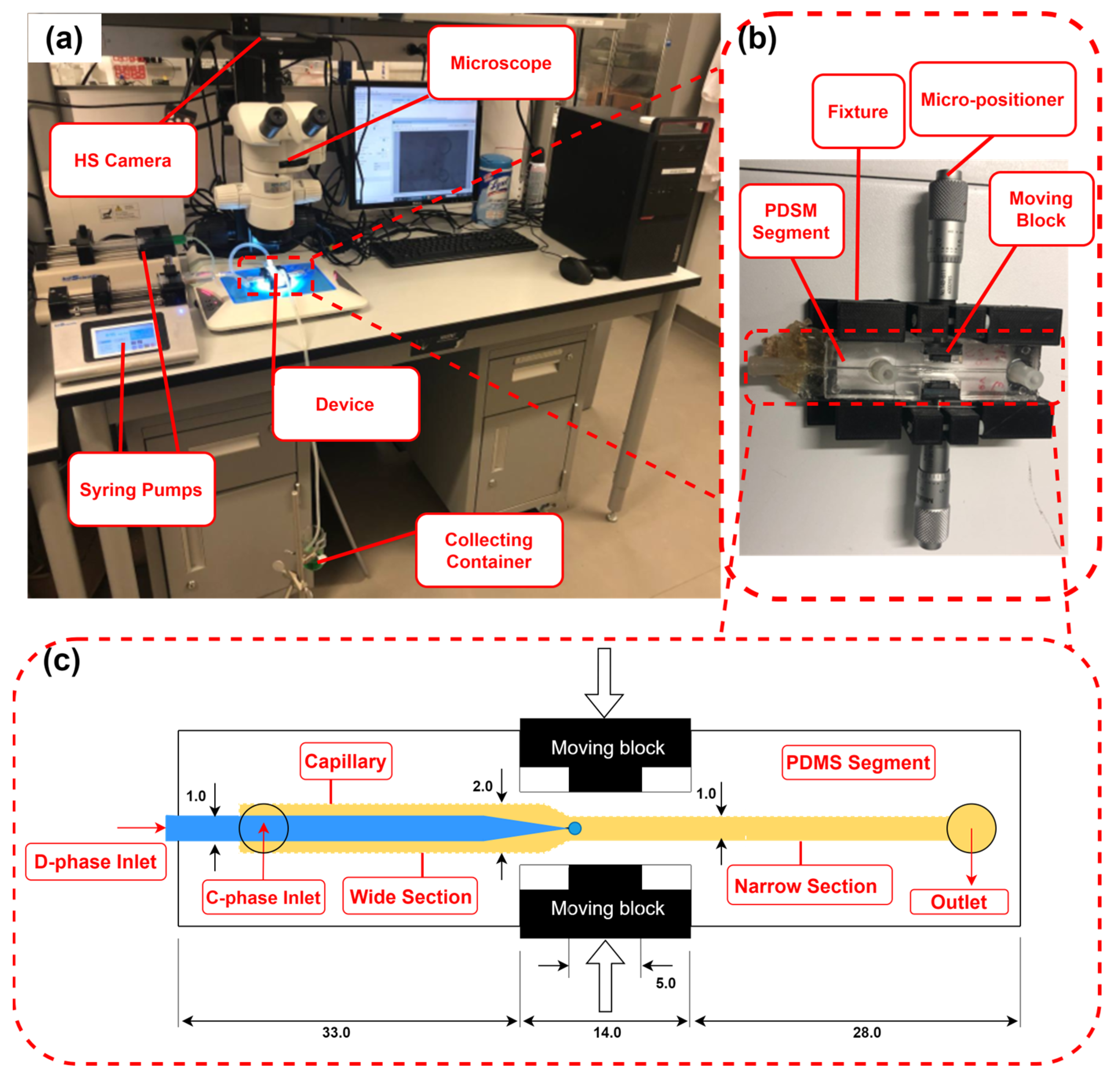
2.2. Experimental Setup
2.3. Microfluidic Co-Flow Droplet-Generation Device
2.4. Experimental Procedure
3. Working Principle of the Co-Flow Droplet-Generation Device with Flexible Walls
4. Results and Discussion
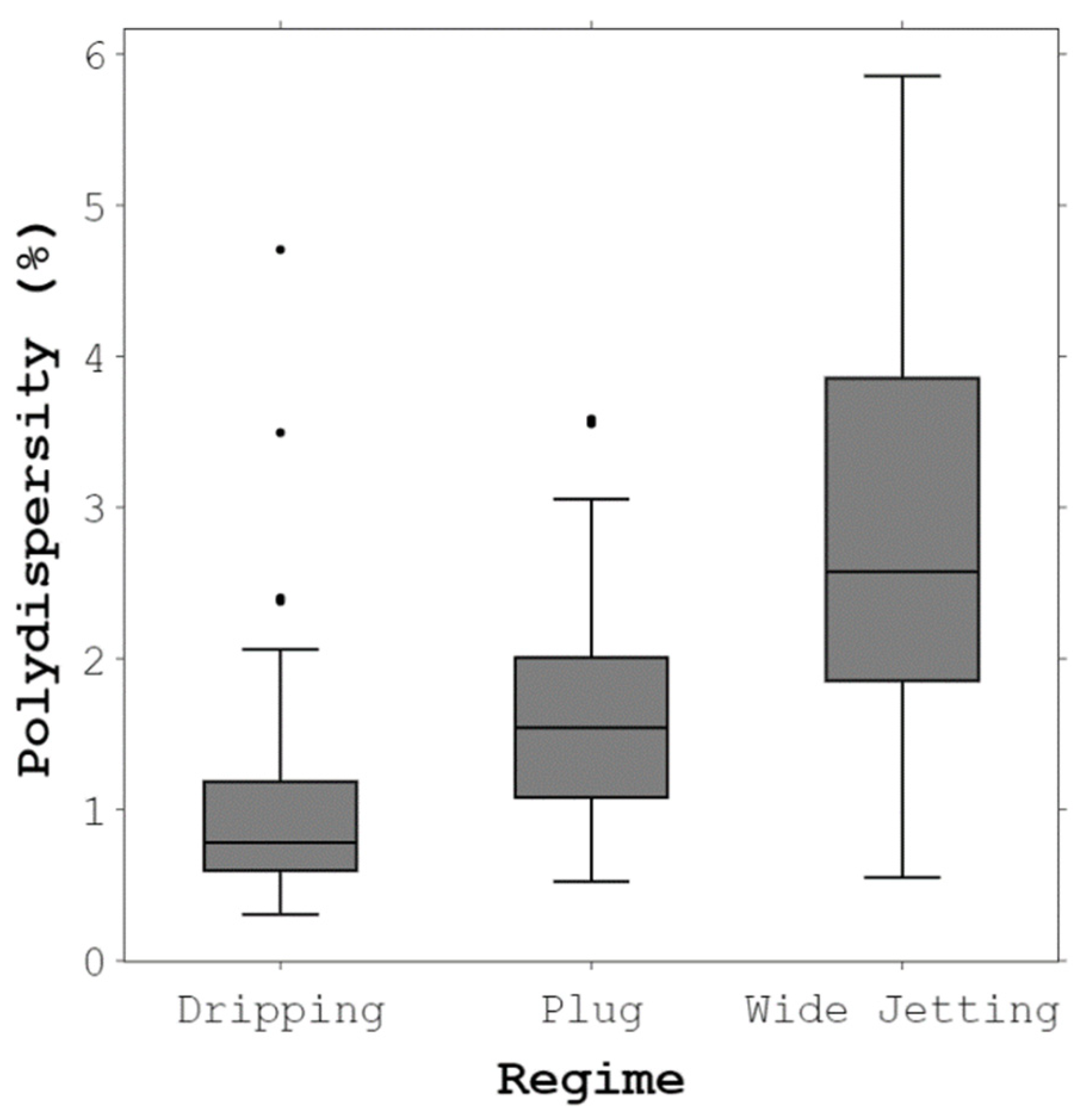
4.1. Droplet-Generation Regimes and Monodispersity in the Proposed Device
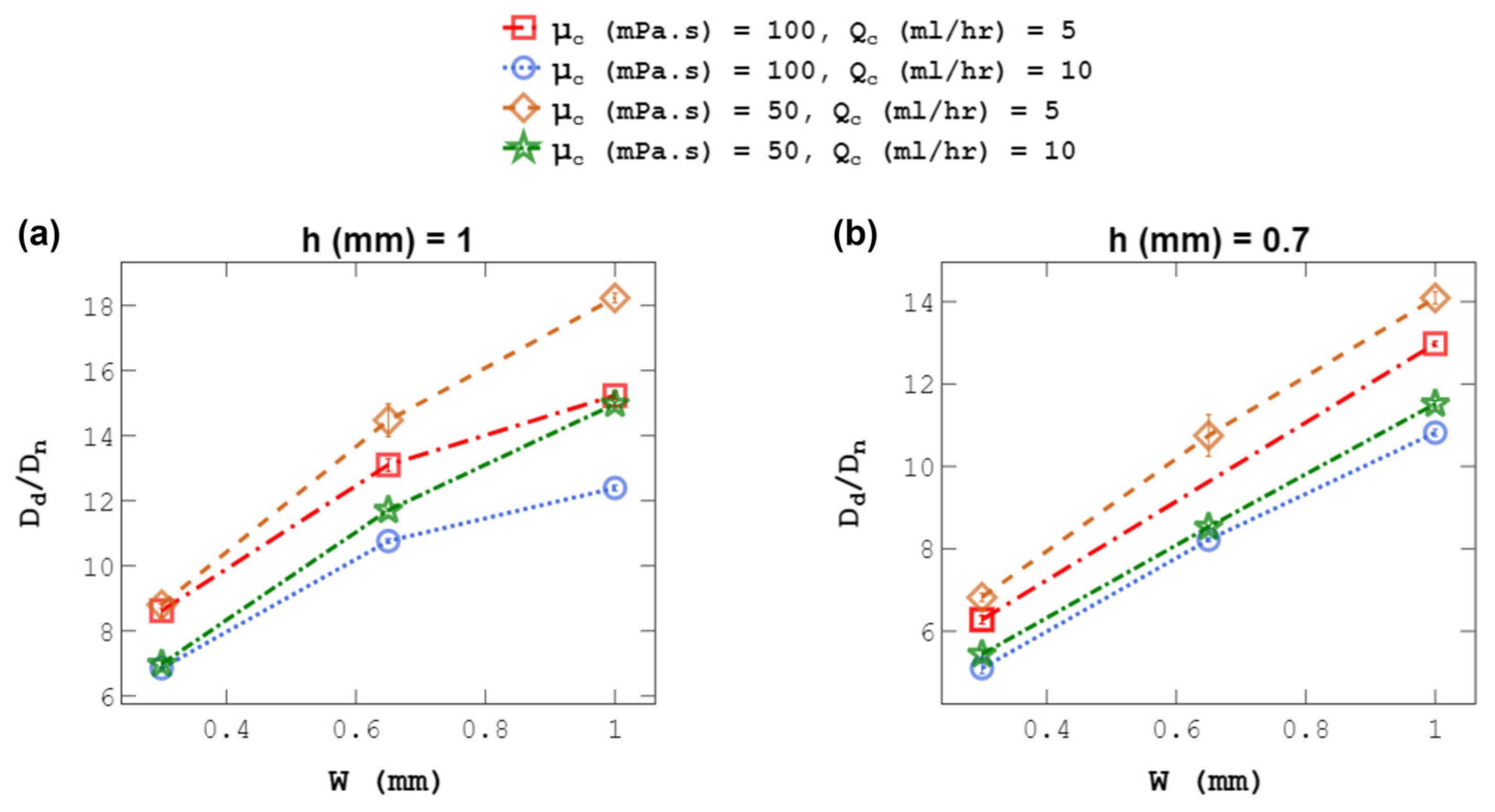
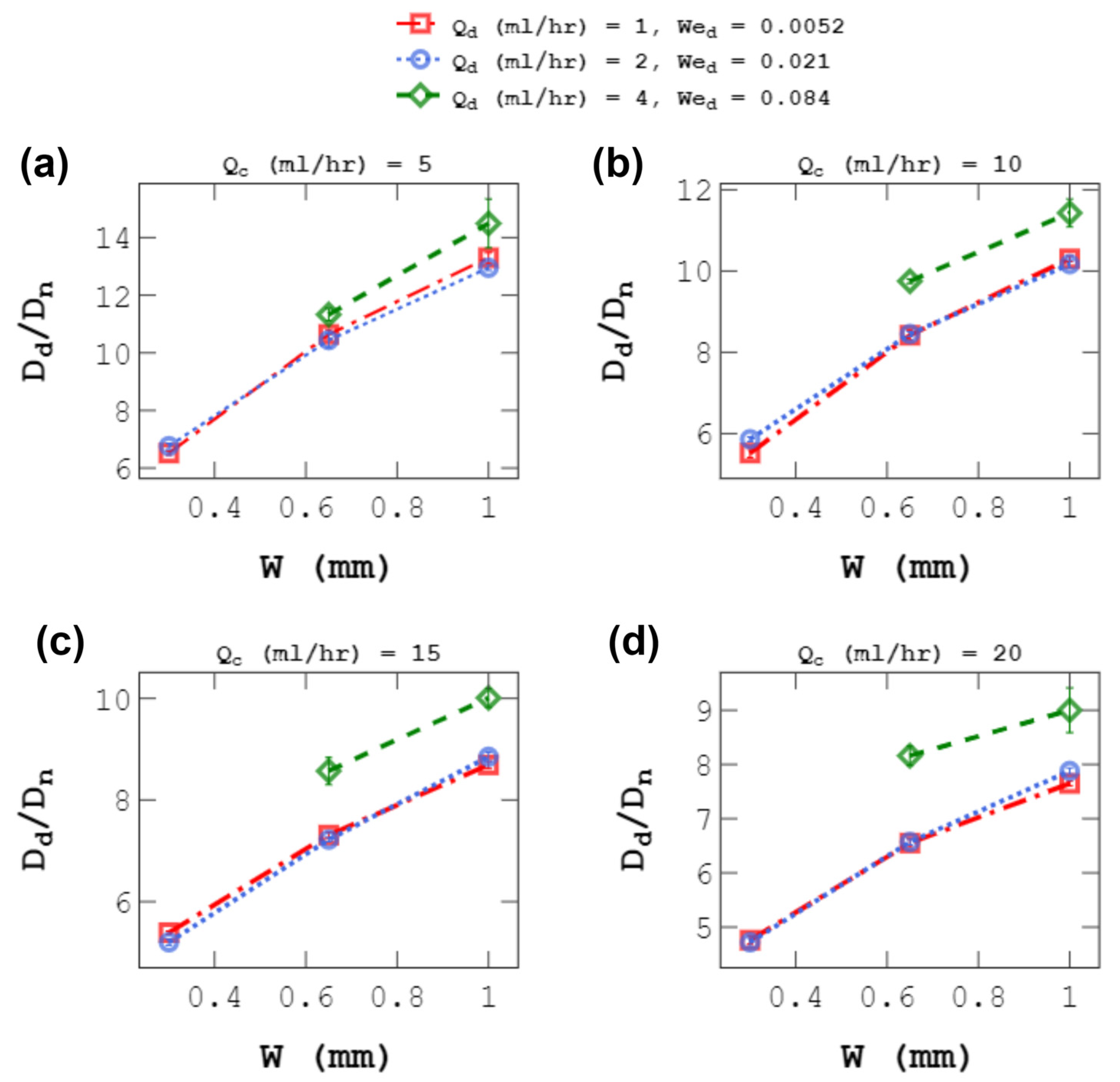
4.2. Droplet Size at a Constant C-Phase Flow Rate
4.3. Effect of D-Phase Flow Rate on Droplet Size
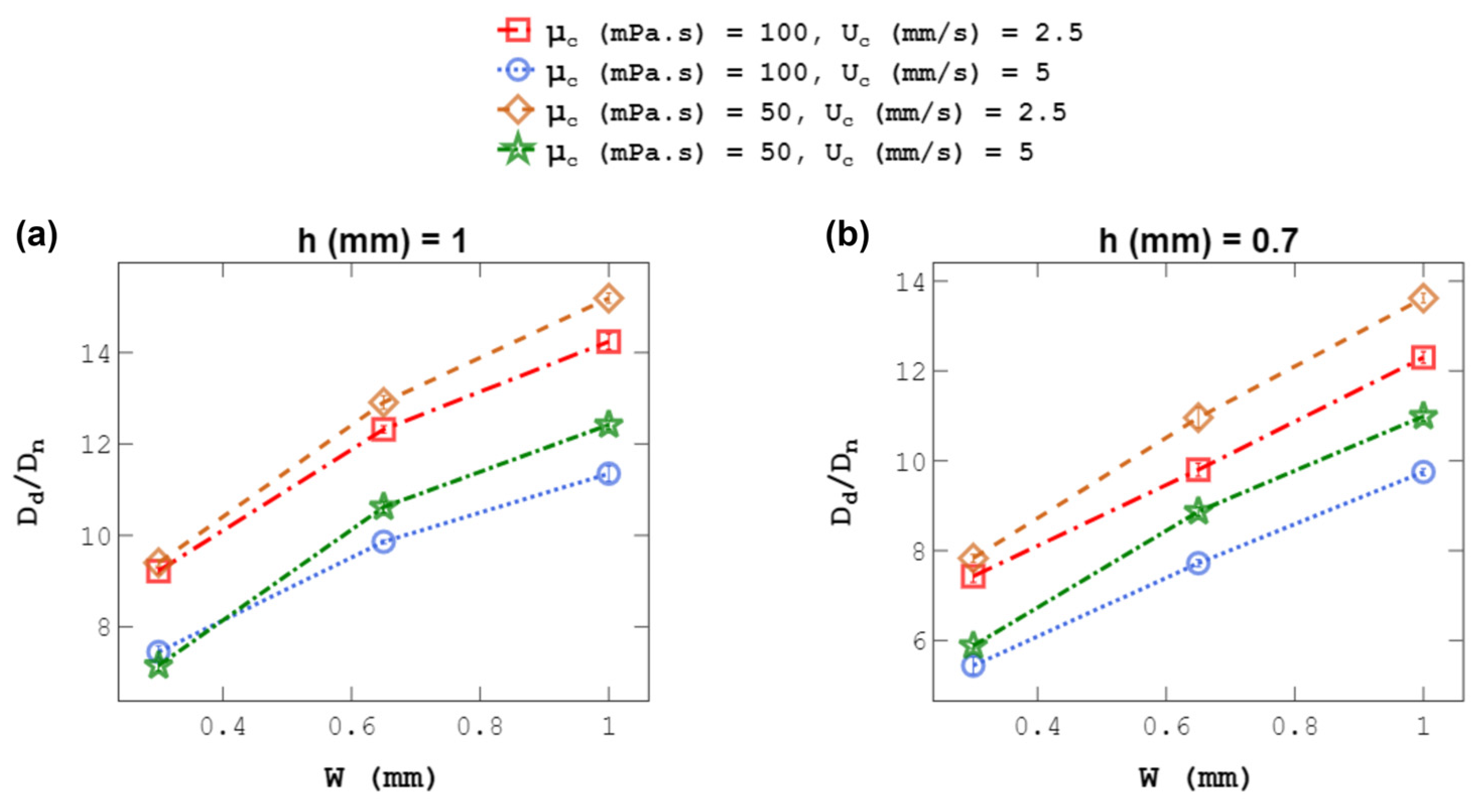
4.4. Droplet Size at a Constant C-Phase Velocity
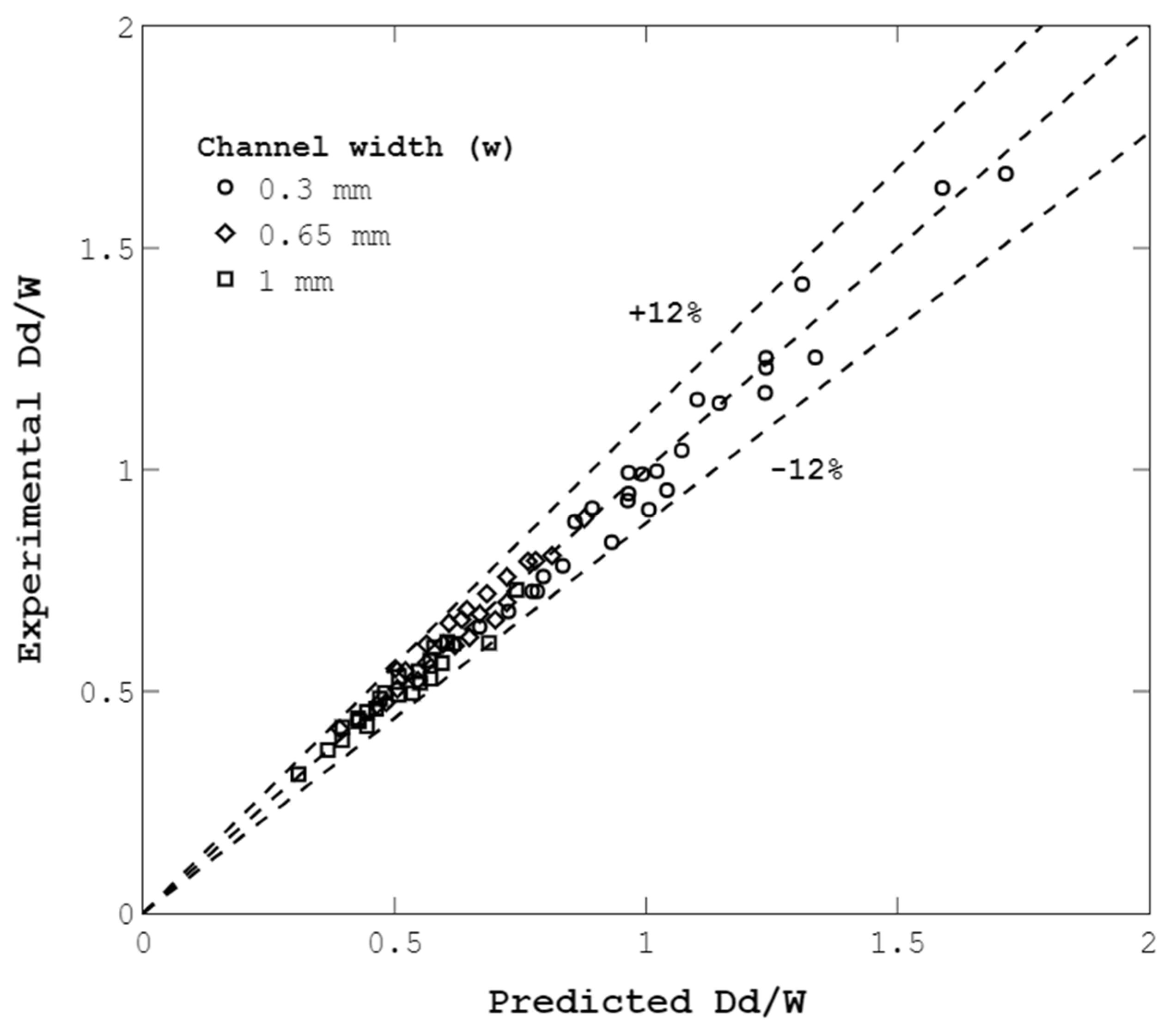
4.5. Droplet-Size Prediction Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baroud, C.N.; Gallaire, F.; Dangla, R. Dynamics of microfluidic droplets. Lab Chip 2010, 10, 2032–2045. [Google Scholar] [CrossRef]
- Chou, W.-L.; Lee, P.-Y.; Yang, C.-L.; Huang, W.-Y.; Lin, Y.-S. Recent Advances in Applications of Droplet Microfluidics. Micromachines 2015, 6, 1249–1271. [Google Scholar] [CrossRef]
- Shang, L.; Cheng, Y.; Zhao, Y. Emerging Droplet Microfluidics. Chem. Rev. 2017, 117, 7964–8040. [Google Scholar] [CrossRef]
- Hattori, S.; Tang, C.; Tanaka, D.; Yoon, D.H.; Nozaki, Y.; Fujita, H.; Akitsu, T.; Sekiguchi, T.; Shoji, S. Development of Microdroplet Generation Method for Organic Solvents Used in Chemical Synthesis. Molecules 2020, 25, 5360. [Google Scholar] [CrossRef] [PubMed]
- Norian, H.; Field, R.M.; Kymissis, I.; Shepard, K.L. An integrated CMOS quantitative-polymerase-chain-reaction lab-on-chip for point-of-care diagnostics. Lab Chip 2014, 14, 4076–4084. [Google Scholar] [CrossRef]
- Golberg, A.; Yarmush, M.L.; Konry, T. Picoliter droplet microfluidic immunosorbent platform for point-of-care diagnostics of tetanus. Microchim. Acta 2013, 180, 855–860. [Google Scholar] [CrossRef]
- Pessi, J.; Santos, H.A.; Miroshnyk, I.; Yliruusi, J.; Weitz, D.A.; Mirza, S. Microfluidics-assisted engineering of polymeric microcapsules with high encapsulation efficiency for protein drug delivery. Int. J. Pharm. 2014, 472, 82–87. [Google Scholar] [CrossRef] [PubMed]
- Herranz-Blanco, B.; Arriaga, L.R.; Mäkilä, E.; Correia, A.; Shrestha, N.; Mirza, S.; Weitz, D.A.; Salonen, J.; Hirvonen, J.; Santos, H.A. Microfluidic assembly of multistage porous silicon–lipid vesicles for controlled drug release. Lab Chip 2014, 14, 1083–1086. [Google Scholar] [CrossRef]
- Song, H.; Chen, D.L.; Ismagilov, R.F. Reactions in Droplets in Microfluidic Channels. Angew. Chem. Int. Ed. 2006, 45, 7336–7356. [Google Scholar] [CrossRef]
- Rademeyer, P.; Carugo, D.; Lee, J.Y.; Stride, E. Microfluidic system for high throughput characterisation of echogenic particles. Lab Chip 2014, 15, 417–428. [Google Scholar] [CrossRef]
- Duncanson, W.J.; Arriaga, L.R.; Ung, W.L.; Kopechek, J.A.; Porter, T.M.; Weitz, D.A. Microfluidic Fabrication of Perfluorohexane-Shelled Double Emulsions for Controlled Loading and Acoustic-Triggered Release of Hydrophilic Agents. Langmuir 2014, 30, 13765–13770. [Google Scholar] [CrossRef] [PubMed]
- Sheeran, P.S.; Rojas, J.D.; Puett, C.; Hjelmquist, J.; Arena, C.B.; Dayton, P.A. Contrast-Enhanced Ultrasound Imaging and in Vivo Circulatory Kinetics with Low-Boiling-Point Nanoscale Phase-Change Perfluorocarbon Agents. Ultrasound Med. Biol. 2015, 41, 814–831. [Google Scholar] [CrossRef] [PubMed]
- Maan, A.A.; Nazir, A.; Khan, M.K.I.; Boom, R.; Schroën, K. Microfluidic emulsification in food processing. J. Food Eng. 2015, 147, 1–7. [Google Scholar] [CrossRef]
- Shewan, H.M.; Stokes, J.R. Review of techniques to manufacture micro-hydrogel particles for the food industry and their applications. J. Food Eng. 2013, 119, 781–792. [Google Scholar] [CrossRef]
- Joscelyne, S.M.; Trägårdh, G. Membrane emulsification—A literature review. J. Memb. Sci. 2000, 169, 107–117. [Google Scholar] [CrossRef]
- Vladisavljević, G.T.; Kobayashi, I.; Nakajima, M. Production of uniform droplets using membrane, microchannel and microfluidic emulsification devices. Microfluid. Nanofluidics 2012, 13, 151–178. [Google Scholar] [CrossRef]
- Manz, A.; Harrison, D.; Verpoorte, E.M.; Fettinger, J.; Paulus, A.; Lüdi, H.; Widmer, H. Planar chips technology for miniaturization and integration of separation techniques into monitoring systems: Capillary electrophoresis on a chip. J. Chromatogr. A 1992, 593, 253–258. [Google Scholar] [CrossRef]
- Tong, J.; Nakajima, M.; Nabetani, H.; Kikuchi, Y.; Maruta, Y. Production of Oil-in-Water Microspheres Using a Stainless Steel Microchannel. J. Colloid Interface Sci. 2001, 237, 239–248. [Google Scholar] [CrossRef]
- Liu, H.; Nakajima, M.; Nishi, T.; Kimura, T. Effect of channel structure on preparation of a water-in-oil emulsion by polymer microchannels. Eur. J. Lipid Sci. Technol. 2005, 107, 481–487. [Google Scholar] [CrossRef]
- Xu, X.; Song, R.; He, M.; Peng, C.; Yu, M.; Hou, Y.; Qiu, H.; Zou, R.; Yao, S. Microfluidic production of nanoscale perfluorocarbon droplets as liquid contrast agents for ultrasound imaging. Lab Chip 2017, 17, 3504–3513. [Google Scholar] [CrossRef]
- Utada, A.S.; Lorenceau, E.; Link, D.R.; Kaplan, P.D.; Stone, H.A.; Weitz, D.A. Monodisperse Double Emulsions Generated from a Microcapillary Device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Nabavi, S.A.; Vladisavljević, G.T.; Gu, S.; Ekanem, E.E. Double emulsion production in glass capillary microfluidic device: Parametric investigation of droplet generation behaviour. Chem. Eng. Sci. 2015, 130, 183–196. [Google Scholar] [CrossRef]
- Hsiung, S.-K.; Chen, C.-T.; Lee, G.-B. Micro-droplet formation utilizing microfluidic flow focusing and controllable moving-wall chopping techniques. J. Micromech. Microeng. 2006, 16, 2403–2410. [Google Scholar] [CrossRef]
- Nabavi, S.A.; Vladisavljević, G.T.; Manović, V. Mechanisms and control of single-step microfluidic generation of multi-core double emulsion droplets. Chem. Eng. J. 2017, 322, 140–148. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, C.; Liu, G.; Xu, W.; Zhu, Z.; Si, T.; Xu, R.X. Multiplex coaxial flow focusing for producing multicompartment Janus microcapsules with tunable material compositions and structural characteristics. Lab Chip 2017, 17, 3168–3175. [Google Scholar] [CrossRef] [PubMed]
- Anna, S.L.; Bontoux, N.; Stone, H.A. Formation of dispersions using ‘flow focusing’ in microchannels. Appl. Phys. Lett. 2003, 82, 364–366. [Google Scholar] [CrossRef]
- Dreyfus, R.; Tabeling, P.; Willaime, H. Ordered and Disordered Patterns in Two-Phase Flows in Microchannels. Phys. Rev. Lett. 2003, 90, 144505. [Google Scholar] [CrossRef]
- Ward, T.; Faivre, M.; Abkarian, M.; Stone, H.A. Microfluidic flow focusing: Drop size and scaling in pressure versus flow-rate-driven pumping. Electrophoresis 2005, 26, 3716–3724. [Google Scholar] [CrossRef]
- Cubaud, T.; Mason, T.G. Capillary threads and viscous droplets in square microchannels. Phys. Fluids 2008, 20, 053302. [Google Scholar] [CrossRef]
- Lee, W.; Walker, L.M.; Anna, S.L. Role of geometry and fluid properties in droplet and thread formation processes in planar flow focusing. Phys. Fluids 2009, 21, 032103. [Google Scholar] [CrossRef]
- Funfschilling, D.; Debas, H.; Li, H.-Z.; Mason, T.G. Flow-field dynamics during droplet formation by dripping in hydrodynamic-focusing microfluidics. Phys. Rev. E 2009, 80, 015301. [Google Scholar] [CrossRef]
- Rahimi, M.; Khorrami, A.S.; Rezai, P. Effect of device geometry on droplet size in co-axial flow-focusing microfluidic droplet generation devices. Colloids Surf. A Physicochem. Eng. Asp. 2019, 570, 510–517. [Google Scholar] [CrossRef]
- Rahimi, M.; Yazdanparast, S.; Rezai, P. Parametric study of droplet size in an axisymmetric flow-focusing capillary device. Chin. J. Chem. Eng. 2020, 28, 1016–1022. [Google Scholar] [CrossRef]
- Thorsen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef] [PubMed]
- van der Graaf, S.; Steegmans, M.L.J.; van der Sman, R.G.M.; Schroën, C.G.P.H.; Boom, R.M. Droplet formation in a T-shaped microchannel junction: A model system for membrane emulsification. Colloids Surf. A Physicochem. Eng. Asp. 2005, 266, 106–116. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Stone, H.A.; Whitesides, G.M. Formation of droplets and bubbles in a microfluidic T-junction—Scaling and mechanism of break-up. Lab Chip 2006, 6, 437–446. [Google Scholar] [CrossRef] [PubMed]
- Christopher, G.F.; Anna, S.L. Microfluidic methods for generating continuous droplet streams. J. Phys. D Appl. Phys. 2007, 40, R319–R336. [Google Scholar] [CrossRef]
- DE Menech, M.; Garstecki, P.; Jousse, F.; Stone, H.A. Transition from squeezing to dripping in a microfluidic T-shaped junction. J. Fluid Mech. 2008, 595, 141–161. [Google Scholar] [CrossRef]
- Christopher, G.F.; Noharuddin, N.N.; Taylor, J.A.; Anna, S.L. Experimental observations of the squeezing-to-dripping transition in T-shaped microfluidic junctions. Phys. Rev. E 2008, 78, 036317. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, R. Effect of geometry on droplet formation in the squeezing regime in a microfluidic T-junction. Microfluid. Nanofluidics 2009, 8, 799–812. [Google Scholar] [CrossRef]
- Sivasamy, J.; Wong, T.-N.; Nguyen, N.-T.; Kao, L.T.-H. An investigation on the mechanism of droplet formation in a microfluidic T-junction. Microfluid. Nanofluidics 2011, 11, 1–10. [Google Scholar] [CrossRef]
- Tarchichi, N.; Chollet, F.; Manceau, J.-F. New regime of droplet generation in a T-shape microfluidic junction. Microfluid. Nanofluidics 2012, 14, 45–51. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, Q.; Fan, L.-S. Three-dimensional numerical study on droplet formation and cell encapsulation process in a micro T-junction. Chem. Eng. Sci. 2013, 87, 100–110. [Google Scholar] [CrossRef]
- Wehking, J.D.; Gabany, M.; Chew, L.; Kumar, R. Effects of viscosity, interfacial tension, and flow geometry on droplet formation in a microfluidic T-junction. Microfluid. Nanofluidics 2013, 16, 441–453. [Google Scholar] [CrossRef]
- Jamalabadi, M.Y.A.; DaqiqShirazi, M.; Kosar, A.; Shadloo, M.S. Effect of injection angle, density ratio, and viscosity on droplet formation in a microfluidic T-junction. Theor. Appl. Mech. Lett. 2017, 7, 243–251. [Google Scholar] [CrossRef]
- Cramer, C.; Fischer, P.; Windhab, E.J. Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 2004, 59, 3045–3058. [Google Scholar] [CrossRef]
- Utada, A.S.; Fernandez-Nieves, A.; Stone, H.A.; Weitz, D.A. Dripping to Jetting Transitions in Coflowing Liquid Streams. Phys. Rev. Lett. 2007, 99, 094502. [Google Scholar] [CrossRef] [PubMed]
- Guillot, P.; Colin, A.; Utada, A.S.; Ajdari, A. Stability of a Jet in Confined Pressure-Driven Biphasic Flows at Low Reynolds Numbers. Phys. Rev. Lett. 2007, 99, 104502. [Google Scholar] [CrossRef]
- Utada, A.S.; Fernandez-Nieves, A.; Gordillo, J.M.; Weitz, D.A. Absolute Instability of a Liquid Jet in a Coflowing Stream. Phys. Rev. Lett. 2008, 100, 014502. [Google Scholar] [CrossRef]
- Deng, C.; Wang, H.; Huang, W.; Cheng, S. Numerical and experimental study of oil-in-water (O/W) droplet formation in a co-flowing capillary device. Colloids Surf. A Physicochem. Eng. Asp. 2017, 533, 1–8. [Google Scholar] [CrossRef]
- Khorrami, A.S.; Rezai, P. Oscillating dispersed-phase co-flow microfluidic droplet generation: Jet length reduction effect. Soft Matter 2018, 14, 9870–9876. [Google Scholar] [CrossRef] [PubMed]
- Khorrami, A.S.; Rezai, P. Oscillating dispersed-phase co-flow microfluidic droplet generation: Multi-droplet size effect. Biomicrofluidics 2018, 12, 034113. [Google Scholar] [CrossRef]
- Okushima, S.; Nisisako, T.; Torii, T.; Higuchi, T. Controlled Production of Monodisperse Double Emulsions by Two-Step Droplet Breakup in Microfluidic Devices. Langmuir 2004, 20, 9905–9908. [Google Scholar] [CrossRef]
- Nisisako, T.; Okushima, S.; Torii, T. Controlled formulation of monodisperse double emulsions in a multiple-phase microfluidic system. Soft Matter 2005, 1, 23–27. [Google Scholar] [CrossRef]
- Perro, A.; Nicolet, C.; Angly, J.; Lecommandoux, S.; Le Meins, J.-F.; Colin, A. Mastering a Double Emulsion in a Simple Co-Flow Microfluidic to Generate Complex Polymersomes. Langmuir 2010, 27, 9034–9042. [Google Scholar] [CrossRef] [PubMed]
- Umbanhowar, P.B.; Prasad, V.; Weitz, D.A. Monodisperse Emulsion Generation via Drop Break Off in a Coflowing Stream. Langmuir 1999, 16, 347–351. [Google Scholar] [CrossRef]
- Erb, R.M.; Obrist, D.; Chen, P.W.; Studer, J.; Studart, A.R. Predicting sizes of droplets made by microfluidic flow-induced dripping. Soft Matter 2011, 7, 8757–8761. [Google Scholar] [CrossRef]
- Fox, H.; Taylor, P.; Zisman, W. Polyorganosiloxanes… surface active properties. Ind. Eng. Chem. 1947, 39, 1401–1409. [Google Scholar] [CrossRef]
- Peters, F.; Arabali, D. Interfacial tension between oil and water measured with a modified contour method. Colloids Surf. A Physicochem. Eng. Asp. 2013, 426, 1–5. [Google Scholar] [CrossRef]
- Seemann, R.; Brinkmann, M.; Pfohl, T.; Herminghaus, S. Droplet based microfluidics. Rep. Prog. Phys. 2011, 75, 16601. [Google Scholar] [CrossRef]
- Lee, C.-H.; Hsiung, S.-K.; Lee, G.-B. A tunable microflow focusing device utilizing controllable moving walls and its applications for formation of micro-droplets in liquids. J. Micromech. Microeng. 2007, 17, 1121–1129. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder—Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]







| Material | Density ρ (Kg/m3) | Viscosity μ (cSt) | Interfacial Tension γ in Water (mN/m) |
|---|---|---|---|
| Silicone oil 1 | 960 | 100 | 35.18 [59] 35.26 [60] |
| DI water | 998 | 1 | |
| Silicone oil 2 | 950 | 50 |
| Condition | Qc (mL/h) | uc (mm/s) | 10−3 | w (mm) | Qd (mL/h) | μc (cSt) | h (mm) |
|---|---|---|---|---|---|---|---|
| Mode i: Constant C-phase flow rate (Qc) | 2, 5, 10, 15, 20, 22, 50 | 16 values between 1.5–11.9, depending on Qc and w | 24 values between 2.1–34 depending on Qc, w, and μc | 0.3, 0.65, 1 | 1, 2, 4 | 50, 100 | 0.7, 1 |
| Mode ii: Constant C-phase velocity (uc) | 12 values between 2.0–16.75, depending on uc and w | 2.5, 5 | 1.8, 3.6, 7.1, 14.3 | 0.3, 0.65, 1 | 1 | 50, 100 | 0.7, 1 |
| Mode iii: Constant C-phase Capillary number (Cac) | 12 values between 3.4–57.3, depending on Cac and w | 2.1, 4.3, 8.5, 17.1 | 6.1, 12.2, 24.4 | 0.3, 0.65, 1 | 1 | 50, 100 | 0.7, 1 |
| Dc [μm] | w [μm] | h [μm] | μc [mPa.s] | Dn [μm] | Camin | Camax | Dd_min [μm] | Dd_max [μm] | Dd_Range [μm] | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| 600 | NA | NA | NA | 40 | NA | NA | 255 | 553 | 298 | Chu et al. (2007) [61] |
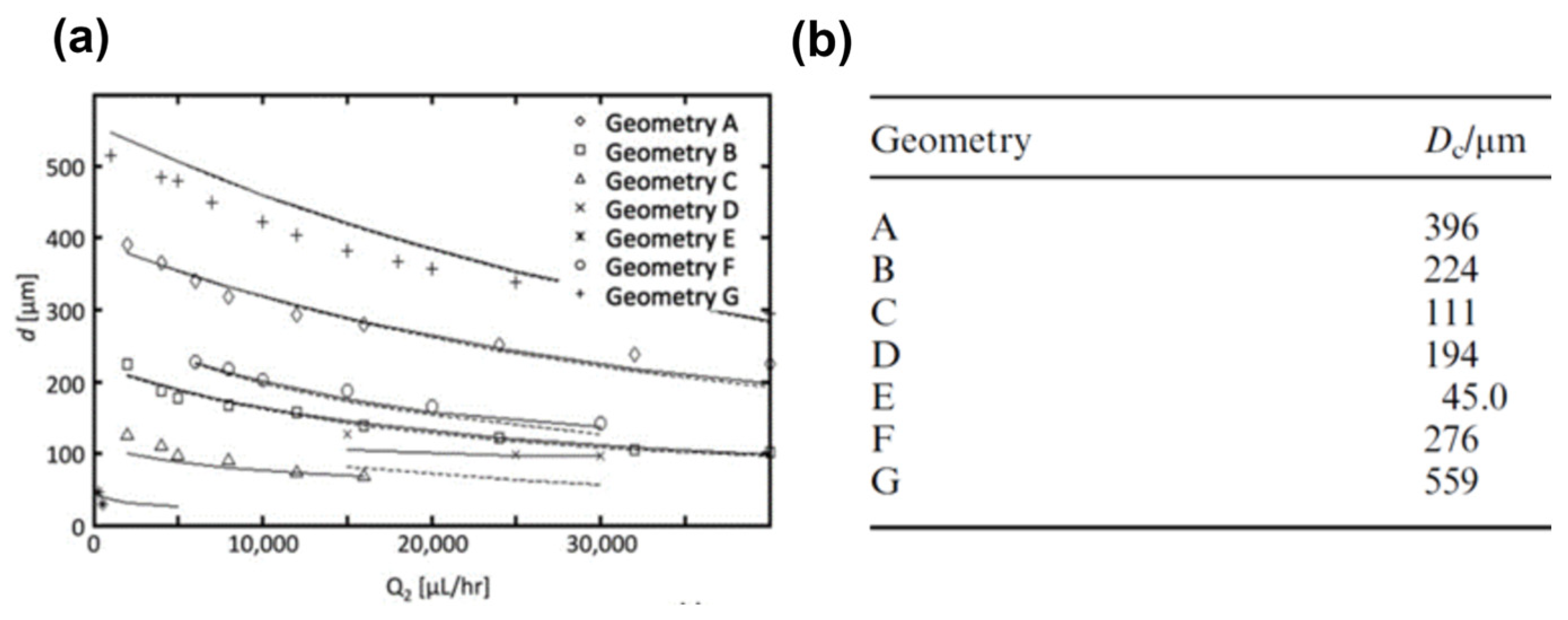
| 559 | NA | NA | 1.2 | 41 | 0.00002 | 0.00096 | 280 | 550 | 270 | Erb et al. (2011) [57] |
| 396 | NA | NA | 1.2 | 47.4 | 0.00012 | 0.0019 | 223 | 389 | 166 | Erb et al. (2011) [57] |
| 224 | NA | NA | 1.2 | 47 | 0.00037 | 0.0060 | 100 | 200 | 100 | Erb et al. (2011) [57] |
| 111 | NA | NA | 1.2 | 45.4 | 0.0015 | 0.0099 | 80 | 100 | 20 | Erb et al. (2011) [57] |
| 150 | NA | NA | 1 | 40 | 0.00034 | 0.010 | 126 | 241 | 115 | Perro et al. (2011) [55] |
| 300 | NA | NA | 49.5 | 40 | 0.11 | 0.51 | 80 | 168 | 166 | Deng et al. (2017) [50] |
| NA | 300 to 1000 | 1000 | 100 | 40 | 0.00085 | 0.044 | 175 | 913 | 738 | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yazdanparast, S.; Rezai, P.; Amirfazli, A. Microfluidic Droplet-Generation Device with Flexible Walls. Micromachines 2023, 14, 1770. https://doi.org/10.3390/mi14091770
Yazdanparast S, Rezai P, Amirfazli A. Microfluidic Droplet-Generation Device with Flexible Walls. Micromachines. 2023; 14(9):1770. https://doi.org/10.3390/mi14091770
Chicago/Turabian StyleYazdanparast, Sajad, Pouya Rezai, and Alidad Amirfazli. 2023. "Microfluidic Droplet-Generation Device with Flexible Walls" Micromachines 14, no. 9: 1770. https://doi.org/10.3390/mi14091770
APA StyleYazdanparast, S., Rezai, P., & Amirfazli, A. (2023). Microfluidic Droplet-Generation Device with Flexible Walls. Micromachines, 14(9), 1770. https://doi.org/10.3390/mi14091770







