Optical Forces on Chiral Particles: Science and Applications
Abstract
1. Introduction
2. Physical Mechanics
2.1. Optical Gradient Force on Chiral Particles

2.2. Optical Radiation Pressure on Chiral Particles
2.3. Optical Pulling Force on Chiral Particles
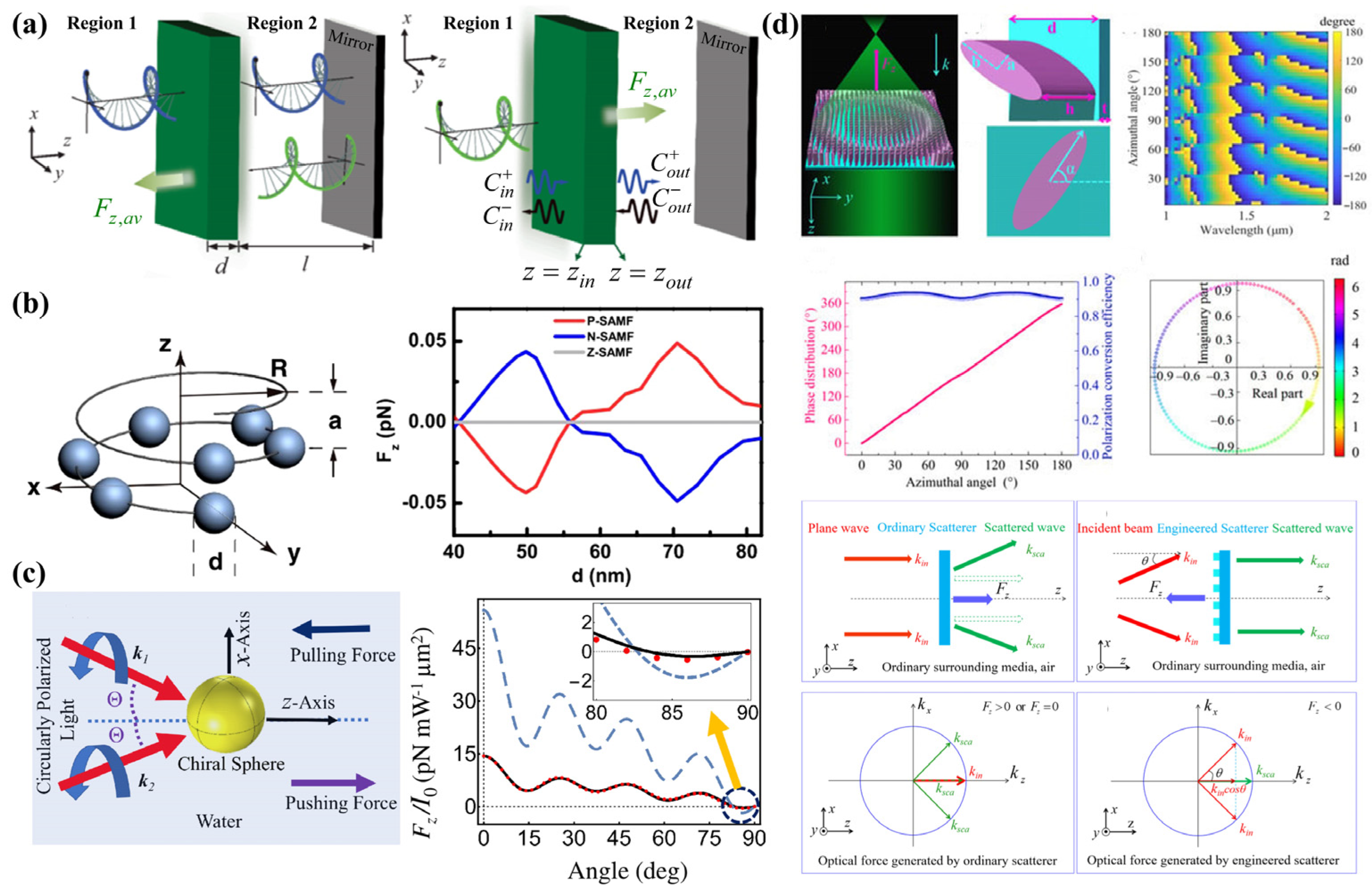
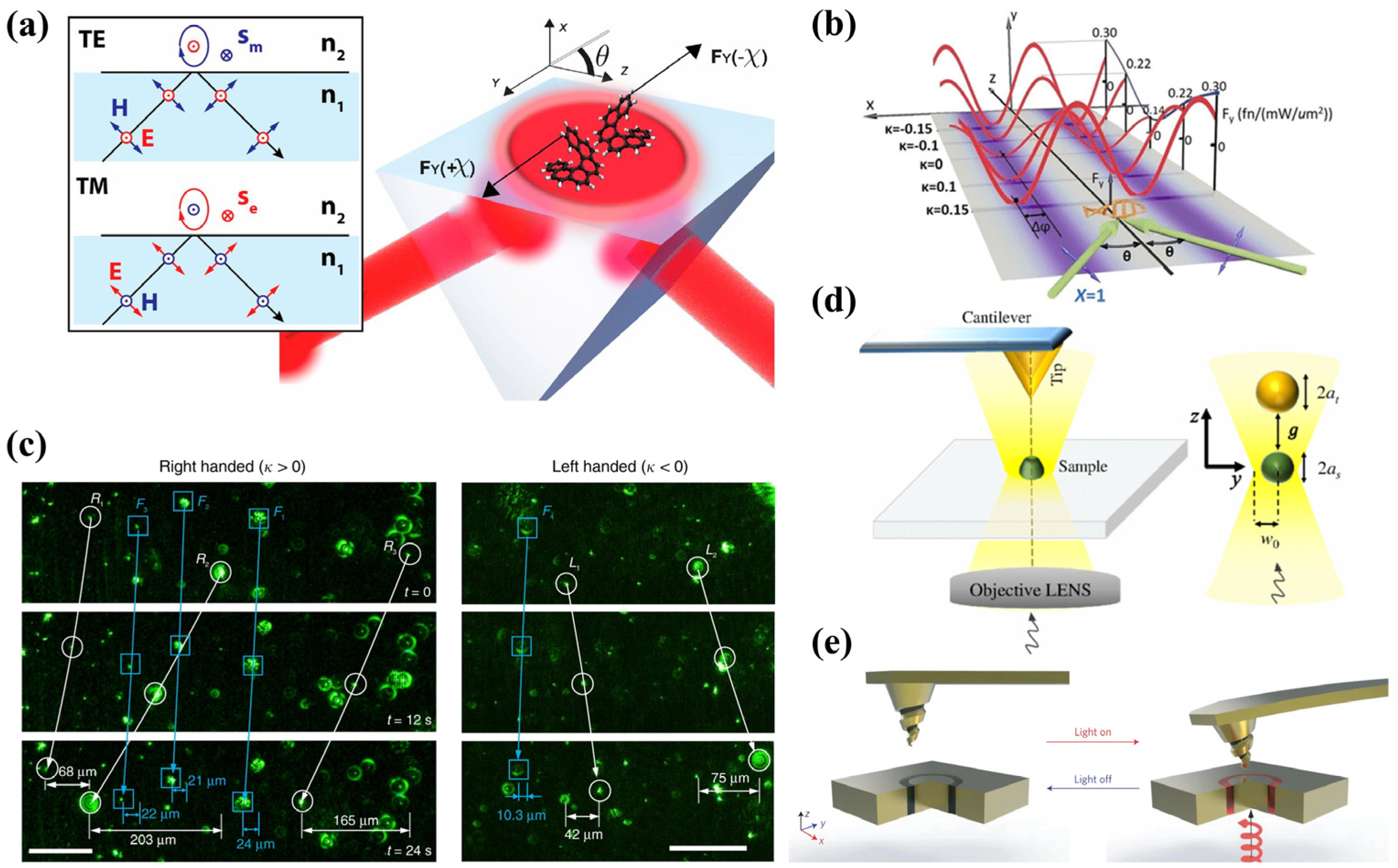
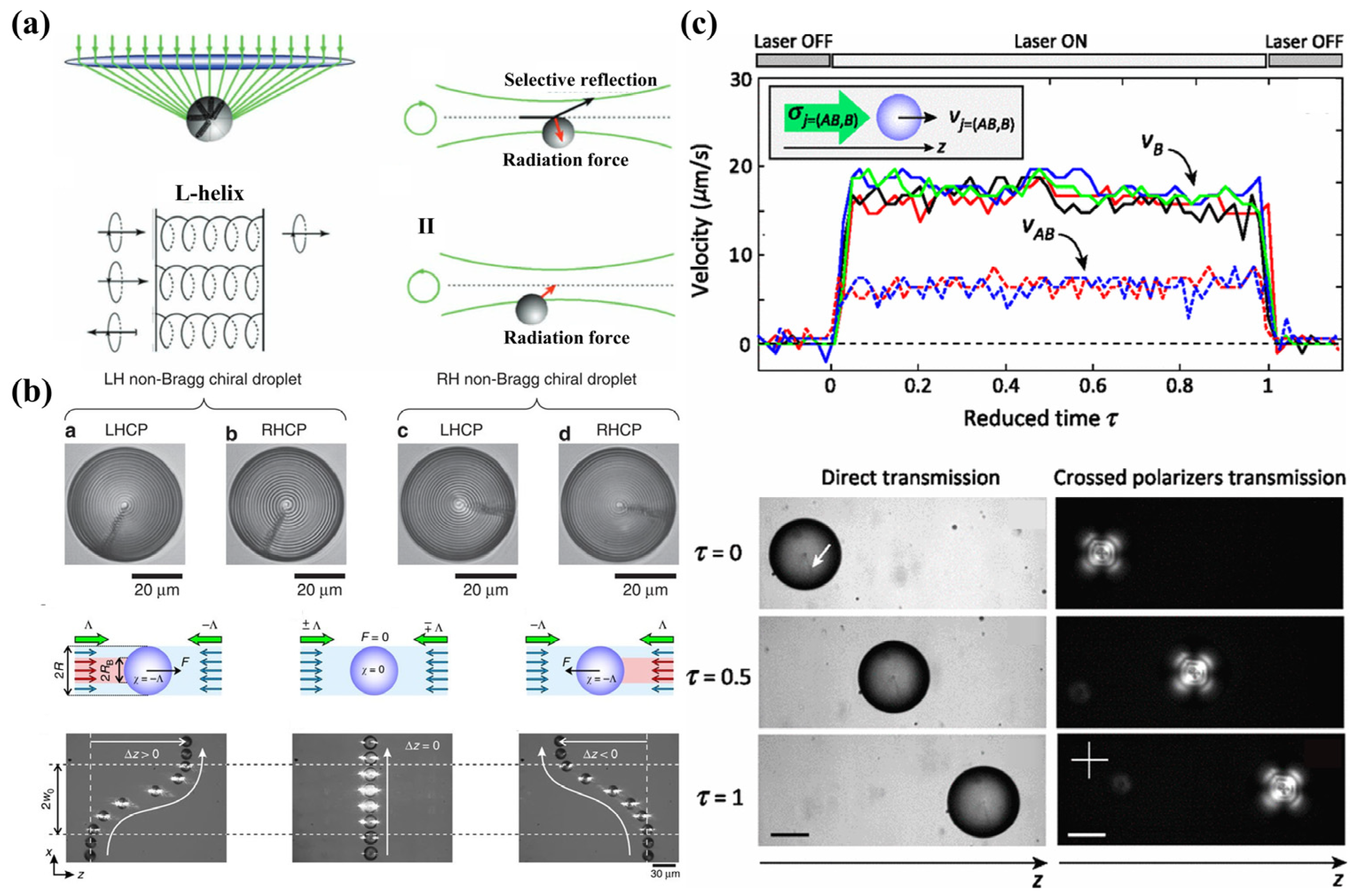
2.4. Optical Lateral Force on Chiral Particles
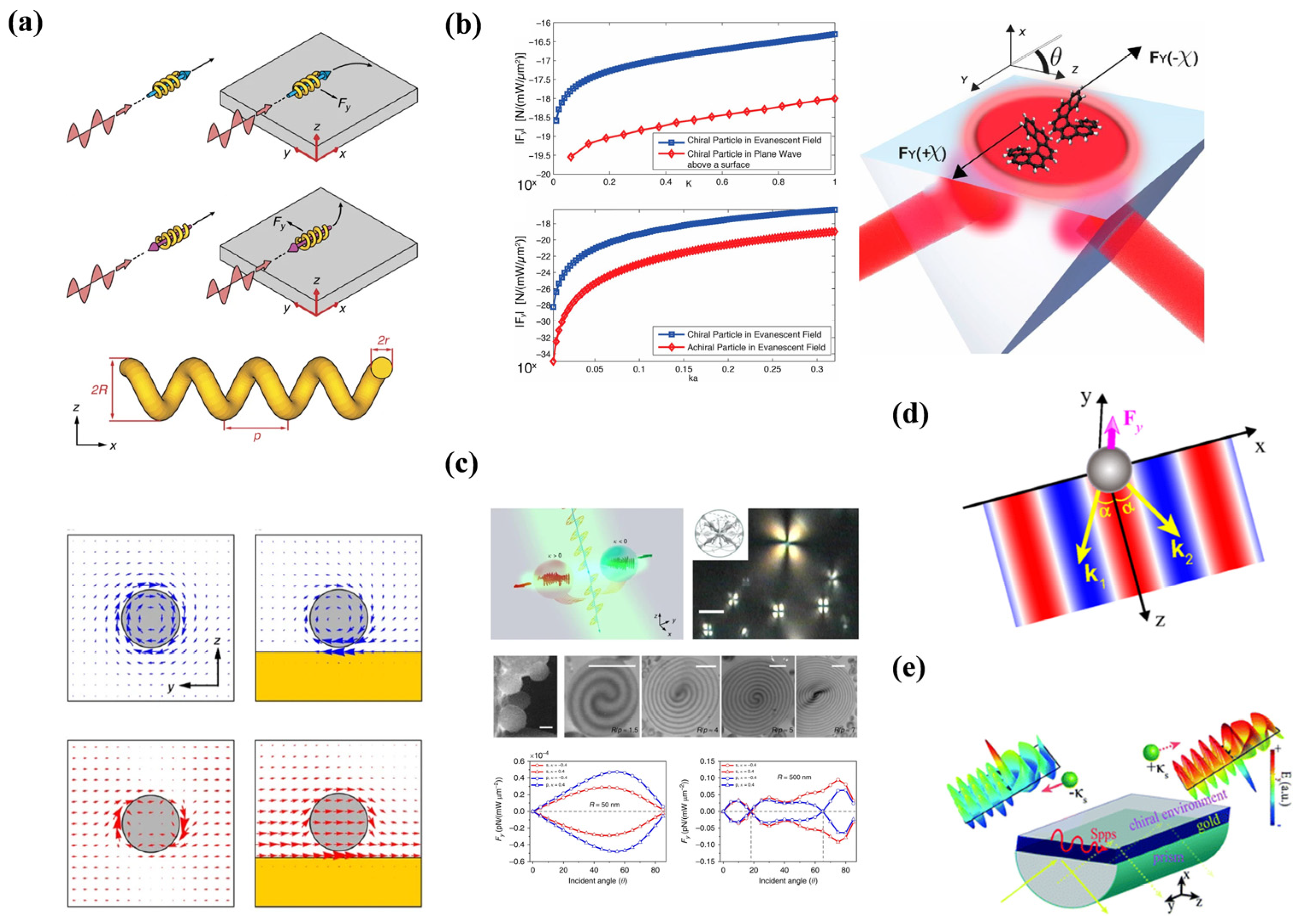
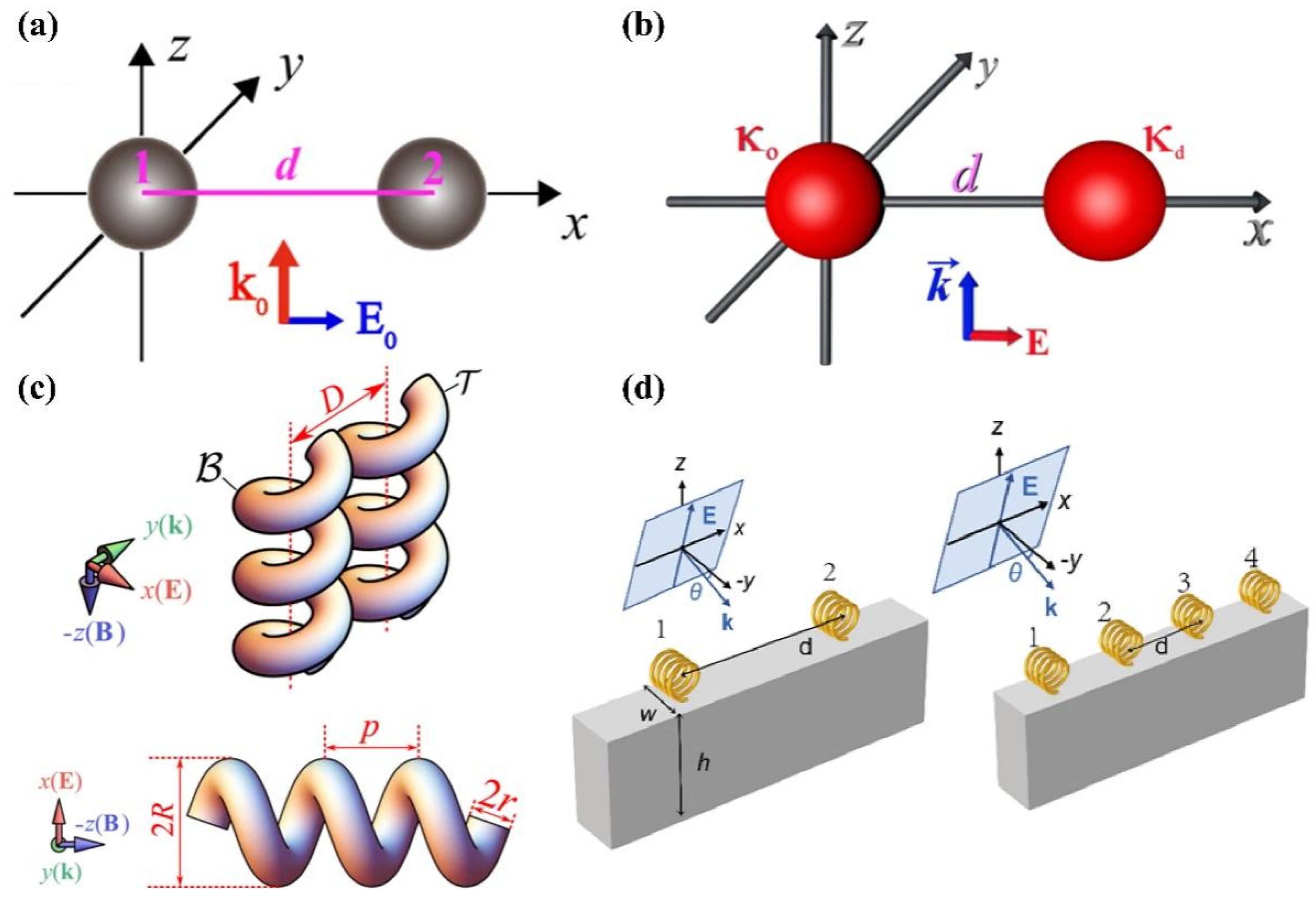
2.5. Optical Force on Coupled Chiral Particles
3. Applications
4. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kemp, B.A. Resolution of the Abraham-Minkowski debate: Implications for the electromagnetic wave theory of light in matter. J. Appl. Phys. 2011, 109, 111101. [Google Scholar] [CrossRef]
- Ashkin, A. Acceleration and Trapping of Particles by Radiation Pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 816–818. [Google Scholar] [CrossRef]
- Ashkin, A. Optical Trapping and Manipulation of Neutral Particles Using Lasers. Opt. Photonics News 1999, 10, 41. [Google Scholar] [CrossRef]
- Qiu, C.-W.; Palima, D.; Novitsky, A.; Gao, D.; Ding, W.; Zhukovsky, S.V.; Gluckstad, J. Engineering light-matter interaction for emerging optical manipulation applications. Nanophotonics 2014, 3, 181–201. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M.; Sáenz, J.J.; Gómez-Medina, R.; Chantada, L. Optical forces on small magnetodielectric particle. Opt. Express 2010, 18, 11428–11443. [Google Scholar] [CrossRef]
- Kahr, B. Polarization in France. Chirality 2018, 30, 351–368. [Google Scholar] [CrossRef]
- Kucirka, J.; Shekhtman, A.G. On the deracemization of a chiral molecular beam by interaction with circularly polarized light. Phys. Lett. A 1996, 221, 273–276. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Nieto-Vesperinas, M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt. Lett. 2000, 25, 1065–1067. [Google Scholar] [CrossRef]
- Guzatov, D.V.; Klimov, V.V. Chiral particles in a circularly polarised light field: New effects and applications. Quantum Electron. 2011, 41, 526–533. [Google Scholar] [CrossRef]
- Cameron, R.P.; Barnett, S.M.; Yao, A.M. Discriminatory optical force for chiral molecules. New J. Phys. 2014, 16, 013020. [Google Scholar] [CrossRef]
- Brzobohaty, O.; Hernandez, R.J.; Simpson, S.; Mazzulla, A.; Cipparrone, G.; Zemanek, P. Chiral particles in the dual-beam optical trap. Opt. Express 2016, 24, 26382–26391. [Google Scholar] [CrossRef]
- Donato, M.G.; Hernandez, J.; Mazzulla, A.; Provenzano, C.; Saija, R.; Sayed, R.; Vasi, S.; Magazzu, A.; Pagliusi, P.; Bartolino, R.; et al. Polarization-dependent optomechanics mediated by chiral microresonators. Nat. Commun. 2014, 5, 3656. [Google Scholar] [CrossRef]
- Eilam, A.; Shapiro, M. Spatial separation of dimers of chiral molecules. Phys. Rev. Lett. 2013, 110, 213004. [Google Scholar] [CrossRef]
- Jacob, A.; Hornberger, K. Effect of molecular rotation on enantioseparation. J. Chem. Phys. 2012, 137, 044313. [Google Scholar] [CrossRef]
- Ross, B.M.; Lakhtakia, A. Light pressure on chiral sculptured thin films and the circular Bragg phenomenon. Optik 2008, 119, 7–12. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, X.; Nieto-Vesperinas, M.; Song, Q.; Liu, A.Q.; Cipparrone, G.; Su, Z.; Yao, B.; Wang, Z.; Qiu, C.-W.; et al. Advances in light transverse momenta and optical lateral forces. Adv. Opt. Photonics 2023, 15, 835–906. [Google Scholar] [CrossRef]
- Shi, Y.; Song, Q.; Toftul, I.; Zhu, T.; Yu, Y.; Zhu, W.; Tsai, D.P.; Kivshar, Y.; Liu, A.Q. Optical manipulation with metamaterial structures. Appl. Phys. Rev. 2022, 9, 031303. [Google Scholar] [CrossRef]
- Gao, D.; Ding, W.; Nieto-Vesperinas, M.; Ding, X.; Rahman, M.; Zhang, T.; Lim, C.; Qiu, C.W. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light Sci. Appl. 2017, 6, e17039. [Google Scholar] [CrossRef]
- Jia, W.Z.; Wei, L.F. Probing molecular chirality by coherent optical absorption spectra. Phys. Rev. A 2011, 84, 053849. [Google Scholar] [CrossRef]
- Zhou, W.; Ruan, Y.-P.; Wu, H.; Zhang, H.; Tang, J.-S.; Xie, Z.; Tang, L.; Wang, Y.; Ji, Y.-E.; Jia, K.; et al. Magnetic-free chiral eigenmode spectroscopy for simultaneous sensitive measurement of optical rotary dispersion and circular dichroism. eLight 2024, 4, 12. [Google Scholar] [CrossRef]
- Li, X.; Shapiro, M. Theory of the optical spatial separation of racemic mixtures of chiral molecules. J. Chem. Phys. 2010, 132, 194315. [Google Scholar] [CrossRef]
- Li, Y.; Deng, K.; Shen, C.; Liang, X.; Zeng, Z.; Liu, L.; Xu, X. Enantiomeric Virus-Inspired Oncolytic Particles for Efficient Antitumor Immunotherapy. ACS Nano 2023, 17, 17320–17331. [Google Scholar] [CrossRef]
- Cao, T.; Qiu, Y.M. Lateral sorting of chiral nanoparticles using Fano-enhanced chiral force in visible region. Nanoscale 2018, 10, 566–574. [Google Scholar] [CrossRef]
- Tkachenko, G.; Brasselet, E. Spin controlled optical radiation pressure. Phys. Rev. Lett. 2013, 111, 033605. [Google Scholar] [CrossRef]
- Ali, R.; Dutra, R.S.; Pinheiro, F.A.; Maia Neto, P.A. Enantioselection and chiral sorting of single microspheres using optical pulling forces. Opt. Lett. 2021, 46, 1640–1643. [Google Scholar] [CrossRef]
- Hayat, A.; Mueller, J.P.; Capasso, F. Lateral chirality-sorting optical forces. Proc. Natl. Acad. Sci. USA 2015, 112, 13190–13194. [Google Scholar] [CrossRef]
- Wo, K.J.; Peng, J.; Prasad, M.K.; Shi, Y.; Li, J.; Wang, S. Optical forces in coupled chiral particles. Phys. Rev. A 2020, 102, 043526. [Google Scholar] [CrossRef]
- Shi, Y.; Zhu, T.; Zhang, T.; Mazzulla, A.; Tsai, D.P.; Ding, W.; Liu, A.Q.; Cipparrone, G.; Saenz, J.J.; Qiu, C.W. Chirality-assisted lateral momentum transfer for bidirectional enantioselective separation. Light Sci. Appl. 2020, 9, 62. [Google Scholar] [CrossRef]
- Solomon, M.L.; Saleh, A.A.E.; Poulikakos, L.V.; Abendroth, J.M.; Tadesse, L.F.; Dionne, J.A. Nanophotonic Platforms for Chiral Sensing and Separation. Acc. Chem. Res. 2020, 53, 588–598. [Google Scholar] [CrossRef]
- Mun, J.; Kim, M.; Yang, Y.; Badloe, T.; Ni, J.; Chen, Y.; Qiu, C.W.; Rho, J. Electromagnetic chirality: From fundamentals to nontraditional chiroptical phenomena. Light Sci. Appl. 2020, 9, 139. [Google Scholar] [CrossRef]
- Zhou, L.-M.; Shi, Y.; Zhu, X.; Hu, G.; Cao, G.; Hu, J.; Qiu, C.-W. Recent Progress on Optical Micro/Nanomanipulations: Structured Forces, Structured Particles, and Synergetic Applications. ACS Nano 2022, 16, 13264–13278. [Google Scholar] [CrossRef]
- Yokota, M.; He, S.; Takenaka, T. Scattering of a Hermite–Gaussian beam field by a chiral sphere. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 2001, 18, 1681–1689. [Google Scholar] [CrossRef]
- Wang, S.B.; Chan, C.T. Lateral optical force on chiral particles near a surface. Nat. Commun. 2014, 5, 3307. [Google Scholar] [CrossRef]
- Chen, H.; Liang, C.; Liu, S.; Lin, Z. Chirality sorting using two-wave-interference–induced lateral optical force. Phys. Rev. A 2016, 93, 053833. [Google Scholar] [CrossRef]
- Zhang, T.; Mahdy, M.R.C.; Liu, Y.; Teng, J.H.; Lim, C.T.; Wang, Z.; Qiu, C.W. All-Optical Chirality-Sensitive Sorting via Reversible Lateral Forces in Interference Fields. ACS Nano 2017, 11, 4292–4300. [Google Scholar] [CrossRef]
- Ding, K.; Ng, J.; Zhou, L.; Chan, C.T. Realization of optical pulling forces using chirality. Phys. Rev. A 2014, 89, 063825. [Google Scholar] [CrossRef]
- Chaumet, P.C.; Rahmani, A. Electromagnetic force and torque on magnetic and negative-index scatterers. Opt. Express 2009, 17, 2224–2234. [Google Scholar] [CrossRef]
- Shi, H.; Zheng, H.; Chen, H.; Lu, W.; Liu, S.; Lin, Z. Optical binding and lateral forces on chiral particles in linearly polarized plane waves. Phys. Rev. A 2020, 101, 043808. [Google Scholar] [CrossRef]
- Chen, J.; Ng, J.; Lin, Z.; Chan, C.T. Optical pulling force. Nat. Photonics 2011, 5, 531–534. [Google Scholar] [CrossRef]
- Zheng, H.; Chen, H.; Ng, J.; Lin, Z. Optical gradient force in the absence of light intensity gradient. Phys. Rev. B 2021, 103, 035103. [Google Scholar] [CrossRef]
- Kravets, N.; Aleksanyan, A.; Brasselet, E. Chiral Optical Stern-Gerlach Newtonian Experiment. Phys. Rev. Lett. 2019, 122, 024301. [Google Scholar] [CrossRef]
- Yamanishi, J.; Ahn, H.-Y.; Yamane, H.; Hashiyada, S.; Ishihara, H.; Nam, K.T.; Okamoto, H. Optical gradient force on chiral particles. Sci. Adv. 2022, 8, eabq2604. [Google Scholar] [CrossRef]
- Zhao, Y.; Saleh, A.A.E.; Dionne, J.A. Enantioselective Optical Trapping of Chiral Nanoparticles with Plasmonic Tweezers. ACS Photonics 2016, 3, 304–309. [Google Scholar] [CrossRef]
- Fang, L.; Wang, J. Optical Trapping Separation of Chiral Nanoparticles by Subwavelength Slot Waveguides. Phys. Rev. Lett. 2021, 127, 233902. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; He, L.; Zhang, X. All-optical separation of chiral nanoparticles on silicon-based microfluidic chips with vector exceptional points. APL Photonics 2023, 8, 036112. [Google Scholar] [CrossRef]
- Pellegrini, G.; Finazzi, M.; Celebrano, M.; Duò, L.; Iatì, M.A.; Maragò, O.M.; Biagioni, P. Superchiral Surface Waves for All-Optical Enantiomer Separation. J. Phys. Chem. C 2019, 123, 28336–28342. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiu, Z.; Fan, X.; Li, R.; Chen, H.; Zheng, H.; Lu, W.; Lin, Z. Enhanced transverse optical gradient force on Rayleigh particles in two plane waves. Opt. Express 2022, 30, 2143–2155. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, S.; Zhang, W.; Zhang, X. Tunable Manipulation of Enantiomers by Vector Exceptional Points. J. Phys. Chem. C 2022, 126, 3127–3133. [Google Scholar] [CrossRef]
- Yao, J.; Bai, Y.; Liu, Y.-D.; Wang, J.; Yang, Y. Sorting of enantiomers using optical chirality in uniform light field. Appl. Phys. Lett. 2024, 124, 191104. [Google Scholar] [CrossRef]
- Dalibard, J.; Cohen-Tannoudji, C. Laser cooling below the Doppler limit by polarization gradients: Simple theoretical models. J. Opt. Soc. Am. B-Opt. Phys. 1989, 6, 721–741. [Google Scholar] [CrossRef]
- Phillips, W.D. Nobel Lecture: Laser cooling and trapping of neutral atoms. Rev. Mod. Phys. 1998, 70, 721–741. [Google Scholar] [CrossRef]
- Mitra, D.; Vilas, N.B.; Hallas, C.; Anderegg, L.; Augenbraun, B.L.; Baum, L.; Miller, C.; Raval, S.; Doyle, J.M. Direct laser cooling of a symmetric top molecule. Science 2020, 369, 1366–1369. [Google Scholar] [CrossRef]
- Chu, S.; Hollberg, L.; Bjorkholm, J.E.; Cable, A.; Ashkin, A. Three-dimensional viscous confinement and cooling of atoms by resonance radiation pressure. Phys. Rev. Lett. 1985, 55, 48–51. [Google Scholar] [CrossRef]
- Kasevich, M.; Chu, S. Laser cooling below a photon recoil with three-level atoms. Phys. Rev. Lett. 1992, 69, 1741–1744. [Google Scholar] [CrossRef]
- Lett, P.D.; Watts, R.N.; Westbrook, C.I.; Phillips, W.D.; Gould, P.L.; Metcalf, H.J. Observation of atoms laser cooled below the Doppler limit. Phys. Rev. Lett. 1988, 61, 169–172. [Google Scholar] [CrossRef]
- Cipparrone, G.; Mazzulla, A.; Pane, A.; Hernandez, R.J.; Bartolino, R. Chiral self-assembled solid microspheres: A novel multifunctional microphotonic device. Adv. Mater. 2011, 23, 5773–5778. [Google Scholar] [CrossRef]
- Tkachenko, G.; Brasselet, E. Optofluidic sorting of material chirality by chiral light. Nat. Commun. 2014, 5, 3577. [Google Scholar] [CrossRef]
- Lakhtakia, A.; Varadan, V.K.; Varadan, V.V. Scattering and absorption characteristics of lossy dielectric, chiral, nonspherical objects. Appl. Opt. 1985, 24, 4146–4154. [Google Scholar] [CrossRef]
- Worasawate, D.; Mautz, J.R.; Arvas, E. Electromagnetic scattering from an arbitrarily shaped three-dimensional homogeneous chiral body. IEEE Trans. Antennas Propag. 2003, 51, 1077–1084. [Google Scholar] [CrossRef]
- Yuceer, M.; Mautz, J.R.; Arvas, E. Method of moments solution for the radar cross section of a chiral body of revolution. IEEE Trans. Antennas Propag. 2005, 53, 1163–1167. [Google Scholar] [CrossRef]
- Demir, V.; Elsherbeni, A.Z.; Arvas, E. FDTD formulation for dispersive chiral media using the Z transform method. IEEE Trans. Antennas Propag. 2005, 53, 3374–3384. [Google Scholar] [CrossRef]
- Kuzu, L.; Demir, V.; Elsherbeni, A.Z.; Arvas, E. Electromagnetic Scattering from Arbitrarily Shaped Chiral Objects Using the Finite Difference Frequency Domain Method. Prog. Electromagn. Res. 2007, 67, 1–24. [Google Scholar] [CrossRef]
- Gordon, D.J. Mie scattering by optically active particles. Biochemistry 2002, 11, 413–420. [Google Scholar] [CrossRef]
- Shang, Q.C.; Wu, Z.S.; Qu, T.; Li, Z.J.; Bai, L.; Gong, L. Analysis of the radiation force and torque exerted on a chiral sphere by a Gaussian beam. Opt. Express 2013, 21, 8677–8688. [Google Scholar] [CrossRef]
- Wu, Z.-S.; Shang, Q.-C.; Li, Z.-J. Calculation of electromagnetic scattering by a large chiral sphere. Appl. Opt. 2012, 51, 6661–6668. [Google Scholar] [CrossRef]
- Zheng, H.; Li, X.; Jiang, Y.; Ng, J.; Lin, Z.; Chen, H. General formulations for computing the optical gradient and scattering forces on a spherical chiral particle immersed in generic monochromatic optical fields. Phys. Rev. A 2020, 101, 053830. [Google Scholar] [CrossRef]
- Lee, S.-H.; Roichman, Y.; Grier, D.G. Optical solenoid beams. Opt. Express 2010, 18, 6988–6993. [Google Scholar] [CrossRef]
- Sukhov, S.; Dogariu, A. On the concept of “tractor beams”. Opt. Lett. 2010, 35, 3847–3849. [Google Scholar] [CrossRef]
- Novitsky, A.; Qiu, C.W.; Wang, H. Single gradientless light beam drags particles as tractor beams. Phys. Rev. Lett. 2011, 107, 203601. [Google Scholar] [CrossRef]
- Marston, P.L. Axial radiation force of a Bessel beam on a sphere and direction reversal of the force. J. Acoust. Soc. Am. 2006, 120, 3518–3524. [Google Scholar] [CrossRef]
- Ding, W.; Zhu, T.; Zhou, L.-M.; Qiu, C.-W. Photonic tractor beams: A review. Adv. Photonics 2019, 1, 024001. [Google Scholar] [CrossRef]
- Fernandes, D.E.; Silveirinha, M.G. Optical tractor beam with chiral light. Phys. Rev. A 2015, 91, 061801. [Google Scholar] [CrossRef]
- Zhao, R.; Koschny, T.; Soukoulis, C.M. Chiral metamaterials: Retrieval of the effective parameters with and without substrate. Opt. Express 2010, 18, 14553–14567. [Google Scholar] [CrossRef]
- Nguyen, L.A.; He, H.; Pham-Huy, C. Chiral drugs: An overview. Int. J. Biomed. Sci. 2006, 2, 85–100. [Google Scholar]
- Zheng, H.; Li, X.; Chen, H.; Lin, Z. Selective transport of chiral particles by optical pulling forces. Opt. Express 2021, 29, 42684–42695. [Google Scholar] [CrossRef]
- Peng, M.; Luo, H.; Zhang, Z.; Kuang, T.; Chen, D.; Bai, W.; Chen, Z.; Yang, J.; Xiao, G. Optical Pulling Using Chiral Metalens as a Photonic Probe. Nanomaterials 2021, 11, 3376. [Google Scholar] [CrossRef]
- Zhu, T.; Shi, Y.; Ding, W.; Tsai, D.P.; Cao, T.; Liu, A.Q.; Nieto-Vesperinas, M.; Saenz, J.J.; Wu, P.C.; Qiu, C.W. Extraordinary Multipole Modes and Ultra-Enhanced Optical Lateral Force by Chirality. Phys. Rev. Lett. 2020, 125, 043901. [Google Scholar] [CrossRef]
- Chen, H.; Zheng, H.; Lu, W.; Liu, S.; Ng, J.; Lin, Z. Lateral Optical Force due to the Breaking of Electric-Magnetic Symmetry. Phys. Rev. Lett. 2020, 125, 073901. [Google Scholar] [CrossRef]
- Sukhov, S.; Kajorndejnukul, V.; Naraghi, R.R.; Dogariu, A. Dynamic consequences of optical spin–orbit interaction. Nat. Photonics 2015, 9, 809–812. [Google Scholar] [CrossRef]
- Rodríguez-Fortuño, F.J.; Engheta, N.; Martínez, A.; Zayats, A.V. Lateral forces on circularly polarizable particles near a surface. Nat. Commun. 2015, 6, 8799. [Google Scholar] [CrossRef]
- Zhang, Z.; Min, C.; Fu, Y.; Zhang, Y.; Liu, W.; Yuan, X. Controllable transport of nanoparticles along waveguides by spin-orbit coupling of light. Opt. Express 2021, 29, 6282–6292. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Liu, X. Optical lateral forces and torques induced by chiral surface-plasmon-polaritons and their potential applications in recognition and separation of chiral enantiomers. Phys. Chem. Chem. Phys. 2019, 21, 1308–1314. [Google Scholar] [CrossRef]
- Sukhov, S.; Dogariu, A. Non-conservative optical forces. Rep. Prog. Phys. 2017, 80, 112001. [Google Scholar] [CrossRef]
- Quidant, R.; Girard, C. Surface-plasmon-based optical manipulation. Laser Photonics Rev. 2008, 2, 47–57. [Google Scholar] [CrossRef]
- Chen, H.; Wang, N.; Lu, W.; Liu, S.; Lin, Z. Tailoring azimuthal optical force on lossy chiral particles in Bessel beams. Phys. Rev. A 2014, 90, 043850. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Zhang, Q.; Dirbeba, M.G. Separation of chiral enantiomers by optical force and torque induced by tightly focused vector polarized hollow beams. Phys. Chem. Chem. Phys. 2019, 21, 15339–15345. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, Y.; Wang, N.; Lu, W.; Liu, S.; Lin, Z. Lateral optical force on paired chiral nanoparticles in linearly polarized plane waves. Opt. Lett. 2015, 40, 5530–5533. [Google Scholar] [CrossRef]
- Li, M.; Yan, S.; Zhang, Y.; Liang, Y.; Zhang, P.; Yao, B. Optical sorting of small chiral particles by tightly focused vector beams. Phys. Rev. A 2019, 99, 033825. [Google Scholar] [CrossRef]
- Alizadeh, M.H.; Reinhard, B.M. Dominant chiral optical forces in the vicinity of optical nanofibers. Opt. Lett. 2016, 41, 4735–4738. [Google Scholar] [CrossRef]
- Mulholland, G.W.; Bohren, C.F.; Fuller, K.A. Light Scattering by Agglomerates: Coupled Electric and Magnetic Dipole Method. Langmuir 2002, 10, 2533–2546. [Google Scholar] [CrossRef]
- Lemaire, T. Coupled-multipole formulation for the treatment of electromagnetic scattering by a small dielectric particle of arbitrary shape. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1997, 14, 470–474. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M. Optical torque: Electromagnetic spin and orbital-angular-momentum conservation laws and their significance. Phys. Rev. A 2015, 92, 043843. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, Y.; Wang, S. Enhanced optical forces on coupled chiral particles at arbitrary order exceptional points. Opt. Express 2023, 31, 28929–28938. [Google Scholar] [CrossRef]
- Forbes, K.A.; Andrews, D.L. Chiral discrimination in optical binding. Phys. Rev. A 2015, 91, 053824. [Google Scholar] [CrossRef]
- Biswas, S.; Rumi, R.K.; Raima, T.R.; Das, S.C.; Mahdy, M.R.C. On chip chiral and plasmonic hybrid dimer or tetramer: Generic way to reverse longitudinal and lateral optical binding forces. Chin. Phys. B 2022, 31, 054202. [Google Scholar] [CrossRef]
- Ali, R.; Pinheiro, F.A.; Dutra, R.S.; Alegre, T.P.M.; Wiederhecker, G.S. Enantioselective optical forces in gain-functionalized single core-shell chiral nanoparticles. Phys. Rev. A 2023, 108, 043704. [Google Scholar] [CrossRef]
- Abujetas, D.R.; Marques, M.I.; Sanchez-Gil, J.A. Modulated flipping torque, spin-induced radiation pressure, and chiral sorting exerted by guided light. Opt. Express 2021, 29, 16969–16979. [Google Scholar] [CrossRef]
- Das, S.C.; Mahdy, M.R.C.; Islam, M.S.; Jani, R.; Bhuiyan, M.S. An Optical Cluster: Near-Field Optical Sorting and Separation of Plasmonic, Dielectric, and Chiral Nanoparticle. Ann. Phys. 2021, 533, 2100299. [Google Scholar] [CrossRef]
- Zheng, H.; Li, X.; Ng, J.; Chen, H.; Lin, Z. Tailoring the gradient and scattering forces for longitudinal sorting of generic-size chiral particles. Opt. Lett. 2020, 45, 4515–4518. [Google Scholar] [CrossRef]
- Shi, Y.Z.; Xiong, S.; Zhang, Y.; Chin, L.K.; Chen, Y.Y.; Zhang, J.B.; Zhang, T.H.; Ser, W.; Larrson, A.; Lim, S.H.; et al. Sculpting nanoparticle dynamics for single-bacteria-level screening and direct binding-efficiency measurement. Nat. Commun. 2018, 9, 815. [Google Scholar] [CrossRef]
- Forbes, K.A.; Green, D.; Andrews, D.L.; Nunzi, J.-M.; Bain, A.J. Optical tweezing chiral particles with 3D structured light. In Proceedings of the Nanophotonics IX, Strasbourg, France, 3–7 April 2022; p. 12131E. [Google Scholar]
- Shi, Y.; Xiong, S.; Chin, L.K.; Zhang, J.; Ser, W.; Wu, J.; Chen, T.; Yang, Z.; Hao, Y.; Liedberg, B.; et al. Nanometer-precision linear sorting with synchronized optofluidic dual barriers. Sci. Adv. 2018, 4, eaao0773. [Google Scholar] [CrossRef]
- Cheng, J.J. Efficient spatial separation for chiral molecules via optically induced forces. J. Chem. Phys. 2024, 161, 034115. [Google Scholar] [CrossRef]
- Li, H.; Ren, Y.; He, M.; Qi, H. Nanoparticle manipulation based on chiral plasmon effects. Phys. Chem. Chem. Phys. 2024, 26, 17860–17868. [Google Scholar] [CrossRef]
- Martínez-Romeu, J.; Diez, I.; Golat, S.; Rodríguez-Fortuño, F.J.; Martínez, A. Longitudinal chiral forces in photonic integrated waveguides to separate particles with realistically small chirality. Nanophotonics 2024. [Google Scholar] [CrossRef]
- Kamandi, M.; Albooyeh, M.; Guclu, C.; Veysi, M.; Zeng, J.; Wickramasinghe, K.; Capolino, F. Enantiospecific Detection of Chiral Nanosamples Using Photoinduced Force. Phys. Rev. Appl. 2017, 8, 064010. [Google Scholar] [CrossRef]
- Sifat, A.A.; Capolino, F.; Potma, E.O. Force Detection of Electromagnetic Chirality of Tightly Focused Laser Beams. ACS Photonics 2022, 9, 2660–2667. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, S.; Wang, Z.; Cheng, X.; Li, B.; Shi, Y.; Tsai, D.P.; Liu, A.Q.; Huang, W.; Zhu, W. Metasurface Micro/Nano-Optical Sensors: Principles and Applications. ACS Nano 2022, 16, 11598–11618. [Google Scholar] [CrossRef]
- Li, C.; He, T.; Yang, X.; Feng, C.; Zhang, Z.; Zhu, J.; Dong, S.; Shi, Y.; Wei, Z.; Jiao, H.; et al. Enhanced Circular Dichroism for Achiral Sensing Based on a DNA-Origami-Empowered Anapole Metasurface. Nano Lett. 2024, 24, 9451–9458. [Google Scholar] [CrossRef]
- Chen, Y.; Ai, B.; Wong, Z.J. Soft optical metamaterials. Nano Converg. 2020, 7, 18. [Google Scholar] [CrossRef]
- Zhao, Y.; Saleh, A.A.E.; van de Haar, M.A.; Baum, B.; Briggs, J.A.; Lay, A.; Reyes-Becerra, O.A.; Dionne, J.A. Nanoscopic control and quantification of enantioselective optical forces. Nat. Nanotechnol. 2017, 12, 1055–1059. [Google Scholar] [CrossRef]
- Alizadeh, M.H.; Reinhard, B.M. Plasmonically Enhanced Chiral Optical Fields and Forces in Achiral Split Ring Resonators. ACS Photonics 2015, 2, 361–368. [Google Scholar] [CrossRef]
- Huang, S.; Yu, H.; Li, Q. Supramolecular Chirality Transfer toward Chiral Aggregation: Asymmetric Hierarchical Self-Assembly. Adv. Sci. 2021, 8, 2002132. [Google Scholar] [CrossRef]
- Mu, X.; Hu, L.; Cheng, Y.; Fang, Y.; Sun, M. Chiral surface plasmon-enhanced chiral spectroscopy: Principles and applications. Nanoscale 2021, 13, 581–601. [Google Scholar] [CrossRef]
- Stoev, I.D.; Seelbinder, B.; Erben, E.; Maghelli, N.; Kreysing, M. Highly sensitive force measurements in an optically generated, harmonic hydrodynamic trap. eLight 2021, 1, 7. [Google Scholar] [CrossRef]
- Warning, L.A.; Miandashti, A.R.; McCarthy, L.A.; Zhang, Q.; Landes, C.F.; Link, S. Nanophotonic Approaches for Chirality Sensing. ACS Nano 2021, 15, 15538–15566. [Google Scholar] [CrossRef]
- Bai, J.; Ge, C.-X.; Wu, Z.-S. Optical Trapping of Chiral Particles by Dual Laser Beams. Photonics 2023, 10, 905. [Google Scholar] [CrossRef]
- Genet, C. Chiral Light–Chiral Matter Interactions: An Optical Force Perspective. ACS Photonics 2022, 9, 319–332. [Google Scholar] [CrossRef]
- Oh, S.S.; Hess, O. Chiral metamaterials: Enhancement and control of optical activity and circular dichroism. Nano Converg. 2015, 2, 24. [Google Scholar] [CrossRef]
- Kwon, J.; Choi, W.J.; Jeong, U.; Jung, W.; Hwang, I.; Park, K.H.; Ko, S.G.; Park, S.M.; Kotov, N.A.; Yeom, J. Recent advances in chiral nanomaterials with unique electric and magnetic properties. Nano Converg. 2022, 9, 32. [Google Scholar] [CrossRef]
- Lee, H.; Kecebas, A.; Wang, F.; Chang, L.; Özdemir, S.K.; Gu, T. Chiral exceptional point and coherent suppression of backscattering in silicon microring with low loss Mie scatterer. eLight 2023, 3, 20. [Google Scholar] [CrossRef]
- Ma, X.; Huang, C.; Pu, M.; Wang, Y.; Zhao, Z.; Wang, C.; Luo, X. Dual-band asymmetry chiral metamaterial based on planar spiral structure. Appl. Phys. Lett. 2012, 101, 161901. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, F.; Pu, M.; Chen, Y.; Guo, Y.; Xie, T.; Feng, X.; Ma, X.; Li, X.; Yu, H.; et al. All-metallic high-efficiency generalized Pancharatnam–Berry phase metasurface with chiral meta-atoms. Nanophotonics 2022, 11, 1961–1968. [Google Scholar] [CrossRef]
- Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Meta-Chirality: Fundamentals, Construction and Applications. Nanomaterials 2017, 7, 116. [Google Scholar] [CrossRef]
- Lee, D.; So, S.; Hu, G.; Kim, M.; Badloe, T.; Cho, H.; Kim, J.; Kim, H.; Qiu, C.-W.; Rho, J. Hyperbolic metamaterials: Fusing artificial structures to natural 2D materials. eLight 2022, 2, 1. [Google Scholar] [CrossRef]
- Luo, X.; Pu, M.; Guo, Y.; Li, X.; Ma, X. Electromagnetic Architectures: Structures, Properties, Functions and Their Intrinsic Relationships in Subwavelength Optics and Electromagnetics. Adv. Photonics Res. 2021, 2, 2100023. [Google Scholar] [CrossRef]
- Jin, R.; Zhang, X.; Huo, P.; Cai, Z.; Lu, Y.; Xu, T.; Liu, Y. Harnessing Enantioselective Optical Forces by Quasibound States in the Continuum. Phys. Rev. Lett. 2024, 133, 086901. [Google Scholar] [CrossRef]
- Fein, Y.Y.; Geyer, P.; Zwick, P.; Kiałka, F.; Pedalino, S.; Mayor, M.; Gerlich, S.; Arndt, M. Quantum superposition of molecules beyond 25 kDa. Nat. Phys. 2019, 15, 1242–1245. [Google Scholar] [CrossRef]
- Kien, F.L.; Kornovan, D.F.; Hejazi, S.S.S.; Truong, V.G.; Petrov, M.I.; Chormaic, S.N.; Busch, T. Force of light on a two-level atom near an ultrathin optical fiber. New J. Phys. 2018, 20, 093031. [Google Scholar] [CrossRef]
- Le Kien, F.; Hejazi, S.S.S.; Truong, V.G.; Nic Chormaic, S.; Busch, T. Chiral force of guided light on an atom. Phys. Rev. A 2018, 97, 063849. [Google Scholar] [CrossRef]
- Lodahl, P.; Mahmoodian, S.; Stobbe, S.; Rauschenbeutel, A.; Schneeweiss, P.; Volz, J.; Pichler, H.; Zoller, P. Chiral quantum optics. Nature 2017, 541, 473–480. [Google Scholar] [CrossRef]
- Zhao, R.; Li, L.; Yang, S.; Bao, W.; Xia, Y.; Ashby, P.; Wang, Y.; Zhang, X. Stable Casimir equilibria and quantum trapping. Science 2019, 364, 984–987. [Google Scholar] [CrossRef]
- Zhao, R.; Zhou, J.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Repulsive Casimir Force in Chiral Metamaterials. Phys. Rev. Lett. 2009, 103, 103602. [Google Scholar] [CrossRef]
- Munday, J.N.; Capasso, F.; Parsegian, V.A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 2009, 457, 170–173. [Google Scholar] [CrossRef]
- Esteso, V.; Carretero-Palacios, S.; Míguez, H. Casimir–Lifshitz Force Based Optical Resonators. J. Phys. Chem. Lett. 2019, 10, 5856–5860. [Google Scholar] [CrossRef]
- Jiang, Q.-D.; Wilczek, F. Chiral Casimir forces: Repulsive, enhanced, tunable. Phys. Rev. B 2019, 99, 125403. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.M. Tunable Stable Levitation Based on Casimir Interaction between Nanostructures. Phys. Rev. Appl. 2016, 5, 034004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, W.; Huang, H.; Lai, C.; He, T.; Wang, Z.; Dai, X.; Shi, Y.; Cheng, X. Optical Forces on Chiral Particles: Science and Applications. Micromachines 2024, 15, 1267. https://doi.org/10.3390/mi15101267
Yi W, Huang H, Lai C, He T, Wang Z, Dai X, Shi Y, Cheng X. Optical Forces on Chiral Particles: Science and Applications. Micromachines. 2024; 15(10):1267. https://doi.org/10.3390/mi15101267
Chicago/Turabian StyleYi, Weicheng, Haiyang Huang, Chengxing Lai, Tao He, Zhanshan Wang, Xinhua Dai, Yuzhi Shi, and Xinbin Cheng. 2024. "Optical Forces on Chiral Particles: Science and Applications" Micromachines 15, no. 10: 1267. https://doi.org/10.3390/mi15101267
APA StyleYi, W., Huang, H., Lai, C., He, T., Wang, Z., Dai, X., Shi, Y., & Cheng, X. (2024). Optical Forces on Chiral Particles: Science and Applications. Micromachines, 15(10), 1267. https://doi.org/10.3390/mi15101267






