Screen-Printed PVDF Piezoelectric Pressure Transducer for Unsteadiness Study of Oblique Shock Wave Boundary Layer Interaction
Abstract
:1. Introduction
2. Methodology: Processing and Characterization
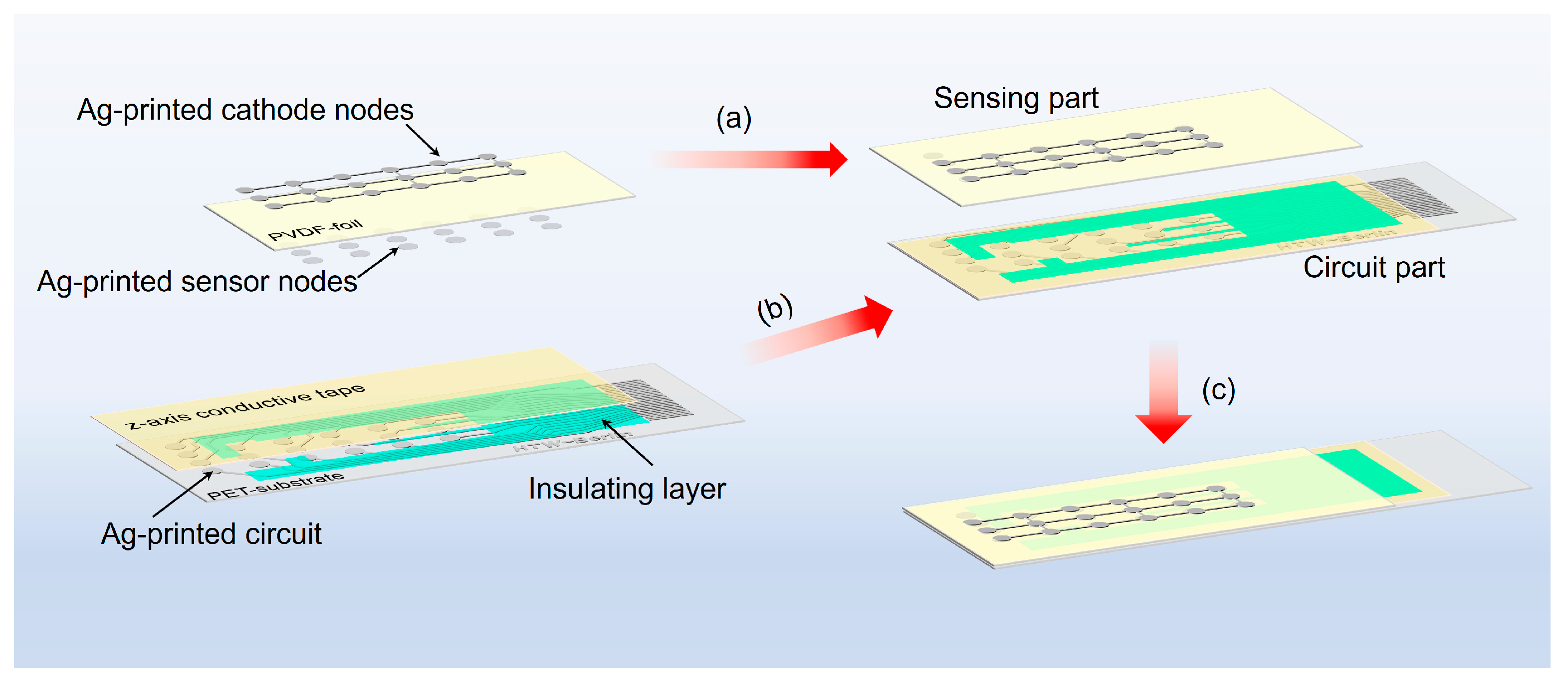
2.1. Material Properties and Design
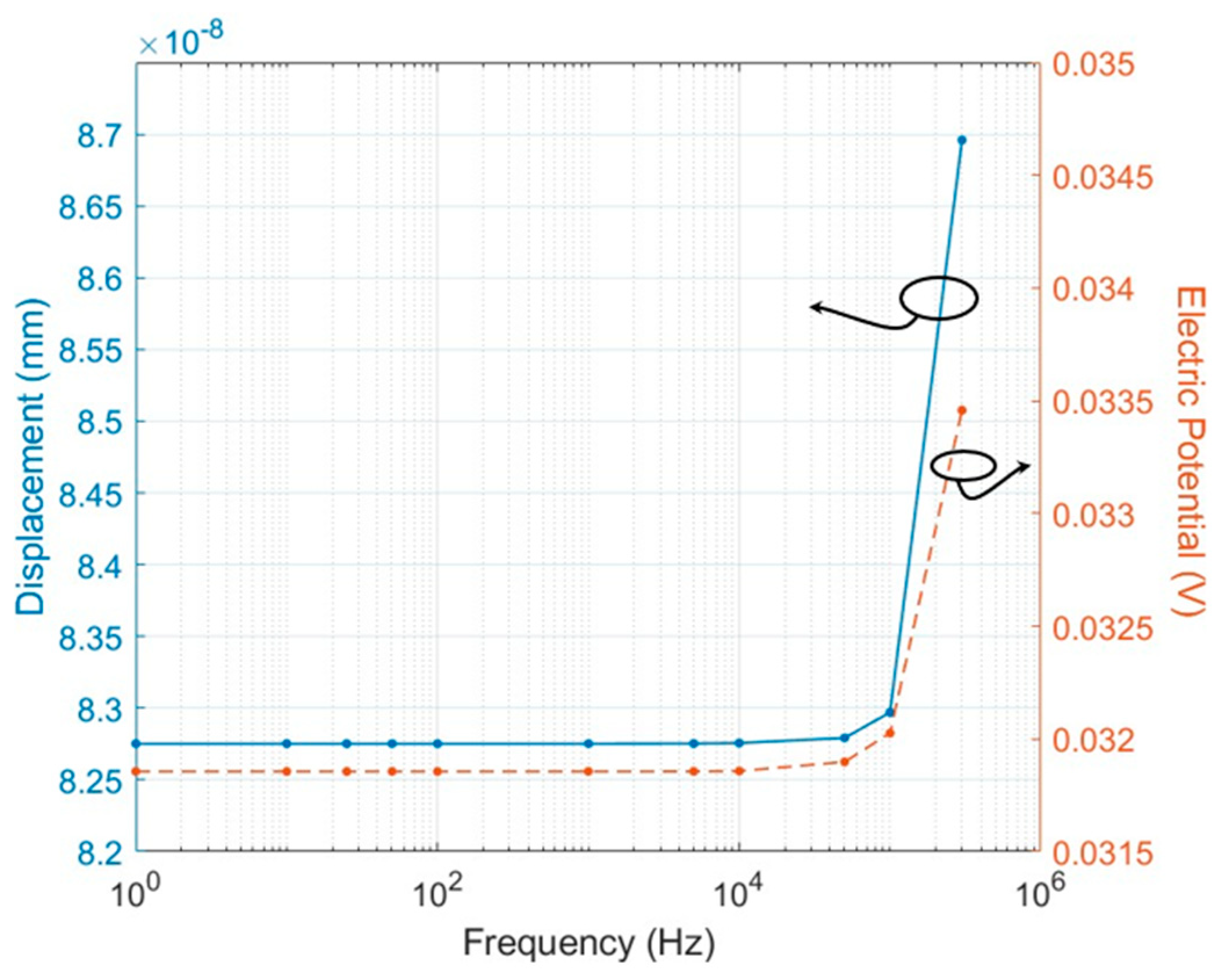
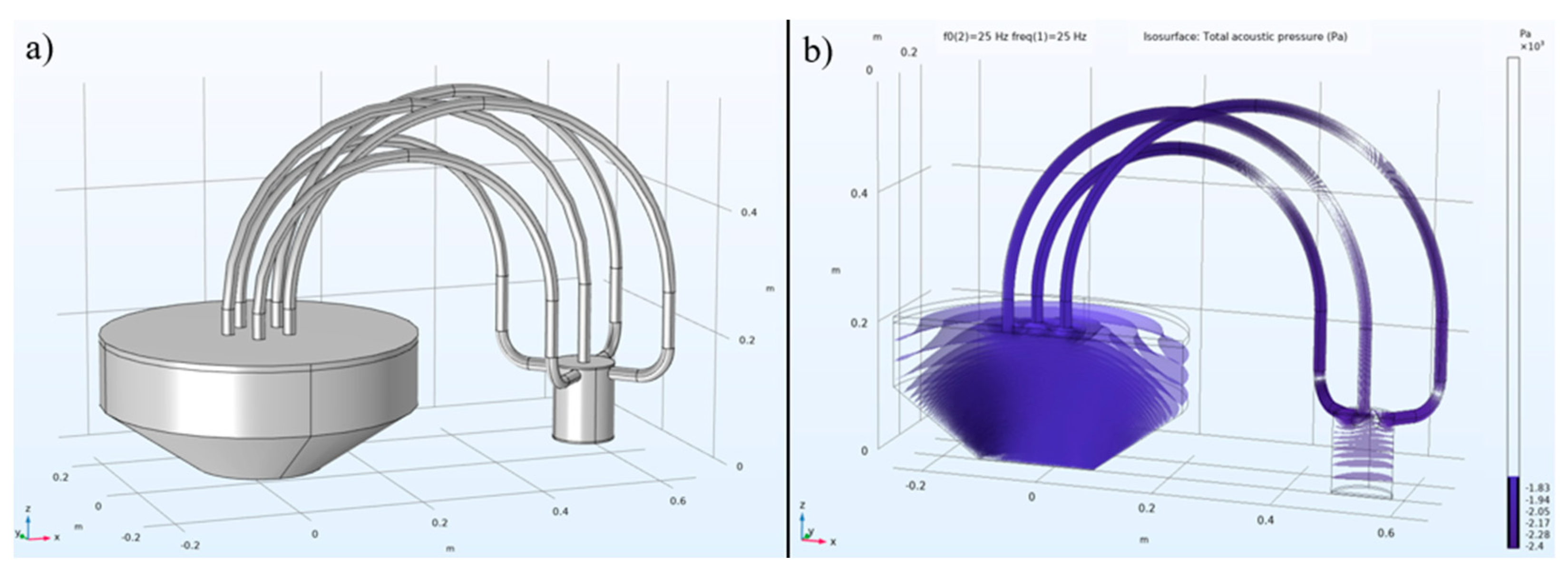
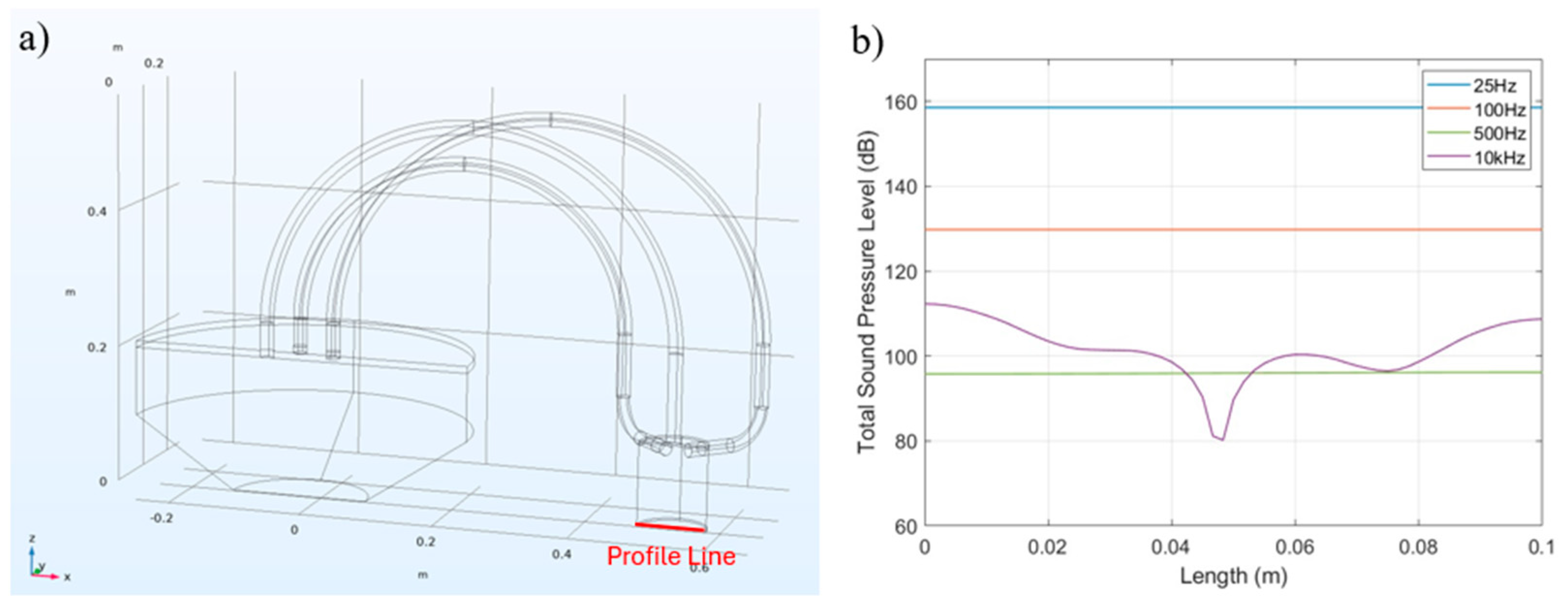
2.2. FEM Simulation in Frequency Domain
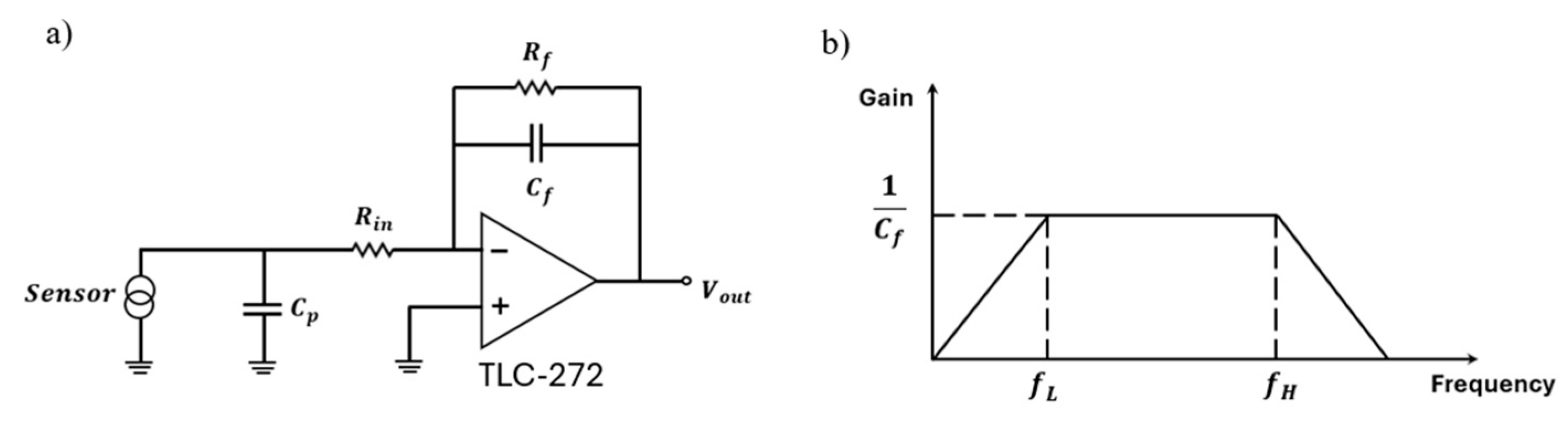
2.3. Processing and Its Electrical Circuit
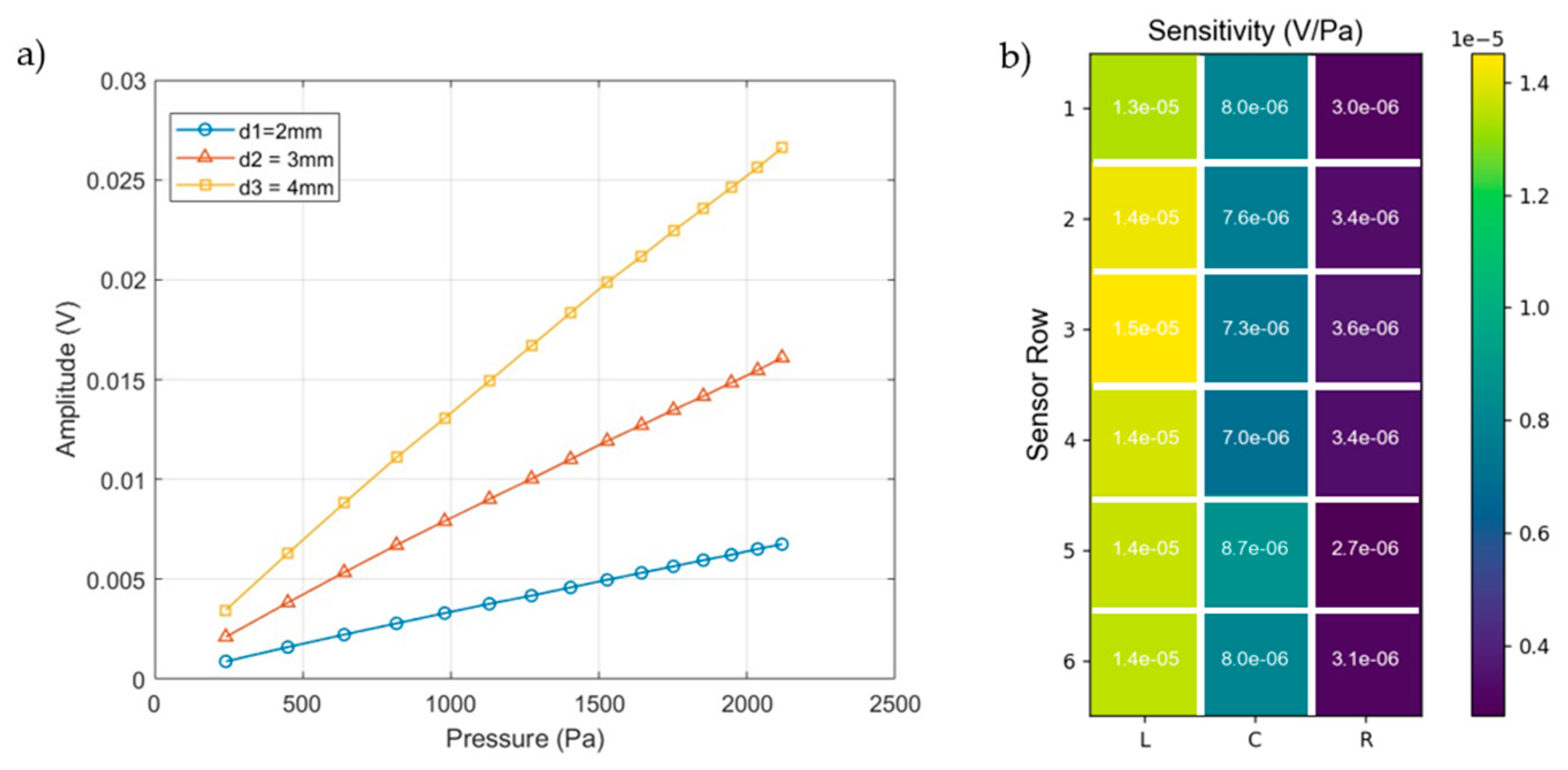
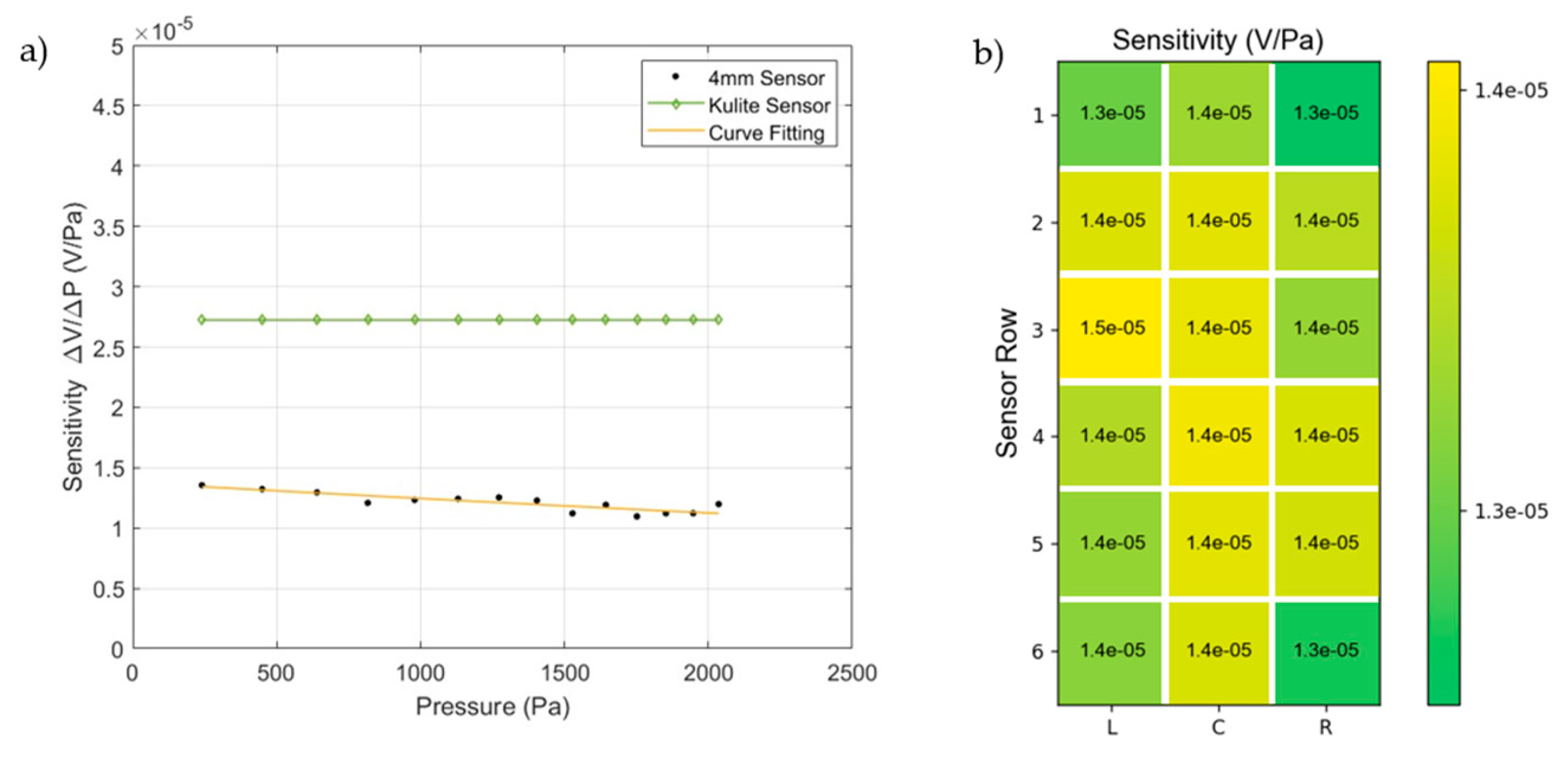
3. Calibration
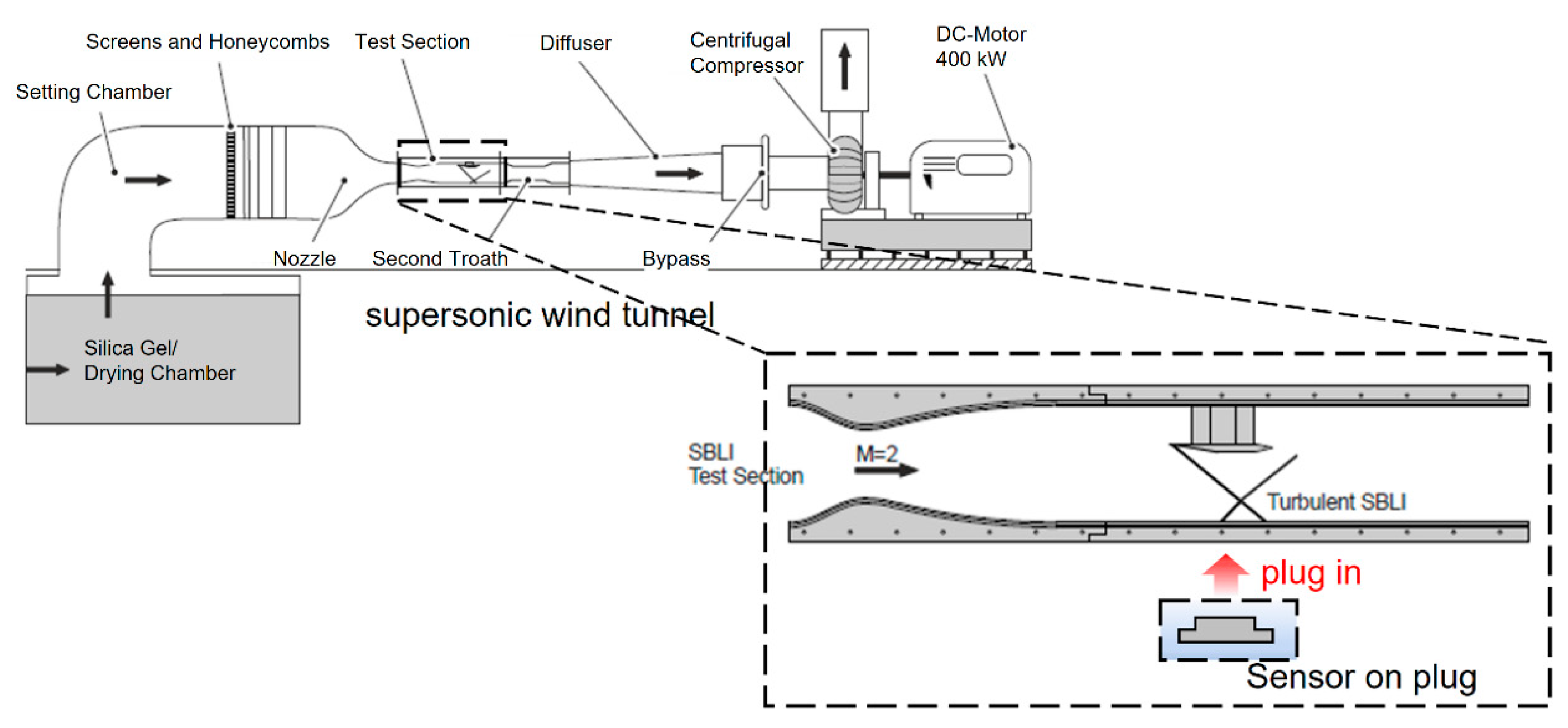
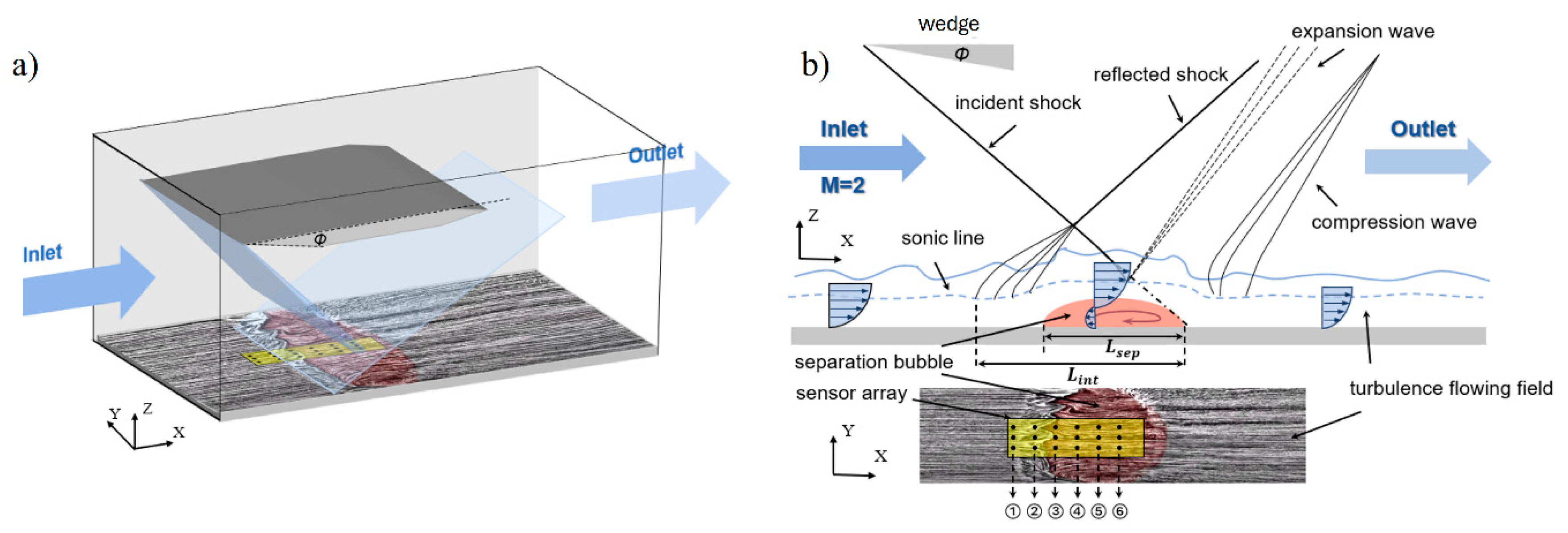
4. SWBLI Study in Mach 2 Wind Tunnel
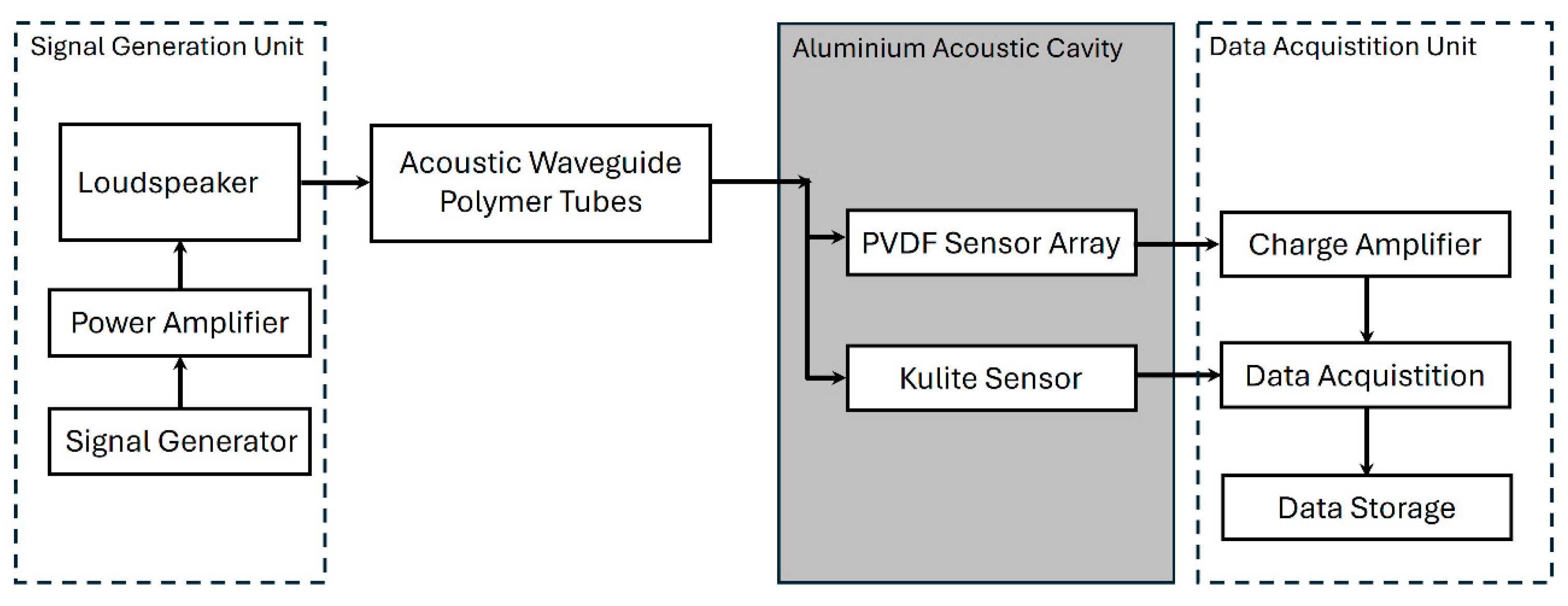
4.1. Experimental and Measurement Setup
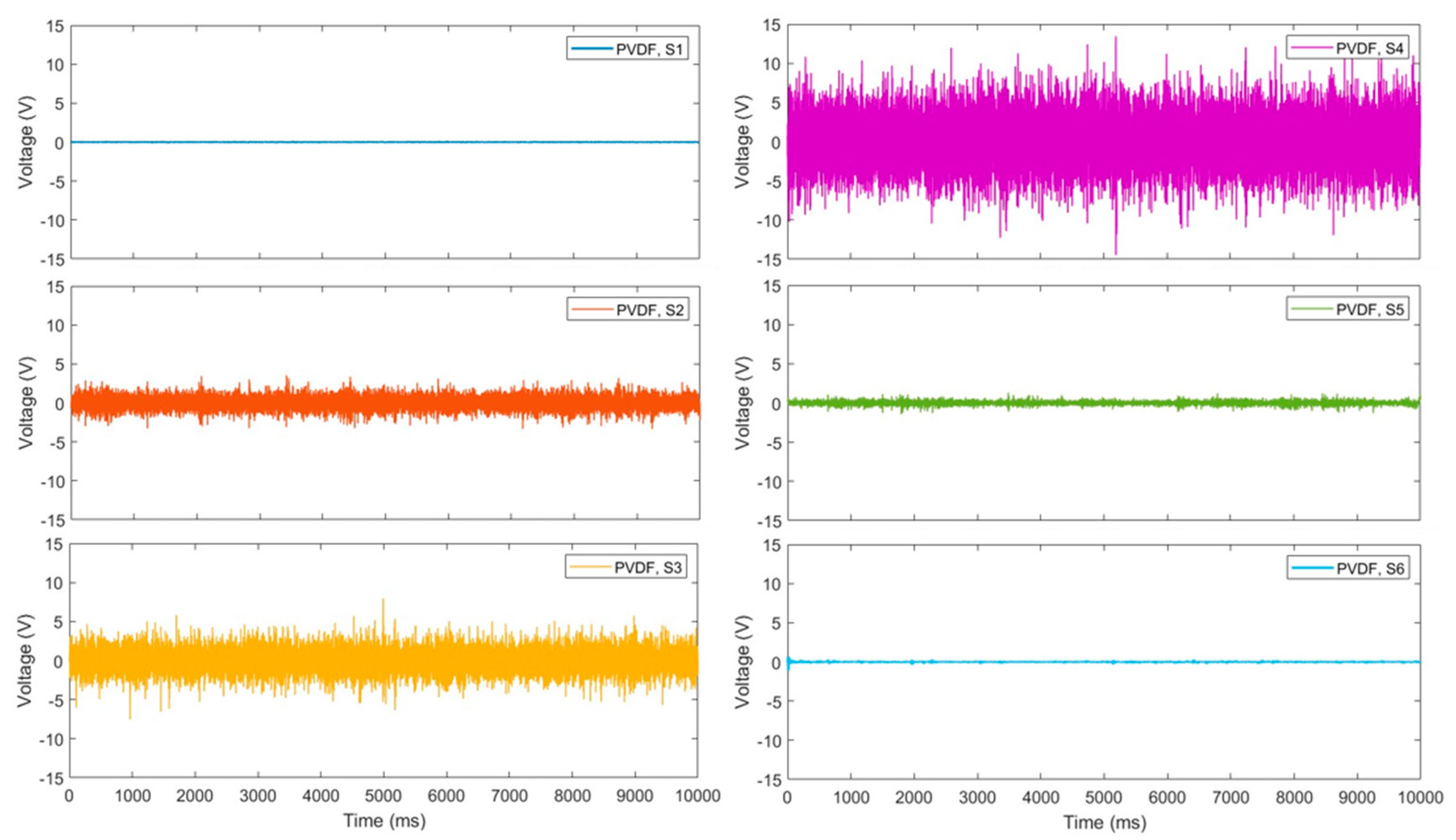
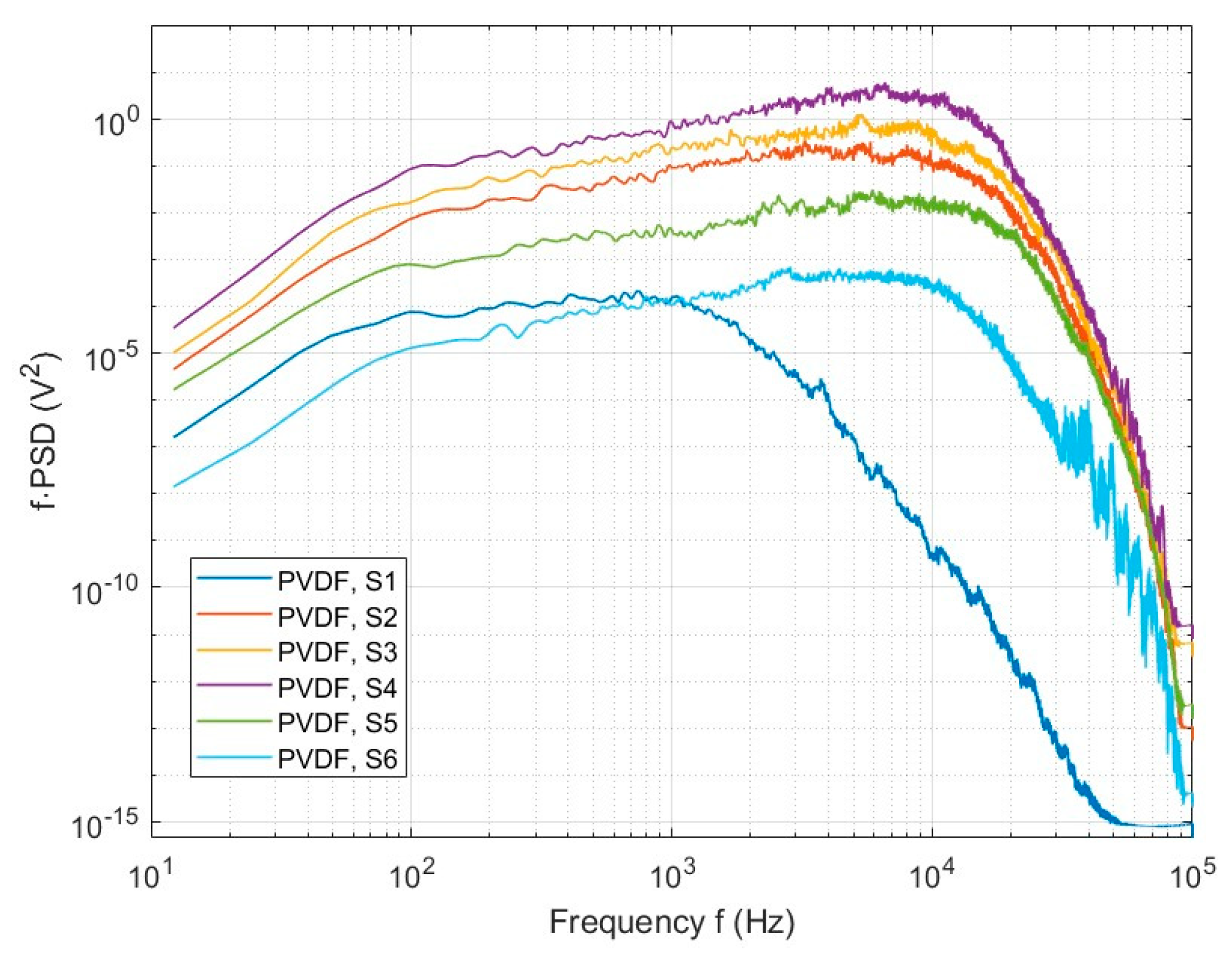
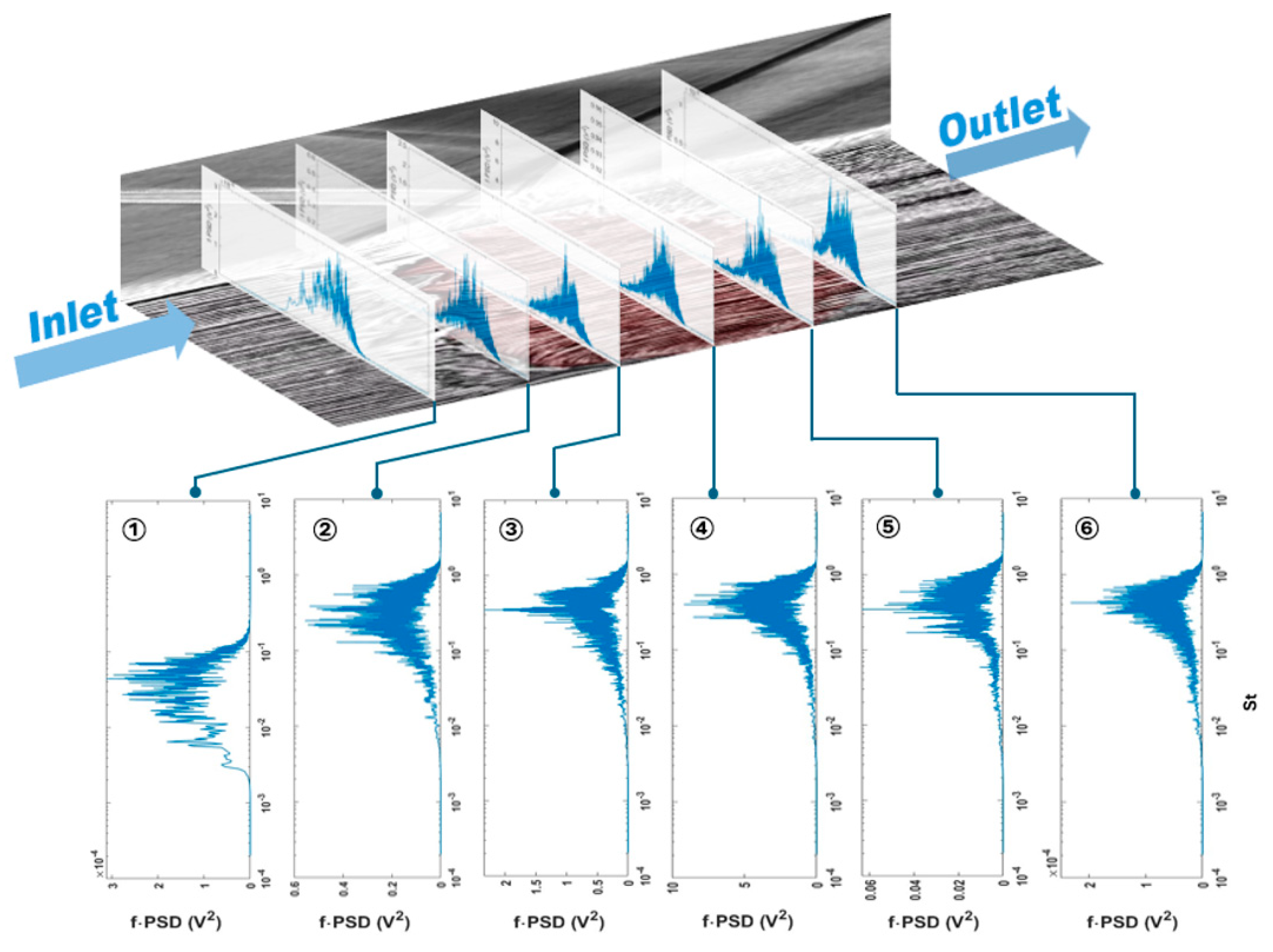
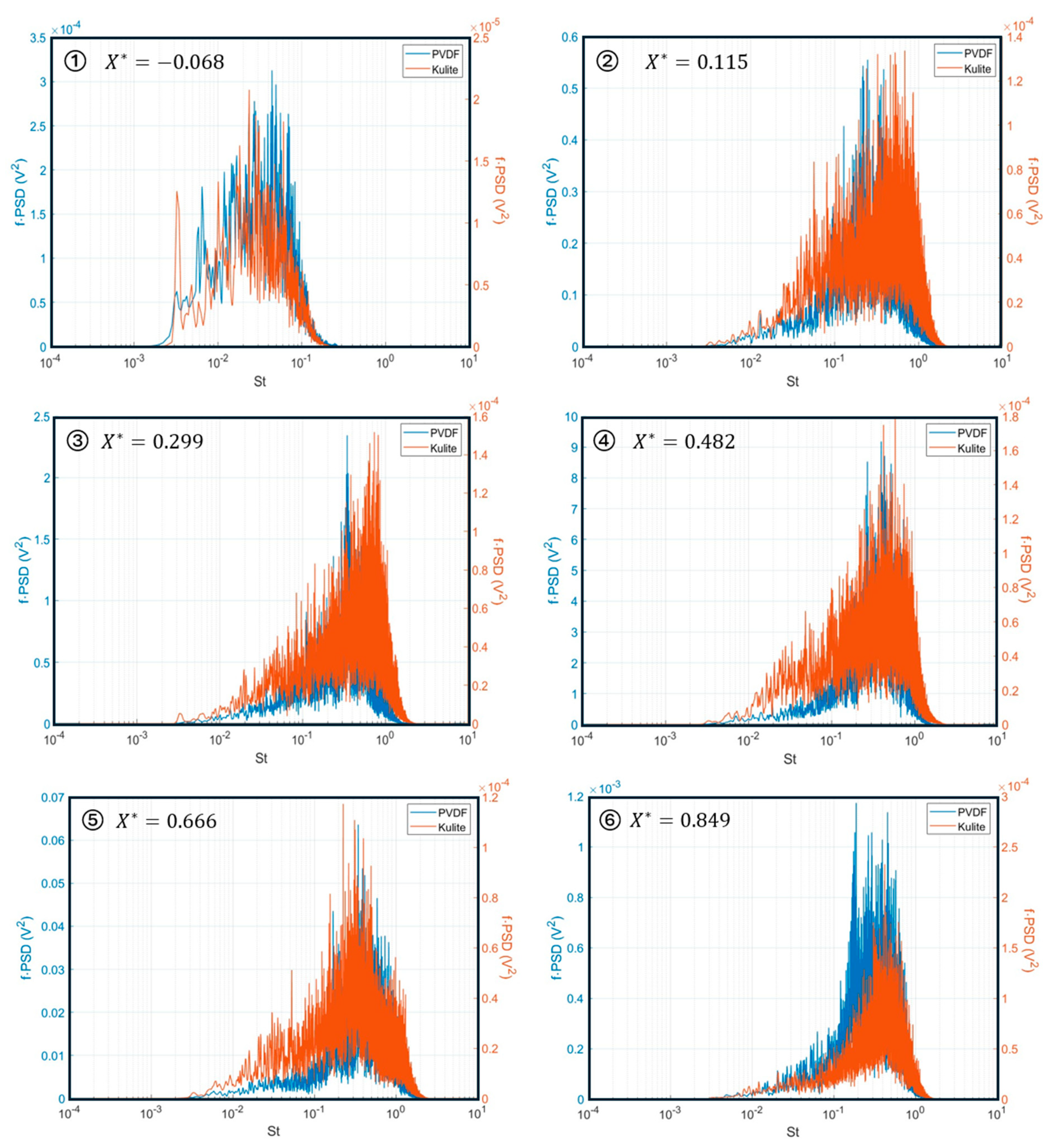
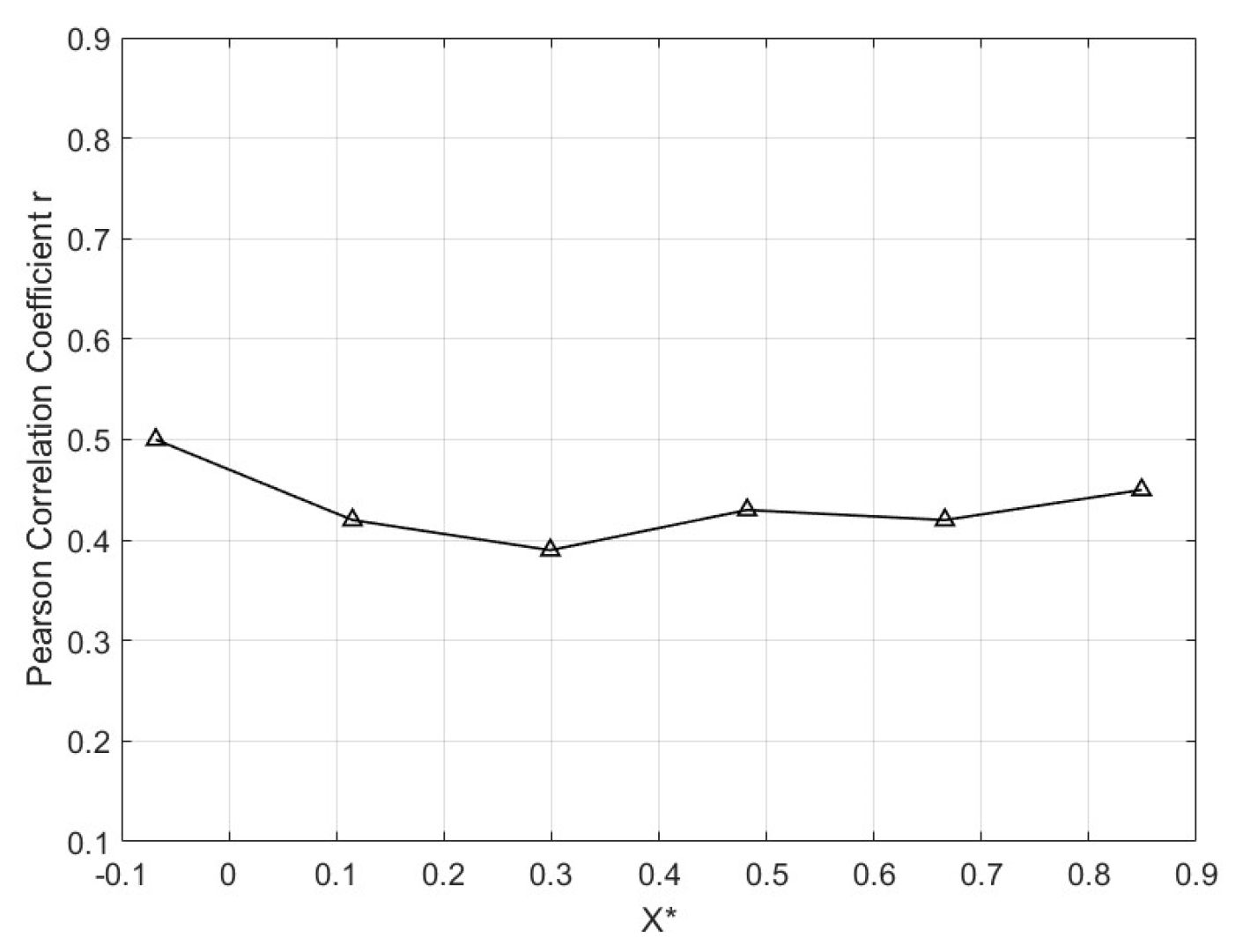
4.2. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harvey, J.; Babinsky, H. Shock Wave-Boundary-Layer Interactions; Cambridge University Press: Navi Mumbai, India, 2011; pp. 25–42. [Google Scholar] [CrossRef]
- Hu, W.; Hickel, S.; van Oudheusden, B.W. Low-frequency unsteadiness mechanisms in shock wave/turbulent boundary layer interactions over a backward-facing step. J. Fluid Mech. 2021, 915, A107. [Google Scholar] [CrossRef]
- Bernardini, M.; Posta, G.D.; Salvadore, F.; Martelli, E. Unsteadiness characterization of shock wave/turbulent boundary-layer interaction at moderate Reynolds number. J. Fluid Mech. 2023, 954, A43. [Google Scholar] [CrossRef]
- Gaitonde, D.V. Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 2015, 72, 80–99. [Google Scholar] [CrossRef]
- Mullenix, N.J.; Gaitonde, D.V. Analysis of unsteady behavior in shock/turbulent boundary layer interactions with Large-Eddy simulations. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Pasquariello, V.; Hickel, S.; Adams, N.A. Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number. J. Fluid Mech. 2017, 823, 617–657. [Google Scholar] [CrossRef]
- Masini, L.; Timme, S.; Peace, A.J. Analysis of a civil aircraft wing transonic shock buffet experiment. J. Mech. 2019, 884, A1–A41. [Google Scholar] [CrossRef]
- Lin, H.; Lu, X.G. Visualization of the shock wave/boundary layer interaction using polarization imaging. J. Vis. 2020, 23, 839–850. [Google Scholar] [CrossRef]
- Atkins, M.D. Velocity field measurement using Particle Image Velocimetry (PIV). In Thermo-Fluidic Measurement Techniques; Butterworth-Heinemann: Oxford, UK, 2016; pp. 116–125. [Google Scholar] [CrossRef]
- Humble, R.A.; Scarano, F.; van Oudheusden, B.W. Particle image velocimetry measurements of a shock wave/turbulent boundary layer interaction. Exp. Fluids 2007, 43, 173–183. [Google Scholar] [CrossRef]
- Humble, R.A.; Elsinga, G.E.; Scarano, F.; Van Oudheusden, B.W. Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 2009, 622, 33. [Google Scholar] [CrossRef]
- Ganapathisubramani, B.; Clemens, N.; Dolling, D. Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 2007, 585, 369–394. [Google Scholar] [CrossRef]
- Merienne, M.C.; Molton, P.; Bur, R.; Le Sant, Y. Pressure-Sensitive paint application to an oscillating shock wave in transonic flow. AIAA J. 2015, 53, 3208–3220. [Google Scholar] [CrossRef]
- Standield, S.; Kimmel, R.; Adamczak, D. HIFiRE-1 flight data analysis: Turbulent Shock-Boundary-Layer interaction experiment during ascent. In Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- Clemens, N.T.; Naraynaswamy, V. Low-Frequency unsteadiness of shock wave/Turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 2014, 46, 469–492. [Google Scholar] [CrossRef]
- Huang, W.; Wu, H.; Yang, Y.G.; Yan, L.; Li, S.B. Recent advances in the shock wave/boundary layer interaction and its control in internal and external flows. Acta Astronaut. 2020, 174, 103–122. [Google Scholar] [CrossRef]
- Hegde, A.; Changanti, N.; Hubner, J.P.; Olcmen, S.M. Spectral study of wall pressure measurements in an impinging shock-wave boundary layer interaction. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 January 2021; p. 1558. [Google Scholar] [CrossRef]
- Erengil, M.; Dolling, D. Unsteady wave structure near separation in a Mach 5 compression rampinteraction. AIAA J. 1991, 29, 728–735. [Google Scholar] [CrossRef]
- Varadan, V.V.; Roh, Y.R.; Varaden, V.K. Measurement of All the Elastic and Dielectric Constants of Poled PVDF Films; IEEE: Piscataway, NJ, USA, 1989; Volume 2, pp. 727–730. [Google Scholar] [CrossRef]
- Tadaki, D.; Ma, T.; Yamamiya, S.; Matsumoto, S.; Imai, Y.; Hirano-Iwata, A.; Niwano, M. Piezoelectric PVDF-based sensors with high pressure sensitivity induced by chemical modification of electrode surfaces. Sens. Actuators A Phys. 2020, 316, 112424. [Google Scholar] [CrossRef]
- Lynch, C.S. Polyvinylidene fluoride (PVDF) elastic, piezoelectric, pyroelectric, and dielectric coefficients and their non-linearities. Ferroelectrics 1993, 150, 331–342. [Google Scholar] [CrossRef]
- Zhu, M.; Luo, M.; Abdalla, I.; Yu, J.; Li, Z.; Ding, B. Highly shape adaptive fiber based electronic skin for sensitive joint motion monitoring and tactile sensing. Nano Energy 2020, 69, 104429. [Google Scholar] [CrossRef]
- Lu, K.; Huang, W.; Guo, J.X.; Gong, T.X.; Wei, X.B.; Lu, B.W.; Liu, S.Y.; Yu, B. Ultra-sensitive strain sensor based on flexible poly(vinylidene fluoride) piezoelectric film. Nanoscale Res. Lett. 2018, 13, 83. [Google Scholar] [CrossRef]
- Guo, Z.; Hu, Y.; Hu, X.R.; Shang, F.; Xiang, Y. In-situ polarization enhanced high-sensitivity acoustic locating and recognition sensor based on flexible PVDF-TrFE film array. In Proceedings of the IEEE 2020 3rd International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Shenzhen, China, 24–26 April 2020. [Google Scholar] [CrossRef]
- Zhou, Y.M.; Wang, H.B.; Qi, K.; You, X.L.; Shao, W.L.; Wang, L.D.; Ding, B.; Cui, S.Z. Highly sensitive, self-powered and wearable electronic skin based on pressure-sensitive nanofiber woven fabric sensor. Sci. Rep. 2017, 7, 12949. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, S.; Wang, L.L.; Jiang, K.; Shen, G.Z. An ultra-sensitive and rapid response speed graphene pressure sensors for electronic skin and health monitoring. Nano Energy 2016, 23, 7–14. [Google Scholar] [CrossRef]
- Lee, J.H.; Yoon, H.J.; Kim, T.Y.; Gupta, M.K.; Lee, J.H.; Seung, W.; Ryu, H.; Kim, S.W. Micropatterned P(VDF-TrFE) film-based piezoelectric nanogenerators for highly sensitive self-powered pressure sensors. Adv. Funct. Mater. 2015, 25, 3203–3209. [Google Scholar] [CrossRef]
- Rohlfs, L.; Stab, I.; Weiss, J. Experimental Investigations of Incident Shockwave Boundary Layer Interactions in a Continuously Operating Supersonic Wind Tunnel. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Dussauge, J.P.; Dupont, P.; Debieve, J.F. Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 2006, 10, 85–91. [Google Scholar] [CrossRef]
- Datasheet of PVDF Film. Available online: https://piezopvdf.com/piezo-pvdf-film-kit/ (accessed on 10 July 2023).
- Corsi, C.; Rohlfs, L.; Weiss, J.; Wang, B.; Kahf, M.; Obloch, P.; Ngo, H.D. Development of PVDF piezo-film sensor array for unsteady wall-pressure measurements in a turbulent SBLI. In Proceedings of the AIAA Aviation 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Kumar, Y.; Trivedi, A.; Shukla, S.K. Investigating the Influence of Frequency on Piezo-dynamics of Polyvinylidene Fluoride (PVDF) Films Embedded in Confined Geomaterials. J. Vib. Eng. Technol. 2024. [Google Scholar] [CrossRef]
- Saxena, P.; Shukla, P. A comprehensive review on fundamental properties and applications of poly(vinylidene fluoride) (PVDF). Adv. Compos. Hybrid Mater. 2021, 4, 8–26. [Google Scholar] [CrossRef]
- Datasheet of TLC272. Available online: https://www.ti.com/product/TLC272?utm_source=google&utm_medium=cpc&utm_campaign=asc-null-null-GPN_EN-cpc-pf-google-eu&utm_content=TLC272&ds_k=TLC272+Datasheet&DCM=yes&gclid=EAIaIQobChMIiorrz-2DgAMVjLnVCh1qqAbNEAAYASAAEgKu7PD_BwE&gclsrc=aw.ds (accessed on 10 September 2024).
- Tavoularis, S. Measurement in Fluid Mechanics, 1st ed.; Cambridge University Press: Navi Mumbai, India, 2005; pp. 201–205. ISBN 978-0-521-81518-5. [Google Scholar]
- Doerffer, P.; Dallmann, U. Reynolds number effect on separation structures at normal shock wave/boundary-layer interaction. AIAA J. 1989, 27, 1206–1212. [Google Scholar] [CrossRef]
- Doerffer, P. An experimental investigation of the Mach nu ISBN-13: 978-0-521-81518-5 Fmber effect upon a normal shock wave—Turbulent boundary layer interaction on a curved wall. Acta Mech. 1989, 76, 35–51. [Google Scholar] [CrossRef]
- Datasheet. Available online: https://kulite.com/products/product-advisor/product-catalog/ultraminiature-pressure-transducer-xcq-062/ (accessed on 10 July 2023).
- Hurst, A.M.; Olsen, T.R.; Goodman, S.; Van De Weert, J.; Shang, T.H. An experimental frequency response characterization of MEMS piezoresistive pressure transducers. In Proceedings of the ASME Turbo Expo 2014, Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 6. GT2014-27159. [Google Scholar] [CrossRef]
- Hu, N. Sensor-size-related attenuation correction of wall pressure spectra measurements. Phys. Fluids 2022, 34, 067119. [Google Scholar] [CrossRef]
- Welch’s Power Spectral Density Estimate in Matlab. Available online: https://de.mathworks.com/help/signal/ref/pwelch.html (accessed on 10 July 2023).
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 299–303. ISBN 978-1-119-40036-3. [Google Scholar]
- Threadgill, J.A.S.; Bruce, P.J.K. Unsteady Flow Features Across Different Shock/Boundary-Layer Interaction Configurations. AIAA J. 2020, 58, 3063–3075. [Google Scholar] [CrossRef]
- Dussauge, J.-P.; Piponniau, S. Shock/boundary-layer interactions: Possible sources of unsteadiness. J. Fluids Struct. 2008, 24, 1166–1175. [Google Scholar] [CrossRef]
- Weiss, J.; Little, J.C.; Threadgill, J.A.; Gross, A. Low-Frequency Unsteadiness in Pressure-Induced Separation Bubbles. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 January 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021; pp. 1–19. [Google Scholar] [CrossRef]
- Agostini, L.; Larchevêque, L.; Dupont, P. Mechanism of shock unsteadiness in separated shock/boundary-layer interactions. Phys. Fluids 2015, 27, 126103. [Google Scholar] [CrossRef]
- Kiya, M.; Sasaki, K. Structure of a Turbulent Separation Bubble. J. Fluid Mech. 1983, 137, 83–113. [Google Scholar] [CrossRef]
- Bhatta, T.; Maharjan, P.; Cho, H.; Park, C.; Yoon, S.H.; Sharma, S.; Salauddin, M.; Toyabur Rahman, M.; Sohel Rana, S.M.; Park, J.Y. High-performance triboelectric nanogenerator based on MXene functionalized polyvinylidene fluoride composite nanofibers. Nano Energy 2021, 81, 105670. [Google Scholar] [CrossRef]

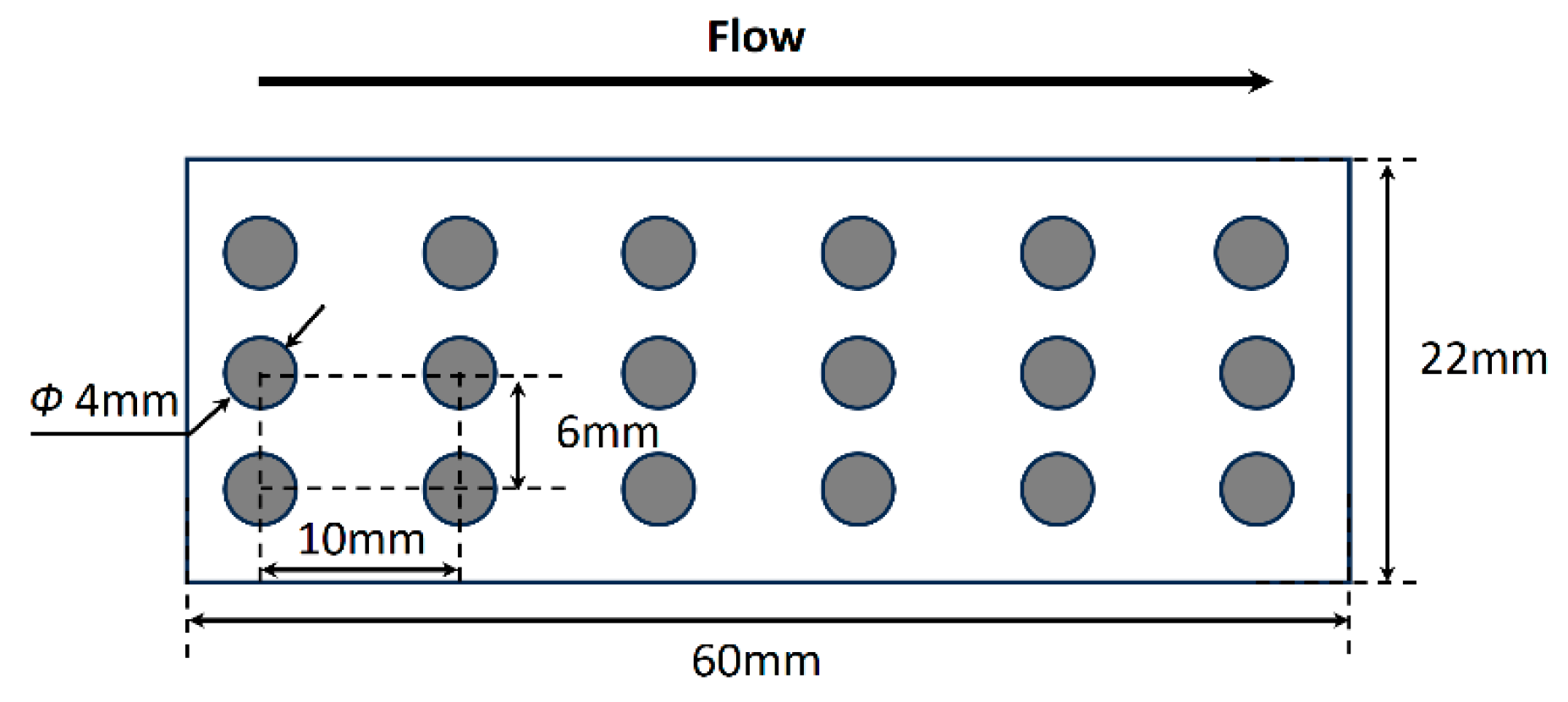

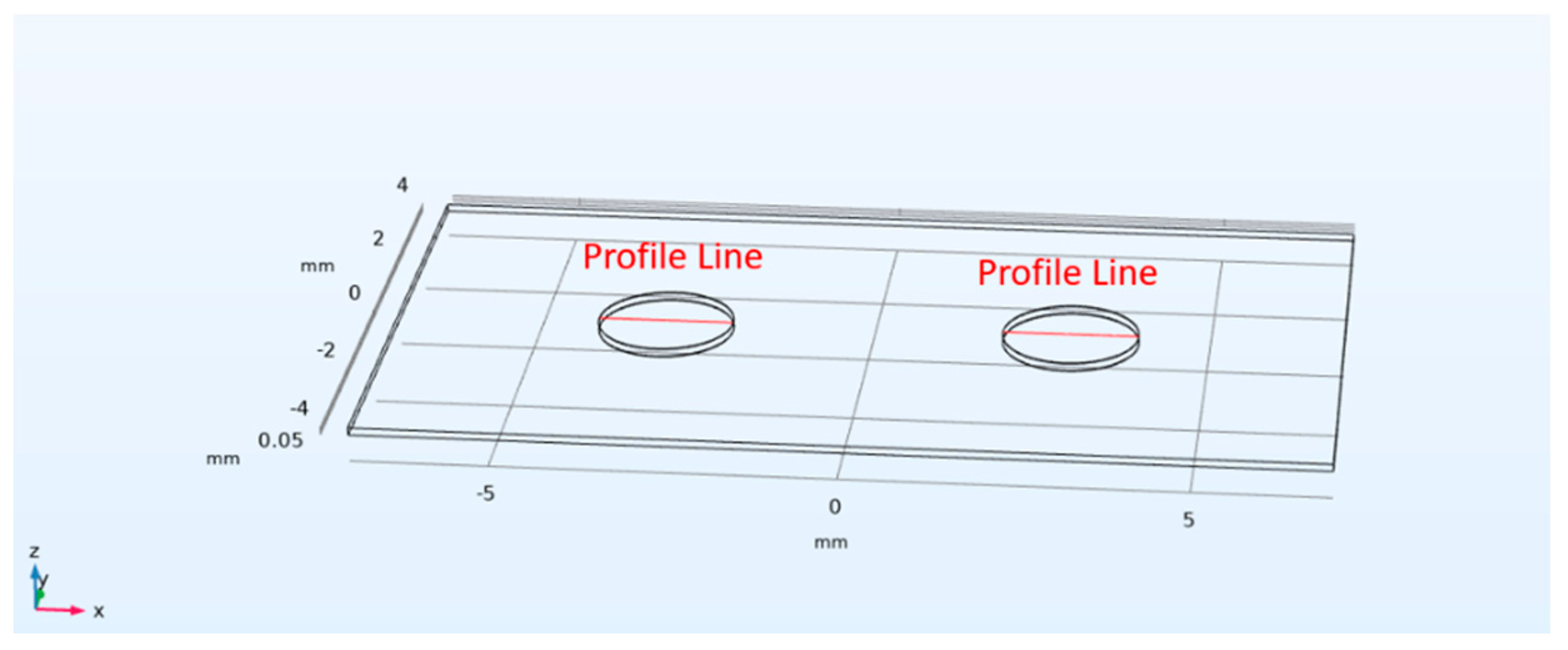
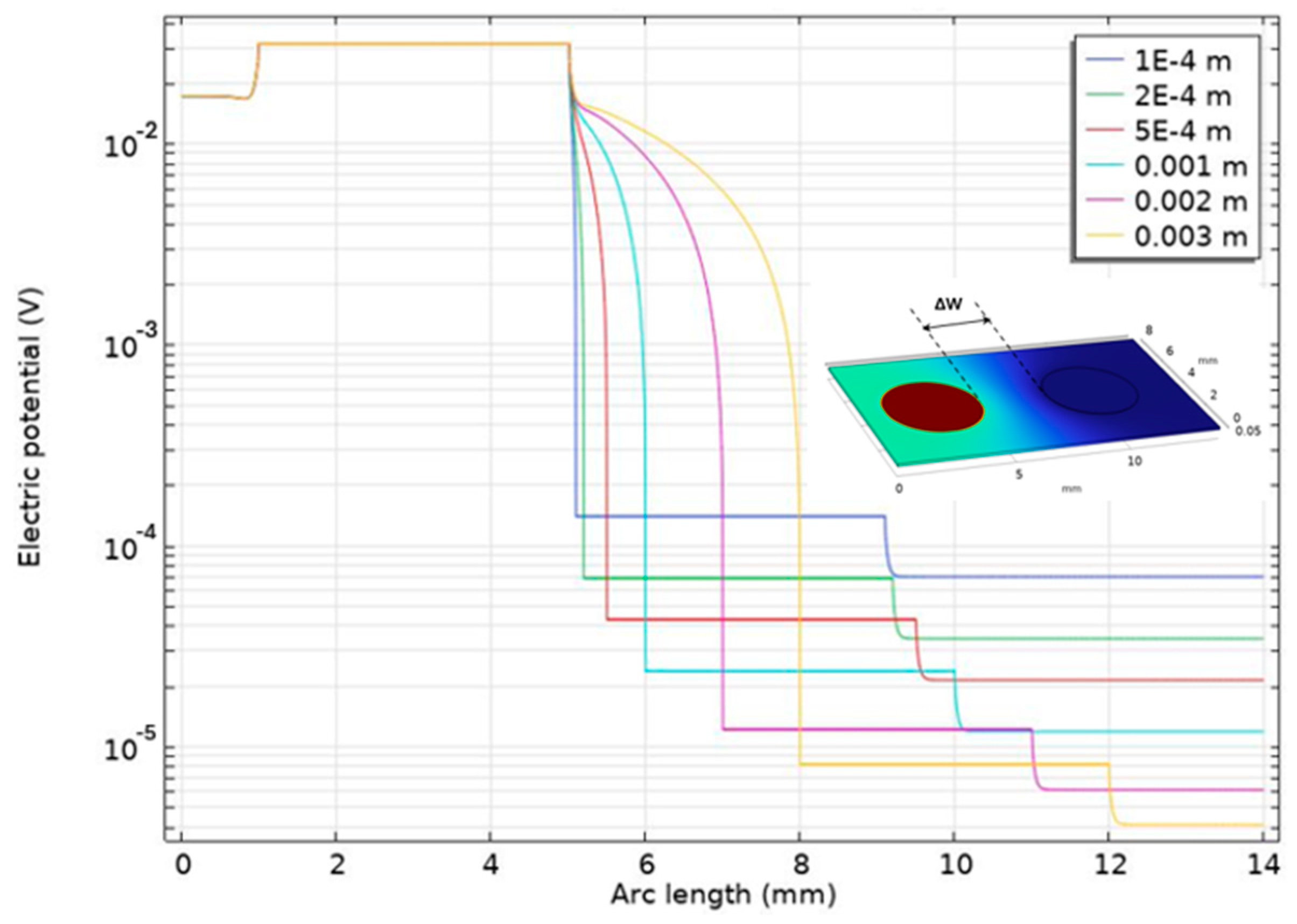
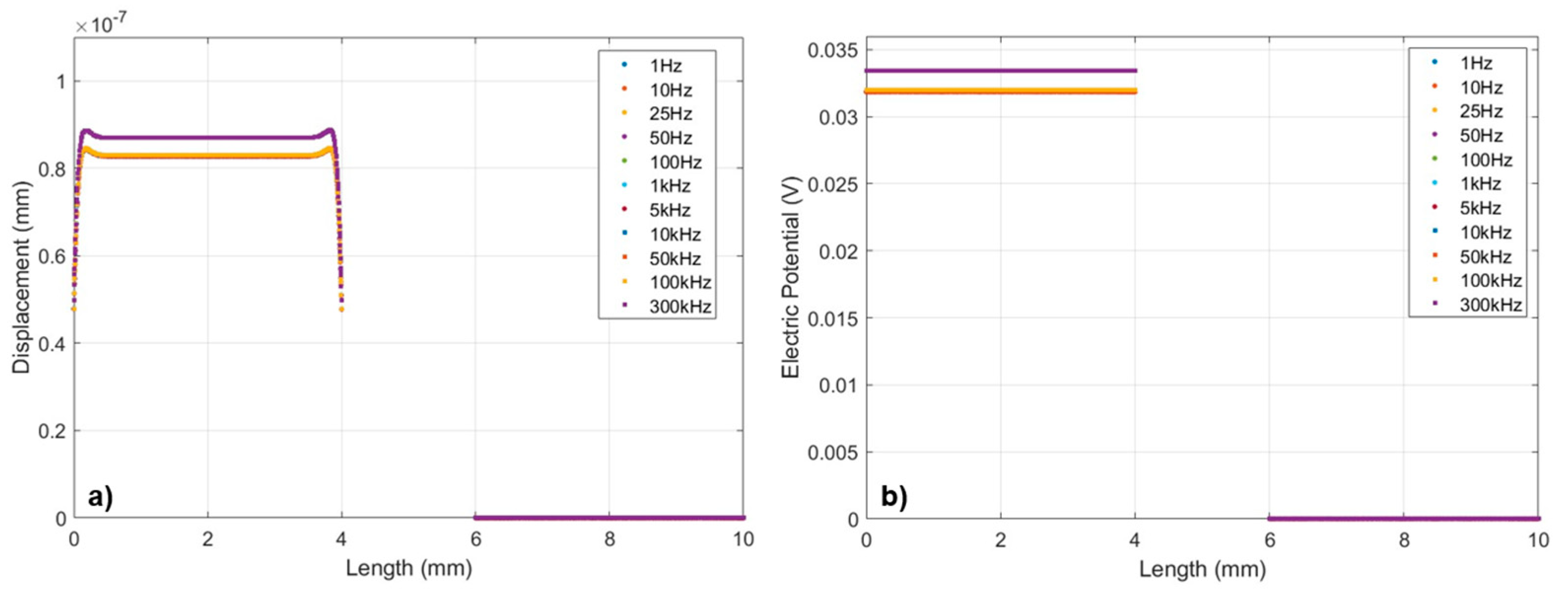





| Item | Value | Unit |
|---|---|---|
| Piezoelectric Strain Constand | 28 | |
| Piezoelectric Voltage Constant | 0.3 | |
| Relative Dielectric Constant | 13.5 | |
| Maximum Operating Voltage | >100 | |
| Tensile Strength | ||
| Young’s Modulus | ||
| Poisson’s Ratio | 0.3 | |
| Density | ||
| Frequency Range | ||
| Pressure Range | ||
| Operating Temperature Range | ||
| Thickness |
| Item | Value | Unit |
|---|---|---|
| Mach Number M | 2 | |
| Freestream Unit Reynolds Number | ||
| Boundary Layer Velocity Thickness | 7.2 | |
| Shock Generator Angle | 10 | |
| Test Section Length | ||
| Cross-Section Dimension |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Corsi, C.; Weiland, T.; Wang, Z.; Grund, T.; Pohl, O.; Bienia, J.M.; Weiss, J.; Ngo, H.D. Screen-Printed PVDF Piezoelectric Pressure Transducer for Unsteadiness Study of Oblique Shock Wave Boundary Layer Interaction. Micromachines 2024, 15, 1423. https://doi.org/10.3390/mi15121423
Wang B, Corsi C, Weiland T, Wang Z, Grund T, Pohl O, Bienia JM, Weiss J, Ngo HD. Screen-Printed PVDF Piezoelectric Pressure Transducer for Unsteadiness Study of Oblique Shock Wave Boundary Layer Interaction. Micromachines. 2024; 15(12):1423. https://doi.org/10.3390/mi15121423
Chicago/Turabian StyleWang, Bei, Cosimo Corsi, Thomas Weiland, Zhenyu Wang, Thomas Grund, Olaf Pohl, Johannes Max Bienia, Julien Weiss, and Ha Duong Ngo. 2024. "Screen-Printed PVDF Piezoelectric Pressure Transducer for Unsteadiness Study of Oblique Shock Wave Boundary Layer Interaction" Micromachines 15, no. 12: 1423. https://doi.org/10.3390/mi15121423
APA StyleWang, B., Corsi, C., Weiland, T., Wang, Z., Grund, T., Pohl, O., Bienia, J. M., Weiss, J., & Ngo, H. D. (2024). Screen-Printed PVDF Piezoelectric Pressure Transducer for Unsteadiness Study of Oblique Shock Wave Boundary Layer Interaction. Micromachines, 15(12), 1423. https://doi.org/10.3390/mi15121423







