Investigations into Capillary Forces and Capillary Rise in a Three-Finger Microgripper and a Plate: Numerical Simulations and Experimental Validation
Abstract
:1. Introduction
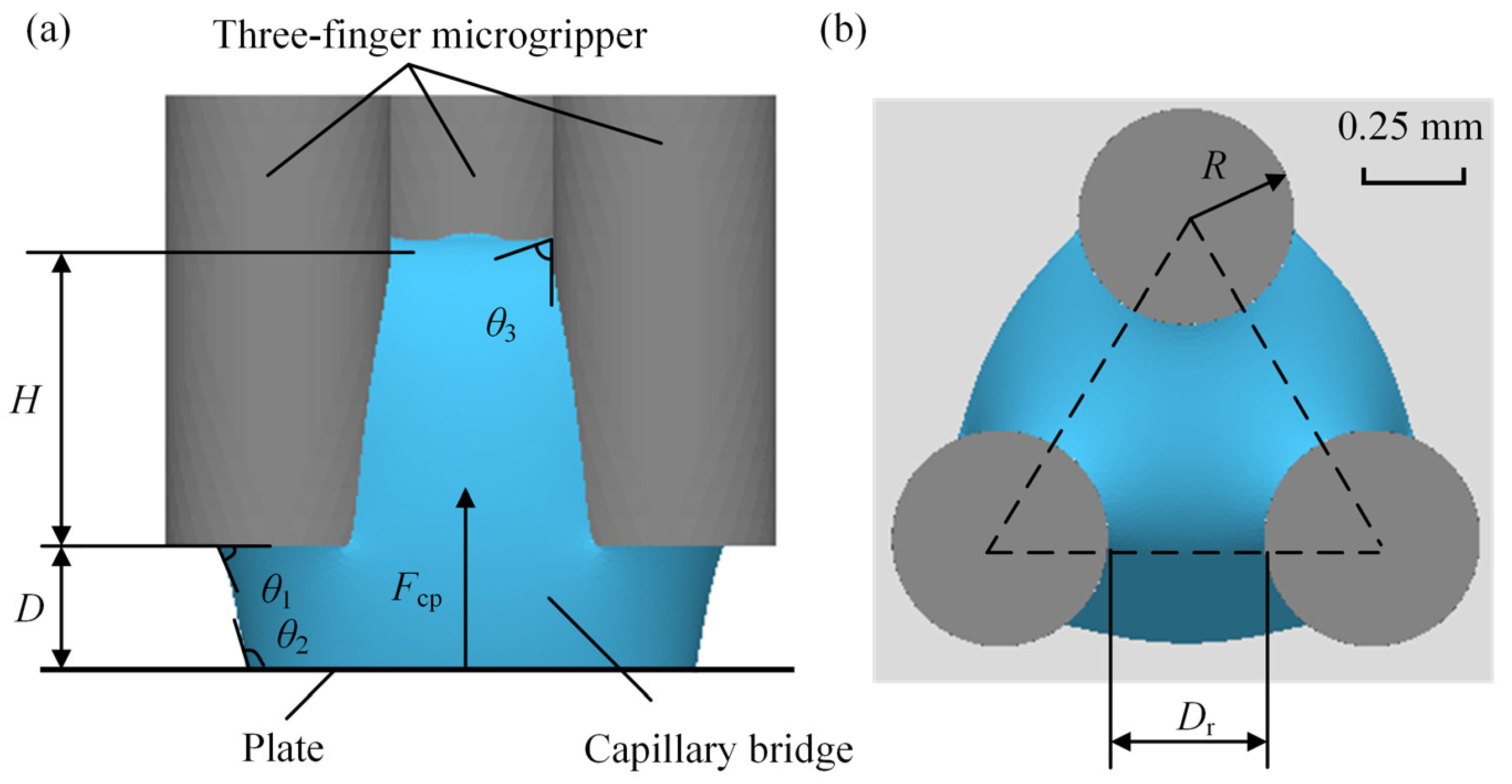
2. Capillary Bridge Model
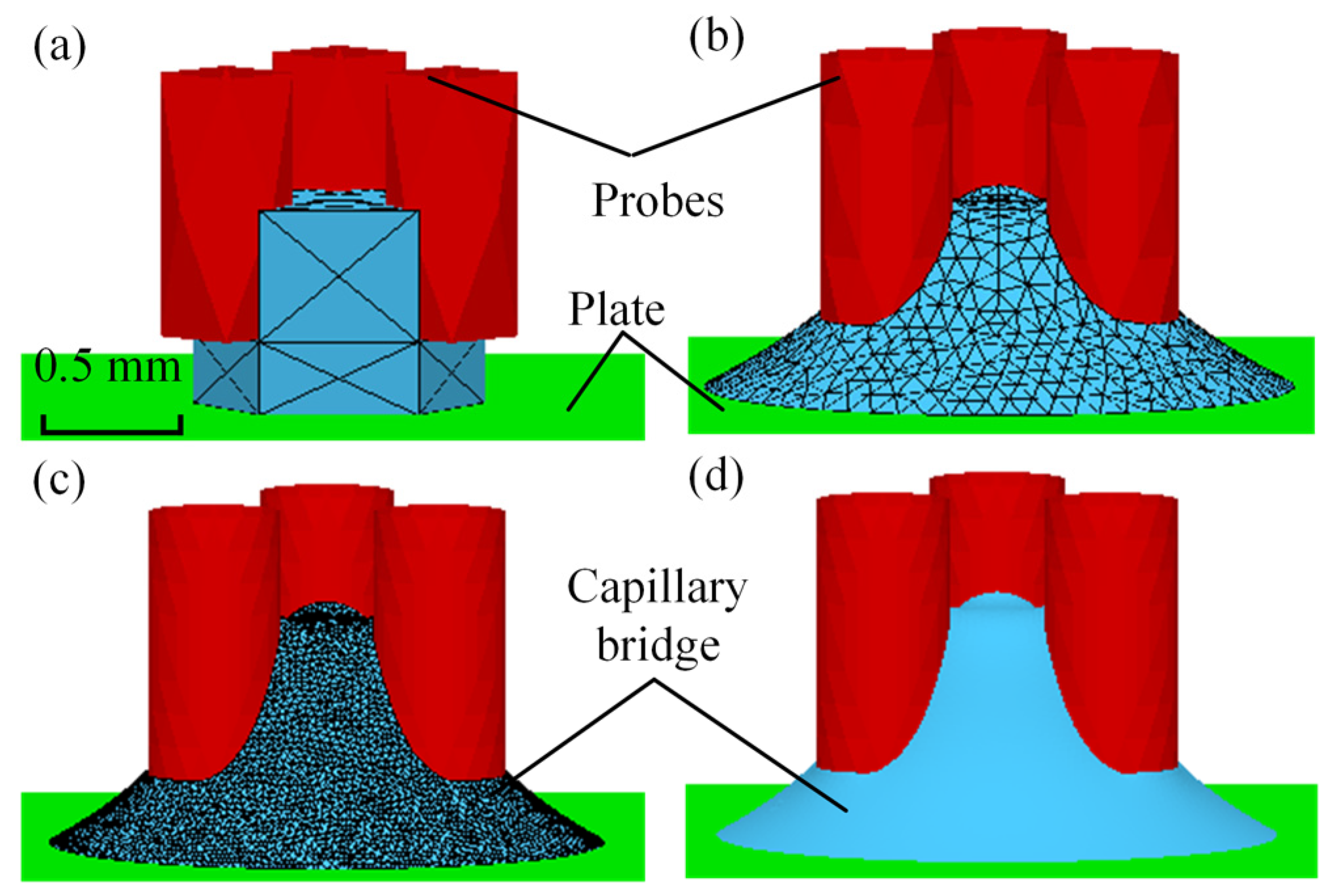
3. Experiments and Simulations
3.1. Experimental Setup
3.2. Experimental Methods
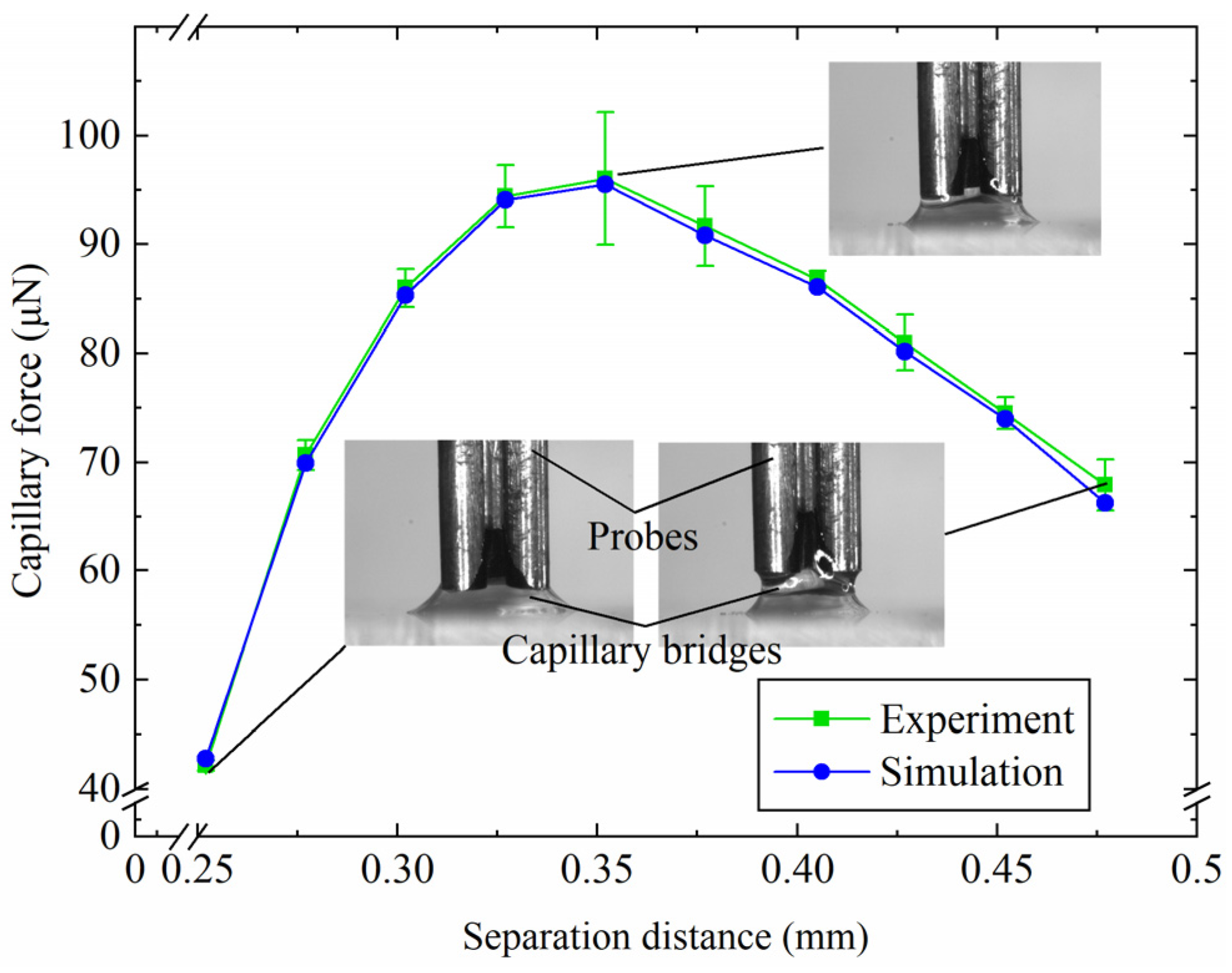
3.3. Comparison Between the Simulation and the Experiment
4. Results and Discussion
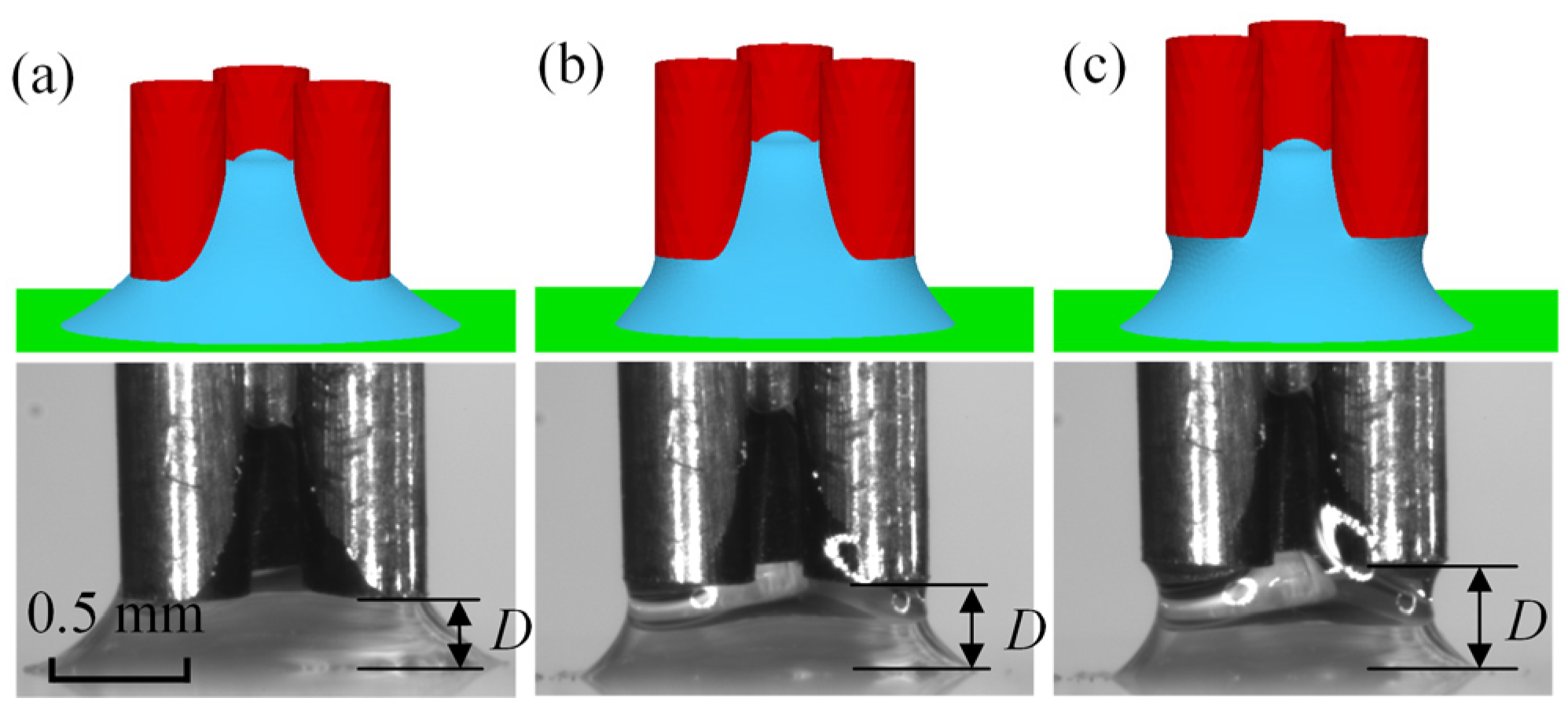
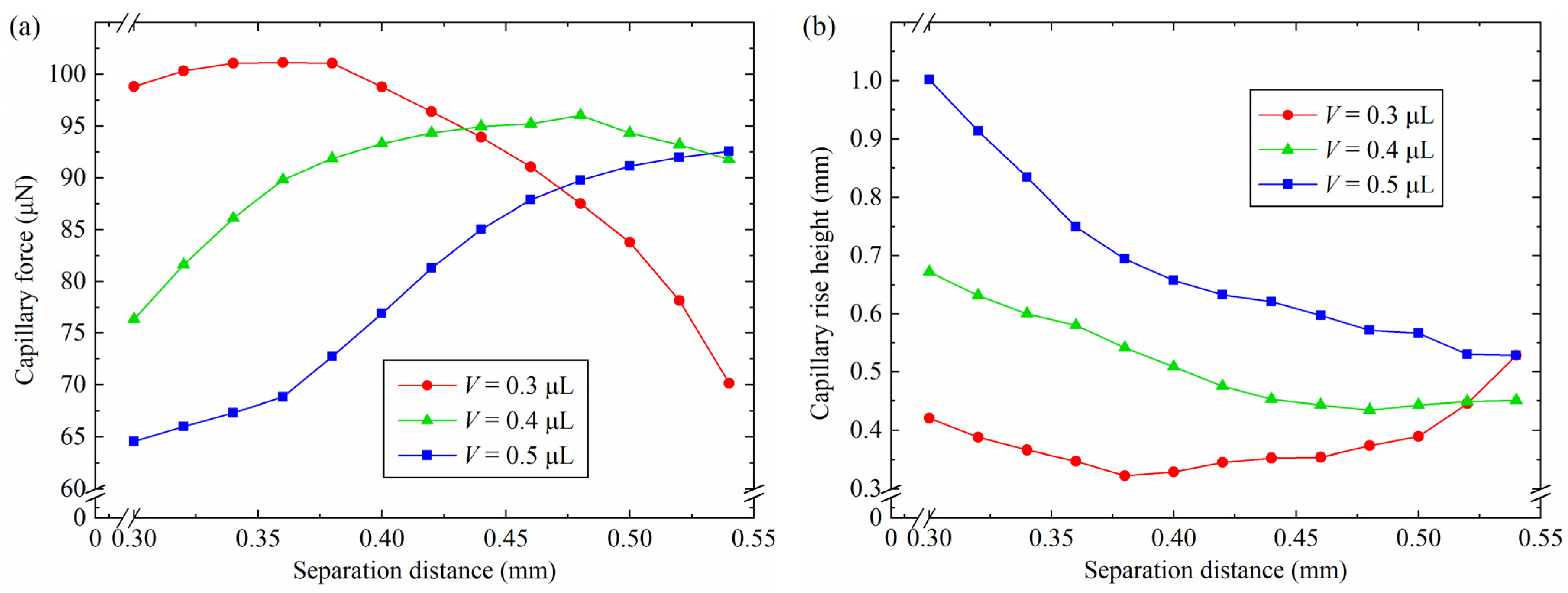
4.1. Influence of Separation Distances
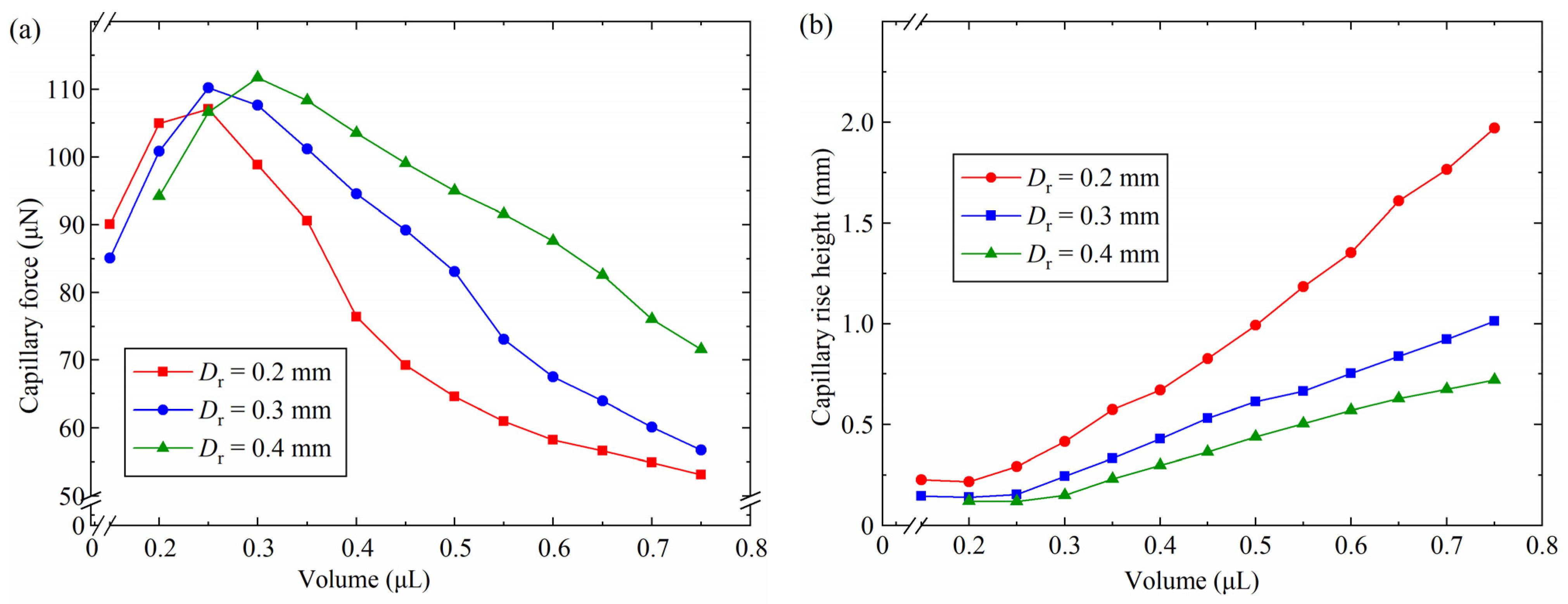
4.2. Influence of the Capillary Bridge Volume
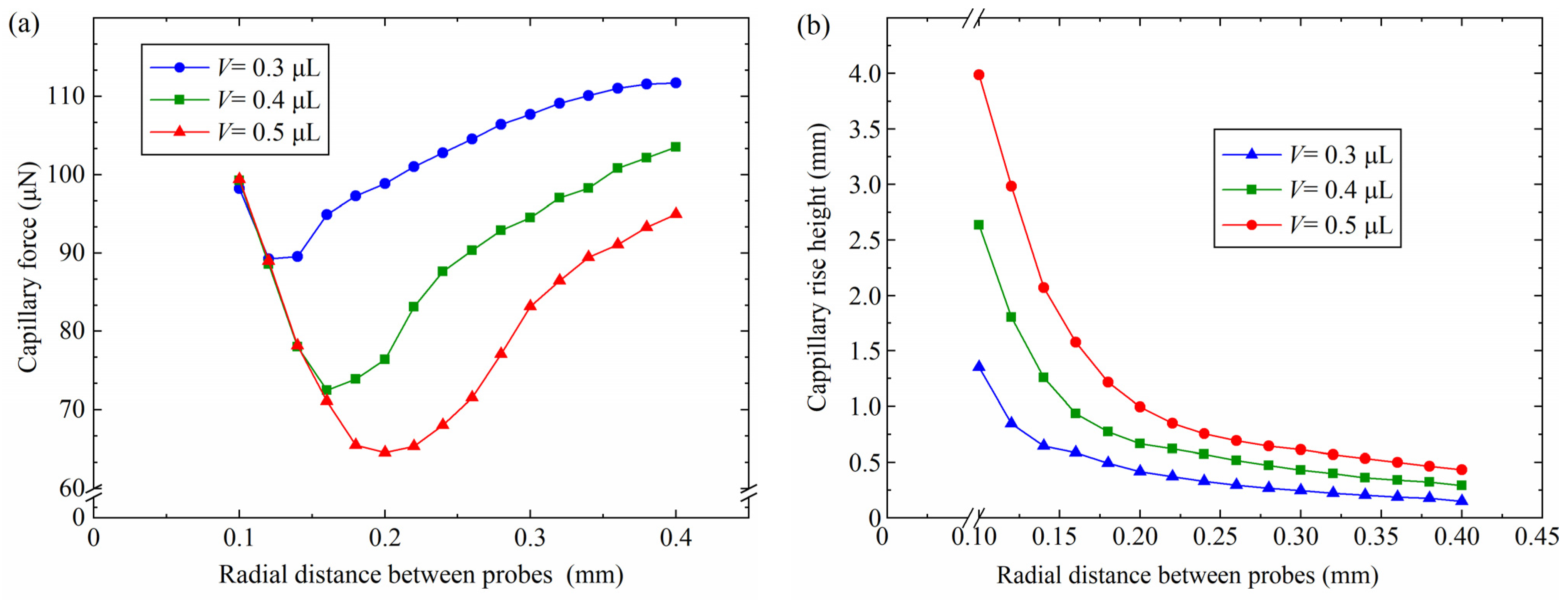
4.3. Influence of the Radial Distance Between Probes
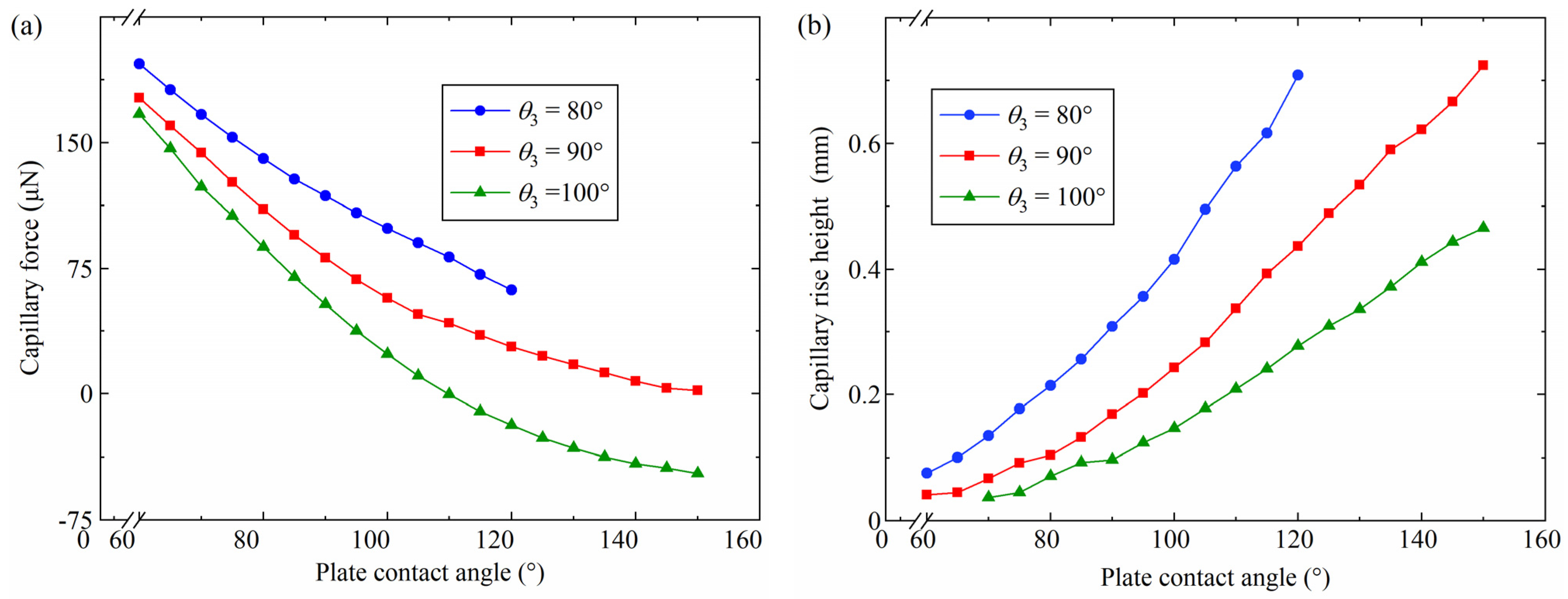
4.4. Influence of the Plate Contact Angle
4.5. Influence of the Probe Side Contact Angle
4.6. Pickup and Release Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dow, A.B.A.; Jazizadeh, B.; Kherani, N.P.; Rangelow, I. Development and modeling of an electrothermally MEMS microactuator with an integrated microgripper. J. Micromech. Microeng. 2011, 21, 125026. [Google Scholar] [CrossRef]
- Nah, S.K.; Zhong, Z. A microgripper using piezoelectric actuation for micro-object manipulation. Sens. Actuator A-Phys. 2007, 133, 218–224. [Google Scholar] [CrossRef]
- Rong, W.; Fan, Z.; Wang, L.; Xie, H.; Sun, L. A vacuum microgripping tool with integrated vibration releasing capability. Rev. Sci. Instrum. 2014, 85, 085002. [Google Scholar] [CrossRef] [PubMed]
- Ford, S.; Macias, G.; Lumia, R. Single active finger IPMC microgripper. Smart Mater. Struct. 2015, 24, 025015. [Google Scholar] [CrossRef]
- Chen, X.; Xie, Z.; Shen, R.; Feng, X.; Tan, H.; Tai, K. High-magnification microgripper with low output displacement loss. Sens. Actuator A-Phys. 2023, 357, 114402. [Google Scholar] [CrossRef]
- Miyazaki, H.; Sato, T. Mechanical assembly of three-dimensional microstructures from fine particles. Adv. Robot. 1996, 11, 169–185. [Google Scholar] [CrossRef]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Lv, J.; Tian, X.; Wang, Y.; Liu, J.; Yu, Y. A remotely driven and controlled micro-gripper fabricated from light-induced deformation smart material. Smart Mater. Struct. 2016, 25, 095009. [Google Scholar] [CrossRef]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef]
- Steager, E.B.; Sakar, M.S.; Kim, D.H.; Kumar, V.; Pappas, G.J.; Kim, M.J. Electrokinetic and optical control of bacterial microrobots. J. Micromech. Microeng. 2011, 21, 035001. [Google Scholar] [CrossRef]
- Chung, S.K.; Kwon, J.O.; Cho, S.K. Manipulation of micro/mini-objects by AC-electrowetting-actuated oscillating bubbles: Capturing, carrying and releasing. J. Adhes. Sci. Technol. 2012, 26, 1965–1983. [Google Scholar] [CrossRef]
- Neild, A.; Oberti, S.; Beyeler, F.; Dual, J.; Nelson, B.J. A micro-particle positioning technique combining an ultrasonic manipulator and a microgripper. J. Micromech. Microeng. 2006, 16, 1562. [Google Scholar] [CrossRef]
- Walker, R.; Gralinski, I.; Keong, L.K.; Alan, T.; Neild, A. Particle manipulation using an ultrasonic micro-gripper. Appl. Phys. Lett. 2012, 101, 163504. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, L.; Rong, W.; Sun, L. Dropwise condensation on a hydrophobic probe-tip for manipulating micro-objects. Appl. Phys. Lett. 2015, 106, 084105. [Google Scholar] [CrossRef]
- Fan, Z.; Rong, W.; Wang, L.; Sun, L. A single-probe capillary microgripper induced by dropwise condensation and inertial release. J. Micromech. Microeng. 2015, 25, 115011. [Google Scholar] [CrossRef]
- Vasudev, A.; Zhe, J. A capillary microgripper based on electrowetting. Appl. Phys. Lett. 2008, 93, 103503. [Google Scholar] [CrossRef]
- Hagiwara, W.; Ito, T.; Tanaka, K.; Tokui, R.; Fuchiwaki, O. Capillary Force Gripper for Complex-Shaped Micro-Objects with Fast Droplet Forming by On–Off Control of a Piston Slider. IEEE Robot. Autom. Lett. 2019, 4, 3695–3702. [Google Scholar] [CrossRef]
- Saito, S.; Motokado, T.; Obata, K.J.; Takahashi, K. Capillary force with a concave probe-tip for micromanipulation. Appl. Phys. Lett. 2005, 87, 234103. [Google Scholar] [CrossRef]
- Iazzolino, A.; Tourtit, Y.; Chafai, A.; Gilet, T.; Lambert, P.; Tadrist, L. Pick up and release of micro-objects: A motion-free method to change the conformity of a capillary contact. Soft Matter. 2020, 16, 754–763. [Google Scholar] [CrossRef]
- Fantoni, G.H.; Hansen, N.; Santochi, M. A new capillary gripper for mini and micro parts. CIRP Annals. 2013, 62, 17–20. [Google Scholar] [CrossRef]
- Biganzoli, F.; Fassi, I.; Pagano, C. Development of a gripping system based on capillary force. In Proceedings of the 6th IEEE International Symposium on Assembly and Task Planning: From Nano to Macro Assembly and Manufacturing, Montreal, QC, Canada, 19–21 July 2005; pp. 36–40. [Google Scholar] [CrossRef]
- Ito, T.; Fukuchi, E.; Tanaka, K.; Nishiyama, Y.; Watanabe, N.; Fuchiwaki, O. Vision Feedback Control for the Automation of the Pick-and-Place of a Capillary Force Gripper. Micromachines 2022, 13, 1270. [Google Scholar] [CrossRef] [PubMed]
- Cavaiani, M.; Dehaeck, S.; Vitry, Y.; Lambert, P. Multi-Scale 3D Printed Capillary Gripper. In Proceedings of the International Conference on Manipulation, Automation and Robotics at Small Scales, Nagoya, Japan, 4–8 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Gan, Y.; Huang, W.; Aoyama, H. Method of orientation control and experimental investigation using a liquid-drop micromanipulator. J. Micromech. Microeng. 2017, 27, 045006. [Google Scholar] [CrossRef]
- Tanaka, K.; Ito, T.; Nishiyama, Y.; Fukuchi, E.; Fuchiwaki, O. Double-Nozzle Capillary Force Gripper for Cubical, Triangular Prismatic, and Helical 1-mm-Sized-Objects. IEEE Robot. Autom. Lett. 2022, 7, 1324–1331. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Z.; Huang, C.; Wang, H.; Fan, M.; Wang, L. Capillary forces and capillary bridges between a three-finger microgripper and a plate. J. Adhes. 2023, 99, 2434–2456. [Google Scholar] [CrossRef]
- Sun, X.; Sakai, M. Direct numerical simulation of gas-solid-liquid flows with capillary effects: An application to liquid bridge forces between spherical particles. Phys. Rev. E 2016, 94, 063301. [Google Scholar] [CrossRef] [PubMed]
- Ata, A.; Rabinovich, Y.; Singh, R. Role of surface roughness in capillary adhesion. J. Adhes. Sci. Technol. 2002, 16, 337–346. [Google Scholar] [CrossRef]
- Iwamatsu, M.; Mori, H. Effect of line tension on axisymmetric nanoscale capillary bridges at the liquid-vapor equilibrium. Phys. Rev. E 2019, 100, 042802. [Google Scholar] [CrossRef]
- Semprebon, C.; Scheel, M.; Herminghaus, S.; Seemann, R.; Brinkmann, M. Liquid morphologies and capillary forces between three spherical beads. Phys. Rev. E 2016, 94, 012907. [Google Scholar] [CrossRef] [PubMed]
- Fan, M.; Fan, Z.; Xu, Z.; Li, J.; Li, C.; Yang, Z. Investigation of capillary forces and capillary bridges between an end-adjusted three-finger microgripper with hydrophobic side surface and a plate. J. Adhes. Sci. Technol. 2024, 38, 1702–1717. [Google Scholar] [CrossRef]
- Yang, L.; Hu, J.; Bai, K. Capillary and van der Waals force between microparticles with different sizes in humid air. J. Adhes. Sci. Technol. 2016, 30, 566–578. [Google Scholar] [CrossRef]
- Wang, L.; Huang, B.; He, Y.; Rong, W. Simulation and experiments on the capillary forces between two continuously fully wet circular disks. J. Adhes. Sci. Technol. 2018, 32, 908–919. [Google Scholar] [CrossRef]
- Chau, A.; Régnier, S.; Delchambre, A.; Lambert, P. Theoretical and Experimental Study of the Influence of AFM Tip Geometry and Orientation on Capillary Force. J. Adhes. Sci. Technol. 2010, 24, 2499–2510. [Google Scholar] [CrossRef]
- Wang, X.; Cui, S.; Zhou, L.; Xu, S.; Sun, Z.; Zhu, R. A generalized Young’s equation for contact angles of droplets on homogeneous and rough substrates. J. Adhes. Sci. Technol. 2014, 28, 161–170. [Google Scholar] [CrossRef]
- Lambert, P.; Chau, A.; Delchambre, A.; Régnier, S. Comparison between Two Capillary Forces Models. Langmuir 2008, 24, 3157–3163. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhou, P.; Wang, G.; Zhao, B.; Howes, T.; Chen, W. Modeling of capillary force between particles with unequal contact angle. Powder Technol. 2020, 376, 390–397. [Google Scholar] [CrossRef]
- Walzel, F.; Requier, A.; Boschi, K.; Farago, J.; Fuchs, P.; Thalmann, F.; Drenckhan, W.; Muller, P.; Charitat, T. Perturbing the catenoid: Stability and mechanical properties of nonaxisymmetric minimal surfaces. Phys. Rev. E 2022, 106, 014803. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, C.; Hong, S.; Sheng, Y.; Tsao, H. Trapped liquid drop in a microchannel: Multiple stable states. Phys. Rev. E 2013, 87, 062401. [Google Scholar] [CrossRef] [PubMed]
- Brakke, K.A. The Surface Evolver. Exp. Math. 1992, 1, 141–165. [Google Scholar] [CrossRef]
- Brakke, K.A. The Surface Evolver and the Stability of Liquid Surfaces. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1996, 354, 2143–2157. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Radius of probes | 0.25 mm |
| Radial distance between probes | 0.2 mm |
| Side contact angle of the probe | 80° |
| Contact angle of the plate | 100° |
| Surface tension | 67.4 mN/m |
| Parameters | Value |
|---|---|
| Radius of probes | 0.25 mm |
| Side contact angle of the probe | 80° |
| Separation distance | 0.3 mm |
| Contact angle of the plate | 100° |
| Surface tension | 67.4 mN/m |
| Parameters | Value |
|---|---|
| Radius of probes | 0.25 mm |
| Side contact angle of the probe | 80° |
| Contact angle of the plate | 100° |
| Separation distance | 0.3 mm |
| Surface tension | 67.4 mN/m |
| Parameters | Value |
|---|---|
| Radius of probes | 0.25 mm |
| Volume of capillary bridge | 0.3 μL |
| Separation distance | 0.3 mm |
| Radial distance between probes | 0.2 mm |
| Surface tension | 67.4 mN/m |
| Parameters | Value |
|---|---|
| Radius of probes | 0.25 mm |
| Volume of capillary bridge | 0.3 μL |
| Separation distance | 0.3 mm |
| Radial distance between probes | 0.2 mm |
| Surface tension | 67.4 mN/m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Fan, Z.; Gao, J.; Zhang, K.; Zhang, X. Investigations into Capillary Forces and Capillary Rise in a Three-Finger Microgripper and a Plate: Numerical Simulations and Experimental Validation. Micromachines 2024, 15, 1459. https://doi.org/10.3390/mi15121459
Xu Z, Fan Z, Gao J, Zhang K, Zhang X. Investigations into Capillary Forces and Capillary Rise in a Three-Finger Microgripper and a Plate: Numerical Simulations and Experimental Validation. Micromachines. 2024; 15(12):1459. https://doi.org/10.3390/mi15121459
Chicago/Turabian StyleXu, Zhi, Zenghua Fan, Jun Gao, Kun Zhang, and Xiang Zhang. 2024. "Investigations into Capillary Forces and Capillary Rise in a Three-Finger Microgripper and a Plate: Numerical Simulations and Experimental Validation" Micromachines 15, no. 12: 1459. https://doi.org/10.3390/mi15121459
APA StyleXu, Z., Fan, Z., Gao, J., Zhang, K., & Zhang, X. (2024). Investigations into Capillary Forces and Capillary Rise in a Three-Finger Microgripper and a Plate: Numerical Simulations and Experimental Validation. Micromachines, 15(12), 1459. https://doi.org/10.3390/mi15121459






