Tool Run-Out in Micro-Milling: Development of an Analytical Model Based on Cutting Force Signal Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Proposed Model
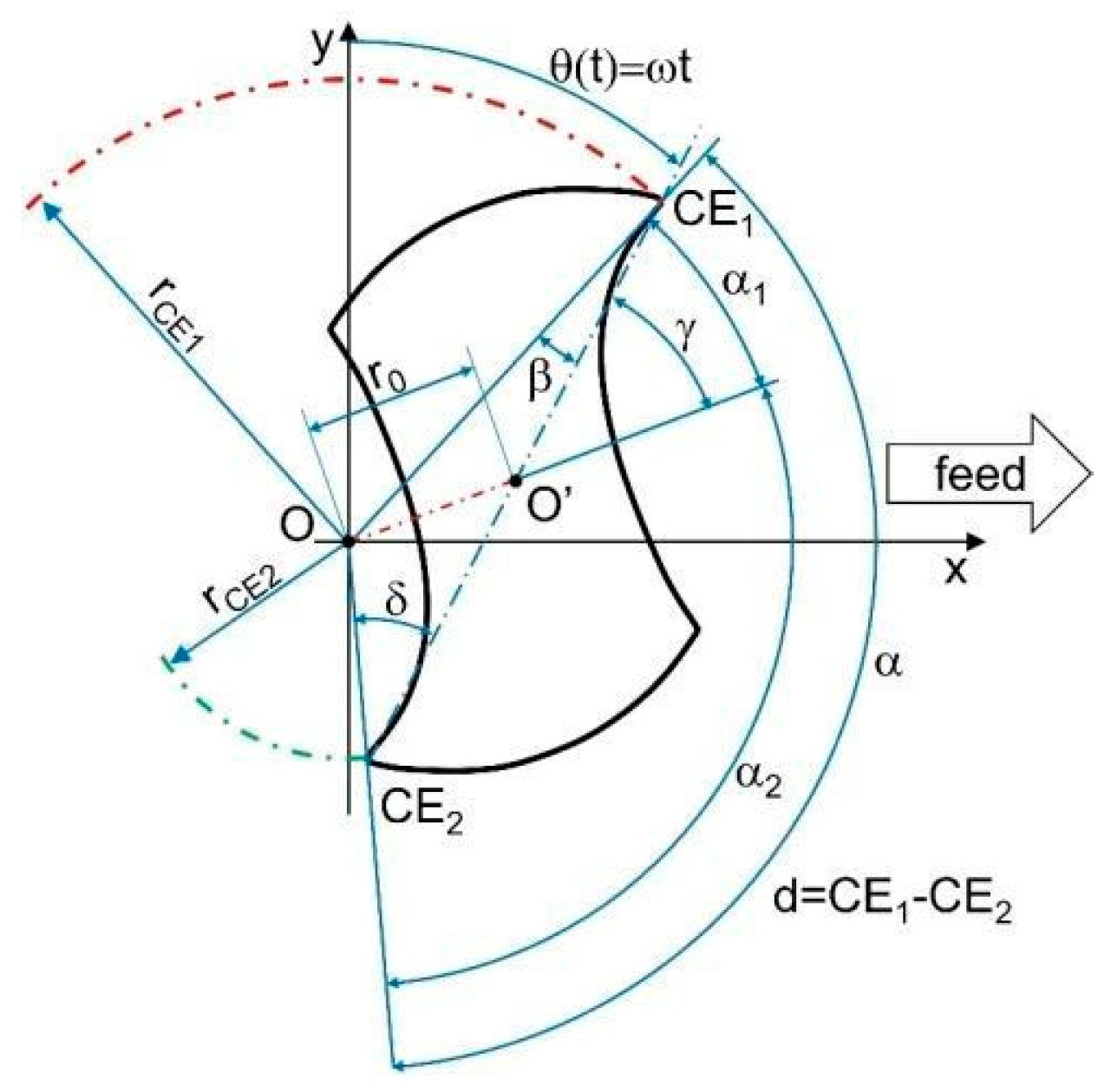
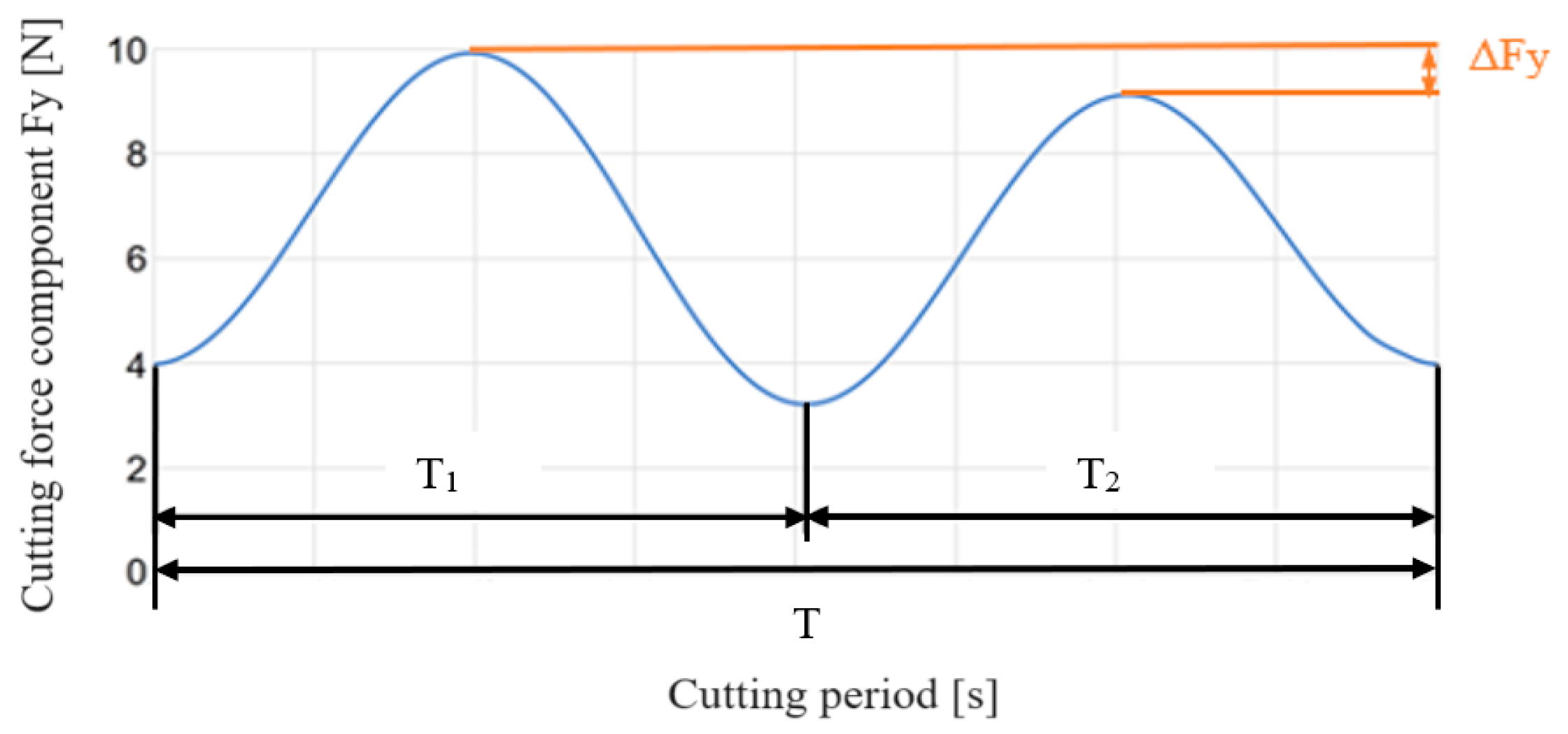
2.1.1. Tool Run-Out
- r0, the distance between the spindle’s rotational center O and the tool one O’;
- γ0, the angle from rce1 and r0.
- the tool diameter d [mm];
- the rotational speed ω [rad/s];
- the cutting edge phase angle α [rad].
- angle α would not be constantly equal to π [rad];
- radius rCE1 would differ from the rotational radius of the second cutting edge rCE2 [mm].
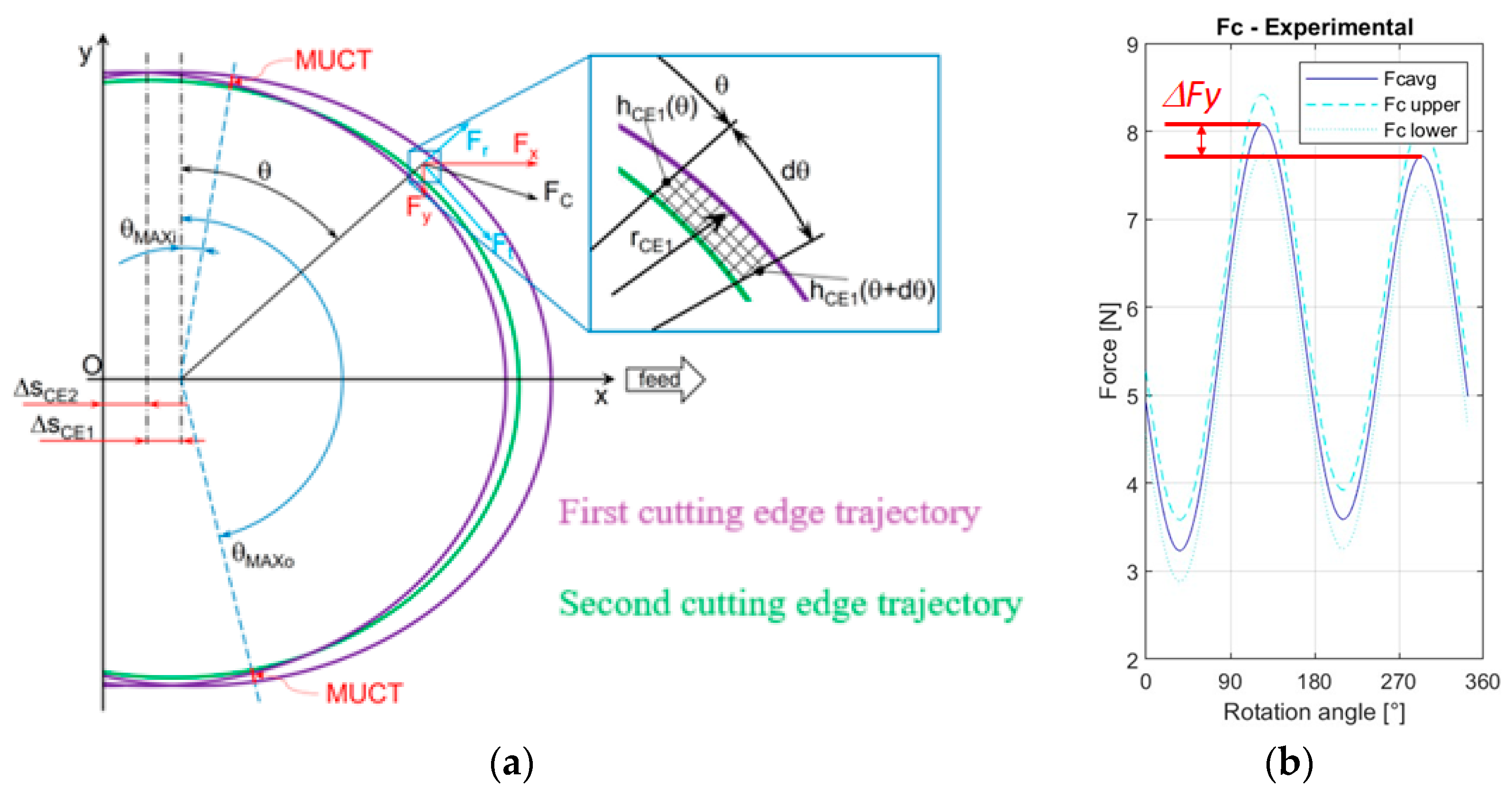
2.1.2. Analytical Model
- ap is the axial depth of cut [mm];
- Kts and Krs are the specific force coefficients for the shearing regime [N/mm2];
- Ktp and Krp are the specific force coefficients for the ploughing regime [N/mm3].
2.2. Experimental Campaign
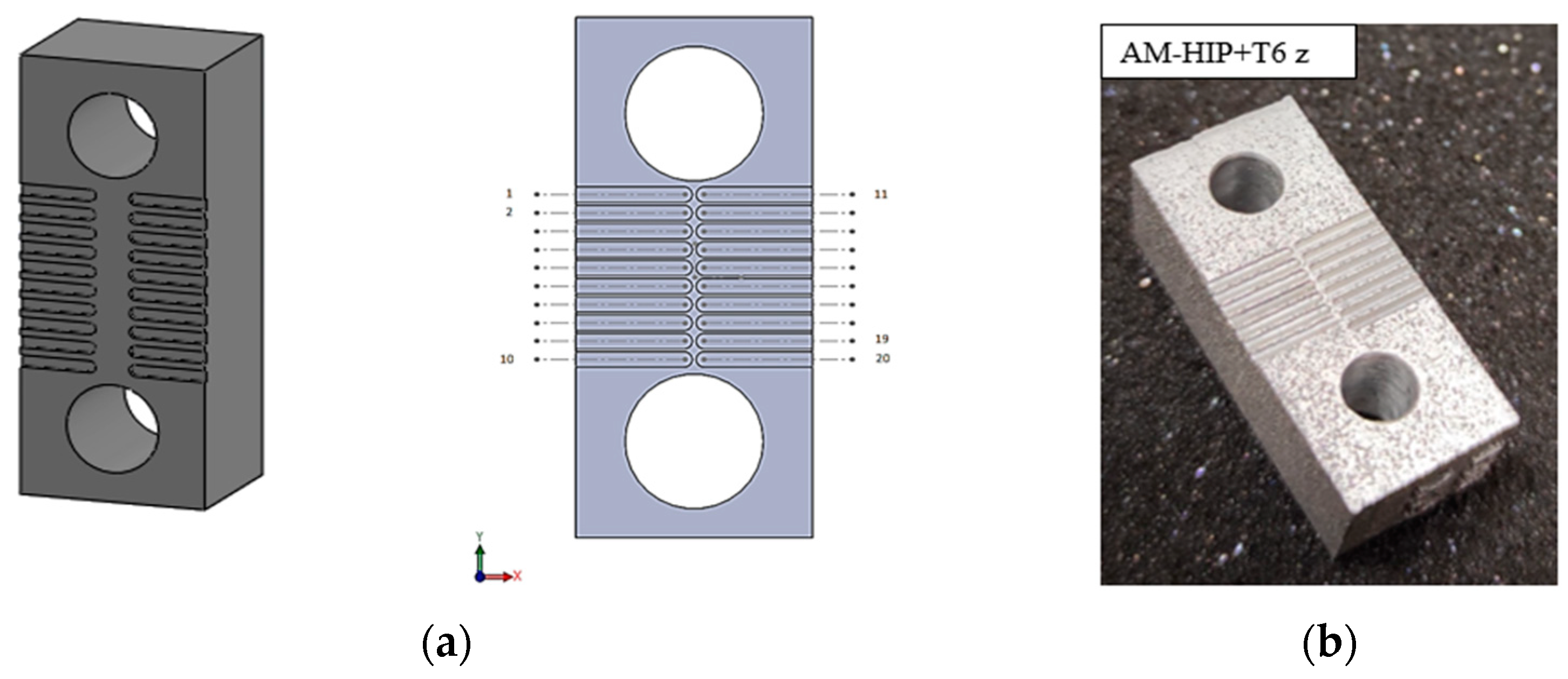
2.2.1. Specimen Preparation
2.2.2. Micro-Milling Experiments
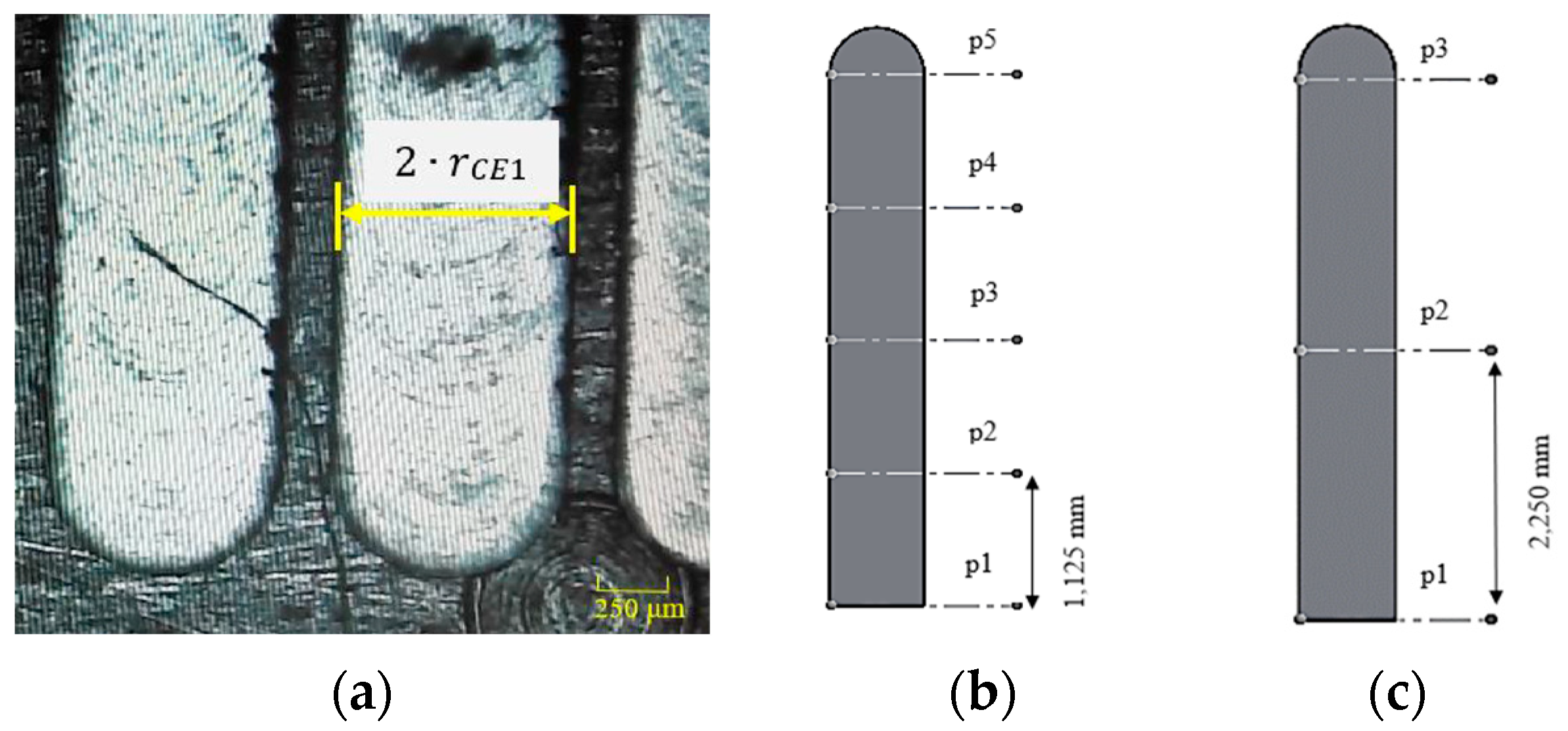
2.2.3. Tool Run-Out Measurement
3. Results and Discussion
3.1. Experimental Measures
3.2. Application of the Analytical Model
3.3. Comparison between the Results
3.4. Simplification of the Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A
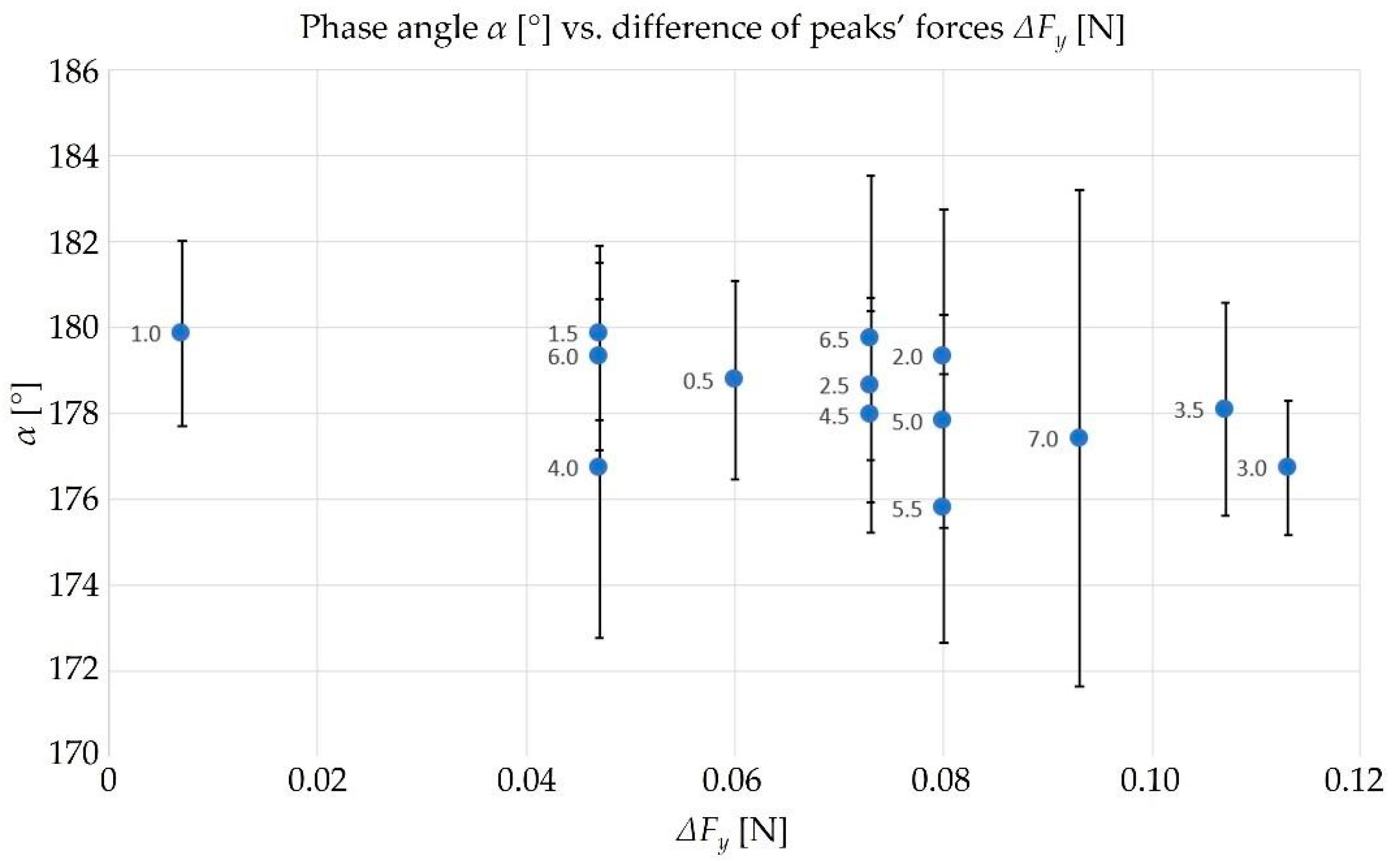
| Test | fz [mm/tooth] | ΔFy [N] | α [°] | Dev St α [°] | α [rad] |
|---|---|---|---|---|---|
| 1 | 0.0010 | 0.007 | 179.87 | 2.16 | 3.14 |
| 2 | 0.0045 | 0.073 | 177.96 | 2.74 | 3.11 |
| 3 | 0.0020 | 0.080 | 179.34 | 3.40 | 3.13 |
| 4 | 0.0060 | 0.047 | 179.33 | 2.19 | 3.13 |
| 5 | 0.0025 | 0.073 | 178.65 | 1.74 | 3.12 |
| 6 | 0.0040 | 0.047 | 176.73 | 3.95 | 3.08 |
| 7 | 0.0015 | 0.047 | 179.87 | 2.03 | 3.14 |
| 8 | 0.0030 | 0.113 | 176.74 | 1.56 | 3.08 |
| 9 | 0.0035 | 0.107 | 178.09 | 2.48 | 3.11 |
| 10 | 0.0005 | 0.060 | 178.78 | 2.32 | 3.12 |
| 11 | 0.0065 | 0.073 | 179.74 | 3.81 | 3.14 |
| 12 | 0.0055 | 0.080 | 175.79 | 3.12 | 3.07 |
| 13 | 0.0050 | 0.080 | 177.82 | 2.49 | 3.10 |
| 14 | 0.0070 | 0.093 | 177.42 | 5.78 | 3.10 |
| Kts [N/mm2] | a∙(rCE1)4 [mm4] | b∙(rCE1)3 [mm4] | c∙(rCE1)2 [mm4] | e∙(rCE1) [mm4] | g [mm4] |
|---|---|---|---|---|---|
| 1 | 8.11 × 10−5 | −8.92 × 10−5 | −9.10 × 10−2 | 5.01 × 10−2 | 8.25 × 10−2 |
| 10 | 8.11 × 10−5 | −8.94 × 10−6 | −9.85 × 10−2 | 5.43 × 10−3 | 9.67 × 10−2 |
| 100 | 8.11 × 10−5 | −9.14 × 10−7 | −9.86 × 10−2 | 5.56 × 10−4 | 9.69 × 10−2 |
| 1000 | 8.11 × 10−5 | −1.11 × 10−7 | −9.86 × 10−2 | 6.77 × 10−5 | 9.69 × 10−2 |
| 10,000 | 8.11 × 10−5 | −3.11 × 10−8 | −9.86 × 10−2 | 1.89 × 10−5 | 9.69 × 10−2 |
| 100,000 | 8.11 × 10−5 | −2.30 × 10−8 | −9.86 × 10−2 | 1.40 × 10−5 | 9.69 × 10−2 |
| 1,000,000 | 8.11 × 10−5 | −2.22 × 10−8 | −9.86 × 10−2 | 1.35 × 10−5 | 9.69 × 10−2 |
| Test | fz [mm] | I [mm] | a [-] | b [mm] | c [mm2] | e [mm3] | g [mm4] |
|---|---|---|---|---|---|---|---|
| 1 | 0.0010 | 0.00000 | 0.00001 | 0.00000 | −0.62252 | 0.00000 | 0.09688 |
| 2 | 0.0045 | 0.00007 | 0.00127 | 0.00000 | −0.62252 | 0.00004 | 0.09688 |
| 3 | 0.0020 | 0.00002 | 0.00013 | 0.00000 | −0.62252 | 0.00002 | 0.09688 |
| 4 | 0.0060 | 0.00003 | 0.00014 | 0.00000 | −0.62252 | 0.00002 | 0.09688 |
| 5 | 0.0025 | 0.00003 | 0.00056 | 0.00000 | −0.62252 | 0.00002 | 0.09688 |
| 6 | 0.0040 | 0.00008 | 0.00326 | 0.00000 | −0.62252 | 0.00005 | 0.09688 |
| 7 | 0.0015 | 0.00001 | 0.00001 | 0.00000 | −0.62252 | 0.00001 | 0.09688 |
| 8 | 0.0030 | 0.00008 | 0.00323 | 0.00000 | −0.62252 | 0.00005 | 0.09688 |
| 9 | 0.0035 | 0.00006 | 0.00111 | 0.00000 | −0.62252 | 0.00004 | 0.09688 |
| 10 | 0.0005 | 0.00001 | 0.00045 | 0.00000 | −0.62252 | 0.00001 | 0.09688 |
| 11 | 0.0065 | 0.00002 | 0.00002 | 0.00000 | −0.62252 | 0.00001 | 0.09688 |
| 12 | 0.0055 | 0.00014 | 0.00540 | 0.00000 | −0.62252 | 0.00009 | 0.09688 |
| 13 | 0.0050 | 0.00007 | 0.00145 | 0.00000 | −0.62252 | 0.00005 | 0.09688 |
| 14 | 0.0070 | 0.00012 | 0.00202 | 0.00000 | −0.62252 | 0.00007 | 0.09688 |
References
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Zhang, M.; Ye, X.; Li, Y.; Wang, H.; Lai, R.; Li, Y. Effect of Heat Treatment States of Feedstock on the Microstructure and Mechanical Properties of AA2219 Layers Deposited by Additive Friction Stir Deposition. Materials 2023, 16, 7591. [Google Scholar] [CrossRef]
- Noga, P.; Skrzekut, T.; Wędrychowicz, M. Microstructure and Mechanical Properties of Al-Si Alloys Produced by Rapid Solidification and Hot Extrusion. Materials 2023, 16, 5223. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Rena, Y.; Rena, J.; Lianga, L.; Lia, R.; Fangb, Q.; Caic, A.; Shand, Q.; Tiane, Y.; Bakerf, I. Selective laser melted AlSi10Mg alloy under melting mode transition: Microstructure evolution, nanomechanical behaviors and tensile properties. J. Alloys Compd. 2021, 873, 159823. [Google Scholar] [CrossRef]
- Wang, P.; Lei, H.; Zhu, X.; Chen, H.; Fang, D. Influence of manufacturing geometric defects on the mechanical properties of AlSi10Mg alloy fabricated by selective laser melting. J. Alloys Compd. 2019, 789, 852–859. [Google Scholar] [CrossRef]
- Thijs, L.; Kempen, K.; Kruth, J.P.; Van Humbeeck, J. Fine-structured aluminium products with controllable texture by selective laser melting of pre-alloyed AlSi10Mg powder. Acta Mater. 2013, 61, 1809–1819. [Google Scholar] [CrossRef]
- Chen, N.; Li, H.N.; Wu, J.; Li, Z.; Li, L.; Liu, G.; He, N. Advances in micro milling: From tool fabrication to process outcomes. Int. J. Mach. Tools Manuf. 2021, 160, 103670. [Google Scholar] [CrossRef]
- Shivakoti, I.; Kibria, G.; Cep, R.; Pradhan, B.B.; Sharma, A. Laser Surface Texturing for Biomedical Applications: A Review. Coatings 2021, 11, 124. [Google Scholar] [CrossRef]
- Pascu, S.; Balc, N. Process Parameter Optimization for Hybrid Manufacturing of PLA Components with Improved Surface Quality. Polymers 2023, 15, 3610. [Google Scholar] [CrossRef]
- Cheng, K.; Huo, D. Micro-Cutting: Fundamentals and Applications; John Wiley & Sons: West Sussex, UK, 2013. [Google Scholar]
- Joshy, J.; George, A.; Kuriachen, B.; Mathew, J. Influence of post processing on the micromachinability of selective laser melted AlSi10Mg: An experimental investigation. Mater. Manuf. Process. 2023, 38, 516–528. [Google Scholar] [CrossRef]
- Pradhana, S.; Singha, S.; Prakasha, C.; Królczykb, G.; Pramanikc, A.; Pruncu, C.I. Investigation of machining characteristics of hard-to-machine Ti-6Al-4V-ELI alloy for biomedical applications. J. Mater. Res. Technol. 2019, 8, 4849–4862. [Google Scholar] [CrossRef]
- Cardoso, P.; Davim, J.P. Optimization of Surface Roughness in Micromilling. Mater. Manuf. Process. 2010, 25, 1115–1119. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, Z.; Li, Y.; Qiao, Y. Swept Mechanism of Micro-Milling Tool Geometry Effect on Machined Oxygen Free High Conductivity Copper (OFHC) Surface Roughness. Materials 2017, 10, 120. [Google Scholar] [CrossRef]
- Dhanorker, A.; Özel, T. Meso/micro scale milling for micro-manufacturing. Int. J. Mechatron. Manuf. Syst. 2008, 1, 23. [Google Scholar] [CrossRef]
- Balázs, B.Z.; Geier, N.; Takács, M.; Davim, J.P. A review on micro-milling: Recent advances and future trends. Int. J. Adv. Manuf. Technol. 2021, 112, 655–684. [Google Scholar] [CrossRef]
- Xie, M.; Yu, X.; Bao, W.; Liu, C.; Xia, M. Side-Milling-Force Model Considering Tool Runout and Workpiece Deformation. Electronics 2023, 12, 968. [Google Scholar] [CrossRef]
- Lu, X.; Cong, C.; Hou, P.; Xv, K.; Liang, S.Y. Improved Cutting Force Modelling in Micro-Milling Aluminum Alloy LF 21 Considering Tool Wear. Appl. Sci. 2022, 12, 5357. [Google Scholar] [CrossRef]
- Cappellini, C.; Malandruccolo, A.; Abeni, A.; Attanasio, A. A feasibility study of promoting osseointegration surface roughness by micro-milling of Ti-6Al-4V biomedical alloy. Int. J. Adv. Manuf. Technol. 2023, 126, 3053–3067. [Google Scholar] [CrossRef]
- Żurawski, K.; Żurek, P.; Kawalec, A.; Bazan, A.; Olko, A. Modeling of Surface Topography after Milling with a Lens-Shaped End-Mill, Considering Runout. Materials 2022, 15, 1188. [Google Scholar] [CrossRef]
- Attanasio, A. Tool Run-Out Measurement in Micro Milling. Micromachines 2017, 8, 221. [Google Scholar] [CrossRef]
- Krüger, M.; Denkena, B. Model-based identification of tool runout in end milling and estimation of surface roughness from measured cutting forces. Int. J. Adv. Manuf. Technol. 2012, 65, 1067–1080. [Google Scholar] [CrossRef]
- Diez, E.; Perez, H.; Guzman, M.; Vizan, A. An improved methodology for the experimental evaluation of tool runout in peripheral milling. Int. J. Adv. Manuf. Technol. 2013, 65, 283–293. [Google Scholar] [CrossRef]
- Abeni, A.; Loda, D.; Özel, T.; Attanasio, A. Analytical force modelling for micro milling additively fabricated Inconel 625. Prod. Eng. 2020, 4, 613–627. [Google Scholar] [CrossRef]
- Chen, W.; Teng, X.; Huo, D.; Wang, Q. An improved cutting force model for micro milling considering machining dynamics. Int. J. Adv. Manuf. Technol. 2017, 93, 3005–3016. [Google Scholar] [CrossRef]
- Cappellini, C.; Abeni, A.; Attanasio, A. Modelling of micro-milling by considering tool run-out and ploughing regime. Proc. CIRP 2023, 118, 402–407. [Google Scholar] [CrossRef]
- Singh, K.; Kartik, V.; Singh, R. Stability modeling with dynamic run-out in high speed micromilling of Ti6Al4V. Int. J. Mech. Sci. 2019, 150, 677–690. [Google Scholar] [CrossRef]
- Jing, X.; Lv, R.; Song, B.; Xu, J.; Jaffery, S.H.I.; Li, H. A novel run-out model based on spatial tool position for micro-milling force prediction. J. Manuf. Process. 2021, 68, 739–749. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, J.; Deng, Q.; Ma, J.; Liao, X. Modeling study of milling force considering tool runout at different types of radial cutting depth. J. Manuf. Process. 2022, 76, 486–503. [Google Scholar] [CrossRef]
- Vogler, M.P.; Kapoor, S.G.; DeVor, R.E. On the modeling and analysis of machining per- formance in micro end milling, part II: Cutting force prediction. ASME J. Manuf. Sci. Eng. 2004, 126, 695–705. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Wang, W. Cutting forces modeling for micro flat end milling by considering tool run-out and bottom edge cutting effect. Proc. Inst. Mech. Eng. Part. B J. Eng. Manuf. 2017, 233, 470–485. [Google Scholar] [CrossRef]
- Wan, M.; Zhang, W.H.; Dang, J.W.; Yang, Y. New procedures for calibration of instantaneous cutting force coefficients and cutter runout parameters in peripheral milling. Int. J. Mach. Tools Manuf. 2009, 49, 1144–1151. [Google Scholar] [CrossRef]
- Sun, Z.; Geng, D.; Meng, F.; Zhou, L.; Jiang, X.; Zhang, D. High performance drilling of T800 CFRP composites by combining ultrasonic vibration and optimized drill structure. Ultrasonics 2023, 134, 107097. [Google Scholar] [CrossRef]
- Sun, Z.; Geng, D.; Guo, H.; Zhang, Q.; Liu, Y.; Liu, L.; Jiang, X.; Zhang, D. Introducing transversal vibration in twist drilling: Material removal mechanisms and surface integrity. J. Mater. Process Technol. 2024, 325, 118296. [Google Scholar] [CrossRef]
- Abeni, A.; Lancini, M. and Attanasio, A. Characterization of machine tools and measurement system for micromilling. Nanotechnol. Precis. Eng. 2019, 2, 23–28. [Google Scholar] [CrossRef]


| AlSi10Mg | Si | Fe | Mn | Mg | Cu | Al |
|---|---|---|---|---|---|---|
| LB-PBF | 10.2 | 0.21 | <0.02 | 0.40 | <0.002 | Balance |
| Parameter | Value |
|---|---|
| Laser power [W] | 370 |
| Scanning speed [mm/s] | 1300 |
| Hatching distance [µm] | 190 |
| Layer thickness [µm] | 30 |
| Building platform temperature [°C] | 80 |
| Scanning direction | Vertical (z) |
| Property | Value |
|---|---|
| Model | 103L008R005-MEGA-64-T |
| Nominal diameter [µm] | 800 |
| Effective diameter [µm] | 789 ± 2 |
| Nom. tool corner radius [µm] | 5 |
| Eff. tool corner radius [µm] | 6.3 |
| Helix angle [°] | 20° |
| Rake angle [°] | 4° |
| Material | Tungsten carbide |
| Coating material | Titanium nitride |
| Parameter | Value |
|---|---|
| Cutting speed vc [m/min] | 80 |
| Axial depth ap [mm] | 0.25 |
| Feed per tooth fz [μm/tooth] | 0.5–7.0 |
| Property | Value |
|---|---|
| Range measurement [mm] | 60 × 60 × 10 |
| x, y resolution [μm] | 0.1 |
| z resolution [μm] | 0.01 |
| Laser spot diameter [μm] | 1 |
| Laser wavelength [nm] | 635 |
| Test | fz [mm/tooth] | f [mm/min] | Average Width [mm] | Dev St Width [mm] | Average ap [mm] | Dev St ap [mm] | Experimental rCE1 [mm] |
|---|---|---|---|---|---|---|---|
| 1 | 0.0010 | 64 | 0.7604 | 0.0219 | 0.2607 | 0.0297 | 0.3802 |
| 2 | 0.0045 | 286 | 0.7755 | 0.0073 | 0.2373 | 0.0317 | 0.3878 |
| 3 | 0.0020 | 127 | 0.7816 | 0.0066 | 0.2385 | 0.0204 | 0.3908 |
| 4 | 0.0060 | 382 | 0.7816 | 0.0035 | 0.2502 | 0.0167 | 0.3908 |
| 5 | 0.0025 | 159 | 0.7662 | 0.0058 | 0.2391 | 0.0192 | 0.3831 |
| 6 | 0.0040 | 255 | 0.7792 | 0.0130 | 0.2374 | 0.0100 | 0.3896 |
| 7 | 0.0015 | 95 | 0.7730 | 0.0135 | 0.2545 | 0.0154 | 0.3865 |
| 8 | 0.0030 | 191 | 0.7960 | 0.0242 | 0.2590 | 0.0172 | 0.3980 |
| 9 | 0.0035 | 223 | 0.7896 | 0.0174 | 0.2616 | 0.0173 | 0.3948 |
| 10 | 0.0005 | 32 | 0.7879 | 0.0171 | 0.2641 | 0.0074 | 0.3940 |
| 11 | 0.0065 | 414 | 0.8021 | 0.0055 | 0.2676 | 0.0140 | 0.4010 |
| 12 | 0.0055 | 350 | 0.7829 | 0.0234 | 0.2541 | 0.0072 | 0.3915 |
| 13 | 0.0050 | 318 | 0.7951 | 0.0198 | 0.3119 | 0.0061 | 0.3975 |
| 14 | 0.0070 | 446 | 0.7997 | 0.0272 | 0.2477 | 0.0167 | 0.3998 |
| Test | fz [mm/tooth] | r0 [mm] | γ [rad] |
|---|---|---|---|
| 1 | 0.0010 | 0.014 | 0.032 |
| 2 | 0.0045 | 0.010 | 0.803 |
| 3 | 0.0020 | 0.004 | 0.552 |
| 4 | 0.0060 | 0.004 | 0.557 |
| 5 | 0.0025 | 0.012 | 0.385 |
| 6 | 0.0040 | 0.012 | 1.149 |
| 7 | 0.0015 | 0.008 | 0.057 |
| 8 | 0.0030 | 0.012 | 1.281 |
| 9 | 0.0035 | 0.007 | 1.535 |
| 10 | 0.0005 | 0.004 | 1.440 |
| 11 | 0.0065 | 0.007 | 0.136 |
| 12 | 0.0055 | 0.015 | 1.346 |
| 13 | 0.0050 | 0.008 | 1.195 |
| 14 | 0.0070 | 0.010 | 1.038 |
| Test | fz [mm] | Experimental rCE1 [mm] | Analytical rCE1 [mm] | Δ Variation [mm] | Percentage Error [%] |
|---|---|---|---|---|---|
| 1 | 0.0010 | 0.38018 | 0.39450 | 0.01432 | 3.63% |
| 2 | 0.0045 | 0.38777 | 0.39460 | 0.00683 | 1.73% |
| 3 | 0.0020 | 0.39082 | 0.39452 | 0.00370 | 0.94% |
| 4 | 0.0060 | 0.39078 | 0.39452 | 0.00374 | 0.95% |
| 5 | 0.0025 | 0.38308 | 0.39454 | 0.01146 | 2.91% |
| 6 | 0.0040 | 0.38961 | 0.39470 | 0.00509 | 1.29% |
| 7 | 0.0015 | 0.38651 | 0.39451 | 0.00799 | 2.03% |
| 8 | 0.0030 | 0.39800 | 0.39470 | −0.00330 | −0.84% |
| 9 | 0.0035 | 0.39479 | 0.39458 | −0.00021 | −0.05% |
| 10 | 0.0005 | 0.39397 | 0.39453 | 0.00056 | 0.14% |
| 11 | 0.0065 | 0.40104 | 0.39451 | −0.00653 | −1.65% |
| 12 | 0.0055 | 0.39145 | 0.39484 | 0.00339 | 0.86% |
| 13 | 0.0050 | 0.39754 | 0.39461 | −0.00293 | −0.74% |
| 14 | 0.0070 | 0.39983 | 0.39466 | −0.00517 | −1.31% |
| Test | fz [mm] | 4th Grade rCE1 [mm] | 2nd Grade rCE1 [mm] | Δ Variation % |
|---|---|---|---|---|
| 1 | 0.0010 | 0.39450 | 0.39450 | 0.00007% |
| 2 | 0.0045 | 0.39460 | 0.39453 | 0.01591% |
| 3 | 0.0020 | 0.39452 | 0.39451 | 0.00166% |
| 4 | 0.0060 | 0.39452 | 0.39452 | 0.00173% |
| 5 | 0.0025 | 0.39454 | 0.39452 | 0.00694% |
| 6 | 0.0040 | 0.39470 | 0.39454 | 0.04082% |
| 7 | 0.0015 | 0.39451 | 0.39451 | 0.00007% |
| 8 | 0.0030 | 0.39470 | 0.39454 | 0.04046% |
| 9 | 0.0035 | 0.39458 | 0.39453 | 0.01384% |
| 10 | 0.0005 | 0.39453 | 0.39451 | 0.00568% |
| 11 | 0.0065 | 0.39451 | 0.39451 | 0.00026% |
| 12 | 0.0055 | 0.39484 | 0.39457 | 0.06759% |
| 13 | 0.0050 | 0.39461 | 0.39454 | 0.01814% |
| 14 | 0.0070 | 0.39466 | 0.39456 | 0.02531% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abeni, A.; Cappellini, C.; Seneci, G.; Del Prete, A.; Attanasio, A. Tool Run-Out in Micro-Milling: Development of an Analytical Model Based on Cutting Force Signal Analysis. Micromachines 2024, 15, 305. https://doi.org/10.3390/mi15030305
Abeni A, Cappellini C, Seneci G, Del Prete A, Attanasio A. Tool Run-Out in Micro-Milling: Development of an Analytical Model Based on Cutting Force Signal Analysis. Micromachines. 2024; 15(3):305. https://doi.org/10.3390/mi15030305
Chicago/Turabian StyleAbeni, Andrea, Cristian Cappellini, Greta Seneci, Antonio Del Prete, and Aldo Attanasio. 2024. "Tool Run-Out in Micro-Milling: Development of an Analytical Model Based on Cutting Force Signal Analysis" Micromachines 15, no. 3: 305. https://doi.org/10.3390/mi15030305
APA StyleAbeni, A., Cappellini, C., Seneci, G., Del Prete, A., & Attanasio, A. (2024). Tool Run-Out in Micro-Milling: Development of an Analytical Model Based on Cutting Force Signal Analysis. Micromachines, 15(3), 305. https://doi.org/10.3390/mi15030305








