A Novel Piezoelectric Energy Harvester for Earcanal Dynamic Motion Exploitation Using a Bistable Resonator Cycled by Coupled Hydraulic Valves Made of Collapsed Flexible Tubes
Abstract
:1. Introduction
2. Energy Source and Harvesting Strategy
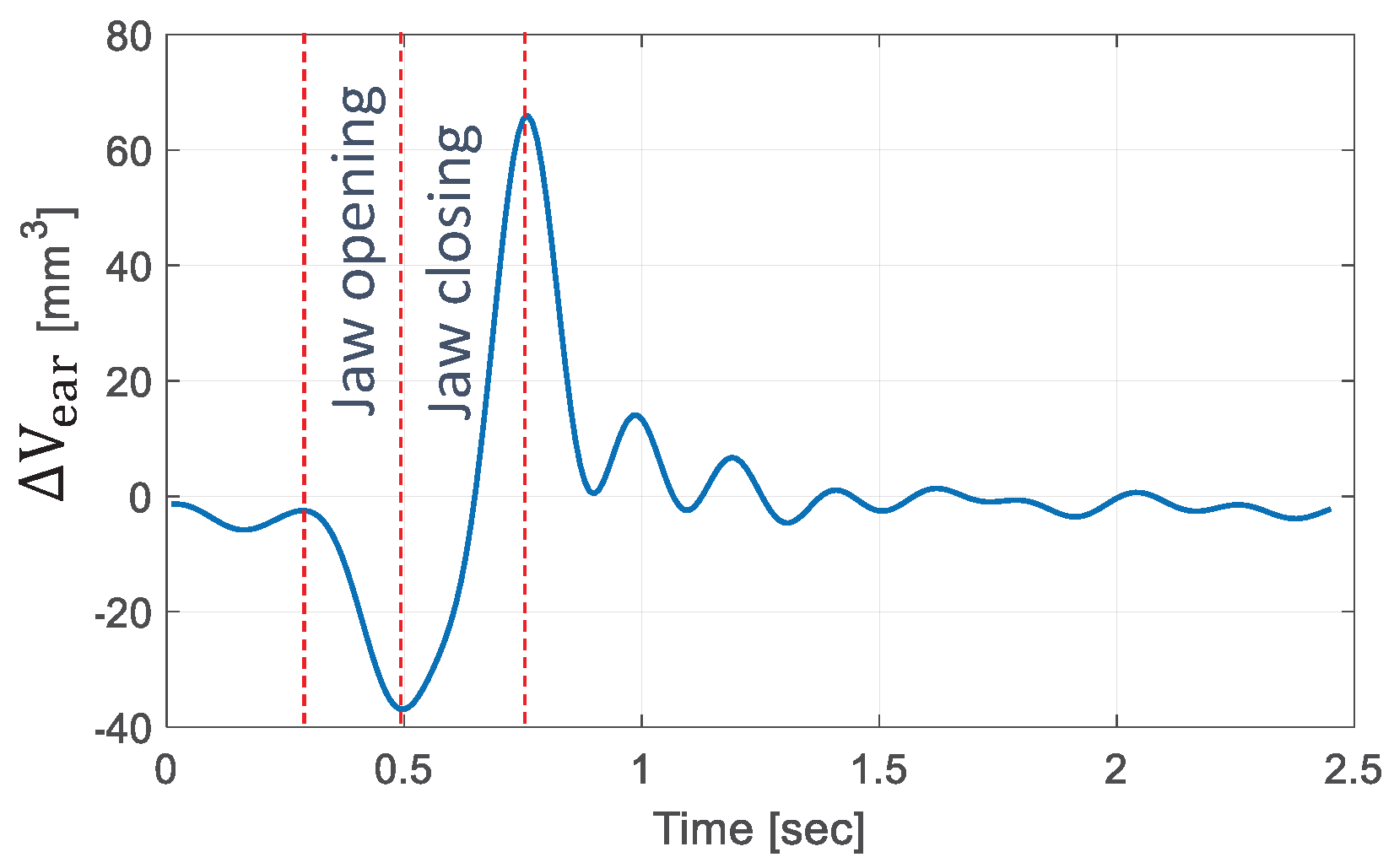
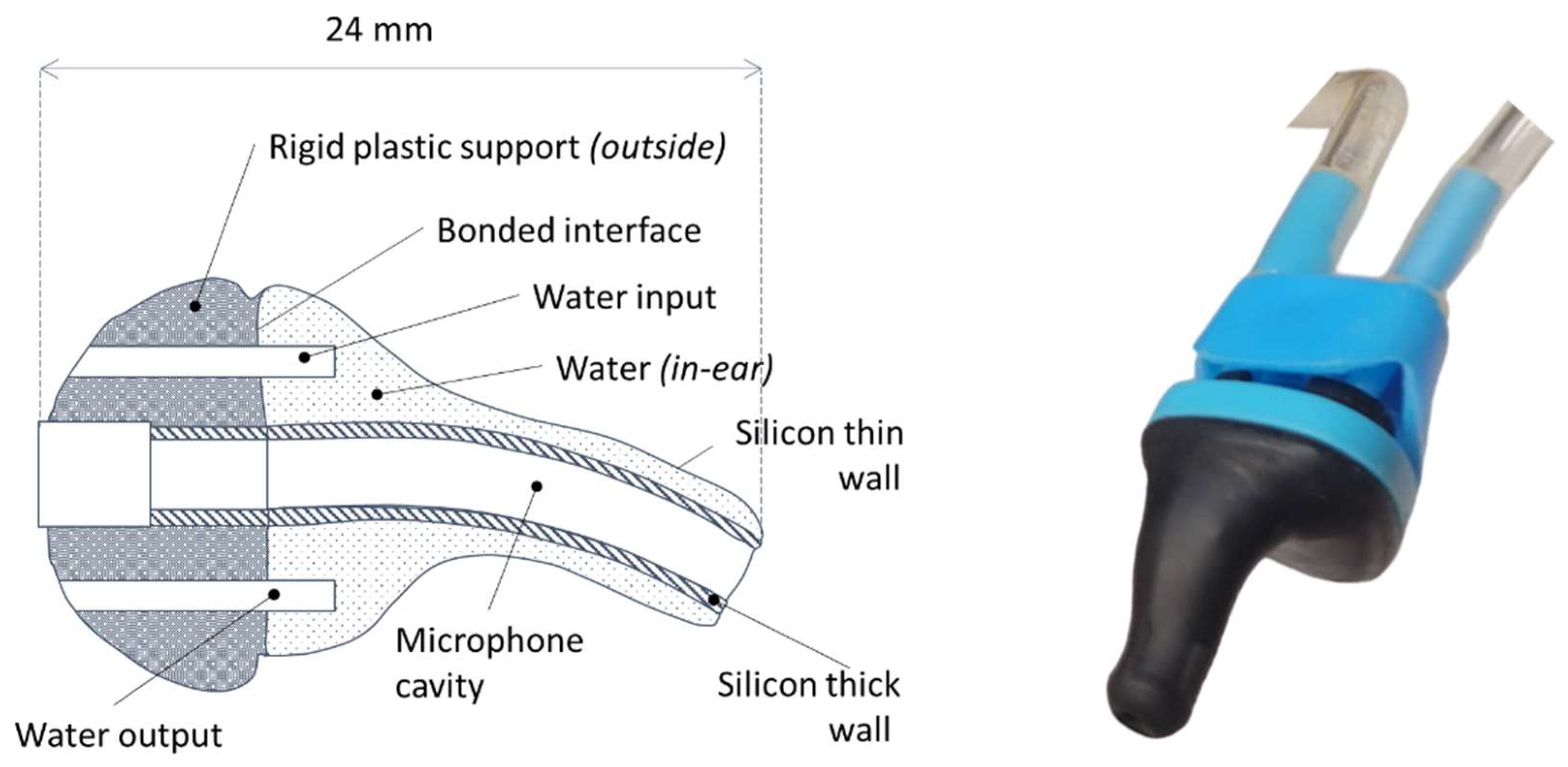
2.1. The Energy Source
2.2. The Energy-Harvesting Strategy
2.2.1. Transducing Method
2.2.2. Power Transmission
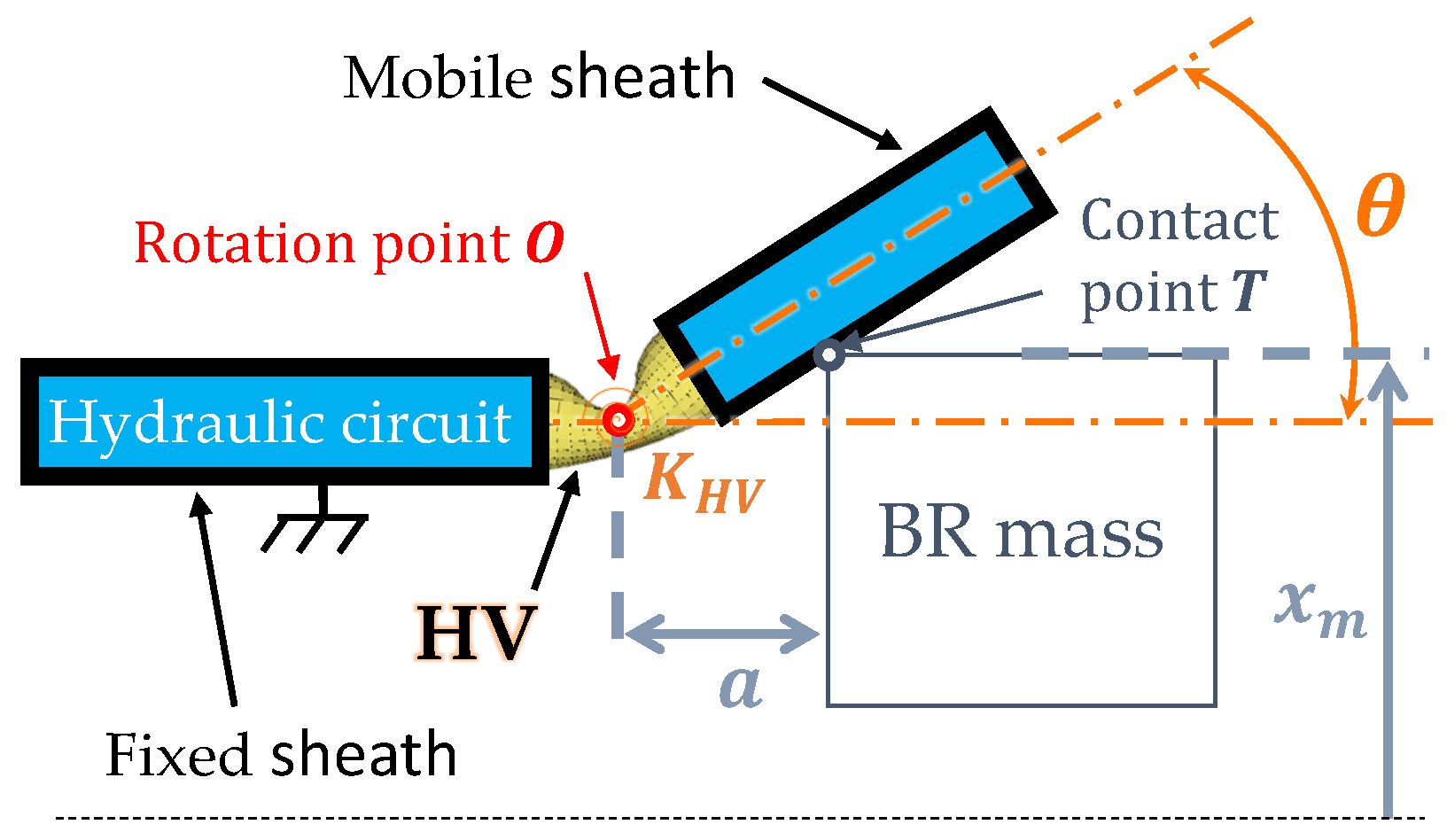
3. Energy Harvester Presentation and Operation Principle
4. System Global Modeling
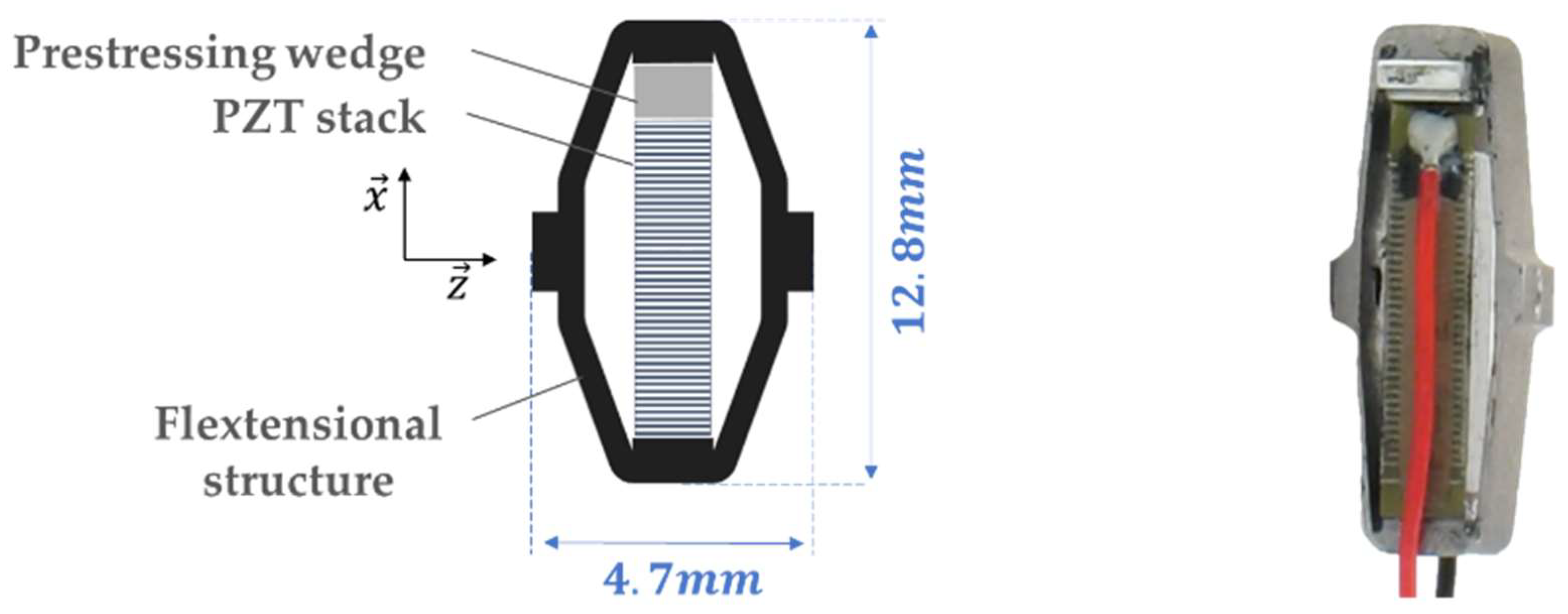
4.1. Modeling of the Electromechanical Converter
- The only mass considered is the BR mass (2).
- All parts are rigid except for the APG (4).
- The hinges are considered elastic: They are defined by their rotational stiffness
- The mechanical damping of the hinges is included in the global viscous damping coefficient .
- .
- The contact between the BR mass (2) and the HC piston head (5) is considered permanent for .
4.2. Modeling of the Hydraulic Circuit
- The flow is incompressible and Newtonian.
- The hydraulic circuit is rigid (no volume change) and there is no leakage.
- The hydraulic actuation is considered quasi-static considering the oscillation frequency of the BR.
5. Numerical Model and Simulations
5.1. Setting the EH Parameters
- The transducer is a APA50XS piezoelectric actuator (Cedrat Technologies, Meylan, France) exploited as a generator [47].
- The hydraulic actuation is ensured by the SMC MQP4-10S HCs, which can operate at 1 kPa pressure [53].
- The usual size of a hearing aid case is 50 × 20 × 10 mm [54]. The mm parameter is chosen to be consistent with this scale.
5.2. Targeted Hydraulic Behavior of the HVs
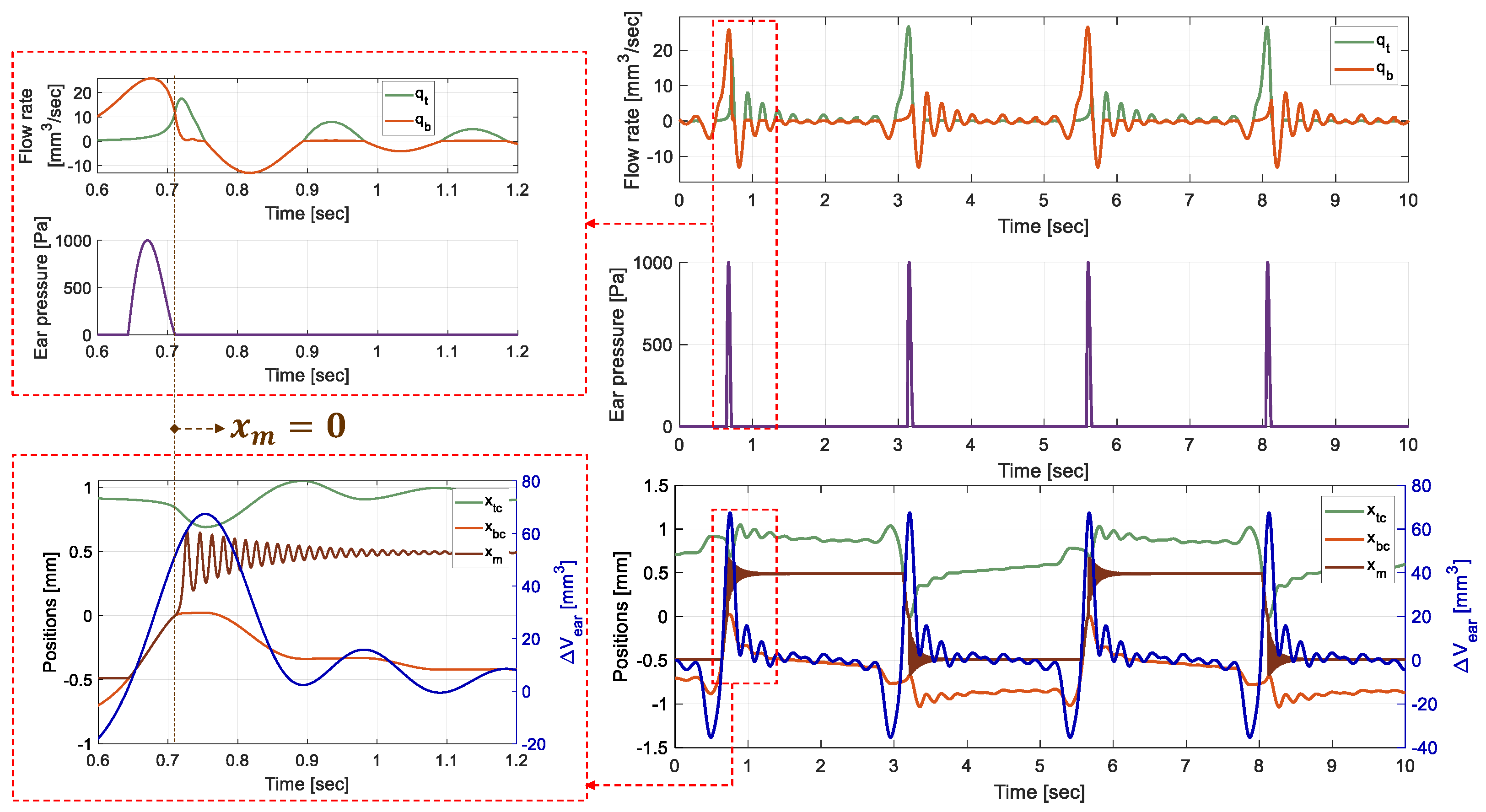
5.3. Simulation Results
- The mass is at the “bottom” equilibrium position .
- The “top” HV is closed () and the “bottom” side HV is opened ().
- There is no contact between the mass and the HCs.
6. Experimental Characterizations of the Electromechanical Converter
6.1. Description of the Electromechanical Converter
6.2. Designing the BR Beams
6.3. Experimental Characterizations
6.4. Analysis and Summary
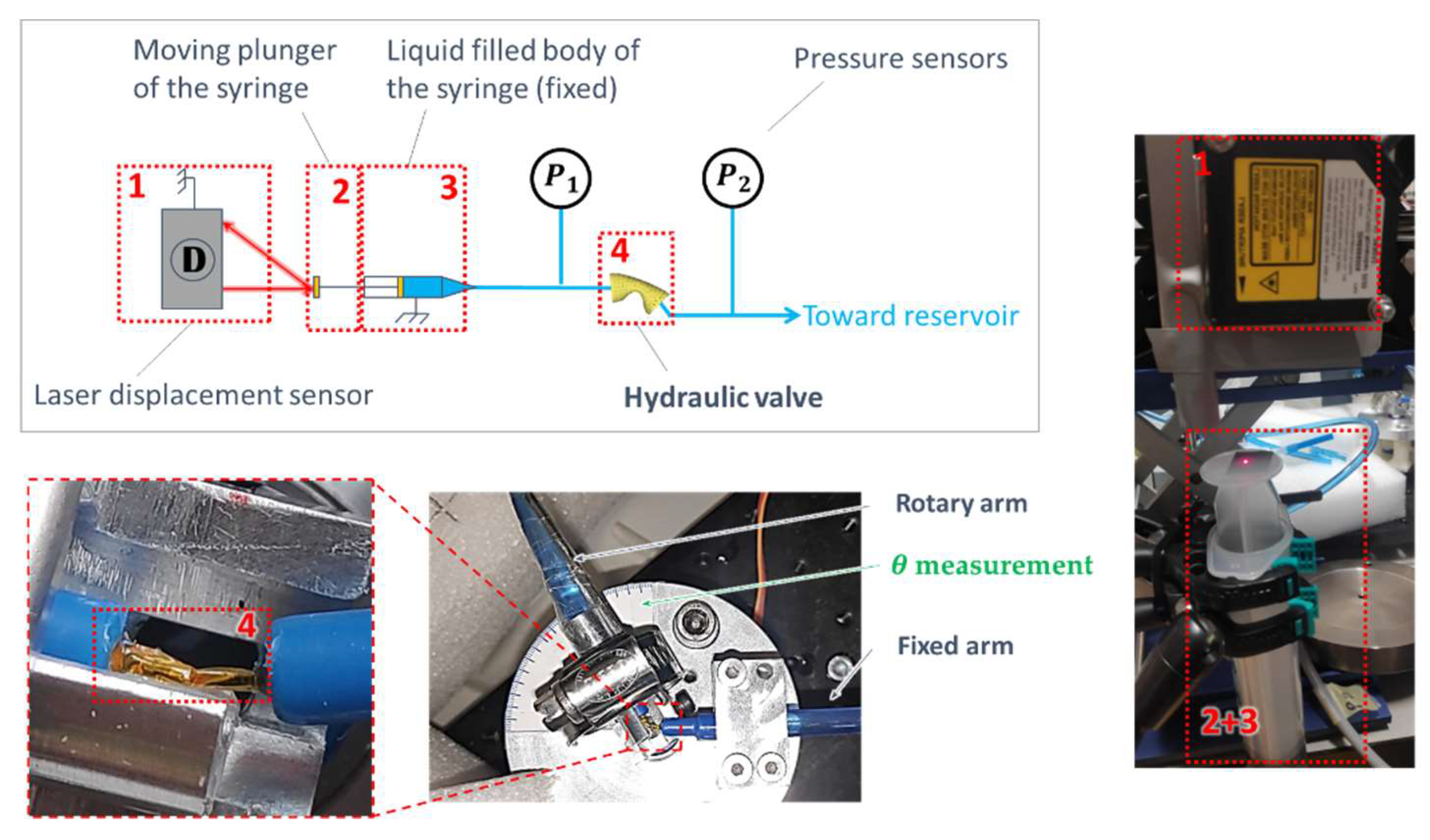
7. Experimental Approach of the HV Design
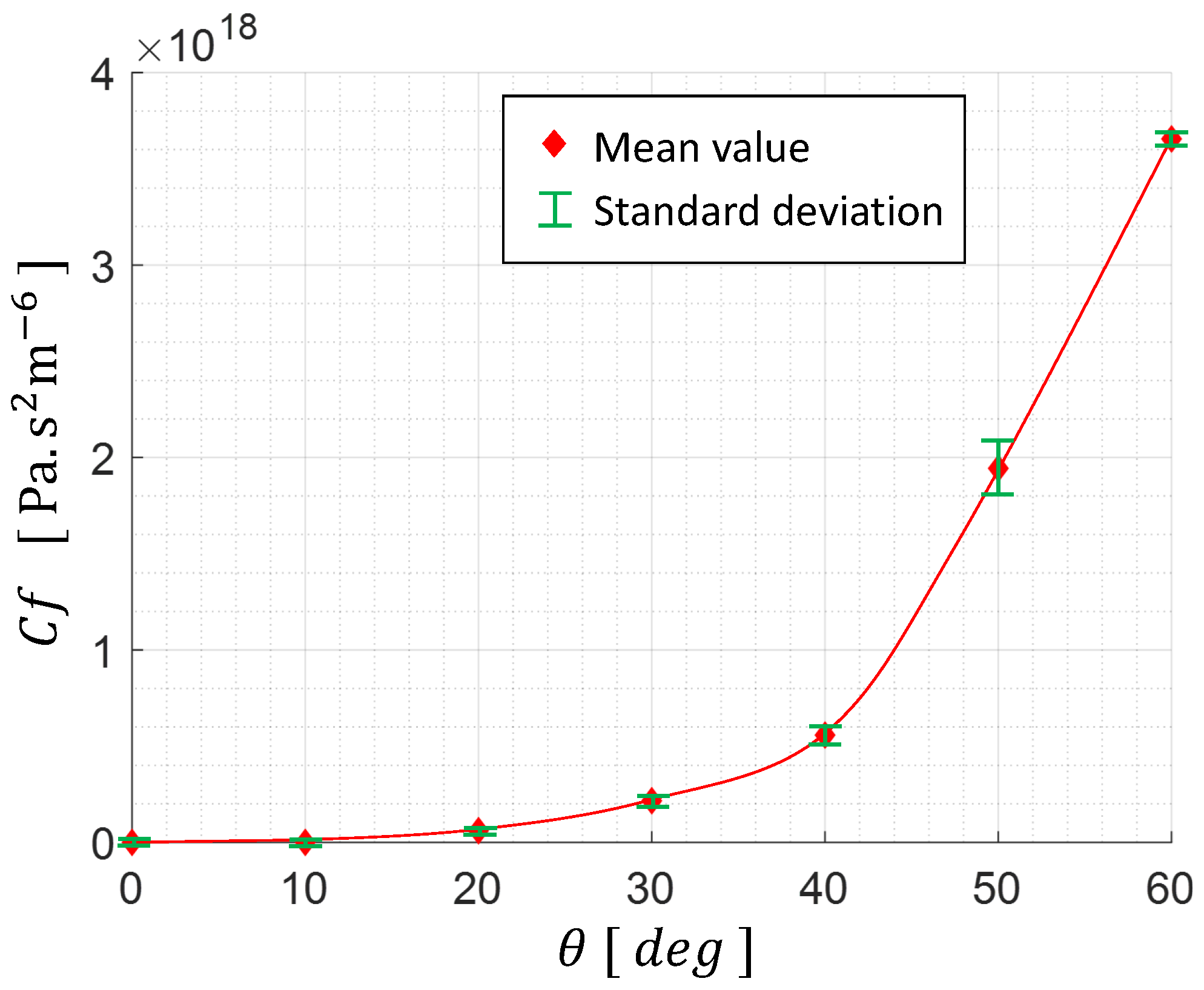
HV Hydraulic Experimental Characterization
8. Global Model Recalibration with Experimental Data
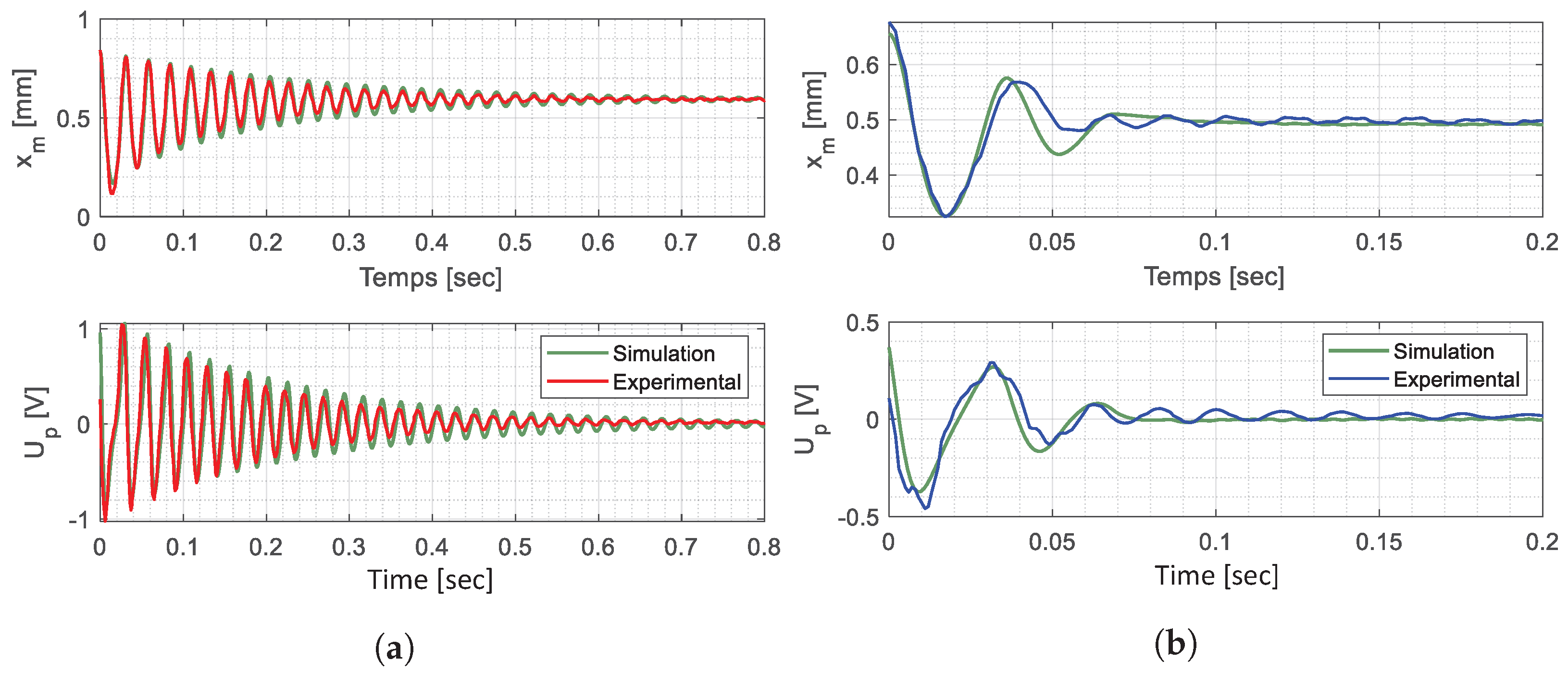
8.1. Recalibration with Release Trials
8.2. Analysis and Discussion
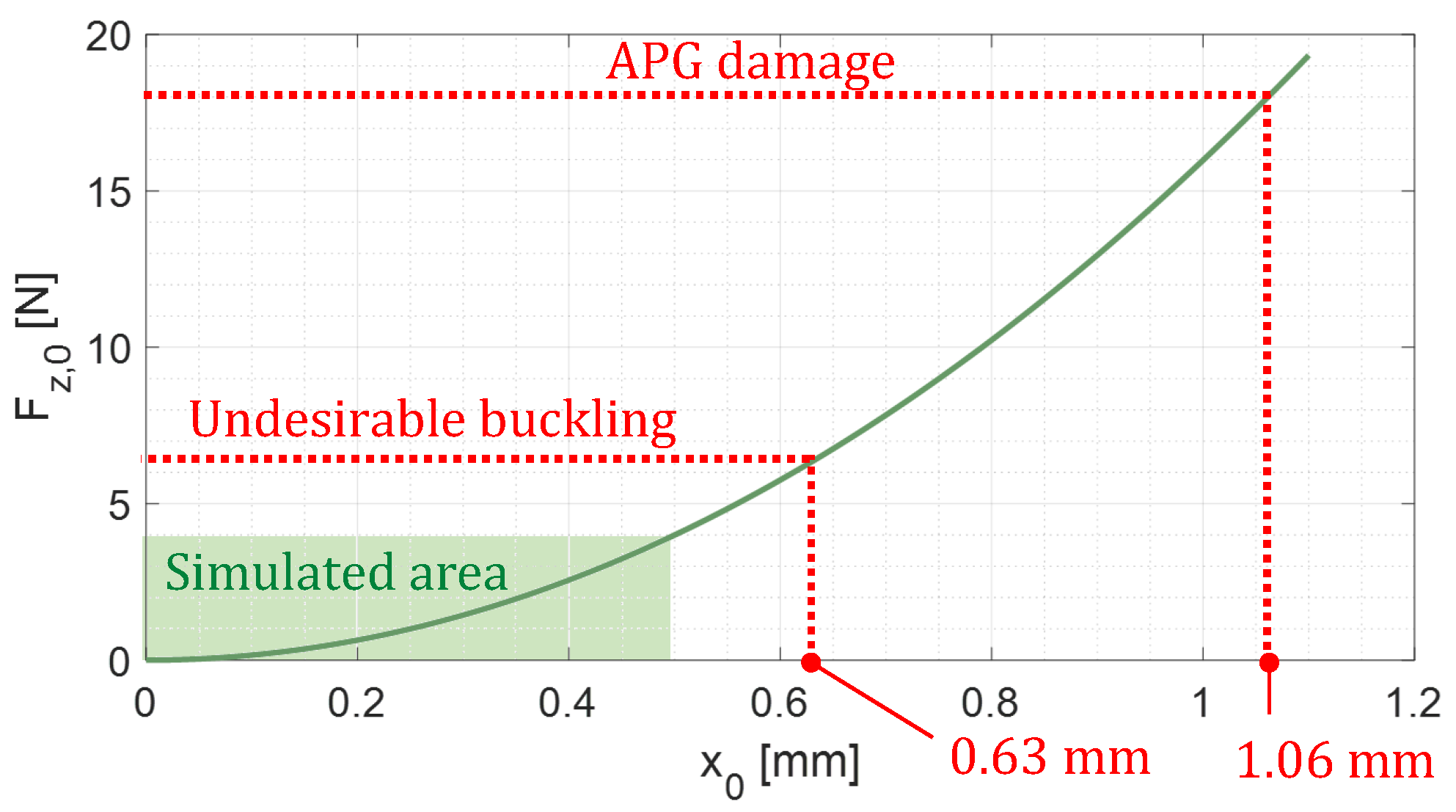
8.3. Directions for Improvements
- The resonator stays bistable with the influence of .
- No mass-piston collision during the oscillation phase.
8.4. Power Capability of the Proposed Energy Harvester
9. Future Work
9.1. Integration Issues
9.1.1. Bio-Compatibility
9.1.2. Power Management and Storage
9.1.3. Geometrical Design
9.2. Other Applications
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Subscripts | |
| APG | Amplified piezoelectric generator |
| BB | Buckled beam |
| BR | Bistable resonator |
| GB | Guide beam |
| EH | Energy harvester |
| HA | Hydraulic amplifier |
| HC | Hydraulic cylinder |
| HFT | High frequency transducer |
| HV | Hydraulic valve |
| LFA | Low frequency absorber |
| PFF | Piezoelectric force factor |
| Roman letters | |
| a [m] | HV bending lever arm |
| [-] | Hydraulic amplification level |
| [Pa·s2·m−6] | Pressure loss coefficient |
| [Pa·s2·m−6] | Opened HV pressure loss coefficient |
| [Pa·s2·m−6] | Closed HV pressure loss coefficient |
| [F] | APG internal capacity |
| D [m] | Diameter of a random tube |
| [m] | Hydraulic diameter of the HV |
| [m] | Hydraulic cylinder internal diameter |
| [m] | HV rigid sheath diameter |
| [m] | Kapton tube initial diameter |
| [J] | Global dissipated energy |
| [J] | Harvested electric energy |
| [J] | Available hydraulic energy from earplug |
| [N] | BR counter reaction force |
| [Hz] | BR natural resonance frequency |
| [-] | Dry friction loss coefficient |
| K [N/m] | APG stiffness |
| [N/m] | 8 BB’s stiffness |
| [N/m] | Equivalent stiffness seen from the APG |
| [N/m] | GB stiffness |
| [N/m/rad] | HV stiffness |
| [N/m] | Spring stiffness |
| [N/m/rad] | Single hinge stiffness |
| [-] | APG electromechanical coupling coefficient |
| [-] | Global electromechanical coupling coefficient |
| L [m] | Distance between 2 BR adjacent hinges on axis |
| [m] | Distance between 2 BR adjacent hinges |
| m [kg] | BR dynamic mass |
| [Pa] | Comfort pressure |
| [Pa] | Hydraulic cylinder internal pressure |
| [W] | Harvested electric power |
| q [m3/s] | Flow rate |
| [m3/s] | Flow rate of the fluid exiting the earplug |
| Q [-] | BR quality factor |
| [-] | Hydraulic restriction coefficient |
| [Ω] | Load resistance |
| [−] | Reynolds number |
| [Pa] | Hydraulic cylinder internal section |
| [m] | BR mass position |
| [m] | HC piston position |
| [m] | BR mass position |
| [m] | BR buckling height |
| [V] | APG tension |
| Greek letters | |
| [N/V] | Piezoelectric force coefficient |
| [Pa] | Earplug pressure variation |
| [m3] | Earplug volume variation |
| [-] | BR buckling level |
| [-] | BR energy conversion efficiency |
| [-] | EH energy conversion efficiency |
| [rad] | HV bending angle |
| [N·s/m] | Air dynamic viscosity |
| [N·s/m] | Water dynamic viscosity |
| [N·s/m] | HC viscous loss coefficient |
| [kg/m3] | Water density |
| [rad] | BR hinge rotational angle |
| [rad/s] | BR natural angular frequency |
| Indexes | |
| Active hydraulic branch | |
| Bottom side hydraulic branch () | |
| Closed HV state | |
| Inactive hydraulic branch () | |
| Opened HV state | |
| Top side hydraulic branch | |
| Upper value | |
| Lowest value |
References
- Scherer, M.; Menachery, K.; Magno, M. SmartAid: A Low-Power Smart Hearing Aid for Stutterers. In Proceedings of the SAS 2019-2019 IEEE Sensors Applications Symposium, Conference Proceedings, Sophia Antipolis, France, 11–13 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Yip, M.; Jin, R.; Nakajima, H.H.; Stankovic, K.M.; Chandrakasan, A.P. A fully-implantable cochlear implant SoC with piezoelectric middle-ear sensor and arbitrary waveform neural stimulation. IEEE J. Solid-State Circuits 2015, 50, 214–229. [Google Scholar] [CrossRef]
- Kulah, H.; Ulusah, H.; Chamanian, S.; Batu, A.; Ugur, M.B.; Yuksel, M.B.; Yilmaz, A.M.; Yigit, H.A.; Koyuncuoglu, A.; Topcu, O.; et al. A Fully-Implantable Mems-Based Autonomous Cochlear Implant. In Proceedings of the IEEE Symposium on Mass Storage Systems and Technologies, Tokyo, Japan, 9–13 January 2022; pp. 396–399. [Google Scholar] [CrossRef]
- Woodruff, T.A.; DiFrancesco, J.; Kurth, M.; Marinelli, A.; Cienkowski, K.M. Disposable Hearing Aid Battery Management: Survey Assessment of Providers and Qualitative Interviews of Patients. Am. J. Audiol. 2021, 30, 730–744. [Google Scholar] [CrossRef]
- Picou, E.M. Hearing Aid Benefit and Satisfaction Results from the MarkeTrak 2022 Survey: Importance of Features and Hearing Care Professionals. Semin. Hear. 2022, 4, 301–316. [Google Scholar] [CrossRef]
- Mercier, P.P.; Lysaght, A.C.; Bandyopadhyay, S.; Chandrakasan, A.P.; Stankovic, K.M. Energy extraction from the biologic battery in the inner ear. Nat. Biotechnol. 2012, 30, 1240–1243. [Google Scholar] [CrossRef]
- Azimi, S.; Golabchi, A.; Nekookar, A.; Rabbani, S.; Amiri, M.H.; Asadi, K.; Abolhasani, M.M. Self-powered cardiac pacemaker by piezoelectric polymer nanogenerator implant. Nano Energy 2021, 83, 105781. [Google Scholar] [CrossRef]
- Smilek, J.; Hadas, Z. A study of kinetic energy harvesting for biomedical application in the head area. Microsyst. Technol. 2016, 22, 1535–1547. [Google Scholar] [CrossRef]
- Kim, S.J.; We, J.H.; Cho, B.J. A wearable thermoelectric generator fabricated on a glass fabric. Energy Environ. Sci. 2014, 7, 1959–1965. [Google Scholar] [CrossRef]
- Jin, C.; Dong, L.; Xu, Z.; Closson, A.; Cabe, A.; Gruslova, A.; Jenney, S.; Escobedo, D.; Elliott, J.; Zhang, M.; et al. Skin-like Elastomer Embedded Zinc Oxide Nanoarrays for Biomechanical Energy Harvesting. Adv. Mater. Interfaces 2021, 8, 2100094. [Google Scholar] [CrossRef]
- Ali, A.; Shaukat, H.; Bibi, S.; Altabey, W.A.; Noori, M.; Kouritem, S.A. Recent progress in energy harvesting systems for wearable technology. Energy Strategy Rev. 2023, 49, 101124. [Google Scholar] [CrossRef]
- Latif, R.; Noor, M.M.; Yunas, J.; Hamzah, A.A. Mechanical Energy Sensing and Harvesting in Micromachined Polymer-Based Piezoelectric Transducers for Fully Implanted Hearing Systems: A Review. Polymers 2021, 13, 2276. [Google Scholar] [CrossRef]
- Delnavaz, A.; Voix, J. Micro-Power Energy Harvesting for In-Ear Devices. In Proceedings of the PowerMEMS 2012, Atlanta, GA, USA, 2–5 December 2012; pp. 488–491. [Google Scholar]
- Carioli, J.; Delnavaz, A.; Zednik, R.J.; Voix, J. Power capacity from earcanal dynamic motion. AIP Adv. 2016, 6, 125203. [Google Scholar] [CrossRef]
- Delnavaz, A.; Voix, J. Piezo-earpiece for micro-power generation from earcanal dynamic motion. J. Micromech. Microeng. 2013, 23, 114001. [Google Scholar] [CrossRef]
- Kulah, H.; Najafi, K. Energy Scavenging from Low-Frequency Vibrations by Using Frequency Up-Conversion for Wireless Sensor Applications. IEEE Sens. J. 2008, 8, 261–268. [Google Scholar] [CrossRef]
- Priya, S.; Song, H.C.; Zhou, Y.; Varghese, R.; Chopra, A.; Kim, S.G.; Kanno, I.; Wu, L.; Ha, D.S.; Ryu, J.; et al. A Review on Piezoelectric Energy Harvesting: Materials, Methods, and Circuits. Energy Harvest. Syst. 2017, 4, 3–39. [Google Scholar] [CrossRef]
- Ashraf, K.; Khir, M.H.M.; Dennis, J.O. Energy harvesting in a low frequency environment. In Proceedings of the 2011 National Postgraduate Conference-Energy and Sustainability: Exploring the Innovative Minds, NPC 2011, Perak, Malaysia, 19–20 September 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Marin, A.; Bressers, S.; Priya, S. Multiple cell configuration electromagnetic vibration energy harvester. J. Phys. D Appl. Phys. 2011, 44, 295501. [Google Scholar] [CrossRef]
- Turcot, M.C.; Voix, J. Pressure Regulation Mechanism for Inflatable in-Ear Device. WO. WO2011041900A1, 14 April 2011. [Google Scholar]
- Bouchard-Roy, J.; Delnavaz, A.; Voix, J. In-Ear Energy Harvesting: Evaluation of the Power Capability of the Temporomandibular Joint. IEEE Sens. J. 2020, 20, 6338–6345. [Google Scholar] [CrossRef]
- Goll, E.; Zenner, H.P.; Dalhoff, E. Upper bounds for energy harvesting in the region of the human head. IEEE Trans. Biomed. Eng. 2011, 58, 3097–3103. [Google Scholar] [CrossRef]
- Mehl, M.R.; Vazire, S.; Ramírez-Esparza, N.; Slatcher, R.B.; Pennebaker, J.W. Are Women Really More Talkative Than Men? Science 2007, 317, 82. [Google Scholar] [CrossRef]
- Allison, K.M.; Yunusova, Y.; Green, J.R. Shorter Sentence Length Maximizes Intelligibility and Speech Motor Performance in Persons with Dysarthria Due to Amyotrophic Lateral Sclerosis. Am. J. Speech-Lang. Pathol. 2019, 28, 96–107. [Google Scholar] [CrossRef]
- Hinderink, E.B.A.; Avison, S.; Boom, R.; Bodnár, I. Dynamic flavor release from chewing gum: Mechanisms of release. Food Res. Int. 2019, 116, 717–723. [Google Scholar] [CrossRef]
- Cǎruntu, G.; Dragomirescu, O. The non-linearity of magnetic sensors. In Proceedings of the International Semiconductor Conference, CAS, Sinaia, Romania, 9–13 October 2001; Volume 2, pp. 375–378. [Google Scholar]
- Yildirim, T.; Ghayesh, M.H.; Li, W.; Alici, G. A review on performance enhancement techniques for ambient vibration energy harvesters. Renew. Sustain. Energy Rev. 2017, 71, 435–449. [Google Scholar] [CrossRef]
- Karadag, C.V.; Topaloglu, N. A Self-Sufficient and Frequency Tunable Piezoelectric Vibration Energy Harvester. J. Vib. Acoust. 2017, 139, 011013. [Google Scholar] [CrossRef]
- Abouzarkhanifard, A.; Chimeh, H.E.; Janaideh, M.A.; Zhang, L. FEM-Inclusive Transfer Learning for Bistable Piezoelectric MEMS Energy Harvester Design. IEEE Sens. J. 2023, 23, 3521–3531. [Google Scholar] [CrossRef]
- Masara, D.O.; El Gamal, H.; Mokhiamar, O. Split Cantilever Multi-Resonant Piezoelectric Energy Harvester for Low-Frequency Application. Energies 2021, 14, 5077. [Google Scholar] [CrossRef]
- Qi, N.; Dai, K.; Wang, X.; You, Z. Optimization for piezoelectric energy harvesters with self-coupled structure: A double kill in bandwidth and power. Nano Energy 2022, 102, 107602. [Google Scholar] [CrossRef]
- Morel, A.; Brenes, A.; Gibus, D.; Lefeuvre, E.; Gasnier, P.; Pillonnet, G.; Badel, A. A comparative study of electrical interfaces for tunable piezoelectric vibration energy harvesting. Smart Mater. Struct. 2022, 31, 045016. [Google Scholar] [CrossRef]
- Richards, C.D.; Anderson, M.J.; Bahr, D.F.; Richards, R.F. Efficiency of energy conversion for devices containing a piezoelectric component. J. Micromech. Microeng. 2004, 14, 717–721. [Google Scholar] [CrossRef]
- Morris, D.J.; Youngsman, J.M.; Anderson, M.J.; Bahr, D.F. A resonant frequency tunable, extensional mode piezoelectric vibration harvesting mechanism. Smart Mater. Struct. 2008, 17, 065021. [Google Scholar] [CrossRef]
- Gibus, D.; Gasnier, P.; Morel, A.; Formosa, F.; Charleux, L.; Boisseau, S.; Pillonnet, G.; Berlitz, C.A.; Quelen, A.; Badel, A. Strongly coupled piezoelectric cantilevers for broadband vibration energy harvesting. Appl. Energy 2020, 277, 115518. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Wang, K.; Chang, Y.; Xu, D.; Wen, G. Bio-inspired bistable piezoelectric vibration energy harvester: Design and experimental investigation. Energy 2021, 228, 120595. [Google Scholar] [CrossRef]
- Peng, Y.; Xu, Z.; Wang, M.; Li, Z.; Peng, J.; Luo, J.; Xie, S.; Pu, H.; Yang, Z. Investigation of frequency-up conversion effect on the performance improvement of stack-based piezoelectric generators. Renew. Energy 2021, 172, 551–563. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, J.; Hu, S.; Rao, J.; Theodossiades, S. A multi-stable ultra-low frequency energy harvester using a nonlinear pendulum and piezoelectric transduction for self-powered sensing. Mech. Syst. Signal Process. 2023, 189, 110034. [Google Scholar] [CrossRef]
- Tang, H.; Hua, C.; Huang, H.; Liu, W.; Yang, Z.; Yuan, Y.; Zhang, Z. Low-frequency vibration energy harvesting: A comprehensive review of frequency up-conversion approaches. Smart Mater. Struct. 2022, 31, 103001. [Google Scholar] [CrossRef]
- Chamanyeta, H.N.; Fath El-Bab, A.M.R.; Ikua, B.W.; Murimi, E. Development of a varying multi-cantilever beam frequency up conversion energy harvester. Energy Convers. Manag. X 2022, 16, 100290. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Z.; Jiang, X.; Peng, Y.; Zhu, C.; Li, Z. Experimental investigation on performance improvement of cantilever piezoelectric energy harvesters via escapement mechanism from extremely Low-Frequency excitations. Sustain. Energy Technol. Assess. 2022, 53, 102591. [Google Scholar] [CrossRef]
- Baù, M.; Alghisi, D.; Dalola, S.; Ferrari, M.; Ferrari, V. Multi-frequency array of nonlinear piezoelectric converters for vibration energy harvesting. Smart Mater. Struct. 2020, 29, 085047. [Google Scholar] [CrossRef]
- Atmeh, M.; Ibrahim, A.; Ramini, A. Static and Dynamic Analysis of a Bistable Frequency Up-Converter Piezoelectric Energy Harvester. Micromachines 2023, 14, 261. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Lallart, M. Parametric analysis for optimized piezoelectric bistable vibration energy harvesters. Smart Mater. Struct. 2019, 28, 115009. [Google Scholar] [CrossRef]
- Abdelnaby, M.A.; Arafa, M. Motion amplification using a flextensional compliant mechanism for enhanced energy harvesting. Act. Passiv. Smart Struct. Integr. Syst. 2016 2016, 9799, 97990M. [Google Scholar] [CrossRef]
- Aubert & Duval APX4 Steel Datasheet. 75015 Paris, France. Available online: https://www.aubertduval.com/wp-media/uploads/sites/2/2017/06/APX4_GB-1.pdf (accessed on 5 August 2023).
- Cedrat Technologies APA50XS Product Web Page. 38240 Meylan, France. Available online: https://cedrat-technologies.com/produit/apa50xs/ (accessed on 5 August 2023).
- Zhou, W.; Zuo, L. A Novel Piezoelectric Multilayer Stack Energy Harvester with Force Amplification. In Proceedings of the Volume 8: 22nd Reliability, Stress Analysis, and Failure Prevention Conference; 25th Conference on Mechanical Vibration and Noise, Portland, OR, USA, 4–7 August 2013; p. V008T13A095. [Google Scholar] [CrossRef]
- Wang, Y.; Toyoda, K.; Uesugi, K.; Morishima, K. A simple micro check valve using a photo-patterned hydrogel valve core. Sens. Actuators A Phys. 2020, 304, 111878. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, H.; Zhu, S.; Pan, G. Research on a hydraulic displacement amplifier for a piezoactuator. J. Phys. Conf. Ser. 2021, 1985. [Google Scholar] [CrossRef]
- Zhu, R.; Malisauskaite, A.; Mescheder, U.; Wallrabe, U. Proof of Concept and Properties of Micro Hydraulic Displacement Amplifier. In Proceedings of the COSMOL Conference in Rotterdam, Rotterdam, The Netherlands, 23–25 October 2013; pp. 1–5. [Google Scholar]
- Liu, W.Q.; Badel, A.; Formosa, F.; Wu, Y.P.; Agbossou, A. Novel piezoelectric bistable oscillator architecture for wideband vibration energy harvesting. Smart Mater. Struct. 2013, 22, 035013. [Google Scholar] [CrossRef]
- SMC. SMC MQP-10S Hydraulic Cylinder Product Page. Available online: https://www.smcusa.com/products/mqp-single-acting-metal-seal-low-friction~32040 (accessed on 5 August 2023).
- Resound. ReSound LiNX Quattro Hearing Aids Datasheets. Available online: https://pro.resound.com/en-us/products/support-materials/linx-quattro-support (accessed on 5 August 2023).
- Clinard, C.G.; Piker, E.G.; Thorne, A.P.; Surface, E.N.; Anderson, A.E.; Beacham, V.A.; Crouse, M.C.; Whitney, V.H.; Depaolis, R.A. Maximum Output and Low-Frequency Limitations of B71 and B81 Clinical Bone Vibrators: Implications for Vestibular Evoked Potentials. Ear Hear. 2020, 41, 847. [Google Scholar] [CrossRef]
- Dupont Kapton. DuPont Kapton HN Kapton Datasheet. Available online: https://www.dupont.com/electronics-industrial/kapton-hn.html (accessed on 5 August 2023).
- Nosonovsky, M.; Kailas, S.V.; Editors, M.R.L. Tribology for Scientists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013; p. 459. [Google Scholar] [CrossRef]
- Kim, S.B.; Park, H.; Kim, S.H.; Wikle, H.C.; Park, J.H.; Kim, D.J. Comparison of MEMS PZT Cantilevers Based on d31 and d33 Modes for Vibration Energy Harvesting. J. Microelectromech. Syst. 2013, 22, 26–33. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, S.; Yang, Z.; Guo, T.; Mei, X. High-performance low-frequency bistable vibration energy harvesting plate with tip mass blocks. Energy 2019, 180, 737–750. [Google Scholar] [CrossRef]
- Catacuzzeno, L.; Orfei, F.; Di Michele, A.; Sforna, L.; Franciolini, F.; Gammaitoni, L. Energy harvesting from a bio cell. Nano Energy 2019, 56, 823–827. [Google Scholar] [CrossRef]
- Montero, K.L.; Laurila, M.M.; Mantysalo, M. Fully Printed Unobtrusive and Skin-conformable Piezoelectric Energy Harvester. In Proceedings of the 2021 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Manchester, UK, 20–23 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Han, S.A.; Naqi, M.; Kim, S.; Kim, J.H. All-day wearable health monitoring system. EcoMat 2022, 4, e12198. [Google Scholar] [CrossRef]
- Koyuncuoğlu, A.; İlik, B.; Chamanian, S.; Uluşan, H.; Ashrafi, P.; Işık, D.; Külah, H. Bulk PZT Cantilever Based MEMS Acoustic Transducer for Cochlear Implant Applications. Proceedings 2017, 1, 584. [Google Scholar] [CrossRef]
- Palosaari, J.; Leinonen, M.; Hannu, J.; Juuti, J.; Jantunen, H. Energy harvesting with a cymbal type piezoelectric transducer from low frequency compression. J. Electroceram. 2012, 28, 214–219. [Google Scholar] [CrossRef]
- Li, H.; Lu, J.; Myjak, M.J.; Liss, S.A.; Brown, R.S.; Tian, C.; Deng, Z.D. An implantable biomechanical energy harvester for animal monitoring devices. Nano Energy 2022, 98, 107290. [Google Scholar] [CrossRef]
- Gupta, S.; Fatma, B.; Bhunia, R.; Prateek; Gupta, R.K.; Garg, A. 7-Biomechanical energy harvesting with piezoelectric materials. In Ferroelectric Materials for Energy Harvesting and Storage; Maurya, D., Pramanick, A., Viehland, D., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Shaston, UK, 2021; pp. 209–247. [Google Scholar] [CrossRef]
- Chamanian, S.; Muhtaroğlu, A.; Külah, H. A Self-Adapting Synchronized-Switch Interface Circuit for Piezoelectric Energy Harvesters. IEEE Trans. Power Electron. 2020, 35, 901–912. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, T.; Zhang, M.; Bowen, C.R.; Yang, Y. Recent Progress in Hybridized Nanogenerators for Energy Scavenging. iScience 2020, 23, 101689. [Google Scholar] [CrossRef] [PubMed]
- AlShuhail, A.S.; Bhatia, S.; Kumar, A.; Bhushan, B. Zigbee-Based Low Power Consumption Wearables Device for Voice Data Transmission. Sustainability 2022, 14, 10847. [Google Scholar] [CrossRef]
- Shaik, M.F.; Subashini, M.M.; Swathi, N. Implementation of a ZigBee Based Network for WBAN. In Proceedings of the 2021 7th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 19–20 March 2021; Volume 1, pp. 188–192. [Google Scholar] [CrossRef]
- Chen, X.; Breiholz, J.; Yahya, F.B.; Lukas, C.J.; Kim, H.S.; Calhoun, B.H.; Wentzloff, D.D. Analysis and Design of an Ultra-Low-Power Bluetooth Low-Energy Transmitter With Ring Oscillator-Based ADPLL and 4× Frequency Edge Combiner. IEEE J. Solid-State Circuits 2019, 54, 1339–1350. [Google Scholar] [CrossRef]
- Ryu, H.; Yoon, H.J.; Kim, S.W. Hybrid Energy Harvesters: Toward Sustainable Energy Harvesting. Adv. Mater. 2019, 31, 1802898. [Google Scholar] [CrossRef] [PubMed]
- Thielen, M.; Kara, G.; Unkovic, I.; Majoe, D.; Hierold, C. Thermal Harvesting Potential of the Human Body. J. Electron. Mater. 2018, 47, 3307–3313. [Google Scholar] [CrossRef]
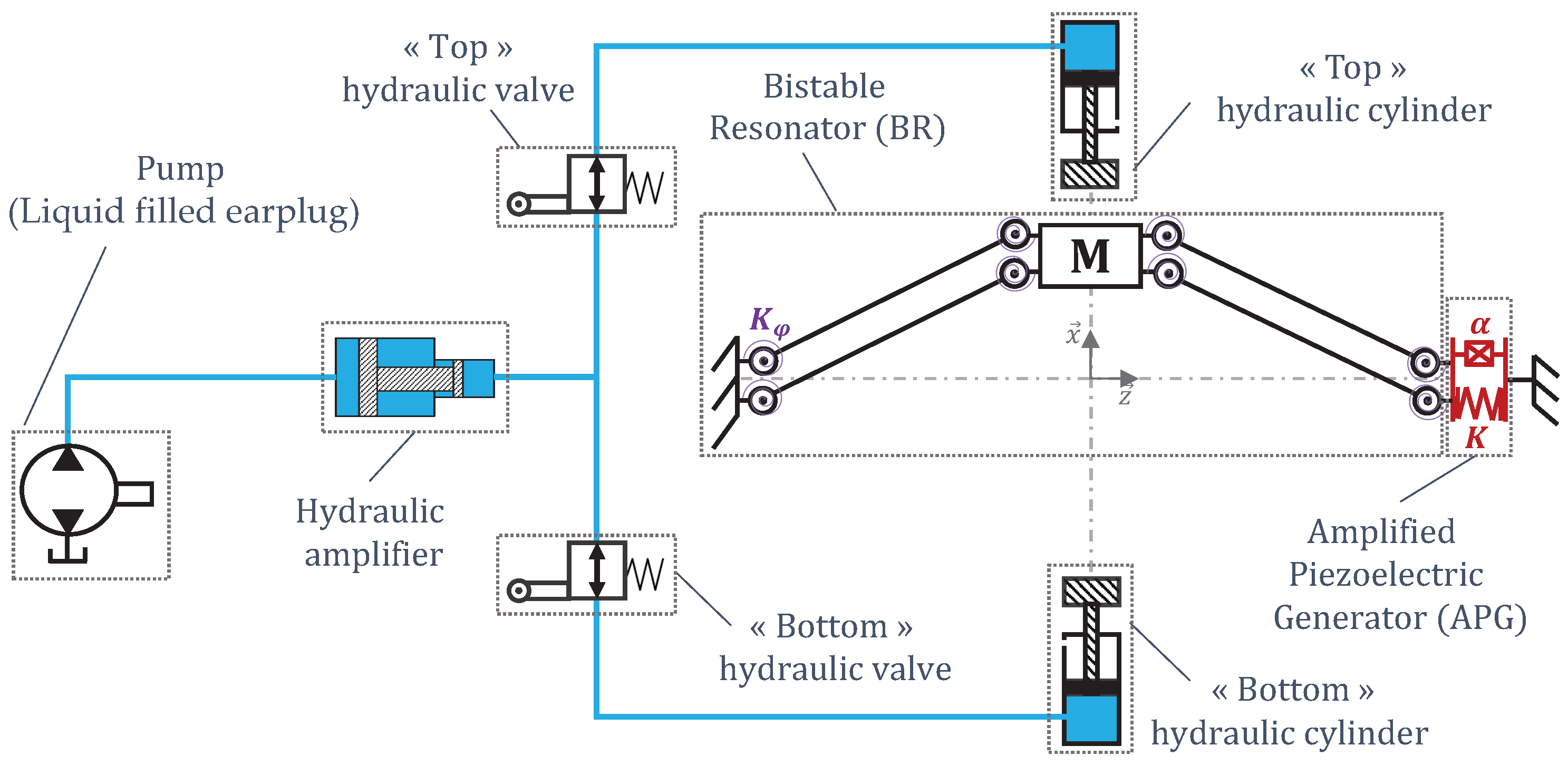
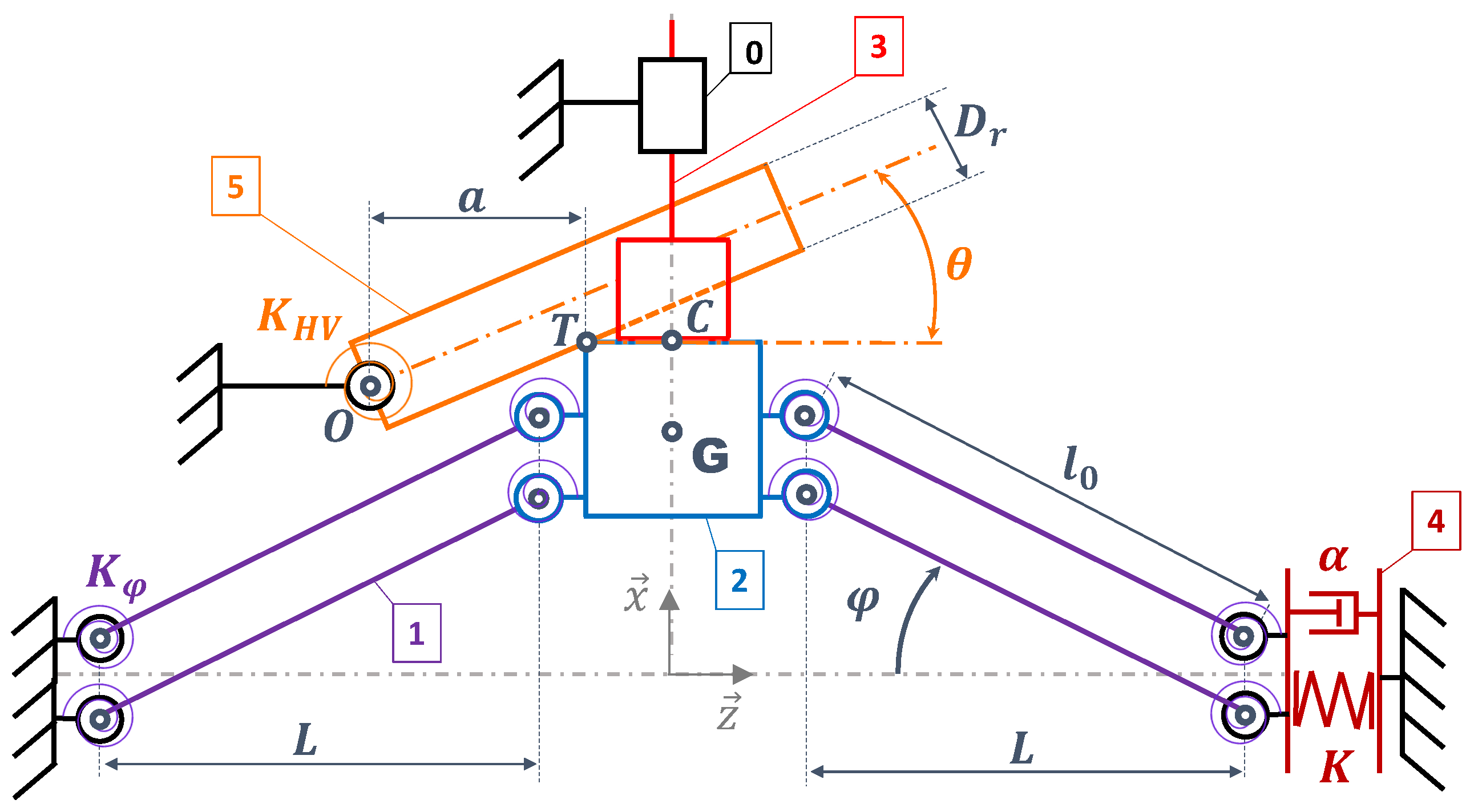



| Num | Name |
|---|---|
| 0 | Fixed frame |
| 1 | BR arm |
| 2 | BR mass |
| 3 | HC piston head |
| 4 | APG |
| 5 | Simplified HV mechanical model |
| Parameter | Value |
|---|---|
| (a) Electromechanical | |
| [N/µm] | 0.256 |
| [mm] | 0.49 |
| L [mm] | 16.0 |
| m [g] | 5.88 |
| [mm] | 0.69 |
| [kΩ] | 6.39 |
| [N/V] | 0.105 |
| [µF] | 0.25 |
| Q [-] | 50 |
| [%] | 85 |
| (b) Hydraulic | |
| [mm] | 4 |
| [-] | 29 |
| [kPa] | 1 |
| [mm3] | 60 |
| [Pa·s2/m6] | 0.21 × 1017 |
| [-] | 26 |
| Parameter Definition | Symbol | Value [Unit] |
|---|---|---|
| APX4 steel Young’s modulus | E | 211 [GPa] |
| APX4 steel elastic resistance | 955 [MPa] | |
| Dimensions of a buckled beam | L × l × e | 16 × 0.07 × 1.2 [mm] |
| Dimensions of the guide beam | × × e | 17.5 × 0.07 × 1.2 [mm] |
| Soft hinge stiffness | 0.006 [N/m/rad] | |
| Stiffness of the guide beam along | 190 [N/m] | |
| Stiffness of four buckled blades along | 1402 [kN/m] | |
| Stiffness of the APG along | K | 252 [kN/m] |
| Symbol | Simulation with Theoretical Parameters | Simulation with Recalibrated Parameters |
|---|---|---|
| Q | 50.0 | 30.0 |
| 47.0 Hz | 27.9 Hz | |
| 0.49 mm | 0.50 mm | |
| 2.56 × 105 N/m | 0.85 × 105 N/m | |
| 14.2 × 105 N/m | 1.27 × 105 N/m | |
| 16% | 1.25% | |
| 85% | 12.9% |
| Parameter | BR | BR + HVT1 |
|---|---|---|
| [mm] | – | 4 |
| [deg] | – | [≈19; ≈36] |
| [Nmm/rad] | – | 0.27 |
| a [mm] | – | 2.24 |
| [-] | – | 0.42 |
| K [N/m] | 84,480 | 84,480 |
| [mm] | 0.59 | 0.50 |
| Q [-] | 24.0 | 5.0 |
| [%] | 1.25 | 1.25 |
| [%] | 12.9 | 2.6 |
| [k] | 15.5 | 15.5 |
| m [g] | 5.88 | 9.00 |
| [Hz] | 32.9 | 27.9 |
| Symbol | Influence on the System | Proportionality | |
|---|---|---|---|
| (*) | (**) | ||
| a |  | Po (1) | Ne (2) |
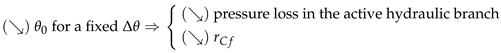 | Ne | Po | |
| m | 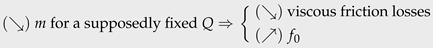 | Ne | Ne |
| Ne | Ne | ||
 | Ne | Ne | |
 | Ne/Po | Ne/Po | |
 | Po | Ne/Po | |
| L | same consequences as for described above | Po | Ne/Po |
| K | same consequences as for described above | Po | Ne/Po |
| Po | Po | ||
| Parameter | Ideal Experimental Design | Actual Experimental Design |
|---|---|---|
| L [mm] | 10 | |
| [mm] | 4 | |
| [kPa] | 12 | |
| [mm3] | 60 | |
| [mm] | 0.91 | 0.89 |
| m [g] | 3.0 | 3.0 |
| [kΩ] | 3.66 | 3.74 |
| [-] | 3.8 | 3.5 |
| [Hz] | 189 | 185 |
| [µJ] | 720 | |
| [µJ] | 362 | 340 |
| [µW] | 359 | 13.3 |
| Excitation Mode | Output Power [µW] (*) | LFA Freq. [Hz] | HFT Freq. [Hz] | Specific Surface [mm2] | Ref. |
|---|---|---|---|---|---|
| 2.4 | 20.8 | 263 | 60 × 10 | [43] | |
| 143 | 4–6 | NA | 100 × 100 | [36] | |
| 1000 | 10.7–20 | NA | 150 × 149 | [59] | |
| 3.4 | 100–200 | NA | 2 × 2 (MEMS) | [29] | |
| 1.7 (1)|66 (2) | 1.5 | 60 | 70 × 70 | This work |
| Energy Source | Transduction Method | Application | Output Power [µW] (*) | Power Density [mW/cm3] | Source Freq. [Hz] | Ref. |
|---|---|---|---|---|---|---|
| Tympan vibration | Piezoelectric (PLD-PZT) | Cochlear implant | 16.3 (p) | 1.5 (p) | 1780 | [3] |
| Inner ear | Biofuel cell | Wireless sensors | 10−3 | NA | NA | [60] |
| earcanal wall flexion | Piezoelectric (PVDF) | Cochlear implant | 70 | 0.04 | 1.5 | [15] |
| Skin deformation | Piezoelectric (PVDF-PTrFE) | Wearable electronics | 10−3 | 0.5 | NA | [61] |
| earcanal wall compression | Piezoelectric (PZT) | Cochlear implant | 1.7 (1)|66 (2) | NA | 1.5 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avetissian, T.; Formosa, F.; Badel, A.; Delnavaz, A.; Voix, J. A Novel Piezoelectric Energy Harvester for Earcanal Dynamic Motion Exploitation Using a Bistable Resonator Cycled by Coupled Hydraulic Valves Made of Collapsed Flexible Tubes. Micromachines 2024, 15, 415. https://doi.org/10.3390/mi15030415
Avetissian T, Formosa F, Badel A, Delnavaz A, Voix J. A Novel Piezoelectric Energy Harvester for Earcanal Dynamic Motion Exploitation Using a Bistable Resonator Cycled by Coupled Hydraulic Valves Made of Collapsed Flexible Tubes. Micromachines. 2024; 15(3):415. https://doi.org/10.3390/mi15030415
Chicago/Turabian StyleAvetissian, Tigran, Fabien Formosa, Adrien Badel, Aidin Delnavaz, and Jérémie Voix. 2024. "A Novel Piezoelectric Energy Harvester for Earcanal Dynamic Motion Exploitation Using a Bistable Resonator Cycled by Coupled Hydraulic Valves Made of Collapsed Flexible Tubes" Micromachines 15, no. 3: 415. https://doi.org/10.3390/mi15030415
APA StyleAvetissian, T., Formosa, F., Badel, A., Delnavaz, A., & Voix, J. (2024). A Novel Piezoelectric Energy Harvester for Earcanal Dynamic Motion Exploitation Using a Bistable Resonator Cycled by Coupled Hydraulic Valves Made of Collapsed Flexible Tubes. Micromachines, 15(3), 415. https://doi.org/10.3390/mi15030415







