On the Aging of OTFTs and Its Impact on PUFs Reliability
Abstract
1. Introduction
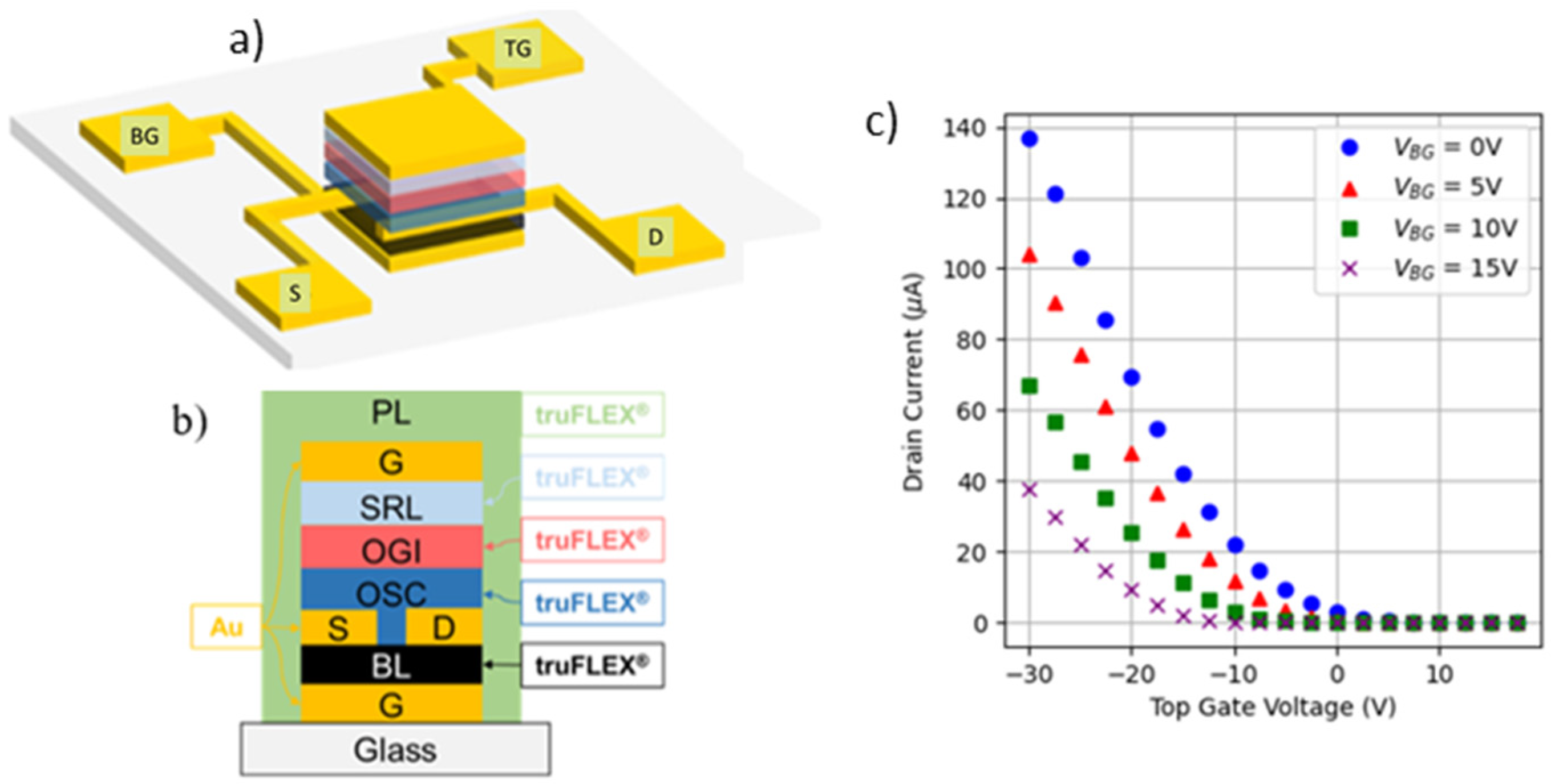
2. Experimental
3. Results
3.1. OTFTs Time-Zero Variability and PUF Performance
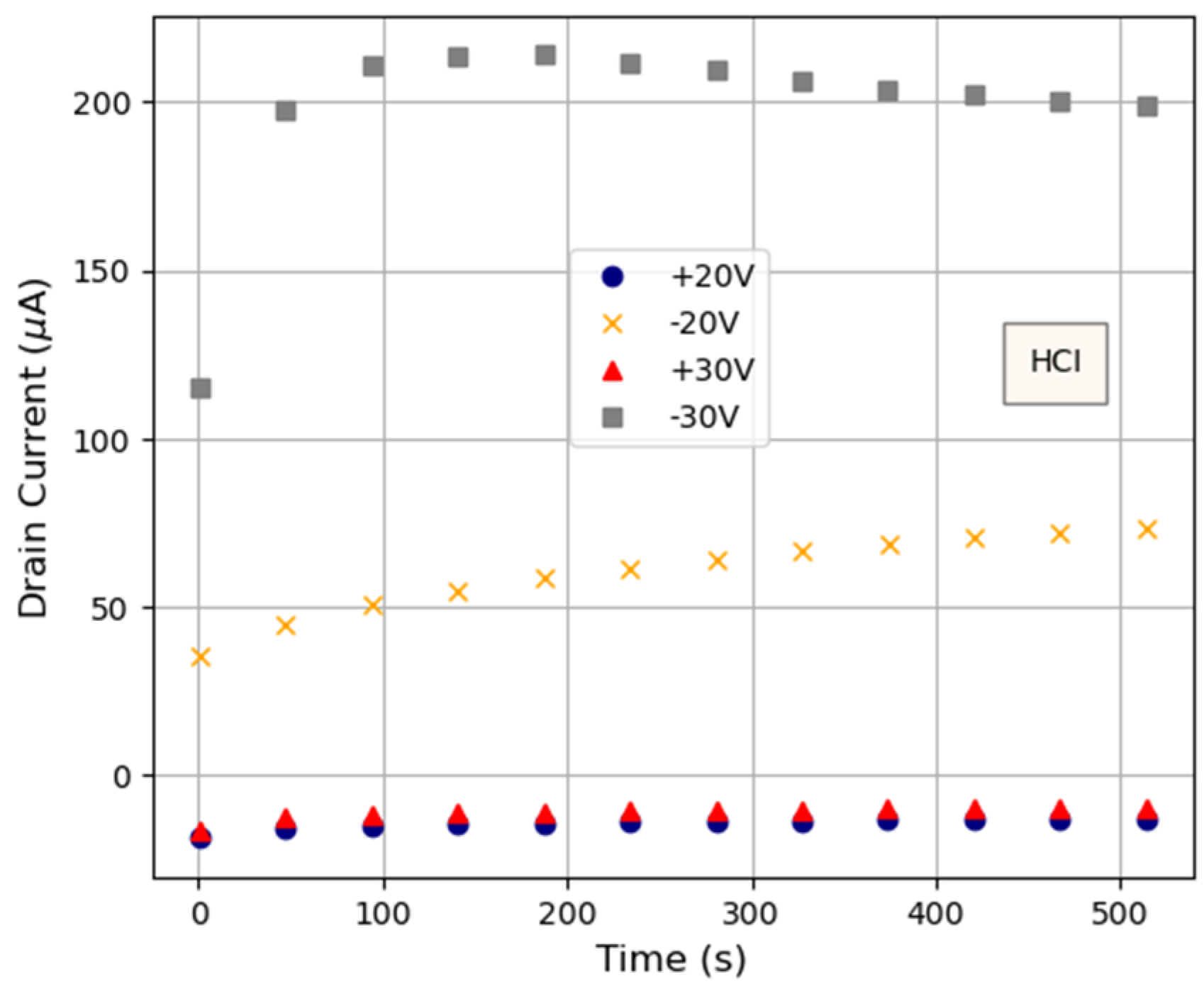
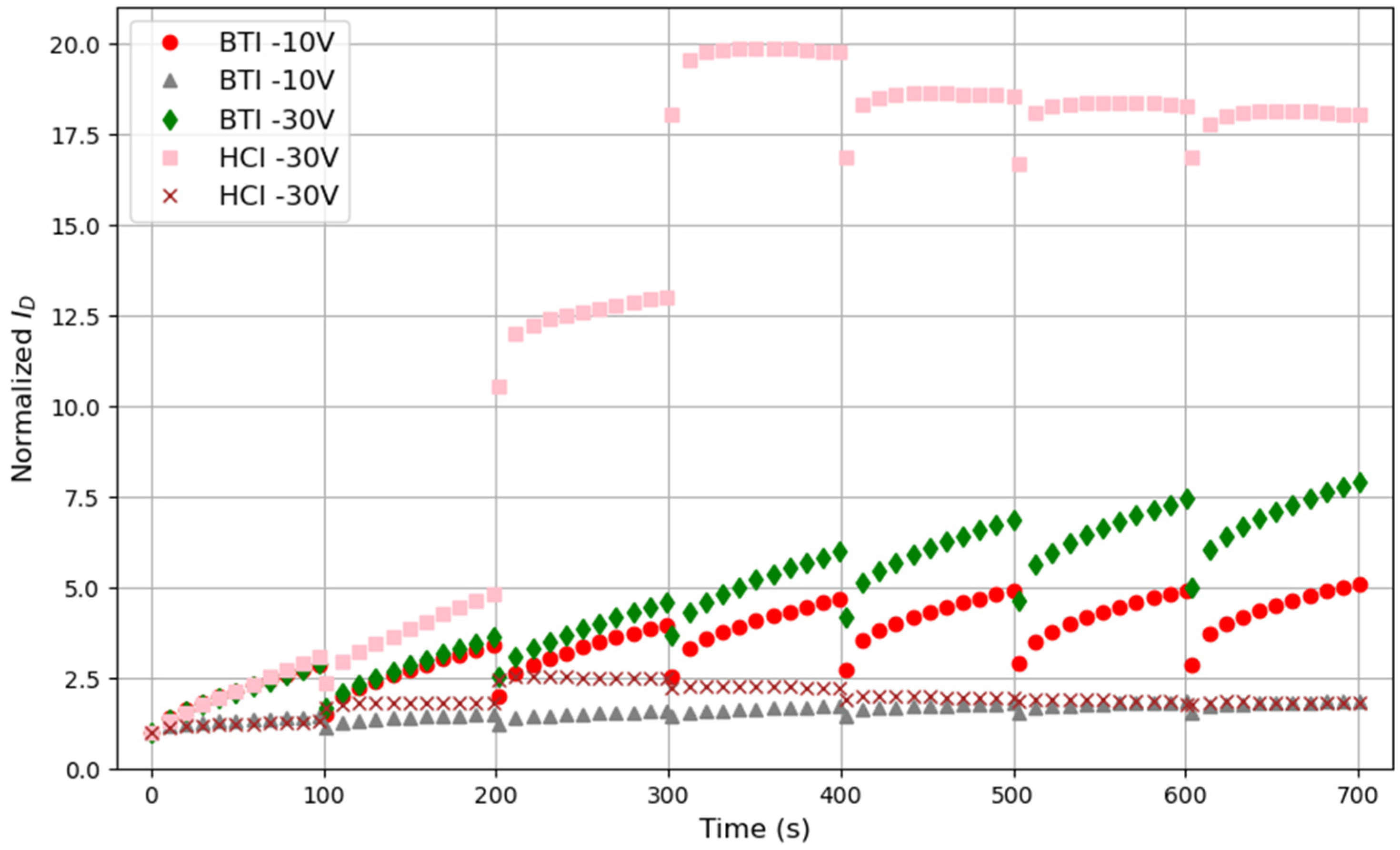
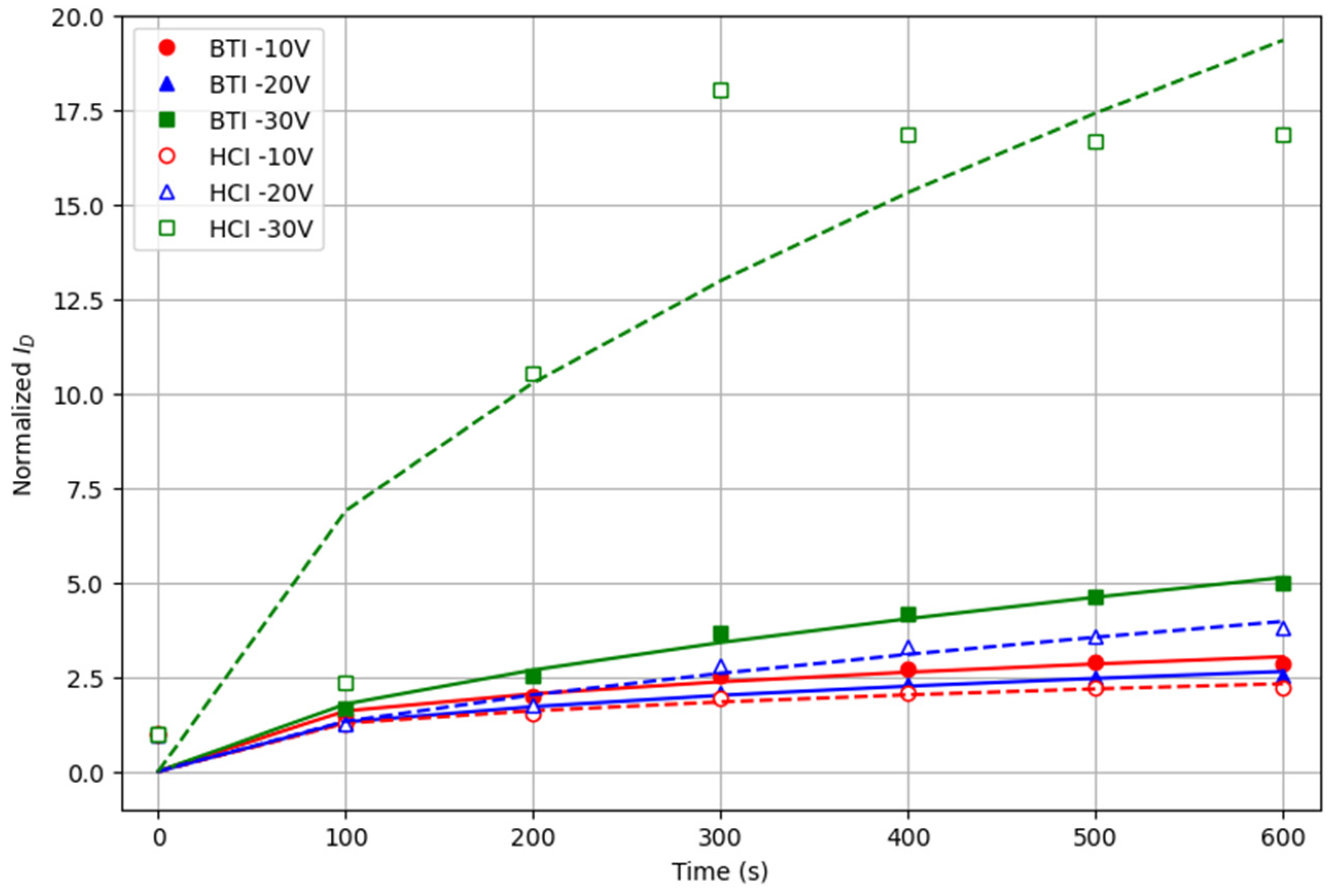
3.2. Impact of Electrical Stresses on the OTFTs’ Performance
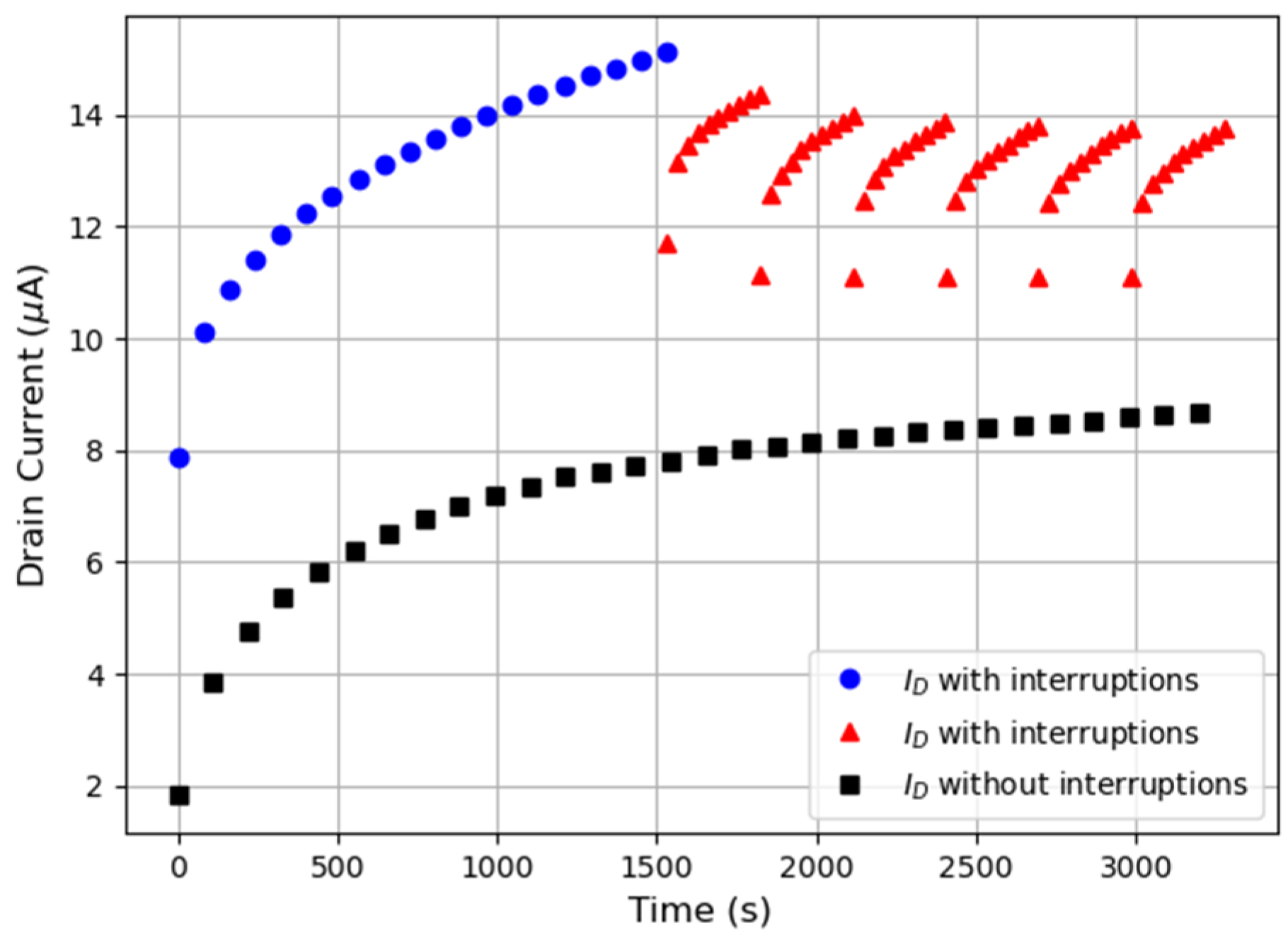
4. Pre-Stress as a Way to Improve PUFs’ Reliability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dimitrakopoulos, C.D.; Malefant, P.R.L. Organic Thin Film Transistors for Large Area Electronics. Adv. Mater. 2002, 14, 99–117. [Google Scholar] [CrossRef]
- Reese, C.; Roberts, M.; Ling, M.; Bao, Z. Organic thin film transistors. Mater. Today 2004, 7, 20–27. [Google Scholar] [CrossRef]
- Guo, X.; Xu, Y.; Ogier, S.; Ng, T.N.; Caironi, M.; Perinot, A.; Li, L.; Zhao, J.; Tang, W.; Sporea, R.A.; et al. Current status and opportunities of organic thin-film transistor technologies. IEEE Trans. Electron Devices 2017, 64, 1906–1921. [Google Scholar] [CrossRef]
- Arnal, A.; Crespo-Yepes, A.; Ramon, E.; Terés, L.; Rodríguez, R.; Nafría, M. DC characterization and fast small-signal parameter extraction of organic thin film transistors with different geometries. IEEE Electron Device Lett. 2020, 41, 1512–1515. [Google Scholar] [CrossRef]
- Ko, S.H.; Pan, H.; Grigoropoulos, C.P.; Luscombe, C.K.; Fréchet, J.M.J.; Poulikakos, D. All-inkjet-printed flexible electronics fabrication on a polymer substrate by low-temperature high-resolution selective laser sintering of metal nanoparticles. Nanotechnology 2007, 18, 345202. [Google Scholar] [CrossRef]
- Jeong, H.; Baek, S.; Han, S.; Jang, H.; Kim, S.H.; Lee, H.S. Novel Eco-Friendly Starch Paper for Use in Flexible, Transparent, and Disposable Organic Electronics. Adv. Funct. Mater. 2018, 28, 1704433. [Google Scholar] [CrossRef]
- Azarova, N.A.; Owen, J.W.; McLellan, C.A.; Grimminger, M.A.; Chapman, E.K.; Anthony, J.E.; Jurchescu, O.D. Fabrication of organic thin-film transistors by spray-deposition for low-cost, large-area electronics. Org. Electron. 2010, 11, 1960–1965. [Google Scholar] [CrossRef]
- Rasheed, F.; Golanbari, M.S.; Marques, G.C.; Tahoori, M.B.; Aghassi-Hagmann, J. A Smooth EKV-Based DC Model for Accurate Simulation of Printed Transistors and Their Process Variations. IEEE Trans. Electron Devices 2018, 65, 667–673. [Google Scholar] [CrossRef]
- Matsui, H.; Takeda, Y.; Tokito, S. Flexible and printed organic transistors: From materials to integrated circuits. Org. Electron. 2019, 75, 105432. [Google Scholar] [CrossRef]
- Ruiz, A.; Claramunt, S.; Crespo-Yepes, A.; Porti, M.; Nafria, M.; Xu, H.; Liu, C.; Wu, Q. Exploiting the KPFM capabilities to analyze at the nanoscale the impact of electrical stresses on OTFTs properties. Solid-State Electron. 2021, 186, 108061. [Google Scholar] [CrossRef]
- Claramunt, S.; Palau, G.; Arnal, A.; Crespo-Yepes, A.; Porti, M.; Ogier, S.; Ramon, E.; Nafria, M. Exploitation of OTFTs variability for PUFs implementation and impact of aging. Solid State Electron. 2023, 207, 108698. [Google Scholar] [CrossRef]
- Qin, Z.; Shintani, M.; Kuribara, K.; Ogasahara, Y.; Sato, T. Organic Current Mirror PUF for Improved Stability Against Device Aging. IEEE Sens. J. 2020, 20, 7569–7578. [Google Scholar] [CrossRef]
- Kim, D.; Im, S.; Kim, D.; Lee, H.; Choi, C.; Cho, J.H.; Ju, H.; Lim, J.A. Reconfigurable Electronic Physically Unclonable Functions Based on Organic Thin-Film Transistors with Multiscale Polycrystalline Entropy for Highly Secure Cryptography Primitives. Adv. Funct. Mater. 2023, 33, 2210367. [Google Scholar] [CrossRef]
- Grasser, T.; Wagner, P.J.; Reisinger, H.; Aichinder, T.; Pobegen, G.; Nelhiebel, M.; Kaczer, B. Analytic modeling of the bias temperature instability using capture/emission time maps. In Proceedings of the 2011 International Electron Devices Meeting, Washington, DC, USA, 5–7 December 2011; pp. 27.4.1–27.4.4. [Google Scholar] [CrossRef]
- Bhargava, M.; Mai, K. A High Reliability PUF Using Hot Carrier Injection Based Response Reinforcement. In Cryptographic Hardware and Embedded Systems—CHES 2013; Bertoni, G., Coron, J.S., Eds.; CHES 2013. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8086. [Google Scholar] [CrossRef]
- Garg, A.; Lee, Z.C.; Lu, L.; Kim, T.T.-H. Improving uniformity and reliability of SRAM PUFs utilizing device aging phenomenon for unique identifier generation. Microelectron. J. 2019, 90, 29–38. [Google Scholar] [CrossRef]



| 300 PUFs Based on ID Digitized into 8-Bit Binary Words (1200 OTFTs) | 300 PUFs Based on ID Digitized into 4-Bit Binary Words (2400 OTFTs) | |||
|---|---|---|---|---|
| Unif. | Uniq. | Unif. | Uniq | |
| 0.50 | 0.51 | 0.52 | 0.54 | |
| SD | 0.07 | 0.09 | 0.06 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porti, M.; Palau, G.; Crespo-Yepes, A.; Arnal Rus, A.; Ogier, S.; Ramon, E.; Nafria, M. On the Aging of OTFTs and Its Impact on PUFs Reliability. Micromachines 2024, 15, 443. https://doi.org/10.3390/mi15040443
Porti M, Palau G, Crespo-Yepes A, Arnal Rus A, Ogier S, Ramon E, Nafria M. On the Aging of OTFTs and Its Impact on PUFs Reliability. Micromachines. 2024; 15(4):443. https://doi.org/10.3390/mi15040443
Chicago/Turabian StylePorti, Marc, Gerard Palau, Albert Crespo-Yepes, August Arnal Rus, Simon Ogier, Eloi Ramon, and Montserrat Nafria. 2024. "On the Aging of OTFTs and Its Impact on PUFs Reliability" Micromachines 15, no. 4: 443. https://doi.org/10.3390/mi15040443
APA StylePorti, M., Palau, G., Crespo-Yepes, A., Arnal Rus, A., Ogier, S., Ramon, E., & Nafria, M. (2024). On the Aging of OTFTs and Its Impact on PUFs Reliability. Micromachines, 15(4), 443. https://doi.org/10.3390/mi15040443







