Optomechanical Microwave-to-Optical Photon Transducer Chips: Empowering the Quantum Internet Revolution
Abstract
1. Introduction
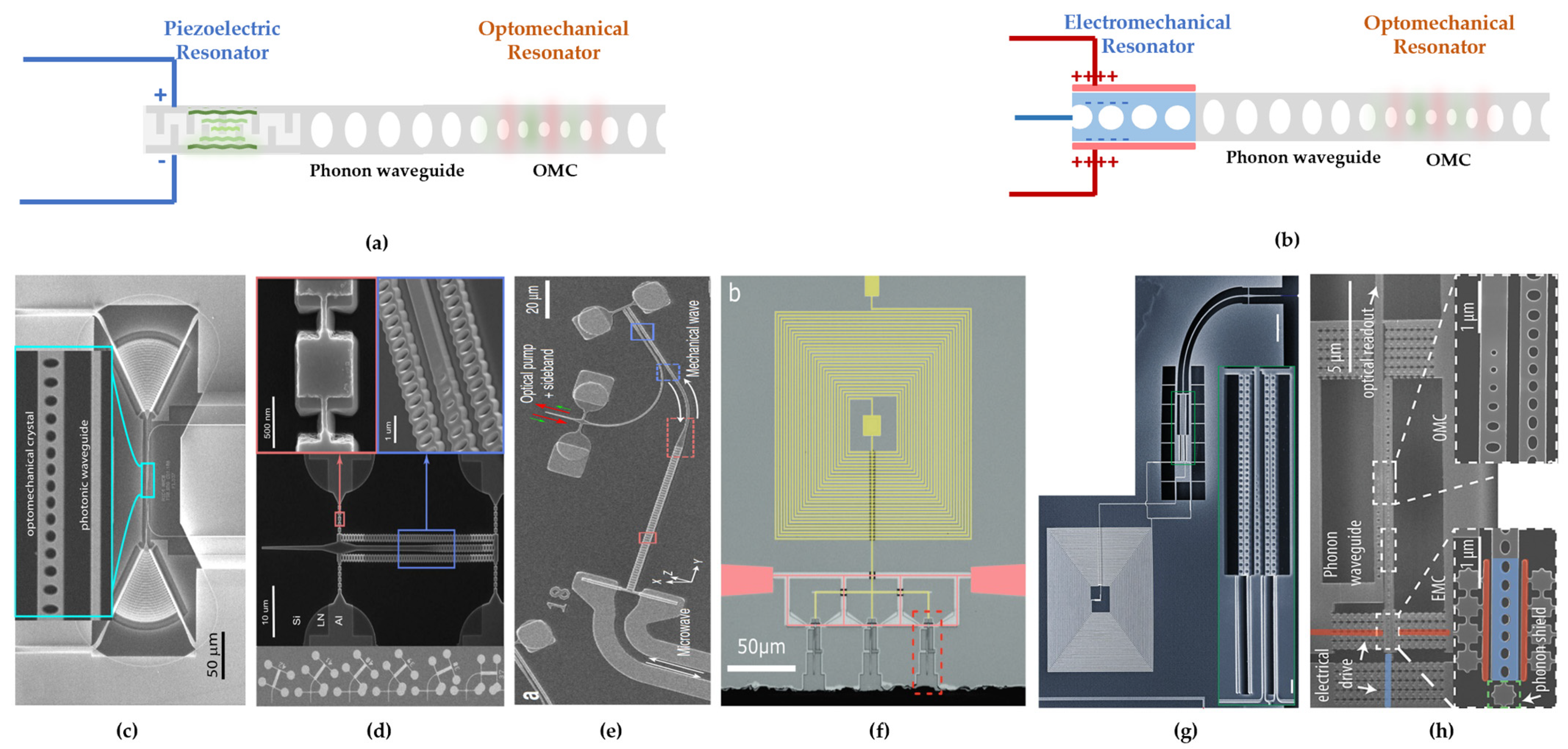
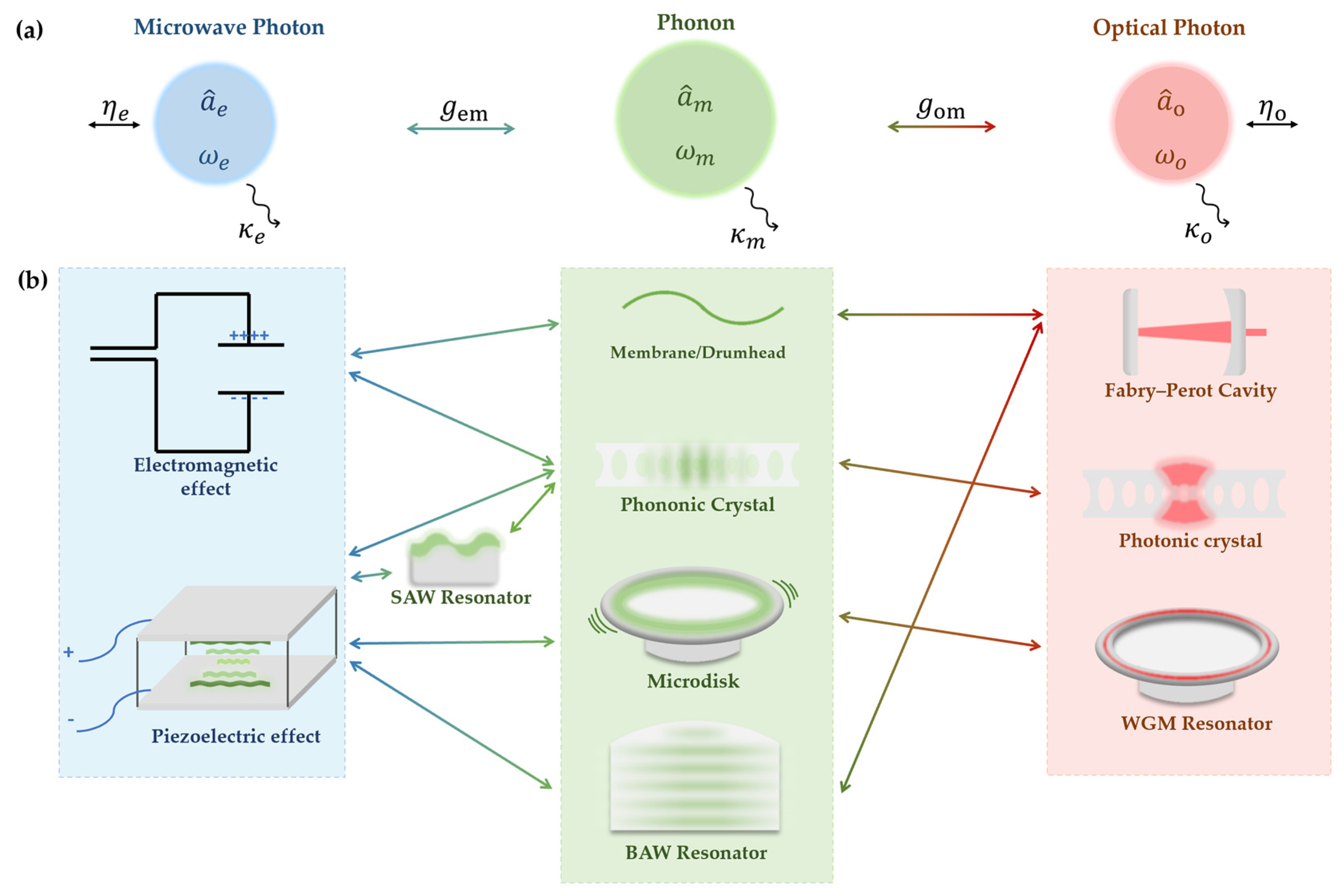
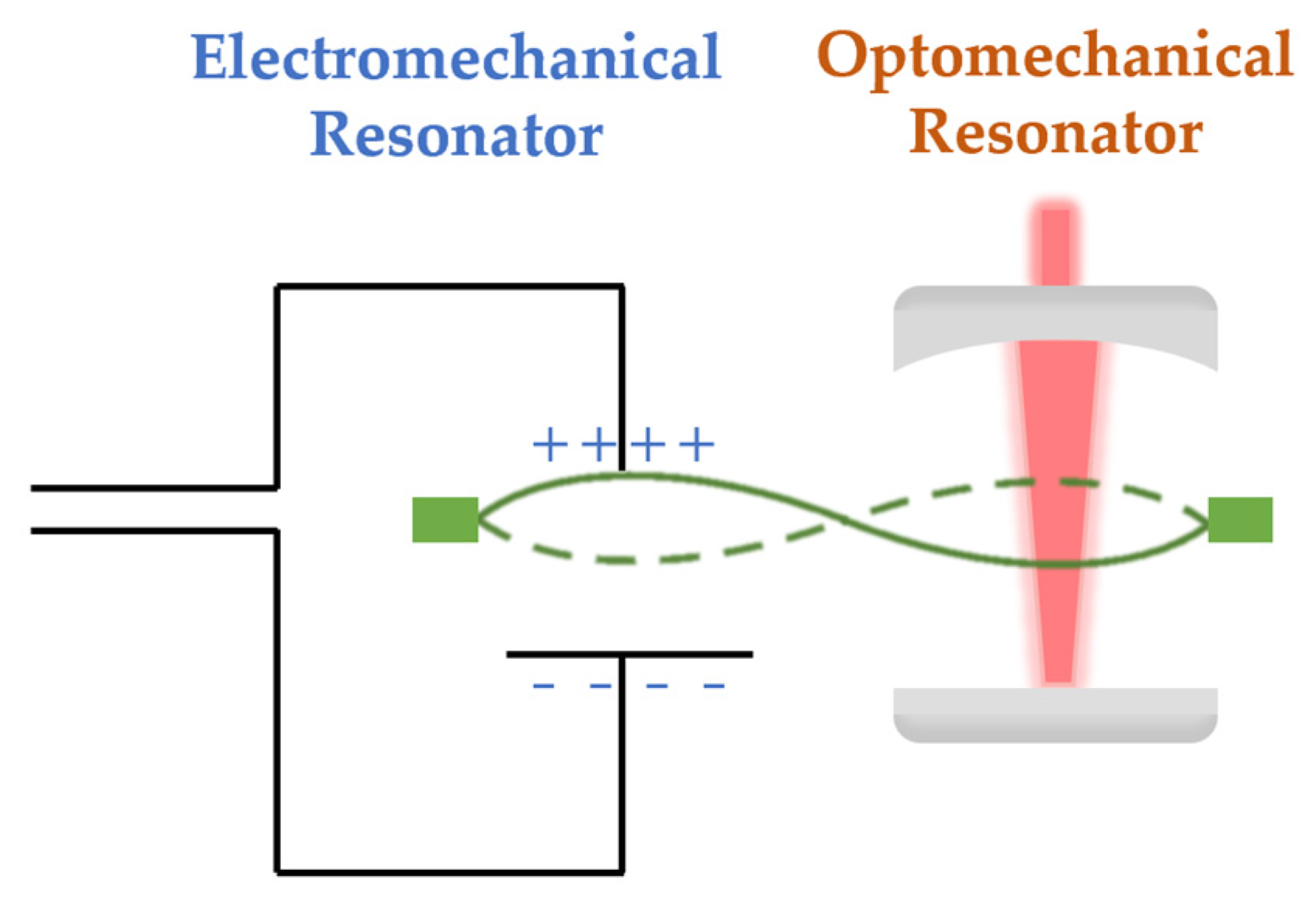
2. Optomechanical Transducer Systems
2.1. Membrane Resonator
2.2. Phononic Crystal Resonator
| Reference | Vainsencher et al. [69] | Jiang et al. [66] | Forsch et al. [36] | Jiang et al. [34] | Mirhosseini et al. [29] | Jiang et al. [36] | Weaver et al. [33] | Stockill et al. [67] | Arnold et al. [61] | Zhao et al. [31] |
|---|---|---|---|---|---|---|---|---|---|---|
| Platform | AIN | LN | GaAs | LN | AlN | LN | LN | GaP | SOI | SOI |
| [MHz] | ~0.115 | 0.12 | 1.3 | 0.08 | 0.5 | 0.41 | 0.53 | ~0.7 | 0.66 | |
| [GHz] | 15.2 | 0.78 | 5.8 | 1.2 | 0.8 | 1.12 | ~1.34 | 4.17 | 1.4 | 1.39 |
[kHz] | 5000 | 500 | 200 | 193 | 19 | 1100 | ~2630 | ~ 67 | 15 | ~ 0.001 |
| 1.73 | 0.04 | 1.74 | 0.9 | |||||||
| 24.2 | 0.57 | |||||||||
| * | 0.05 | 0.09 | ||||||||
| 0.35 | ||||||||||
| 0.57 | 0.36 | (M–O) (O–M) | ||||||||
| T [K] | 300 | 20 | 0.02 | 300 | 0.015 | 0.25 | 4 | 0.15 | 0.02 |
2.3. Microdisk
2.4. Bulk Acoustic Wave Resonator (BAR)
3. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Dowling, J.P.; Milburn, G.J. Quantum Technology: The Second Quantum Revolution. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2003, 361, 1655–1674. [Google Scholar] [CrossRef]
- Awschalom, D.; Berggren, K.K.; Bernien, H.; Bhave, S.; Carr, L.D.; Davids, P.; Economou, S.E.; Englund, D.; Faraon, A.; Fejer, M.; et al. Development of Quantum Interconnects (QuICs) for Next-Generation Information Technologies. PRX Quantum 2021, 2, 017002. [Google Scholar] [CrossRef]
- Lauk, N.; Sinclair, N.; Barzanjeh, S.; Covey, J.P.; Saffman, M.; Spiropulu, M.; Simon, C. Perspectives on Quantum Transduction. Quantum Sci. Technol. 2020, 5, 020501. [Google Scholar] [CrossRef]
- Schneeloch, J.; Sheridan, E.; Smith, A.M.; Tison, C.C.; Campbell, D.L.; LaHaye, M.D.; Fanto, M.L.; Alsing, P.M. Principles for Optimizing Quantum Transduction in Piezo-Optomechanical Systems. arXiv 2023, arXiv:2312,04673. [Google Scholar]
- Tian, L.; Wang, H. Optical Wavelength Conversion of Quantum States with Optomechanics. Phys. Rev. A 2010, 82, 053806. [Google Scholar] [CrossRef]
- Safavi-Naeini, A.H.; Painter, O. Proposal for an Optomechanical Traveling Wave Phonon–Photon Translator. New J. Phys. 2011, 13, 013017. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Abdi, M.; Milburn, G.J.; Tombesi, P.; Vitali, D. Reversible Optical-to-Microwave Quantum Interface. Phys. Rev. Lett. 2012, 109, 130503. [Google Scholar] [CrossRef]
- Wang, Y.-D.; Clerk, A.A. Using Interference for High Fidelity Quantum State Transfer in Optomechanics. Phys. Rev. Lett. 2012, 108, 153603. [Google Scholar] [CrossRef]
- Rueda, A.; Sedlmeir, F.; Collodo, M.C.; Vogl, U.; Stiller, B.; Schunk, G.; Strekalov, D.V.; Marquardt, C.; Fink, J.M.; Painter, O.; et al. Efficient Microwave to Optical Photon Conversion: An Electro-Optical Realization. Optica 2016, 3, 597. [Google Scholar] [CrossRef]
- Fan, L.; Zou, C.; Cheng, R.; Guo, X.; Han, X.; Gong, Z.; Wang, S.; Tang, H. Cavity Electro-Optic Circuit for Microwave-to-Optical Frequency Conversion. In Proceedings of the Nonlinear Optics (NLO); Optica Publishing Group: Washington, DC, USA, 2019; p. NF2A.2. [Google Scholar]
- Soltani, M.; Zhang, M.; Ryan, C.; Ribeill, G.J.; Wang, C.; Loncar, M. Efficient Quantum Microwave-to-Optical Conversion Using Electro-Optic Nanophotonic Coupled Resonators. Phys. Rev. A 2017, 96, 043808. [Google Scholar] [CrossRef]
- Tsang, M. Cavity Quantum Electro-Optics. Phys. Rev. A 2010, 81, 063837. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Tabuchi, Y.; Gloppe, A.; Usami, K.; Nakamura, Y. Hybrid Quantum Systems Based on Magnonics. Appl. Phys. Express 2019, 12, 070101. [Google Scholar] [CrossRef]
- Yuan, H.Y.; Cao, Y.; Kamra, A.; Duine, R.A.; Yan, P. Quantum Magnonics: When Magnon Spintronics Meets Quantum Information Science. Phys. Rep. 2022, 965, 1–74. [Google Scholar] [CrossRef]
- Lachance-Quirion, D.; Wolski, S.P.; Tabuchi, Y.; Kono, S.; Usami, K.; Nakamura, Y. Entanglement-Based Single-Shot Detection of a Single Magnon with a Superconducting Qubit. Science 2020, 367, 425–428. [Google Scholar] [CrossRef]
- Li, Y.; Yefremenko, V.G.; Lisovenko, M.; Trevillian, C.; Polakovic, T.; Cecil, T.W.; Barry, P.S.; Pearson, J.; Divan, R.; Tyberkevych, V.; et al. Coherent Coupling of Two Remote Magnonic Resonators Mediated by Superconducting Circuits. Phys. Rev. Lett. 2022, 128, 047701. [Google Scholar] [CrossRef]
- Shen, Z.; Xu, G.-T.; Zhang, M.; Zhang, Y.-L.; Wang, Y.; Chai, C.-Z.; Zou, C.-L.; Guo, G.-C.; Dong, C.-H. Coherent Coupling between Phonons, Magnons, and Photons. Phys. Rev. Lett. 2022, 129, 243601. [Google Scholar] [CrossRef]
- Hafezi, M.; Kim, Z.; Rolston, S.L.; Orozco, L.A.; Lev, B.L.; Taylor, J.M. Atomic Interface between Microwave and Optical Photons. Phys. Rev. A 2012, 85, 020302. [Google Scholar] [CrossRef]
- Williamson, L.A.; Chen, Y.-H.; Longdell, J.J. Magneto-Optic Modulator with Unit Quantum Efficiency. Phys. Rev. Lett. 2014, 113, 203601. [Google Scholar] [CrossRef]
- Verdú, J.; Zoubi, H.; Koller, C.; Majer, J.; Ritsch, H.; Schmiedmayer, J. Strong Magnetic Coupling of an Ultracold Gas to a Superconducting Waveguide Cavity. Phys. Rev. Lett. 2009, 103, 043603. [Google Scholar] [CrossRef]
- Fernandez-Gonzalvo, X.; Williamson, L.A.; Chen, Y.-H.; Yin, C.; Rogge, S.; Longdell, J.J. Upconversion of Microwave to Optical Photons Using Erbium Impurities in a Solid. In Proceedings of the CLEO: 2015; Optica Publishing Group: Washington, DC, USA, 2015; p. FM3A.7. [Google Scholar]
- Han, X.; Fu, W.; Zou, C.-L.; Jiang, L.; Tang, H.X. Microwave-Optical Quantum Frequency Conversion. Optica 2021, 8, 1050. [Google Scholar] [CrossRef]
- Clerk, A.A.; Lehnert, K.W.; Bertet, P.; Petta, J.R.; Nakamura, Y. Hybrid Quantum Systems with Circuit Quantum Electrodynamics. Nat. Phys. 2020, 16, 257–267. [Google Scholar] [CrossRef]
- Chu, Y.; Gröblacher, S. A Perspective on Hybrid Quantum Opto- and Electromechanical Systems. Appl. Phys. Lett. 2020, 117, 150503. [Google Scholar] [CrossRef]
- Delaney, R.D.; Urmey, M.D.; Mittal, S.; Brubaker, B.M.; Kindem, J.M.; Burns, P.S.; Regal, C.A.; Lehnert, K.W. Superconducting-Qubit Readout via Low-Backaction Electro-Optic Transduction. Nature 2022, 606, 489–493. [Google Scholar] [CrossRef] [PubMed]
- Andrews, R.W.; Peterson, R.W.; Purdy, T.P.; Cicak, K.; Simmonds, R.W.; Regal, C.A.; Lehnert, K.W. Bidirectional and Efficient Conversion between Microwave and Optical Light. Nat. Phys. 2014, 10, 321–326. [Google Scholar] [CrossRef]
- Gao, X.; Yin, Z.; Li, T. High-Speed Quantum Transducer with a Single-Photon Emitter in a 2D Resonator. Ann. Phys. 2020, 532, 2000233. [Google Scholar] [CrossRef]
- Bonaldi, M.; Borrielli, A.; Di Giuseppe, G.; Malossi, N.; Morana, B.; Natali, R.; Piergentili, P.; Sarro, P.M.; Serra, E.; Vitali, D. Low Noise Opto-Electro-Mechanical Modulator for RF-to-Optical Transduction in Quantum Communications. Entropy 2023, 25, 1087. [Google Scholar] [CrossRef]
- Mirhosseini, M.; Sipahigil, A.; Kalaee, M.; Painter, O. Superconducting Qubit to Optical Photon Transduction. Nature 2020, 588, 599–603. [Google Scholar] [CrossRef]
- Chiappina, P.; Banker, J.; Meesala, S.; Lake, D.; Wood, S.; Painter, O. Design of an Ultra-Low Mode Volume Piezo-Optomechanical Quantum Transducer. Opt. Express 2023, 31, 22914. [Google Scholar] [CrossRef]
- Zhao, H.; Bozkurt, A.; Mirhosseini, M. Electro-Optic Transduction in Silicon via Gigahertz-Frequency Nanomechanics. Optica 2023, 10, 790. [Google Scholar] [CrossRef]
- Zhang, J.; Nuño-Ruano, P.; Le Roux, X.; Cassan, E.; Marris-Morini, D.; Vivien, L.; Lanzillotti-Kimura, D.; Alonso-Ramos, C. Optomechanical Cavities in Silicon-on-Insulator. In Proceedings of the Integrated Optics: Devices, Materials, and Technologies XXVII; García-Blanco, S.M., Cheben, P., Eds.; SPIE: Bellingham, WA, USA, 2023; Volume 12424, p. 6. [Google Scholar]
- Weaver, M.J.; Duivestein, P.; Bernasconi, A.C.; Scharmer, S.; Lemang, M.; Thiel, T.C.V.; Hijazi, F.; Hensen, B.; Gröblacher, S.; Stockill, R. An Integrated Microwave-to-Optics Interface for Scalable Quantum Computing. Nat. Nanotechnol. 2023, 19, 166–172. [Google Scholar] [CrossRef]
- Jiang, W.; Sarabalis, C.J.; Dahmani, Y.D.; Patel, R.N.; Mayor, F.M.; McKenna, T.P.; Van Laer, R.; Safavi-Naeini, A.H. Efficient Bidirectional Piezo-Optomechanical Transduction between Microwave and Optical Frequency. Nat. Commun. 2020, 11, 1166. [Google Scholar] [CrossRef]
- Jiang, W.; Mayor, F.M.; Malik, S.; Van Laer, R.; McKenna, T.P.; Patel, R.N.; Witmer, J.D.; Safavi-Naeini, A.H. Optically Heralded Microwave Photon Addition. Nat. Phys. 2023, 19, 1423–1428. [Google Scholar] [CrossRef]
- Forsch, M.; Stockill, R.; Wallucks, A.; Marinković, I.; Gärtner, C.; Norte, R.A.; Van Otten, F.; Fiore, A.; Srinivasan, K.; Gröblacher, S. Microwave-to-Optics Conversion Using a Mechanical Oscillator in Its Quantum Ground State. Nat. Phys. 2020, 16, 69–74. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Fu, W.; Zhong, C.; Zou, C.-L.; Xu, Y.; Sayem, A.A.; Xu, M.; Wang, S.; Cheng, R.; Jiang, L.; et al. Cavity Piezo-Mechanics for Superconducting-Nanophotonic Quantum Interface. Nat. Commun. 2020, 11, 3237. [Google Scholar] [CrossRef]
- Shandilya, P.K.; Lake, D.P.; Mitchell, M.J.; Sukachev, D.D.; Barclay, P.E. Optomechanical Interface between Telecom Photons and Spin Quantum Memory. Nat. Phys. 2021, 17, 1420–1425. [Google Scholar] [CrossRef]
- Yoon, T.; Mason, D.; Jain, V.; Chu, Y.; Kharel, P.; Renninger, W.H.; Collins, L.; Frunzio, L.; Schoelkopf, R.J.; Rakich, P.T. Simultaneous Brillouin and Piezoelectric Coupling to a High-Frequency Bulk Acoustic Resonator. Optica 2023, 10, 110. [Google Scholar] [CrossRef]
- Kharel, P.; Chu, Y.; Mason, D.; Kittlaus, E.A.; Otterstrom, N.T.; Gertler, S.; Rakich, P.T. Multimode Strong Coupling in Cavity Optomechanics. Phys. Rev. Appl. 2022, 18, 024054. [Google Scholar] [CrossRef]
- Shore, K.A. Quantum Optomechanics, by W. P. Bowen and G. J. Milburn. Contemp. Phys. 2016, 57, 616–617. [Google Scholar] [CrossRef]
- Xia, Z.; Tang, J.; Jiang, Q.; Chen, P.; Li, H.; Zhou, Q.; You, L.; Wang, Y.; Song, H.; Guo, G.; et al. Key Technologies for Detecting Acoustic Quantum States in OneDimensional Optomechanical Crystal Nanobeam. J. Univ. Electron. Sci. Technol. China 2023, 52, 322–330. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity Optomechanics. Rev. Modern Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Xuereb, A.; Gröblacher, S.; Paternostro, M.; Regal, C.A.; Weig, E.M. Optomechanics for Quantum Technologies. Nat. Phys. 2022, 18, 15–24. [Google Scholar] [CrossRef]
- Xia, J.; Qiao, Q.; Zhou, G.; Chau, F.S.; Zhou, G. Opto-Mechanical Photonic Crystal Cavities for Sensing Application. Appl. Sci. 2020, 10, 7080. [Google Scholar] [CrossRef]
- Barzanjeh, S.; Guha, S.; Weedbrook, C.; Vitali, D.; Shapiro, J.H.; Pirandola, S. Microwave Quantum Illumination. Phys. Rev. Lett. 2015, 114, 080503. [Google Scholar] [CrossRef]
- Zeuthen, E.; Schliesser, A.; Sørensen, A.S.; Taylor, J.M. Figures of Merit for Quantum Transducers. Quantum Sci. Technol. 2020, 5, 034009. [Google Scholar] [CrossRef]
- Bagci, T.; Simonsen, A.; Schmid, S.; Villanueva, L.G.; Zeuthen, E.; Appel, J.; Taylor, J.M.; Sørensen, A.; Usami, K.; Schliesser, A.; et al. Optical Detection of Radio Waves through a Nanomechanical Transducer. Nature 2014, 507, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Magnard, P.; Storz, S.; Kurpiers, P.; Schär, J.; Marxer, F.; Lütolf, J.; Walter, T.; Besse, J.-C.; Gabureac, M.; Reuer, K.; et al. Microwave Quantum Link between Superconducting Circuits Housed in Spatially Separated Cryogenic Systems. Phys. Rev. Lett. 2020, 125, 260502. [Google Scholar] [CrossRef] [PubMed]
- Brubaker, B.M.; Kindem, J.M.; Urmey, M.D.; Mittal, S.; Delaney, R.D.; Burns, P.S.; Vissers, M.R.; Lehnert, K.W.; Regal, C.A. Optomechanical Ground-State Cooling in a Continuous and Efficient Electro-Optic Transducer. Phys. Rev. X 2022, 12, 021062. [Google Scholar] [CrossRef]
- Dong, C.; Wang, Y.; Wang, H. Optomechanical Interfaces for Hybrid Quantum Networks. Natl. Sci. Rev. 2015, 2, 510–519. [Google Scholar] [CrossRef]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong Dispersive Coupling of a High-Finesse Cavity to a Micromechanical Membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-Based Quantum Control of Mechanical Motion. Nature 2018, 563, 53–58. [Google Scholar] [CrossRef]
- Higginbotham, A.P.; Burns, P.S.; Urmey, M.D.; Peterson, R.W.; Kampel, N.S.; Brubaker, B.M.; Smith, G.; Lehnert, K.W.; Regal, C.A. Harnessing Electro-Optic Correlations in an Efficient Mechanical Converter. Nat. Phys. 2018, 14, 1038–1042. [Google Scholar] [CrossRef]
- Purdy, T.P.; Peterson, R.W.; Regal, C.A. Observation of Radiation Pressure Shot Noise on a Macroscopic Object. Science 2013, 339, 801–804. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.M.; Pérez-García, D.; Giedke, G. Quantum Capacities of Bosonic Channels. Phys. Rev. Lett. 2007, 98, 130501. [Google Scholar] [CrossRef] [PubMed]
- Esmenda, J.C.; Aguila, M.A.C.; Wang, J.-Y.; Lee, T.-H.; Chen, Y.-C.; Yang, C.-Y.; Lin, K.-H.; Chang-Liao, K.-S.; Kafanov, S.; Pashkin, Y.; et al. Optoelectrical Nanomechanical Resonators Made from Multilayered Two-Dimensional Materials. ACS Appl. Nano Mater. 2022, 5, 8875–8882. [Google Scholar] [CrossRef]
- Qiu, L.; Shomroni, I.; Seidler, P.; Kippenberg, T.J. Laser Cooling of a Nanomechanical Oscillator to Its Zero-Point Energy. Phys. Rev. Lett. 2020, 124, 173601. [Google Scholar] [CrossRef] [PubMed]
- Kiesel, N.; Blaser, F.; Delić, U.; Grass, D.; Kaltenbaek, R.; Aspelmeyer, M. Cavity Cooling of an Optically Levitated Nanoparticle. Proc. Natl. Acad. Sci. 2013, 110, 14180–14185. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound Attenuation by Sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Arnold, G.; Wulf, M.; Barzanjeh, S.; Redchenko, E.S.; Rueda, A.; Hease, W.J.; Hassani, F.; Fink, J.M. Converting Microwave and Telecom Photons with a Silicon Photonic Nanomechanical Interface. Nat. Commun. 2020, 11, 4460. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical Crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef]
- Chan, J.; Safavi-Naeini, A.H.; Hill, J.T.; Meenehan, S.; Painter, O. Optimized Optomechanical Crystal Cavity with Acoustic Radiation Shield. Appl. Phys. Lett. 2012, 101, 081115. [Google Scholar] [CrossRef]
- Bochmann, J.; Vainsencher, A.; Awschalom, D.D.; Cleland, A.N. Nanomechanical Coupling between Microwave and Optical Photons. Nat. Phys. 2013, 9, 712–716. [Google Scholar] [CrossRef]
- Balram, K.C.; Davanço, M.I.; Song, J.D.; Srinivasan, K. Coherent Coupling between Radio Frequency, Optical, and Acoustic Waves in Piezo-Optomechanical Circuits. Nat. Photonics 2016, 10, 346–352. [Google Scholar] [CrossRef]
- Jiang, W.; Patel, R.N.; Mayor, F.M.; McKenna, T.P.; Arrangoiz-Arriola, P.; Sarabalis, C.J.; Witmer, J.D.; Van Laer, R.; Safavi-Naeini, A.H. Lithium Niobate Piezo-Optomechanical Crystals. Optica 2019, 6, 845. [Google Scholar] [CrossRef]
- Stockill, R.; Forsch, M.; Hijazi, F.; Beaudoin, G.; Pantzas, K.; Sagnes, I.; Braive, R.; Gröblacher, S. Ultra-Low-Noise Microwave to Optics Conversion in Gallium Phosphide. Nat. Commun. 2022, 13, 6583. [Google Scholar] [CrossRef] [PubMed]
- Hönl, S.; Popoff, Y.; Caimi, D.; Beccari, A.; Kippenberg, T.J.; Seidler, P. Microwave-to-Optical Conversion with a Gallium Phosphide Photonic Crystal Cavity. Nat. Commun. 2022, 13, 2065. [Google Scholar] [CrossRef]
- Vainsencher, A.; Satzinger, K.J.; Peairs, G.A.; Cleland, A.N. Bi-Directional Conversion between Microwave and Optical Frequencies in a Piezoelectric Optomechanical Device. Appl. Phys. Lett. 2016, 109, 033107. [Google Scholar] [CrossRef]
- van Thiel, T.C.; Weaver, M.J.; Berto, F.; Duivestein, P.; Lemang, M.; Schuurman, K.L.; Žemlička, M.; Hijazi, F.; Bernasconi, A.C.; Lachman, E.; et al. Optical Readout of a Superconducting Qubit Using a Scalable Piezo-Optomechanical Transducer. arXiv 2023, arXiv:2310.06026. [Google Scholar]
- Kippenberg, T.J.; Rokhsari, H.; Carmon, T.; Scherer, A.; Vahala, K.J. Analysis of Radiation-Pressure Induced Mechanical Oscillation of an Optical Microcavity. Phys. Rev. Lett. 2005, 95, 033901. [Google Scholar] [CrossRef] [PubMed]
- Meesala, S.; Wood, S.; Lake, D.; Chiappina, P.; Zhong, C.; Beyer, A.D.; Shaw, M.D.; Jiang, L.; Painter, O. Non-Classical Microwave–Optical Photon Pair Generation with a Chip-Scale Transducer. Nat. Phys. 2024, 1–7. [Google Scholar] [CrossRef]
- Meesala, S.; Lake, D.; Wood, S.; Chiappina, P.; Zhong, C.; Beyer, A.D.; Shaw, M.D.; Jiang, L.; Painter, O. Quantum Entanglement between Optical and Microwave Photonic Qubits. arXiv 2023, arXiv:2312.13559. [Google Scholar]
- Liu, H.; Shi, X.; Yao, Y.; Luo, H.; Li, Q.; Huang, H.; Qi, H.; Zhang, Y.; Ren, Y.; Kelly, S.D.; et al. Emergence of High Piezoelectricity from Competing Local Polar Order-Disorder in Relaxor Ferroelectrics. Nat. Commun. 2023, 14, 1007. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Zhang, S.-J.; Xu, Z. Electronic Materials Research Laboratory, Key Laboratory of the Ministry of Education, Xi’an Jiaotong University, Xi’an 710049, China; Australian Institute of Advanced Materials, Wollongong University, Wollongong, NSW 2500, Australia Piezoelectricity—An important property for ferroelectrics during last 100 years. Acta Phys. Sin. 2020, 69, 217703. [Google Scholar] [CrossRef]
- Meenehan, S.M.; Cohen, J.D.; MacCabe, G.S.; Marsili, F.; Shaw, M.D.; Painter, O. Pulsed Excitation Dynamics of an Optomechanical Crystal Resonator near Its Quantum Ground State of Motion. Phys. Rev. X 2015, 5, 041002. [Google Scholar] [CrossRef]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum Ground State and Single-Phonon Control of a Mechanical Resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Lau, H.-K.; Clerk, A.A. Ground-State Cooling and High-Fidelity Quantum Transduction via Parametrically Driven Bad-Cavity Optomechanics. Phys. Rev. Lett. 2020, 124, 103602. [Google Scholar] [CrossRef] [PubMed]
- Rueda, A.; Hease, W.; Barzanjeh, S.; Fink, J.M. Electro-Optic Entanglement Source for Microwave to Telecom Quantum State Transfer. NPJ Quantum Inf. 2019, 5, 108. [Google Scholar] [CrossRef]
- Hease, W.; Rueda, A.; Sahu, R.; Wulf, M.; Arnold, G.; Schwefel, H.G.L.; Fink, J.M. Bidirectional Electro-Optic Wavelength Conversion in the Quantum Ground State. PRX Quantum 2020, 1, 020315. [Google Scholar] [CrossRef]
- Sahu, R.; Hease, W.; Rueda, A.; Arnold, G.; Qiu, L.; Fink, J.M. Quantum-Enabled Operation of a Microwave-Optical Interface. Nat. Commun. 2022, 13, 1276. [Google Scholar] [CrossRef]
- Han, X.; Fong, K.Y.; Tang, H.X. A 10-GHz Film-Thickness-Mode Cavity Optomechanical Resonator. Appl. Phys. Lett. 2015, 106, 161108. [Google Scholar] [CrossRef]
- Xu, M.; Han, X.; Fu, W.; Zou, C.-L.; Tang, H.X. Frequency-Tunable High-Q Superconducting Resonators via Wireless Control of Nonlinear Kinetic Inductance. Appl. Phys. Lett. 2019, 114, 192601. [Google Scholar] [CrossRef]
- Cai, L.; Pan, J.; Zhao, Y.; Wang, J.; Xiao, S. Whispering Gallery Mode Optical Microresonators: Structures and Sensing Applications. Phys. Status Solidi 2020, 217, 1900825. [Google Scholar] [CrossRef]
- Lambert, N.J.; Rueda, A.; Sedlmeir, F.; Schwefel, H.G.L. Coherent Conversion Between Microwave and Optical Photons—An Overview of Physical Implementations. Adv. Quantum Technol. 2020, 3, 1900077. [Google Scholar] [CrossRef]
- Galliou, S.; Goryachev, M.; Bourquin, R.; Abbé, P.; Aubry, J.P.; Tobar, M.E. Extremely Low Loss Phonon-Trapping Cryogenic Acoustic Cavities for Future Physical Experiments. Sci. Rep. 2013, 3, 2132. [Google Scholar] [CrossRef]
- Kharel, P.; Harris, G.I.; Kittlaus, E.A.; Renninger, W.H.; Otterstrom, N.T.; Harris, J.G.E.; Rakich, P.T. High-Frequency Cavity Optomechanics Using Bulk Acoustic Phonons. Sci. Adv. 2019, 5, eaav0582. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Dong, B.; Skehan, J.C.; Zervas, M.; Kippenberg, T.J.; Bhave, S.A. Hybrid Integrated Photonics Using Bulk Acoustic Resonators. Nat. Commun. 2020, 11, 3073. [Google Scholar] [CrossRef]
- Chou, M.-H.; Dumur, É.; Zhong, Y.P.; Peairs, G.A.; Bienfait, A.; Chang, H.-S.; Conner, C.R.; Grebel, J.; Povey, R.G.; Satzinger, K.J.; et al. Measurements of a Quantum Bulk Acoustic Resonator Using a Superconducting Qubit. Appl. Phys. Lett. 2020, 117, 254001. [Google Scholar] [CrossRef]
- Renninger, W.H.; Kharel, P.; Behunin, R.O.; Rakich, P.T. Bulk Crystalline Optomechanics. Nat. Phys. 2018, 14, 601–607. [Google Scholar] [CrossRef]
- Blésin, T.; Kao, W.; Siddharth, A.; Wang, R.N.; Attanasio, A.; Tian, H.; Bhave, S.A.; Kippenberg, T.J. Bidirectional Microwave-Optical Transduction Based on Integration of High-Overtone Bulk Acoustic Resonators and Photonic Circuits. arXiv 2023, arXiv:2308.02706. [Google Scholar] [CrossRef]
- Liu, J.; Raja, A.S.; Karpov, M.; Ghadiani, B.; Pfeiffer, M.H.P.; Lukashchuk, A.; Engelsen, N.J.; Guo, H.; Zervas, M.; Kippenberg, T.J. Ultralow-Power Chip-Based Soliton Microcombs for Photonic Integration. In Proceedings of the Optical Fiber Communication Conference (OFC) 2019; Optica Publishing Group: Washington, DC, USA, 2019; p. 1. [Google Scholar]



| Mechanical Resonator | [kHz] | BW [MHz] | [K] | |||||
|---|---|---|---|---|---|---|---|---|
| Membrane [25,26,54] | 0.06 | 132 | 132 | * | 0.99 | 38 | 0.012 | 0.035 |
| Phononic Crystal [29] | 500 | 0.04 | 0.57 | * | 0.57 | 1 | 0.015 | |
| Microdisk [37] | 19 | 0.4 | 7 | 1.6 | 1 | |||
| BAR [91] | 0.42 | - | - | 25 | Room Temperature |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhang, Y.; Tang, J.; Chen, P.; Zeng, L.; Xia, Z.; Xing, W.; Zhou, Q.; Wang, Y.; Song, H.; et al. Optomechanical Microwave-to-Optical Photon Transducer Chips: Empowering the Quantum Internet Revolution. Micromachines 2024, 15, 485. https://doi.org/10.3390/mi15040485
Xu X, Zhang Y, Tang J, Chen P, Zeng L, Xia Z, Xing W, Zhou Q, Wang Y, Song H, et al. Optomechanical Microwave-to-Optical Photon Transducer Chips: Empowering the Quantum Internet Revolution. Micromachines. 2024; 15(4):485. https://doi.org/10.3390/mi15040485
Chicago/Turabian StyleXu, Xinyao, Yifei Zhang, Jindao Tang, Peiqin Chen, Liping Zeng, Ziwei Xia, Wenbo Xing, Qiang Zhou, You Wang, Haizhi Song, and et al. 2024. "Optomechanical Microwave-to-Optical Photon Transducer Chips: Empowering the Quantum Internet Revolution" Micromachines 15, no. 4: 485. https://doi.org/10.3390/mi15040485
APA StyleXu, X., Zhang, Y., Tang, J., Chen, P., Zeng, L., Xia, Z., Xing, W., Zhou, Q., Wang, Y., Song, H., Guo, G., & Deng, G. (2024). Optomechanical Microwave-to-Optical Photon Transducer Chips: Empowering the Quantum Internet Revolution. Micromachines, 15(4), 485. https://doi.org/10.3390/mi15040485







