Design and Implementation of a Four-Unit Array Piezoelectric Bionic MEMS Vector Hydrophone
Abstract
:1. Introduction
2. Materials and Methods Sensor Principle and Structural Design
2.1. Bionic Principle
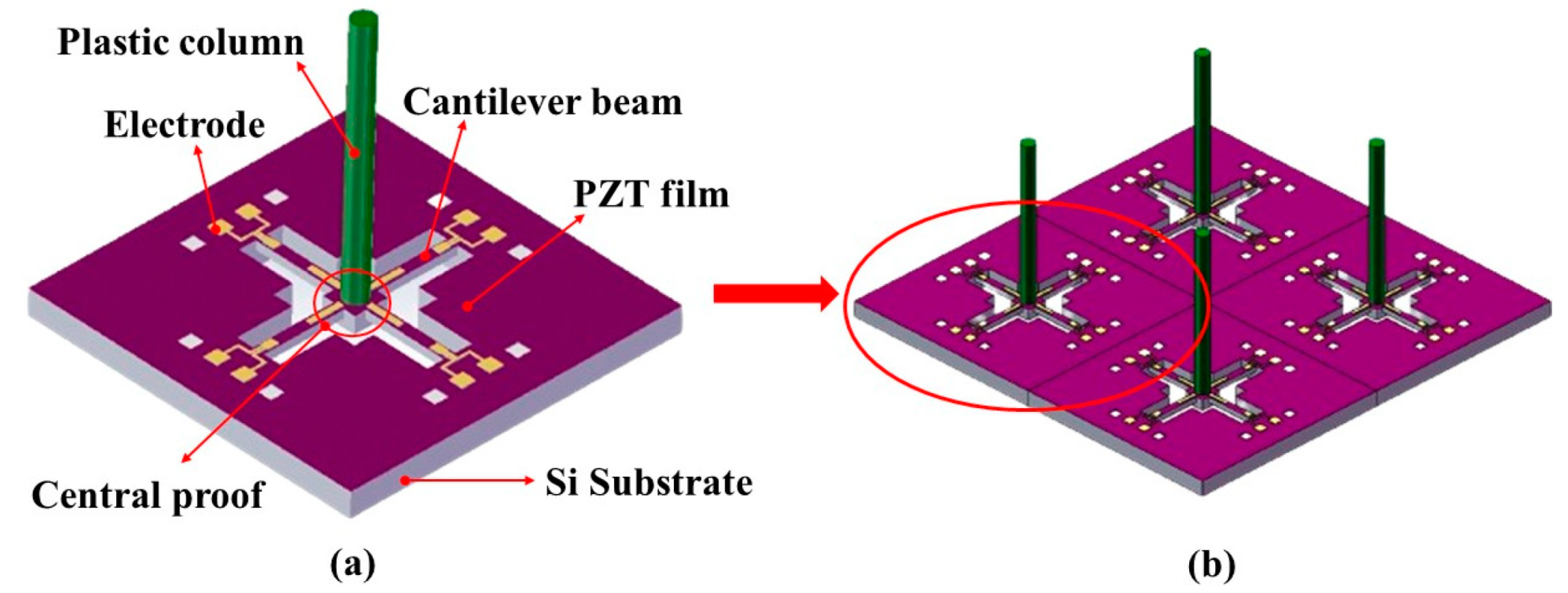
2.2. Structure of the Hydrophone
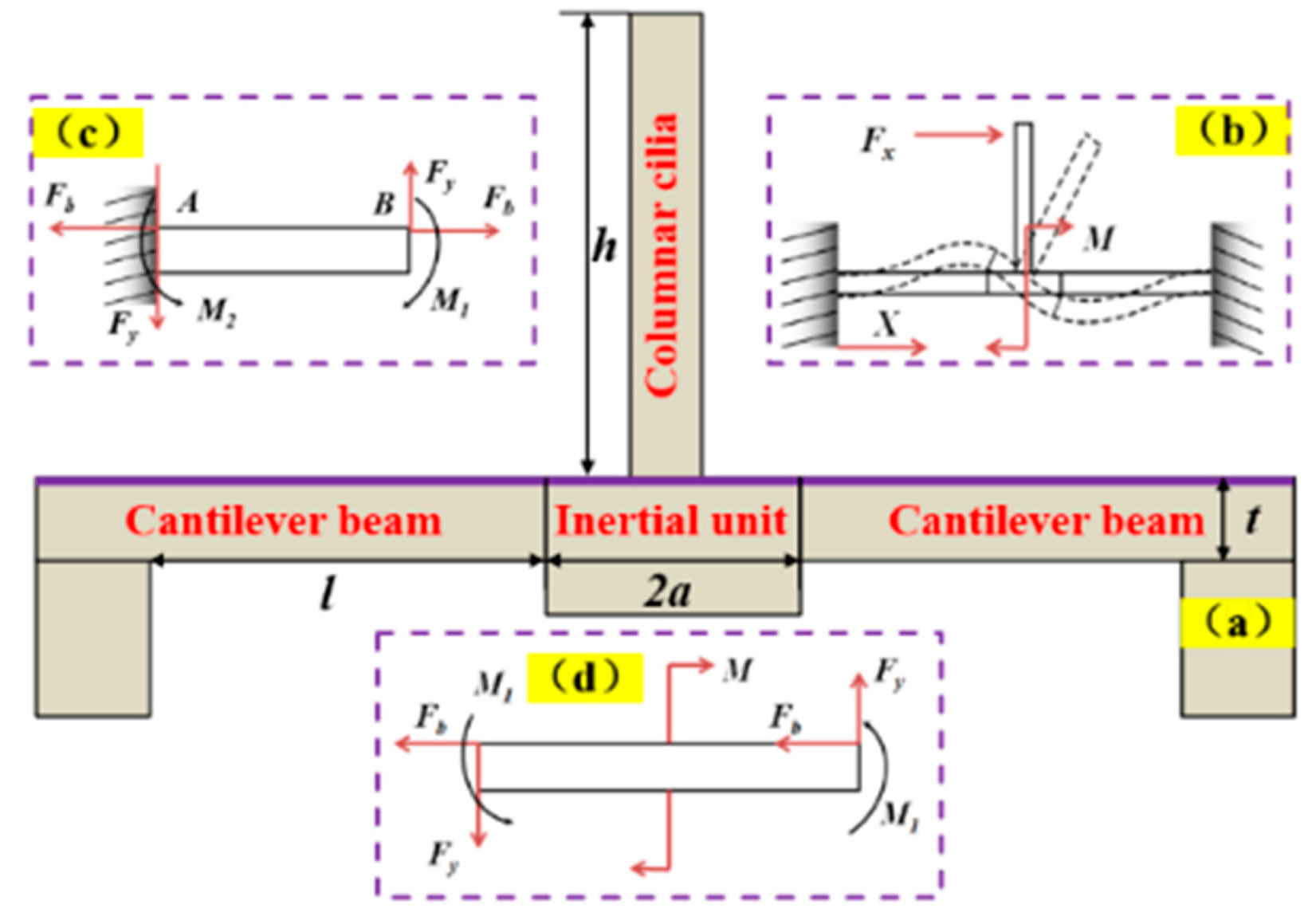
2.3. Stress and Resonance Frequencies of the Cantilever Beam
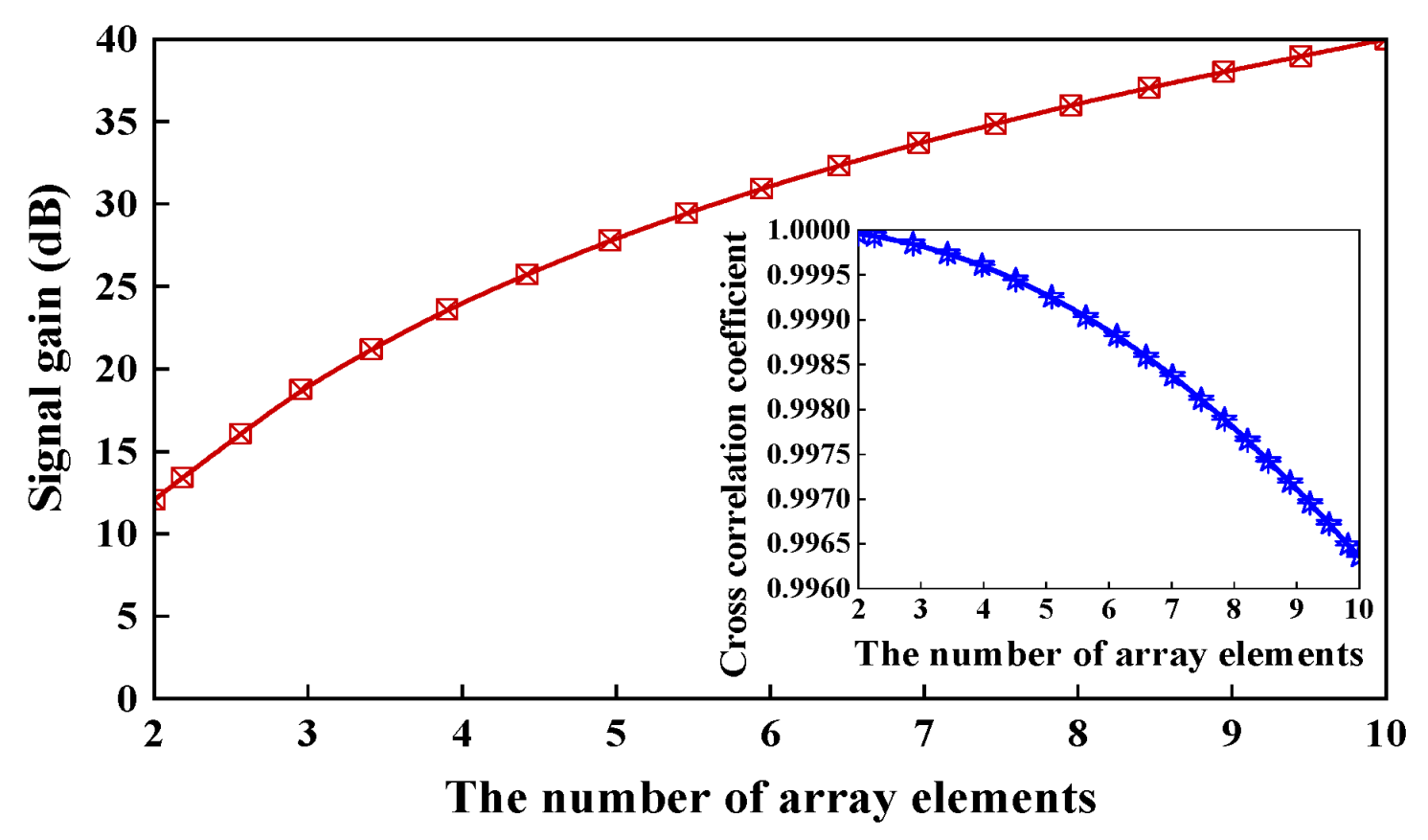
3. Sensitivity Gains of Multi-Unit Hydrophones
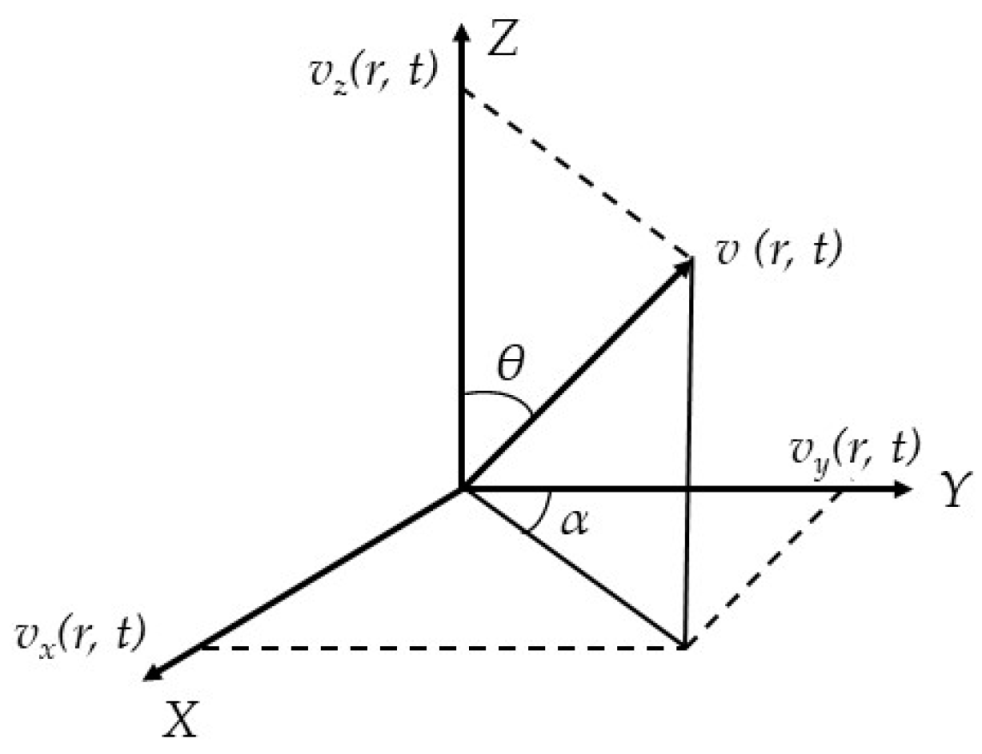
4. Directional Principle of MEMS Vector Hydrophone
5. Simulation Analysis
6. Fabrication and Experiment
6.1. Fabrication
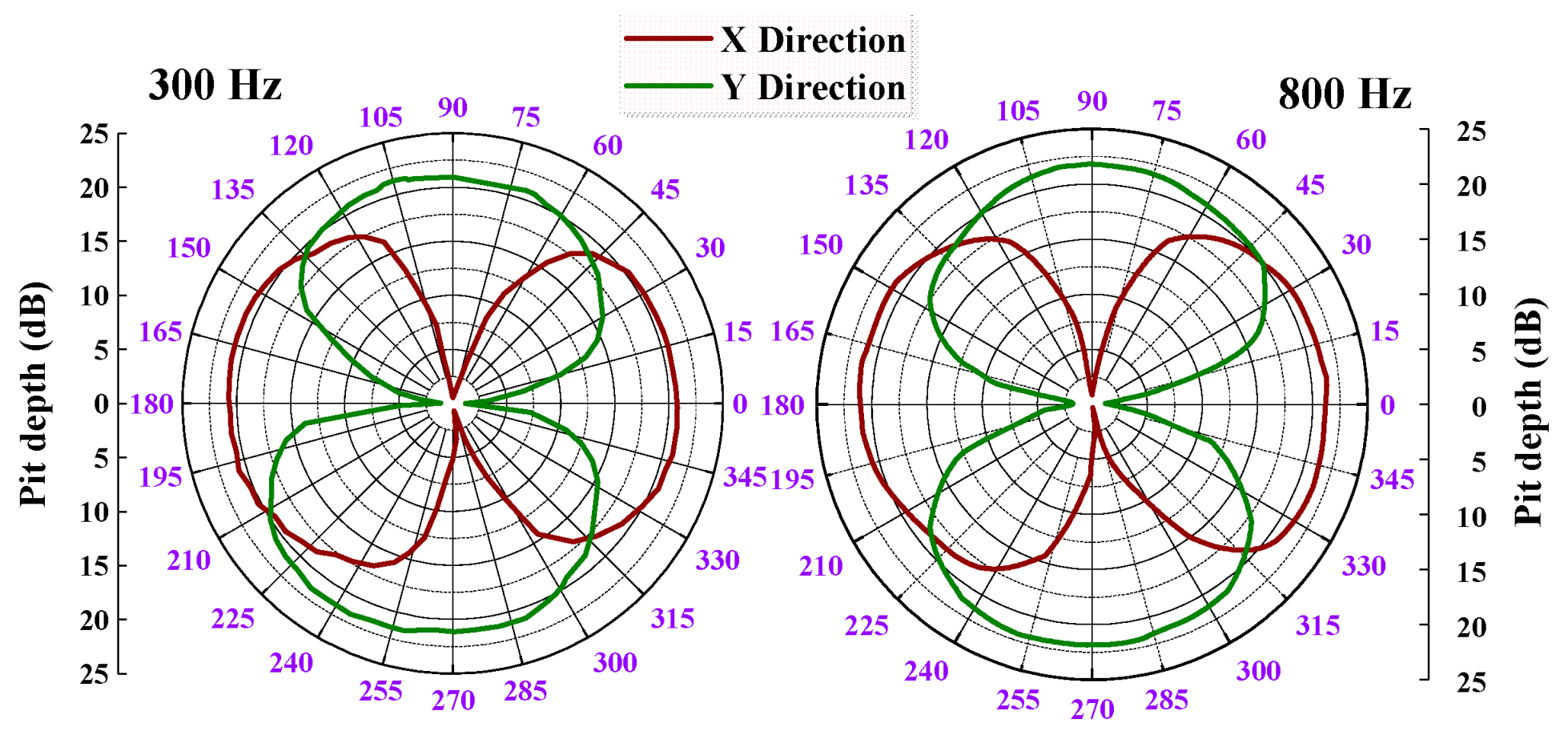
6.2. Experimental Equipment and Characteristics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ge, C.; Cretu, E. Bionic MEMS for Touching and Hearing Sensations: Recent Progress, Challenges, and Solutions. J. Bionic Eng. 2022, 19, 590–615. [Google Scholar] [CrossRef]
- Islam, T.U.; Wang, Y.; Aggarwal, I.; Cui, Z.; Amirabadi, H.E.; Garg, H.; Kooi, R.; Venkataramanachar, B.B.; Wang, T.; Zhang, S.; et al. Microscopic Artificial Cilia—A Review. Lab Chip 2022, 22, 1650–1679. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, P.G.; Walker, R.G. Molecular Basis of Mechanosensory Transduction. Nature 2001, 413, 194–202. [Google Scholar] [CrossRef]
- Krijnen, G.J.M.; Dijkstra, M.; Baar, J.J.V.; Shankar, S.S.; Kuipers, W.J.; Boer, R.J.H.D.; Altpeter, D.; Lammerink, T.S.J.; Wiegerink, R. MEMS Based Hair Flow-sensors as Model Systems for Acoustic Perception Studies. Nanotechnology 2006, 17, S84–S89. [Google Scholar] [CrossRef]
- Ozevin, D. MEMS Acoustic Emission Sensors. Appl. Sci. 2020, 10, 8966. [Google Scholar] [CrossRef]
- Ali, W.R.; Prasad, M. Piezoelectric MEMS Based Acoustic Sensors: A review. Sens. Actuators A Phys. 2020, 301, 111756. [Google Scholar] [CrossRef]
- Xue, C.; Chen, S.; Zhang, W.; Zhang, B.; Zhang, G.; Qiao, H. Design, Fabrication, and Preliminary Characterization of a Novel MEMS Bionic Vector Hydrophone. Microelectron. J. 2007, 38, 1021–1026. [Google Scholar] [CrossRef]
- Bai, B.; Ren, Z.; Ding, J.; Xu, W.; Zhang, G.; Liu, J.; Zhang, W.; Xue, C.; Zhang, B.; Wang, R. Cross-supported Planar MEMS Vector Hydrophone for High Impact Resistance. Sens. Actuators A Phys. 2017, 263, 563–570. [Google Scholar] [CrossRef]
- Shi, S.; Geng, W.; He, J.; Hou, X.; Mu, J.; Li, J.F.; Chou, X. Design and Fabrication of a Novel MEMS Piezoelectric Hydrophone. Sens. Actuators A Phys. 2020, 313, 112203. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, N.; Xu, Q.; Pei, Y.; Lian, Y.; Wang, W.; Zhang, G.; Zhang, W. Design and Implementation of Anulus-shaped Ciliary Structure for Four-unit MEMS Vector Hydrophone. Int. J. Metrol. Qual. Eng. 2021, 12, 4. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, G.; Song, X.; Liu, Y.; Zhang, W. Design of the Monolithic Integrated Array MEMS Hydrophone. IEEE Sens. J. 2016, 16, 989–995. [Google Scholar]
- Liu, M.; Nie, L.; Li, S.; Jia, W.; Zhang, L.; Zhang, G.; Zhang, W. Array MEMS Vector Hydrophone Oriented at Different Direction Angles. Sensors 2019, 19, 4282. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Zhang, G.; Shen, N.; Shang, Z.; Pei, Y.; Ding, J.; Zhang, L.; Wang, R.; Zhang, W. Design and Analysis of a Multiple Sensor Units Vector Hydrophone. AIP Adv. 2018, 8, 085124. [Google Scholar] [CrossRef]
- Saheban, H.; Kordrostami, Z. Hydrophones, Fundamental Features, Design Considerations, and Various Structures: A review. Sens. Actuators A Phys. 2021, 329, 112790. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Fernando, S.N.; Chai, K.T.; Gu, Y. AlN-on-SOI Platform-based Micro-machined Hydrophone. Appl. Phys. Lett. 2016, 109, 60. [Google Scholar] [CrossRef]
- Jia, L.; Shi, L.; Liu, C.; Yao, Y.; Sun, C.; Wu, G. Design and Characterization of an Aluminum Nitride-Based MEMS Hydrophone with Biologically Honeycomb Architecture. IEEE Trans. Electron Devices 2021, 68, 4656–4663. [Google Scholar] [CrossRef]
- Jia, L.; Shi, L.; Lu, Z.; Sun, C.; Wu, G. A High-Performance 9.5% Scandium-Doped Aluminum Nitride Piezoelectric MEMS Hydrophone with Honeycomb Structure. IEEE Electron Device Lett. 2021, 42, 1845–1848. [Google Scholar] [CrossRef]
- Ganji, B.A.; Nateri, M.S.; Dardel, M. Design and modeling of a novel high sensitive MEMS piezoelectric vector hydrophone. Microsyst. Technol. 2018, 24, 2085–2095. [Google Scholar] [CrossRef]
- Zhang, B.; Qiao, H.; Chen, S.; Liu, J.; Zhang, W.; Xiong, J.; Xue, C.; Zhang, G. Modeling and Characterization of a Micromachined Artificial Hair Cell Vector Hydrophone. Microsyst. Technol. 2008, 14, 821–828. [Google Scholar] [CrossRef]
- Xue, C.; Tong, Z.; Zhang, B.; Zhang, W. A Novel Vector Hydrophone Based on the Piezoresistive Effect of Resonant Tunneling Diode. IEEE Sens. J. 2008, 8, 401–402. [Google Scholar] [CrossRef]
- Tiwari, B.; Babu, T.; Choudhary, R.N.P. Piezoelectric Lead Zirconate Titanate as an Energy Material: A review study. Mater. Today 2021, 43, 407–412. [Google Scholar] [CrossRef]
- Zhang, W.; Guan, L.; Zhang, G.; Xue, C.; Zhang, K.; Wang, L. Research of DOA Estimation Based on Single MEMS Vector Hydrophone. Sensors 2009, 9, 6823–6834. [Google Scholar] [CrossRef] [PubMed]
- Pierce, A.D. Acoustics—An Introduction to Its Physical Principles and Applications; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Chen, X.; Qiao, X.; Zhang, L.; Zhang, J.; Zhang, Q.; He, J.; Mu, J.; Hou, X.; Chou, X.; Geng, W. Temperature Dependence of Ferroelectricity and Domain Switching Behavior in Pb(Zr0.3Ti0.7)O3 Ferroelectric Thin Films. Ceram. Int. 2019, 45, 18030–18036. [Google Scholar] [CrossRef]
- Liu, M.; Jian, Z.; Zhang, G.; Guo, N.; Zhang, W. Design of MEMS Bionic Vector Hydrophone Based on NBR Sound-transparent Cap. Sens. Rev. 2015, 35, 303–309. [Google Scholar] [CrossRef]
- Zhao, A.; Zhou, B.; Li, J. Calibration of Vector Hydrophones in Deep Water. Appl. Mech. Mater. 2013, 336, 303–308. [Google Scholar] [CrossRef]
- Kosobrodov, R.A.; Nekrasov, V.N. Effect of the Diffraction of Sound by the Carrier of Hydroacoustic Equipment on the Results of Measurements. Acoust. Phys. 2001, 47, 323–328. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, L.; Zhang, W.; Xue, C. Design of a Monolithic Integrated Three-dimensional MEMS Bionic Vector Hydrophone. Microsyst. Technol. 2014, 21, 1697–1708. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Wu, S.; Xue, C.; Yang, S.; Zhang, W. A Bionic Fish Cilia Median-Low Frequency Three-Dimensional Piezoresistive MEMS Vector Hydrophone. Nano-Micro Lett. 2014, 6, 136–142. [Google Scholar]

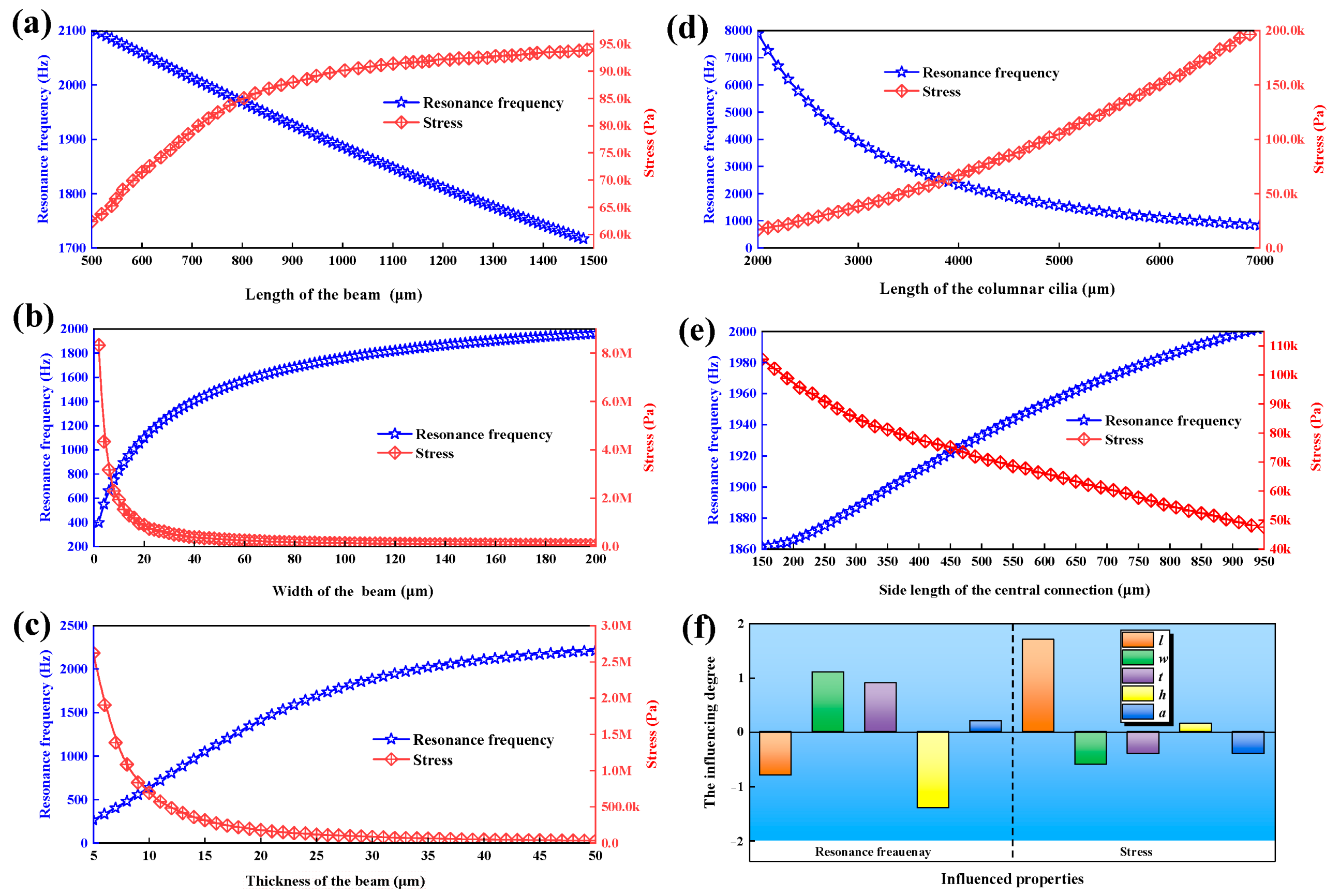
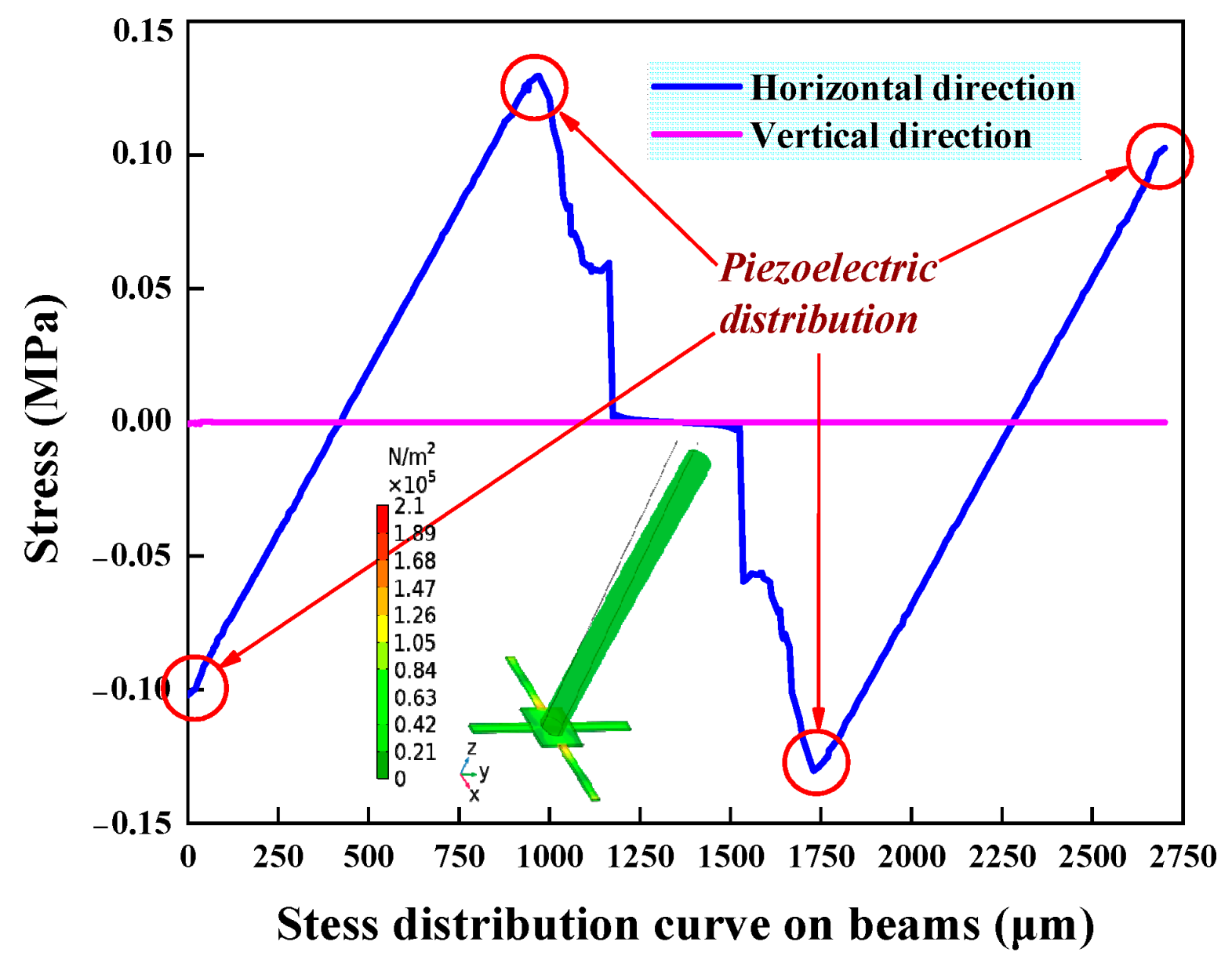
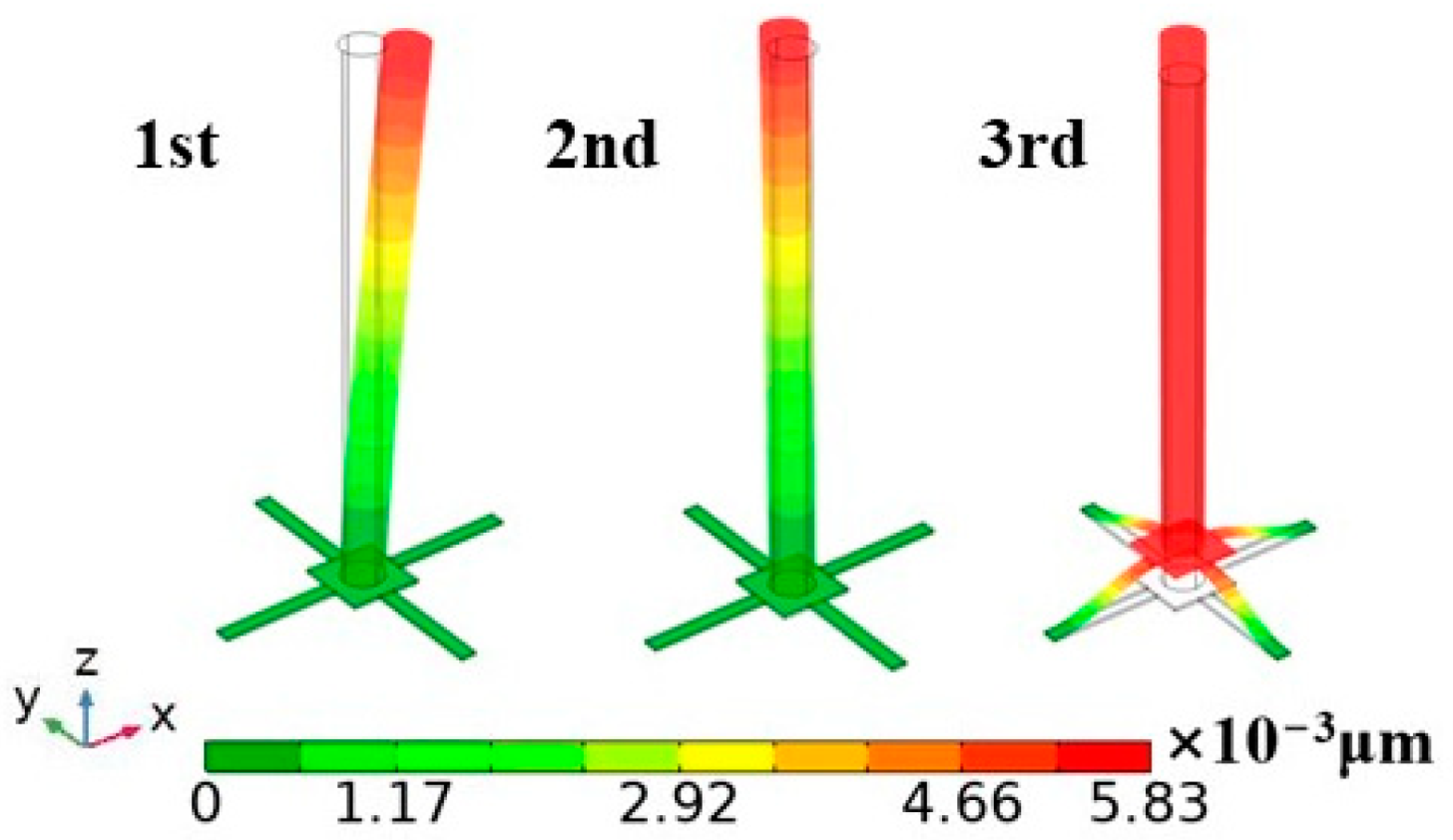

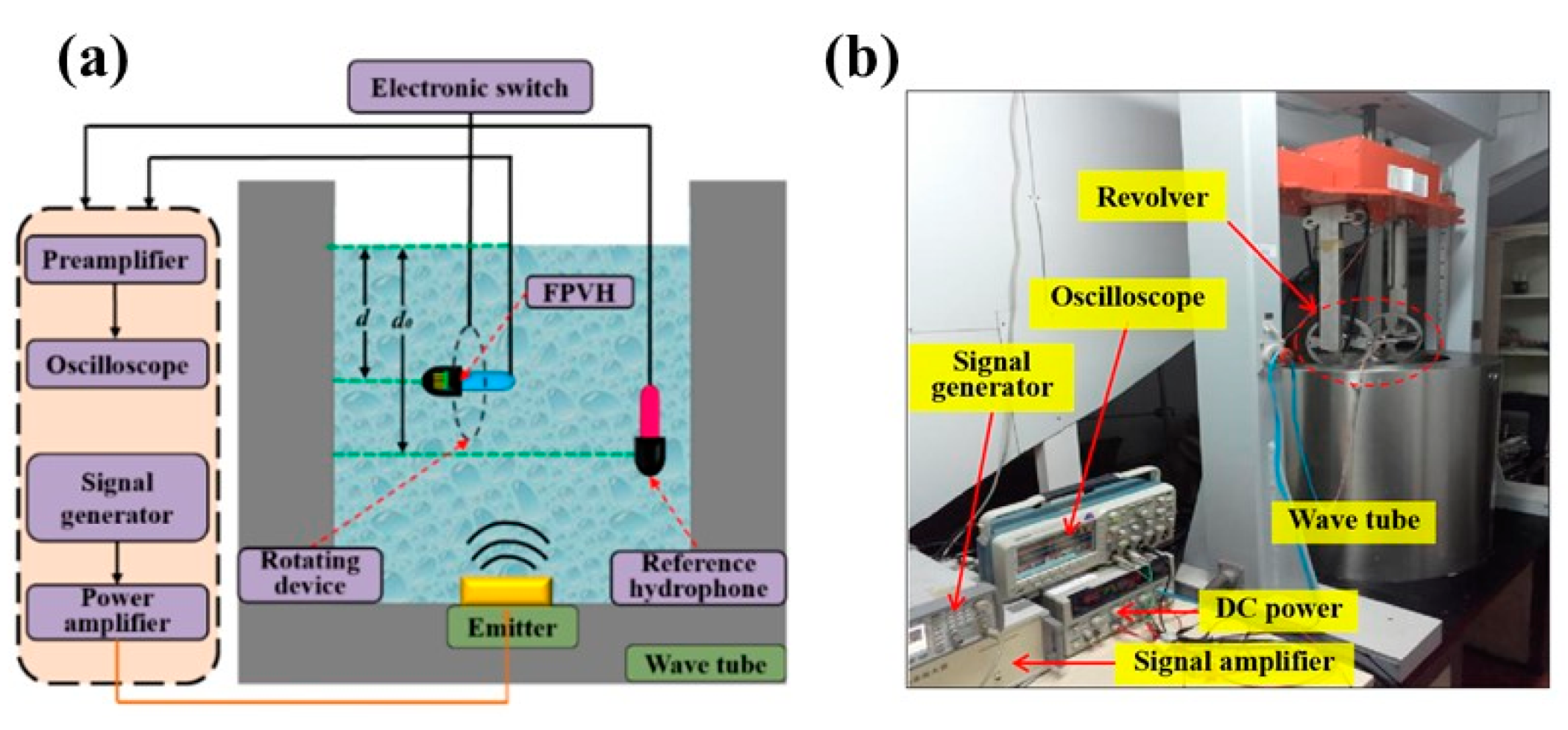

| Structure Parameters | Parameter Value (μm) |
|---|---|
| Length of beam (l) | 1000 |
| width of beam (b) | 130 |
| thickness of beam (t) | 35 |
| side length of central inertial unit (2a) | 700 |
| height of cilium (h) | 4500 |
| diameter of cilium (D) | 400 |
| side length of one-units (N × N units) | 5000 × N |
| Hydrophones | Material | Sensitivity | Bandwidth | Directivity | Ref. | Technology |
|---|---|---|---|---|---|---|
| FPVH | PZT | −167.93 dB@1000 Hz | 20 Hz~1200 Hz | “8” | This work | piezoelectric |
| OPVH | PZT | −179.13 dB@1000 Hz | 20 Hz~1200 Hz | “8” | [9] | piezoelectric |
| FCVH | resistance | −177.14 dB@1000 Hz | 20 Hz~1000 Hz | “8” | [13] | piezoresistive |
| AIN-on-SOI | AIN | −182.5 dB (re: 1 V/μPa) | 10 Hz~100 Hz | “omni” | [15] | piezoelectric |
| Honeycomb | AlN | −178 dB (re: 1 V/μPa) | 10 Hz~50 kHz | / | [16] | piezoelectric |
| Honeycomb | ScAlN | −164.5 dB (re: 1 V/μPa) | 10 Hz~50 kHz | / | [17] | piezoelectric |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Zhang, X.; Wang, Z.; Ma, L.; Kang, K.; Pang, Y.; Ma, H.; Hu, J. Design and Implementation of a Four-Unit Array Piezoelectric Bionic MEMS Vector Hydrophone. Micromachines 2024, 15, 524. https://doi.org/10.3390/mi15040524
Shi S, Zhang X, Wang Z, Ma L, Kang K, Pang Y, Ma H, Hu J. Design and Implementation of a Four-Unit Array Piezoelectric Bionic MEMS Vector Hydrophone. Micromachines. 2024; 15(4):524. https://doi.org/10.3390/mi15040524
Chicago/Turabian StyleShi, Shuzheng, Xiaoyong Zhang, Zhanying Wang, Liyong Ma, Kai Kang, Yongjun Pang, Hong Ma, and Jinjiang Hu. 2024. "Design and Implementation of a Four-Unit Array Piezoelectric Bionic MEMS Vector Hydrophone" Micromachines 15, no. 4: 524. https://doi.org/10.3390/mi15040524
APA StyleShi, S., Zhang, X., Wang, Z., Ma, L., Kang, K., Pang, Y., Ma, H., & Hu, J. (2024). Design and Implementation of a Four-Unit Array Piezoelectric Bionic MEMS Vector Hydrophone. Micromachines, 15(4), 524. https://doi.org/10.3390/mi15040524







