Design, Modeling, and Experimental Validation of an Active Microcatheter Driven by Shape Memory Effects
Abstract
:1. Introduction
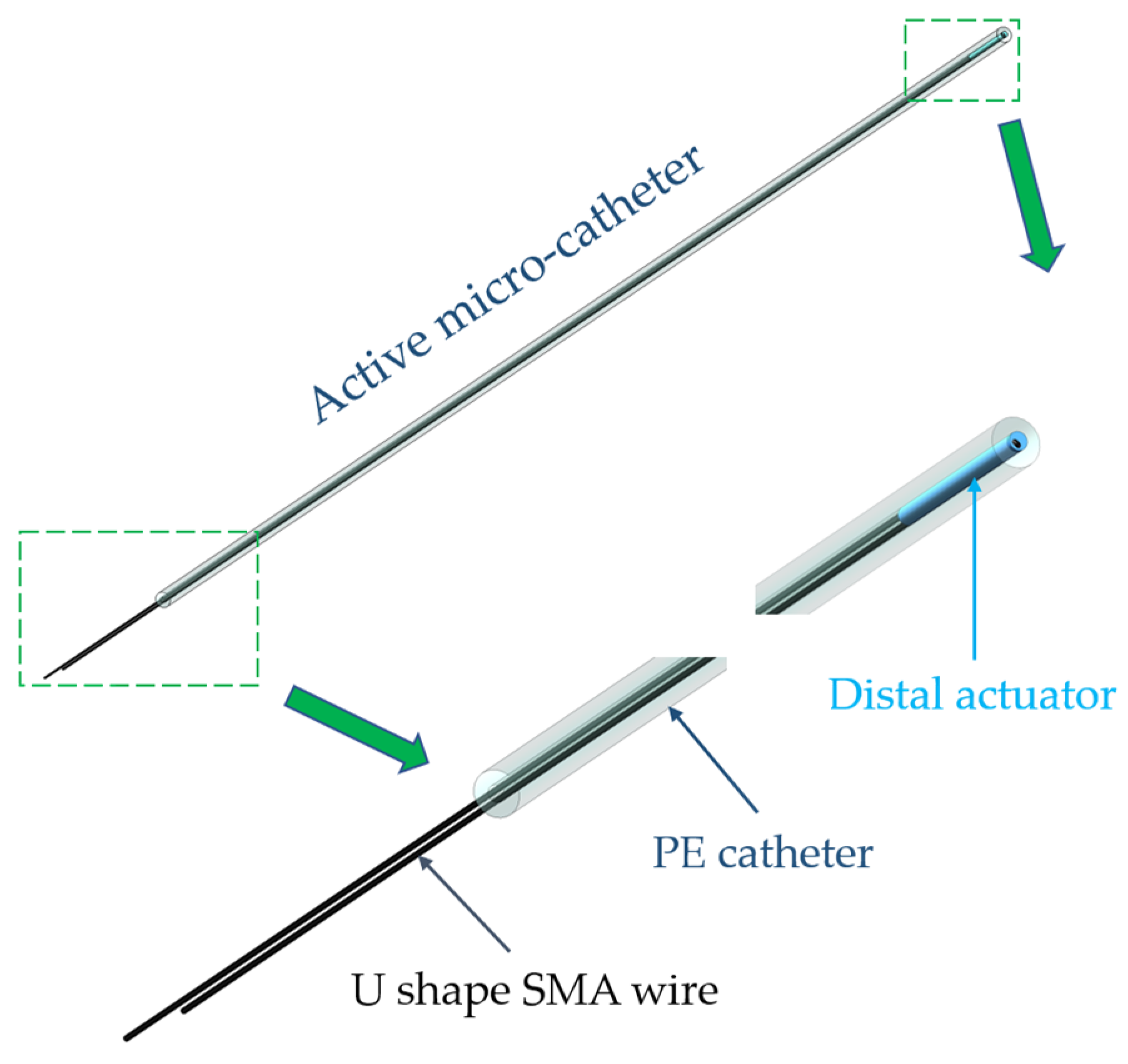
2. Structural Design and Working Mechanism
3. Mathematical Model and Simulation
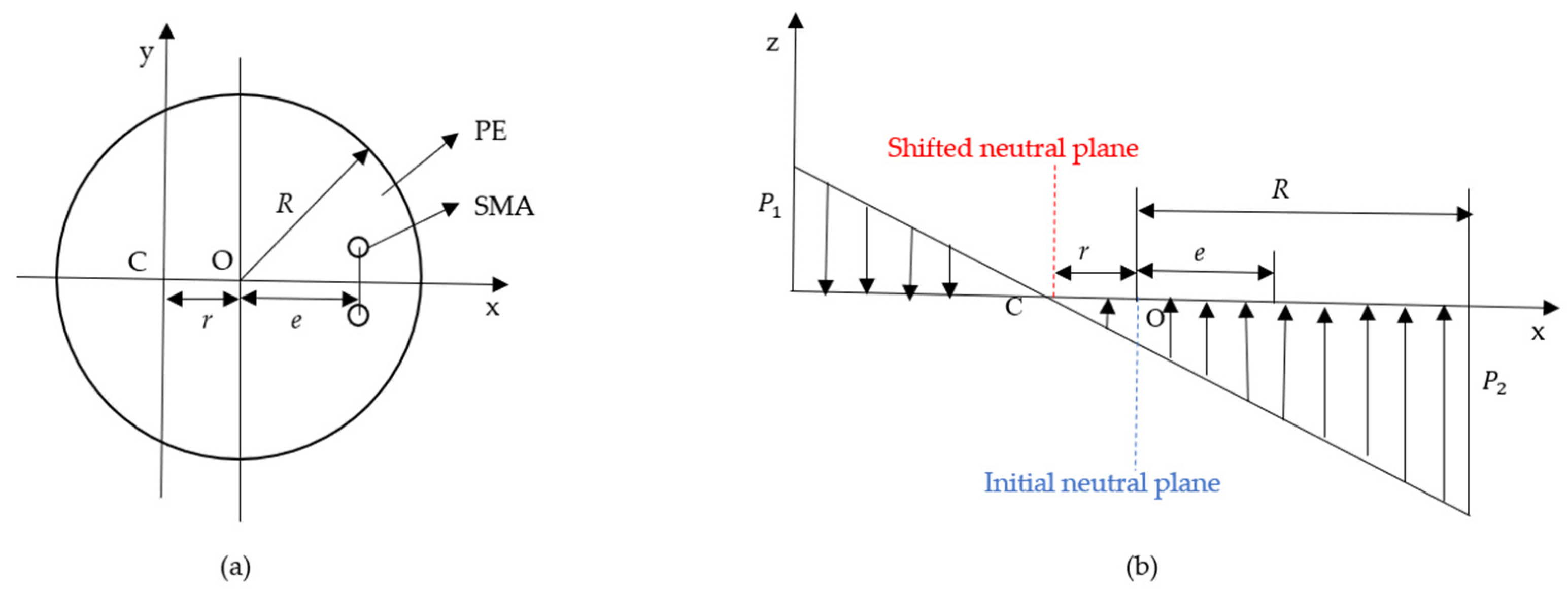
3.1. Mathematical Modeling of the Microcatheter
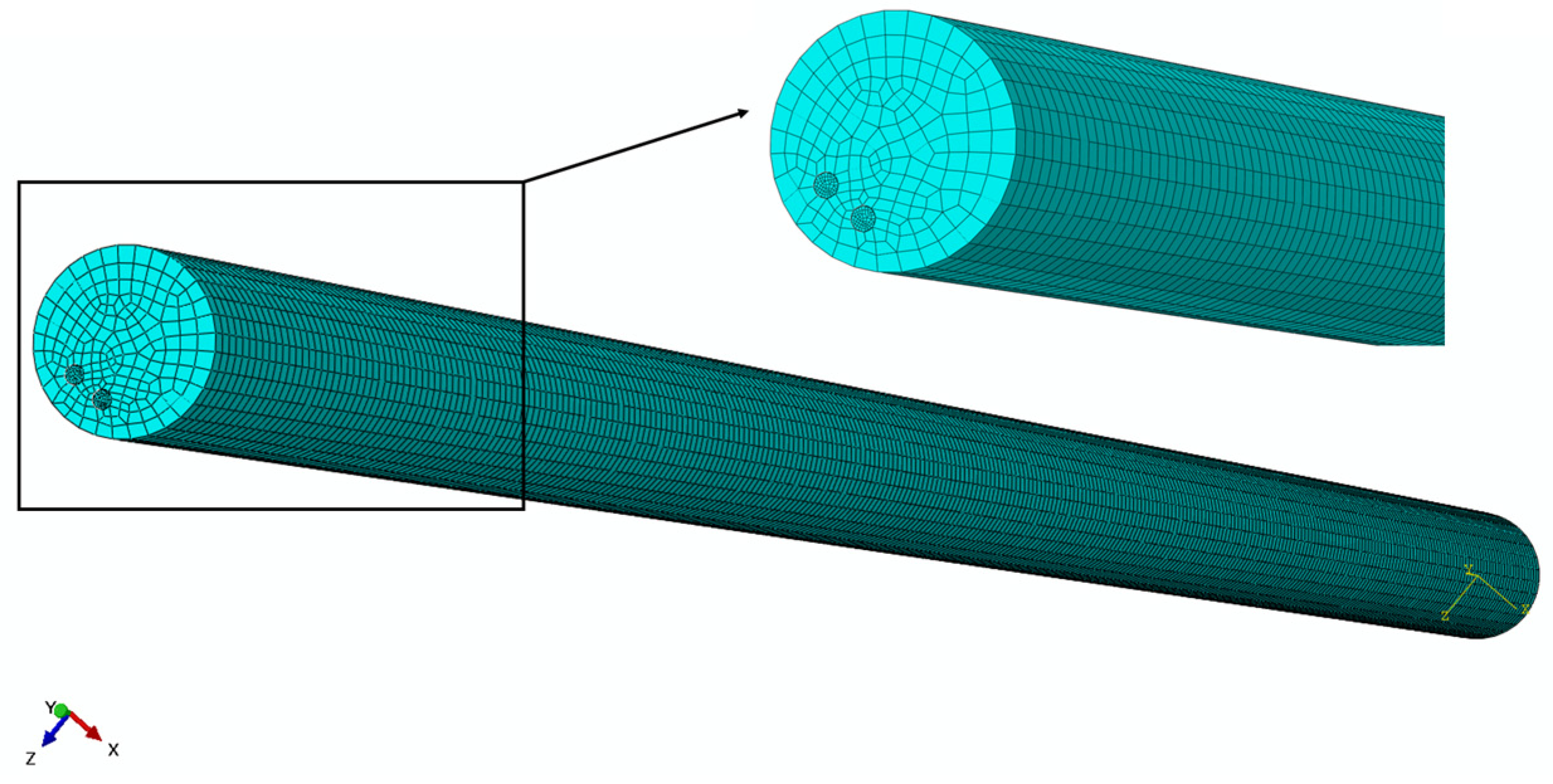
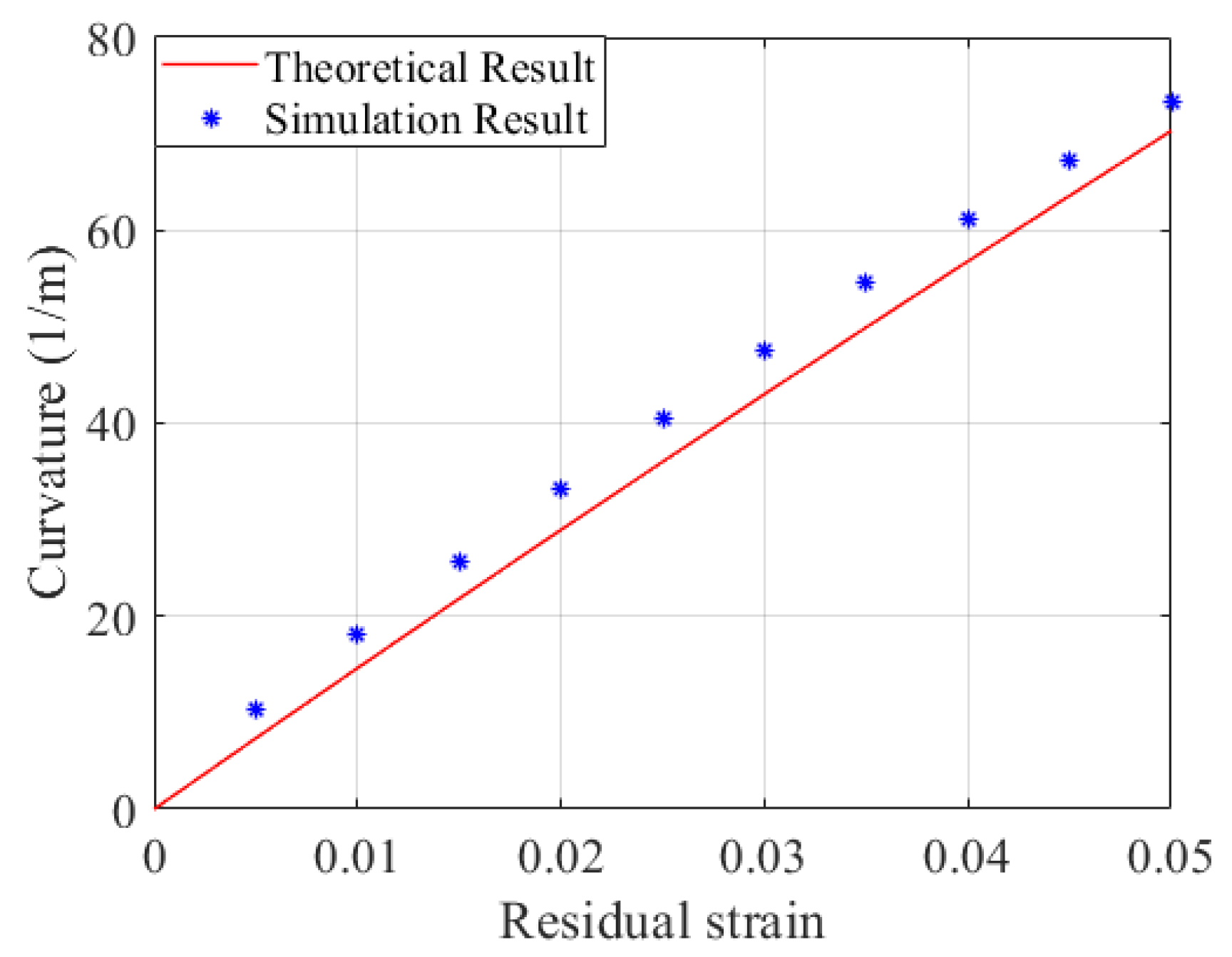
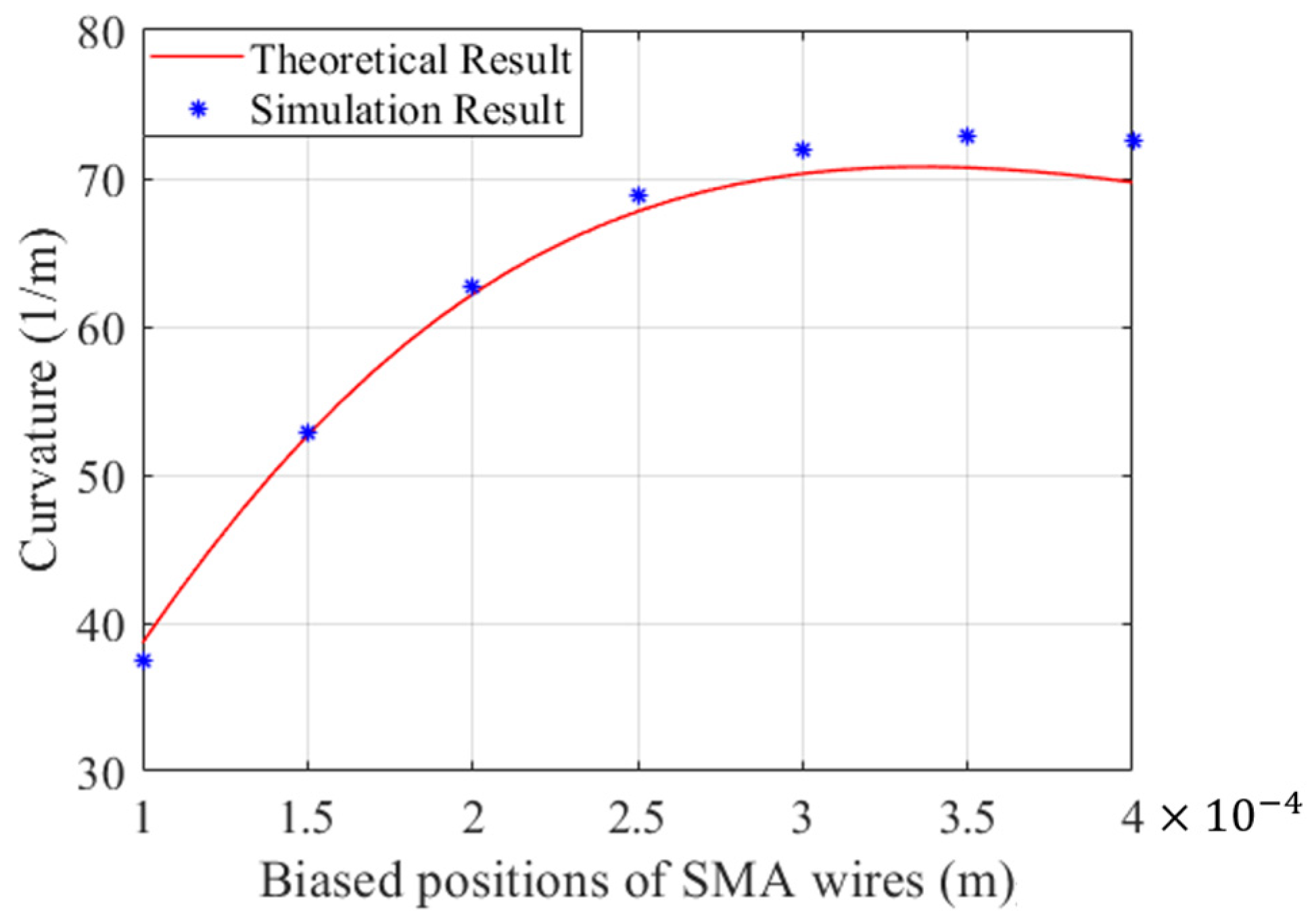
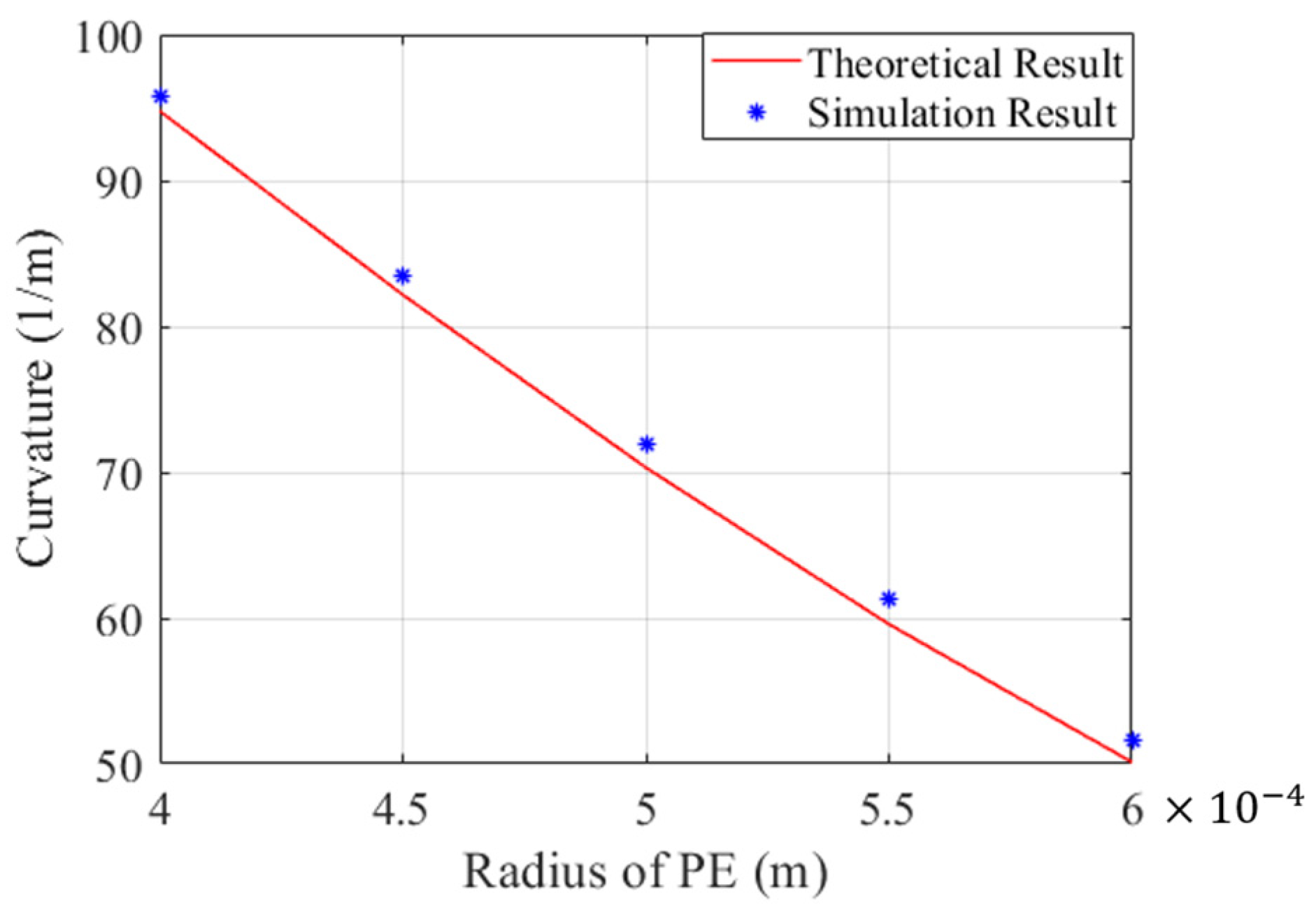
3.2. Simulation by Finite Element Method
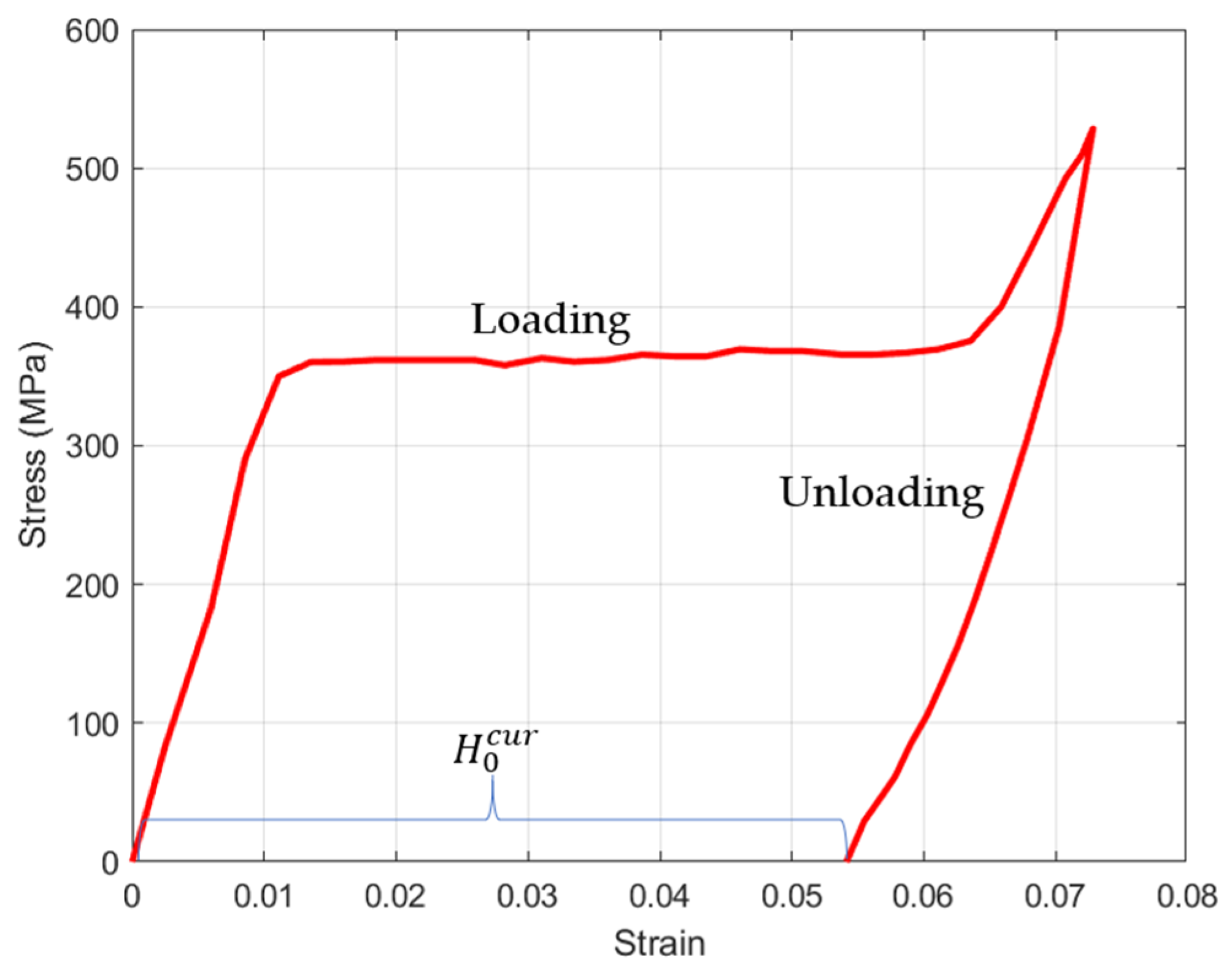
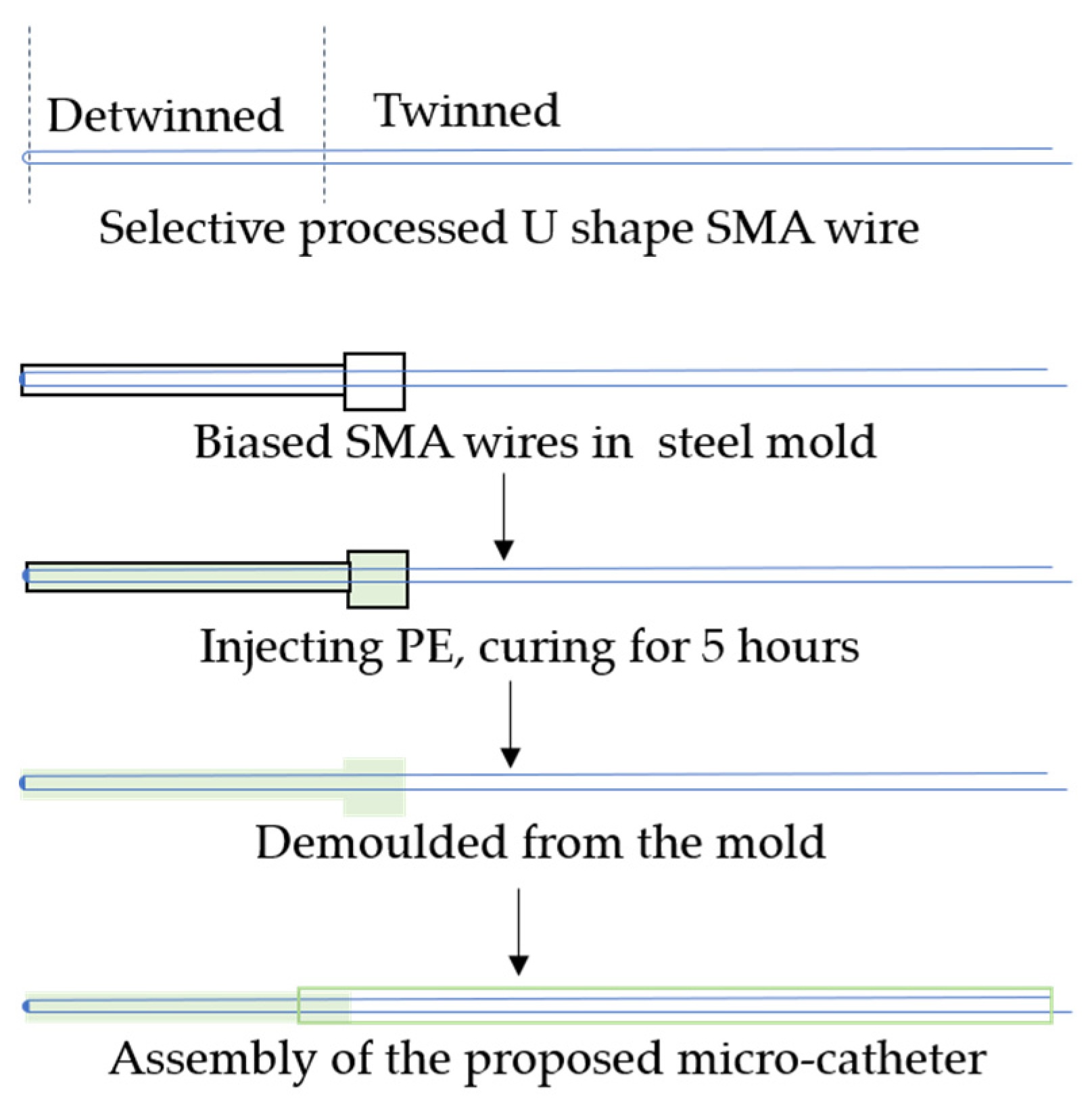
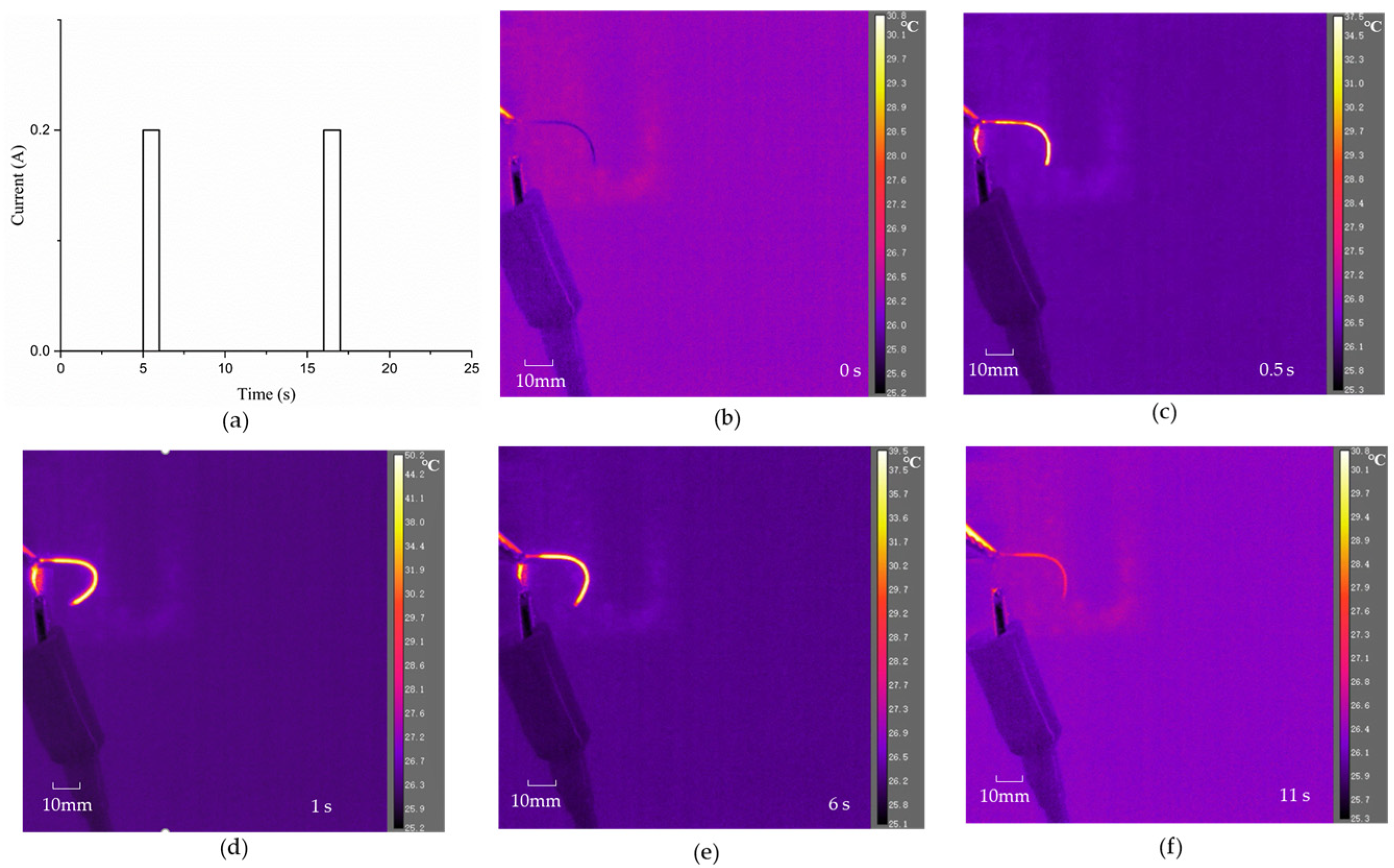
4. Fabrication and Experiment
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dupont, P.E.; Nelson, B.J.; Goldfarb, M.; Hannaford, B.; Menciassi, A.; O’Malley, M.K.; Simaan, N.; Valdastri, P.; Yang, G.-Z. A decade ret-rospective of medical robotics research from 2010 to 2020. Sci. Robot. 2021, 6, eabi8017. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Zhang, X.; Gao, C.; Jiang, S.; Wu, H.; Liu, Z.; Dou, T. Burden and trends of brain and central nervous system can-cer from 1990 to 2019 at the global, regional, and country levels. Arch. Public Health 2022, 80, 209. [Google Scholar] [CrossRef]
- Bhatt, N.; Gurung, H.; Soni, S.; Singla, A. Effect of biasing conditions on the performance of a SMA spring actuator under thermo-mechanical loading. Mech. Adv. Mater. Struct. 2022, 29, 4599–4613. [Google Scholar] [CrossRef]
- Yao, D.R.; Kim, I.; Yin, S.; Gao, W. Multimodal Soft Robotic Actuation and Locomotion. Adv. Mater. 2024, e2308829. [Google Scholar] [CrossRef] [PubMed]
- Gomes da Silva, G.T.; Nobre Dantas Grassi, E.; de Amorim, W.F., Jr.; de Araujo, C.J. Pull-out resistance of shape memory alloy nickel-titanium ribbons embedded in silicone matrix for development of flexible composites. J. Intell. Mater. Syst. Struct. 2021, 32, 430–441. [Google Scholar] [CrossRef]
- Kang, D.-H.; Park, J. Endovascular stroke therapy focused on stent retriever thrombectomy and direct clot aspira-tion: Historical review and modern application. Journal of Korean Neurosurg. Soc. 2017, 60, 335–347. [Google Scholar] [CrossRef]
- Shi, C.; Ishihara, H. Performance Evaluation of a Vascular Interventional Surgery Robotic System with Visual-Based Force Feedback. Machines 2023, 11, 727. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, P.; Jiang, B.; Yan, H. Research trends in methods for controlling macro-micro motion platforms. Nanotechnol. Precis. Eng. 2023, 6, 19384. [Google Scholar] [CrossRef]
- Chen, P.; Wang, Y.; Tian, D.; Guo, Y.; Xu, K. The Catheter and Guidewire Operating Sys-tems of Vascular Interventional Surgical Robots: A Systematic Review. IEEE Trans. Med. Robot. Bionics 2023, 5, 180–195. [Google Scholar] [CrossRef]
- Leber, A.; Dong, C.; Laperrousaz, S.; Banerjee, H.; Abdelaziz, M.E.M.K.; Bartolomei, N.; Schyrr, B.; Temelkuran, B.; Sorin, F. Highly Integrated Multi-Material Fibers for Soft Robotics. Adv. Sci. 2023, 10, 2204016. [Google Scholar] [CrossRef]
- Gopesh, T.; Wen, J.H.; Santiago-Dieppa, D.; Yan, B.; Pannell, J.S.; Khalessi, A.; Norbash, A.; Friend, J. Soft robotic steerable mi-crocatheter for the endovascular treatment of cerebral disorders. Sci. Robot. 2021, 6, eabf0601. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, L.; Xiang, Y.; Liao, F.; Li, N.; Li, J.; Wang, J.; Wu, Q.; Zhou, C.; Yang, Y.; et al. Magnetic soft microfiberbots for robotic embolization. Sci. Robot. 2024, 9, eadh2479. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Genevriere, E.; Harker, P.; Choe, J.; Balicki, M.; Regenhardt, R.W.; Vranic, J.E.; Dmytriw, A.A.; Patel, A.B.; Zhao, X. Telerobotic neurovascular in-terventions with magnetic manipulation. Sci. Robot. 2022, 7, eabg9907. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Parada, G.A.; Liu, S.; Zhao, X. Ferromagnetic soft continuum robots. Sci. Robot. 2019, 4, eaax7329. [Google Scholar] [CrossRef] [PubMed]
- Dreyfus, R.; Boehler, Q.; Lyttle, S.; Gruber, P.; Lussi, J.; Chautems, C.; Gervasoni, S.; Berberat, J.; Seibold, D.; Ochsenbein-Kölble, N.; et al. Dexterous helical magnetic robot for improved endovascular access. Sci. Robot. 2024, 9, eadh0298. [Google Scholar] [CrossRef] [PubMed]
- Piskarev, Y.; Sun, Y.; Righi, M.; Boehler, Q.; Chautems, C.; Fischer, C.; Nelson, B.J.; Shintake, J.; Floreano, D. Fast-Response Variable-Stiffness Magnetic Catheters for Minimally Invasive Surgery. Adv. Sci. 2024, 11, e2305537. [Google Scholar] [CrossRef] [PubMed]
- Mohd-Jani, J.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Lohse, F.; Kopelmann, K.; Grellmann, H.; Ashir, M.; Gereke, T.; Häntzsche, E.; Sennewald, C.; Cherif, C. Experimental and Numerical Analysis of the Deformation Behavior of Adaptive Fiber-Rubber Composites with Integrated Shape Memory Alloys. Materials 2022, 15, 582. [Google Scholar] [CrossRef]
- Scholtes, D.; Schmidt, M.; Linnebach, P.; Seelecke, S.; Motzki, P. A Multifunctional Characterization Test Bench for Shape Memory Alloy Micro-Wires—Design, Implementation and Validation. Materials 2023, 16, 4820. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, C.; Ji, H.; Zhang, C.; Qiu, J. Training, Control and Application of SMA-Based Actuators with Two-Way Shape Memory Effect. Actuators 2023, 12, 25. [Google Scholar] [CrossRef]
- Mineta, T.; Mitsui, T.; Watanabe, Y.; Kobayashi, S.; Haga, Y.; Esashi, M. An active guide wire with shape memory alloy bending actuator fabricated by room temperature process. Sens. Actuators A Phys. 2002, 97, 632–637. [Google Scholar] [CrossRef]
- Miranda, I.; Souza, A.; Sousa, P.; Ribeiro, J.; Castanheira, E.M.S.; Lima, R.; Minas, G. Properties and applications of PDMS for biomedical engineering: A review. J. Funct. Biomater. 2021, 13, 2. [Google Scholar] [CrossRef] [PubMed]
- Niu, D.; Li, D.; Chen, J.; Zhang, M.; Lei, B.; Jiang, W.; Chen, J.; Liu, H. SMA-based soft actuators with electrically responsive and photoresponsive deformations applied in soft robots. Sens. Actuators A Phys. 2022, 341, 113516. [Google Scholar] [CrossRef]
- Cortez, R.; Sandoval-Chileño, M.A.; Lozada-Castillo, N.; Luviano-Juárez, A. Snake Robot with Motion Based on Shape Memory Alloy Spring-Shaped Actuators. Biomimetics 2024, 9, 180. [Google Scholar] [CrossRef] [PubMed]
- Du, T.; Liu, J.; Dong, J.; Xie, H.; Wang, X.; Yang, X.; Yang, Y. Multifunctional coatings of nickel-titanium implant toward promote osseointegration after operation of bone tumor and clinical application: A review. Front. Bioeng. Biotechnol. 2024, 12, 1325707. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Acevedo-Velazquez, A.I.; Annadata, A.R.; Winkler, A.; Röbenack, K.; Modler, N. Closed-loop control of a 3D printed soft actuator with integrated flex sensors and SMA wires. J. Physics: Conf. Ser. 2024, 2716, 8–50. [Google Scholar] [CrossRef]
- Sato, Y.; Guo, Y. Shape-Memory-Alloys Enabled Actuatable Fiber Sensors via the Preform-to-Fiber Fabrication. ACS Appl. Eng. Mater. 2023, 1, 822–831. [Google Scholar] [CrossRef]
- Saver, J.L.; Chapot, R.; Agid, R.; Hassan, A.E.; Jadhav, A.P.; Liebeskind, D.S.; Lobotesis, K.; Meila, D.; Meyer, L.; Gupta RRaphaeli, G.; et al. Thrombectomy for distal, medium vessel occlusions: A consensus statement on present knowledge and promising directions. Stroke 2020, 51, 2872–2884. [Google Scholar] [CrossRef]
- Sharma, S.; Bhaskar, N.; Bose, S.; Basu, B. Biomimetic porous high-density polyethylene/polyethylene- graft-ed-maleic anhydride scaffold with improved in vitro cytocompatibility. J. Biomater. Appl. 2018, 32, 1450–1463. [Google Scholar] [CrossRef]
- Zhou, L.; Fu, J.; He, Y. A Review of 3D Printing Technologies for Soft Polymer Materials. Adv. Funct. Mater. 2020, 30, 2000187. [Google Scholar] [CrossRef]
- Lian, C.; Zhang, X.-F.; Li, X.-L.; Liu, X.-J. Sterile polyethylene film: A novel application for the treatment of facial pediatric scald burns. J. Am. Acad. Dermatol. 2024, 90, e87–e88. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Li, C.; Xie, K.; Mangla, S.; Nam, C.-Y.; Camino, F.; Wang, H.; Yuan, J.; Yan, P. Smart material based multilayered microbeam structures for spatial self-deployment and reconfiguration: A residual stress approach. Compos. Struct. 2023, 304, 116468. [Google Scholar] [CrossRef]
- Su, X.; Ren, Z.; Yan, J.; Shi, Y.; Pan, Q. Microstructure and twisting ability of an adjusted antisymmetric angle ply laminate. Appl. Phys. Lett. 2019, 114, 211902. [Google Scholar] [CrossRef]
- Li, C.; Xie, K.; Wang, J.; Li, J.; Ren, Z.; Yan, P. Submillimeter-scale Flexible Micro-catheters Driven by Shape Memory Alloys for Vascular Interventions. In Proceedings of the 2023 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Chengdu, China, 29 July–2 August 2023; pp. 162–166. [Google Scholar]
- Sun, H.; Luo, J.; Ren, Z.; Lu, M.; Nykypanchuk, D.; Mangla, S.; Shi, Y. Shape memory alloy bimorph microactuators by lift-off process. J. Micro Nano-Manuf. 2020, 8, 031003. [Google Scholar] [CrossRef]
- Sun, H.; Luo, J.; Ren, Z.; Lu, M.; Shi, Y. Effects of deposition and annealing conditions on the crystallisation of NiTi thin films by e-beam evaporation. Micro Nano Lett. 2020, 15, 670–673. [Google Scholar] [CrossRef]
- Tang, T.; Xie, K.; Li, C.; Sun, S.; Ren, Z.; Yuan, J.; Yan, P. A shape memory alloy spring driven soft crawling robot with feet of constant curvature. J. Intell. Mater. Syst. Struct. 2023, 34, 2393–2403. [Google Scholar] [CrossRef]
- Wang, H.; Duan, W.; Ren, Z.; Li, X.; Ma, W.; Guan, Y.; Liu, F.; Chen, L.; Yan, P.; Hou, X. Engineered Sandwich-Structured Composite Wound Dressings with Unidirectional Drainage and Anti-Adhesion Supporting Accelerated Wound Healing. Adv. Health Mater. 2022, 12, e2202685. [Google Scholar] [CrossRef]




| Material | Density (10−9 t/mm3) | Young’s Modulus (MPa) | CTE (1/°C) |
|---|---|---|---|
| SMA | 6.45 | 66,000 | −0.0005 |
| PE | 0.95 | 1070 | 0.0002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, X.; Ren, Z.; Wang, J.; Sun, S.; Fu, J.; Xu, Y.; Duan, W. Design, Modeling, and Experimental Validation of an Active Microcatheter Driven by Shape Memory Effects. Micromachines 2024, 15, 603. https://doi.org/10.3390/mi15050603
Li C, Zhang X, Ren Z, Wang J, Sun S, Fu J, Xu Y, Duan W. Design, Modeling, and Experimental Validation of an Active Microcatheter Driven by Shape Memory Effects. Micromachines. 2024; 15(5):603. https://doi.org/10.3390/mi15050603
Chicago/Turabian StyleLi, Chengyang, Xu Zhang, Zhongjing Ren, Jingkai Wang, Shouyu Sun, Jian Fu, Yang Xu, and Wu Duan. 2024. "Design, Modeling, and Experimental Validation of an Active Microcatheter Driven by Shape Memory Effects" Micromachines 15, no. 5: 603. https://doi.org/10.3390/mi15050603
APA StyleLi, C., Zhang, X., Ren, Z., Wang, J., Sun, S., Fu, J., Xu, Y., & Duan, W. (2024). Design, Modeling, and Experimental Validation of an Active Microcatheter Driven by Shape Memory Effects. Micromachines, 15(5), 603. https://doi.org/10.3390/mi15050603








