Loss-Optimized Design of Magnetic Devices
Abstract
:1. Introduction
2. Winding Loss Modeling
3. Winding Optimization Design
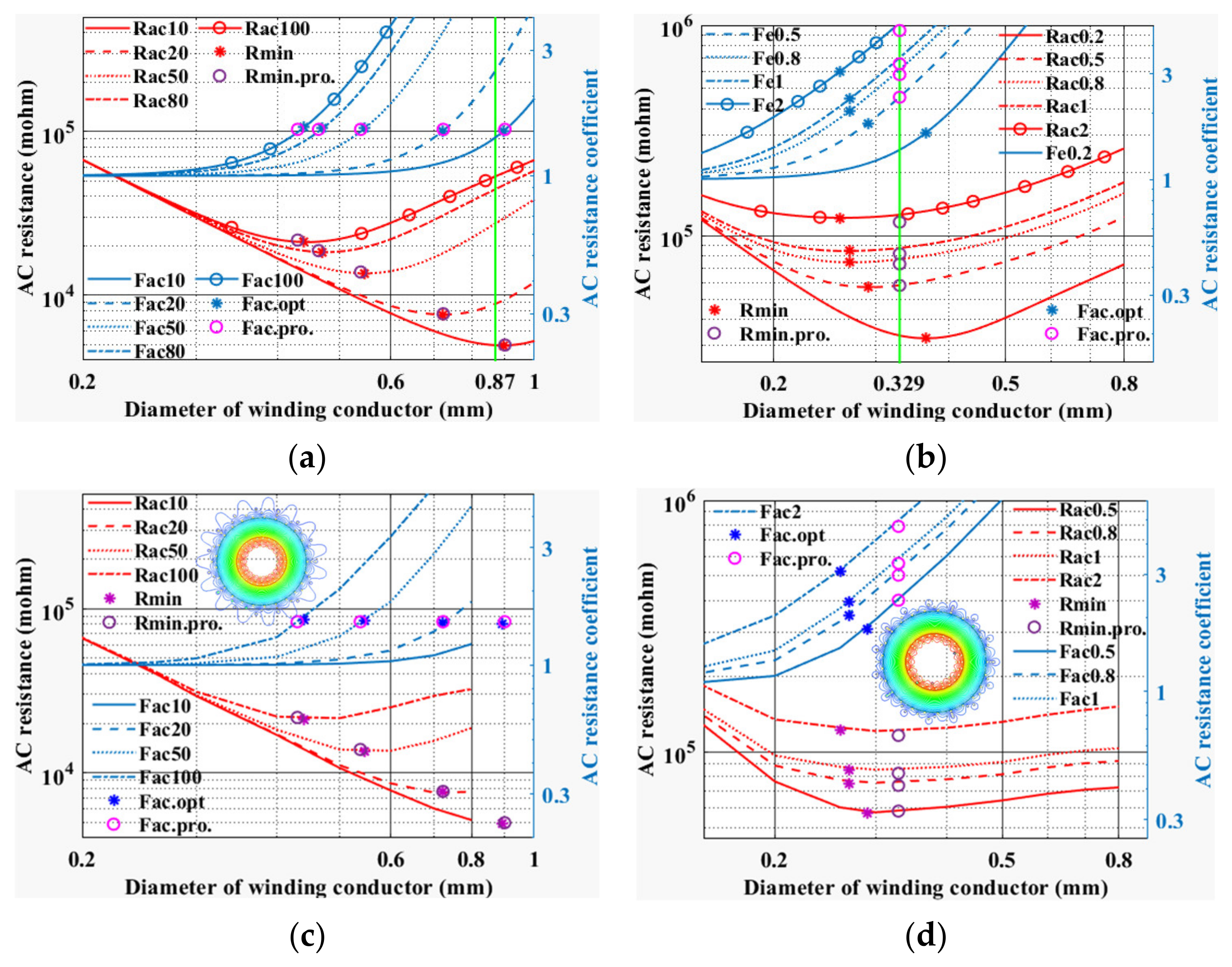
3.1. Diameter of the Wire
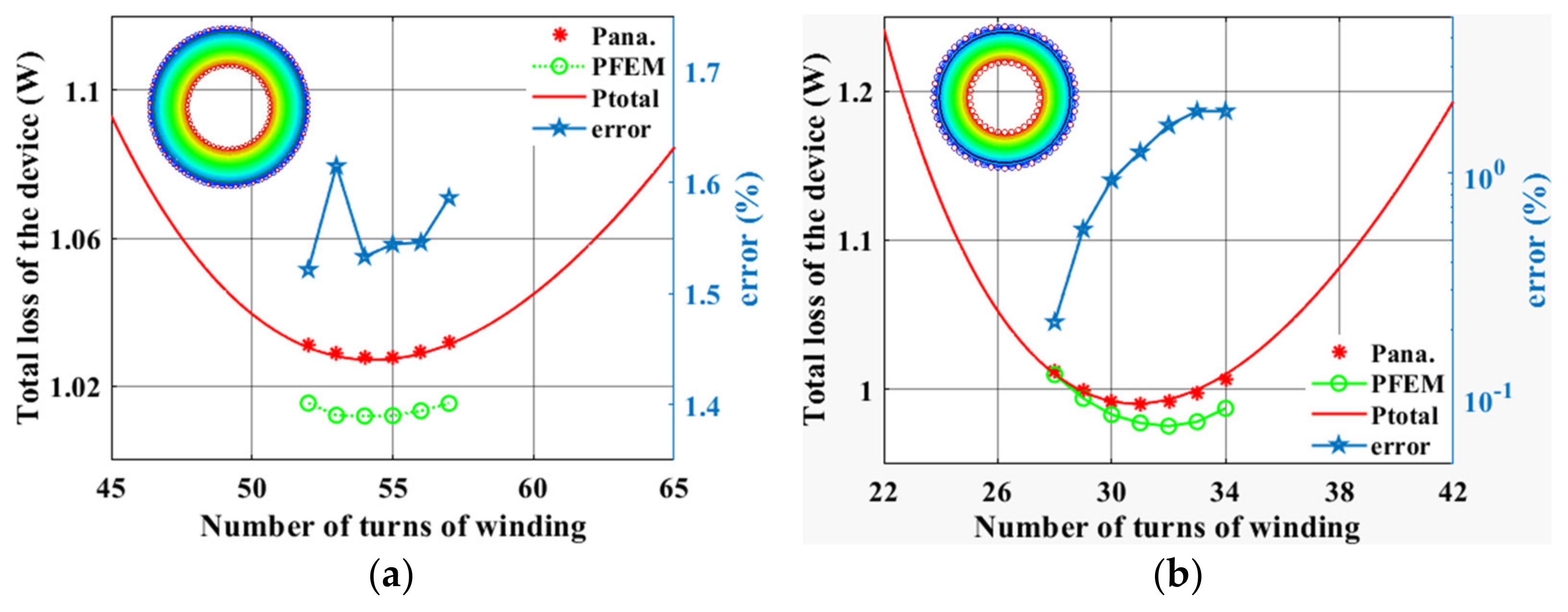
3.2. Number of Turns
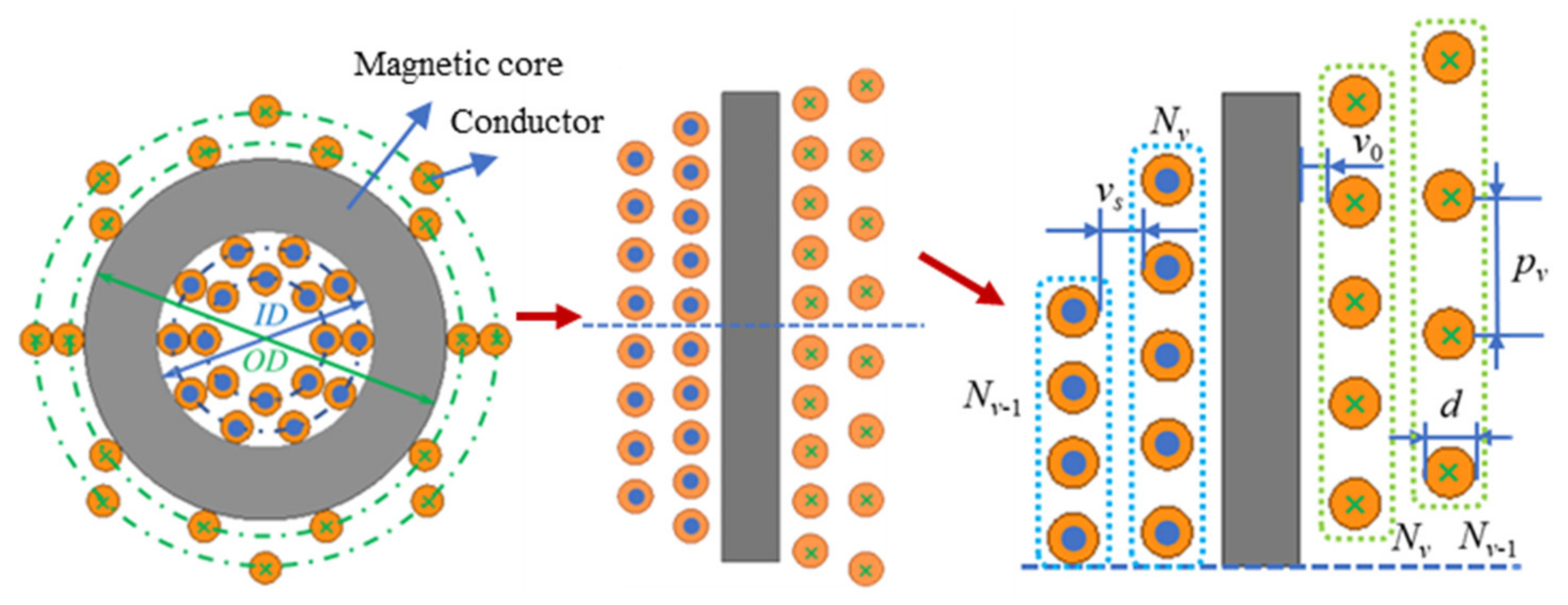
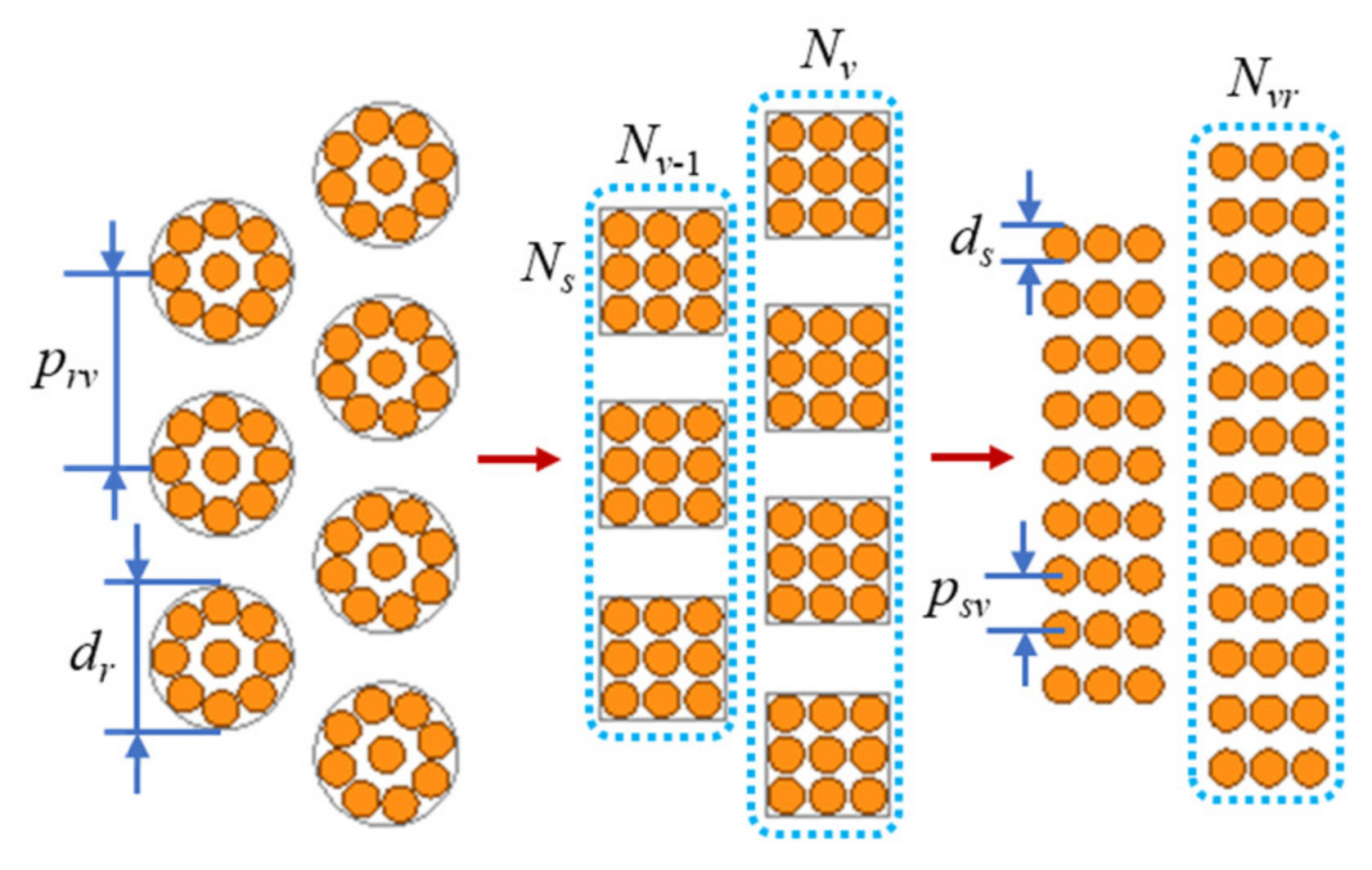
3.3. Winding Arrangement
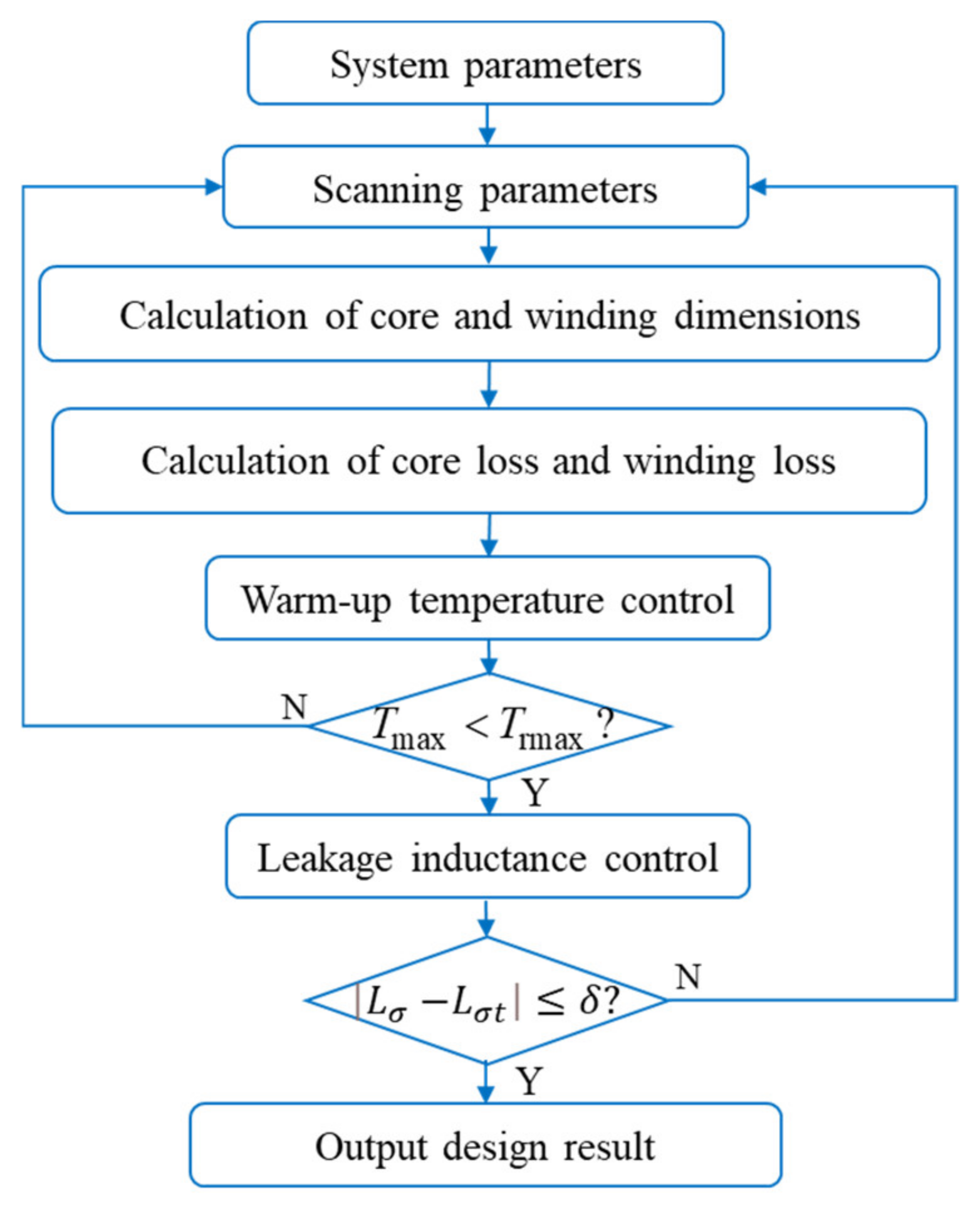
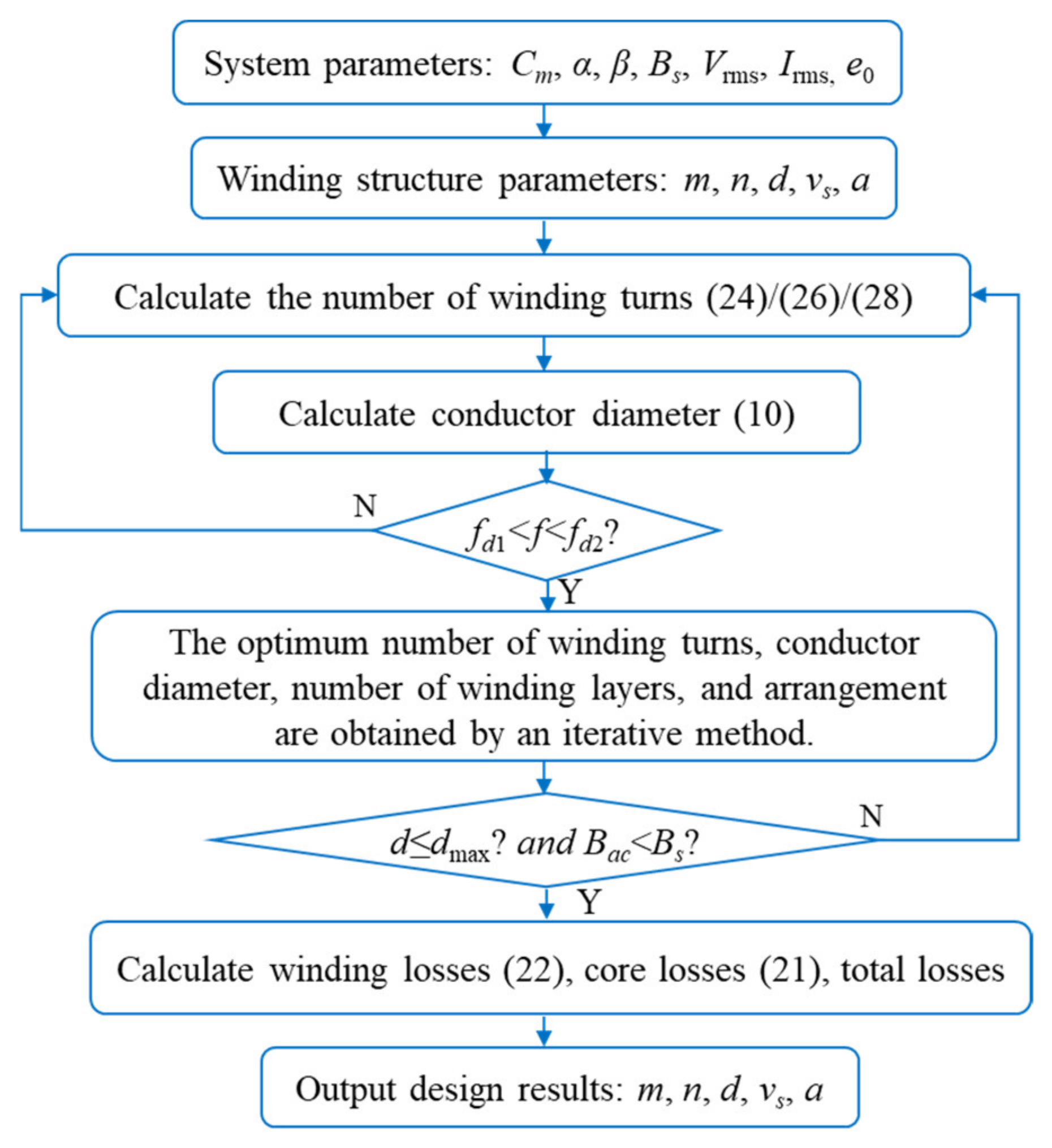
3.4. Optimal Design Model
3.5. Extension of Theory and Miniaturized Systems
4. Finite Element Method Case
4.1. Diameter of the Wire Case
4.2. Number of Turns Case
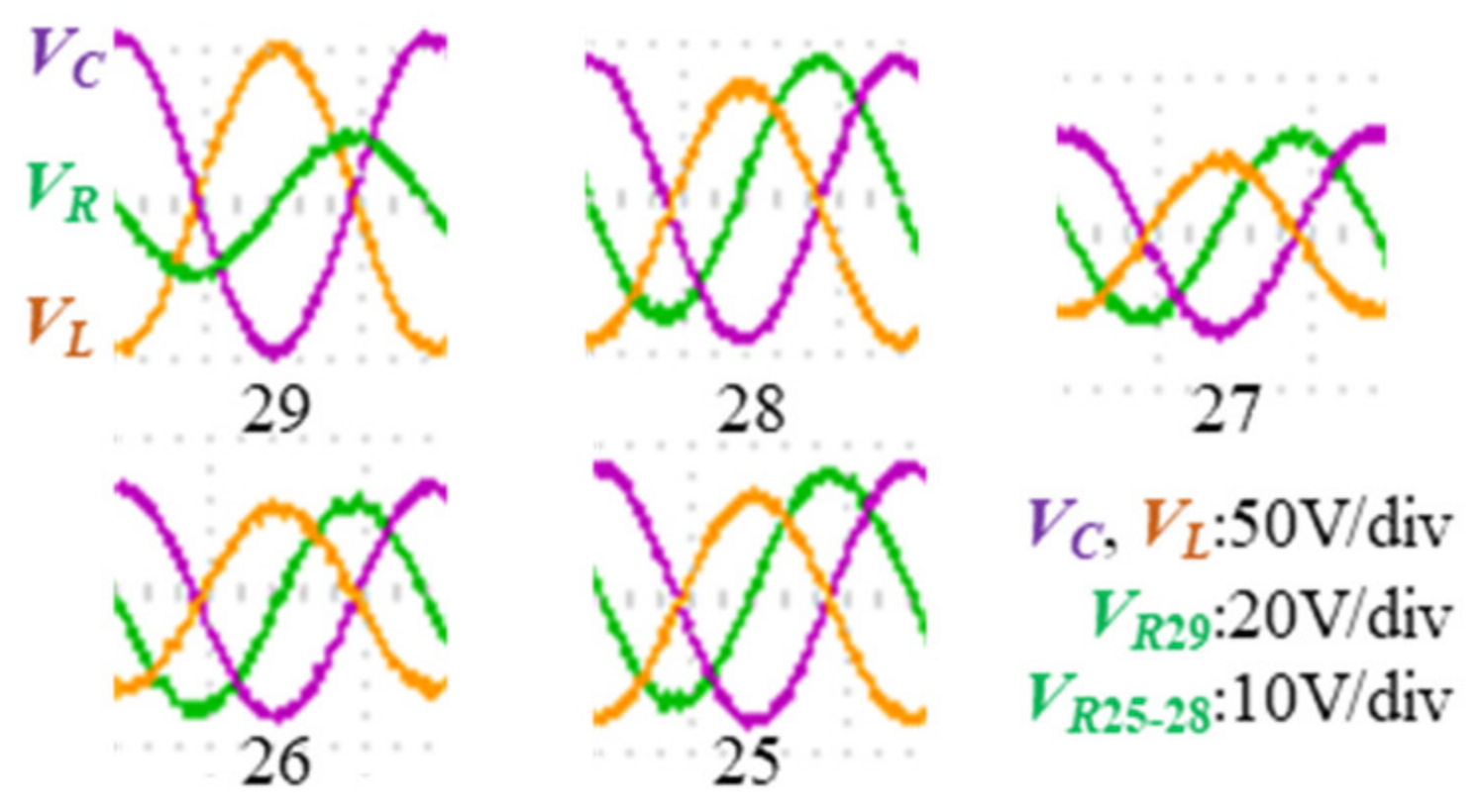
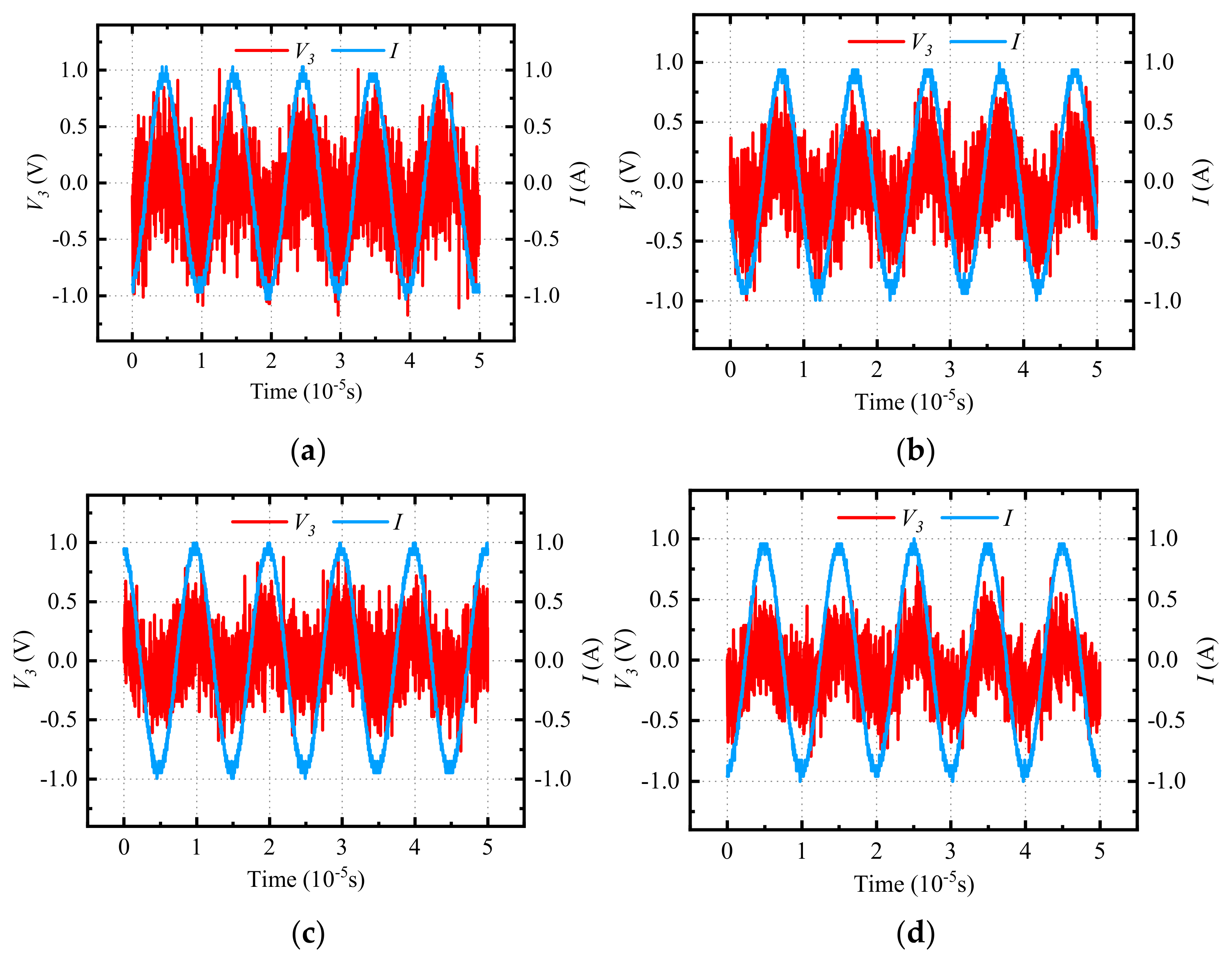
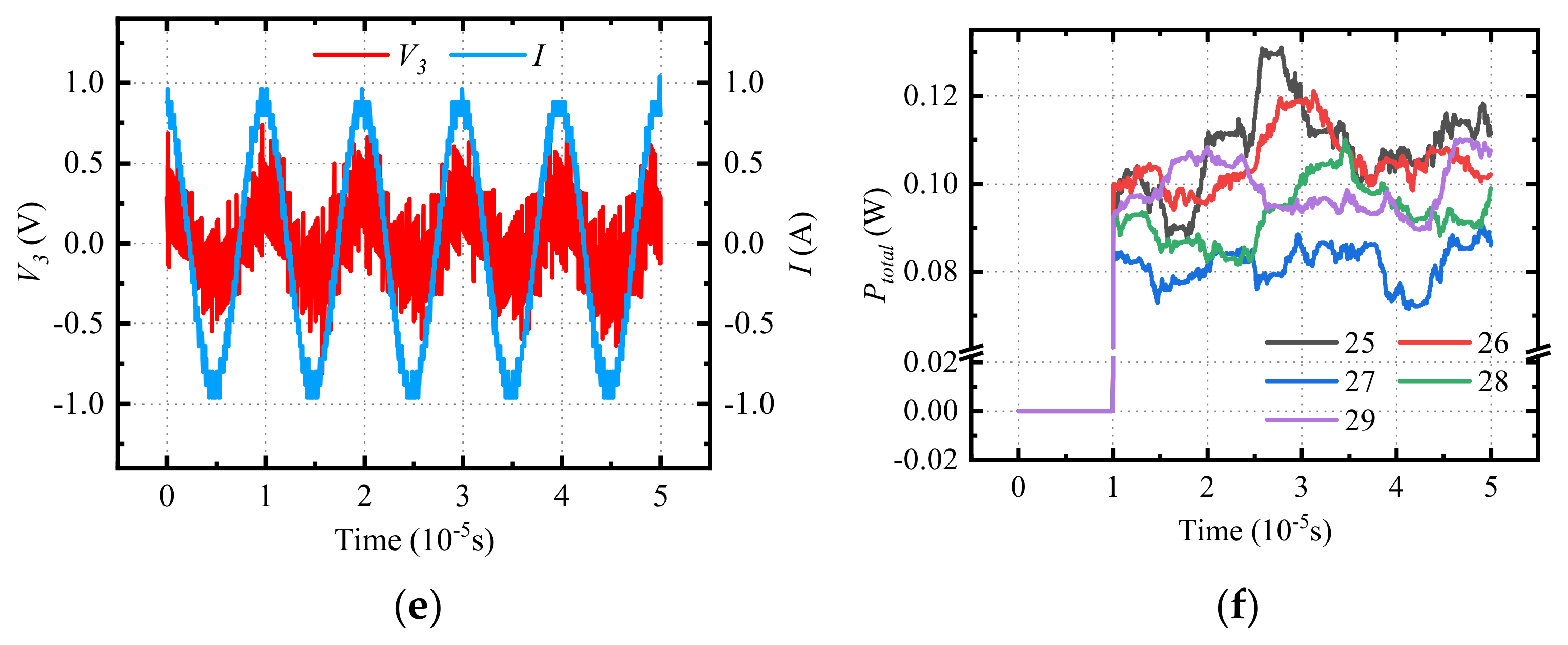
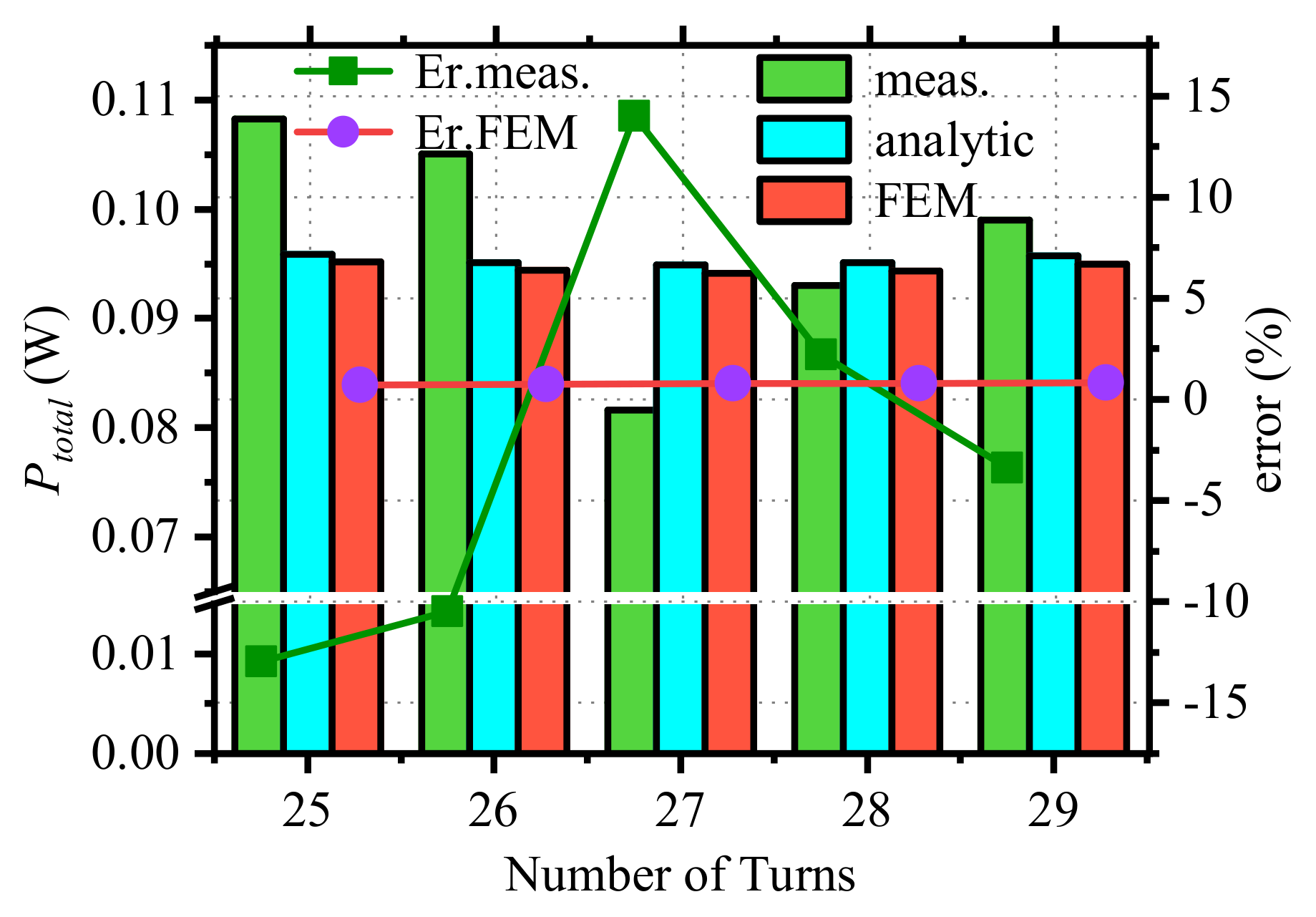
5. Experimental Analysis and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rodriguez-Sotelo, D.; Rodriguez-Licea, M.A.; Araujo-Vargas, I.; Prado-Olivarez, J.; Barranco-Gutiérrez, A.-I.; Perez-Pinal, F.J. Power losses models for magnetic cores: A review. Micromachines 2022, 13, 418. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Dujic, D. Overview of planar magnetics of loosely coupled PCB spiral coils in inductive power transfer systems. IEEE Trans. Power Electron. 2023, 38, 13430–13442. [Google Scholar] [CrossRef]
- Chen, C.; Pan, P.; Gu, J.; Li, X. A high-voltage-isolated MEMS quad–solenoid transformer with specific insulation barriers for miniaturized galvanically isolated power applications. Micromachines 2024, 15, 228. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Wu, Y.; Diao, F.; Lin, N.; Du, X.; Zhao, Y.; Zhu, G. Design and demonstration of a 100kW high-frequency matrix core transformer for more electric aircraft power distribution. IEEE Trans. Transp. Electrif. 2022, 8, 4279–4290. [Google Scholar] [CrossRef]
- Li, H.; Zhu, K.; Xu, T.; Lei, K.; Xia, J. Design and manufacture of millimeter-scale 3D transformers for RF-IC. Micromachines 2022, 13, 2162. [Google Scholar] [CrossRef] [PubMed]
- Lv, S.; Feng, H.; Lou, W.; Xiao, C.; Su, W.; Kan, W.; He, B. Research on the application of micro-cast electromagnetic coil in an Si MEMS bistable recoverable safety and arming device. Micromachines 2023, 14, 1346. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Barbosa, P. Design and optimization of an integrated resonant inductor with high-frequency transformer for wide gain range DC–DC resonant converters in electric vehicle charging applications. IEEE Trans. Power Electron. 2023, 38, 6380–6394. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Ni, S.; Song, Y.; Yang, F. Lower-height-oriented magnetic integration design for onboard power converter of electric vehicles. IEEE Trans. 2024s Transp. Electrif. 2024, 10, 163–173. [Google Scholar] [CrossRef]
- Dong, Z.; Xu, L.; Yang, T. Transient response characteristics analysis of high-power piezoelectric transducers. Micromachines 2022, 13, 1638. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Huang, H.; Yang, Y.; Chen, Y.; Fu, Z.; Jin, Z.; Shi, Z.; Xiong, X.; Zou, X.; Chen, J. A modulation method for tunnel magnetoresistance current sensors noise suppression. Micromachines 2024, 15, 360. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Xue, R.; Cheong, J.; Zhang, X.; Yao, L. Design and optimization of planar spiral coils for powering implantable neural recording microsystem. Micromachines 2023, 14, 1221. [Google Scholar] [CrossRef] [PubMed]
- Jolly, N.; Chandwani, A.; Mallik, A. Multi-constraint optimization and co-design of a 2-MHz all-GaN based 700 W 95.6% efficient LLC converter. CPSS Trans. Power Electron. Appl. 2022, 7, 259–272. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, L. Effect of Bi2O3–CuO flux on the microstructure, soft magnetic properties, and gyromagnetic properties of NiCuZn ferrites for LTCC devices. Micromachines 2024, 15, 215. [Google Scholar] [CrossRef] [PubMed]
- Stiharu, I.; Andronenko, S.; Zinnatullin, A.; Vagizov, F. SiCNFe ceramics as soft magnetic material for MEMS magnetic devices: A Mössbauer Study. Micromachines 2023, 14, 925. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Wang, R.; Xiao, F.; Zhang, X.; Jie, G.; Gao, S.; Wang, H.; Kang, W. Modeling and optimal design of inductor-integrated three-phase 3-D wound core transformer under SPWM excitation. IEEE Trans. Power Electron. 2023, 38, 6196–6211. [Google Scholar] [CrossRef]
- Gadelrab, R.; Lee, F.C. PCB-based magnetic integration and design optimization for three-phase LLC. IEEE Trans. Power Electron. 2023, 38, 14037–14049. [Google Scholar] [CrossRef]
- Yuan, T.; Jin, F.; Li, Z.; Zhao, C.; Li, Q. Design of an integrated transformer with parallel windings for a 30-kW LLC resonant converter. IEEE Trans. Power Electron. 2023, 38, 14317–14333. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Pei, W.; Yang, Z.; Zhuang, J.; Zhang, X. In-depth design and multiobjective optimization of an integrated transformer for five-phase LLC resonant converters. IEEE Trans. Power Electron. 2022, 37, 13538–13553. [Google Scholar] [CrossRef]
- Ahmed, D.; Wang, L. Noniterative design of litz-wire high-frequency gapped-transformer (Lw-HFGT) for LLC converters based on optimal core-geometry factor model (OKGM). IEEE Trans. Ind. Electron. 2021, 68, 3090–3102. [Google Scholar] [CrossRef]
- Li, M.; Wang, C.; Ouyang, Z.; Andersen, M.A.E. Optimal design of a matrix planar transformer in an LLC resonant converter for data center applications. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1778–1787. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Y.; Hu, D.; Li, Y.; Zhang, Z.; Wu, H. Overview of planar magnetics for high-frequency resonant converters. Chin. J. Electr. Eng. 2022, 8, 61–78. [Google Scholar] [CrossRef]
- Kiran, M.R.; Farrok, O.; Islam, M.R.; Zhu, J. Increase in the power transfer capability of advanced magnetic material based high frequency transformer by using a novel distributed winding topology. IEEE Trans. Ind. Appl. 2021, 57, 6306–6317. [Google Scholar] [CrossRef]
- Wang, K.; Gao, Q.; Wei, G.; Yang, X. Integrated fractional-turn planar transformer for MHz and high-current applications. IEEE Trans. Power Electron. 2023, 38, 7374–7384. [Google Scholar] [CrossRef]
- Dey, S.; Reece, C.; Irabor, O.P.; Mallik, A. Comparative analysis and optimization of triple active bridge transformer configuration with integrable leakage inductance. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5102–5119. [Google Scholar] [CrossRef]
- Shimura, K.; Kobayashi, S.; Sato, M.; Mizuno, T. Application of magnetic composite materials in windings to reduce alternating current resistance in leakage transformers. IEEE Trans. Magn. 2023, 59, 8401806. [Google Scholar] [CrossRef]
- Akbar, S.M.; Hasan, A.; Watson, A.J.; Wheeler, P. FEA based transformer loss analysis for dual active bridge dc–dc converter using triple phase shift modulation. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4347–4360. [Google Scholar] [CrossRef]
- Zhao, Y.; Ming, Z.; Han, B. Analytical modelling of high-frequency losses in toroidal inductors. IET Power Electron. 2023, 16, 1538–1547. [Google Scholar] [CrossRef]
- Ehrlich, S.; Rossmanith, H.; Sauer, M.; Joffe, C.; März, M. Fast numerical power loss calculation for high-frequency litz wires. IEEE Trans. Power Electron. 2021, 36, 2018–2032. [Google Scholar] [CrossRef]
- Pniak, L.; Quéval, L.; Revol, B.; Teu, J.-S.N.; Gautier, C.; Béthoux, O. AC resistance and leakage inductance estimation for planar transformers with parallel-connected windings. IEEE Trans. Power Electron. 2023, 38, 728–738. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, X.; Xu, Y.; Gao, Q.; Zhou, Y.; Wu, J.; Wang, K.; Zhang, F.; Wang, L.; Chen, W. 2-D analytical copper loss model for pcb and copper foil magnetics with arbitrary air gaps. IEEE Trans. Power Electron. 2023, 38, 14274–14291. [Google Scholar] [CrossRef]
- Umetani, K.; Kawahara, S.; Acero, J.; Sarnago, H.; Lucía, Ó.; Hiraki, E. Analytical formulation of copper loss of litz wire with multiple levels of twisting using measurable parameters. IEEE Trans. Ind. Appl. 2021, 57, 2407–2420. [Google Scholar] [CrossRef]
- Li, W.; Zhou, L.; Chen, J.; Liu, B.; Gao, S.; Zhang, C.; Wang, D. Numerical model for eddy-current loss of wound core in single-phase transformer. IEEE Trans. Transp. Electrif. 2024, 10, 150–162. [Google Scholar] [CrossRef]
- Yan, Z.; Weibo, Z.; Guanghui, T. A core loss calculation method for dc/dc power converters based on sinusoidal losses. IEEE Trans. Power Electron. 2023, 38, 692–702. [Google Scholar] [CrossRef]
- Li, Z.; Hsieh, E.; Li, Q.; Lee, F.C. High-frequency transformer design with medium-voltage insulation for resonant converter in solid-state transformer. IEEE Trans. Power Electron. 2023, 38, 9917–9932. [Google Scholar] [CrossRef]
- Wang, Z.; Bak, C.L.; Wang, H.; Sørensen, H.; da Silva, F.F. Multiphysics digital model of the high frequency transformer for power electronics application considering electro-thermal interactions. IEEE Trans. Power Electron. 2023, 38, 14345–14359. [Google Scholar] [CrossRef]
- Ho, G.K.Y.; Fang, Y.; Pong, B.M.H. A multiphysics design and optimization method for air-core planar transformers in high-frequency LLC resonant converters. IEEE Trans. Ind. Electron. 2020, 67, 1605–1614. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, X.; Li, X.; Chaohui, L.; Ma, H. Parameter design for symmetrical CLLC-type dc transformer considering cascaded system stability and power efficiency. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6219–6231. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Z.; Chen, Z. Pareto optimum design of the magnetic components in DAB converters based on nondominated sorting genetic algorithms-II. IEEE Trans. Power Electron. 2023, 38, 12961–12974. [Google Scholar] [CrossRef]
- D’Antonio, M.; Chakraborty, S.; Khaligh, A. Planar transformer with asymmetric integrated leakage inductance using horizontal air gap. IEEE Trans. Power Electron. 2021, 36, 14014–14028. [Google Scholar] [CrossRef]
- Ahmed, D.; Wang, L.; Dai, Z.; Wu, M. Pareto-optimal design of litz-wire gapped-core high-frequency transformer for LLC Converters. IEEE Trans. Ind. Electron. 2022, 69, 8883–8894. [Google Scholar] [CrossRef]
- Elizondo, D.; Barrios, E.L.; Ursua, A.; Sanchis, P. Analytical modeling of high-frequency winding loss in round-wire toroidal inductors. IEEE Trans. Ind. Electron 2022, 70, 5581–5591. [Google Scholar] [CrossRef]
- Yu, X.; Su, J.; Lai, J. Winding loss calculation revisited for medium frequency transformer in applications of dc generation of new energy. In Proceedings of the 8th Renewable Power Generation Conference (RPG 2019), Shanghai, China, 24–25 October 2019; pp. 384–392. [Google Scholar]
- Yu, X.; Su, J.; Lai, J.; Guo, S. Analytical optimization of non-saturated thermally limited high-frequency transformer/inductor design considering discreteness of design variables. IEEE Trans. Power Electron. 2020, 35, 6231–6250. [Google Scholar] [CrossRef]
- Khan, S.R.; Pavuluri, S.K.; Desmulliez, M.P. New analytical model for the characterisation of printed spiral coils for wireless power transfer. In Proceedings of the 12th European Conference on Antennas and Propagation (EuCAP 2018), London, UK, 9–13 April 2018; pp. 1–5. [Google Scholar]
- Yue, S.; Li, Y.; Yang, Q.; Yu, X.; Zhang, C. Comparative analysis of core loss calculation methods for magnetic materials under non-sinusoidal excitations. IEEE Trans. Magn. 2018, 54, 6300605. [Google Scholar] [CrossRef]
- Zhu, S.; Cheng, M.; Dong, J.; Du, J. Core loss analysis and calculation of stator permanent-magnet machine considering DC-biased magnetic induction. IEEE Trans. Ind. Electron. 2014, 61, 5203–5212. [Google Scholar] [CrossRef]
- Liu, B.; Chen, W.; Wang, J.; Chen, Q. A practical inductor loss testing scheme and device with high frequency pulsewidth modulation excitations. IEEE Trans. Ind. Electron. 2021, 68, 4457–4467. [Google Scholar] [CrossRef]
- Hou, D.; Mu, M.; Lee, F.C.; Li, Q. New high-frequency core loss measurement method with partial cancellation concept. IEEE Trans. Power Electron. 2017, 32, 2987–2994. [Google Scholar] [CrossRef]

| Symbol | m | Nv | d (mm) | ID (mm) | OD (mm) | vs (mm) |
|---|---|---|---|---|---|---|
| devices | 3 | N1 = 25, N2 = 20, N3 = 15 | 0.1, 0.2, 0.26, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 | 9.1 | 21.1 | 0.1 |
| Symbol | Nv | h (mm) | ID (mm) | OD (mm) |
|---|---|---|---|---|
| Group 1 devices (100 kHz) | 52, 53, 54, 55, 56, 57 | 7.62 | 13.34 | 23.62 |
| Group 2 devices (800 kHz) | 28, 29, 30, 31, 32, 33, 34 | 7.62 | 13.34 | 23.62 |
| Symbol | Nv | d (mm) | ID (mm) | OD (mm) | h (mm) |
|---|---|---|---|---|---|
| Devices (100 kHz) | 25, 26, 27, 28, 29 | 0.65 | 13.34 | 23.62 | 7.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Ming, Z.; Du, C. Loss-Optimized Design of Magnetic Devices. Micromachines 2024, 15, 697. https://doi.org/10.3390/mi15060697
Zhao Y, Ming Z, Du C. Loss-Optimized Design of Magnetic Devices. Micromachines. 2024; 15(6):697. https://doi.org/10.3390/mi15060697
Chicago/Turabian StyleZhao, Yuhu, Zhengfeng Ming, and Chaofan Du. 2024. "Loss-Optimized Design of Magnetic Devices" Micromachines 15, no. 6: 697. https://doi.org/10.3390/mi15060697
APA StyleZhao, Y., Ming, Z., & Du, C. (2024). Loss-Optimized Design of Magnetic Devices. Micromachines, 15(6), 697. https://doi.org/10.3390/mi15060697






