Evaluation of an Active Disturbance Rejection Controller for Ophthalmic Robots with Piezo-Driven Injector
Abstract
:1. Introduction
2. Materials and Methods
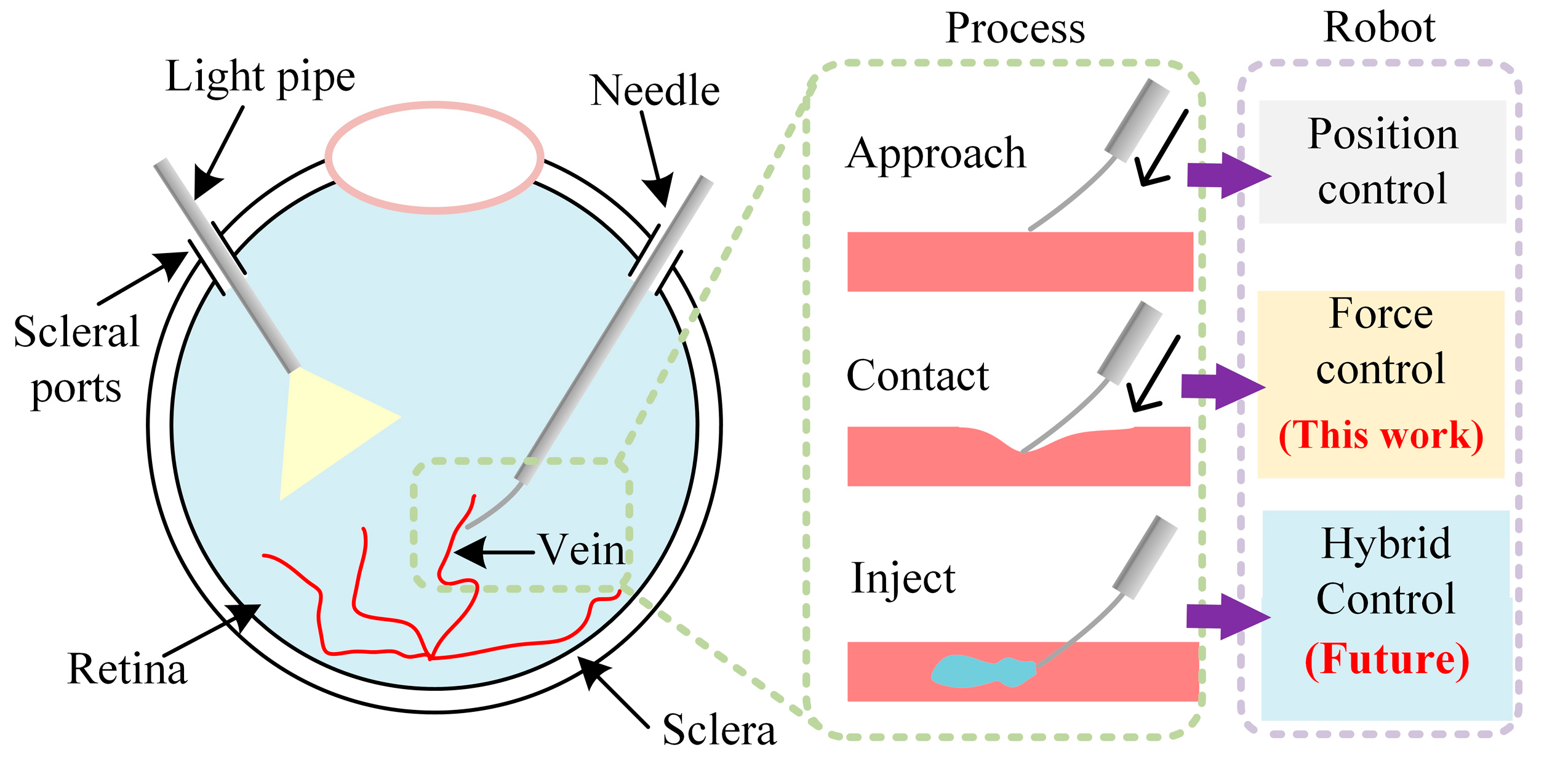
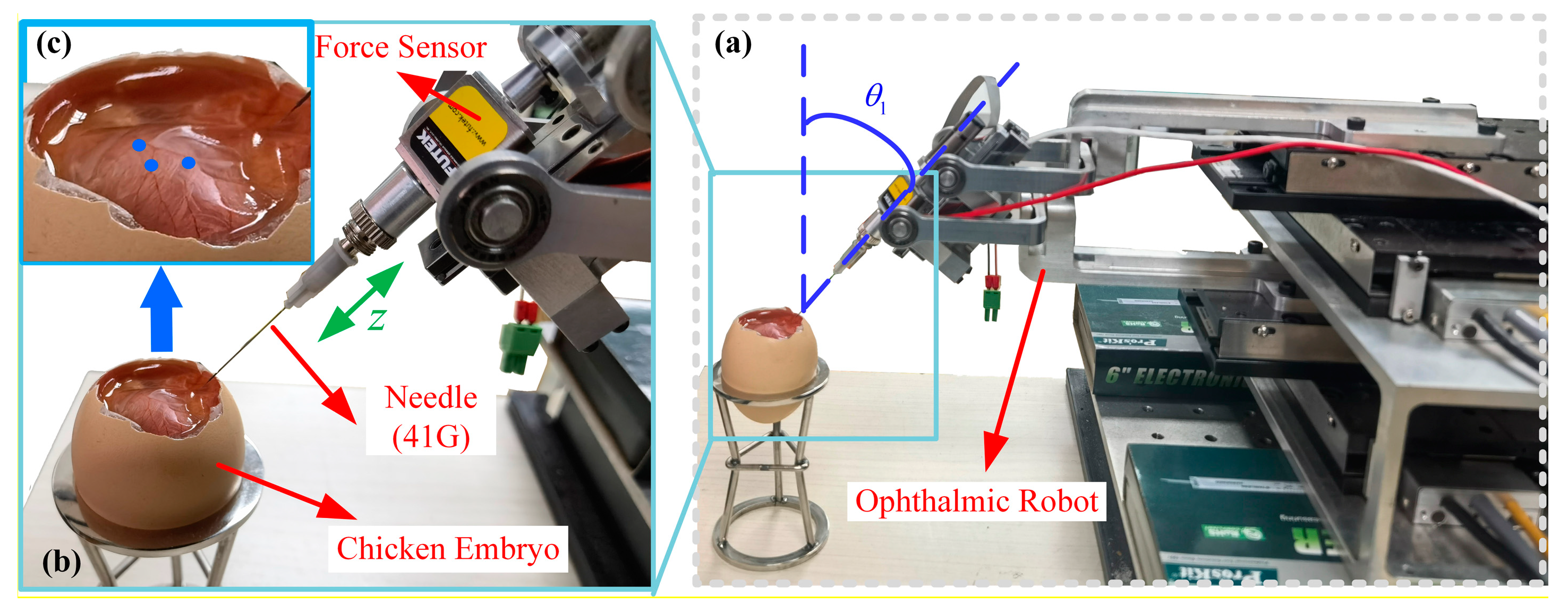
2.1. Ophthalmic Surgical Robot
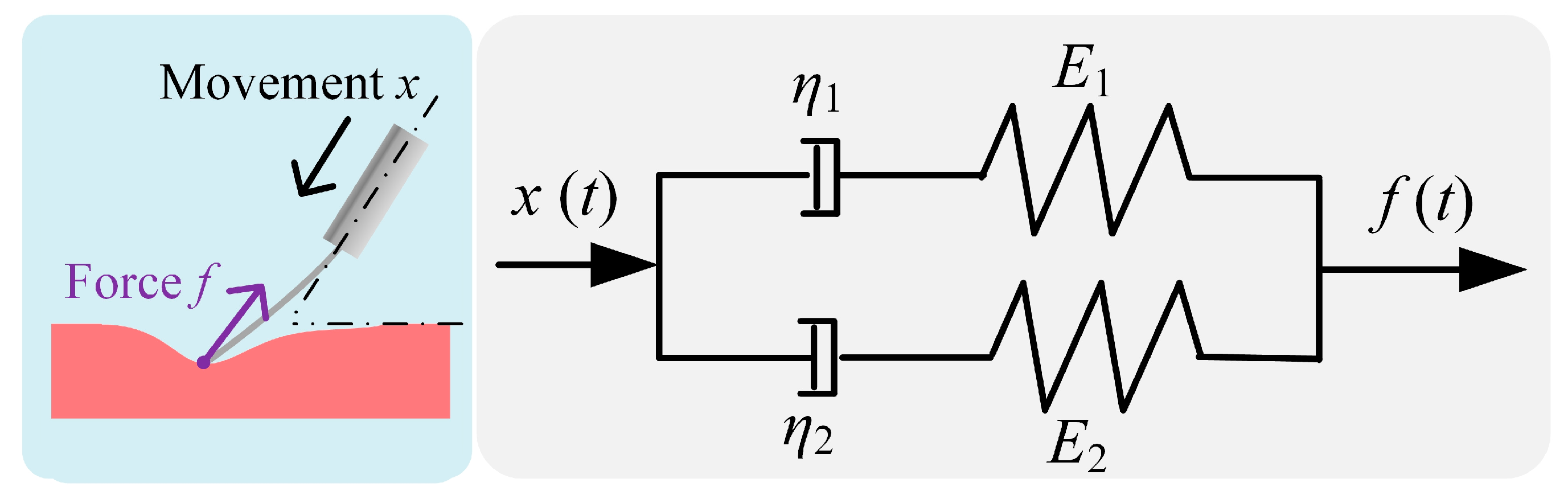
2.2. Viscoelastic Contact Model
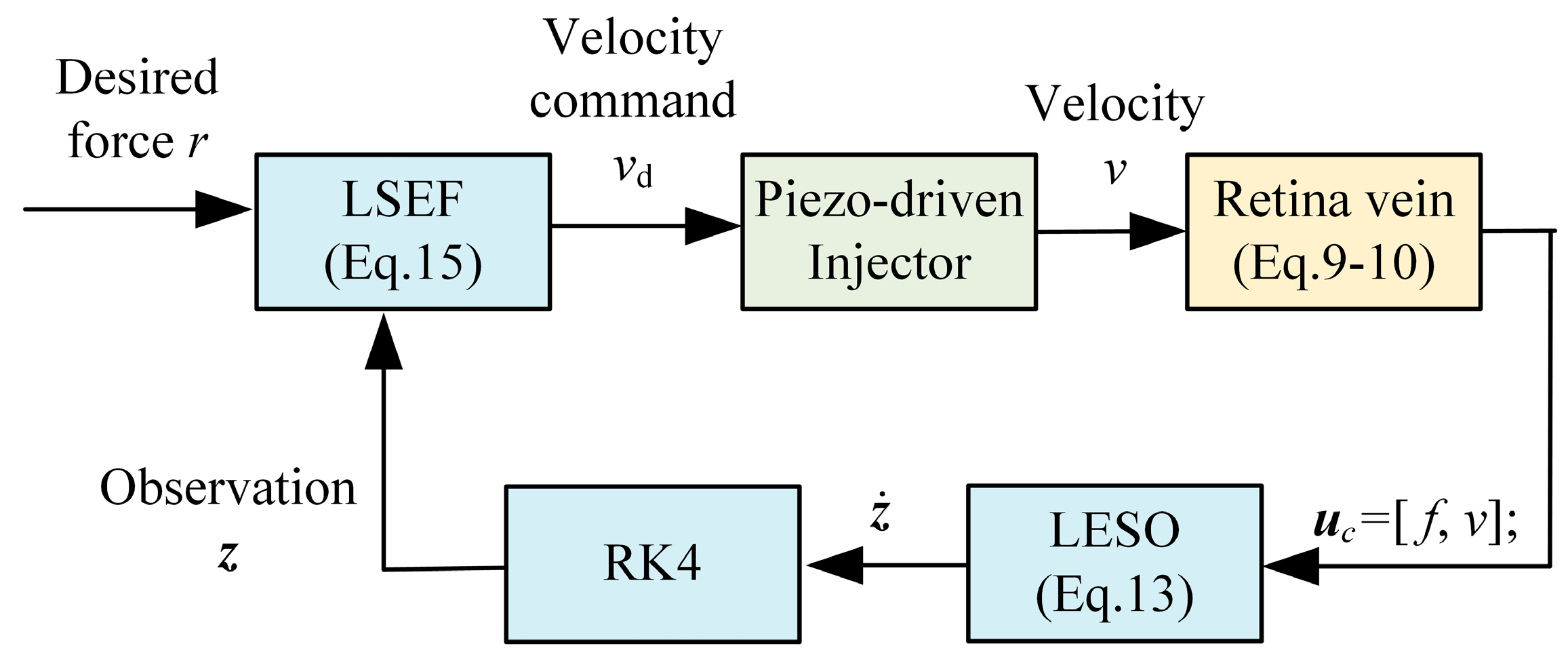
2.3. Active Disturbance Rejection Force Controller
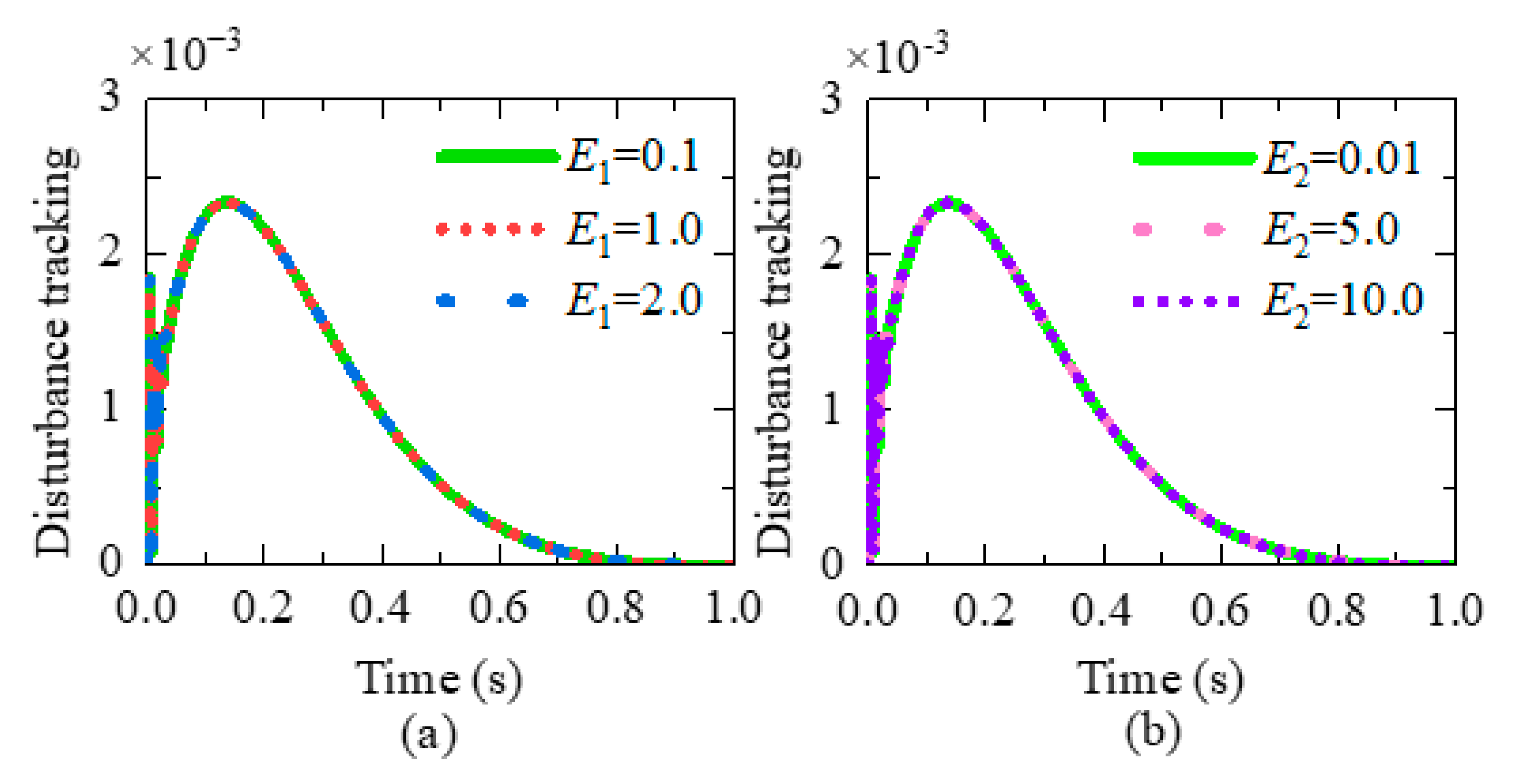
3. Disturbance Rejection Capability Analysis
4. Experimental Results and Discussion
4.1. Experimental Setup
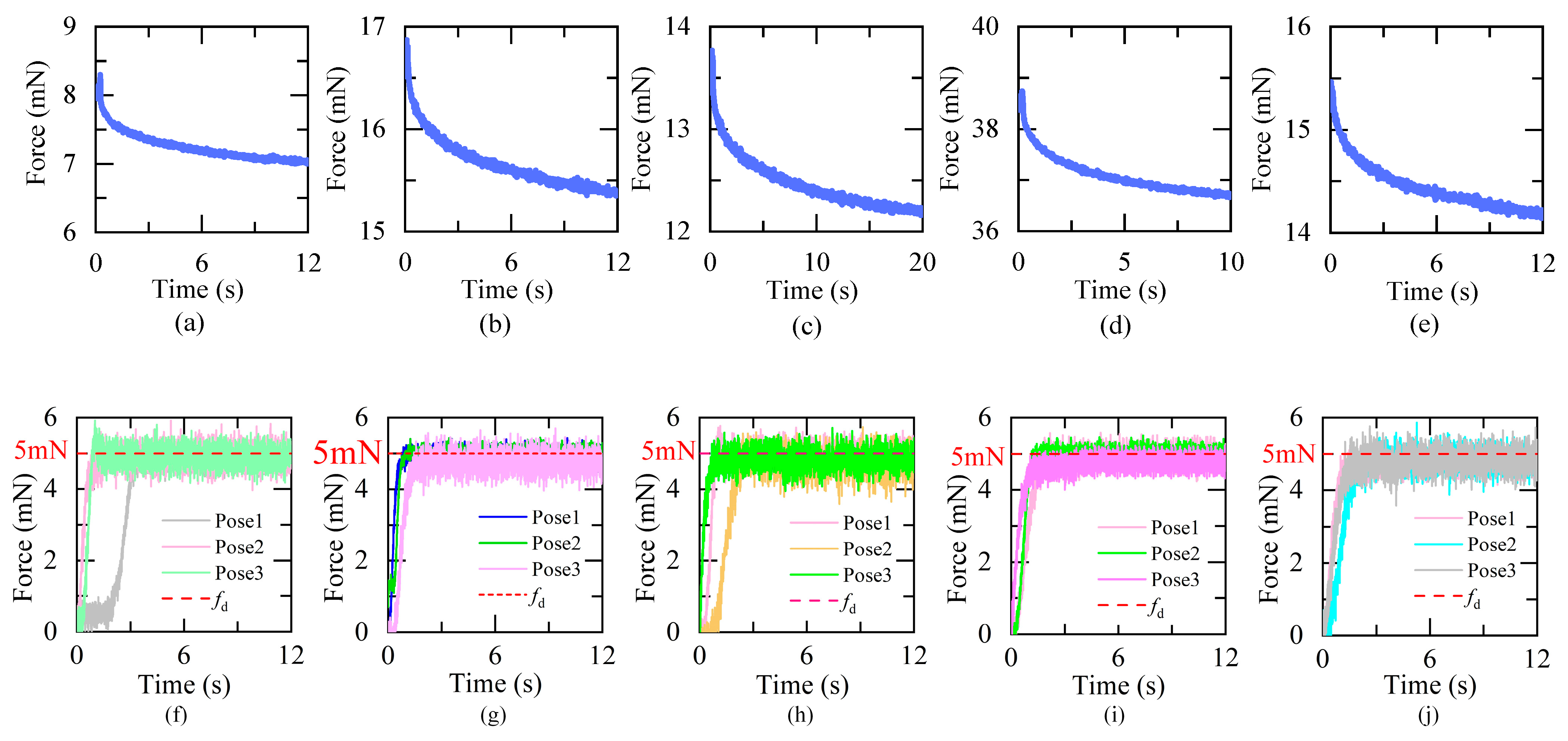
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rehak, J.; Rehak, M. Branch retinal vein occlusion: Pathogenesis, visual prognosis, and treatment modalities. Curr. Eye Res. 2008, 33, 111–131. [Google Scholar] [CrossRef] [PubMed]
- Wong, T.Y.; Scott, I.U. Retinal-vein occlusion. N. Engl. J. Med. 2010, 363, 2135–2144. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Yang, X.H.; Mo, B.; Qi, Y.; Yang, Y.; Lin, C.; Han, S.F.; Wang, N.L.; Guang, C.H.; Liu, W. Evaluation of the Hand Motion and Peeling Force in Inner Limiting Membrane Peeling. Transl. Vis. Sci. Technol. 2023, 12, 32. [Google Scholar] [CrossRef] [PubMed]
- Bynoe, L.A.; Hutchins, R.K.; Lazarus, H.S.; Friedberg, M.A. Retinal endovascular surgery for central retinal vein occlusion: Initial experience of four surgeons. Retina 2005, 25, 625–632. [Google Scholar] [CrossRef]
- Poorten, E.V.; Riviere, C.N.; Abbott, J.J.; Bergeles, C.; Nasseri, M.A.; Kang, J.U.; Sznitman, R.; Faridpooya, K.; Iordachita, I. Physiologicalbook of Robotic and Image-Guided Surgery-Part 36: Robotic Retinal Surgery; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Zhou, M.C.; Yu, Q.M.; Huang, K.; Mahov, S.; Eslami, A.; Maier, M.; Lohmann, C.P.; Navab, N.; Zapp, D.; Knoll, A.; et al. Towards Robotic-Assisted Subretinal Injection: A Hybrid Parallel-Serial Robot System Design and Preliminary Evaluation. IEEE Trans. Ind. Electron. 2024, 67, 6617–6628. [Google Scholar] [CrossRef]
- He, C.Y.; Yang, E.; Patel, N.; Ebrahimi, A.; Shahbazi, M.; Gehlbach, P.; Iordachita, I. Automatic Light Pipe Actuating System for Bimanual Robot-Assisted Retinal Surgery. IEEE-ASME Trans. Mechatron. 2020, 25, 2846–2857. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Yang, Y.; Lin, C.; Guang, C.H.; Zong, J.J.; Ma, K. Preliminary Estimation of the Friction between Force-sensing Forceps and Cornea. In Proceedings of the IEEE RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Seoul, Republic of Korea, 21–24 August 2022; pp. 1–6. [Google Scholar]
- Yang, S.; MacLachlan, R.A.; Martel, J.N.; Lobes, L.A.; Riviere, C.N. Comparative Evaluation of Handheld Robot-Aided Intraocular Laser Surgery. IEEE Trans. Robot. 2016, 32, 246–251. [Google Scholar] [CrossRef] [PubMed]
- Charreyron, S.L.; Boehler, Q.; Danun, A.N.; Mesot, A.; Becker, M.; Nelson, B.J. A Magnetically Navigated Microcannula for Subretinal Injections. IEEE Trans. Biomed. Eng. 2021, 68, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Keller, B.; Draelos, M.; Zhou, K.; Qian, R.B.; Konidaris, N.G.A.; Hauser, K.; Izatt, J.A. Optical Coherence Tomography-Guided Robotic Ophthalmic Microsurgery via Reinforcement Learning from Demonstration. IEEE Trans. Robot. 2020, 36, 1207–1218. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.C.; Hao, X.; Eslami, A.; Huang, K.; Cai, C.X.; Lohmann, C.P.; Navab, N.; Knoll, A.; Nasseri, M.A. 6DOF Needle Pose Estimation for Robot-Assisted Vitreoretinal Surgery. IEEE Access 2019, 7, 63113–63122. [Google Scholar] [CrossRef]
- Schoevaerdts, L.; Esteveny, L.; Gijbels, A.; Smits, J.; Reynaerts, D.; Vander Poorten, E. Design and evaluation of a new bioelectrical impedance sensor for micro-surgery: Application to retinal vein cannulation. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 311–320. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Urias, M.G.; Patel, N.; Taylor, R.H.; Gehlbach, P.; Iordachita, I. Adaptive control improves sclera force safety in robot-assisted eye surgery: A clinical study. IEEE Trans. Biomed. Eng. 2021, 68, 3356–3365. [Google Scholar] [CrossRef]
- He, C.Y.; Patel, N.; Shahbazi, M.; Yang, Y.; Gehlbach, P.; Kobilarov, M.; Iordachita, I. Toward Safe Retinal Microsurgery: Development and Evaluation of an RNN-Based Active Interventional Control Framework. IEEE Trans. Biomed. Eng. 2020, 67, 966–977. [Google Scholar] [CrossRef]
- He, C.Y.; Patel, N.; Iordachita, I.; Kobilarov, M. Enabling Technology for Safe Robot-Assisted Retinal Surgery: Early Warning for Unsafe Scleral Force. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3889–3894. [Google Scholar]
- He, C.Y.; Ebrahimi, A.; Yang, E.; Urias, M.; Yang, Y.; Gehlbach, P.; Iordachita, I. Towards Bimanual Vein Cannulation: Preliminary Study of a Bimanual Robotic System With a Dual Force Constraint Controller. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May 2020–31 August 2020; pp. 4441–4447. [Google Scholar]
- Wells, T.S.; Yang, S.; MacLachlan, R.A.; Lobes, L.A.; Martel, J.N.; Riviere, C.N. Hybrid position/force control of an active handheld micromanipulator for membrane peeling. Int. J. Med. Robot. Comput. Assist. Surg. 2016, 12, 85–95. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Patel, N.; He, C.Y.; Gehlbach, P.; Kobilarov, M.; Iordachita, I. Adaptive Control of Sclera Force and Insertion Depth for Safe Robot-Assisted Retinal Surgery. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9073–9079. [Google Scholar]
- Avetisov, K.S.; Bakhchieva, N.A.; Avetisov, S.E.; Novikov, I.A.; Frolova, A.A.; Akovantseva, A.A.; Efremov, Y.M.; Kotova, S.L.; Timashev, P.S. Biomechanical properties of the lens capsule: A review. J. Mech. Behav. Biomed. Mater. 2020, 103, 103600. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Liu, H.; Bu, F.; Huang, W.; Qin, H.; Tan, Y.; Qian, Z. Linear active disturbance rejection control for dual-stator winding induction generator AC power system. IEEE Trans. Ind. Electron. 2022, 70, 6597–6607. [Google Scholar] [CrossRef]
- Zhou, R.; Fu, C.; Tan, W. Implementation of linear controllers via active disturbance rejection control structure. IEEE Trans. Ind. Electron. 2020, 68, 6217–6226. [Google Scholar] [CrossRef]
- Lin, C.; Guang, C.H.; Zheng, Y.; Ma, K.; Yang, Y. Preliminary evaluation of a novel vision-guided hybrid robot system for capsulotomy in cataract surgery. Displays 2022, 74, 102262. [Google Scholar] [CrossRef]
- Moreira, P.; Zemiti, N.; Liu, C.; Poignet, P. Viscoelastic model based force control for soft tissue interaction and its application in physiological motion compensation. Comput. Meth. Programs Biomed. 2014, 116, 52–67. [Google Scholar] [CrossRef]
- Patel, N.; Urias, M.; He, C.Y.; Gehlbach, P.L.; Iordachita, I. A Comparison of Manual and Robot Assisted Retinal Vein Cannulation in Chicken Chorioallantoic Membrane. In Proceedings of the 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 5101–5105. [Google Scholar]
- Gonenc, B.; Patel, N.; Iordachita, I. Evaluation of a Force-Sensing Handheld Robot for Assisted Retinal Vein Cannulation. In Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 3664–3668. [Google Scholar]
- Bian, G.B.; Wang, J.; Fu, P.; Wei, B.T.; Li, M.J.; Li, Z. A Tremor Suppression and Noise Removal Algorithm for Microscopic Robot-Assisted Cataract Surgery. IEEE-ASME Trans. Mechatron. 2023, 28, 2941–2952. [Google Scholar] [CrossRef]
- Iordachita, I.; Smet, M.D.; Naus, G.; Mitsuishi, M.; Riviere, C.N. Robotic Assistance for Intraocular Microsurgery: Challenges and Perspectives. Proc. IEEE 2022, 110, 893–908. [Google Scholar] [CrossRef] [PubMed]
- Gonenc, B.; Chamani, A.; Handa, J.; Gehlbach, P.; Taylor, R.H.; Iordachita, I. 3-DOF Force-Sensing Motorized Micro-Forceps for Robot-Assisted Vitreoretinal Surgery. IEEE Sens. J. 2017, 17, 3526–3541. [Google Scholar] [CrossRef] [PubMed]
- Haidegger, T. Autonomy for Surgical Robots: Concepts and Paradigms. IEEE Trans. Med. Robot. Bionics 2019, 1, 65–76. [Google Scholar] [CrossRef]
- Haidegger, T.; Speidel, S.; Stoyanov, D.; Satava, R.M. Robot-Assisted Minimally Invasive Surgery—Surgical Robotics in the Data Age. Proc. IEEE 2022, 110, 835–846. [Google Scholar] [CrossRef]



| Group I | Group II | ||||||
|---|---|---|---|---|---|---|---|
| E1 | τ1 | E2 | τ2 | R2 | SSE (mN) | Response Time (s) | |
| Embryo 1 | 0.692 | 1.042 | 7.405 | 0.004611 | 0.9789 | 0.31 | 1.41 |
| Embryo 2 | 0.7765 | 1.038 | 15.865 | 0.00272 | 0.9834 | 0.29 | 1.93 |
| Embryo 3 | 0.801 | 0.6156 | 12.665 | 0.002042 | 0.9812 | 0.35 | 1.97 |
| Embryo 4 | 1.254 | 1.068 | 37.31 | 0.001693 | 0.9735 | 0.24 | 1.80 |
| Embryo 5 | 0.701 | 0.9863 | 14.62 | 0.002621 | 0.9881 | 0.32 | 2.23 |
| Tech | Max Relative Error | Surgical Procedure | |
|---|---|---|---|
| JHU LCSR lab (SHER) [15] | CM | 25.56% | RVC |
| Carnegie Mellon (Micron) [18] | HH | 40% | RVC/membrane peeling |
| Chinese Academy of Sciences [28] | TM | O | Cataract surgery |
| TU Munich [6] | TM | O | RVC |
| Wenzhou Univ [29] | TM | O | RVC |
| This work | TM | 9.4% | RVC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Q.; Liu, J.; Zheng, Y.; Yang, Y.; Lin, C.; Guang, C. Evaluation of an Active Disturbance Rejection Controller for Ophthalmic Robots with Piezo-Driven Injector. Micromachines 2024, 15, 833. https://doi.org/10.3390/mi15070833
Tao Q, Liu J, Zheng Y, Yang Y, Lin C, Guang C. Evaluation of an Active Disturbance Rejection Controller for Ophthalmic Robots with Piezo-Driven Injector. Micromachines. 2024; 15(7):833. https://doi.org/10.3390/mi15070833
Chicago/Turabian StyleTao, Qiannan, Jianjun Liu, Yu Zheng, Yang Yang, Chuang Lin, and Chenhan Guang. 2024. "Evaluation of an Active Disturbance Rejection Controller for Ophthalmic Robots with Piezo-Driven Injector" Micromachines 15, no. 7: 833. https://doi.org/10.3390/mi15070833
APA StyleTao, Q., Liu, J., Zheng, Y., Yang, Y., Lin, C., & Guang, C. (2024). Evaluation of an Active Disturbance Rejection Controller for Ophthalmic Robots with Piezo-Driven Injector. Micromachines, 15(7), 833. https://doi.org/10.3390/mi15070833






