Dynamics of a 3D Piezo-Magneto-Elastic Energy Harvester with Axisymmetric Multi-Stability
Abstract
:1. Introduction
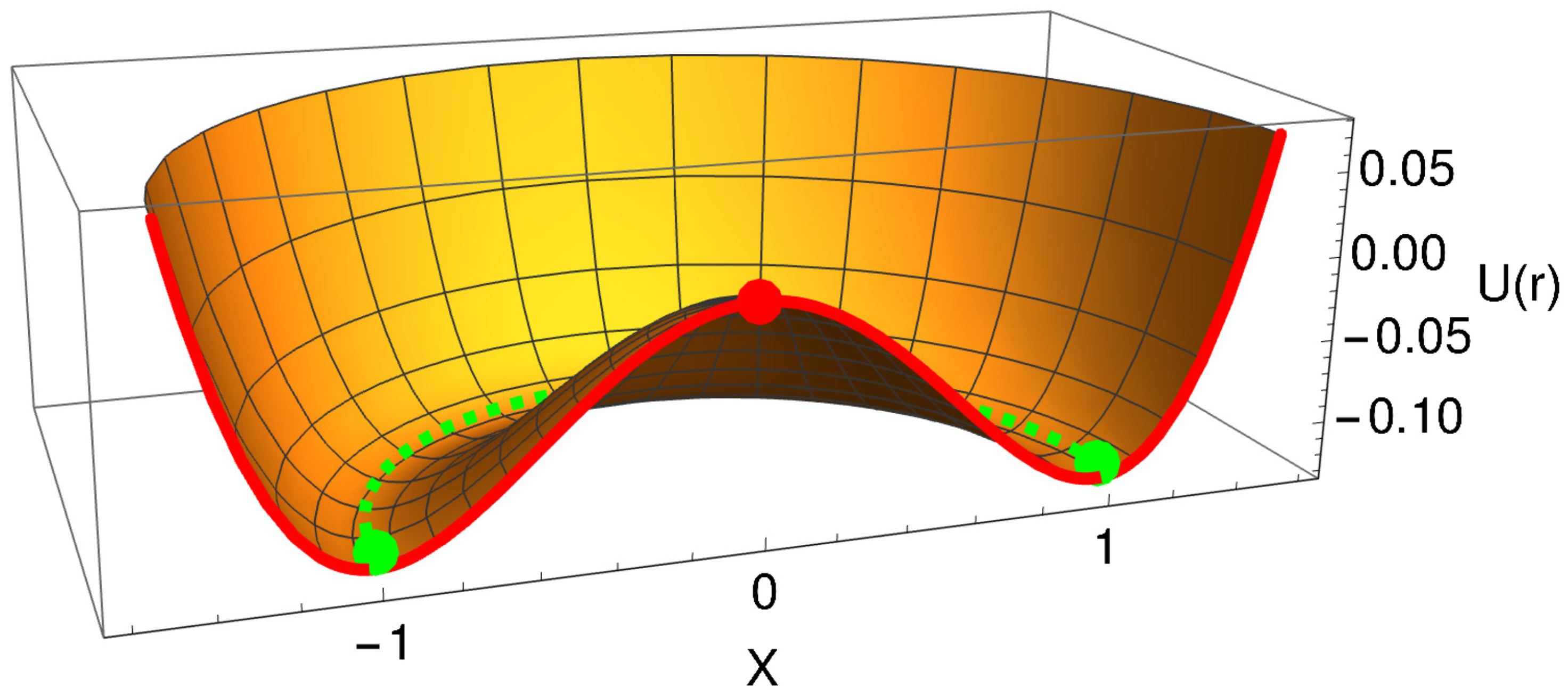
2. Description of the Model
Description of Model and Excitation Parameters
3. Numerical Simulations and Results
3.1. Results and Discussion
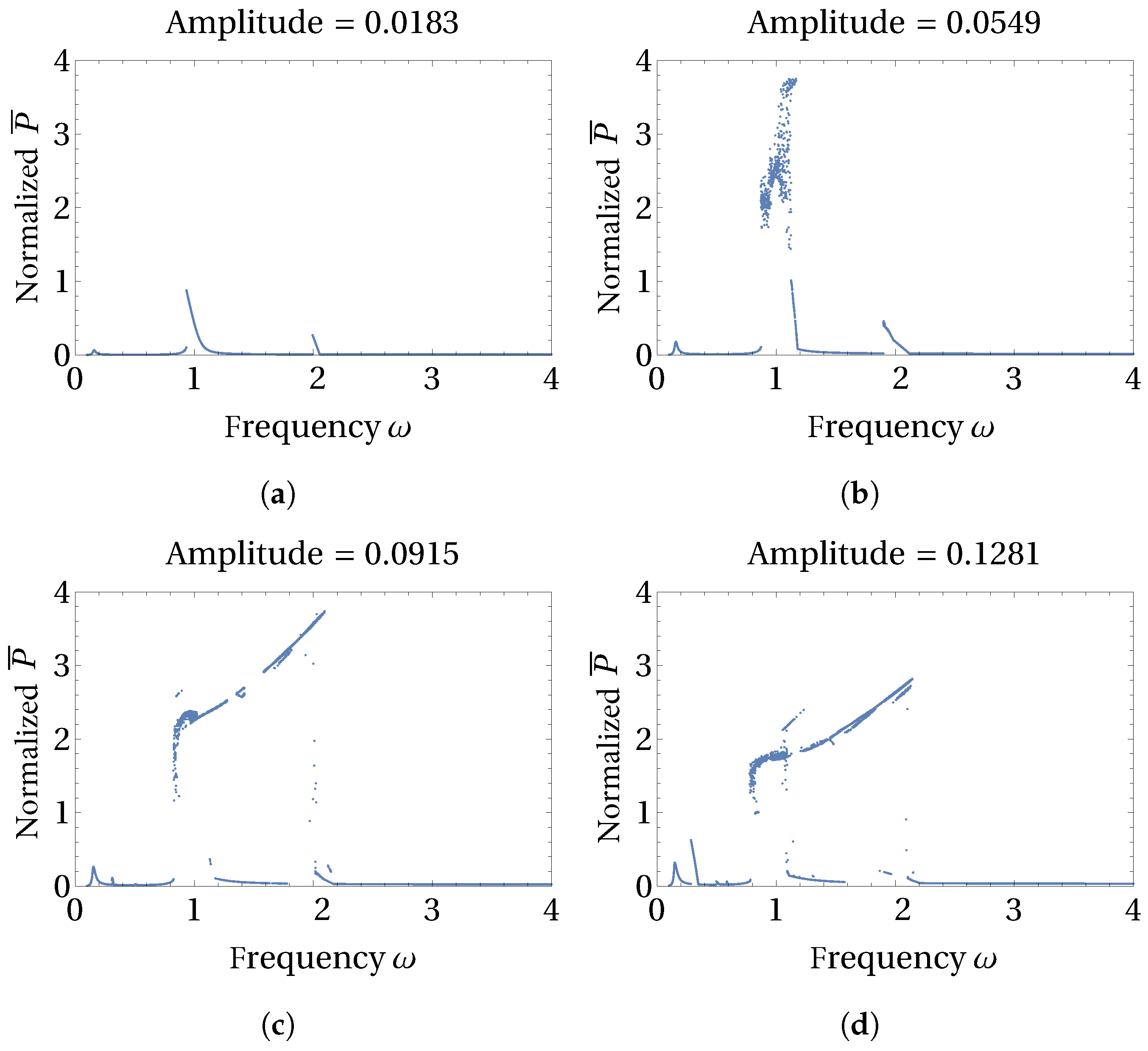
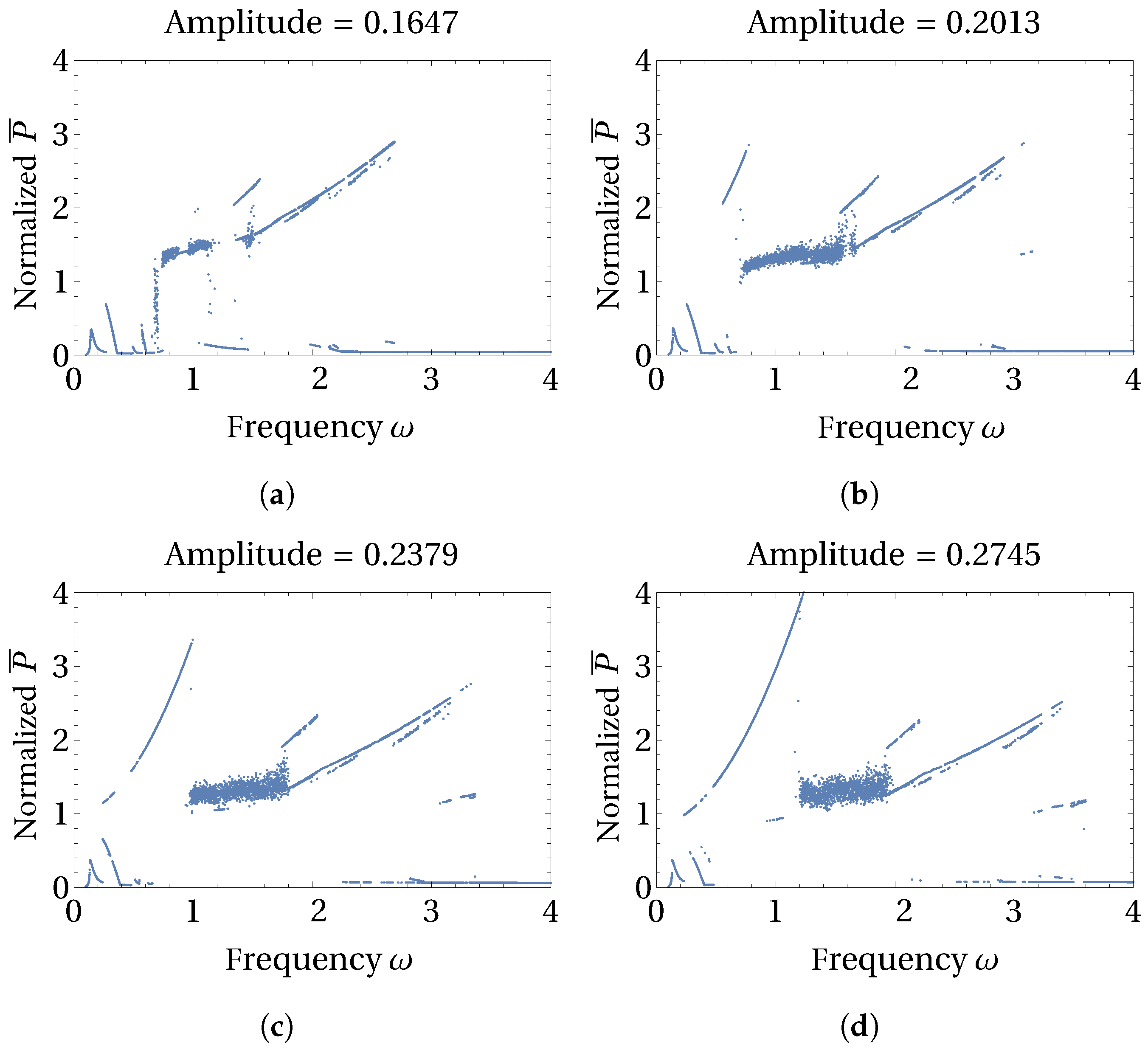
3.2. Influence of the Excitation Amplitude on the Average Power
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- White, N.M.; Glynne-Jones, P.; Beeby, S.P. A novel thick-film piezoelectric micro-generator. Smart Mater. Struct. 2001, 10, 850–852. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K. A piezoelectric vibration based generator for wireless electronics. Smart Mater. Struct. 2004, 13, 1131–1142. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-performance piezoelectric energy harvesters and their applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Vocca, H.; Neri, I.; Travasso, F.; Gammaitoni, L. Kinetic energy harvesting with bistable oscillators. Appl. Energy 2012, 97, 771–776. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Lett. 2009, 101, 080601. [Google Scholar] [CrossRef] [PubMed]
- Litak, G.; Friswell, M.I.; Adhikari, S. Magnetopiezoelastic energy harvesting driven by random excitations. Appl. Phys. Lett. 2010, 96, 214103. [Google Scholar] [CrossRef]
- Friswell, M.I.; Ali, S.F.; Adhikari, S.; Lees, A.W.; Bilgen, O.; Litak, G. Nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. J. Intell. Mater. Syst. Struct. 2012, 23, 1505–1521. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Lallart, M. Exploting bistable oscillator subharmonics for magnified broadband vibration energy harvesting. Appl. Phys. Lett. 2017, 111, 173905. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Druet, O.; Lallart, M. Drastic bandwidth enhancement of bistable energy harvesters: Study of subharmonic behaviors and their stability robustness. Appl. Energy 2018, 226, 607–617. [Google Scholar] [CrossRef]
- Huguet, T.; Lallart, M.; Badel, A. Orbit jump in bistable energy harvesters through buckling level modification. Mech. Syst. Signal Process. 2019, 128, 202–215. [Google Scholar] [CrossRef]
- Litak, G.; Ambrożkiewicz, B.; Wolszczak, P. Dynamics of a nonlinear energy harvester with subharmonic responses. J. Phys. Conf. Ser. 2021, 1736, 012032. [Google Scholar] [CrossRef]
- Giri, A.M.; Ali, S.F.; Arockiarajan, A. Characterizing harmonic and subharmonic solutions of the bi-stable piezoelectric harvester with a modified Harmonic Balance approach. Mech. Syst. Signal Process. 2023, 198, 110437. [Google Scholar] [CrossRef]
- Stanton, S.C.; Erturk, A.; Mann, B.P.; Inman, D.J. Nonlinear piezoelectricity in electroelastic energy harvesters: Modeling and experimental identification. J. Appl. Phys. 2010, 108, 074903. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved energy harvesting from wideband vibrations by nonlinear piezoelectric converters. Sens. Actuators A Phys. 2010, 162, 425–431. [Google Scholar] [CrossRef]
- Zhou, S.; Lallart, M.; Erturk, A. Multistable vibration energy harvesters: Principle, progress, and perspectives. J. Sound Vib. 2022, 528, 116886. [Google Scholar] [CrossRef]
- Litak, G.; Margielewicz, J.; Gąska, D.; Wolszczak, P.; Zhou, S. Multiple solutions of the tristable energy harvester. Energies 2021, 14, 1284. [Google Scholar] [CrossRef]
- Giri, A.M.; Ali, S.F.; Arockiarajan, A. Influence of asymmetric potential on multiple solutions of the bi-stable piezoelectric harvester. Eur. Phys. J. Spec. Top. 2022, 231, 1443–1464. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A novel two-degrees-of-freedom piezoelectric energy harvester. Intell. Mater. Syst. Struct. 2013, 24, 357–368. [Google Scholar] [CrossRef]
- Febbo, M.; Prado, B.F.A.; Smarzaro, V.C.; Bavastri, C.A. Multi-beam piezoelectric systems by means of dynamically equivalent stiffness concept. Smart Mater. Struct. 2023, 32, 085007. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Zhu, P. A broadband quad-stable energy harvester and its advantages over bi-stable harvester: Simulation and experiment verification. Mech. Syst. Signal Process. 2017, 84, 158–168. [Google Scholar] [CrossRef]
- Kim, P.; Seok, J. A multi-stable energy harvester: Dynamic modeling and bifurcation analysis. J. Sound Vib. 2014, 333, 5525–5547. [Google Scholar] [CrossRef]
- Giri, A.M.; Ali, S.F. A Arockiarajan, Dynamics of symmetric and asymmetric potential well-based piezoelectric harvesters: A comprehensive review. J. Intell. Mater. Syst. Struct. 2021, 32, 1881–1947. [Google Scholar] [CrossRef]
- Upadrashta, D.; Yang, Y. Experimental investigation of performance reliability of macro fiber composite for piezoelectric energy harvesting applications. Sens. Actuators A Phys. 2016, 244, 223–232. [Google Scholar] [CrossRef]
- Wang, P.; Liu, X.; Zhao, H.; Zhang, W.; Zhang, X.; Zhong, Y.; Guo, Y. A two-dimensional energy harvester with radially distributed piezoelectric array for vibration with arbitrary in-plane directions. J. Intell. Mater. Syst. Struct. 2019, 30, 1094–1104. [Google Scholar] [CrossRef]
- Borowiec, M.; Bochenski, M.; Litak, G.; Teter, A. Analytical model and energy harvesting analysis of a vibrating slender rod with added tip mass in three-dimensional space. Eur. Phys. J. Spec. Top. 2021, 230, 3581–3590. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behaviour; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Iwaniec, J.; Litak, G.; Iwaniec, M.; Margielewicz, J.; Gąska, D.; Melnyk, M.; Zabierowski, W. Response Identification in a Vibration Energy-Harvesting System with Quasi-Zero Stiffness and Two Potential Wells. Energies 2021, 14, 3926. [Google Scholar] [CrossRef]



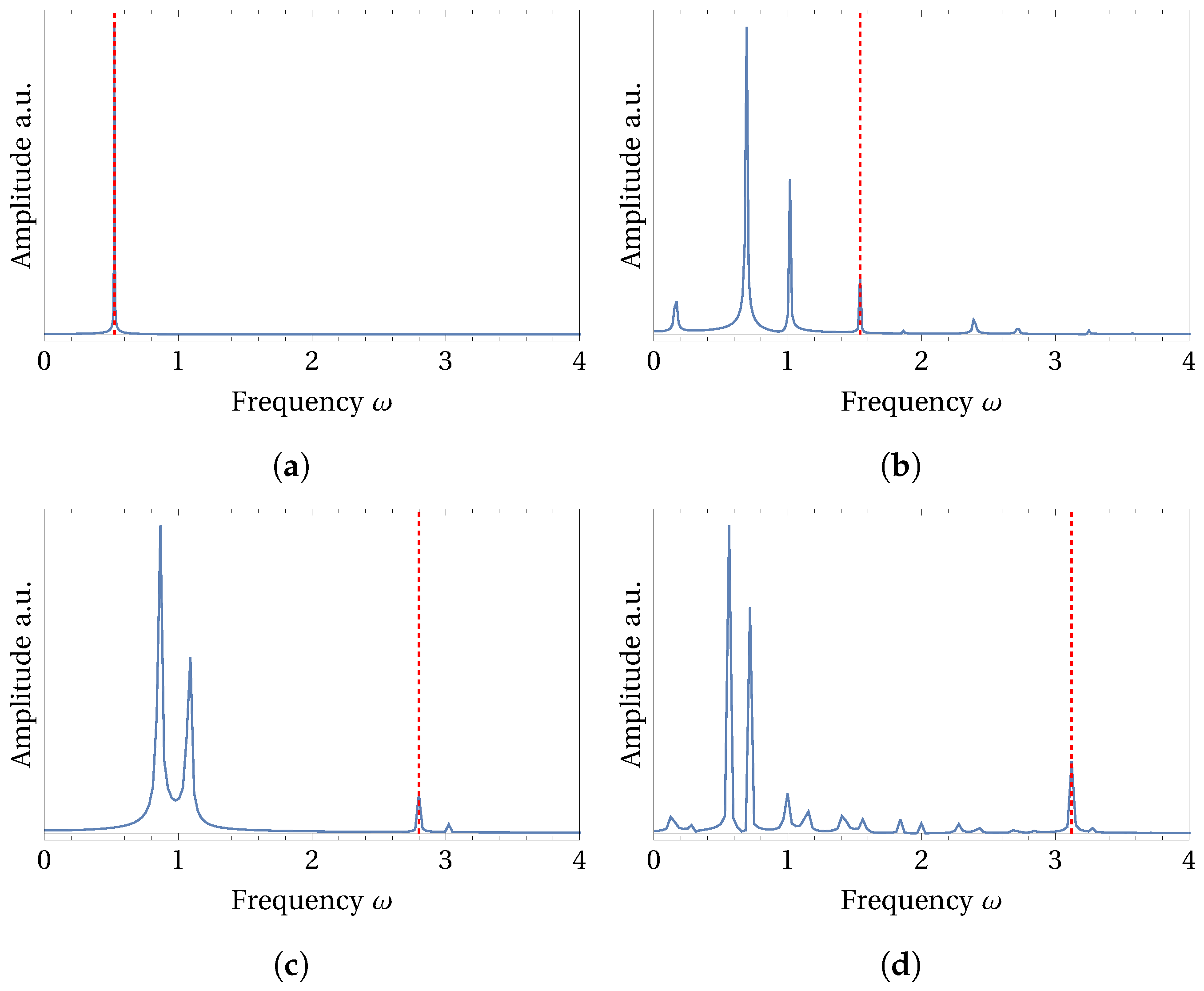
| Excitation Frequency | Frequencies of the Harmonics in FFT |
|---|---|
| 0.5235 | 0.5235 |
| 1.5405 | 0.169455, 0.693225, 1.01673, 1.5405 |
| 2.7985 | 0.867535, 1.09142, 2.7985 |
| 3.1210 | 0.56178, 0.71783, 0.99872, 3.1210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Litak, G.; Klimek, M.; Giri, A.M.; Wolszczak, P. Dynamics of a 3D Piezo-Magneto-Elastic Energy Harvester with Axisymmetric Multi-Stability. Micromachines 2024, 15, 906. https://doi.org/10.3390/mi15070906
Litak G, Klimek M, Giri AM, Wolszczak P. Dynamics of a 3D Piezo-Magneto-Elastic Energy Harvester with Axisymmetric Multi-Stability. Micromachines. 2024; 15(7):906. https://doi.org/10.3390/mi15070906
Chicago/Turabian StyleLitak, Grzegorz, Mariusz Klimek, Abhijeet M. Giri, and Piotr Wolszczak. 2024. "Dynamics of a 3D Piezo-Magneto-Elastic Energy Harvester with Axisymmetric Multi-Stability" Micromachines 15, no. 7: 906. https://doi.org/10.3390/mi15070906






