Parametric Synthesis of Single-Stage Lattice-Type Acoustic Wave Filters and Extended Multi-Stage Design
Abstract
:1. Introduction
2. Basic Synthesis Theory of Single-Stage Filter
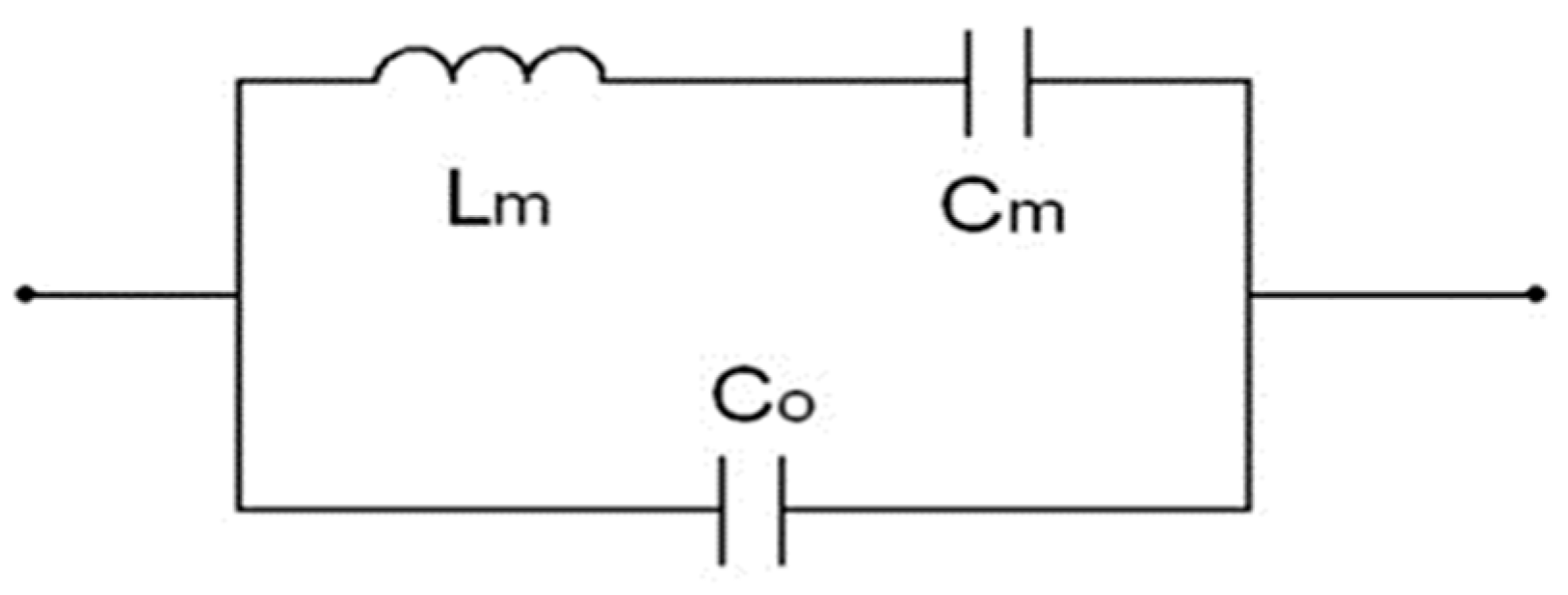
2.1. Equivalent Circuit of Acoustic Resonator
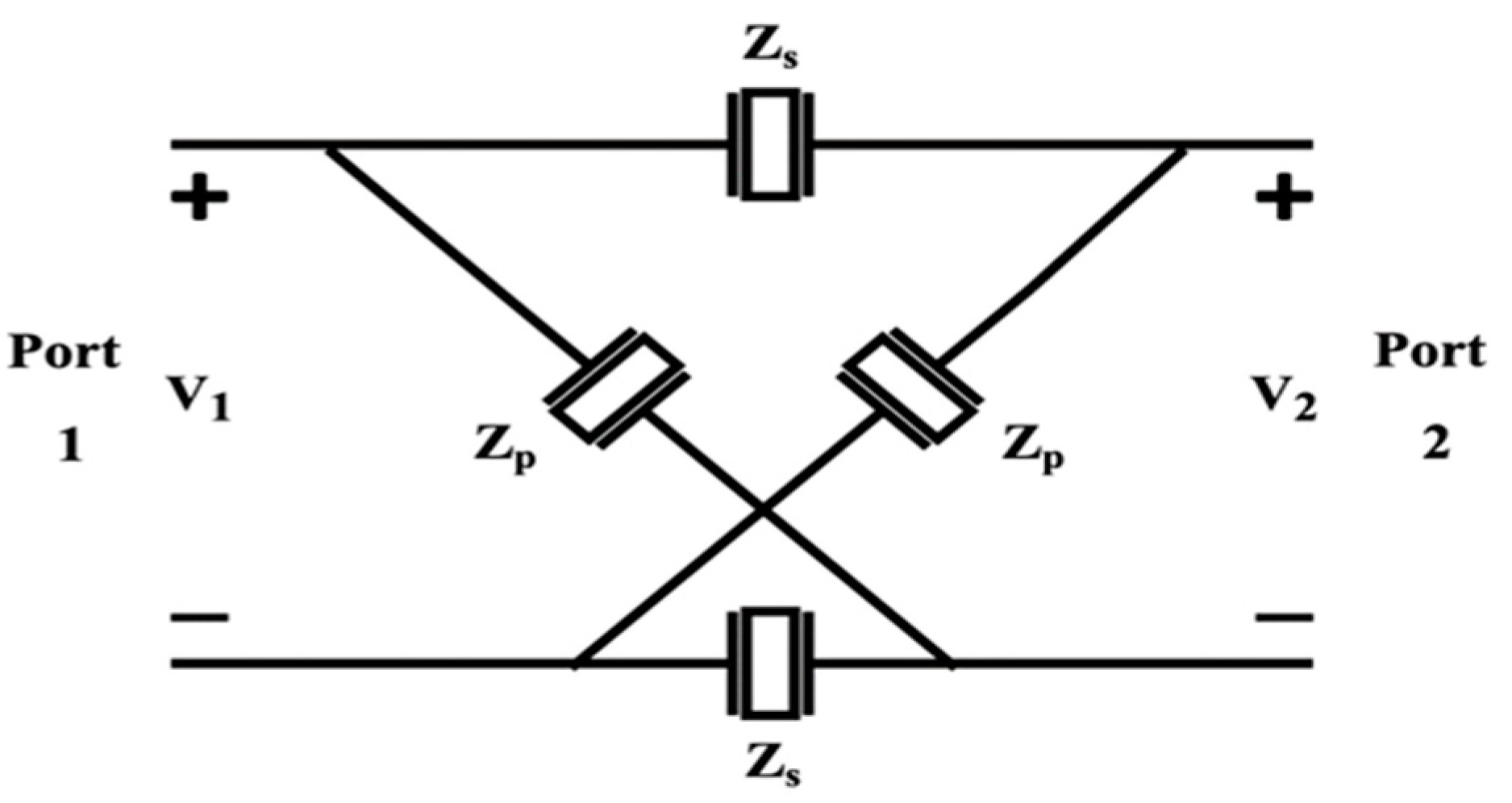
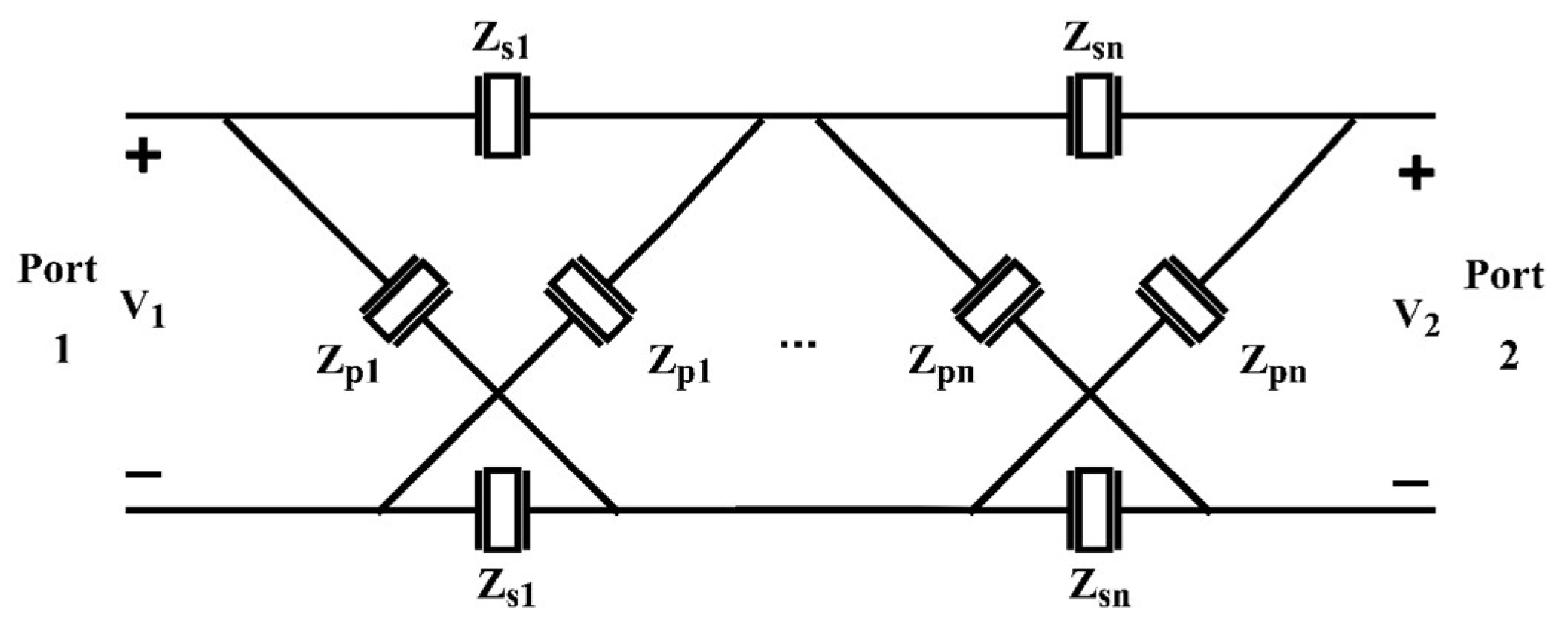
2.2. One Stage Lattice Network Analysis
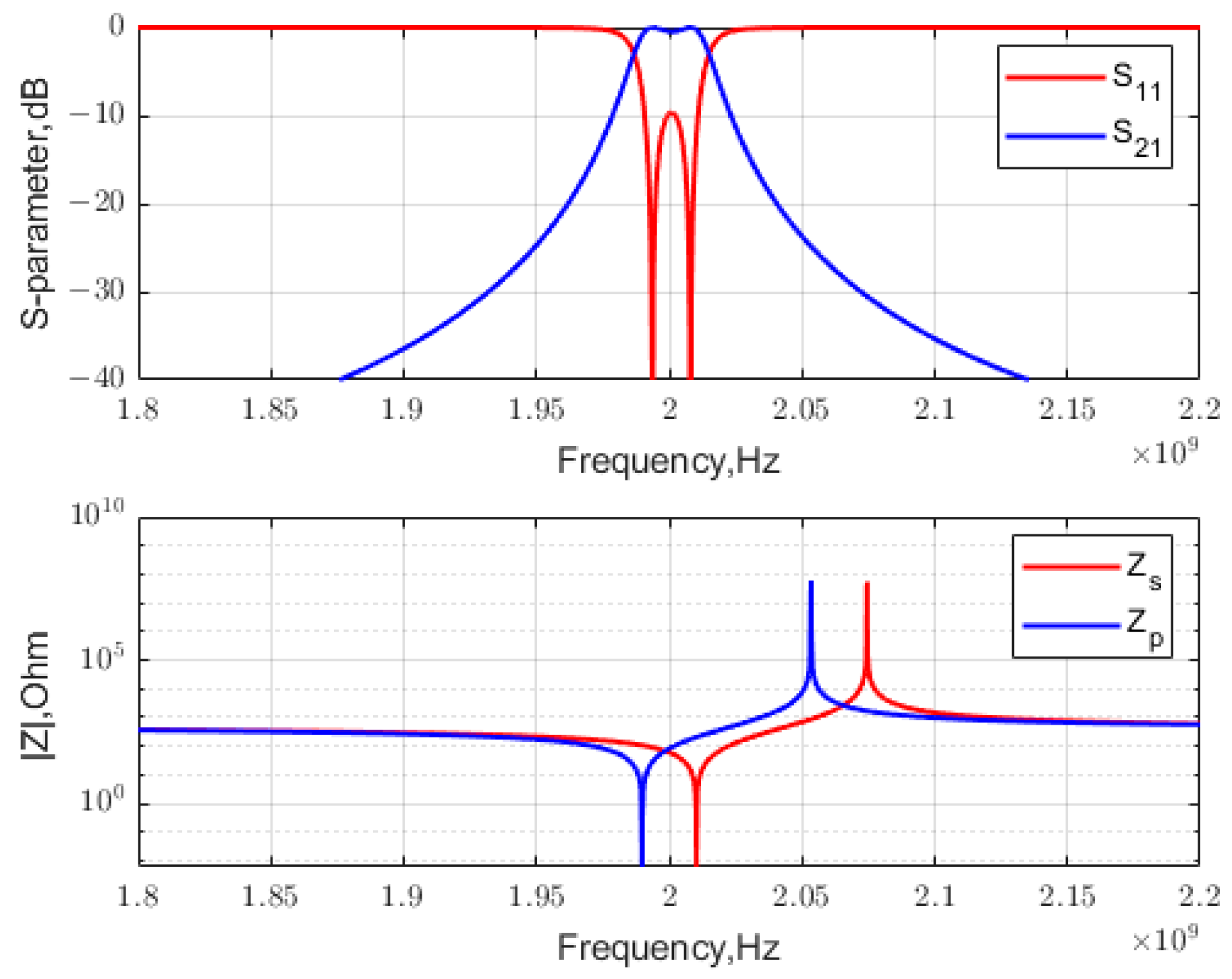
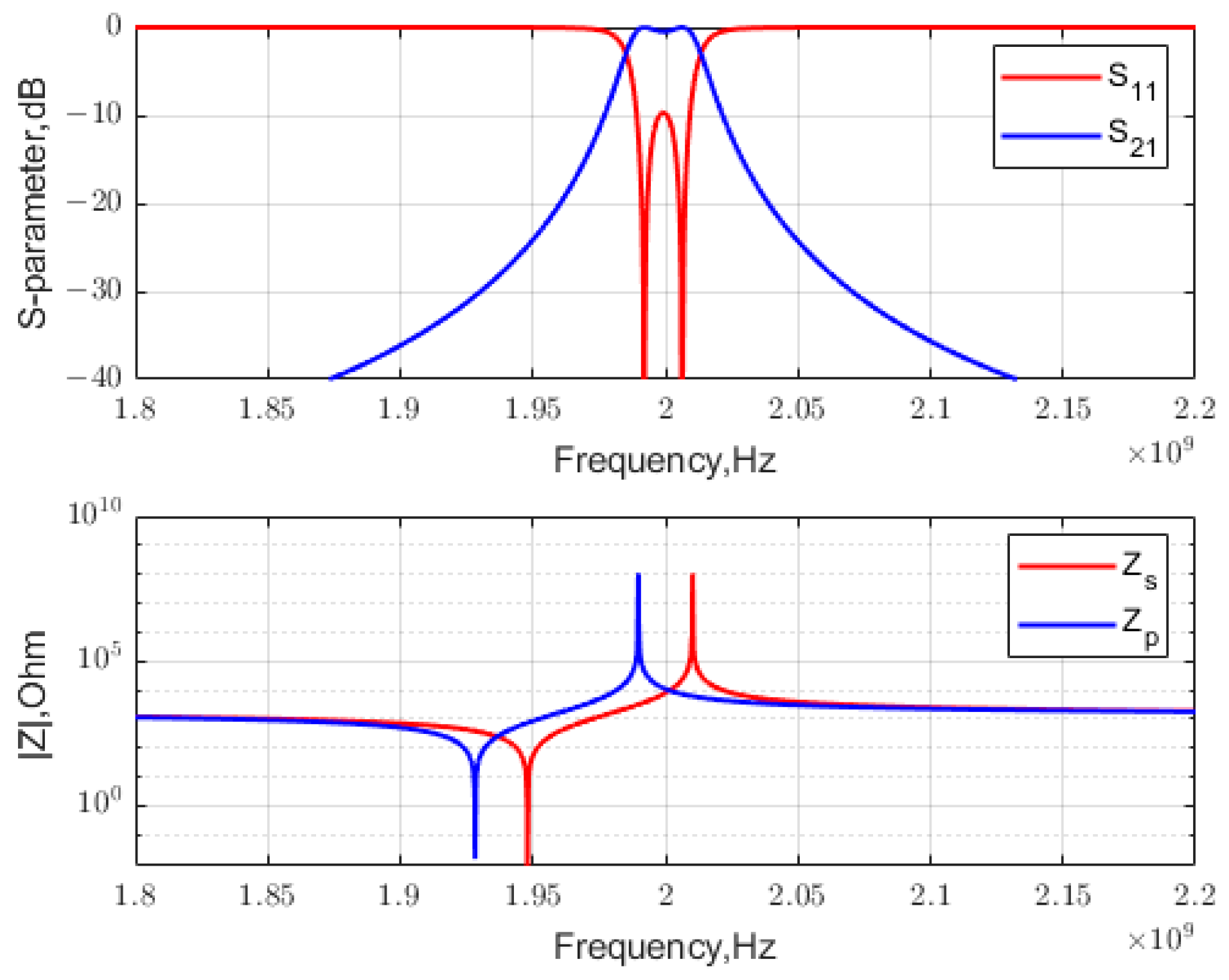
2.3. Synthesis for a Narrow-Band Single-Stage Design
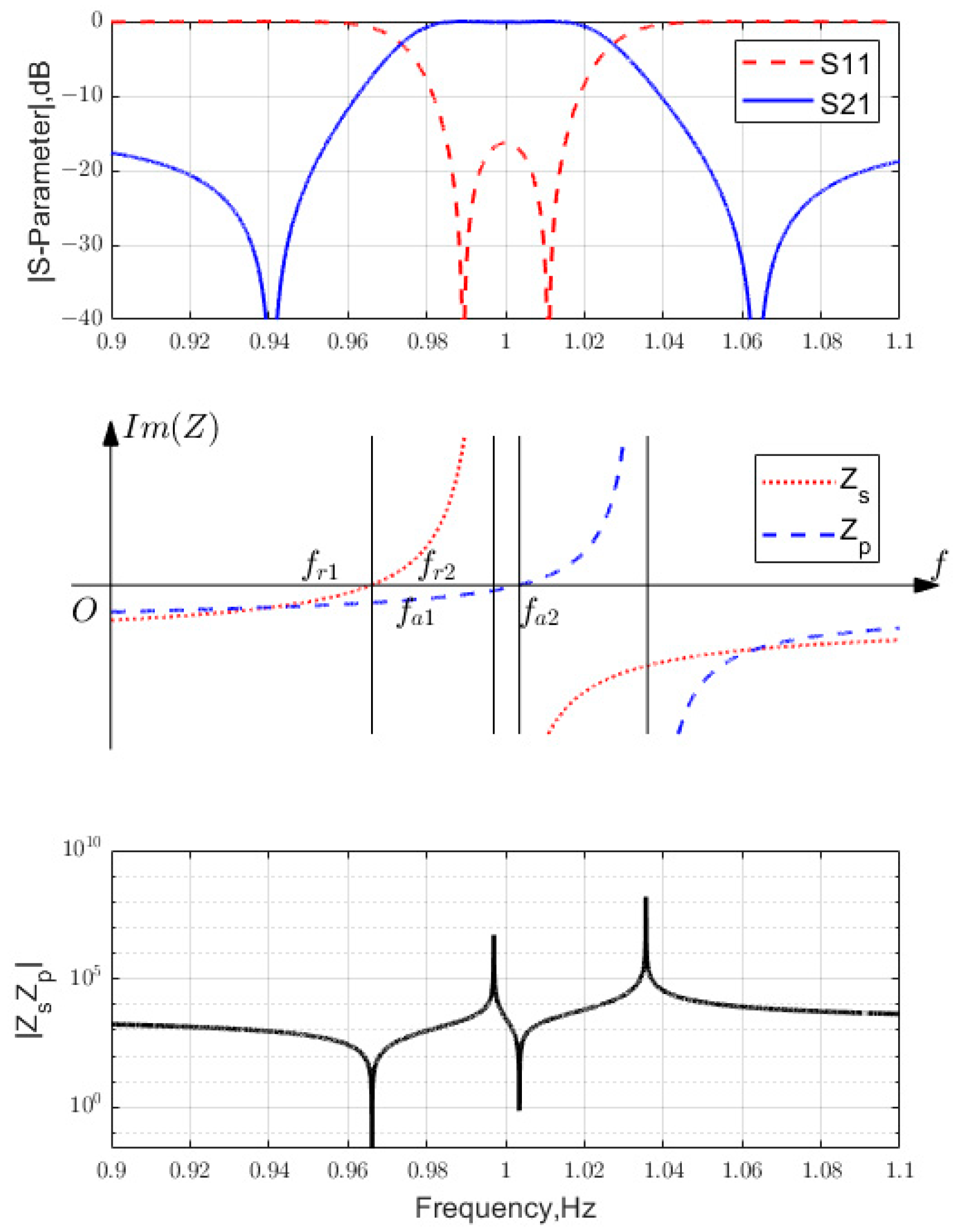
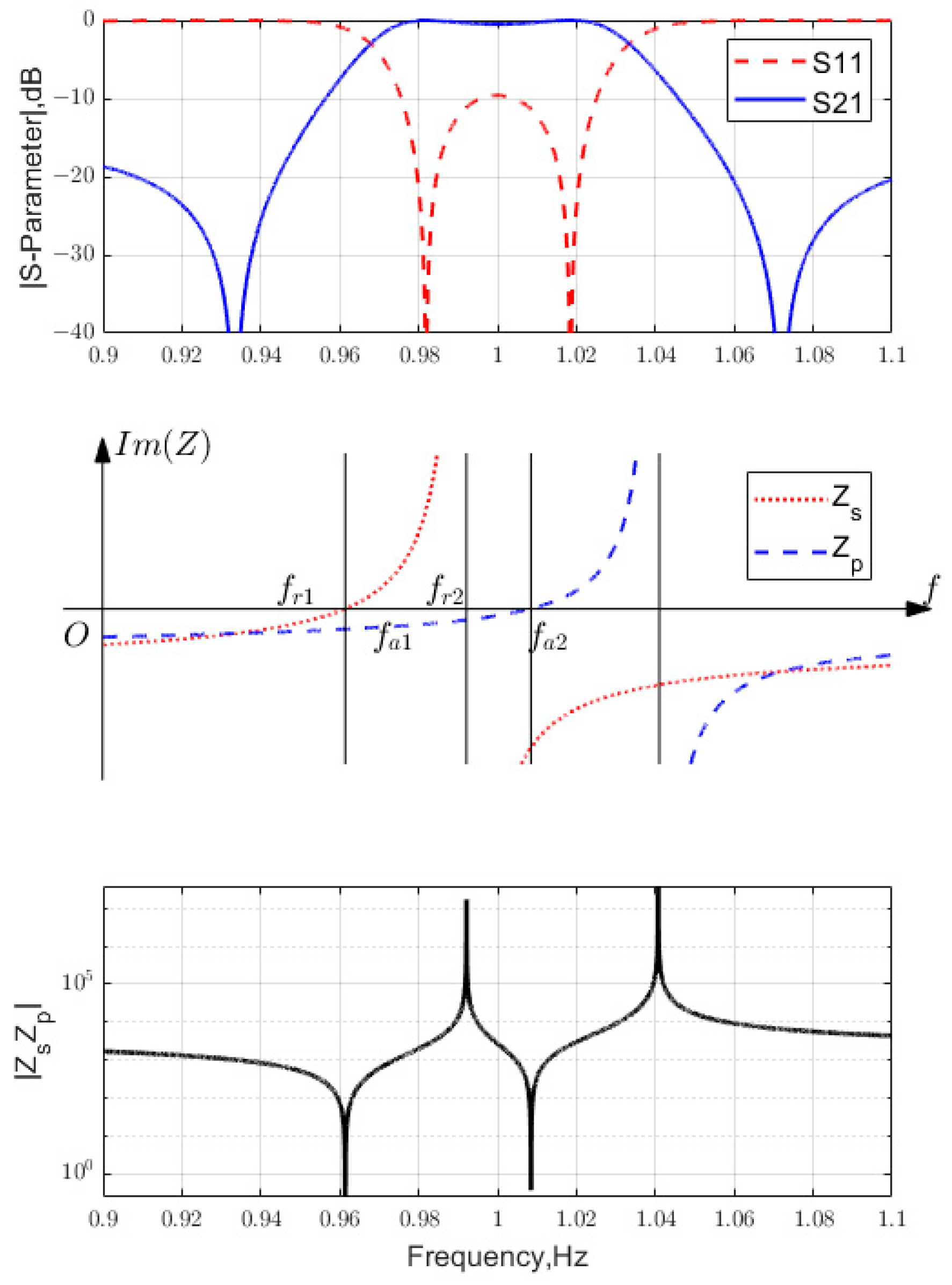
2.4. Passband Conditions
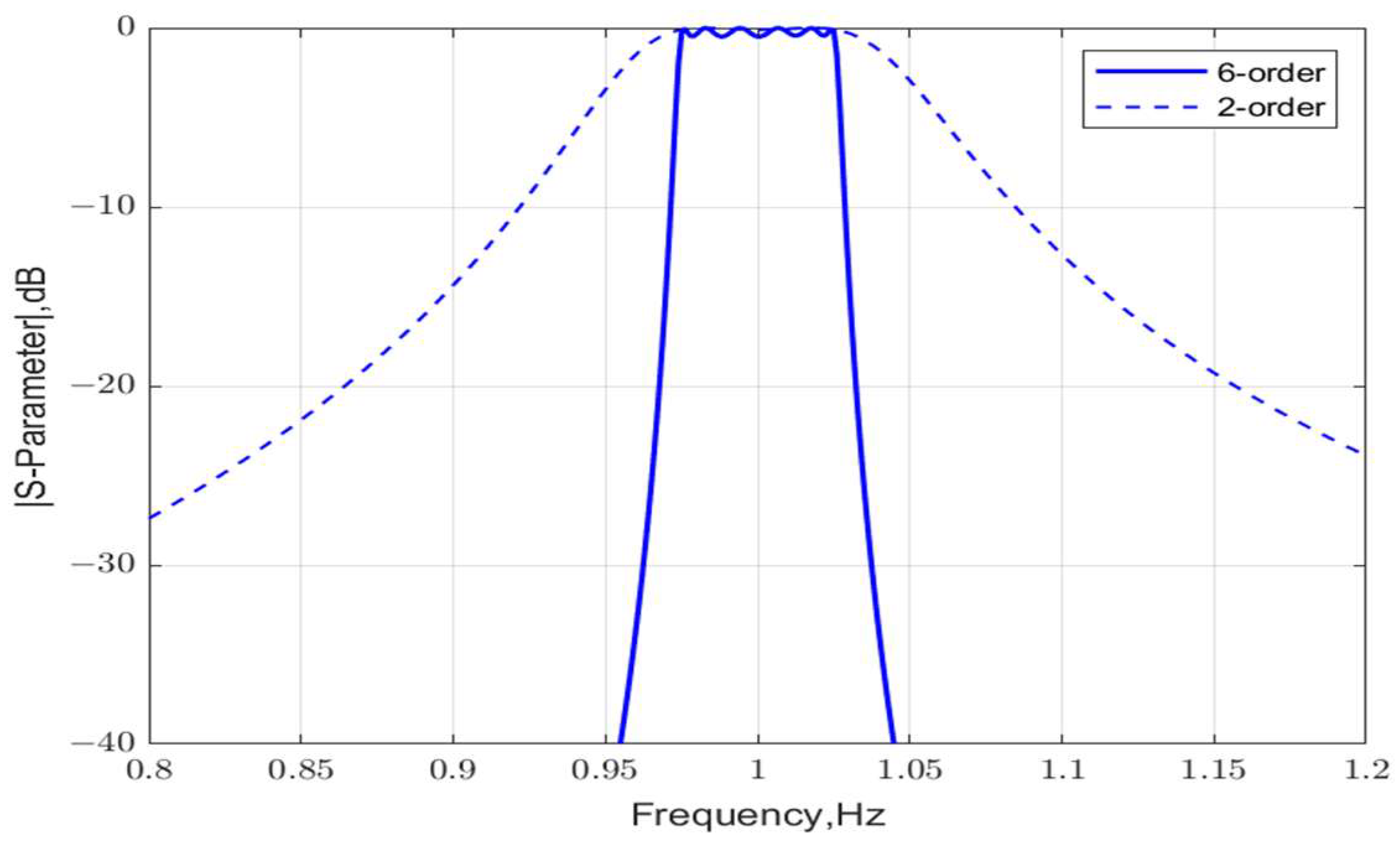
2.5. Multi-Stage Design
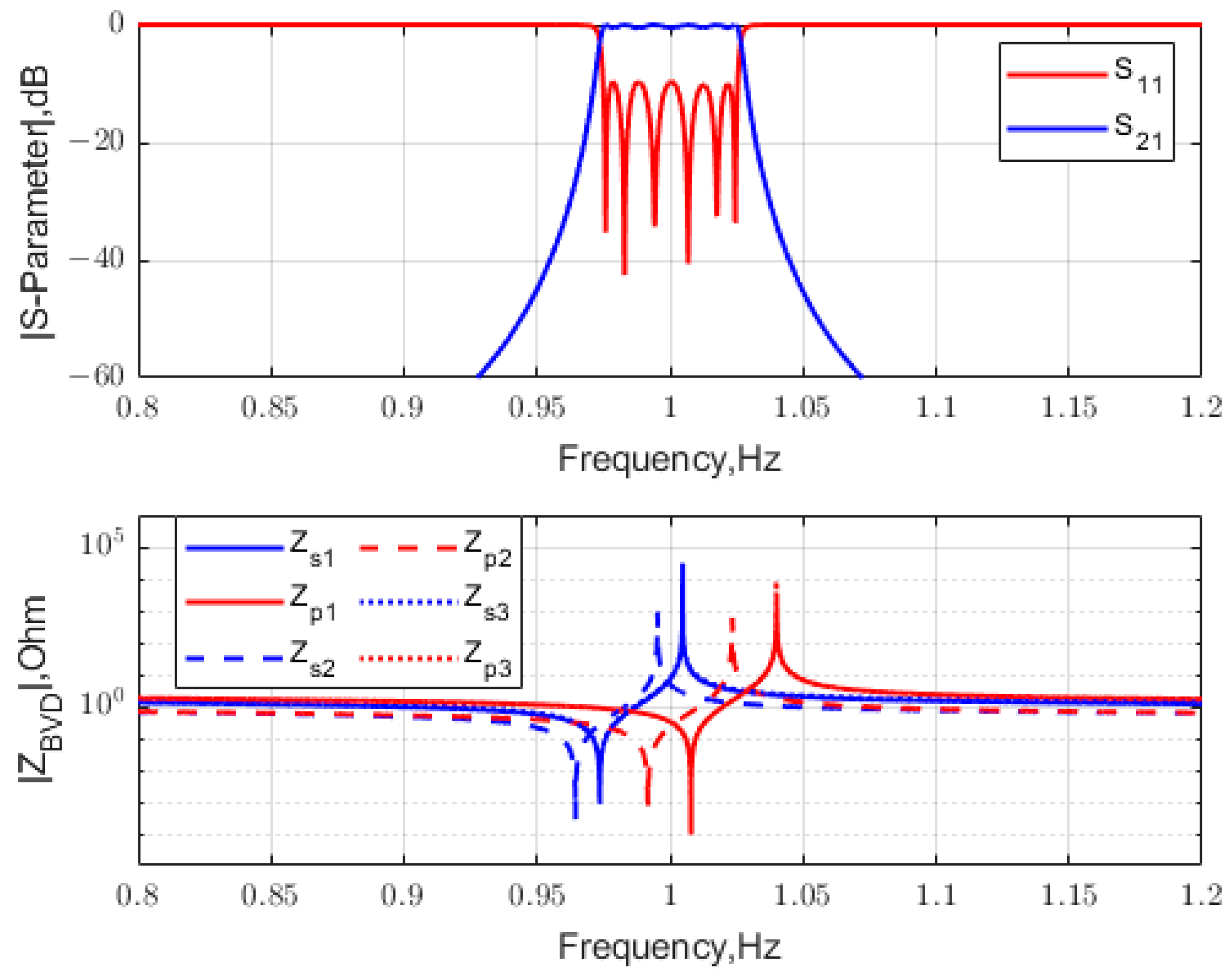
2.6. Mult-Stage Lattice Network Analysis
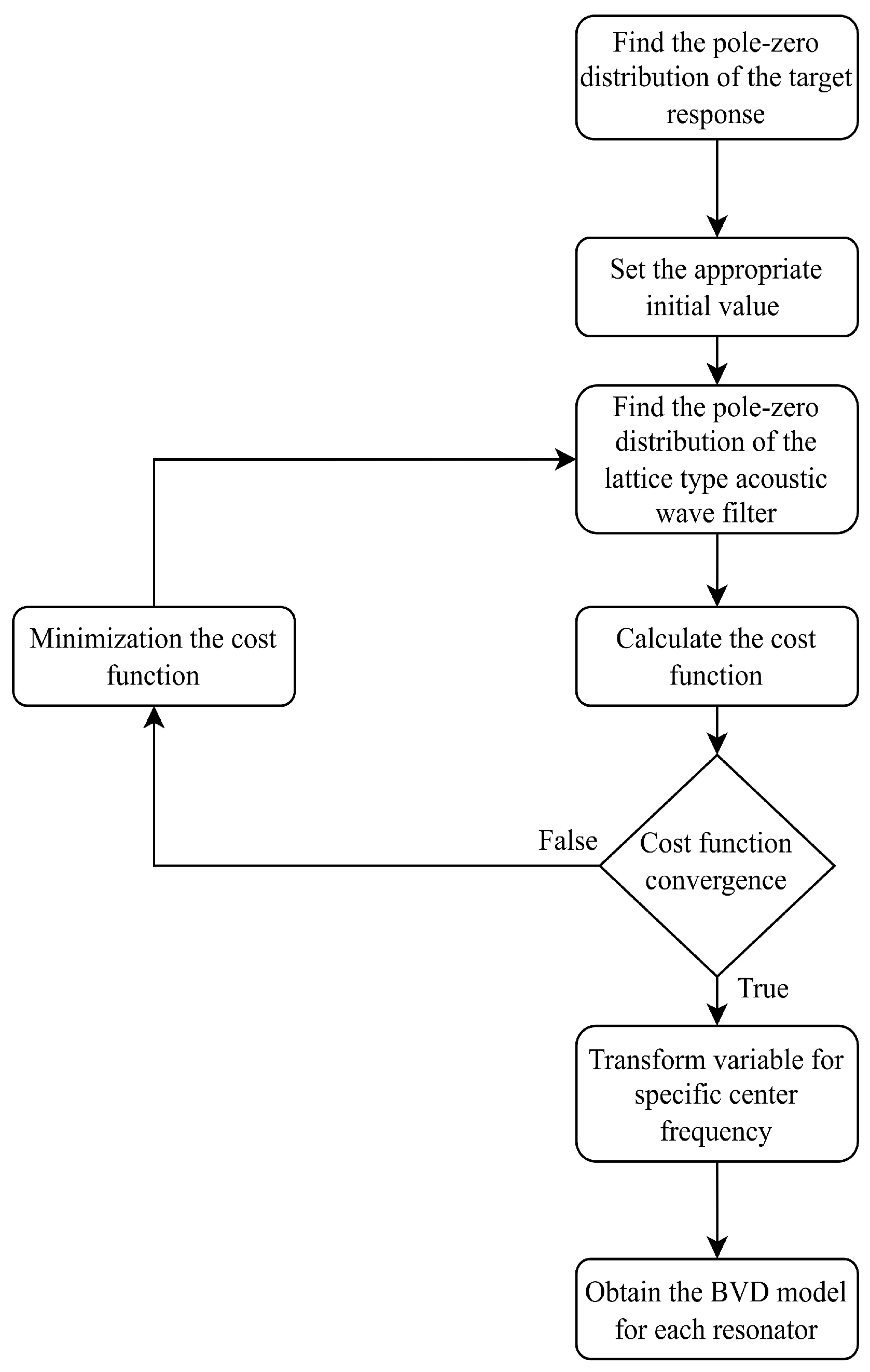
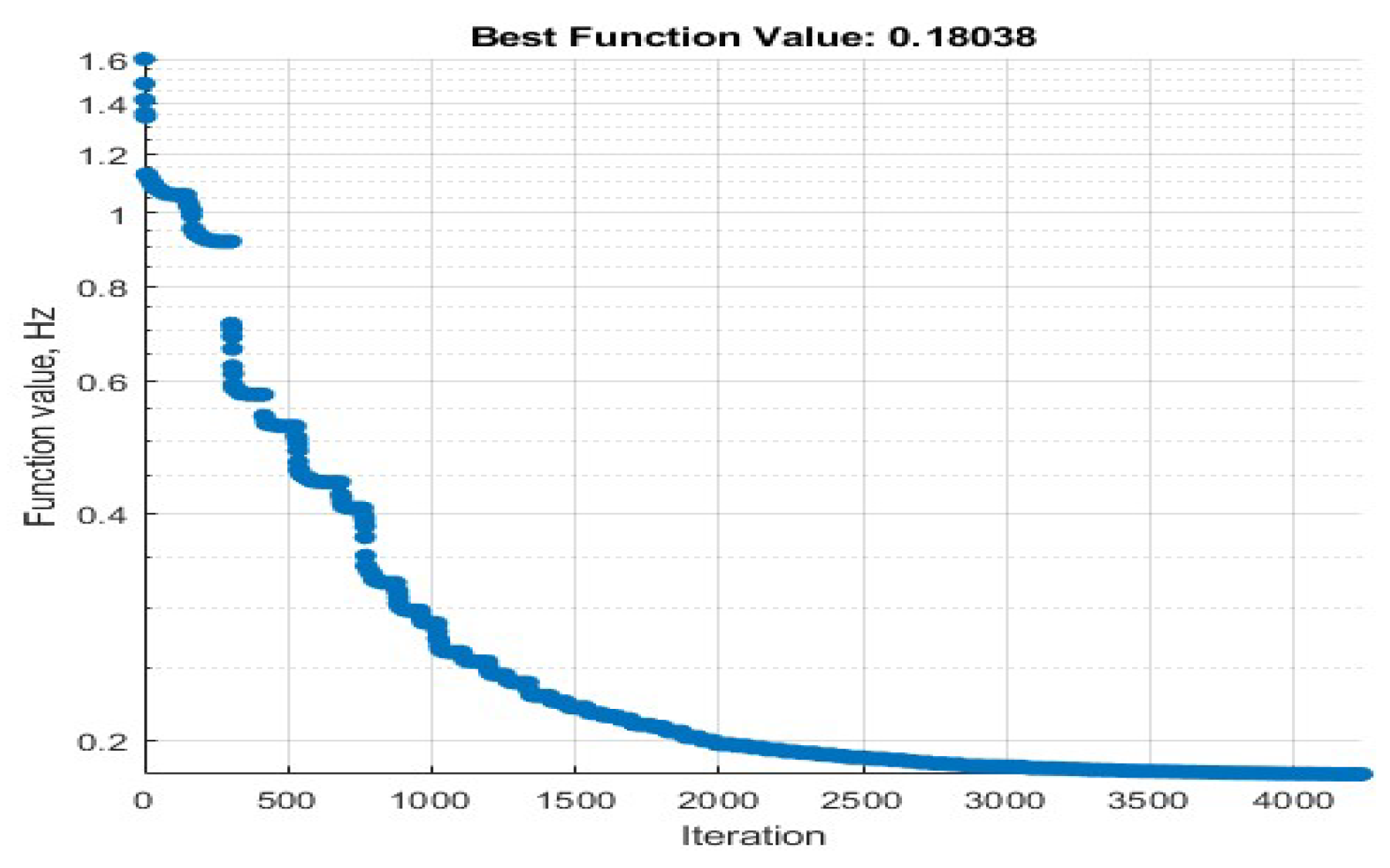
2.7. Pole-Zero Distribution Optimization Process
2.8. Conversion Formula of the New System Parameters
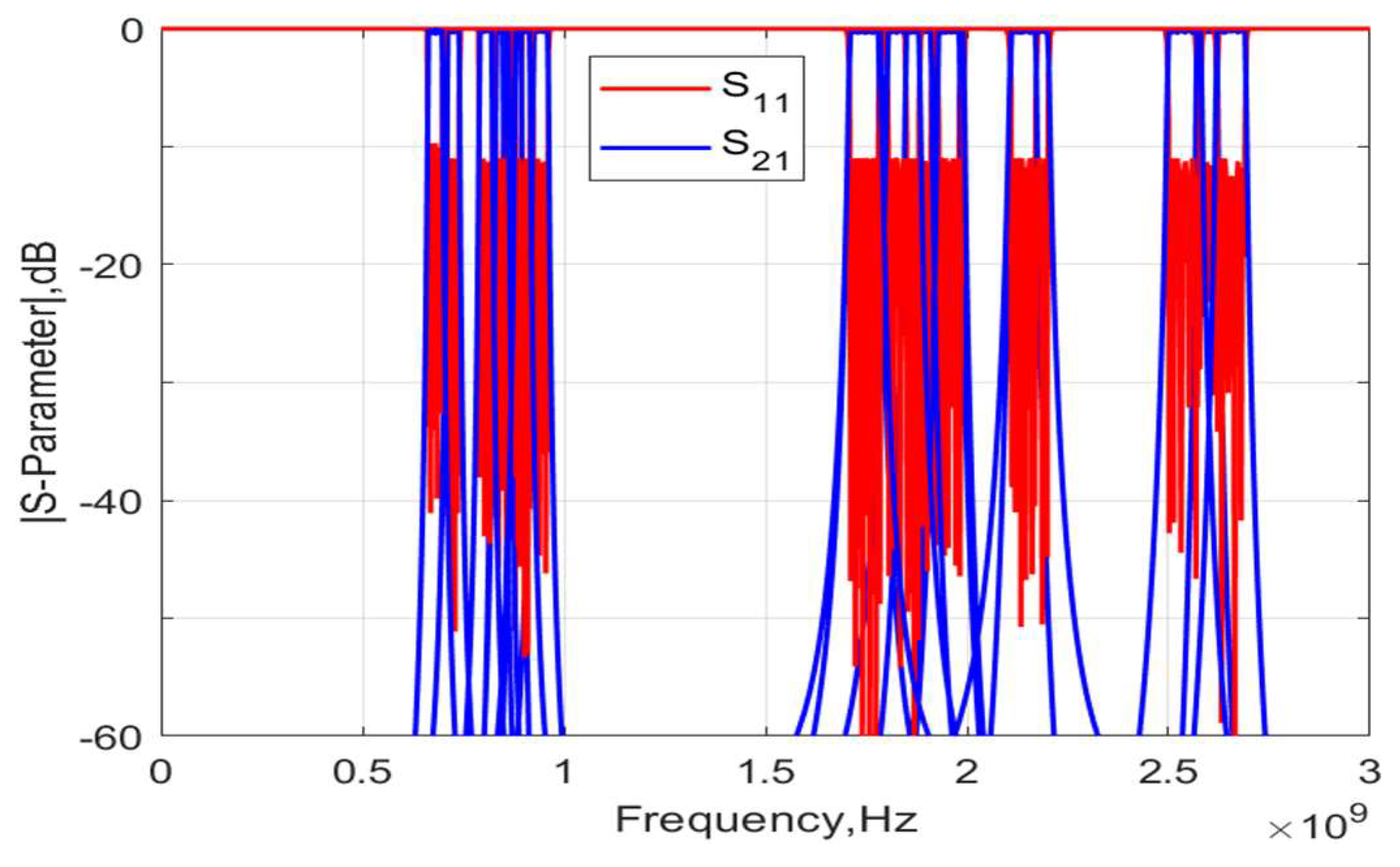
2.9. Application in the 5G Bands
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tag, A.; Schaefer, M.; Sadhu, J.; Tajic, A.; Stokes, P.; Koohi, M.; Yusuf, W.; Heeren, W.; Fatemi, H.; Celii, F.; et al. Next generation of BAW: The new benchmark for RF acoustic technologies. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022. [Google Scholar]
- Wang, W.; Fu, S.; Xu, Z.; Xu, H.; Liu, P.; Xiao, B.; Pan, F. High-performance wideband SAW filters on LNOI platform. In Proceedings of the 2024 IEEE MTT-S International Conference on Microwave Acoustics & Mechanics (IC-MAM 2024), Chengdu, China, 13–15 May 2024. [Google Scholar]
- Sun, M.; Zhang, S.; Zheng, P.; Zhang, L.; Wu, J.; Ou, X. Exploring surface acoustic wave transversal filters on heterogeneous substrates for 5G n77 band. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022. [Google Scholar]
- Fu, H.X.S.; Su, R.; Liu, P.; Zhang, S.; Lu, Z.; Xiao, B.; Wang, R.; Song, C.; Zeng, F.; Wang, W.; et al. SAW filters on LiNbO3/SiC heterostructure for 5G n77 and n78 band applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 1157–1169. [Google Scholar]
- Shen, J.; Fu, S.; Su, R.; Xu, H.; Lu, Z.; Zhang, Q.; Zeng, F.; Song, C.; Wang, W. Ultra-wideband surface acoustic wave filters based on the Cu/LiNbO3/SiO2/SiC structure. In Proceedings of the 2021 IEEE International Ultrasonics Symposium, Virtual, 11–16 September 2021. [Google Scholar]
- Balysheva, O.L. SAW filters and mobile communication systems 5G. In Proceedings of the 2021 Wave Electronics and Its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 31 May–4 June 2021; pp. 1–5. [Google Scholar]
- Dolle, H.K.J.T.; Lobeek, J.-W.; Tuinhout, A.; Foekema, J. Balanced lattice-ladder bandpass filter in bulk acoustic wave technology. In Proceedings of the IEEE International Microwave Symposium 2004, Fort Worth, TX, USA, 9–11 June 2004; pp. 391–394. [Google Scholar]
- Ariturk, G.; Almuqati, N.R.; Yu, Y.; Yen, E.T.-T.; Fruehling, A.; Sigmarsson, H.H. Wideband hybrid acoustic-electromagnetic filters with prescribed Chebyshev functions. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Denver, CO, USA, 19–24 June 2022. [Google Scholar]
- Yang, Q.; Pang, W.; Zhang, D.; Zhang, H. Modified lattice configuration design for compact wideband bulk acoustic wave filter applications. Micromachines 2016, 7, 133. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Piazza, G. Design and analysis of Lithium–Niobate-based high electro-mechanical coupling RF-MEMS resonators for wideband filtering. IEEE Trans. Microw. Theory Tech. 2013, 61, 403–414. [Google Scholar] [CrossRef]
- Driscoll, M.; Moore, R.; Rosenbaum, J.; Krishnaswamy, S.; Szedon, I. Design and evaluation of UHF monolithic film resonator—Stabilized oscillators and bandpass filters. In 1987 IEEE MTT-S International Microwave Symposium Digest; IEEE: New York, NY, USA, 1987; Volume 87, pp. 801–804. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011; Chapter 4. [Google Scholar]
- Lewis, R.M.; Torczon, V. A globally convergent augmented Lagrangian pattern search algorithm for optimization with general constraints and simple bounds. SIAM J. Optim. 2002, 12, 10751089. [Google Scholar] [CrossRef]
- Tseng, S.-Y.; Hsiao, C.-C.; Wu, R.-B. Synthesis and realization of Chebyshev filters based on constant electromechanical coupling coefficient acoustic wave resonators. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 257–260. [Google Scholar]
- Tseng, S.-Y.; Yang, M.-Y.; Hsiao, C.-C.; Chen, Y.-Y.; Wu, R.-B. Design for acoustic wave multiplexers with single inductor matching network using frequency response fitting method. IEEE Open J. Ultrason. Ferroelectr. Freq. Control 2022, 2, 140–151. [Google Scholar] [CrossRef]
- Yang, M.-Y.; Wu, R.-B. Design for SAW antenna-plexers with improved matching inductance circuits. Micromathines 2024, 15, 89. [Google Scholar] [CrossRef] [PubMed]


| BVD | |||||
|---|---|---|---|---|---|
| 19.6946 | 0.9736 | 3.2196 | 0.0083 | 0.1278 | |
| 25.8630 | 1.0079 | 4.0840 | 0.0061 | 0.0940 | |
| 10.2497 | 0.9645 | 1.6914 | 0.0161 | 0.2478 | |
| 10.0815 | 0.9917 | 1.6180 | 0.0159 | 0.2454 | |
| 21.8005 | 0.9736 | 3.5638 | 0.0075 | 0.1154 | |
| 25.6740 | 1.0078 | 4.0546 | 0.0062 | 0.0947 |
| 5GNR FR1 Band | Uplink Operating Band User Equipment Transmit (MHz) | FBW of Uplink Operating Band | Downlink Operating Band User Equipment Receive (MHz) | FBW of Downlink Operating Band | Duplex Mode | Band Width (MHz) |
|---|---|---|---|---|---|---|
| n1 | 1920–1980 | 3.1% | 2110–2170 | 2.8% | FDD | 60 |
| n2 | 1850–1910 | 3.2% | 1930–1990 | 3.1% | FDD | 60 |
| n3 | 1805–1880 | 4.1% | 1710–1785 | 4.3% | FDD | 75 |
| n5 | 869–894 | 2.8% | 824–849 | 2.9% | FDD | 25 |
| n7 | 2620–2690 | 2.6% | 2500–2579 | 3.1% | FDD | 70 |
| n8 | 925–960 | 3.7% | 880–915 | 3.9% | FDD | 35 |
| n20 | 832–862 | 3.5% | 791–821 | 3.7% | FDD | 20 |
| n28 | 703–748 | 6.2% | 758–803 | 5.8% | FDD | 45 |
| n38 | 2570–2620 | 1.9% | 2570–2620 | 1.9% | TDD | 50 |
| n41 | 2496–2690 | 7.5% | 2496–2690 | 7.5% | FDD | 194 |
| n66 | 1710–1780 | 4.0% | 2110–2200 | 4.2% | FDD | 70/90 |
| n71 | 663–698 | 5.1% | 617–652 | 5.5% | FDD | 35 |
| n77 | 3300–4200 | 24% | 330–4200 | 24% | TDD | 900 |
| n78 | 3300–3800 | 14% | 3300–3800 | 14% | TDD | 500 |
| n79 | 4400–5000 | 12.7% | 4400–5000 | 12.7% | TDD | 600 |
| n81 | 880–915 | 3.9% | N/A | SUL | 35 | |
| n83 | 703–748 | 6.2% | N/A | SUL | 45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tseng, W.-H.; Wu, R.-B. Parametric Synthesis of Single-Stage Lattice-Type Acoustic Wave Filters and Extended Multi-Stage Design. Micromachines 2024, 15, 1075. https://doi.org/10.3390/mi15091075
Tseng W-H, Wu R-B. Parametric Synthesis of Single-Stage Lattice-Type Acoustic Wave Filters and Extended Multi-Stage Design. Micromachines. 2024; 15(9):1075. https://doi.org/10.3390/mi15091075
Chicago/Turabian StyleTseng, Wei-Hsien, and Ruey-Beei Wu. 2024. "Parametric Synthesis of Single-Stage Lattice-Type Acoustic Wave Filters and Extended Multi-Stage Design" Micromachines 15, no. 9: 1075. https://doi.org/10.3390/mi15091075
APA StyleTseng, W.-H., & Wu, R.-B. (2024). Parametric Synthesis of Single-Stage Lattice-Type Acoustic Wave Filters and Extended Multi-Stage Design. Micromachines, 15(9), 1075. https://doi.org/10.3390/mi15091075







