Scan-Rate-Dependent Ion Current Rectification in Bipolar Interfacial Nanopores
Abstract
1. Introduction
2. Theoretical Model
- (1)
- Poisson–Nernst–Planck equation
- (2)
- Navier–Stokes equation
3. Results and Discussion
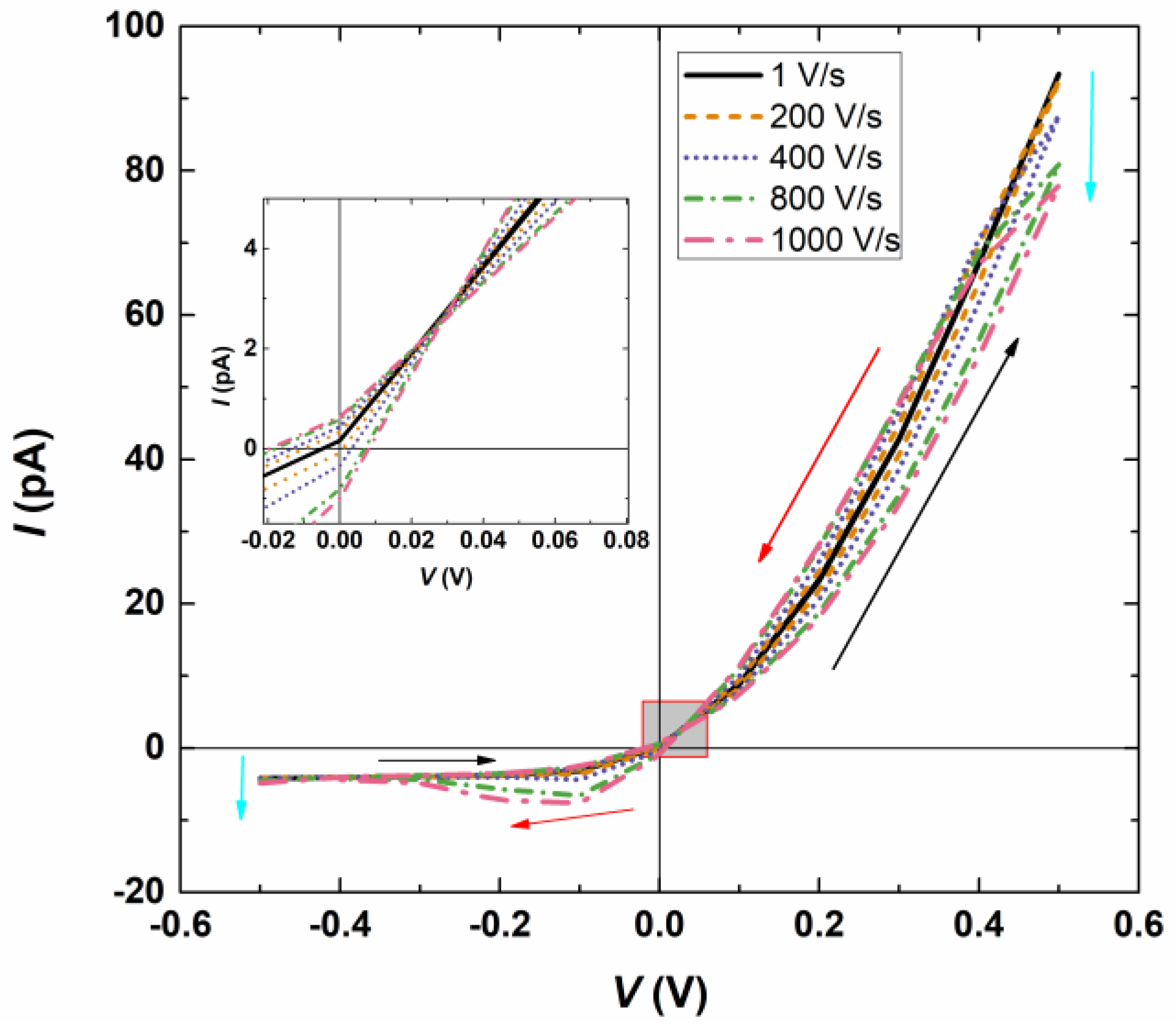
3.1. Effect of the Potential Scan Rate
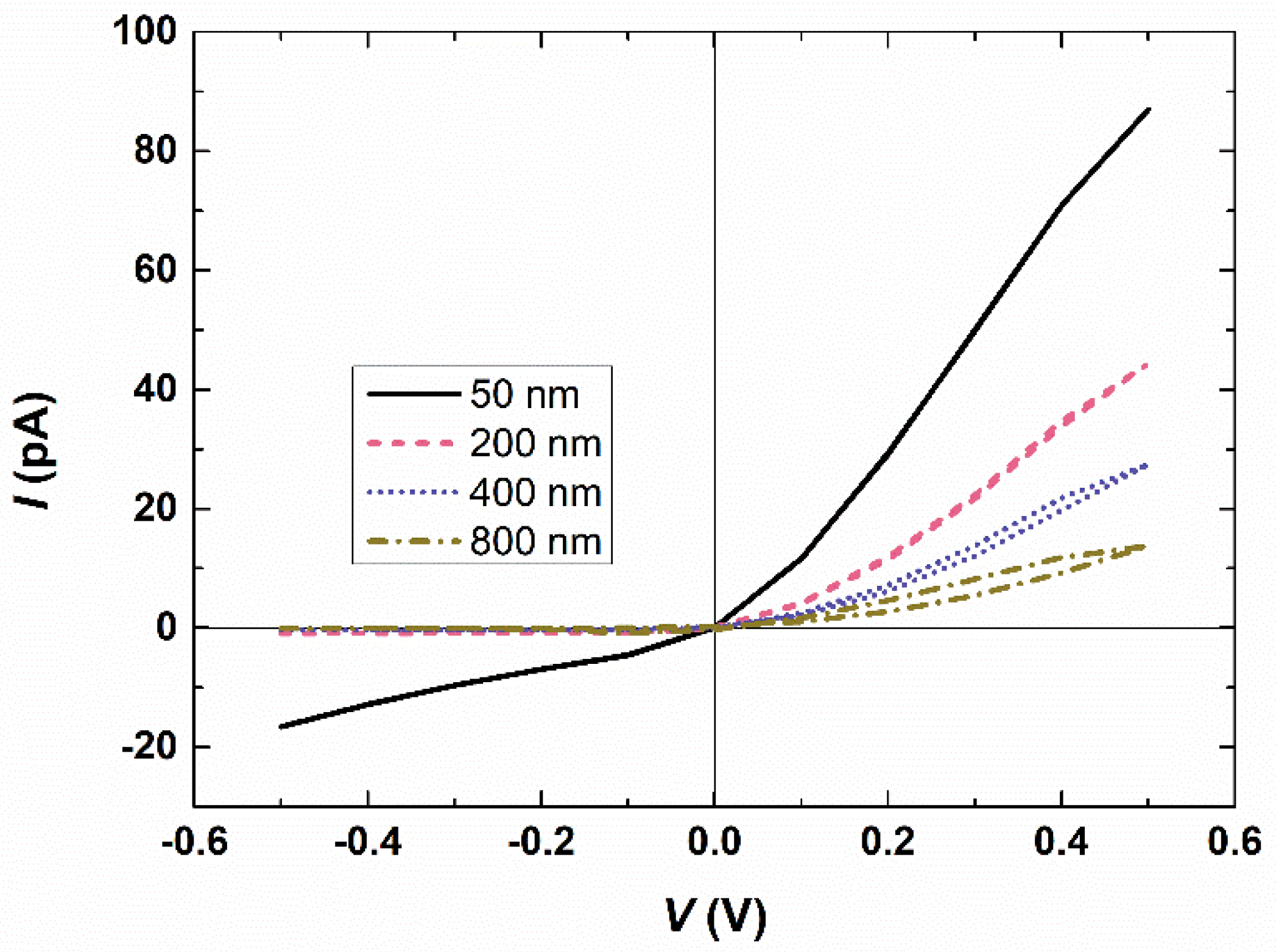
3.2. Effect of the Membrane Thickness
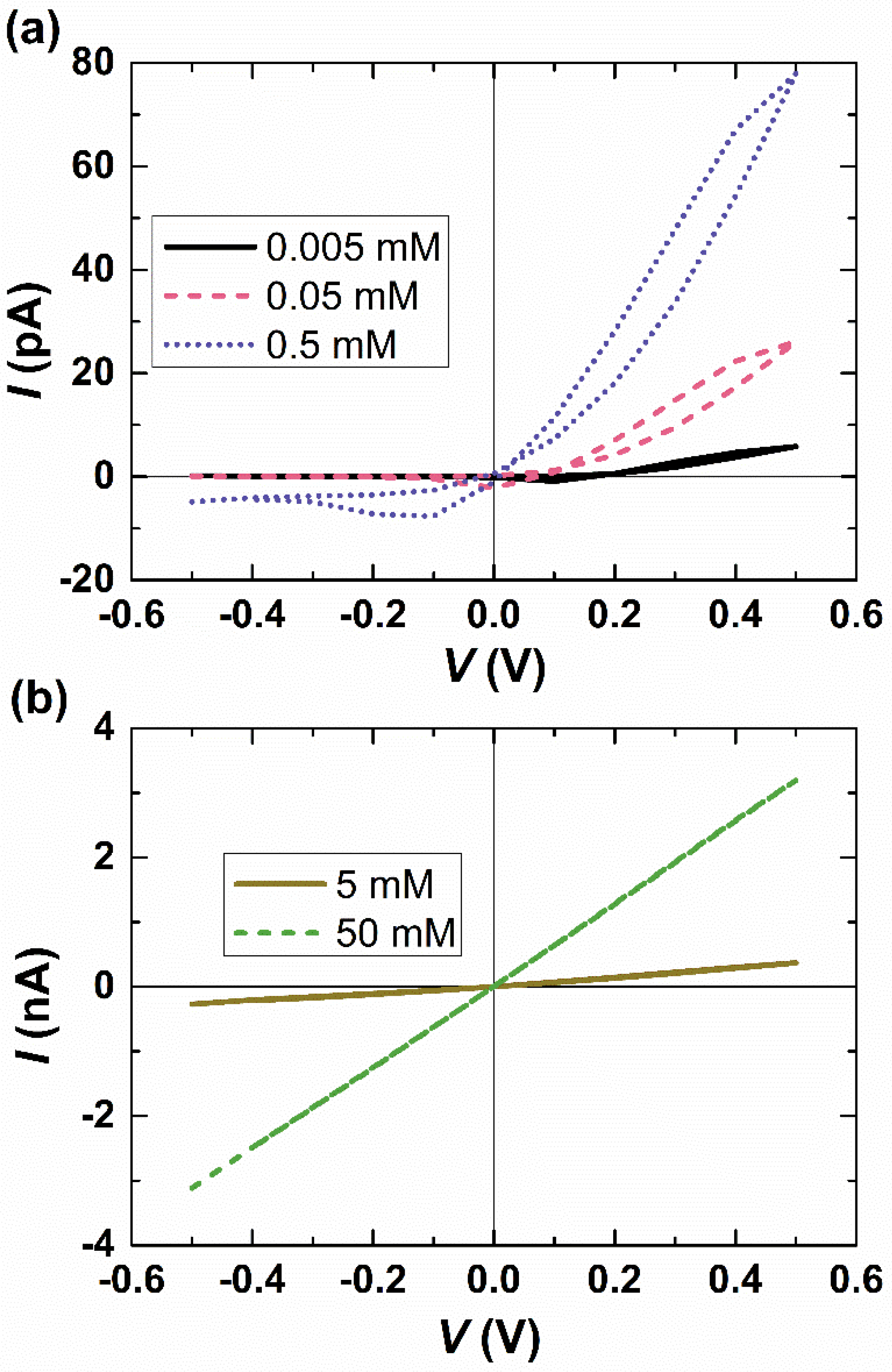
3.3. Effect of the Salt Concentration
3.4. Comparison with the Conventional Nanopore
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sheng, Q.; Xie, Y.B.; Li, J.; Wang, X.W.; Xue, J.M. Transporting an ionic-liquid/water mixture in a conical nanochannel: A nanofluidic memristor. Chem. Commun. 2017, 53, 6125–6127. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Ling, Y.; Wang, Y.; Wang, M.; Chen, Y.; Li, X.; Hou, X. Learning from the Brain: Bioinspired Nanofluidics. J. Phys. Chem. Lett. 2023, 14, 2891–2900. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, P.; Gomez, V.; Cervera, J.; Mafe, S.; Bisquert, J. Synaptical Tunability of Multipore Nanofluidic Memristors. J. Phys. Chem. Lett. 2023, 14, 10930–10934. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, P.; Portillo, S.; Cervera, J.; Nasir, S.; Ali, M.; Ensinger, W.; Mafe, S. Neuromorphic responses of nanofluidic memristors in symmetric and asymmetric ionic solutions. J. Chem. Phys. 2024, 160, 044701. [Google Scholar] [CrossRef] [PubMed]
- Emmerich, T.; Teng, Y.; Ronceray, N.; Lopriore, E.; Chiesa, R.; Chernev, A.; Artemov, V.; Di Ventra, M.; Kis, A.; Radenovic, A. Nanofluidic logic with mechano-ionic memristive switches. Nat. Electron. 2024, 7, 271–278. [Google Scholar] [CrossRef]
- Xiong, T.; Li, W.; Yu, P.; Mao, L. Fluidic memristor: Bringing chemistry to neuromorphic devices. Innovation 2023, 4, 100435. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, P.; Peng, H. Polyelectrolyte-confined fluidic memristor for neuromorphic computing in aqueous environment. Sci. Bull. 2023, 68, 767–769. [Google Scholar] [CrossRef]
- Kamsma, T.M.; Boon, W.Q.; Spitoni, C.; van Roij, R. Unveiling the capabilities of bipolar conical channels in neuromorphic iontronics. Faraday Discuss. 2023, 246, 125–140. [Google Scholar] [CrossRef]
- Kamsma, T.M.; Boon, W.Q.; Rele, T.T.; Spitoni, C.; van Roij, R. Iontronic Neuromorphic Signaling with Conical Microfluidic Memristors. Phys. Rev. Lett. 2023, 130, 268401. [Google Scholar] [CrossRef]
- Ling, Y.X.; Yu, L.J.; Guo, Z.W.; Bian, F.Z.; Wang, Y.Q.; Wang, X.; Hou, Y.Q.; Hou, X. Single-Pore Nanofluidic Logic Memristor with Reconfigurable Synaptic Functions and Designable Combinations. J. Am. Chem. Soc. 2024, 146, 14558–14565. [Google Scholar] [CrossRef]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Lett. 2010, 10, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Xiong, T.; Li, W.; Gao, T.; Zong, J.; Liu, Y.; Yu, P. Perspective on Nanofluidic Memristors: From Mechanism to Application. Chem.-Asian J. 2022, 17, e202200682. [Google Scholar] [CrossRef] [PubMed]
- Robin, P.; Kavokine, N.; Bocquet, L. Modeling of emergent memory and voltage spiking in ionic transport through angstrom-scale slits. Science 2021, 373, 687–691. [Google Scholar] [CrossRef]
- Leong, I.W.; Tsutsui, M.; Murayama, S.; Hayashida, T.; He, Y.H.; Taniguchi, M. Quasi-Stable Salt Gradient and Resistive Switching in Solid-State Nanopores. ACS Appl. Mater. Interfaces 2020, 12, 52175–52181. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Xia, M.; Zhuge, F.W.; Zhou, Y.; Wang, Z.Y.; Dong, B.Y.; Fu, Y.Y.; Yang, K.C.; Li, Y.; He, Y.H.; et al. Nanochannel-Based Transport in an Interfacial Memristor Can Emulate the Analog Weight Modulation of Synapses. Nano Lett. 2019, 19, 4279–4286. [Google Scholar] [CrossRef]
- Najem, J.S.; Taylor, G.J.; Weiss, R.J.; Hasan, M.S.; Rose, G.; Schuman, C.D.; Belianinov, A.; Collier, C.P.; Sarles, S.A. Memristive Ion Channel-Doped Biomembranes as Synaptic Mimics. ACS Nano 2018, 12, 4702–4711. [Google Scholar] [CrossRef]
- Tuszynski, J.A.; Friesen, D.; Freedman, H.; Sbitnev, V.I.; Kim, H.; Santelices, I.; Kalra, A.P.; Patel, S.D.; Shankar, K.; Chua, L.O. Microtubules as Sub-Cellular Memristors. Sci. Rep. 2020, 10, 2108. [Google Scholar] [CrossRef]
- Feng, J.Y.; Liu, J.; Wu, B.H.; Wang, G.L. Impedance Characteristics of Amine Modified Single Glass Nanopores. Anal. Chem. 2010, 82, 4520–4528. [Google Scholar] [CrossRef] [PubMed]
- Momotenko, D.; Girault, H.H. Scan-Rate-Dependent Ion Current Rectification and Rectification Inversion in Charged Conical Nanopores. J. Am. Chem. Soc. 2011, 133, 14496–14499. [Google Scholar] [CrossRef]
- Wang, D.; Kvetny, M.; Liu, J.; Brown, W.; Li, Y.; Wang, G. Transmembrane Potential across Single Conical Nanopores and Resulting Memristive and Memcapacitive Ion Transport. J. Am. Chem. Soc. 2012, 134, 3651–3654. [Google Scholar] [CrossRef]
- Guerrette, J.P.; Zhang, B. Scan-Rate-Dependent Current Rectification of Cone-Shaped Silica Nanopores in Quartz Nanopipettes. J. Am. Chem. Soc. 2010, 132, 17088–17091. [Google Scholar] [CrossRef] [PubMed]
- Conroy, D.T.; Craster, R.V.; Matar, O.K.; Cheng, L.J.; Chang, H.C. Nonequilibrium hysteresis and Wien effect water dissociation at a bipolar membrane. Phys. Rev. E 2012, 86, 056104. [Google Scholar] [CrossRef] [PubMed]
- Robin, P.; Emmerich, T.; Ismail, A.; Nigues, A.; You, Y.; Nam, G.H.; Keerthi, A.; Siria, A.; Geim, A.K.; Radha, B.; et al. Long-term memory and synapse-like dynamics in two-dimensional nanofluidic channels. Science 2023, 379, 161–167. [Google Scholar] [CrossRef]
- Shi, D.; Wang, W.; Liang, Y.; Duan, L.; Du, G.; Xie, Y. Ultralow Energy Consumption Angstrom-Fluidic Memristor. Nano Lett. 2023, 23, 11662–11668. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Yeh, L.-H.; Hsu, J.-P.; Tseng, S. Regulating Current Rectification and Nanoparticle Transport Through a Salt Gradient in Bipolar Nanopores. Small 2015, 11, 4594–4602. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-Y.; Hsu, J.-P.; Yeh, L.-H. Rectification of ionic current in nanopores functionalized with bipolar polyelectrolyte brushes. Sens. Actuators B 2018, 258, 1223–1229. [Google Scholar] [CrossRef]
- Daiguji, H.; Oka, Y.; Shirono, K. Nanofluidic diode and bipolar transistor. Nano Lett. 2005, 5, 2274–2280. [Google Scholar] [CrossRef]
- Kim, J.; Wang, C.; Park, J. Multi-Layered Bipolar Ionic Diode Working in Broad Range Ion Concentration. Micromachines 2023, 14, 1311. [Google Scholar] [CrossRef]
- Wu, C.-T.; Hsu, J.-P. Electrokinetic behavior of bullet-shaped nanopores modified by functional groups: Influence of finite thicknessy-20 of modified layer. J. Colloid Interface Sci. 2021, 582, 741–751. [Google Scholar] [CrossRef]
- Hsu, J.-P.; Wu, H.-H.; Lin, C.-Y.; Tseng, S. Ion Current Rectification Behavior of Bioinspired Nanopores Having a pH-Tunable Zwitterionic Surface. Anal. Chem. 2017, 89, 3952–3958. [Google Scholar] [CrossRef]
- Lin, D.-H.; Lin, C.-Y.; Tseng, S.; Hsu, J.-P. Influence of electroosmotic flow on the ionic current rectification in a pH-regulated, conical nanopore. Nanoscale 2015, 7, 14023–14031. [Google Scholar] [CrossRef] [PubMed]
- Alidoosti, E.; Zhao, H. The effects of electrostatic correlations on the ionic current rectification in conical nanopores. Electrophoresis 2019, 40, 2655–2661. [Google Scholar] [CrossRef] [PubMed]
- Qian, S.; Joo, S.W.; Ai, Y.; Cheney, M.A.; Hou, W. Effect of linear surface-charge non-uniformities on the electrokinetic ionic-current rectification in conical nanopores. J. Colloid Interface Sci. 2009, 329, 376–383. [Google Scholar] [CrossRef]
- Hsu, J.-P.; Yang, S.-T.; Lin, C.-Y.; Tseng, S. Ionic Current Rectification in a Conical Nanopore: Influences of Electroosmotic Flow and Type of Salt. J. Phys. Chem. C 2017, 121, 4576–4582. [Google Scholar] [CrossRef]
- Tseng, S.; Lin, S.-C.; Lin, C.-Y.; Hsu, J.-P. Influences of Cone Angle and Surface Charge Density on the Ion Current Rectification Behavior of a Conical Nanopore. J. Phys. Chem. C 2016, 120, 25620–25627. [Google Scholar] [CrossRef]
- Chu, C.W.; Fauziah, A.R.; Yeh, L.H. Optimizing Membranes for Osmotic Power Generation. Angew. Chem.-Int. Ed. 2023, 62, e202303582. [Google Scholar] [CrossRef]
- Chang, C.W.; Chu, C.W.; Su, Y.S.; Yeh, L.H. Space charge enhanced ion transport in heterogeneous polyelectrolyte/alumina nanochannel membranes for high-performance osmotic energy conversion. J. Mater. Chem. A. 2022, 10, 2867–2875. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, J.; Wang, C.; Chang, G.T.; Park, J. Asymmetric Nanochannel Network-Based Bipolar Ionic Diode for Enhanced Heavy Metal Ion Detection. ACS Nano 2022, 16, 8253–8263. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.Z.; Cheng, W.; Zhang, X.L.; Li, J.; Ma, J.; Zhang, T. Engineering a protective surface layer to resist membrane scaling and scale-induced wetting in membrane distillation for the treatment of hypersaline wastewater. Chem. Eng. J. 2023, 452, 139167. [Google Scholar] [CrossRef]
- Sun, Y.; Dong, T.D.; Lu, C.X.; Xin, W.W.; Yang, L.S.; Liu, P.; Qian, Y.C.; Zhao, Y.Y.; Kong, X.Y.; Wen, L.P.; et al. Tailoring A Poly(ether sulfone) Bipolar Membrane: Osmotic-Energy Generator with High Power Density. Angew. Chem.-Int. Ed. 2020, 59, 17423–17428. [Google Scholar] [CrossRef]
- Su, Y.S.; Hung, W.H.; Fauziah, A.R.; Siwy, Z.S.; Yeh, L.H. A pH gradient induced rectification inversion in asymmetric nanochannels leads to remarkably improved osmotic power. Chem. Eng. J. 2023, 456, 141064. [Google Scholar] [CrossRef]
- Fauziah, A.R.; Chu, C.-W.; Yeh, L.-H. Engineered subnanochannel ionic diode membranes based on metal–organic frameworks for boosted lithium ion transport and osmotic energy conversion in organic solution. Chem. Eng. J. 2023, 452, 139244. [Google Scholar] [CrossRef]
- Luan, B.; Bai, J.; Stolovitzky, G. Fabricatable nanopore sensors with an atomic thickness. Appl. Phys. Lett. 2013, 103, 183501. [Google Scholar] [CrossRef]
- Zhang, X.; Han, X.; Qian, S.; Yang, Y.; Hu, N. Tuning Ion Transport through a Nanopore by Self-Oscillating Chemical Reactions. Anal. Chem. 2019, 91, 4600–4607. [Google Scholar] [CrossRef] [PubMed]
- Yeh, L.-H.; Zhang, M.; Qian, S. Ion Transport in a pH-Regulated Nanopore. Anal. Chem. 2013, 85, 7527–7534. [Google Scholar] [CrossRef]
- Yeh, L.H.; Hughes, C.; Zeng, Z.P.; Qian, S.Z. Tuning Ion Transport and Selectivity by a Salt Gradient in a Charged Nanopore. Anal. Chem. 2014, 86, 2681–2686. [Google Scholar] [CrossRef]
- Su, Y.S.; Hsu, S.C.; Peng, P.H.; Yang, J.Y.; Gao, M.Y.; Yeh, L.H. Unraveling the anomalous channel-length-dependent blue energy conversion using engineered alumina nanochannels. Nano Energy 2021, 84, 105930. [Google Scholar] [CrossRef]
- Wu, Y.-Y.; Chen, L.-D.; Cai, X.-H.; Zhao, Y.; Chen, M.; Pan, X.-H.; Li, Y.-Q. Smart pH-Modulated Two-Way Photoswitch Based on a Polymer-Modified Single Nanochannel. ACS Appl. Mater. Interfaces 2021, 13, 25241–25249. [Google Scholar] [CrossRef]
- Gao, M.Y.; Tsai, P.C.; Su, Y.S.; Peng, P.H.; Yeh, L.H. Single Mesopores with High Surface Charges as Ultrahigh Performance Osmotic Power Generators. Small 2020, 16, 2006013. [Google Scholar] [CrossRef]
- Yeh, L.-H.; Zhang, M.; Joo, S.W.; Qian, S.; Hsu, J.-P. Controlling pH-Regulated Bionanoparticles Translocation through Nanopores with Polyelectrolyte Brushes. Anal. Chem. 2012, 84, 9615–9622. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, L.; Zhang, H.W.; Zhuang, J.K.; Man, J.; Siwy, Z.S.; Qiu, Y.H. Dynamic Response of Ionic Current in Conical Nanopores. ACS Appl. Mater. Interfaces 2024, 16, 30496–30505. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.-P.; Chu, Y.-Y.; Lin, C.-Y.; Tseng, S. Ion transport in a pH-regulated conical nanopore filled with a power-law fluid. J. Colloid Interface Sci. 2019, 537, 358–365. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, M.; Yang, J.; Hu, N. Ion Transport in pH-Regulated Double-Barreled Nanopores. Anal. Chem. 2022, 94, 5642–5650. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, X.; Yang, Y.; Hu, N. Ion Transport in Multi-Nanochannels Regulated by pH and Ion Concentration. Anal. Chem. 2024, 96, 5648–5657. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, Y.; Zheng, J.; Yang, C.; Wang, D. Scan-Rate-Dependent Ion Current Rectification in Bipolar Interfacial Nanopores. Micromachines 2024, 15, 1176. https://doi.org/10.3390/mi15091176
Zhang X, Wang Y, Zheng J, Yang C, Wang D. Scan-Rate-Dependent Ion Current Rectification in Bipolar Interfacial Nanopores. Micromachines. 2024; 15(9):1176. https://doi.org/10.3390/mi15091176
Chicago/Turabian StyleZhang, Xiaoling, Yunjiao Wang, Jiahui Zheng, Chen Yang, and Deqiang Wang. 2024. "Scan-Rate-Dependent Ion Current Rectification in Bipolar Interfacial Nanopores" Micromachines 15, no. 9: 1176. https://doi.org/10.3390/mi15091176
APA StyleZhang, X., Wang, Y., Zheng, J., Yang, C., & Wang, D. (2024). Scan-Rate-Dependent Ion Current Rectification in Bipolar Interfacial Nanopores. Micromachines, 15(9), 1176. https://doi.org/10.3390/mi15091176





