A Review of Optical Interferometry for High-Precision Length Measurement
Abstract
:1. Introduction
2. Grating Interferometry
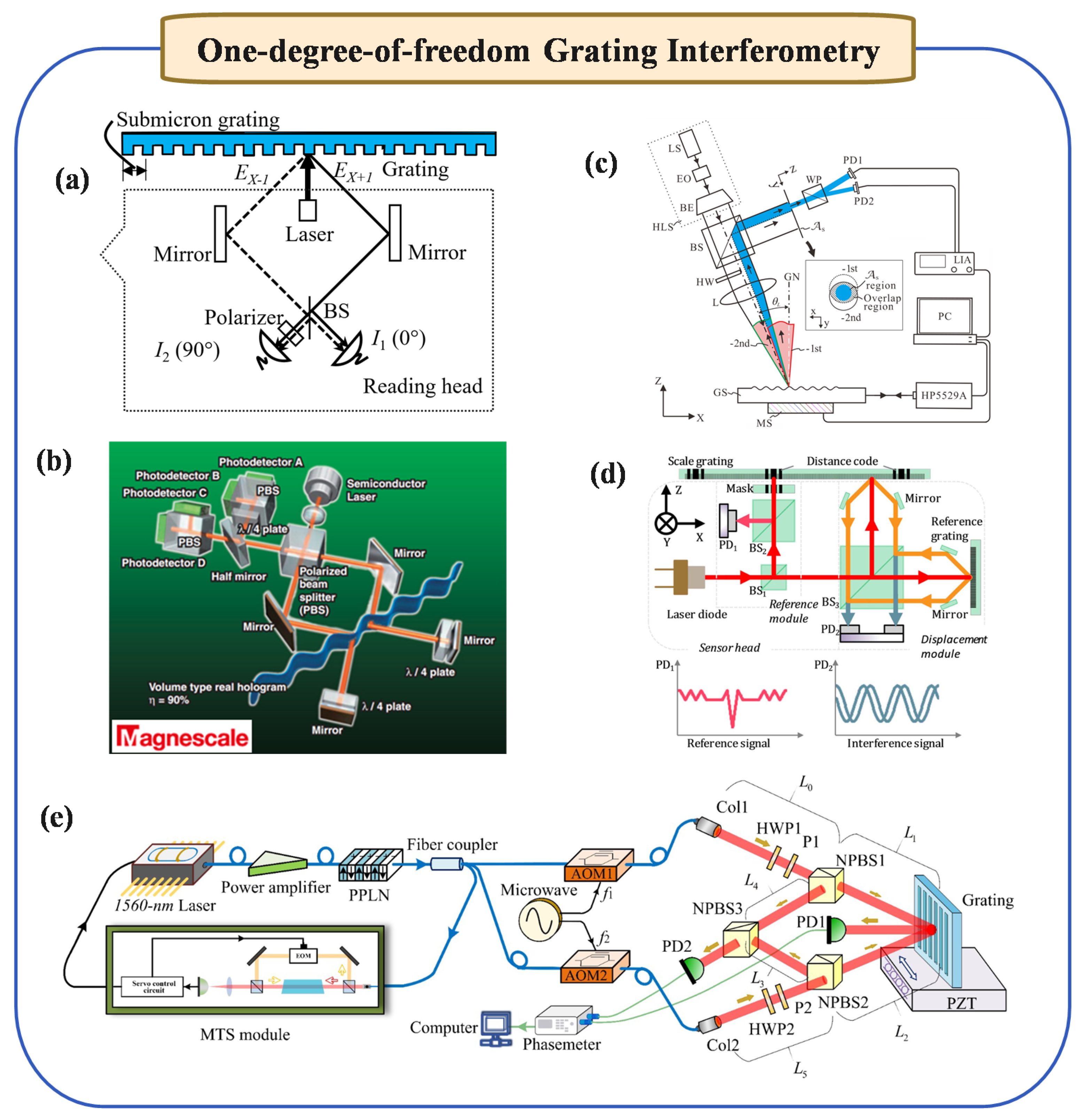
2.1. One-Degree-of-Freedom Grating Interferometry
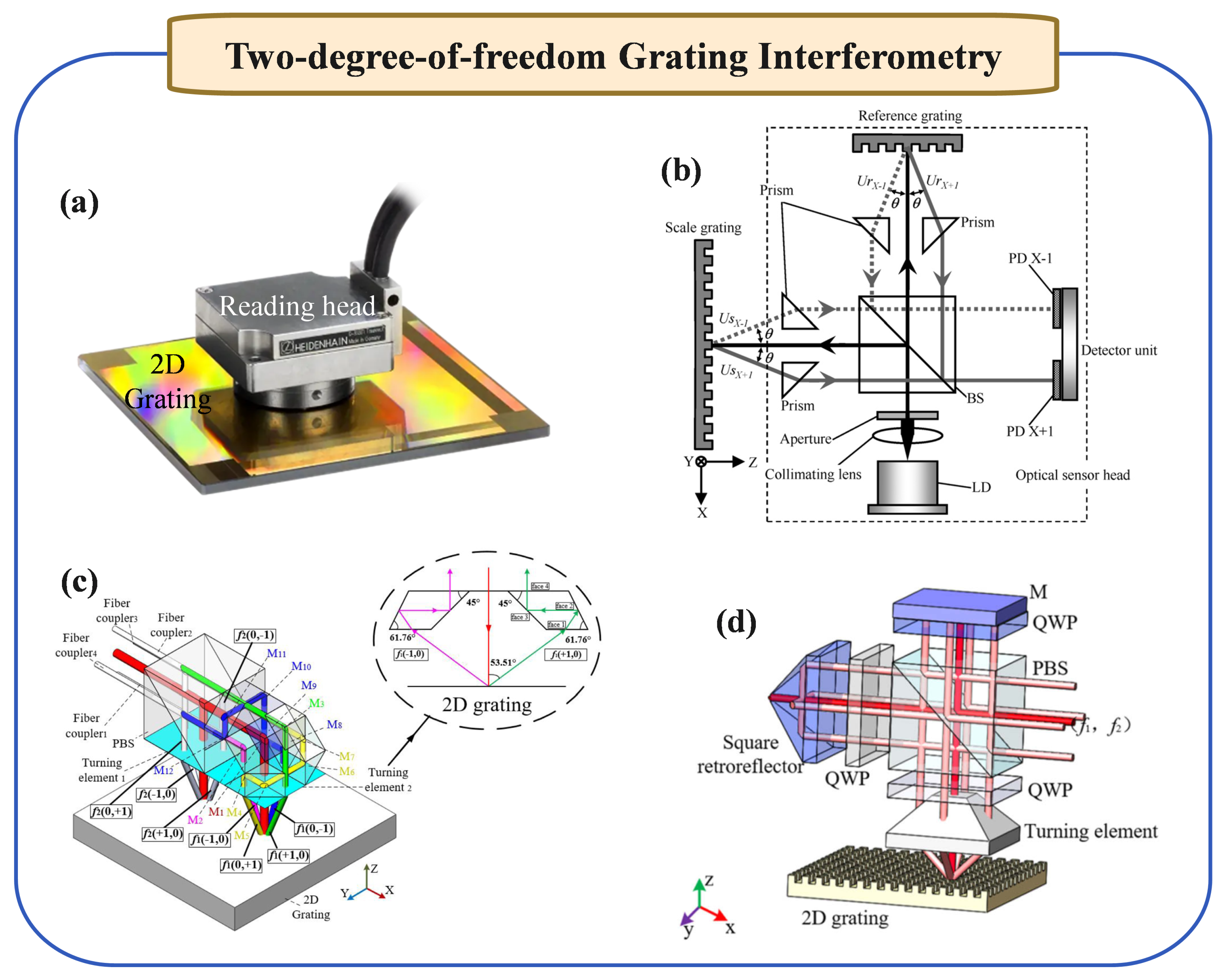
2.2. Two-Degree-of-Freedom Grating Interferometry
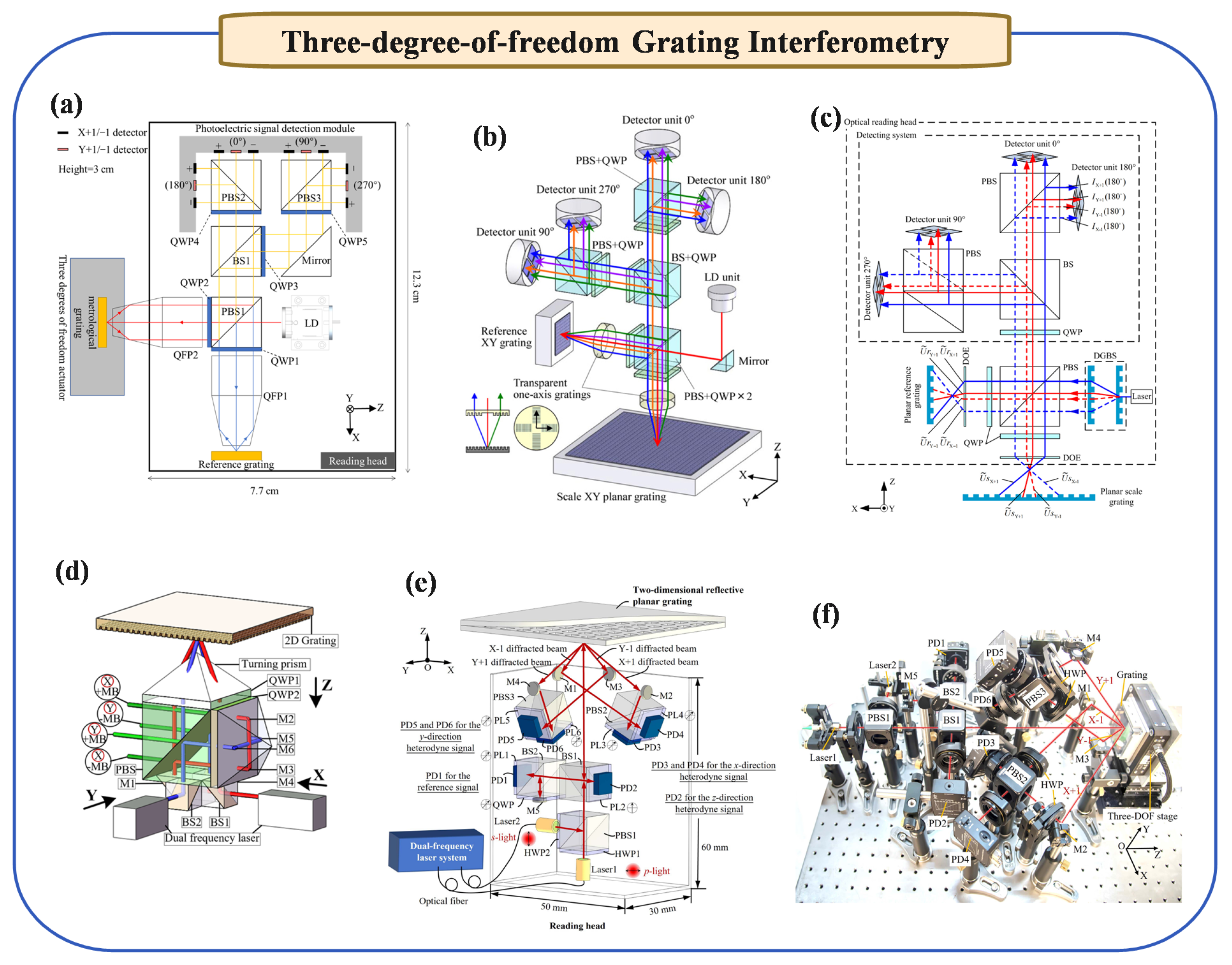
2.3. Three-Degree-of-Freedom Grating Interferometry
2.4. Multi-Degree-of-Freedom Grating Interferometry
2.4.1. Multi-DOF Grating Interferometry (Single Optical Head)
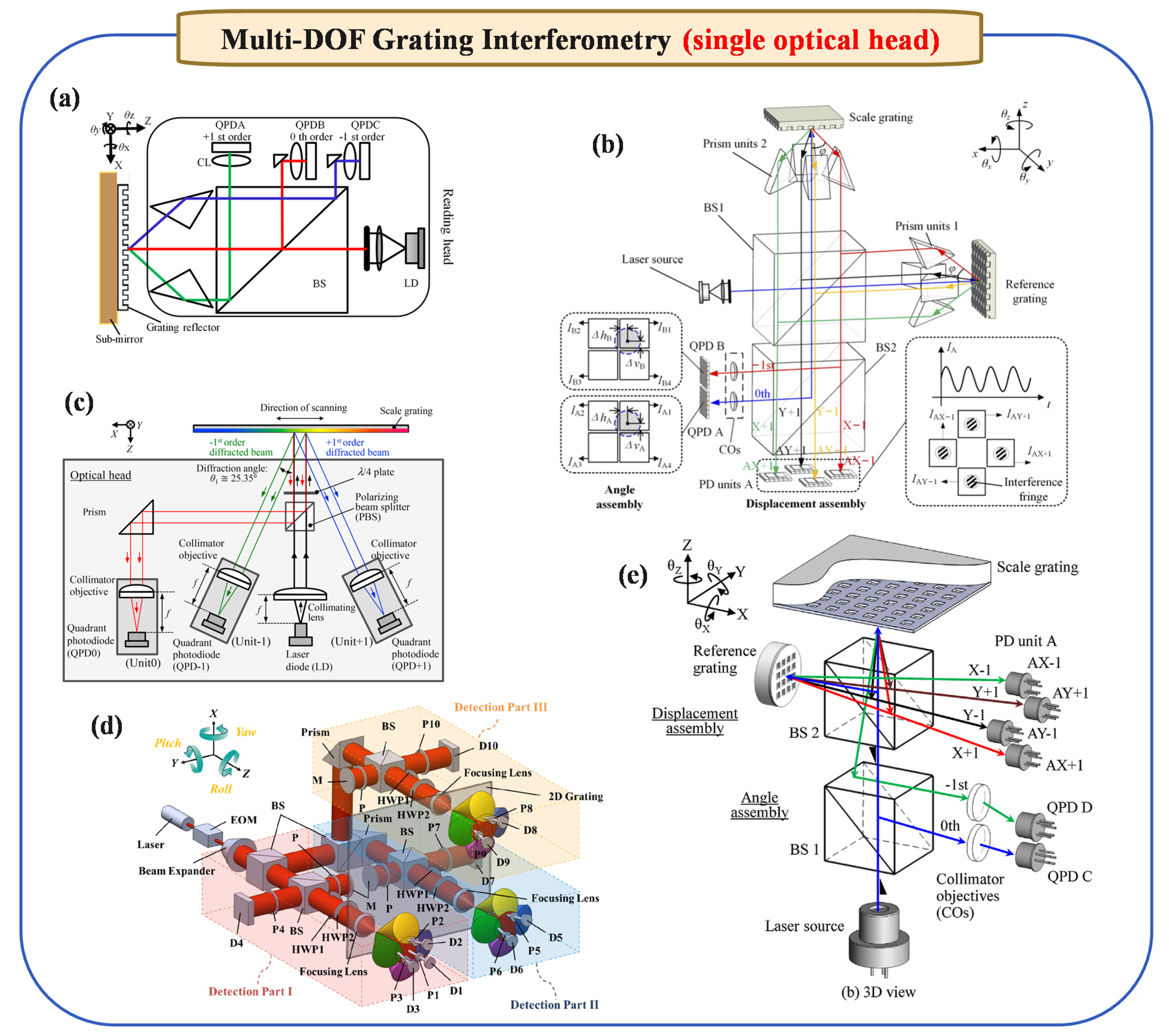
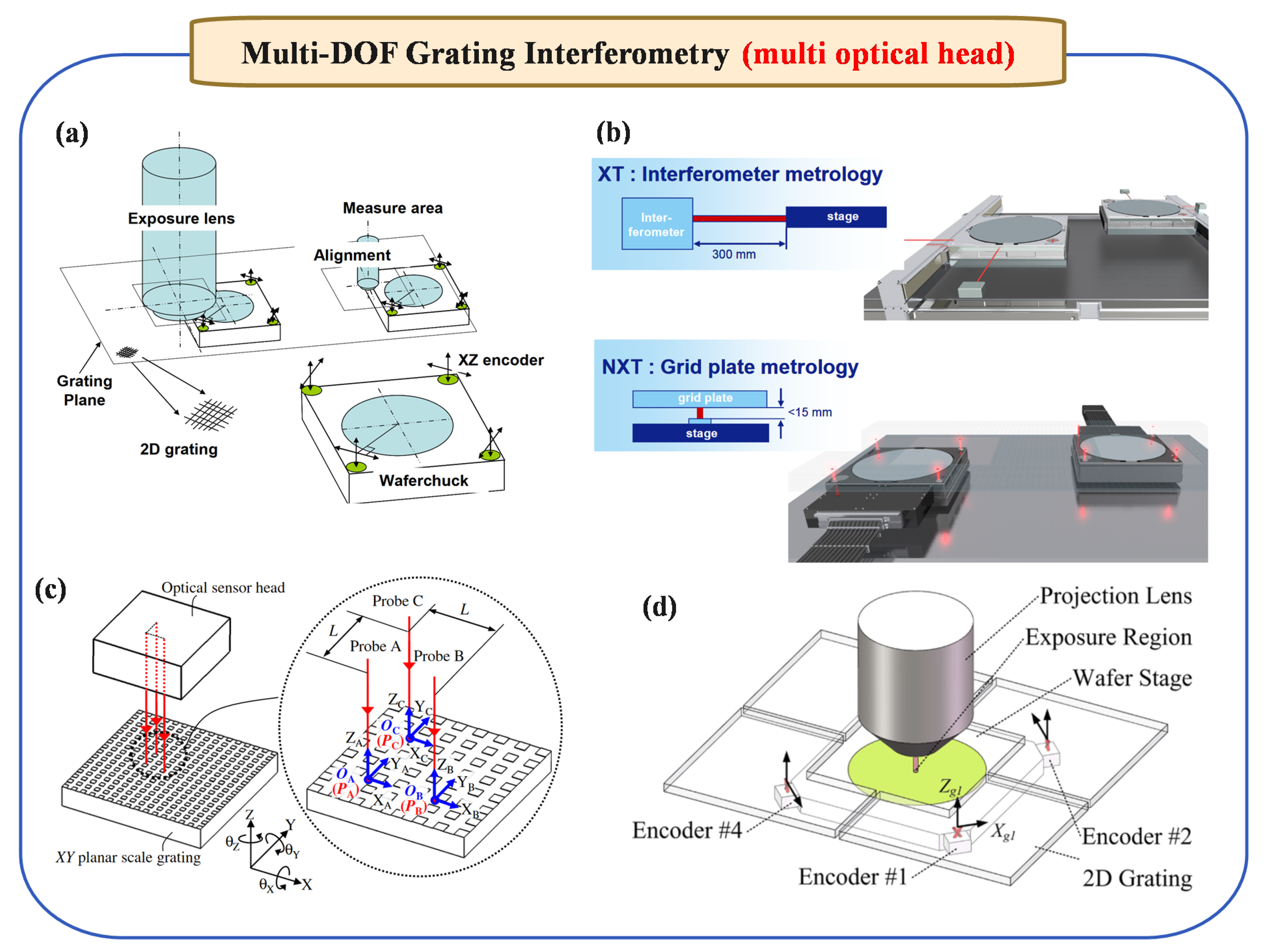
2.4.2. Multi-DOF Grating Interferometry (Multi-Optical Heads)
3. Laser Interferometry
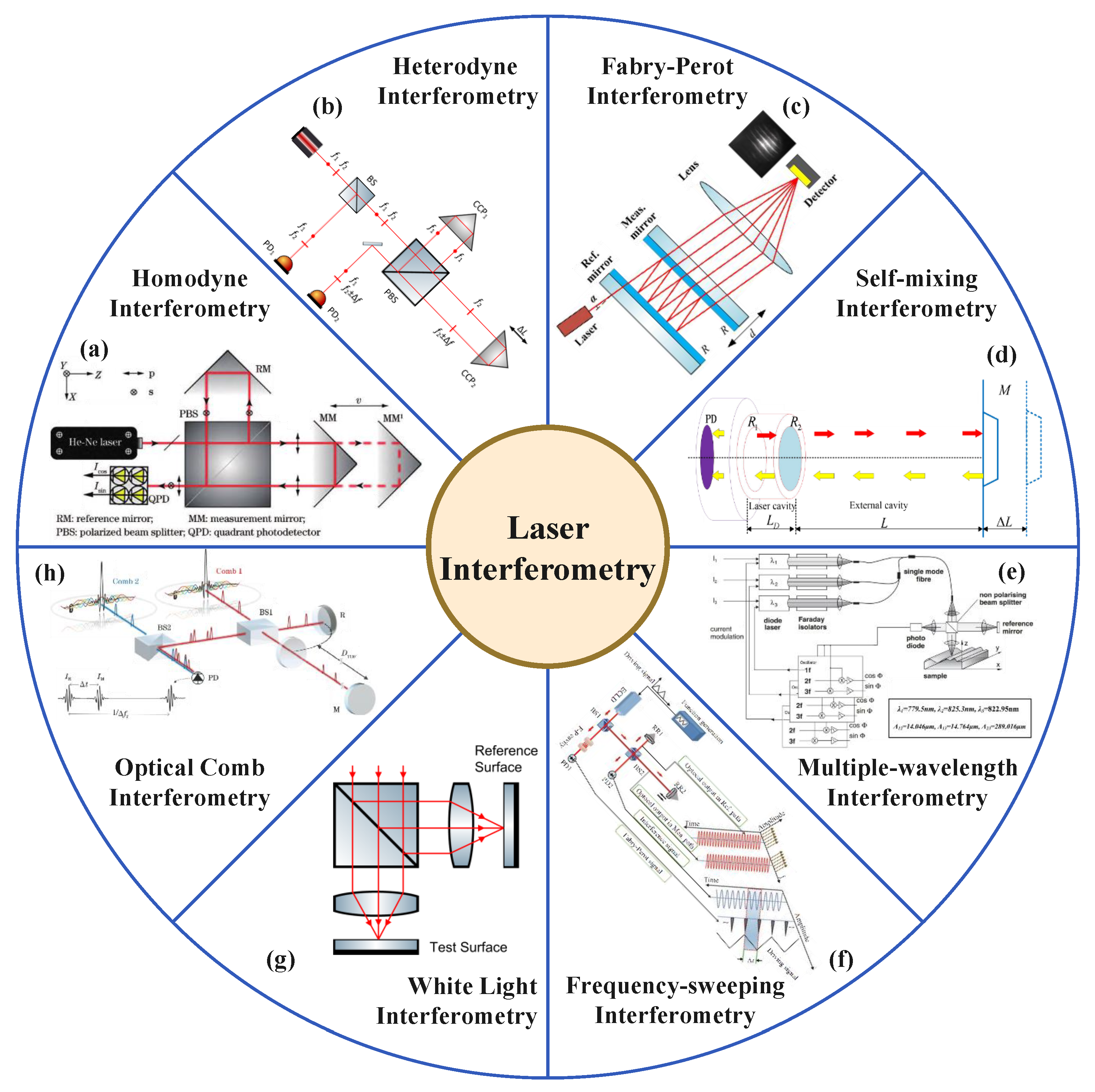
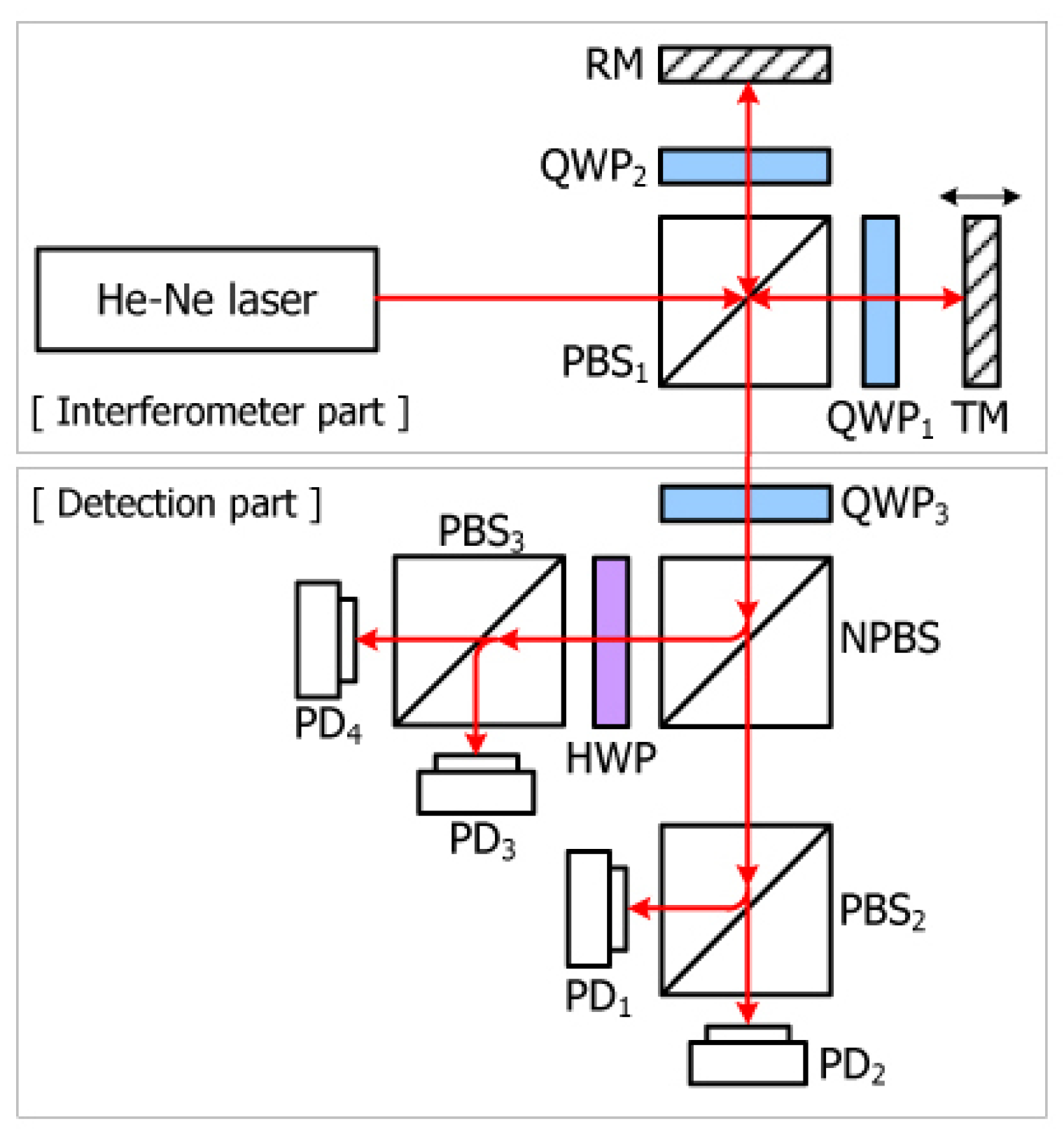
3.1. Homodyne Interferometry
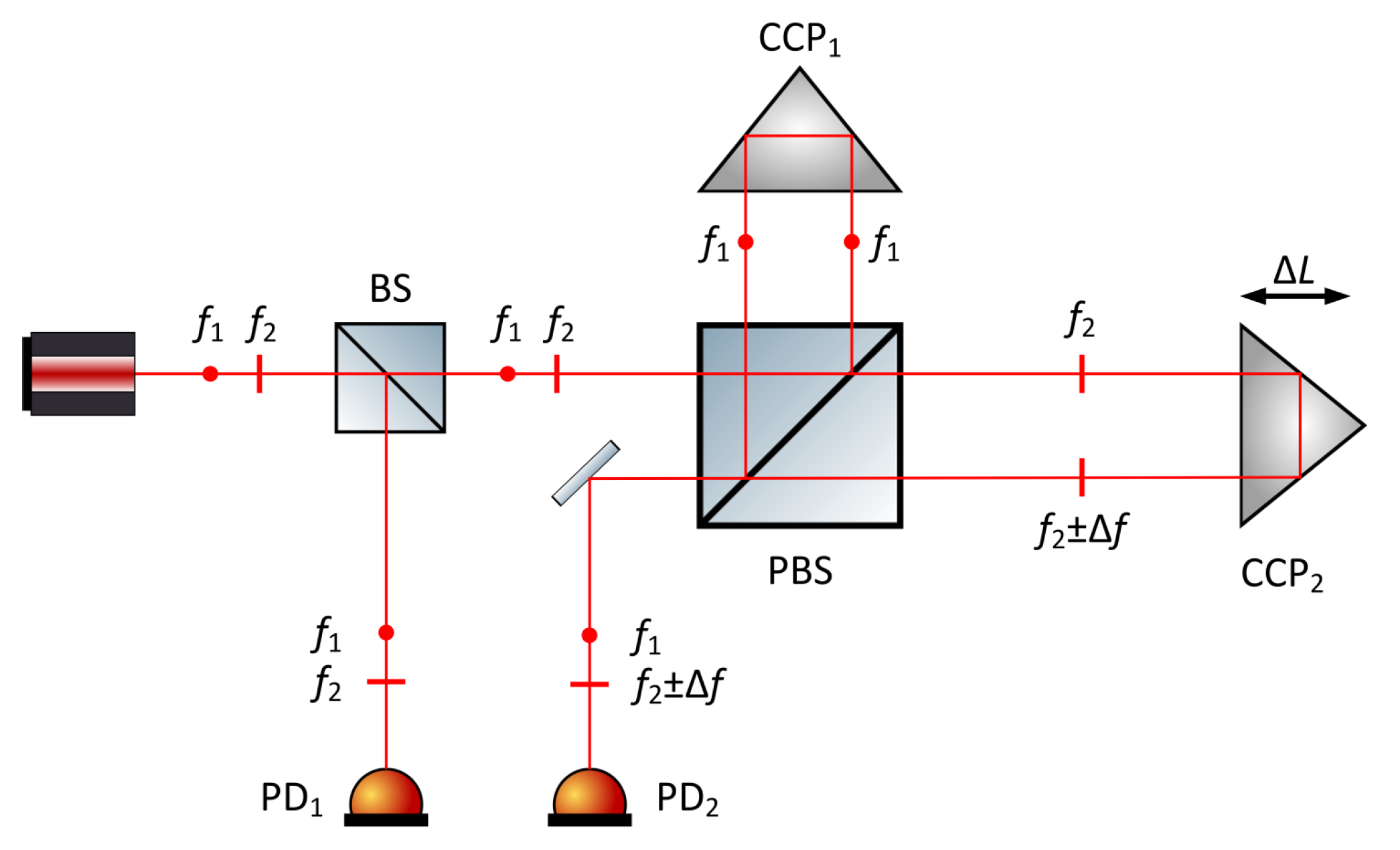
3.2. Heterodyne Interferometry
3.3. Sinusoidal Phase Modulation Interferometry
3.4. Fabry–Perot Interferometry
3.5. Self-Mixing Interferometry
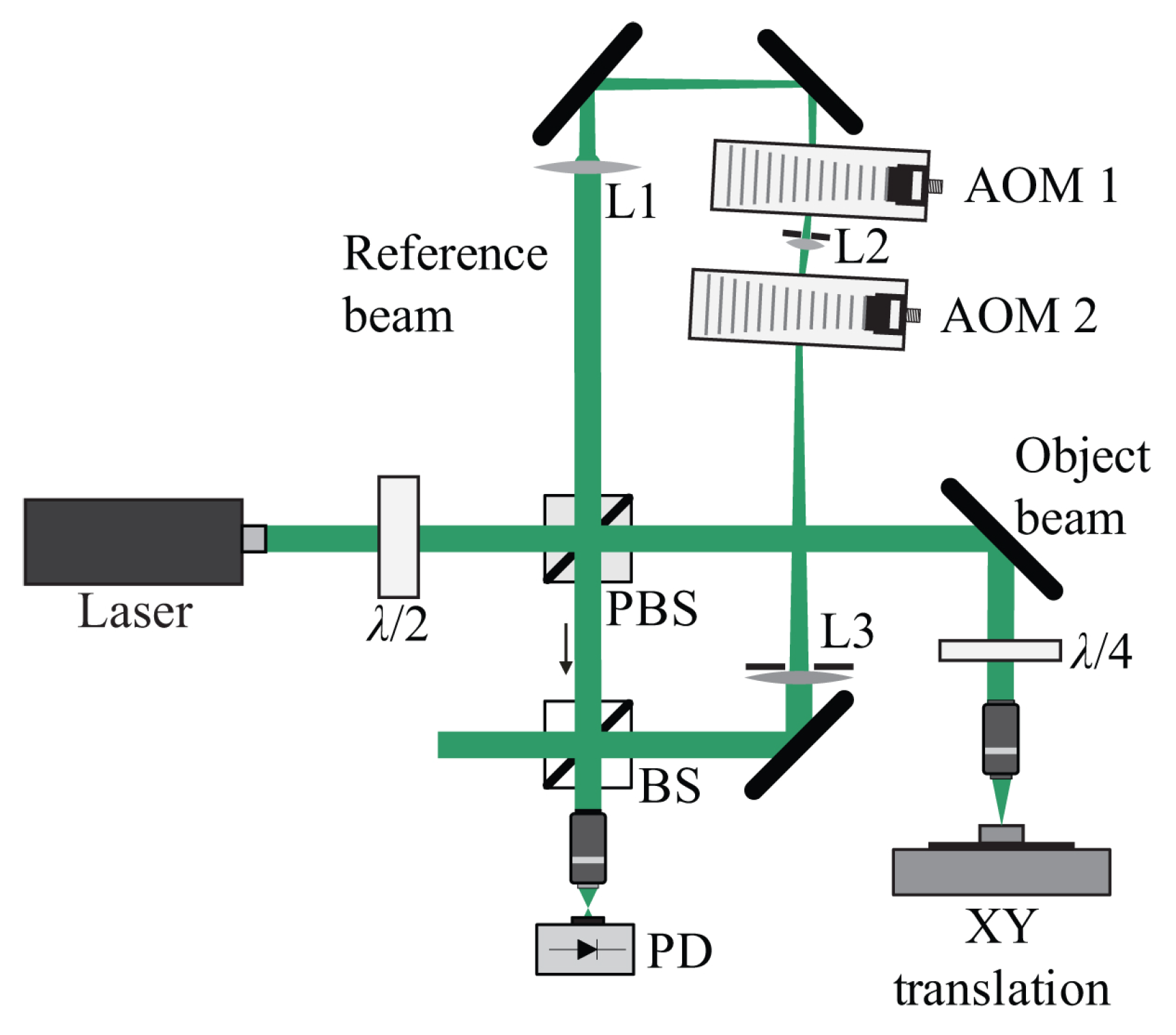
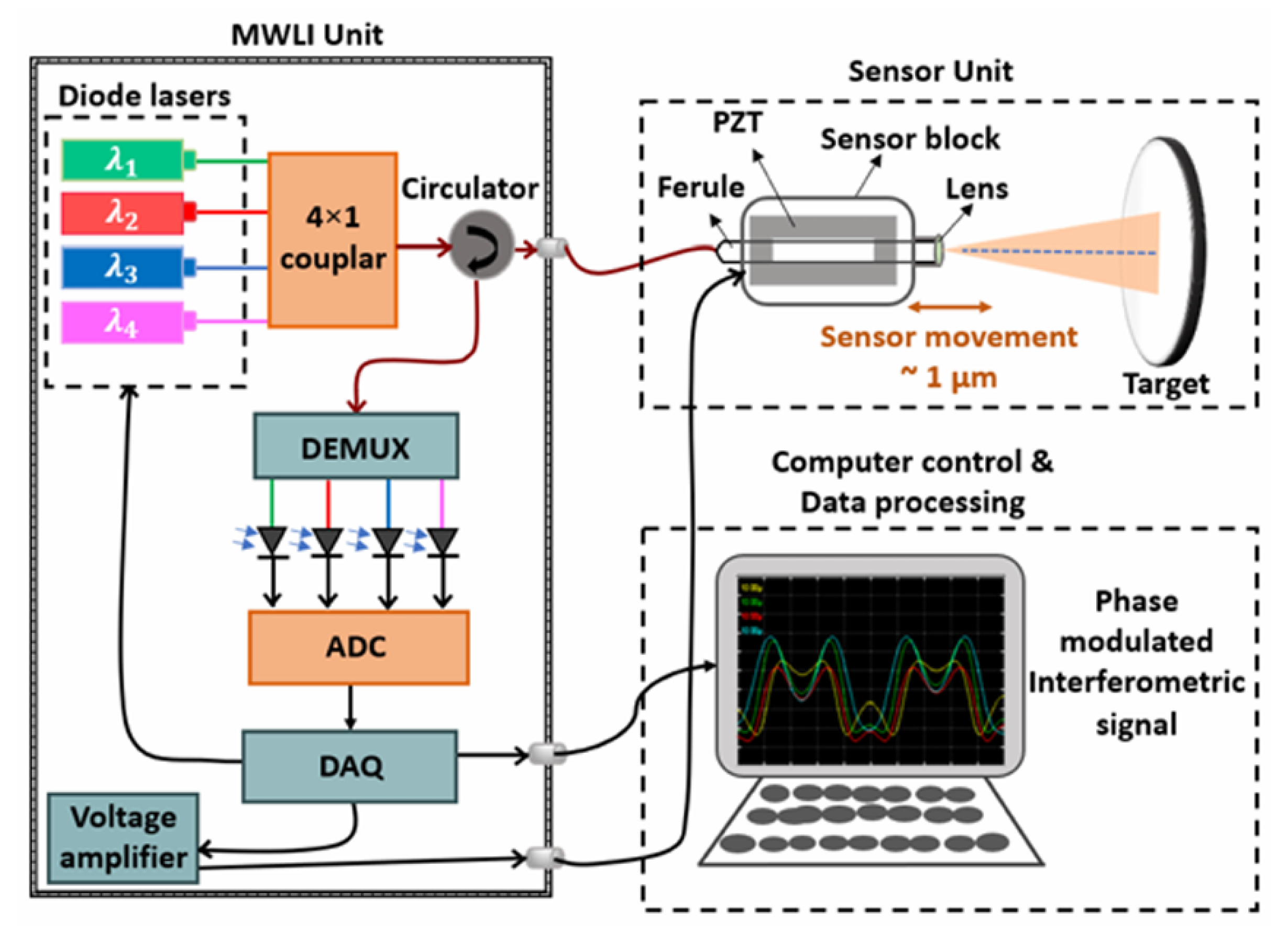
3.6. Multi-Wavelength Interferometry
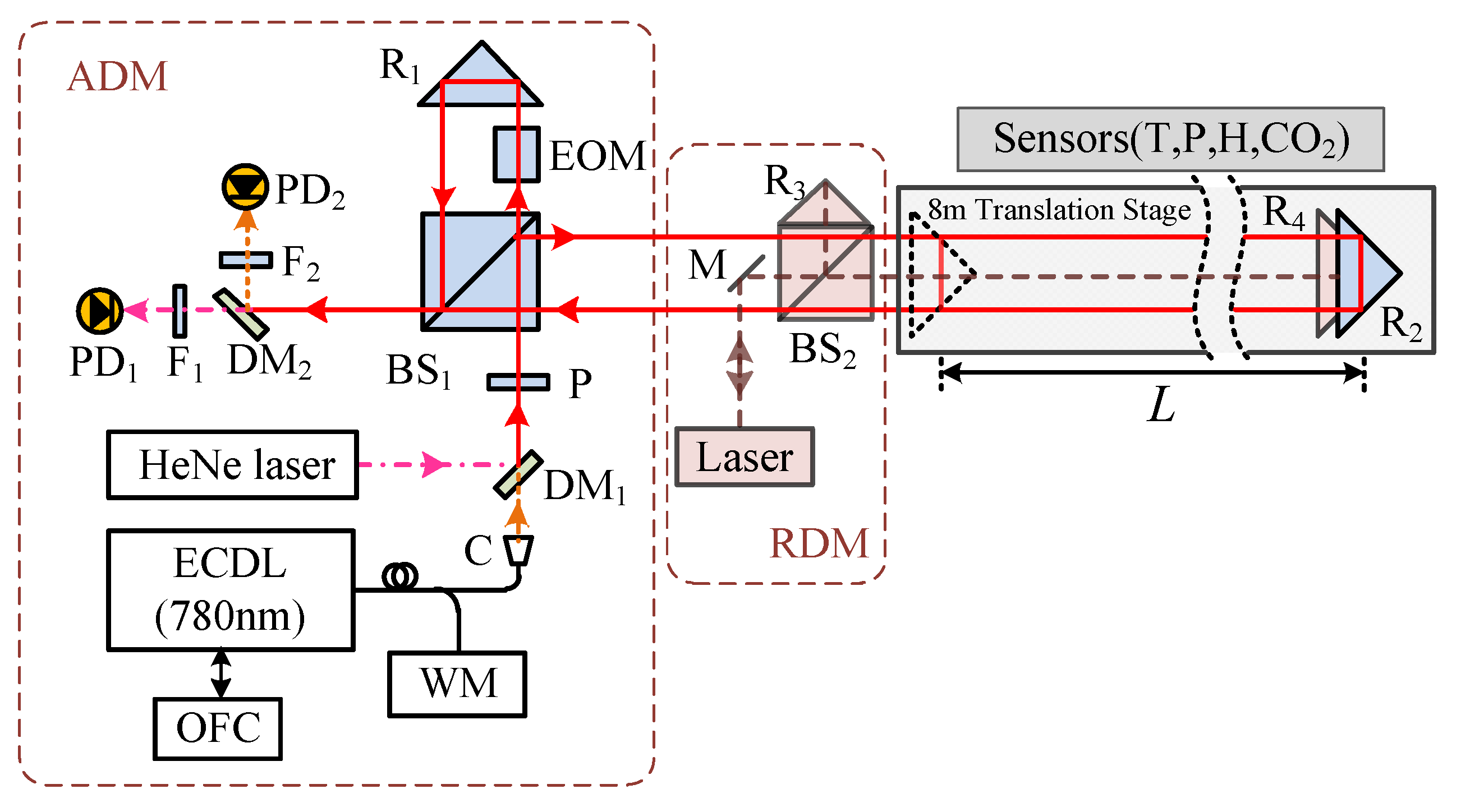
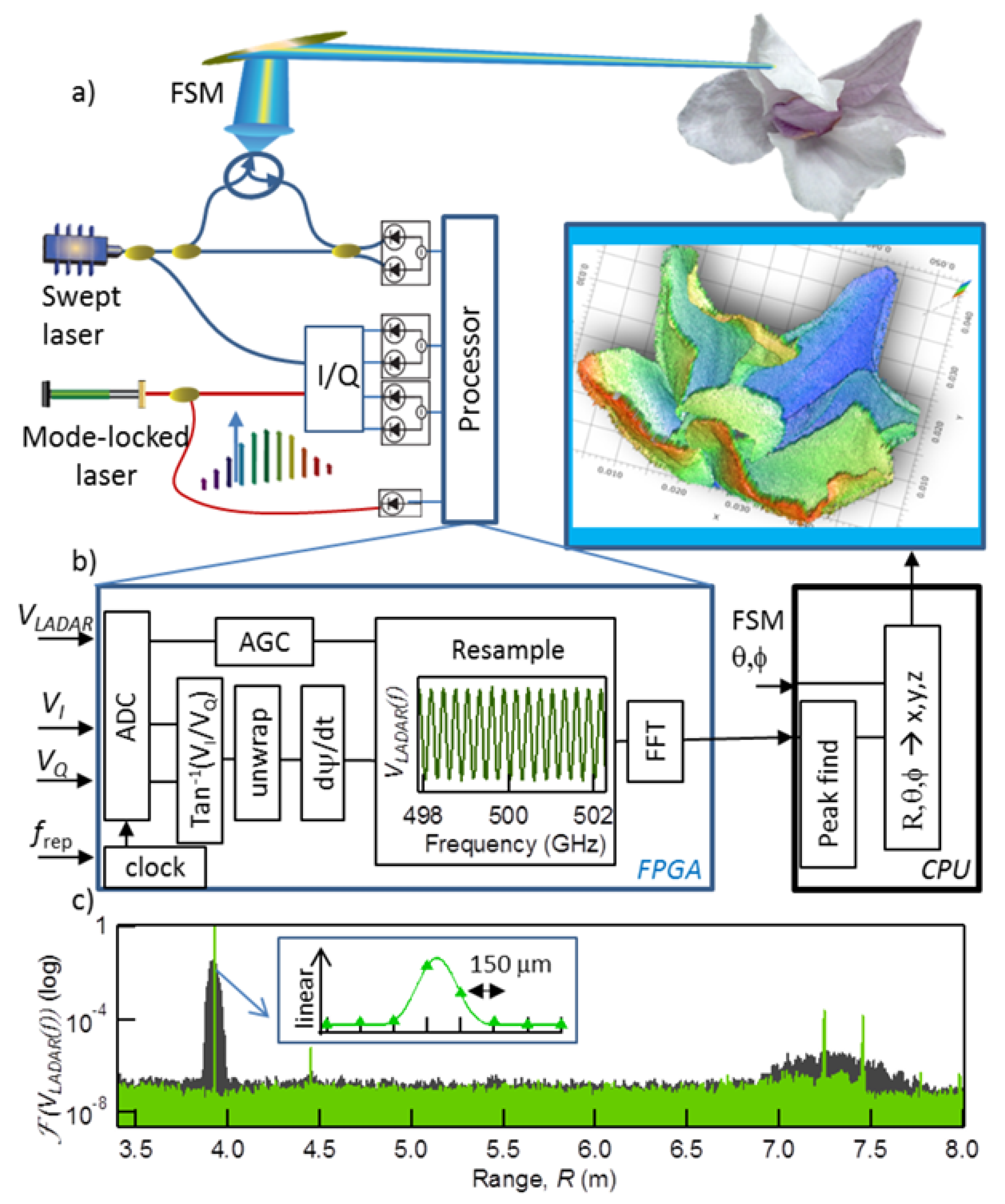
3.7. Frequency-Sweeping Interferometry
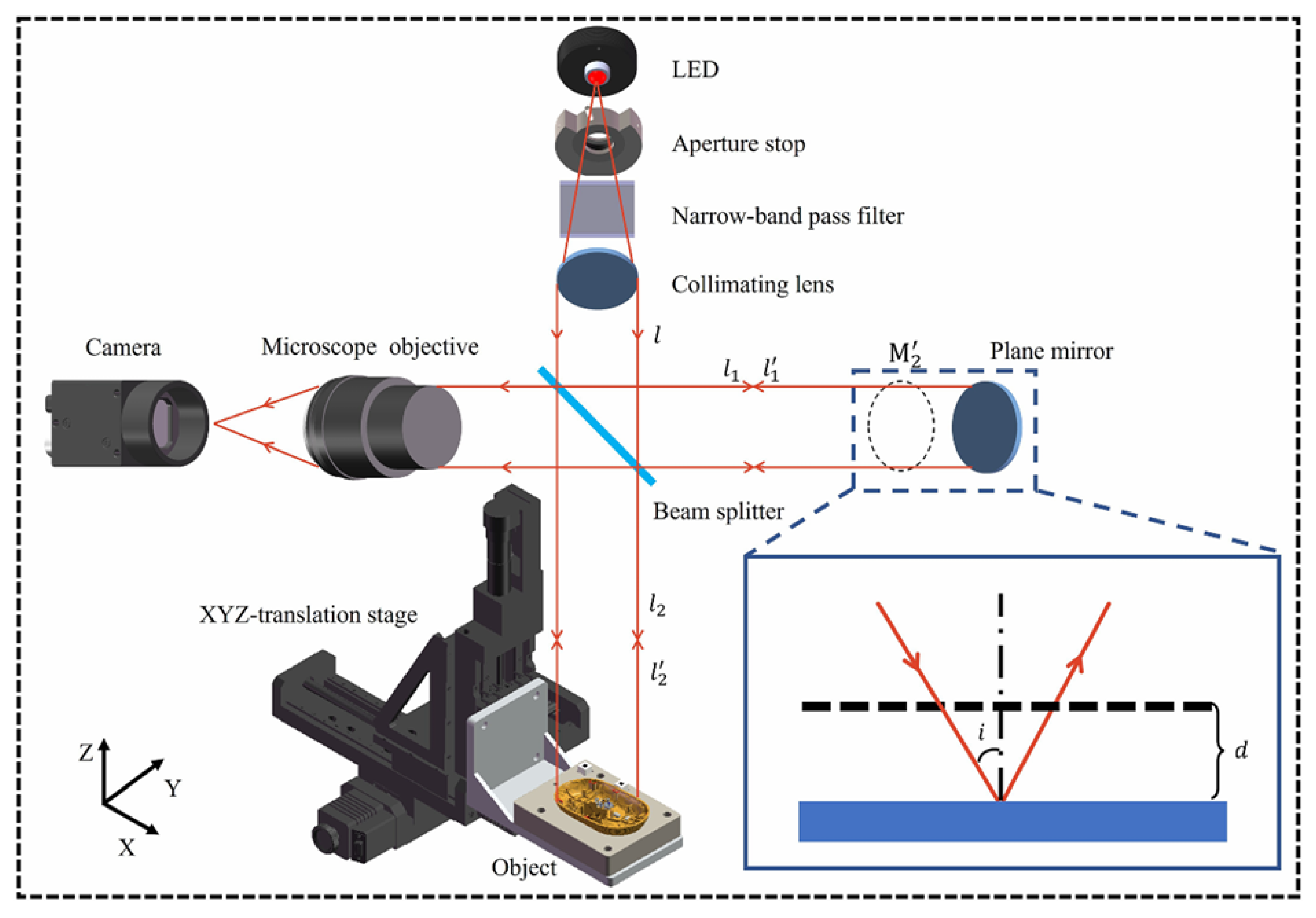
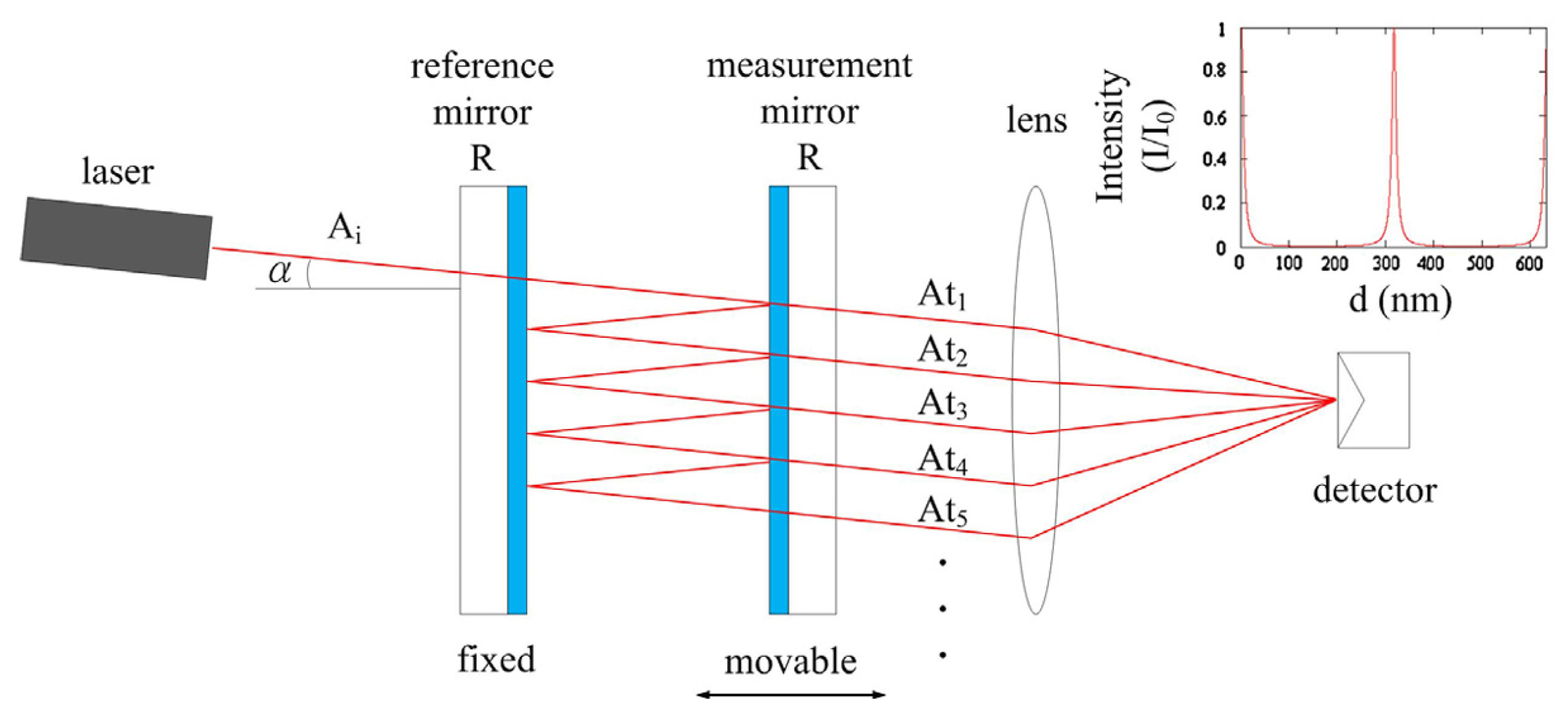
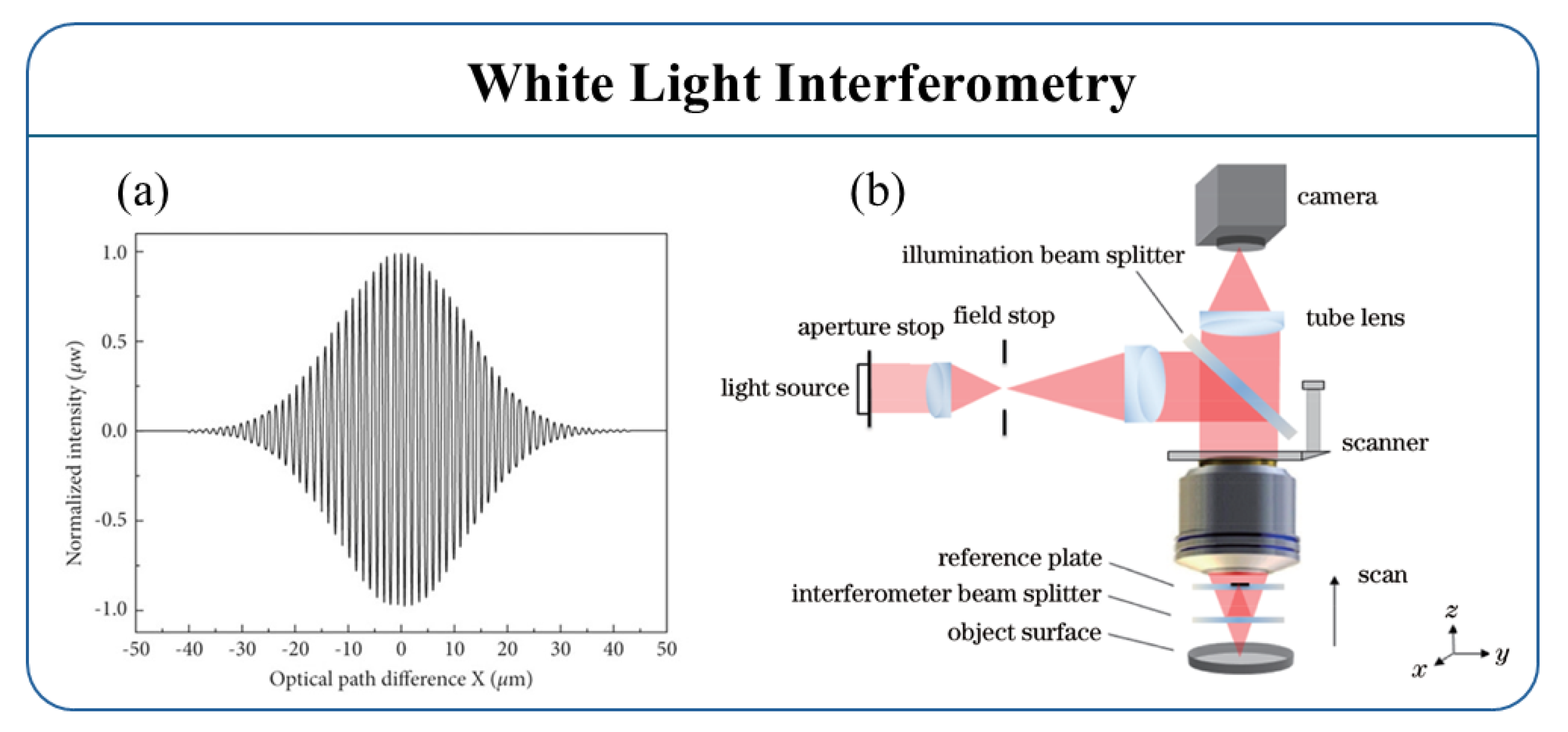
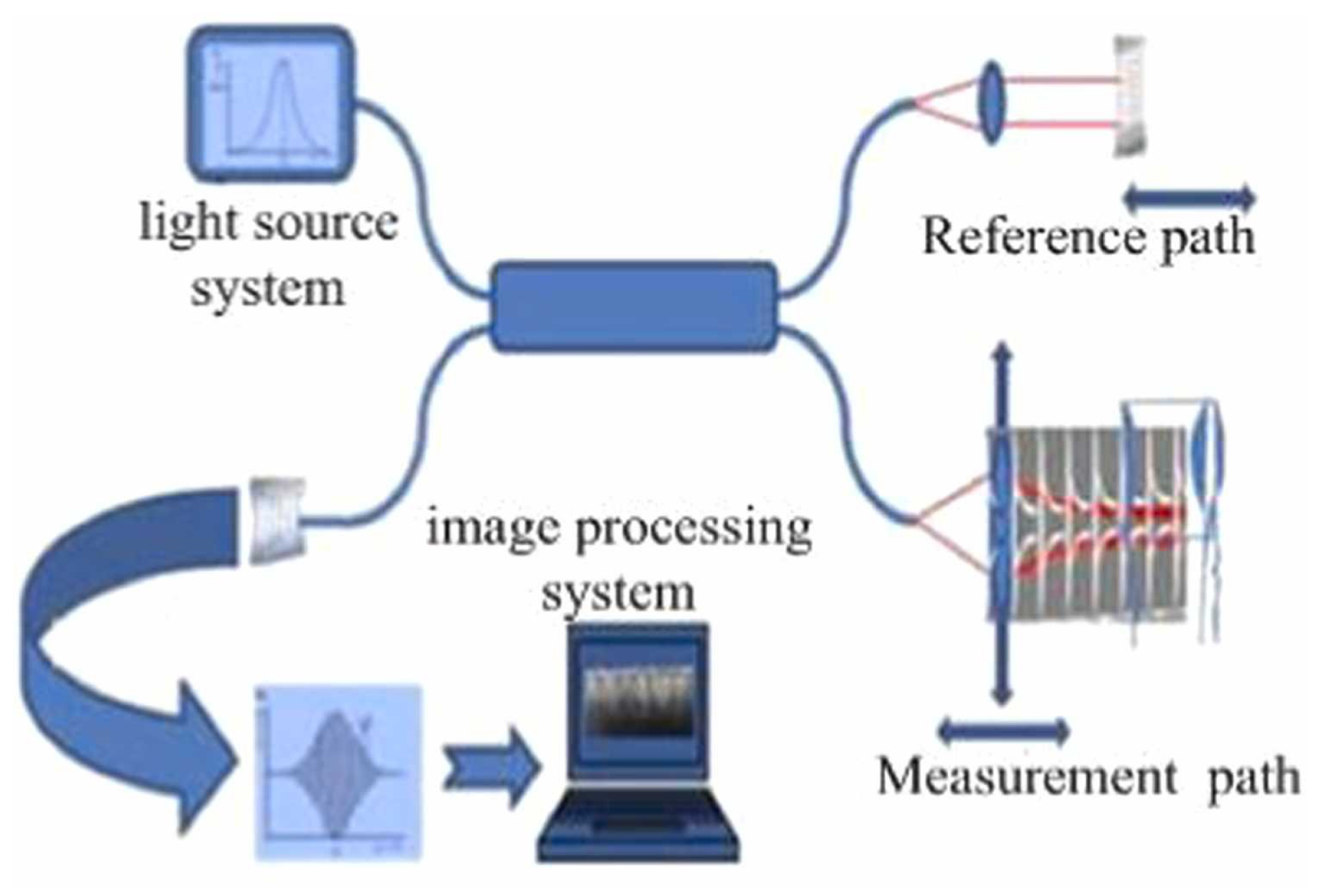
3.8. White Light Interferometry
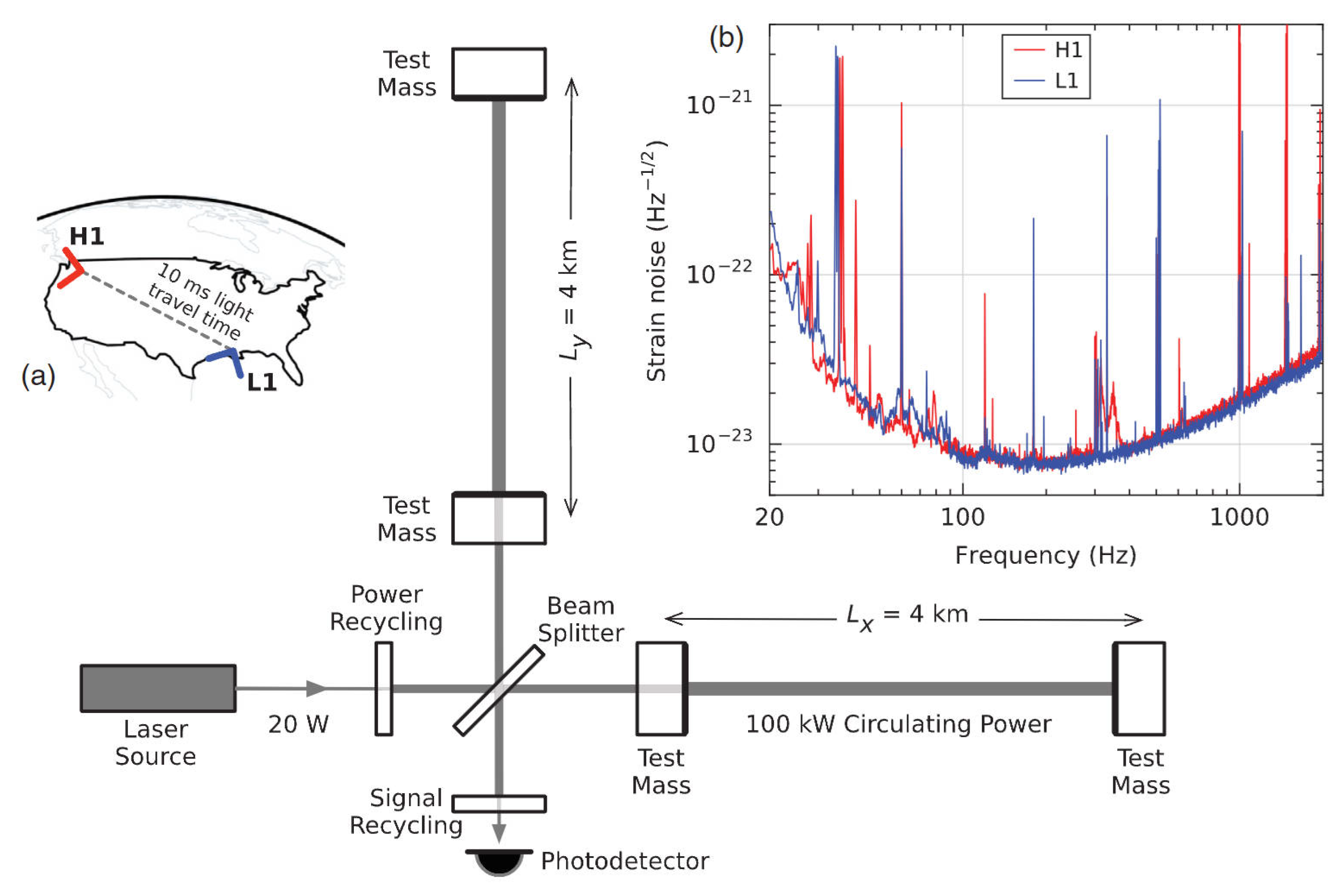
3.9. LIGO Interferometer
3.10. Optical Coherence Tomography
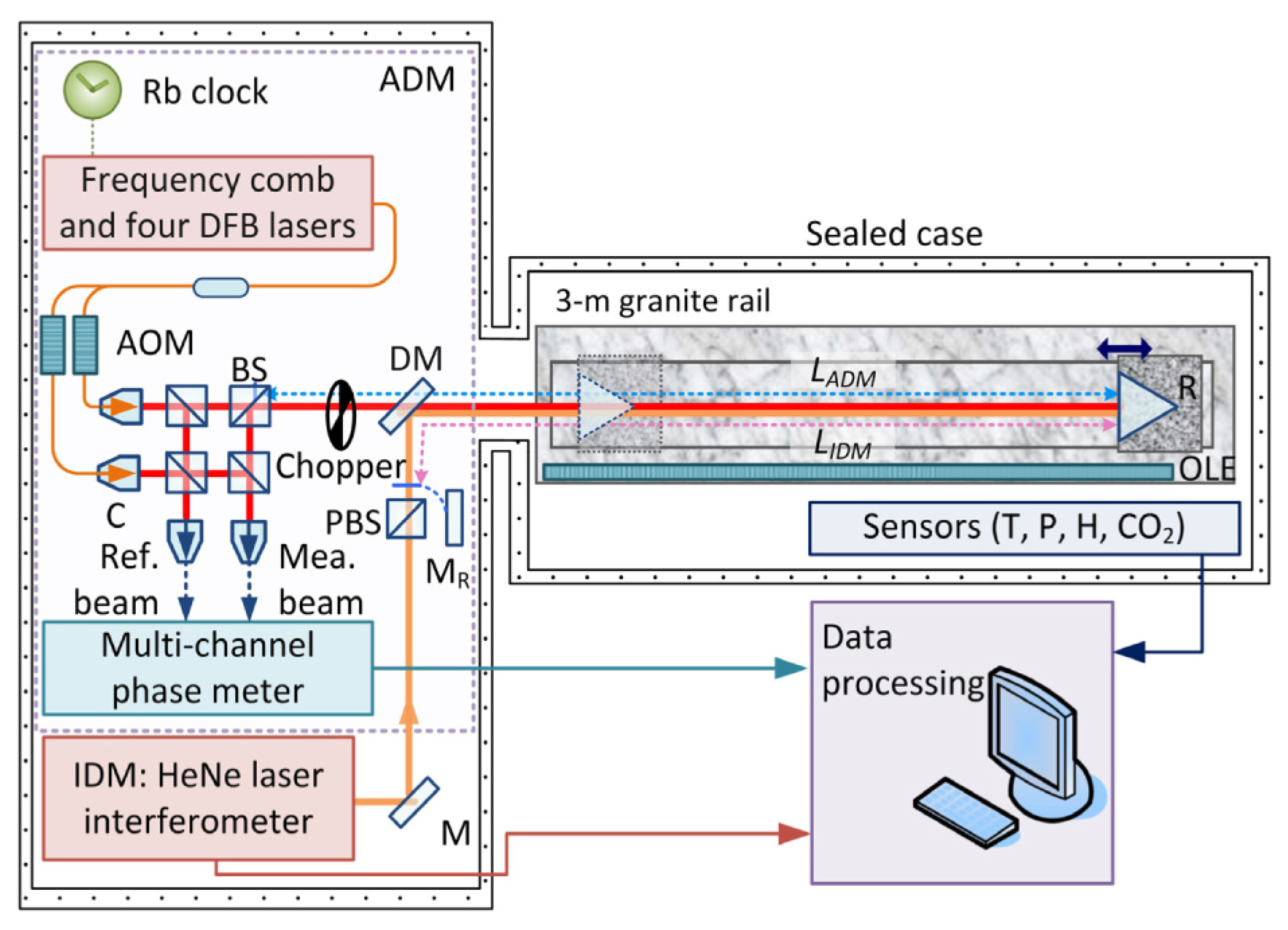
4. Optical Frequency Comb Interferometry
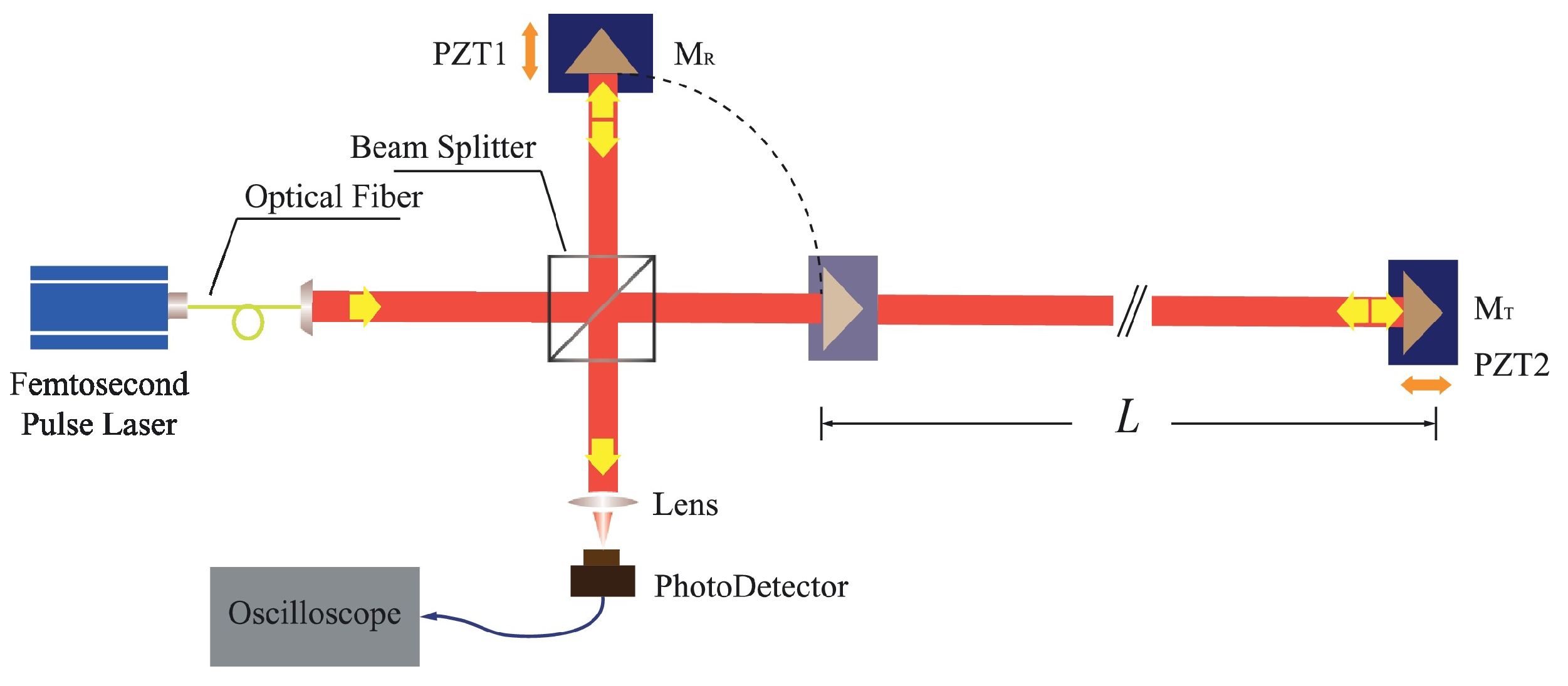
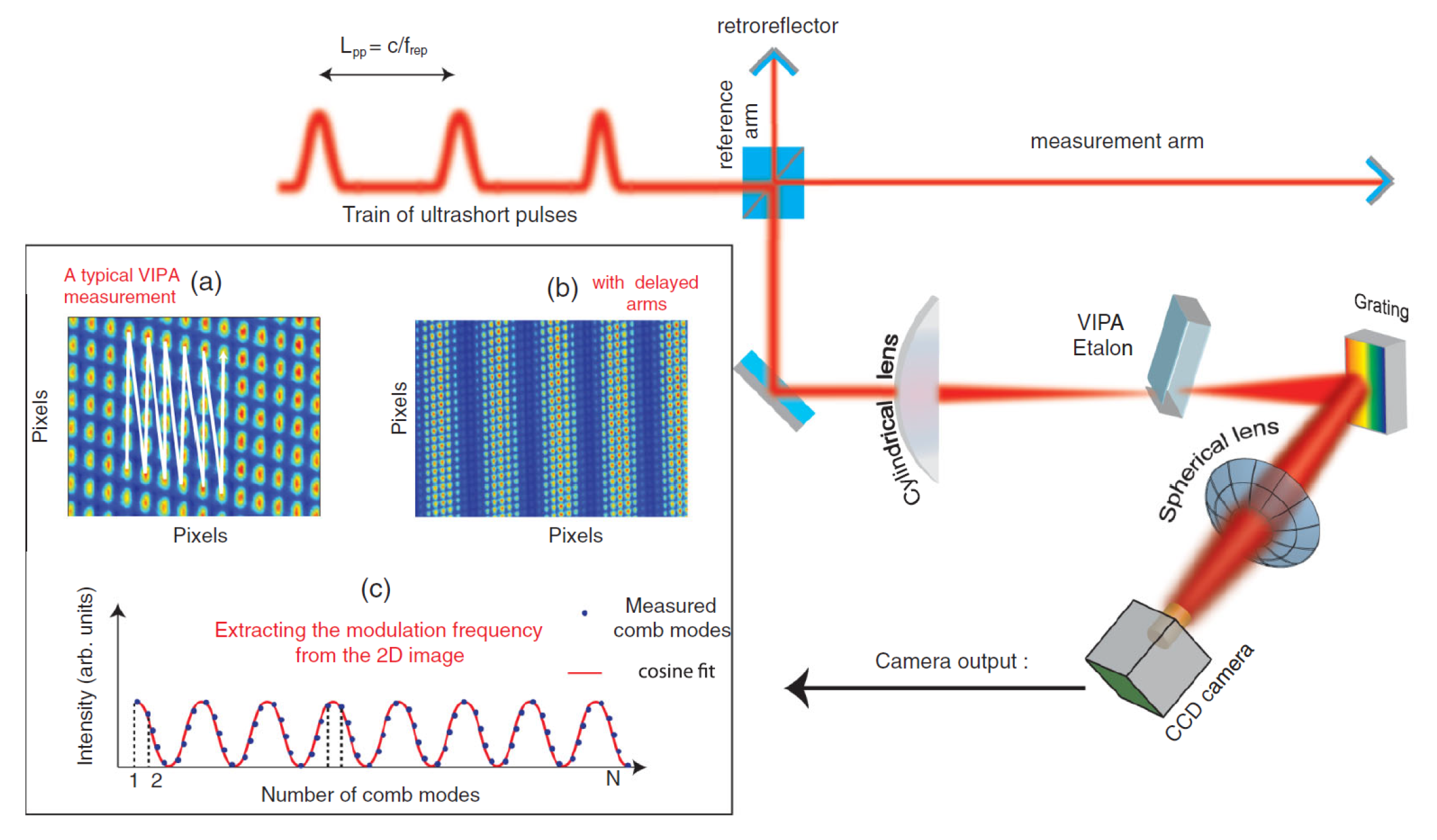
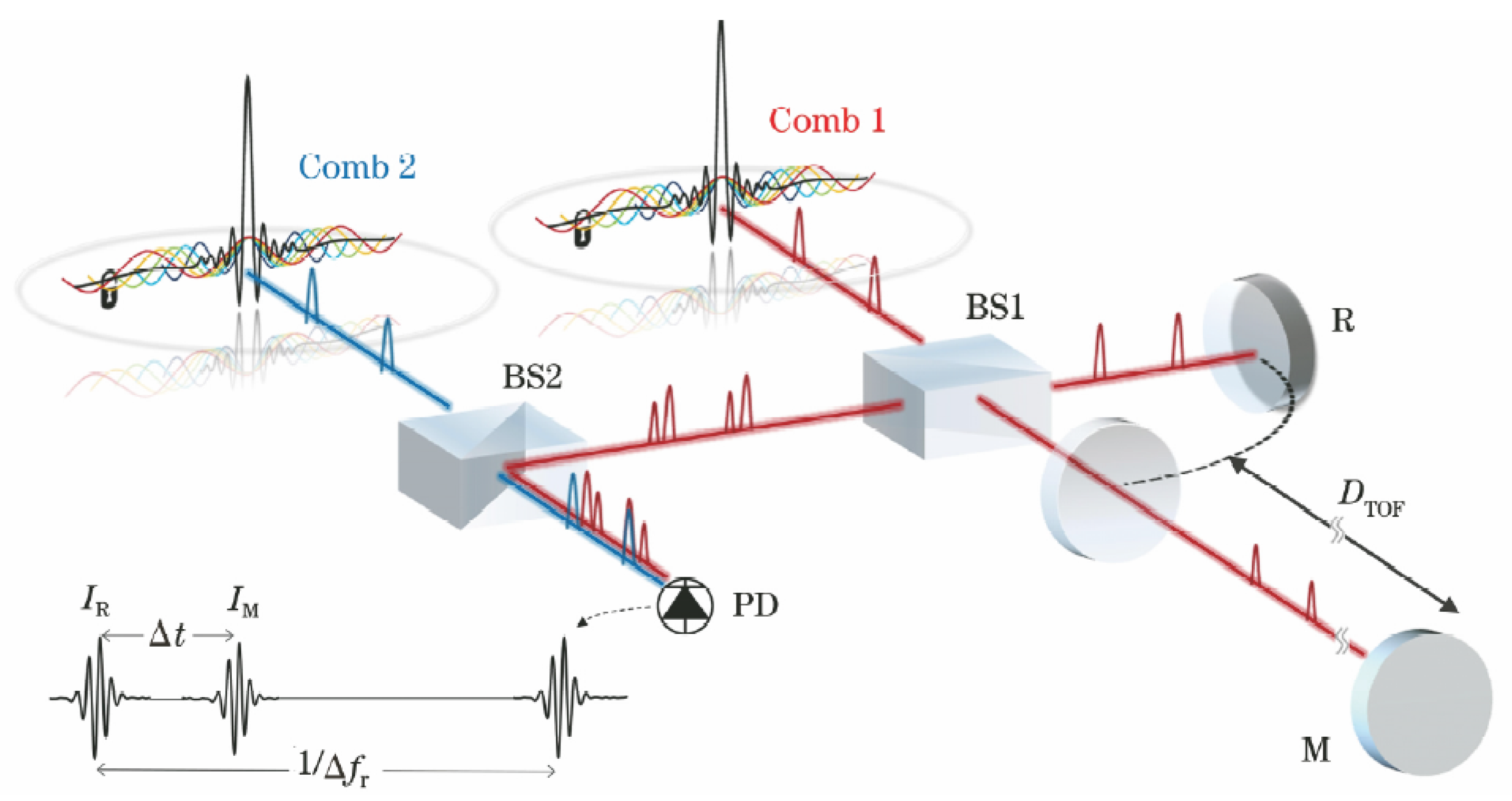
4.1. Time-of-Flight Method
4.2. Synthetic Wavelength Interferometry
4.3. Multi-Wavelength Interferometry
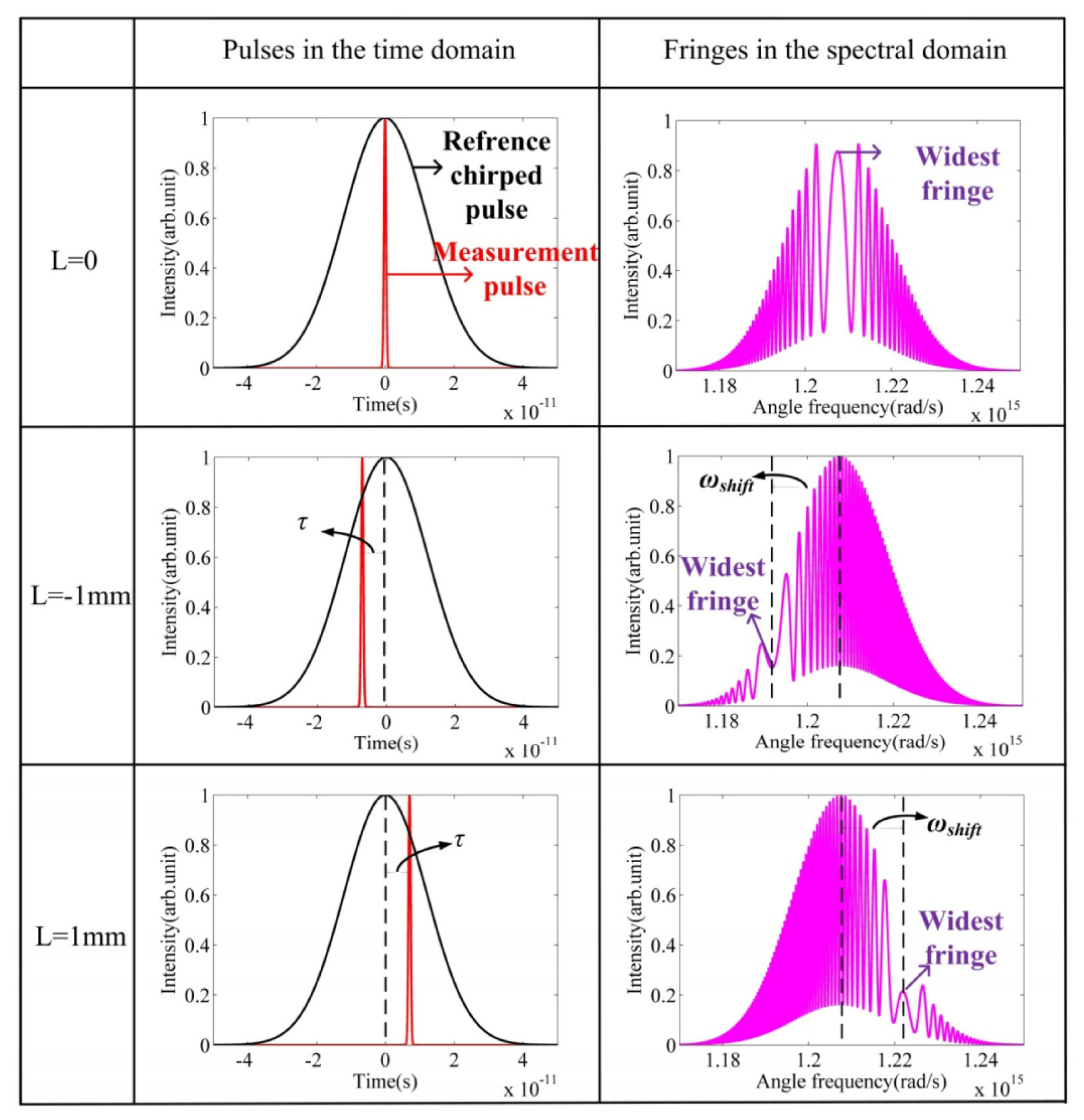
4.4. Dispersive Interferometry
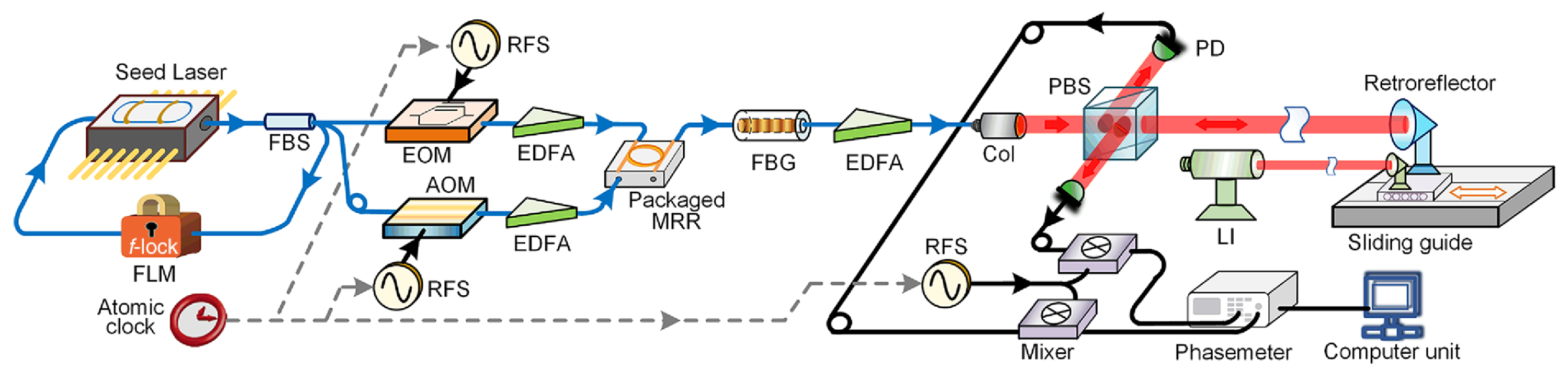
4.5. Dual-Comb Interferometry
5. Discussions
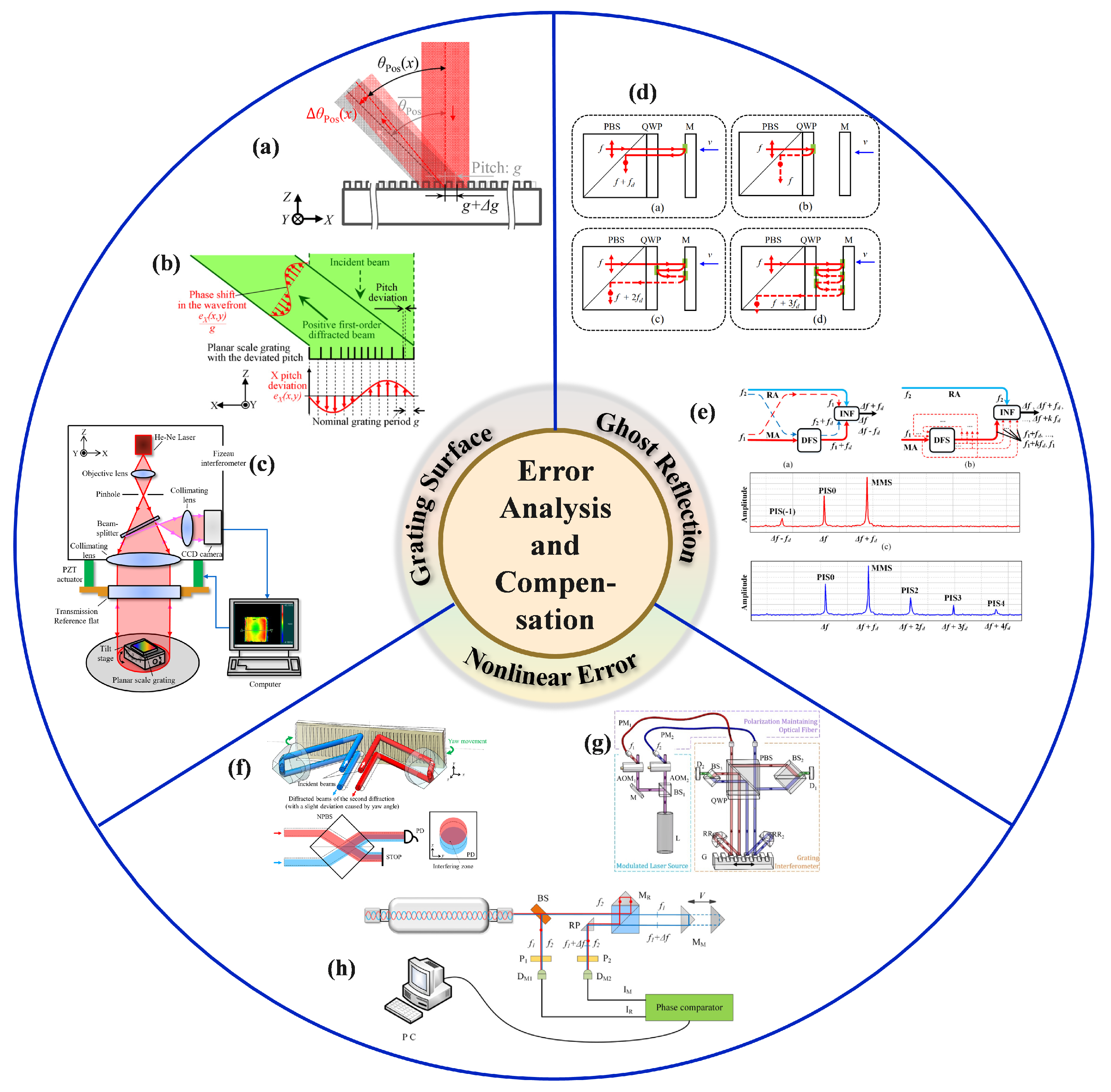
5.1. Error Analysis and Compensation Methods
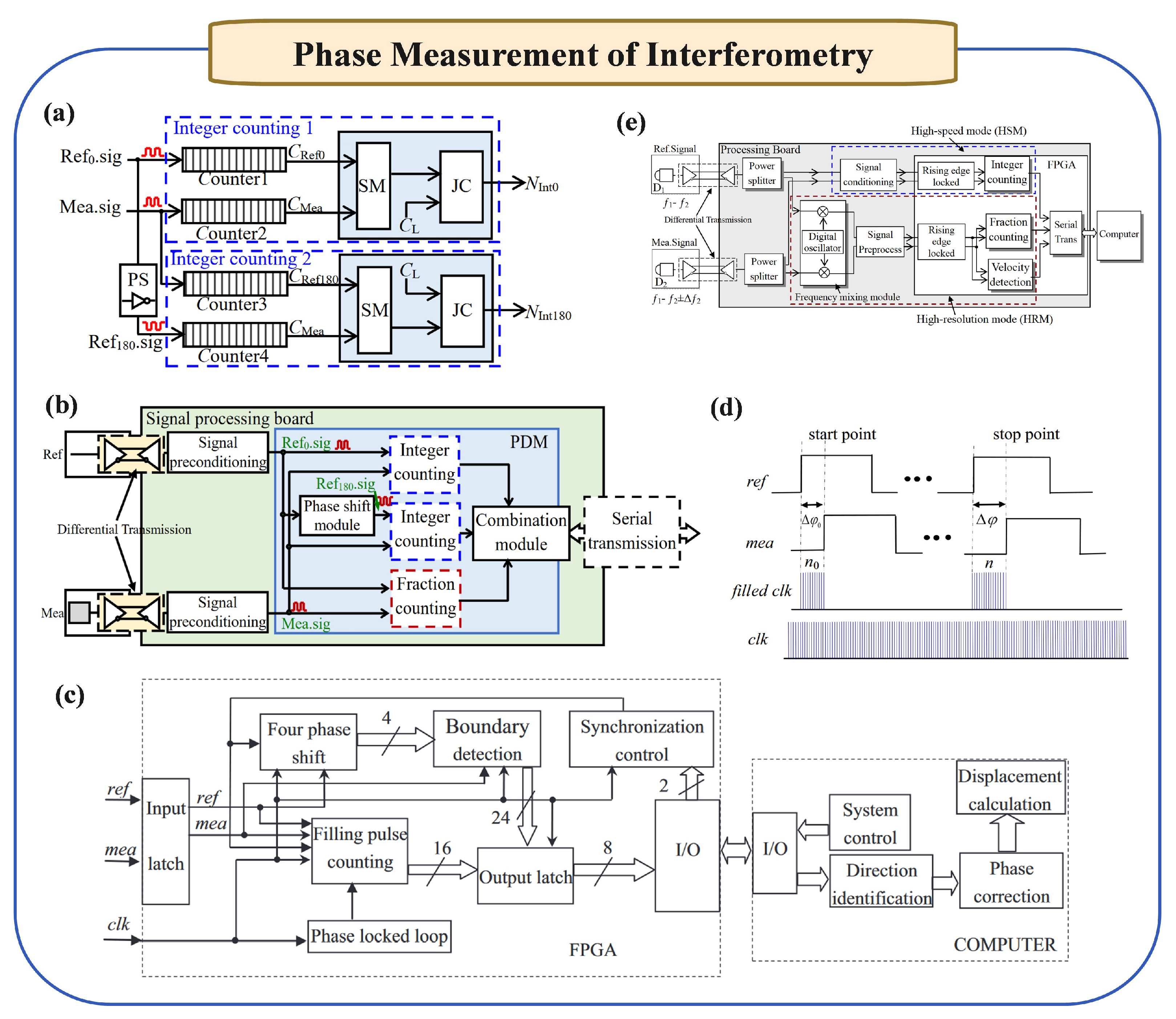
5.2. Phase Measurement Methods
6. Conclusions and Perspectives
6.1. Grating Interferometry: Future Directions
6.2. Laser Interferometry: Future Directions
6.3. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Joo, K.N.; Kim, Y.; Kim, S.W. Distance measurements by combined method based on a femtosecond pulse laser. Opt. Express 2008, 16, 19799–19806. [Google Scholar] [CrossRef]
- Hyun, S.; Kim, Y.J.; Kim, Y.; Jin, J.; Kim, S.W. Absolute length measurement with the frequency comb of a femtosecond laser. Meas. Sci. Technol. 2009, 20, 095302. [Google Scholar] [CrossRef]
- Matsumoto, H.; Wang, X.; Takamasu, K.; Aoto, T. Absolute Measurement of Baselines up to 403 m Using Heterodyne Temporal Coherence Interferometer with Optical Frequency Comb. Appl. Phys. Express 2012, 5, 046601. [Google Scholar] [CrossRef]
- Kosarevsky, S. Practical way to measure large-scale 2D parts using repositioning on coordinate-measuring machines. Measurement 2010, 43, 837–841. [Google Scholar] [CrossRef]
- Petley, B. New definition of the metre. Nature 1983, 303, 373–376. [Google Scholar] [CrossRef]
- Felder, R. Practical realization of the definition of the metre, including recommended radiations of other optical frequency standards (2003). Metrologia 2005, 42, 323. [Google Scholar] [CrossRef]
- Yang, J.; Gu, G.; Qian, W.; Ren, K.; Lu, D.; Zhang, J.; Guo, P.; Gao, Q.; Wan, M.; Chen, Q. Pulsed light time-of-flight measurement based on a differential hysteresis timing discrimination method. Opt. Express 2020, 28, 23554–23568. [Google Scholar] [CrossRef]
- Lyu, L.; Li, D.; Wu, T.; Mi, Q.; Jiang, Y.; Xu, L. Signal flux and time-of-flight estimation based on waveform optimization for single-photon LiDAR. Measurement 2025, 242, 116239. [Google Scholar] [CrossRef]
- Sarbolandi, H.; Plack, M.; Kolb, A. Pulse Based Time-of-Flight Range Sensing. Sensors 2018, 18, 1679. [Google Scholar] [CrossRef]
- Limi Jaya, G.; Chen, S.; Siek, L. The Design of Clocked-Comparator-Based Time-Interval Measurement Circuit for Pulse ToF Measurement. IEEE Sens. J. 2017, 17, 6699–6706. [Google Scholar] [CrossRef]
- Wang, S.; Ma, R.; Cao, F.; Luo, L.; Li, X. A Review: High-Precision Angle Measurement Technologies. Sensors 2024, 24, 1755. [Google Scholar] [CrossRef]
- Luo, L.; Shan, S.; Li, X. A Review: Laser Interference Lithography for Diffraction Gratings and Their Applications in Encoders and Spectrometers. Sensors 2024, 24, 6617. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.; Lu, X.; Knapp, W.; Weckenmann, A.; Estler, W.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Wang, G.; Gao, L.; Huang, G.; Lei, X.; Cui, C.; Wang, S.; Yang, M.; Zhu, J.; Yan, S.; Li, X. A wavelength-stabilized and quasi-common-path heterodyne grating interferometer with sub-nanometer precision. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Liu, C.; Cai, G.; Wang, W. A survey on the grating based optical position encoder. Opt. Laser Technol. 2021, 143, 107352. [Google Scholar] [CrossRef]
- Schuhler, N.; Salvadé, Y.; Lévêque, S.; Dändliker, R.; Holzwarth, R. Frequency-comb-referenced two-wavelength source for absolute distance measurement. Opt. Lett. 2006, 31, 3101–3103. [Google Scholar] [CrossRef] [PubMed]
- Salvadé, Y.; Schuhler, N.; Lévêque, S.; Floch, S.L. High-accuracy absolute distance measurement using frequency comb referenced multiwavelength source. Appl. Opt. 2008, 47, 2715–2720. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Q.; Zhu, X.; Lu, H.; Yang, L.; Ma, D.; Sun, J.; Ni, K.; Wang, X. Holographic fabrication of an arrayed one-axis scale grating for a two-probe optical linear encoder. Opt. Express 2017, 25, 16028–16039. [Google Scholar] [CrossRef]
- Shan, S.; Li, J.; Liu, P.; Li, Q.; Wang, X.; Li, X. A Microlens Array Grating for Miniature Multi-Channel Spectrometers. Sensors 2023, 23, 8381. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Chen, L.C.; Kim, D.W.; Chen, X.; Li, X.; Matsukuma, H. An insight into optical metrology in manufacturing. Meas. Sci. Technol. 2021, 32, 042003. [Google Scholar] [CrossRef]
- Xue, G.; Lu, H.; Li, X.; Zhou, Q.; Wu, G.; Wang, X.; Zhai, Q.; Ni, K. Patterning nanoscale crossed grating with high uniformity by using two-axis Lloyd’s mirrors based interference lithography. Opt. Express 2020, 28, 2179–2191. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Shimizu, Y.; Ito, S. A two-axis Lloyd’s mirror interferometer for fabrication of two-dimensional diffraction gratings. CIRP Ann. 2014, 63, 461–464. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, J.; Xu, T.; Yuan, S.; Zhang, Z.; Jiang, H.; Gu, H.; Zhou, R.; Liu, S. Optical wafer defect inspection at the 10 nm technology node and beyond. Int. J. Extrem. Manuf. 2022, 4, 032001. [Google Scholar] [CrossRef]
- Teimel, A. Technology and applications of grating interferometers in high-precision measurement. Precis. Eng. 1992, 14, 147–154. [Google Scholar] [CrossRef]
- Resolution, L. Finally Reaches the Realm of Picometer. Available online: https://www.magnescale.com/en/laserscale/ (accessed on 9 December 2024).
- Wu, C.C.; Hsu, C.C.; Lee, J.Y.; Chen, Y.Z. Heterodyne common-path grating interferometer with Littrow configuration. Opt. Express 2013, 21, 13322–13332. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, K.; Li, X.; Zhou, Q.; Wang, X. Highly accurate, absolute optical encoder using a hybrid-positioning method. Opt. Lett. 2019, 44, 5258–5261. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, M.; Zhu, Y.; Lu, S.; Yang, K. A displacement measurement system for ultra-precision heterodyne Littrow grating interferometer. Opt. Precis. Eng. 2017, 25, 2975–2985. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Lee, J.Y.; Wu, W.T.; Chen, J.C.; Deturche, R.; Lerondel, G. Quasi-common-optical-path heterodyne grating interferometer for displacement measurement. Meas. Sci. Technol. 2010, 21, 115304. [Google Scholar] [CrossRef]
- Lin, C.; Yan, S.; Du, Z.; Wang, G.; Wei, C. Symmetrical short-period and high signal-to-noise ratio heterodyne grating interferometer. Chin. Opt. Lett. 2015, 13, 100501. [Google Scholar]
- Xing, X.; Chang, D.; Hu, P.; Tan, J. Spatially separated heterodyne grating interferometer for eliminating periodic nonlinear errors. Opt. Express 2017, 25, 31384–31393. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, H.; Ni, K.; Zhou, Q.; Mao, X.; Zeng, L.; Wang, X.; Xiao, X. Two-probe optical encoder for absolute positioning of precision stages by using an improved scale grating. Opt. Express 2016, 24, 21378–21391. [Google Scholar] [CrossRef]
- Shi, Y.; Zhou, Q.; Li, X.; Ni, K.; Wang, X. Design and testing of a linear encoder capable of measuring absolute distance. Sens. Actuators A Phys. 2020, 308, 111935. [Google Scholar] [CrossRef]
- Xia, H.J. Research on Precise 2-D Plane Grating Measurement System and Key Technology. PHD Thesis, Hefei University of Technology, Hefei, China, 2006. [Google Scholar]
- Heidenhain. PP281 Two-Coordinate Encoder. Available online: https://www.heidenhain.com/products/linear-encoders/exposed/pp-281. (accessed on 9 December 2024).
- Kimura, A.; Gao, W.; Arai, Y.; Lijiang, Z. Design and construction of a two-degree-of-freedom linear encoder for nanometric measurement of stage position and straightness. Precis. Eng. 2010, 34, 145–155. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Jiri, G.; Hao, Q.; Li, W. High-precision 2D grating displacement measurement system based on double-spatial heterodyne optical path interleaving. Opt. Lasers Eng. 2022, 158, 107167. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Jiang, S.; Wang, W.; Yu, H.; Li, W. Grating-based 2D displacement measurement with quadruple optical subdivision of a single incident beam. Opt. Express 2021, 29, 24169–24181. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.C.; Wu, C.C.; Lee, J.Y.; Chen, H.Y.; Weng, H.F. Reflection type heterodyne grating interferometry for in-plane displacement measurement. Opt. Commun. 2008, 281, 2582–2589. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhang, M.; Zhu, Y.; Wu, Y.F.; Hu, C.X.; Liu, Z. A novel heterodyne grating interferometer system for in-plane and out-of-plane displacement measurement with nanometer resolution. In Proceedings of the 29th Annual Meeting of the American Society for Precision Engineering, Boston, MA, USA, 9–15 November 2014; pp. 173–177. [Google Scholar]
- Lin, C.; Yan, S.; Du, Z.; Wei, C.; Wang, G. High-efficiency gold-coated cross-grating for heterodyne grating interferometer with improved signal contrast and optical subdivision. Opt. Commun. 2015, 339, 86–93. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Pan, S.W. Development of a grating-based interferometer for six-degree-of-freedom displacement and angle measurements. Opt. Express 2015, 23, 2451–2465. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, G. Dual-Comb Ranging. Engineering 2018, 4, 772–778, Correction in Engineering 2019, 5, 350. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, M.; Zhu, Y.; Ye, W.; Wang, L.; Xia, Y. Two Degree-of-Freedom Fiber-Coupled Heterodyne Grating Interferometer with Milli-Radian Operating Range of Rotation. Sensors 2019, 19, 3219. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liao, B.; Shi, N.; Li, X. A compact and high-precision three-degree-of-freedom grating encoder based on a quadrangular frustum pyramid prism. Sensors 2023, 23, 4022. [Google Scholar] [CrossRef] [PubMed]
- Kimura, A.; Gao, W.; Kim, W.; Hosono, K.; Shimizu, Y.; Shi, L.; Zeng, L. A sub-nanometric three-axis surface encoder with short-period planar gratings for stage motion measurement. Precis. Eng. 2012, 36, 576–585. [Google Scholar] [CrossRef]
- Lin, J.; Guan, J.; Wen, F.; Tan, J. High-resolution and wide range displacement measurement based on planar grating. Opt. Commun. 2017, 404, 132–138. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, L.; Bai, Y.; Jirigalantu; Yu, H.; Bayanheshig; Liu, Z.; Li, W. Littrow 3D measurement based on 2D grating dual-channel equal-optical path interference. Opt. Express 2022, 30, 41671–41684. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Wang, G.; Wang, S.; Li, X. A reflective-type heterodyne grating interferometer for three-degree-of-freedom subnanometer measurement. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Gao, W.; Kimura, A. A Three-axis Displacement Sensor with Nanometric Resolution. CIRP Ann. 2007, 56, 529–532. [Google Scholar] [CrossRef]
- Shimizu, Y.; Ito, T.; Li, X.; Kim, W.; Gao, W. Design and testing of a four-probe optical sensor head for three-axis surface encoder with a mosaic scale grating. Meas. Sci. Technol. 2014, 25, 094002. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Pan, S.W. Three-degree-of-freedom displacement measurement using grating-based heterodyne interferometry. Appl. Opt. 2013, 52, 6840–6848. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Guan, J.; Jin, P.; Tan, J. Three-Dimensional Grating Displacement Measuring System with Dual-Frequency Laser. CN103644848A, 19 March 2014. [Google Scholar]
- Tan, J.B.; Lu, Z.G.; Wei, P.P. A Three-Dimensional Displacement Measurement Device Using Dual-Frequency Laser and Diffraction Grating. CN104567695A, 29 April 2015. [Google Scholar]
- Gao, W.; Saito, Y.; Muto, H.; Arai, Y.; Shimizu, Y. A three-axis autocollimator for detection of angular error motions of a precision stage. CIRP Ann. 2011, 60, 515–518. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Muto, H.; Shimizu, Y.; Ito, S.; Dian, S. A six-degree-of-freedom surface encoder for precision positioning of a planar motion stage. Precis. Eng. 2013, 37, 771–781. [Google Scholar] [CrossRef]
- Quan, L.; Shimizu, Y.; Xiong, X.; Matsukuma, H.; Gao, W. A new method for evaluation of the pitch deviation of a linear scale grating by an optical angle sensor. Precis. Eng. 2021, 67, 1–13. [Google Scholar] [CrossRef]
- Yu, K.; Zhu, J.; Yuan, W.; Zhou, Q.; Xue, G.; Wu, G.; Wang, X.; Li, X. Two-channel six degrees of freedom grating-encoder for precision-positioning of sub-components in synthetic-aperture optics. Opt. Express 2021, 29, 21113–21128. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Luo, L.; Zhu, J.; Shi, N.; Li, X. An ultra-precision absolute-type multi-degree-of-freedom grating encoder. Sensors 2022, 22, 9047. [Google Scholar] [CrossRef]
- Li, X.; Shi, Y.; Xiao, X.; Zhou, Q.; Wu, G.; Lu, H.; Ni, K. Design and Testing of a Compact Optical Prism Module for Multi-Degree-of-Freedom Grating Interferometry Application. Appl. Sci. 2018, 8, 2495. [Google Scholar] [CrossRef]
- Shi, N.; Wang, S.; Xue, G.; Liu, M.; Han, Y.; Zhu, J.; Ni, K.; Wang, X.; Li, X. A real-time processing system for dual-channel six-degree-of-freedom grating ruler based on FPGA. In Proceedings of the Optical Design and Testing XI; SPIE: Bellingham, WA, USA, 2021; Volume 11895, pp. 250–260. [Google Scholar]
- de Jong, F.; van der Pasch, B.; Castenmiller, T.; Vleeming, B.; Droste, R.; van de Mast, F. Enabling the lithography roadmap: An immersion tool based on a novel stage positioning system. In Proceedings of the Optical Microlithography XXII; SPIE: Bellingham, WA, USA, 2009; Volume 7274, pp. 608–617. [Google Scholar]
- Castenmiller, T.; van de Mast, F.; de Kort, T.; van de Vin, C.; de Wit, M.; Stegen, R.; van Cleef, S. Towards ultimate optical lithography with NXT: 1950i dual stage immersion platform. In Proceedings of the Optical Microlithography XXIII; SPIE: Bellingham, WA, USA, 2010; Volume 7640, pp. 623–634. [Google Scholar]
- Li, X.; Shimizu, Y.; Ito, T.; Cai, Y.; Ito, S.; Gao, W. Measurement of six-degree-of-freedom planar motions by using a multiprobe surface encoder. Opt. Eng. 2014, 53, 122405. [Google Scholar] [CrossRef]
- Ye, W.; Zhang, M.; Zhu, Y.; Wang, L.; Hu, J.; Li, X.; Hu, C. Real-time displacement calculation and offline geometric calibration of the grating interferometer system for ultra-precision wafer stage measurement. Precis. Eng. 2019, 60, 413–420. [Google Scholar] [CrossRef]
- Lee, C.; Kim, G.H.; Lee, S.K. Design and construction of a single unit multi-function optical encoder for a six-degree-of-freedom motion error measurement in an ultraprecision linear stage. Meas. Sci. Technol. 2011, 22, 105901. [Google Scholar] [CrossRef]
- Matsukuma, H.; Ishizuka, R.; Furuta, M.; Li, X.; Shimizu, Y.; Gao, W. Reduction in cross-talk errors in a six-degree-of-freedom surface encoder. Nanomanuf. Metrol. 2019, 2, 111–123. [Google Scholar] [CrossRef]
- Lin, X.; Su, X.; Wang, J.; Sun, Y.; Hu, P. Laser Interferometer Technology and Instruments for Sub-Nanometer and Picometer Displacement Measurements. Laser Optoelectron. Prog. 2023, 60, 312016. (In Chinese) [Google Scholar]
- Wang, Y.C.; Shyu, L.H.; Chang, C.P. The Comparison of Environmental Effects on Michelson and Fabry-Perot Interferometers Utilized for the Displacement Measurement. Sensors 2010, 10, 2577–2586. [Google Scholar] [CrossRef]
- Cui, X.; Liu, Y.; Chen, P.; Li, C. Measuring two vibrations using dual-external-cavity structure in a self-mixing system. Opt. Lasers Eng. 2021, 141, 106557. [Google Scholar] [CrossRef]
- Meiners-Hagen, K.; Burgarth, V.; Abou-Zeid, A. Profilometry with a multi-wavelength diode laser interferometer. Meas. Sci. Technol. 2004, 15, 741. [Google Scholar] [CrossRef]
- Song, L.; Zhang, F.; Sun, D.; Lin, H.; Huang, X.; Yu, M.; Zhang, Q. Research progress of absolute distance measurement methods based on tunable laser frequency sweeping interference. Infrared Laser Eng. 2022, 51, 20210406-1. (In Chinese) [Google Scholar]
- Wu, G.; Zhou, S.; Yang, Y.; Ni, K. Dual-Comb Ranging and Its Applications. Chin. J. Lasers 2021, 48, 1504002. (In Chinese) [Google Scholar]
- Bobroff, N. Recent advances in displacement measuring interferometry. Meas. Sci. Technol. 1993, 4, 907. [Google Scholar] [CrossRef]
- Xu, X.; Gu, D.; Gao, S.; Sun, L.; Lu, X.; Wang, K.; Bai, J. Back to Michelson interferometer: A precise inspection system for industrial intricate structures defect detection. Meas. Sci. Technol. 2023, 35, 035026. [Google Scholar] [CrossRef]
- Yan, L.; Chen, B.; Wang, B. A differential Michelson interferometer with orthogonal single frequency laser for nanometer displacement measurement. Meas. Sci. Technol. 2017, 28, 045001. [Google Scholar] [CrossRef]
- Yatabe, K.; Ishikawa, K.; Oikawa, Y. Signal processing for optical sound field measurement and visualization. In Proceedings of Meetings on Acoustics; AIP Publishing: Melville, NY, USA, 2017. [Google Scholar] [CrossRef]
- Kim, J.A.; Kim, J.W.; Kang, C.S.; Eom, T.B.; Ahn, J. A digital signal processing module for real-time compensation of nonlinearity in a homodyne interferometer using a field-programmable gate array. Meas. Sci. Technol. 2009, 20, 017003. [Google Scholar] [CrossRef]
- Hu, P.; Zhu, J.; Zhai, X.; Tan, J. DC-offset-free homodyne interferometer and its nonlinearity compensation. Opt. Express 2015, 23, 8399. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Zhu, J.; Guo, X.; Tan, J. Compensation for the Variable Cyclic Error in Homodyne Laser Interferometers. Sensors 2015, 15, 3090–3106. [Google Scholar] [CrossRef]
- Požar, T.; Gregorčič, P.; Možina, J. A precise and wide-dynamic-range displacement-measuring homodyne quadrature laser interferometer. Appl. Phys. B 2011, 105, 575–582. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Jiu, Y.; Tan, J.; Sun, T. Homodyne laser interferometer involving minimal quadrature phase error to obtain subnanometer nonlinearity. Appl. Opt. 2016, 55, 7086. [Google Scholar] [CrossRef] [PubMed]
- Pisani, M. A homodyne Michelson interferometer with sub-picometer resolution. Meas. Sci. Technol. 2009, 20, 084008. [Google Scholar] [CrossRef]
- Keem, T.; Gonda, S.; Misumi, I.; Huang, Q.; Kurosawa, T. Removing nonlinearity of a homodyne interferometer by adjusting the gains of its quadrature detector systems. Appl. Opt. 2004, 43, 2443–2448. [Google Scholar] [CrossRef] [PubMed]
- Pisani, M. Multiple reflection Michelson interferometer with picometer resolution. Opt. Express 2008, 16, 21558. [Google Scholar] [CrossRef] [PubMed]
- Ahn, J.; Kim, J.A.; Kang, C.S.; Kim, J.W.; Kim, S. A passive method to compensate nonlinearity in a homodyne interferometer. Opt. Express 2009, 17, 23299. [Google Scholar] [CrossRef]
- Dobosz, M.; Zamiela, G. Interference fringe detection system for distance measuring interferometer. Optics Laser Technology 2012, 44, 1620–1628. [Google Scholar] [CrossRef]
- Yan, L.; Chen, B.; Chen, Z.; Xie, J.; Zhang, E.; Zhang, S. Phase-modulated dual-homodyne interferometer without periodic nonlinearity. Meas. Sci. Technol. 2017, 28, 115006. [Google Scholar] [CrossRef]
- Choi, H.; Park, K.; La, J. Novel phase measurement technique of the heterodyne laser interferometer. Rev. Sci. Instrum. 2005, 76, 093105. [Google Scholar] [CrossRef]
- Park, Y.; Cho, K. Heterodyne interferometer scheme using a double pass in an acousto-optic modulator. Opt. Lett. 2011, 36, 331. [Google Scholar] [CrossRef]
- Kimachi, A. Real-time heterodyne imaging interferometry: Focal-plane amplitude and phase demodulation using a three-phase correlation image sensor. Appl. Opt. 2007, 46, 87. [Google Scholar] [CrossRef]
- Yin, Z.; Li, F.; Sun, Y.; Zou, Y.; Wang, Y.; Yang, H.; Hu, P.; Fu, H.; Tan, J. High synchronization absolute distance measurement using a heterodyne and superheterodyne combined interferometer. Chin. Opt. Lett. 2024, 22, 011204. [Google Scholar] [CrossRef]
- Meskers, A.J.H.; Spronck, J.W.; Munnig Schmidt, R.H. Heterodyne displacement interferometer, insensitive for input polarization. Opt. Lett. 2014, 39, 1949. [Google Scholar] [CrossRef] [PubMed]
- Demarest, F.C. High-resolution, high-speed, low data age uncertainty, heterodyne displacement measuring interferometer electronics. Meas. Sci. Technol. 1998, 9, 1024–1030. [Google Scholar] [CrossRef]
- Eom, T.B.; Choi, T.Y.; Lee, K.H.; Choi, H.S.; Lee, S.K. A simple method for the compensation of the nonlinearity in the heterodyne interferometer. Meas. Sci. Technol. 2002, 13, 222–225. [Google Scholar] [CrossRef]
- Schmitz, T.L.; Chu, D.; Houck, L., III. First-order periodic error correction: Validation for constant and non-constant velocities with variable error magnitudes. Meas. Sci. Technol. 2006, 17, 3195–3203. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Spronck, J.W.; van Kan, P.J.M.; Schmidt, R.H.M. Simple heterodyne laser interferometer with subnanometer periodic errors. Opt. Lett. 2009, 34, 386. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Buice, E.S.; Spronck, J.W.; Schmidt, R.H.M. High resolution heterodyne interferometer without detectable periodic nonlinearity. Opt. Express 2010, 18, 1159. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J.D.; Meskers, A.J.H.; Spronck, J.W.; Schmidt, R.H.M. Fiber-coupled displacement interferometry without periodic nonlinearity. Opt. Lett. 2011, 36, 3584–3586. [Google Scholar] [CrossRef] [PubMed]
- Leirset, E.; Engan, H.E.; Aksnes, A. Heterodyne interferometer for absolute amplitude vibration measurements with femtometer sensitivity. Opt. Express 2013, 21, 19900. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.; Duan, H.Z.; Li, L.T.; Liang, Y.R.; Luo, J.; Yeh, H.C. A dual-heterodyne laser interferometer for simultaneous measurement of linear and angular displacements. Rev. Sci. Instrum. 2015, 86, 123102. [Google Scholar] [CrossRef]
- Zhu, M.; Wei, H.; Zhao, S.; Wu, X.; Li, Y. Subnanometer absolute displacement measurement using a frequency comb referenced dual resonance tracking Fabry–Perot interferometer. Appl. Opt. 2015, 54, 4594. [Google Scholar] [CrossRef]
- Hsieh, H.L.; Lee, J.Y.; Chen, L.Y.; Yang, Y. Development of an angular displacement measurement technique through birefringence heterodyne interferometry. Opt. Express 2016, 24, 6802. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Li, B. Laser Displacement Sensor in the Application of Aero-Engine Blade Measurement. IEEE Sens. J. 2016, 16, 1377–1384. [Google Scholar] [CrossRef]
- Joo, K.N.; Clark, E.; Zhang, Y.; Ellis, J.D.; Guzmán, F. A compact high-precision periodic-error-free heterodyne interferometer. J. Opt. Soc. Am. A 2020, 37, B11. [Google Scholar] [CrossRef] [PubMed]
- Dong Nguyen, T.; Higuchi, M.; Tung Vu, T.; Wei, D.; Aketagawa, M. 10-pm-order mechanical displacement measurements using heterodyne interferometry. Appl. Opt. 2020, 59, 8478. [Google Scholar] [CrossRef]
- Dong, N.T.; Tai, N.T.; Hoang, D.V.; Mai, N.T.P.; Tung, V.T.; Thang, V.T. Sub-nanometer Displacement Measurement Using Heterodyne Interferometer and Down-Beat Frequency Technique. In Regional Conference in Mechanical Manufacturing Engineering, Proceedings of the AUN/SEED-Net Joint Regional Conference in Transportation, Hanoi, Vietnam, 10–12 December 2021; Springer Nature: Singapore, 2022; pp. 1170–1176. [Google Scholar] [CrossRef]
- Sasaki, O.; Takahashi, K. Sinusoidal phase modulating interferometer using optical fibers for displacement measurement. Appl. Opt. 1988, 27, 4139–4142. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, O.; Takahashi, K.; Suzuki, T. Sinusoidal phase modulating laser diode interferometer with feedback control system to eliminate external disturbance. Opt. Eng. 1990, 29, 1511–1515. [Google Scholar] [CrossRef]
- Minoni, U.; Sardini, E.; Gelmini, E.; Docchio, F.; Marioli, D. A high-frequency sinusoidal phase-modulation interferometer using an electro-optic modulator: Development and evaluation. Rev. Sci. Instrum. 1991, 62, 2579–2583. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Z.; Chen, B.; Yan, L.; Xie, J. Sinusoidal phase modulating absolute distance measurement interferometer combining frequency-sweeping and multi-wavelength interferometry. Opt. Express 2018, 26, 9273–9284. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Shan, D.; Jin, H.; Lou, Y.; Yan, L.; Chen, B. Absolute distance measurement using sinusoidal phase modulating frequency sweeping interferometry with a reference interferometer. Opt. Express 2022, 30, 38880–38895. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.C.; Huang, Y.F.; Hwang, F.H. An improved sensitivity normalization technique of PGC demodulation with low minimum phase detection sensitivity using laser modulation to generate carrier signal. Sens. Actuators A Phys. 2013, 191, 1–10. [Google Scholar] [CrossRef]
- Zhang, A.; Zhang, S. High Stability Fiber-Optics Sensors With an Improved PGC Demodulation Algorithm. IEEE Sens. J. 2016, 16, 7681–7684. [Google Scholar] [CrossRef]
- Xia, W.; Liu, Q.; Hao, H.; Guo, D.; Wang, M.; Chen, X. Sinusoidal phase-modulating self-mixing interferometer with nanometer resolution and improved measurement velocity range. Appl. Opt. 2015, 54, 7820–7827. [Google Scholar] [CrossRef] [PubMed]
- Dandridge, A.; Tveten, A.; Giallorenzi, T. Homodyne demodulation scheme for fiber optic sensors using phase generated carrier. IEEE J. Quantum Electron. 1982, 18, 1647–1653. [Google Scholar] [CrossRef]
- Christian, T.R.; Frank, P.A.; Houston, B.H. Real-time analog and digital demodulator for interferometric fiber optic sensors. In Proceedings of the Smart Structures and Materials 1994: Smart Sensing, Processing, and Instrumentation; Sirkis, J.S., Ed.; International Society for Optics and Photonics; SPIE: Bellingham, WA, USA, 1994; Volume 2191, pp. 324–336. [Google Scholar] [CrossRef]
- He, J.; Wang, L.; Li, F.; Liu, Y. An Ameliorated Phase Generated Carrier Demodulation Algorithm With Low Harmonic Distortion and High Stability. J. Light. Technol. 2010, 28, 3258–3265. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, A.; Pan, H. Eliminating Light Intensity Disturbance With Reference Compensation in Interferometers. IEEE Photonics Technol. Lett. 2015, 27, 1888–1891. [Google Scholar] [CrossRef]
- Zhang, A.; Li, D. Interferometric sensor with a PGC-AD-DSM demodulation algorithm insensitive to phase modulation depth and light intensity disturbance. Appl. Opt. 2018, 57, 7950–7955. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yan, L.; Chen, B.; Xu, Z.; Xie, J. Real-time phase delay compensation of PGC demodulation in sinusoidal phase-modulation interferometer for nanometer displacement measurement. Opt. Express 2017, 25, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Chen, B.; Yan, L.; Xu, Z. Real-time normalization and nonlinearity evaluation methods of the PGC-arctan demodulation in an EOM-based sinusoidal phase modulating interferometer. Opt. Express 2018, 26, 605–616. [Google Scholar] [CrossRef]
- Hillmer, H.; Woidt, C.; Kobylinskiy, A.; Kraus, M.; Istock, A.; Iskhandar, M.S.Q.; Brunner, R.; Kusserow, T. Miniaturized Interferometric Sensors with Spectral Tunability for Optical Fiber Technology—A Comparison of Size Requirements, Performance, and New Concepts. Photonics 2021, 8, 332. [Google Scholar] [CrossRef]
- Hillmer, H.; Woidt, C.; Istock, A.; Kobylinskiy, A.; Nguyen, D.T.; Ahmed, N.; Brunner, R.; Kusserow, T. Role of Nanoimprint Lithography for Strongly Miniaturized Optical Spectrometers. Nanomaterials 2021, 11, 164. [Google Scholar] [CrossRef]
- Chang, C.P.; Tung, P.C.; Shyu, L.H.; Wang, Y.C.; Manske, E. Fabry–Perot displacement interferometer for the measuring range up to 100 mm. Measurement 2013, 46, 4094–4099. [Google Scholar] [CrossRef]
- Rabinowitz, P.; Jacobs, S.F.; Schultz, T.; Gould, G. Cube-corner fabry-perot interfermometer. J. Opt. Soc. Am. (1917–1983) 1962, 52, 452. [Google Scholar] [CrossRef]
- Durand, M.; Lawall, J.; Wang, Y. High-accuracy Fabry-Perot displacement interferometry using fiber lasers. Meas. Sci. Technol. 2011, 22, 094025. [Google Scholar] [CrossRef]
- Nowakowski, B.K.; Smith, D.T.; Smith, S.T. Highly compact fiber Fabry-Perot interferometer: A new instrument design. Rev. Sci. Instrum. 2016, 87, 115102. [Google Scholar] [CrossRef]
- Liu, B.; Wang, B.; Ruan, Y.; Yu, Y.; Xi, J.; Ji, H.; Tang, P. Time-multiplexed laser self-mixing sensor for measurement of multiple material elastic moduli. Opt. Laser Technol. 2024, 176, 110963. [Google Scholar] [CrossRef]
- Donati, S.; Giuliani, G.; Merlo, S. Laser diode feedback interferometer for measurement of displacements without ambiguity. IEEE J. Quantum Electron. 1995, 31, 113–119. [Google Scholar] [CrossRef]
- Ning, Y.; Grattan, K.T.V.; Meggitt, B.T.; Palmer, A.W. Characteristics of laser diodes for interferometric use. Applied Optics 1989, 28, 3657. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, S.; Yoshida, H.; Ikeda, H.; Nishide, K.; Sumi, M. Compact and high-precision range finder with wide dynamic range and its application. IEEE Trans. Instrum. Meas. 1992, 41, 40–44. [Google Scholar] [CrossRef]
- Gagnon, E.; Rivest, J.F. Laser range imaging using the self-mixing effect in a laser diode. IEEE Trans. Instrum. Meas. 1999, 48, 693–699. [Google Scholar] [CrossRef]
- Kou, K.; Li, X.; Li, L.; Xiang, H. Injected current reshaping in distance measurement by laser self-mixing interferometry. Appl. Opt. 2014, 53, 6280. [Google Scholar] [CrossRef]
- Moench, H.; Carpaij, M.; Gerlach, P.; Gronenborn, S.; Gudde, R.; Hellmig, J.; Kolb, J.; van der Lee, A. VCSEL-based sensors for distance and velocity. In Proceedings of the Vertical-Cavity Surface-Emitting Lasers XX; Choquette, K.D., Guenter, J.K., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2016; Volume 9766, p. 97660A. [Google Scholar] [CrossRef]
- Michalzik, R. VCSELs: A Research Review; Springer: Berlin/Heidelberg, Germany, 2013; Volume 166, p. 3. [Google Scholar] [CrossRef]
- Bosch, T.; Servagent, N.; Chellali, R.; Lescure, M. Three-dimensional object construction using a self-mixing type scanning laser range finder. IEEE Trans. Instrum. Meas. 1998, 47, 1326–1329. [Google Scholar] [CrossRef]
- Polhemus, C. Two-wavelength interferometry. Appl. Opt. 1973, 12, 2071. [Google Scholar] [CrossRef] [PubMed]
- Daendliker, R.; Thalmann, R.; Prongue, D. Two-wavelength laser interferometry using superheterodyne detection. Opt. Lett. 1988, 13, 339–341. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Wyant, J.C. Multiple-wavelength phase-shifting interferometry. Appl. Opt. 1985, 24, 804–807. [Google Scholar] [CrossRef]
- Kuschmierz, R.; Czarske, J.; Fischer, A. Multiple wavelength interferometry for distance measurements of moving objects with nanometer uncertainty. Meas. Sci. Technol. 2014, 25, 085202. [Google Scholar] [CrossRef]
- Falaggis, K.; Towers, D.P.; Towers, C.E. Multiwavelength interferometry: Extended range metrology. Opt. Lett. 2009, 34, 950. [Google Scholar] [CrossRef] [PubMed]
- van den Berg, S.A.; Persijn, S.T.; Kok, G.J.P.; Zeitouny, M.G.; Bhattacharya, N. Many-Wavelength Interferometry with Thousands of Lasers for Absolute Distance Measurement. Phys. Rev. Lett. 2012, 108, 183901. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Eiswirt, P.; Petter, J. Electro optic sensor for high precision absolute distance measurement using multiwavelength interferometry. Opt. Express 2018, 26, 3443. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Q.; Lou, Y.; Sun, Z.; Yan, L. Simultaneous Phase Detection of Multi-Wavelength Interferometry Based on Frequency Division Multiplexing. J. Light. Technol. 2022, 40, 4990–4998. [Google Scholar] [CrossRef]
- Thiel, J.; Pfeifer, T.; Hartmann, M. Interferometric measurement of absolute distances of up to 40 m. Measurement 1995, 16, 1–6. [Google Scholar] [CrossRef]
- Bechstein, K.H.; Fuchs, W. Absolute interferometric distance measurements applying a variable synthetic wavelength. J. Opt. 1998, 29, 179–182. [Google Scholar] [CrossRef]
- Xiaoli, D.; Katuo, S. High-accuracy absolute distance measurement by means of wavelength scanning heterodyne interferometry. Meas. Sci. Technol. 1998, 9, 1031–1035. [Google Scholar] [CrossRef]
- Cabral, A.; Rebordão, J. Accuracy of frequency-sweeping interferometry for absolute distance metrology. Opt. Eng. 2007, 46, 073602. [Google Scholar] [CrossRef]
- Kinder, T.; Salewski, K.D. Absolute distance interferometer with grating-stabilized tunable diode laser at 633 nm. J. Opt. A Pure Appl. Opt. 2002, 4, S364–S368. [Google Scholar] [CrossRef]
- Swinkels, B.L.; Bhattacharya, N.; Braat, J.J.M. Correcting movement errors in frequency-sweeping interferometry. Opt. Lett. 2005, 30, 2242–2244. [Google Scholar] [CrossRef]
- Kikuta, H.; Iwata, K.; Nagata, R. Distance measurement by the wavelength shift of laser diode light. Appl. Opt. 1986, 25, 2976–2980. [Google Scholar] [CrossRef] [PubMed]
- Satyan, N.; Vasilyev, A.; Rakuljic, G.; Leyva, V.; Yariv, A. Precise control of broadband frequency chirps using optoelectronic feedback. Opt. Express 2009, 17, 15991. [Google Scholar] [CrossRef]
- Iiyama, K.; Matsui, S.I.; Kobayashi, T.; Maruyama, T. High-Resolution FMCW Reflectometry Using a Single-Mode Vertical-Cavity Surface-Emitting Laser. IEEE Photonics Technol. Lett. 2011, 23, 703–705. [Google Scholar] [CrossRef]
- Baumann, E.; Giorgetta, F.R.; Deschênes, J.D.; Swann, W.C.; Coddington, I.; Newbury, N.R. Comb-calibrated laser ranging for three-dimensional surface profiling with micrometer-level precision at a distance. Opt. Express 2014, 22, 24914. [Google Scholar] [CrossRef]
- Liyama, K.; Wang, L.T.; Hayashi, K. Linearizing Optical Frequency-Sweep of a Laser Diode for FMCW Reflectometry. J. Light. Technol. 1996, 14, 173. [Google Scholar] [CrossRef]
- Greiner, C.; Boggs, B.; Wang, T.; Mossberg, T.W. Laser frequency stabilization by means of optical self-heterodyne beat-frequency control. Opt. Lett. 1998, 23, 1280–1282. [Google Scholar] [CrossRef] [PubMed]
- Gorju, G.; Jucha, A.; Jain, A.; Crozatier, V.; Lorgeré, I.; Le Gouët, J.L.; Bretenaker, F.; Colice, M. Active stabilization of a rapidly chirped laser by an opto-electronic digital servo-loop control. Opt. Lett. 2007, 32, 484–486. [Google Scholar] [CrossRef]
- Satyan, N.; Vasilyev, A.; Rakuljic, G.; White, J.O.; Yariv, A. Phase-locking and coherent power combining of broadband linearly chirped optical waves. Opt. Express 2012, 20, 25213. [Google Scholar] [CrossRef]
- Roos, P.A.; Reibel, R.R.; Berg, T.; Kaylor, B.; Barber, Z.W.; Babbitt, W.R. Ultrabroadband optical chirp linearization for precision metrology applications. Opt. Lett. 2009, 34, 3692. [Google Scholar] [CrossRef] [PubMed]
- Barber, Z.W.; Giorgetta, F.R.; Roos, P.A.; Coddington, I.; Dahl, J.R.; Reibel, R.R.; Greenfield, N.; Newbury, N.R. Characterization of an actively linearized ultrabroadband chirped laser with a fiber-laser optical frequency comb. Opt. Lett. 2011, 36, 1152. [Google Scholar] [CrossRef] [PubMed]
- Mateo, A.B.; Barber, Z.W. Precision and accuracy testing of FMCW ladar-based length metrology. Appl. Opt. 2015, 54, 6019. [Google Scholar] [CrossRef]
- Mateo, A.B.; Barber, Z.W. Multi-dimensional, non-contact metrology using trilateration and high resolution FMCW ladar. Appl. Opt. 2015, 54, 5911. [Google Scholar] [CrossRef]
- Qin, J.; Zhou, Q.; Xie, W.; Xu, Y.; Yu, S.; Liu, Z.; Tong, Y.t.; Dong, Y.; Hu, W. Coherence enhancement of a chirped DFB laser for frequency-modulated continuous-wave reflectometry using a composite feedback loop. Opt. Lett. 2015, 40, 4500. [Google Scholar] [CrossRef] [PubMed]
- Danielson, B.L.; Boisrobert, C.Y. Absolute optical ranging using low coherence interferometry. Appl. Opt. 1991, 30, 2975–2979. [Google Scholar] [CrossRef]
- Pavlíček, P.; Häusler, G. White-light interferometer with dispersion: An accurate fiber-optic sensor for the measurement of distance. Appl. Opt. 2005, 44, 2978. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, A.; Huang, H. Development of an in-fiber white-light interferometric distance sensor for absolute measurement of arbitrary small distances. Appl. Opt. 2008, 47, 2821–2828. [Google Scholar] [CrossRef] [PubMed]
- Ullmann, V.; Emam, S.; Manske, E. White-light interferometers with polarizing optics for length measurements with an applicable zero-point detection. Meas. Sci. Technol. 2015, 26, 084010. [Google Scholar] [CrossRef]
- Lv, H.; Kong, X.; Ren, J.; Zhao, X.; Sun, C. Research on Real-Time Monitoring of Strain Behavior of Concrete under Freezing-Thawing Cycle by White Light Interferometer. Adv. Mater. Sci. Eng. 2022, 2022, 8049092. [Google Scholar] [CrossRef]
- Hu, J.; Yuan, Q.; Yu, H.; Wang, S.; Sun, Y.; Gao, Z. Assembly Error Tolerance of Interferometer Plate in Mirau Interference-Microscope Objective. Chin. J. Lasers 2019, 46, 0904001. [Google Scholar] [CrossRef]
- Koch, A.; Ulrich, R. Fiber-optic displacement sensor with 0.02 µm resolution by white-light interferometry. Sens. Actuators A Phys. 1990, 25, 201–207. [Google Scholar] [CrossRef]
- Winarno, A.; Masuda, S.; Takahashi, S.; Matsumoto, H.; Takamasu, K. Noncontact method of point-to-point absolute distance measurement using tandem low-coherence interferometry. Meas. Sci. Technol. 2018, 29, 025006. [Google Scholar] [CrossRef]
- Niehues, J.; Lehmann, P.; Bobey, K. Dual-wavelength vertical scanning low-coherence interferometric microscope. Appl. Opt. 2007, 46, 7141–7148. [Google Scholar] [CrossRef] [PubMed]
- Niehues, J.; Lehmann, P. Improvement of lateral resolution and reduction of batwings in vertical scanning white-light interferometry. In Proceedings of the Optical Measurement Systems for Industrial Inspection VII; Lehmann, P.H., Osten, W., Gastinger, K., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2011; Volume 8082, p. 80820W. [Google Scholar] [CrossRef]
- Lehmann, P.; Xie, W.; Kühnhold, P.; Niehues, J. Interferometric measurement of functional surfaces. In Proceedings of the International Conference on Optics in Precision Engineering and Nanotechnology (icOPEN2013); Quan, C., Qian, K., Asundi, A., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2013; Volume 8769, p. 876904. [Google Scholar] [CrossRef]
- Tapilouw, A.M.; Chang, Y.W.; Yu, L.Y.; Wang, H.W. Reduction of batwing effect in white light interferometry for measurement of patterned sapphire substrates (PSS) wafer. In Proceedings of the Interferometry XVIII; Creath, K., Burke, J., Albertazzi Gonçalves, A., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2016; Volume 9960, p. 996006. [Google Scholar] [CrossRef]
- Allendorf, B.; Käkel, E.; Ha, U.M.; Hagemeier, S.; Hillmer, H.; Lehmann, P. Adaptive high-resolution Linnik interferometry for 3D measurement of microparticles. Opt. Lett. 2019, 44, 3550. [Google Scholar] [CrossRef] [PubMed]
- Chong, W.K.; Li, X.; Soh, Y.C. Harnessing spectral property of dual wavelength white LED to improve vertical scanning interferometry. Appl. Opt. 2013, 52, 4652. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; LIGO Scientific Collaboration; Virgo Collaboration; et al. The Virgo Collaboration GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Observation of gravitational waves from two neutron star–black hole coalescences. Astrophys. J. Lett. 2021, 915, L5. [Google Scholar] [CrossRef]
- Smith, J.R.; for the LIGO Scientific Collaboration. The path to the enhanced and advanced LIGO gravitational-wave detectors. Class. Quantum Gravity 2009, 26, 114013. [Google Scholar] [CrossRef]
- Harry, G.M.; for the LIGO Scientific Collaboration. Advanced LIGO: The next generation of gravitational wave detectors. Class. Quantum Gravity 2010, 27, 084006. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2014, 32, 024001. [Google Scholar] [CrossRef]
- Wang, Z.B.; Shi, G.H.; He, Y.; Ding, Z.H.; Zhang, Y.D. Application of optical coherence tomography to distance measurement of optical surface. Opt. Precis. Eng. 2012, 20, 1469–1474. [Google Scholar] [CrossRef]
- Schmitt, J.M. Optical coherence tomography (OCT): A review. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 1205–1215. [Google Scholar] [CrossRef]
- Sampson, D.D. Trends and prospects for optical coherence tomography. In Proceedings of the Second European Workshop on Optical Fibre Sensors; Lopez-Higuera, J.M., Culshaw, B., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2004; Volume 5502, pp. 25–32. [Google Scholar] [CrossRef]
- Standish, B.A.; Mariampillai, A.; Leung, M.K.K.; Vitkin, I.A. Optical Coherence Tomography: Principles and Applications of Microvascular Imaging. In Handbook of Coherent-Domain Optical Methods; Tuchin, V.V., Ed.; Springer: New York, NY, USA, 2013; p. 945. [Google Scholar] [CrossRef]
- Fercher, A.F.; Hitzenberger, C.K.; Kamp, G.; El-Zaiat, S.Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- Yasuno, Y.; Madjarova, V.D.; Makita, S.; Akiba, M.; Morosawa, A.; Chong, C.; Sakai, T.; Chan, K.P.; Itoh, M.; Yatagai, T. Three-dimensional and high-speed swept-source optical coherence tomography for in vivo investigation of human anterior eye segments. Opt. Express 2005, 13, 10652. [Google Scholar] [CrossRef] [PubMed]
- Savini, G.; Barboni, P.; Carbonelli, M.; Sbreglia, A.; Deluigi, G.; Parisi, V. Comparison of Optic Nerve Head Parameter Measurements Obtained by Time-domain and Spectral-domain Optical Coherence Tomography. J. Glaucoma 2013, 22, 384–389. [Google Scholar] [CrossRef] [PubMed]
- Keane, P.A.; Bhatti, R.A.; Brubaker, J.W.; Liakopoulos, S.; Sadda, S.R.; Walsh, A.C. Comparison of Clinically Relevant Findings from High-Speed Fourier-Domain and Conventional Time-Domain Optical Coherence Tomography. Am. J. Ophthalmol. 2009, 148, 242–248.e1. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.S.; Li, K.Z.; Lim, T.H. Calculating the predicted retinal thickness from spectral domain and time domain optical coherence tomography–comparison of different methods. Graefe’s Arch. Clin. Exp. Ophthalmol. 2014, 252, 1491–1499. [Google Scholar] [CrossRef]
- Schrems, W.A.; Schrems-Hoesl, L.M.; Bendschneider, D.; Mardin, C.Y.; Laemmer, R.; Kruse, F.E.; Horn, F.K. Predicted and Measured Retinal Nerve Fiber Layer Thickness From Time-Domain Optical Coherence Tomography Compared with Spectral-Domain Optical Coherence Tomography. JAMA Ophthalmol. 2015, 133, 1135. [Google Scholar] [CrossRef]
- Vergnole, S.; Lévesque, D.; Lamouche, G.; Dufour, M.; Gauthier, B. Characterization of Thin Layered Structures Using Deconvolution Techniques in Time-Domain and Fourier-Domain Optical Coherence Tomography. SPIE: Bellingham, WA, USA, 2007; Volume 6796, p. 7961H. [Google Scholar] [CrossRef]
- de Boer, J.F.; Cense, B.; Park, B.H.; Pierce, M.C.; Tearney, G.J.; Bouma, B.E. Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography. Opt. Lett. 2003, 28, 2067–2069. [Google Scholar] [CrossRef] [PubMed]
- Öhnell, H.M.; Heijl, A.; Bengtsson, B. Ageing and glaucoma progression of the retinal nerve fibre layer using spectral-domain optical coherence tomography analysis. Acta Ophthalmol. 2021, 99, 260–268. [Google Scholar] [CrossRef]
- Jiang, Z.; Jiang, Z.; Ding, H. Optical coherence tomography for laser welding applications. Optik 2022, 257, 168784. [Google Scholar] [CrossRef]
- Chen, S.; Ni, S.; Jiménez-Villar, A.; Jian, Y.; Jia, Y.; Huang, D. Optical coherence tomography split-spectrum amplitude-decorrelation optoretinography. Opt. Lett. 2023, 48, 3921. [Google Scholar] [CrossRef]
- Chinn, S.R.; Swanson, E.A.; Fujimoto, J.G. Optical coherence tomography using a frequency-tunable optical source. Opt. Lett. 1997, 22, 340–342. [Google Scholar] [CrossRef] [PubMed]
- Wartak, A.; Schenk, M.S.; Bühler, V.; Kassumeh, S.A.; Birngruber, R.; Tearney, G.J. Micro-optical coherence tomography for high-resolution morphologic imaging of cellular and nerval corneal micro-structures. Biomed. Opt. Express 2020, 11, 5920. [Google Scholar] [CrossRef]
- Auksorius, E.; Borycki, D.; Stremplewski, P.; Lizewski, K.; Tomczewski, S.; Niedzwiedziuk, P.; Sikorski, B.L.; Wojtkowski, M. In vivo imaging of human cornea with high-speed and high-resolution Fourier-domain full-field optical coherence tomography. arXiv 2020, arXiv:2003.12085. [Google Scholar] [CrossRef]
- Jones, D.J.; Diddams, S.A.; Ranka, J.K.; Stentz, A.; Windeler, R.S.; Hall, J.L.; Cundiff, S.T. Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis. Science 2000, 288, 635–639. [Google Scholar] [CrossRef]
- Wu, G.; Liao, L.; Xiong, S.; Li, G.; Gai, Z.; Zhu, Z. Synthetic wavelength interferometry of an optical frequency comb for absolute distance measurement. Sci. Rep. 2018, 8, 4362. [Google Scholar] [CrossRef]
- Wang, G.; Jang, Y.S.; Hyun, S.; Chun, B.J.; Kang, H.J.; Yan, S.; Kim, S.W.; Kim, Y.J. Absolute positioning by multi-wavelength interferometry referenced to the frequency comb of a femtosecond laser. Opt. Express 2015, 23, 9121. [Google Scholar] [CrossRef] [PubMed]
- Joo, K.N.; Kim, S.W. Absolute distance measurement by dispersive interferometry using a femtosecond pulse laser. Opt. Express 2006, 14, 5954–5960. [Google Scholar] [CrossRef]
- Ye, J. Absolute measurement of a long, arbitrary distance to less than an optical fringe. Opt. Lett. 2004, 29, 1153–1155. [Google Scholar] [CrossRef] [PubMed]
- Cui, M.; Schouten, R.N.; Bhattacharya, N.; van den Berg, S.A. Experimental demonstration of distance measurement with a femtosecond frequency comb laser. J. Eur. Opt. Soc.-Rapid Publ. 2008, 3, 08003. [Google Scholar] [CrossRef]
- Cui, M.; Zeitouny, M.G.; Bhattacharya, N.; van den Berg, S.A.; Urbach, H.P.; Braat, J.J.M. High-accuracy long-distance measurements in air with a frequency comb laser. Opt. Lett. 2009, 34, 1982. [Google Scholar] [CrossRef]
- Kim, Y.J. Laser ranging by time-of-flight measurement of femtosecond light pulses. Meas. Sci. Technol. 2014, 23, 217. [Google Scholar] [CrossRef]
- Wei, D.; Takahashi, S.; Takamasu, K.; Matsumoto, H. Time-of-flight method using multiple pulse train interference as a time recorder. Opt. Express 2011, 19, 4881. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yang, L.; Guo, Y.; Lin, J.; Cui, P.; Zhu, J. Optimization methods of pulse-to-pulse alignment using femtosecond pulse laser based on temporal coherence function for practical distance measurement. Opt. Lasers Eng. 2018, 101, 35–43. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, Y.; Wang, X.; Zhang, F.; Wang, W.; Ma, X.; Wang, J.; Chen, J.; Jia, L.; Song, M.; et al. Optical ranging system based on multiple pulse train interference using soliton microcomb. Appl. Phys. Lett. 2021, 118, 261106. [Google Scholar] [CrossRef]
- Minoshima, K.; Matsumoto, H. High-Accuracy Measurement of 240-m Distance in an Optical Tunnel by use of a Compact Femtosecond Laser. Appl. Opt. 2000, 39, 5512–5517. [Google Scholar] [CrossRef] [PubMed]
- Minoshima, K. High-precision absolute length metrology using fiber-based optical frequency combs. In Proceedings of the 2010 International Conference on Electromagnetics in Advanced Applications, Sydney, Australia, 20–24 September 2010; Volume 28, pp. 800–802. [Google Scholar] [CrossRef]
- Minoshima, K.; Arai, K.; Inaba, H. High-accuracy self-correction of refractive index of air using two-color interferometry of optical frequency combs. Opt. Express 2011, 19, 26095. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Arai, K.; Takahashi, M.; Inaba, H.; Minoshima, K. High-accuracy correction of air refractive index by using two-color heterodyne interferometry of optical frequency combs. Meas. Sci. Technol. 2013, 24, 015203. [Google Scholar] [CrossRef]
- Wu, G.; Takahashi, M.; Arai, K.; Inaba, H.; Minoshima, K. CORRIGENDUM: Extremely high-accuracy correction of air refractive index using two-colour optical frequency combs. Sci. Rep. 2014, 4, 5789. [Google Scholar] [CrossRef]
- Doloca, N.R.; Meiners-Hagen, K.; Wedde, M.; Pollinger, F.; Abou-Zeid, A. Absolute distance measurement system using a femtosecond laser as a modulator. Meas. Sci. Technol. 2010, 21, 115302. [Google Scholar] [CrossRef]
- Jang, Y.S.; Lee, K.; Han, S.; Lee, J.; Kim, Y.J.; Kim, S.W. Absolute distance measurement with extension of nonambiguity range using the frequency comb of a femtosecond laser. Opt. Eng. 2014, 53, 122403. [Google Scholar] [CrossRef]
- Zhao, X.; Qu, X.; Zhang, F.; Zhao, Y.; Tang, G. Absolute distance measurement by multi-heterodyne interferometry using an electro-optic triple comb. Opt. Lett. 2018, 43, 807. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Wang, G.; Wang, Z.; Li, X.; Zhu, L.; Wang, W.; Zhang, W.; Yan, S.; Yang, J. Micrometer-precision absolute distance measurement with a repetition-rate-locked soliton microcomb. Opt. Lett. 2023, 48, 4356. [Google Scholar] [CrossRef]
- Jin, J.; Kim, Y.J.; Kim, Y.; Kim, S.W.; Kang, C.S. Absolute length calibration of gauge blocks using optical comb of a femtosecond pulse laser. Opt. Express 2006, 14, 5968. [Google Scholar] [CrossRef] [PubMed]
- Guochao, W.; Chunhua, W.; Shuhua, Y. Wavelength Selection and Non-Ambiguity Range Analysis for Optical-Comb-Referenced Multi-Wavelength Absolute Distance Measurement. Acta Opt. Sin. 2014, 34, 0412002. [Google Scholar] [CrossRef]
- Cui, M.; Zeitouny, M.G.; Bhattacharya, N.; van den Berg, S.A.; Urbach, H.P. Long distance measurement with femtosecond pulses using a dispersive interferometer. Opt. Express 2011, 19, 6549. [Google Scholar] [CrossRef]
- van den Berg, S.A.; van Eldik, S.; Bhattacharya, N. Mode-resolved frequency comb interferometry for high-accuracy long distance measurement. Sci. Rep. 2015, 5, 14661. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zhang, F.; Meng, F.; Liu, T.; Li, J.; Pan, L.; Qu, X. Absolute distance measurement in a combined-dispersive interferometer using a femtosecond pulse laser. Meas. Sci. Technol. 2016, 27, 015202. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, F.; Liu, T.; Meng, F.; Li, J.; Qu, X. Absolute distance measurement by chirped pulse interferometry using a femtosecond pulse laser. Opt. Express 2015, 23, 31582–31593. [Google Scholar] [CrossRef] [PubMed]
- Minoshima, K.; Matsumoto, H.; Zhang, Z.; Yagi, T. Simultaneous 3-D Imaging Using Chirped Ultrashort Optical Pulses. Jpn. J. Appl. Phys. 1994, 33, L1348. [Google Scholar] [CrossRef]
- Zhai, X.; Meng, Z.; Zhang, H.; Xu, X.; Qian, Z.; Xue, B.; Wu, H. Underwater distance measurement using frequency comb laser. Opt. Express 2019, 27, 6757–6769. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photonics 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Liu, T.A.; Newbury, N.R.; Coddington, I. Sub-micron absolute distance measurements in sub-millisecond times with dual free-running femtosecond Er fiber-lasers. Opt. Express 2011, 19, 18501. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Han, S.; Lee, K.; Bae, E.; Kim, S.; Lee, S.; Kim, S.W.; Kim, Y.J. Absolute distance measurement by dual-comb interferometry with adjustable synthetic wavelength. Meas. Sci. Technol. 2013, 24, 045201. [Google Scholar] [CrossRef]
- Wang, G.; Yan, S.; Yang, J.; Lin, C.; Yang, D.; Zou, P. Analysis of an innovative method for large-scale high-precision absolute distance measurement based on multi-heterodyne interference of dual optical frequency combs. Sensors 2013, 62, 070601. [Google Scholar] [CrossRef]
- Li, Y.; Cai, Y.; Li, R.; Shi, H.; Tian, H.; He, M.; Song, Y.; Hu, M. Large-scale absolute distance measurement with dual free-running all-polarization-maintaining femtosecond fiber lasers. Chin. Opt. Lett. 2019, 17, 091202. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, G.; Ni, K.; Zhou, Q.; Wu, G. Synthetic-wavelength-based dual-comb interferometry for fast and precise absolute distance measurement. Opt. Express 2018, 26, 5747. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Ni, K.; Zhou, Q.; Wu, G. Two-color phase-stable dual-comb ranging without precise environmental sensing. Opt. Express 2019, 27, 4660. [Google Scholar] [CrossRef]
- Kim, W.; Jang, J.; Han, S.; Kim, S.; Oh, J.S.; Kim, B.S.; Kim, Y.J.; Kim, S.W. Absolute laser ranging by time-of-flight measurement of ultrashort light pulses [Invited]. J. Opt. Soc. Am. A 2020, 37, B27. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, T.; Sun, J.; Reid, D.T. Dynamic measurements at up to 130-kHz sampling rates using Ti:sapphire dual-comb distance metrology. Opt. Express 2021, 29, 42119. [Google Scholar] [CrossRef]
- Jiang, R.; Zhou, S.; Wu, G. Aliasing-free dual-comb ranging system based on free-running fiber lasers. Opt. Express 2021, 29, 33527. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Kimura, A. A fast evaluation method for pitch deviation and out-of-flatness of a planar scale grating. CIRP Ann. 2010, 59, 505–508. [Google Scholar] [CrossRef]
- Xiong, X.; Shimizu, Y.; Chen, X.; Matsukuma, H.; Gao, W. Uncertainty evaluation for measurements of pitch deviation and out-of-flatness of planar scale gratings by a Fizeau interferometer in Littrow configuration. Appl. Sci. 2018, 8, 2539. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Y.; Hu, P.; Tan, J.; Fan, Z. Nonlinear errors resulting from ghost reflection and its coupling with optical mixing in heterodyne laser interferometers. Sensors 2018, 18, 758. [Google Scholar] [CrossRef] [PubMed]
- Hu, P.; Bai, Y.; Zhao, J.; Wu, G.; Tan, J. Toward a nonlinearity model for a heterodyne interferometer: Not based on double-frequency mixing. Opt. Express 2015, 23, 25935–25941. [Google Scholar] [CrossRef]
- Chang, D.; Xing, X.; Hu, P.; Wang, J.; Tan, J. Double-diffracted spatially separated heterodyne grating interferometer and analysis on its alignment tolerance. Appl. Sci. 2019, 9, 263. [Google Scholar] [CrossRef]
- Yang, Y.; Deng, Y.; Tan, Y.; Huang, Z.; Zhang, Y.; Wang, Y.; Zhang, S. Nonlinear error analysis and experimental measurement of Birefringence-Zeeman dual-frequency laser interferometer. Opt. Commun. 2019, 436, 264–268. [Google Scholar] [CrossRef]
- Li, X.; Shimizu, Y.; Ito, S.; Gao, W. Fabrication of scale gratings for surface encoders by using laser interference lithography with 405 nm laser diodes. Int. J. Precis. Eng. Manuf. 2013, 14, 1979–1988. [Google Scholar] [CrossRef]
- Li, X.; Lu, H.; Zhou, Q.; Wu, G.; Ni, K.; Wang, X. An orthogonal type two-axis Lloyd’s mirror for holographic fabrication of two-dimensional planar scale gratings with large area. Appl. Sci. 2018, 8, 2283. [Google Scholar] [CrossRef]
- Xue, G.; Zhai, Q.; Lu, H.; Zhou, Q.; Ni, K.; Lin, L.; Wang, X.; Li, X. Polarized holographic lithography system for high-uniformity microscale patterning with periodic tunability. Microsyst. Nanoeng. 2021, 7, 31. [Google Scholar] [CrossRef]
- Wang, G.; Xue, G.; Zhai, Q.; Zhu, J.; Yu, K.; Huang, G.; Wang, M.; Zhong, A.; Zhu, L.; Yan, S.; et al. Planar diffractive grating for magneto-optical trap application: Fabrication and testing. Appl. Opt. 2021, 60, 9358–9364. [Google Scholar] [CrossRef]
- Xue, G.; Lin, L.; Zhai, Q.; Zeng, C.; Wang, X.; Li, X. Development of dielectric-film-based polarization modulation scheme for patterning highly uniform 2d array structures with periodic tunability. Opt. Lasers Eng. 2023, 167, 107627. [Google Scholar] [CrossRef]
- Guan, J.; Köchert, P.; Weichert, C.; Köning, R.; Siaudinyte, L.; Flügge, J. A differential interferometric heterodyne encoder with 30 picometer periodic nonlinearity and sub-nanometer stability. Precis. Eng. 2017, 50, 114–118. [Google Scholar] [CrossRef]
- Fu, H.; Wang, Y.; Hu, P.; Yang, H.; Yang, R.; Xing, X.; Tan, J. Real-time compensation of nonlinearity in heterodyne interferometers based on quadrature demodulation and extremum operation. Opt. Eng. 2020, 59, 044101. [Google Scholar] [CrossRef]
- Wang, S.; Luo, L.; Li, X. Design and Parameter Optimization of Zero Position Code Considering Diffraction Based on Deep Learning Generative Adversarial Networks. Nanomanuf. Metrol. 2024, 7, 2. [Google Scholar] [CrossRef]
- Hu, P.; Wang, J.; Lin, X.; Xing, X.; Fu, H.; Tan, J. Phase Measurement Method Based on Digital Dual Frequency Comb for High-Precision High-Speed Heterodyne Interferometry. IEEE Sens. J. 2023, 23, 9707–9715. [Google Scholar] [CrossRef]
- Zhang, E.; Chen, B.; Zheng, H.; Teng, X. Laser heterodyne interference signal processing method based on phase shift of reference signal. Opt. Express 2018, 26, 8656–8668. [Google Scholar] [CrossRef]
- Han, Y.; Ni, K.; Li, X.; Wu, G.; Yu, K.; Zhou, Q.; Wang, X. An fpga platform for next-generation grating encoders. Sensors 2020, 20, 2266. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Yan, L.; Chen, B.; Liu, Y.; Tian, Q. Signal processing method of phase correction for laser heterodyne interferometry. Opt. Lasers Eng. 2014, 57, 93–100. [Google Scholar] [CrossRef]
- Zhang, E.; Chen, B.; Yan, L.; Yang, T.; Hao, Q.; Dong, W.; Li, C. Laser heterodyne interferometric signal processing method based on rising edge locking with high frequency clock signal. Opt. Express 2013, 21, 4638–4652. [Google Scholar] [CrossRef]
- Wang, C.; Ellis, J.D. Data age error compensation for nonconstant velocity metrology. IEEE Trans. Instrum. Meas. 2016, 65, 2601–2611. [Google Scholar] [CrossRef]




| Method | Advantages | Challenges |
|---|---|---|
| Homodyne Interferometry | Simple setup; Compact structure; Low cost; High accuracy and sensitivity. | Sensitive to ambient light and environment; Combined light intensity is not stable; High requirement for environment. |
| Heterodyne Interferometry | High signal-to-noise ratio; Strong anti-interference ability to the environment; High accuracy; Large dynamic range | Target speed is limited; periodic nonlinear error needs to be further reduced. |
| Fabry–Perot Interferometry | High sensitivity; miniaturization and light weight; Multiplexing ability; Low requirements on measurement environment. | The relative accuracy of the measurement is limited by the cavity length; Folding structure or optical fiber structure is required to extend the measurement range. |
| Self-mixing Interferometry | Simple and compact structure; Low cost; Easy to collimate; Not affected by light source coherence or laser type. | The system debugging is complicated; The measurement accuracy is affected by the laser modulation performance |
| Multi-wavelength Interferometry | Fast and accurate absolute length measurement ability; No measurement dead area; Retain the resolution and accuracy of single wavelength interferometry over a large scale. | High requirements for laser frequency stability and synchronous phase measurement accuracy; Reasonable selection of wavelength combinations to build a synthetic wavelength chain; Integrated high-performance multi-wavelength light source is required. |
| Frequency-sweeping Interferometry | No measurement dead zone; No need for cooperative targets; High signal-to-noise ratio; Capable of large-scale absolute length measurement | Susceptible to laser mode hopping, frequency modulation nonlinearity, and environmental vibration; Signal spectrum broadening caused by fiber dispersion mismatch; FFT transform spectrum leakage. |
| White Light Interferometry | No phase ambiguity; Applicable to a wide range of materials and surface types; Insensitive to environmental fluctuations. | Interference fringe clarity is affected by coherence length; Lateral crosstalk; Data processing is computationally intensive; Real-time performance is affected by scanning rate. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, G.; Cui, C.; Lei, X.; Li, Q.; Yan, S.; Li, X.; Wang, G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines 2025, 16, 6. https://doi.org/10.3390/mi16010006
Huang G, Cui C, Lei X, Li Q, Yan S, Li X, Wang G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines. 2025; 16(1):6. https://doi.org/10.3390/mi16010006
Chicago/Turabian StyleHuang, Guangyao, Can Cui, Xiaoyang Lei, Qixue Li, Shuhua Yan, Xinghui Li, and Guochao Wang. 2025. "A Review of Optical Interferometry for High-Precision Length Measurement" Micromachines 16, no. 1: 6. https://doi.org/10.3390/mi16010006
APA StyleHuang, G., Cui, C., Lei, X., Li, Q., Yan, S., Li, X., & Wang, G. (2025). A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines, 16(1), 6. https://doi.org/10.3390/mi16010006







