High-Precision Small-Signal Model for Double-Channel–High-Electron-Mobility Transistors Based on the Double-Channel Coupling Effect
Abstract
:1. Introduction
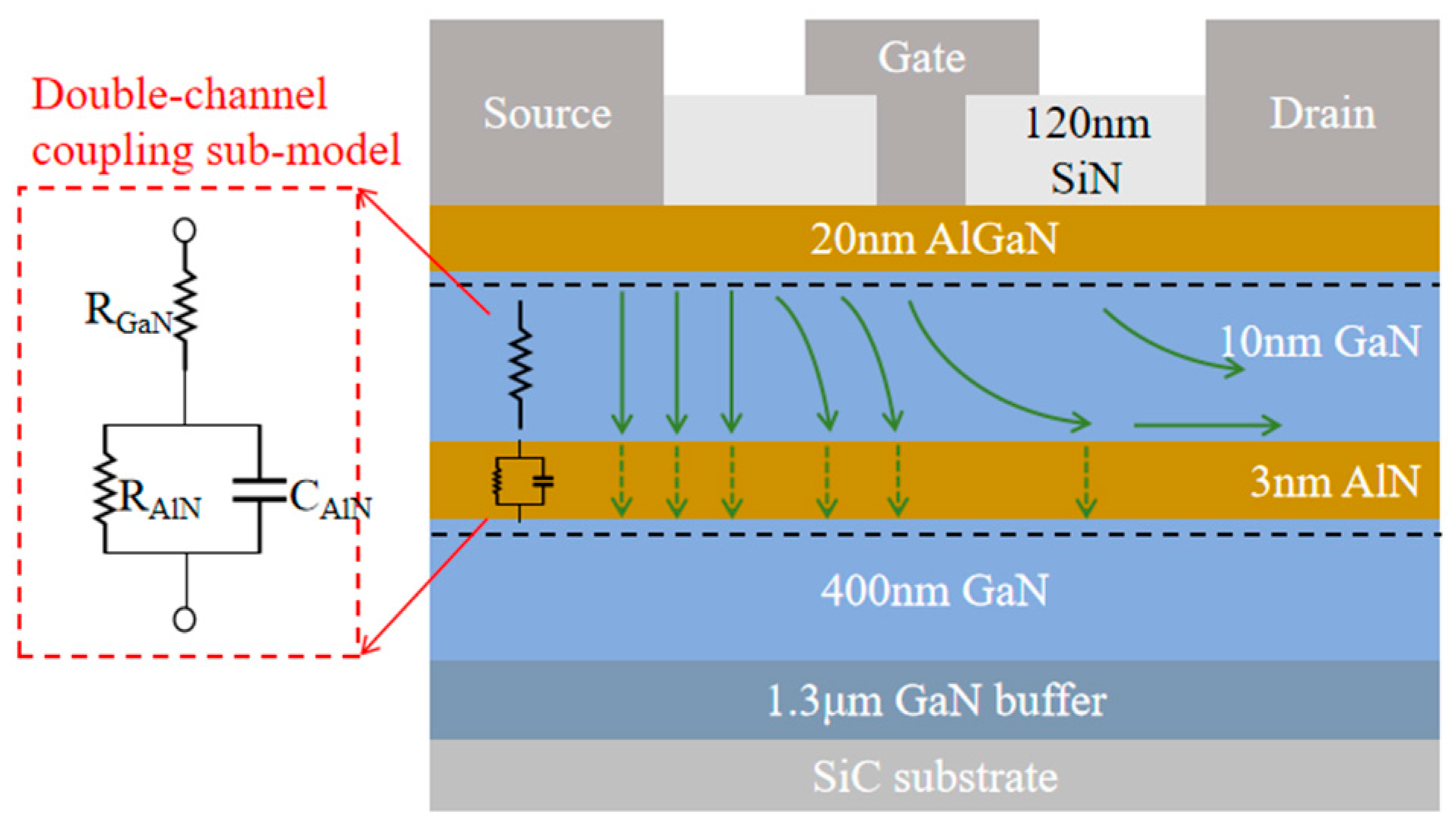
2. Device Structures and Process
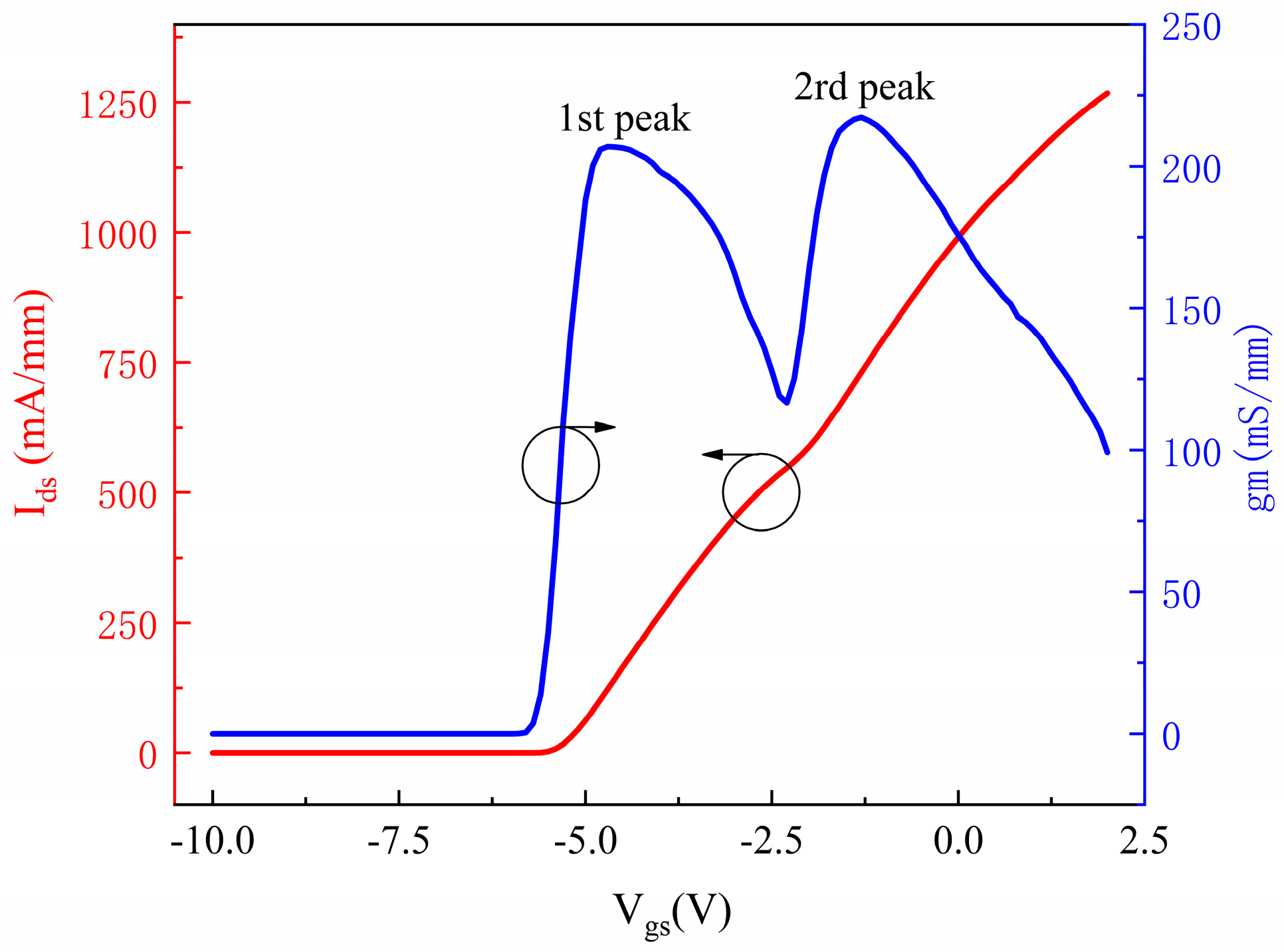
3. Measurement and Analysis
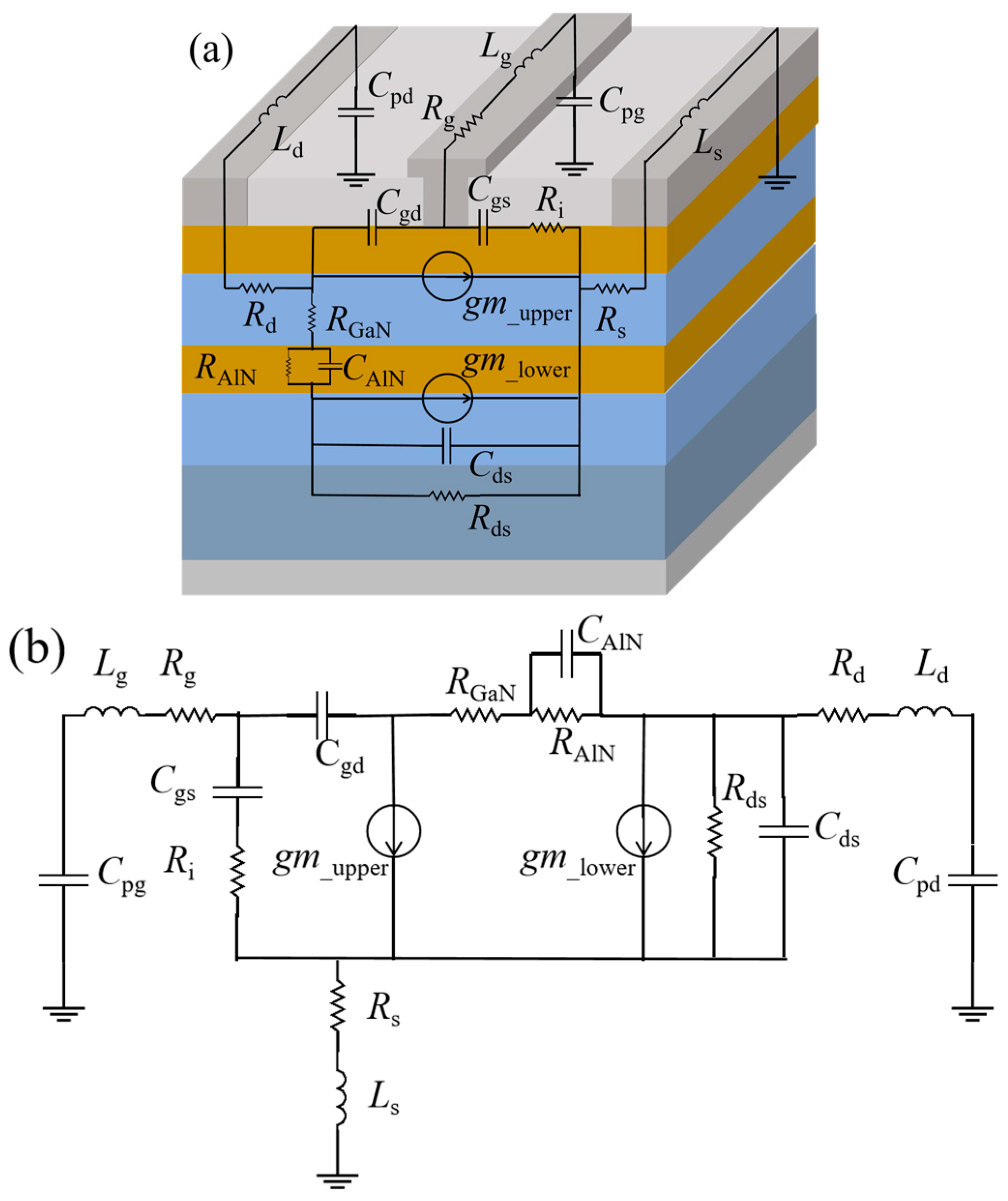
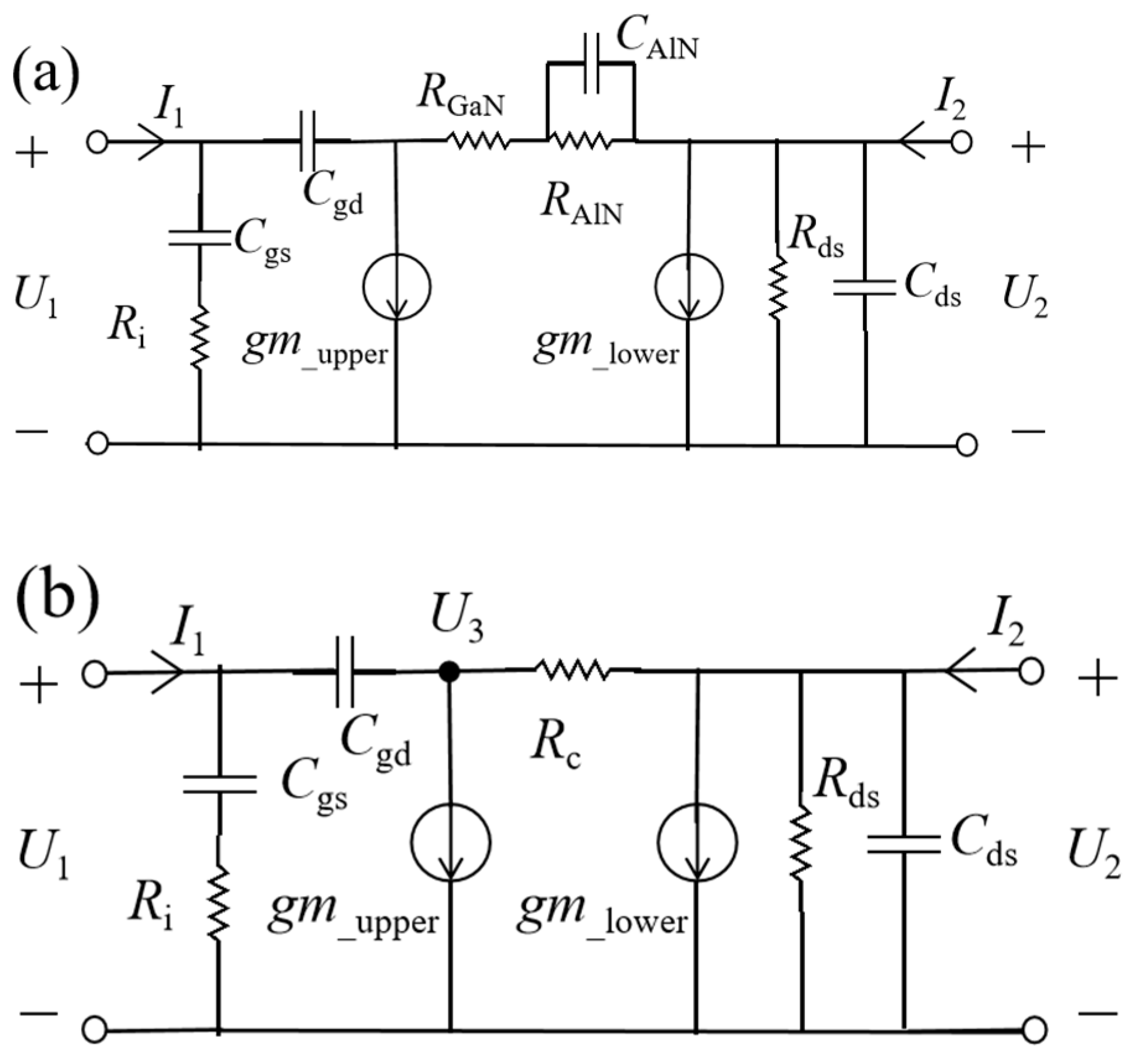
4. The New Small-Signal Model
4.1. Double-Channel Coupling Effect
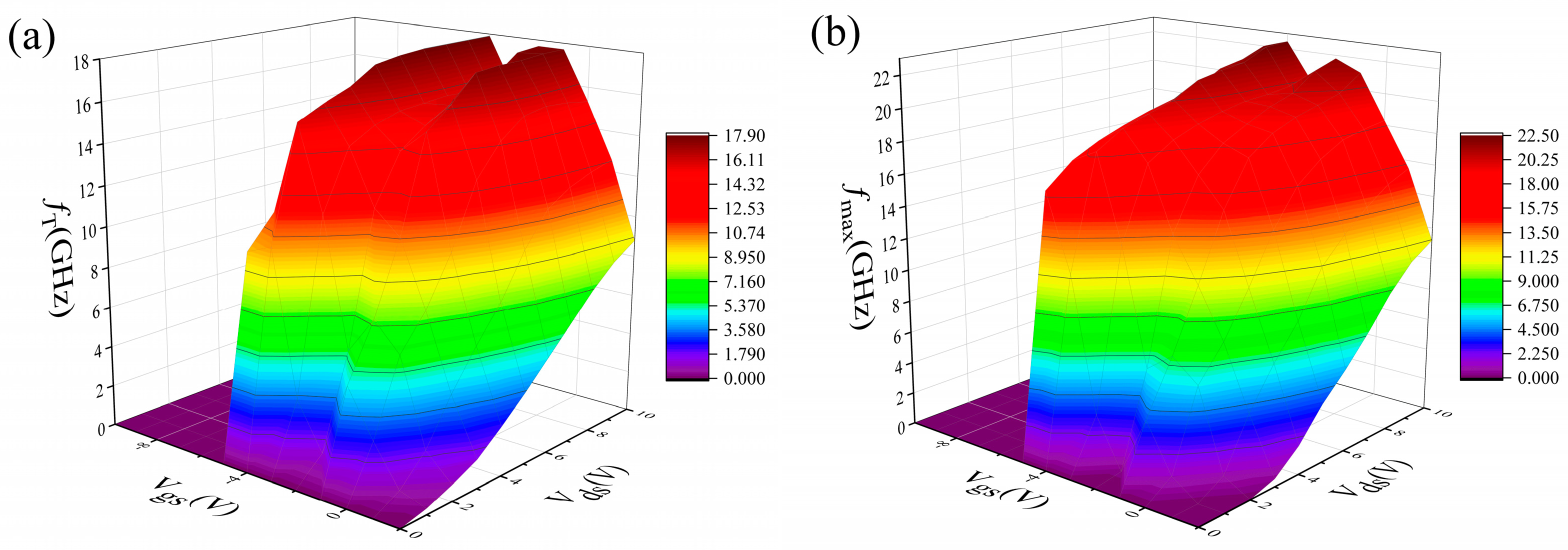
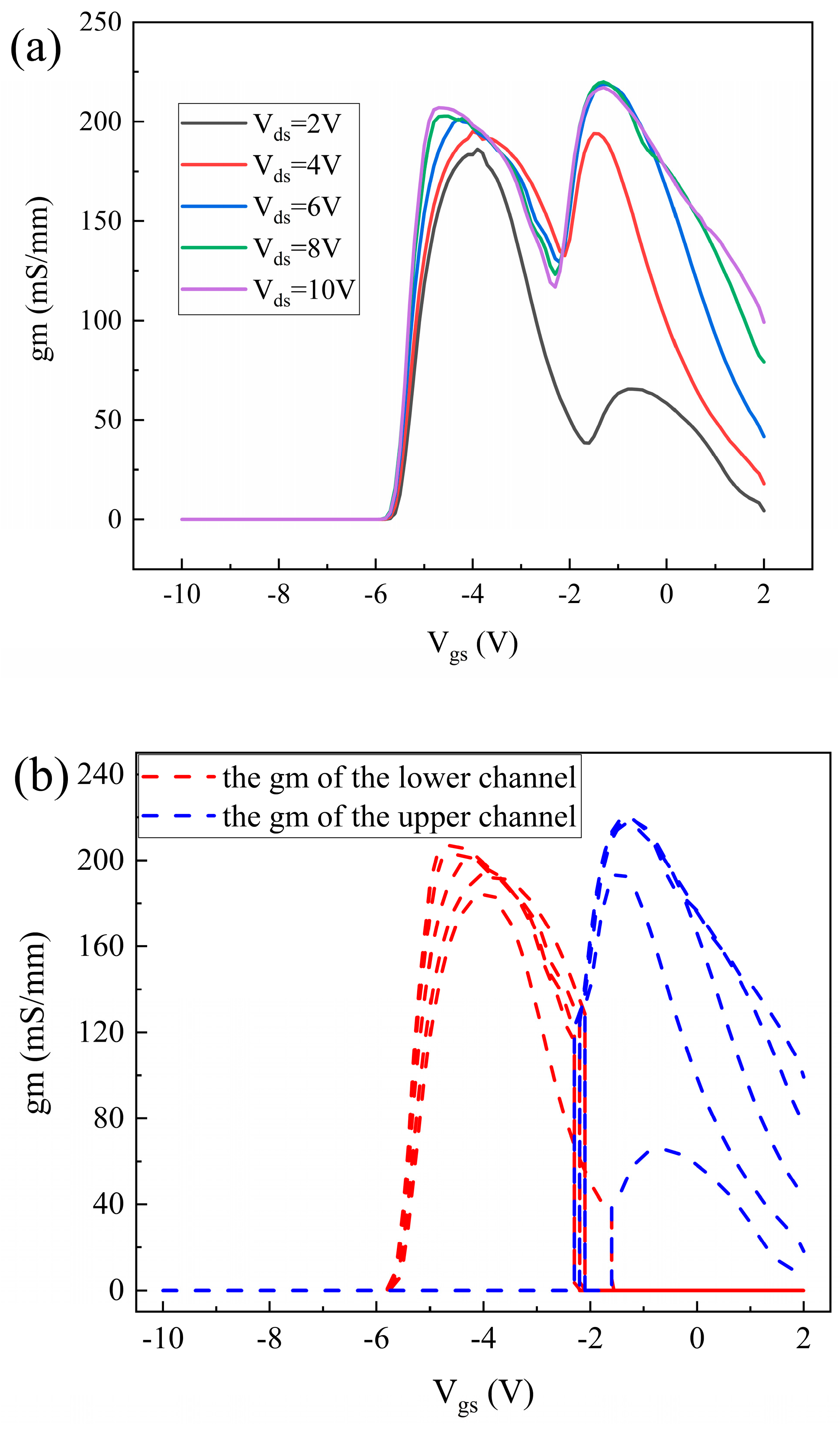
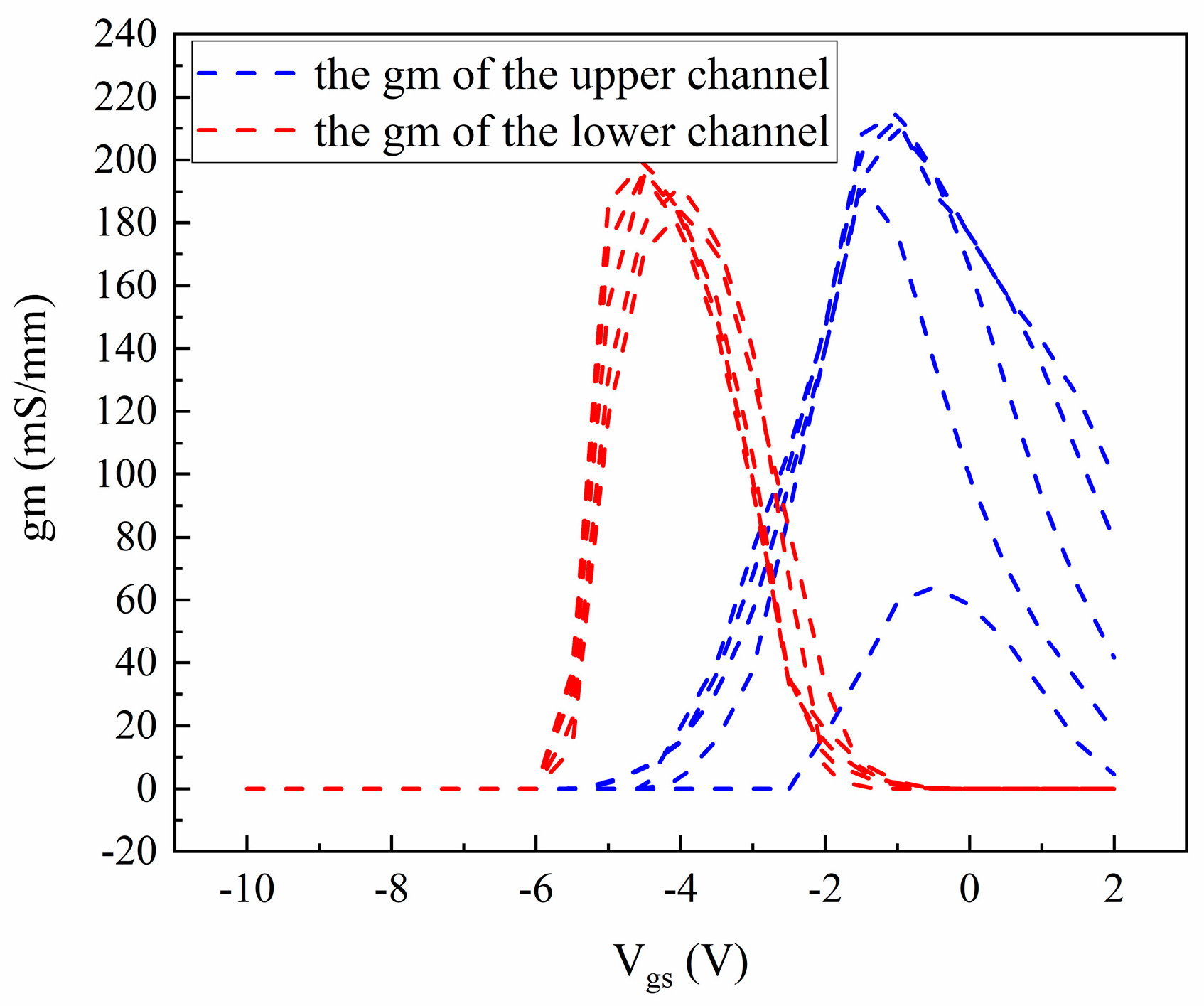
4.2. Device Simulation Results
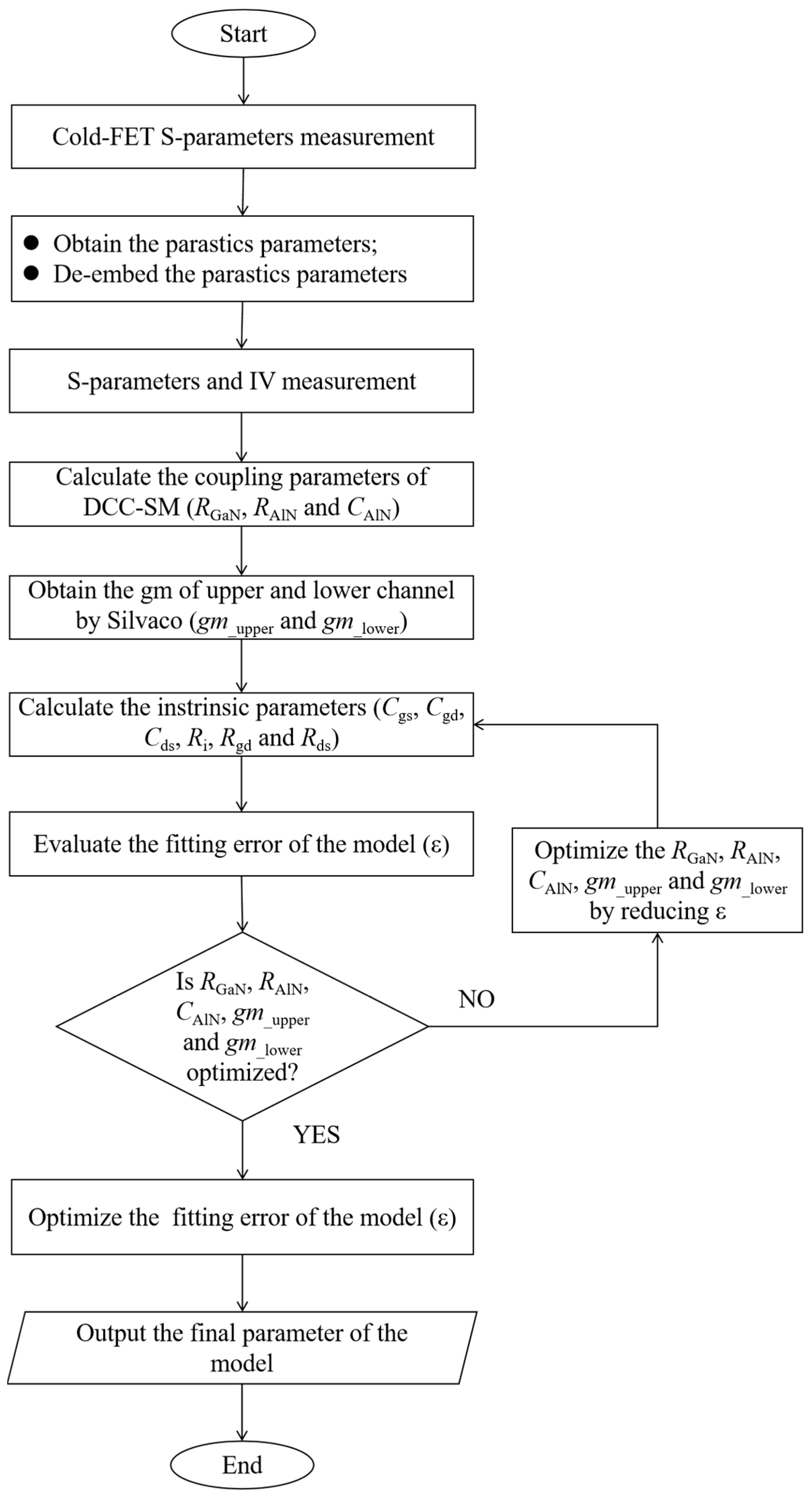
4.3. Extracting Model Parameters
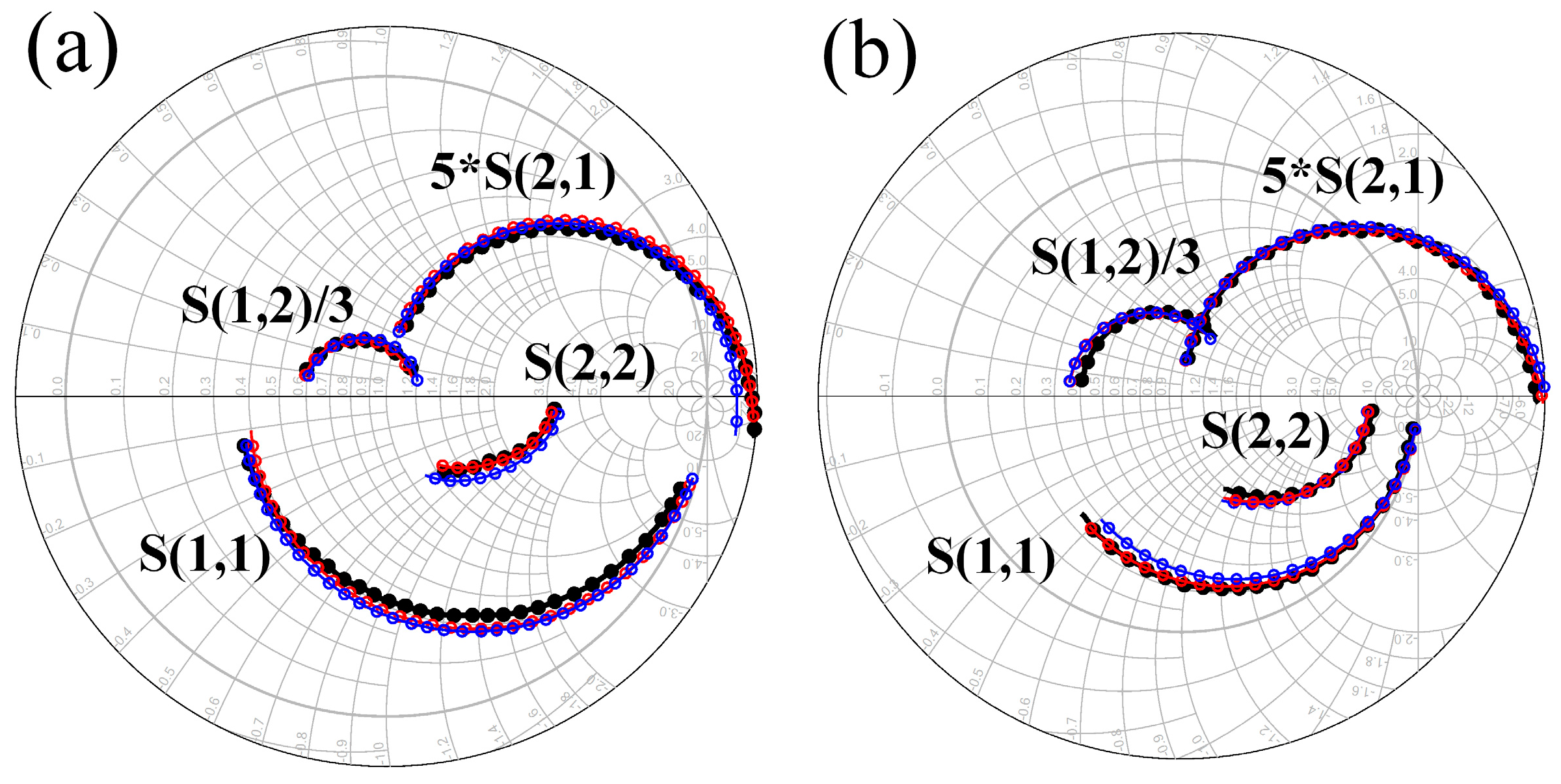
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shinohara, K.; Regan, D.C.; Tang, Y.; Corrion, A.L.; Brown, D.F.; Wong, J.C.; Robinson, J.F.; Fung, H.H.; Schmitz, A.; Oh, T.C.; et al. Scaling of GaN HEMTs and Schottky diodes for submillimeter-wave MMIC applications. IEEE Electron Device Lett. 2013, 60, 2982–2996. [Google Scholar] [CrossRef]
- Wu, S.; Gao, J.; Wang, W.; Zhang, J. W-band MMIC PA with ultrahigh power density in 100-nm AlGaN/GaN technology. IEEE Trans. Electron Devices 2016, 63, 3882–3886. [Google Scholar] [CrossRef]
- Xue, J.S.; Zhang, J.C.; Zhang, K.; Zhao, Y.; Zhang, L.; Ma, X.; Li, X.; Meng, F.; Hao, Y. Fabrication and characterization of InAlN/GaN-based double-channel high electron mobility transistors for electronic applications. J. Appl. Phys. 2012, 111, 2408. [Google Scholar] [CrossRef]
- Chung, J.W.; Hoke, W.E.; Chumbes, E.M.; Palacios, T. AlGaN/GaN HEMT with 300-GHz fmax. IEEE Electron Device Lett. 2010, 31, 195–197. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Zhang, J.; Han, Z.; You, S.; Chen, L.; Wang, L.; Li, Z.; Yang, W.; Chang, J.; et al. 1700 V High-Performance GaN HEMTs on 6-inch Sapphire with 1.5 μm Thin Buffer. IEEE Trans. Electron Devices 2024, 5, 84–87. [Google Scholar] [CrossRef]
- Palacios, T.; Chakraborty, A.; Rajan, S.; Poblenz, C.; Keller, S.; DenBaars, S.; Speck, J.; Mishra, U. High-power AlGaN/GaN HEMTs for Ka-band applications. IEEE Electron Device Lett. 2005, 26, 781–783. [Google Scholar] [CrossRef]
- Moon, J.S.; Wong, D.; Hu, M.; Hashimoto, P.; Antcliffe, M.; McGuire, C.; Micovic, M.; Willadson, P. 55% PAE and high power Ka-band GaN HEMTs with linearized transconductance via n+ GaN source contact ledge. IEEE Electron Device Lett. 2008, 29, 834–837. [Google Scholar] [CrossRef]
- Palacios, T.; Rajan, S.; Chakraborty, A.; Heikman, S. Influence of the Dynamic Access Resistance in the gm and fT Linearity of AlGaN/GaN HEMTs. IEEE Trans. Electron Devices 2005, 52, 2117–2123. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Bajaj, S.; Rajan, S. Amplified spontaneous emission of phonons as a likely mechanism for density-dependent velocity saturation in GaN transistors. Appl. Phys. Express 2016, 9, 094101. [Google Scholar] [CrossRef]
- Khalil, I.; Bahat-Treidel, E.; Schnieder, F.; Wurfl, J. Improving the linearity of GaN HEMTs by optimizing epitaxial structure. IEEE Trans. Electron Devices 2009, 56, 361–364. [Google Scholar] [CrossRef]
- Sohel, S.H.; Rahman, M.W.; Xie, A.; Beam, E.; Cui, Y.; Kruzich, M.; Xue, H.; Razzak, T.; Bajaj, S.; Cao, Y.; et al. Linearity improvement with AlGaN polarization-graded field effect transistors with low pressure chemical vapor deposi-tion grown SiNx passivation. IEEE Electron Device Lett. 2020, 41, 19–22. [Google Scholar] [CrossRef]
- Sohel, S.H.; Xie, A.; Beam, E.; Xue, H.; Roussos, J.A.; Razzak, T.; Bajaj, S.; Cao, Y.; Meyer, D.J.; Lu, W.; et al. X-band power and linearity performance of compositionally graded AlGaN channel transistors. IEEE Electron Device Lett. 2018, 39, 1884–1887. [Google Scholar] [CrossRef]
- Moon, J.S.; Wong, J.; Grabar, B.; Antcliffe, M.; Chen, P.; Arkun, E.; Khalaf, I.; Corrion, A.; Chappell, J.; Venkatesan, N.; et al. 360 GHz fMAX graded-channel AlGaN/GaN HEMTs for mmW low-noise applications. IEEE Electron Device Lett. 2020, 41, 1173–1176. [Google Scholar] [CrossRef]
- Yang, L.; Lu, H.; Zhang, M.; Niu, X.; Shi, C.; Hou, B.; Mi, M.; Wu, M.; Zhu, Q.; Lu, Y.; et al. Investigation on the Influence of Ohmic Structure on Channel-to-Channel Coupling Effect in InAlN/GaN Double Channel HEMTs. IEEE J. Electron Devices Soc. 2022, 10, 474–480. [Google Scholar] [CrossRef]
- Priyesh, K.; Jhuma, S. A Comprehensive analysis of Interlayer variabilities in double-channel AlGaN/GaN HEMT heterostructure. In Proceedings of the 2024 8th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), Bangalore, India, 3–6 March 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Wei, J.; Liu, S.; Li, B.; Tang, X.; Lu, Y.; Liu, C.; Hua, M.; Zhang, Z.; Tang, G.; Chen, K.J. Low on-resistance normally-off GaN double-channel metal-oxide-semiconductor high-electron-mobility transistor. IEEE Electron Device Lett. 2015, 36, 1287–1290. [Google Scholar] [CrossRef]
- Rahman, I.K.M.R.; Khan, M.I.; Khosru, Q.D.M. A rigorous investigation of electrostatic and transport phenomena of GaN double-channel HEMT. IEEE Trans. Electron Devices 2019, 66, 2923–2931. [Google Scholar] [CrossRef]
- Zhao, Z.; Lu, Y.; Yi, C.; Chen, Y.; Cai, X.; Zhang, Y.; Duan, X.; Ma, X.; Hao, Y. A fast small signal modeling method for GaN HEMTs. Solid-State Electron. 2021, 175, 107946. [Google Scholar] [CrossRef]
- Yadav, R.K.; Pathak, P.; Mehra, R.M. Small Signal Parameter Extraction and DC Simulation of Asymmetric Dual Channel AlGaN/GaN Heterojunction Field Effect Transistor. Indian J. Sci. Technol. 2017, 10, 16. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices; Wiley: New York, NY, USA, 1981; pp. 342–343. [Google Scholar]
- Jarndal, A.; Kompa, G. A new small-signal modeling approach applied to GaN devices. IEEE Trans. Microw. Theory Tech. 2005, 53, 3440–3448. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, C.; Sun, H.; Wen, Z.; Wu, Y.; Xu, R.; Yu, X.; Ren, C.; Wang, Z.; Zhang, B.; et al. A scalable large-signal multiharmonic model of AlGaN/GaN HEMTs and its application in C-band high power amplifier MMIC. IEEE Trans. Microw. Theory Techn. 2017, 65, 2836–2846. [Google Scholar] [CrossRef]
- Crupi, G.; Raffo, A.; Vadalà, V.; Vannini, G.; Schreurs, D.M.M.-P.; Caddemi, A. Scalability of multifinger HEMT performance. IEEE Microw. Wireless Compon. Lett. 2020, 30, 869–872. [Google Scholar] [CrossRef]

| Parameters | (Vgs = −1 V, Vds = 8 V) | (Vgs = −3 V, Vds = 6 V) |
|---|---|---|
| Cgs (F) | 2.85 × 10−13 | 1.14 × 10−13 |
| Cgd (F) | 8.68 × 10−14 | 5.57 × 10−14 |
| Cds (F) | 1.99 × 10−15 | 1.71 × 10−14 |
| Ri (Ω) | 14.86 | 5.61 |
| Rgd (Ω) | 21.24 | 12.93 |
| gds (S) | 7.15 × 10−3 | 2.51 × 10−3 |
| gm_upper (S) | 9.58 × 10−3 | 7.49 × 10−3 |
| gm_lower (S) | 1.86 × 10−3 | 6.93 × 10−2 |
| RGaN (Ω) | 6.12 | 1.53 |
| RAlN (Ω) | 14.88 | 2.17 |
| CAlN (F) | 10.01 × 10−14 | 9.03 × 10−12 |
| Error(ε) | (Vgs = −1 V, Vds = 8 V) | (Vgs = −3 V, Vds = 6V) | ||
|---|---|---|---|---|
| The New Model | The Traditional Model [18] | The New Model | The Traditional Model [18] | |
| ε(S11) | 1.61% | 4.12% | 1.92% | 3.28% |
| ε(S12) | 1.32% | 4.31% | 3.35% | 4.27% |
| ε(S21) | 3.10% | 9.68% | 4.73% | 8.42% |
| ε(S22) | 2.41% | 2.64% | 1.71% | 2.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Yu, Q.; Lu, Y.; Yi, C.; Liu, X.; Feng, T.; Zhao, W.; Chen, Y.; Yang, L.; Ma, X.; et al. High-Precision Small-Signal Model for Double-Channel–High-Electron-Mobility Transistors Based on the Double-Channel Coupling Effect. Micromachines 2025, 16, 200. https://doi.org/10.3390/mi16020200
Zhao Z, Yu Q, Lu Y, Yi C, Liu X, Feng T, Zhao W, Chen Y, Yang L, Ma X, et al. High-Precision Small-Signal Model for Double-Channel–High-Electron-Mobility Transistors Based on the Double-Channel Coupling Effect. Micromachines. 2025; 16(2):200. https://doi.org/10.3390/mi16020200
Chicago/Turabian StyleZhao, Ziyue, Qian Yu, Yang Lu, Chupeng Yi, Xin Liu, Ting Feng, Wei Zhao, Yilin Chen, Ling Yang, Xiaohua Ma, and et al. 2025. "High-Precision Small-Signal Model for Double-Channel–High-Electron-Mobility Transistors Based on the Double-Channel Coupling Effect" Micromachines 16, no. 2: 200. https://doi.org/10.3390/mi16020200
APA StyleZhao, Z., Yu, Q., Lu, Y., Yi, C., Liu, X., Feng, T., Zhao, W., Chen, Y., Yang, L., Ma, X., & Hao, Y. (2025). High-Precision Small-Signal Model for Double-Channel–High-Electron-Mobility Transistors Based on the Double-Channel Coupling Effect. Micromachines, 16(2), 200. https://doi.org/10.3390/mi16020200






