Optimization of Cutting Parameters to Minimize Wall Deformation in Micro-Milling of Thin-Wall Geometries
Abstract
:1. Introduction
2. Materials and Methods
2.1. Workpiece Material and Cutting Tool
2.2. Taguchi Optimisation Draft
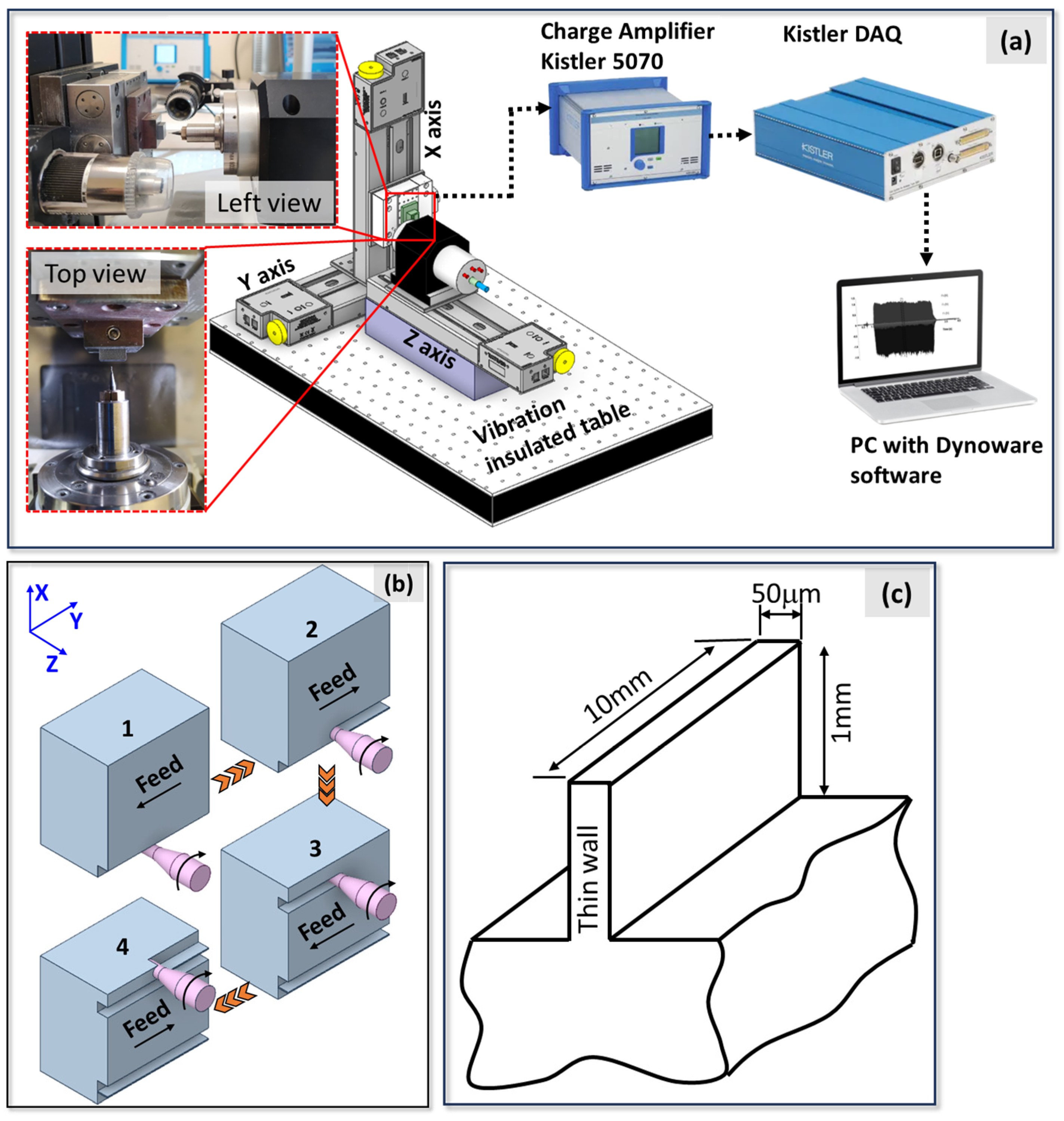
2.3. Experimental Setup
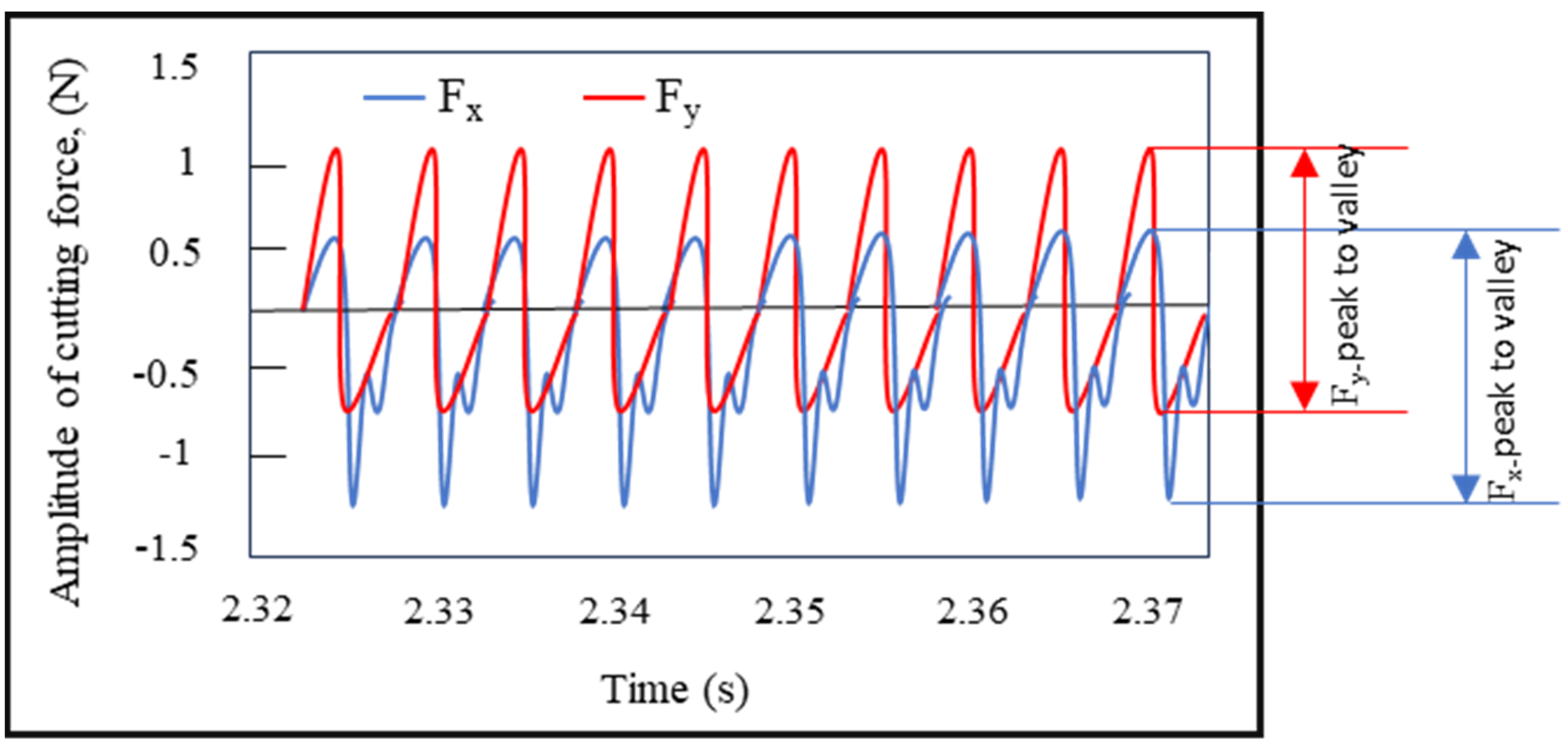
2.4. Deformation Measurement in Micro Thin Wall
3. Results and Discussion
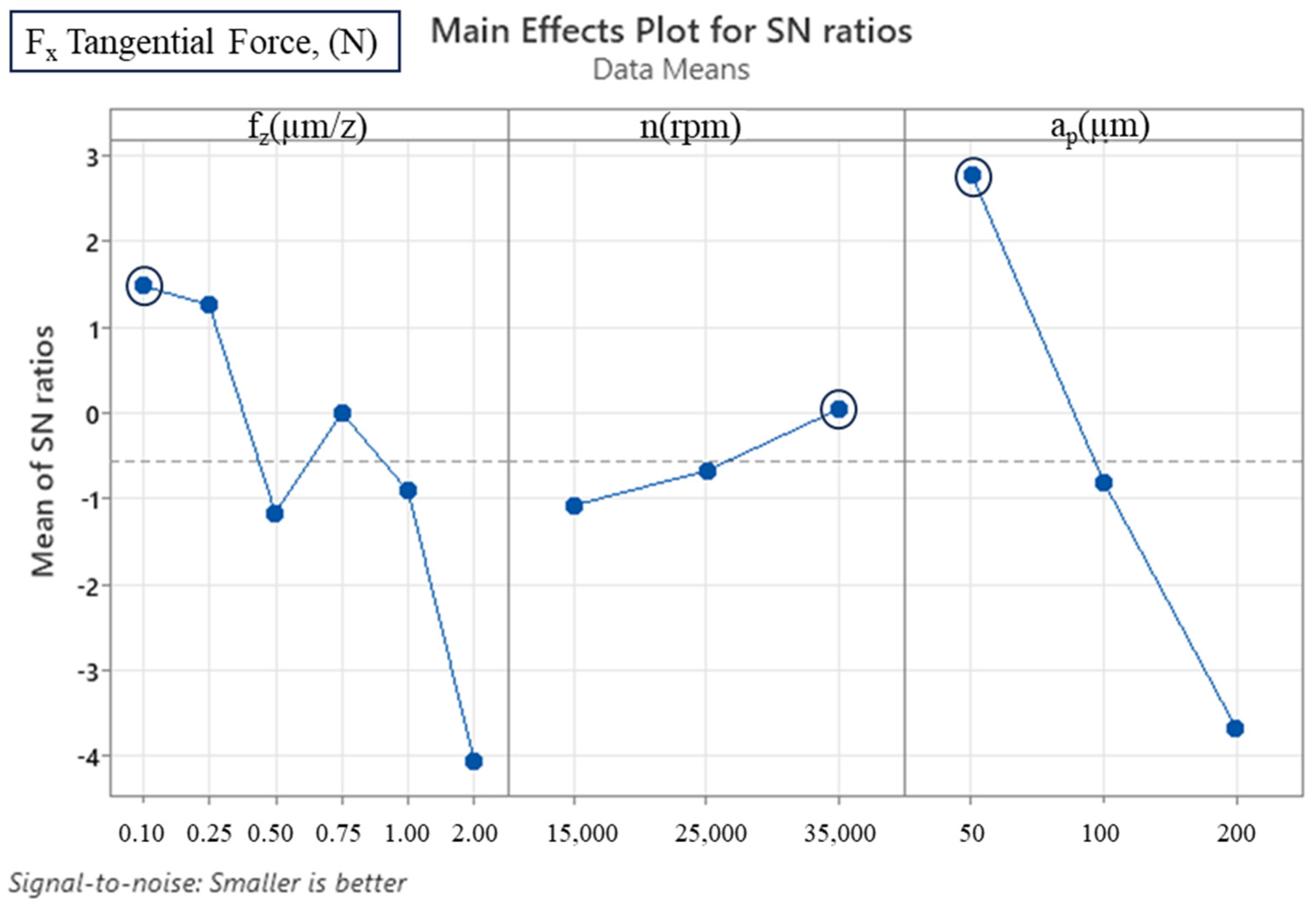
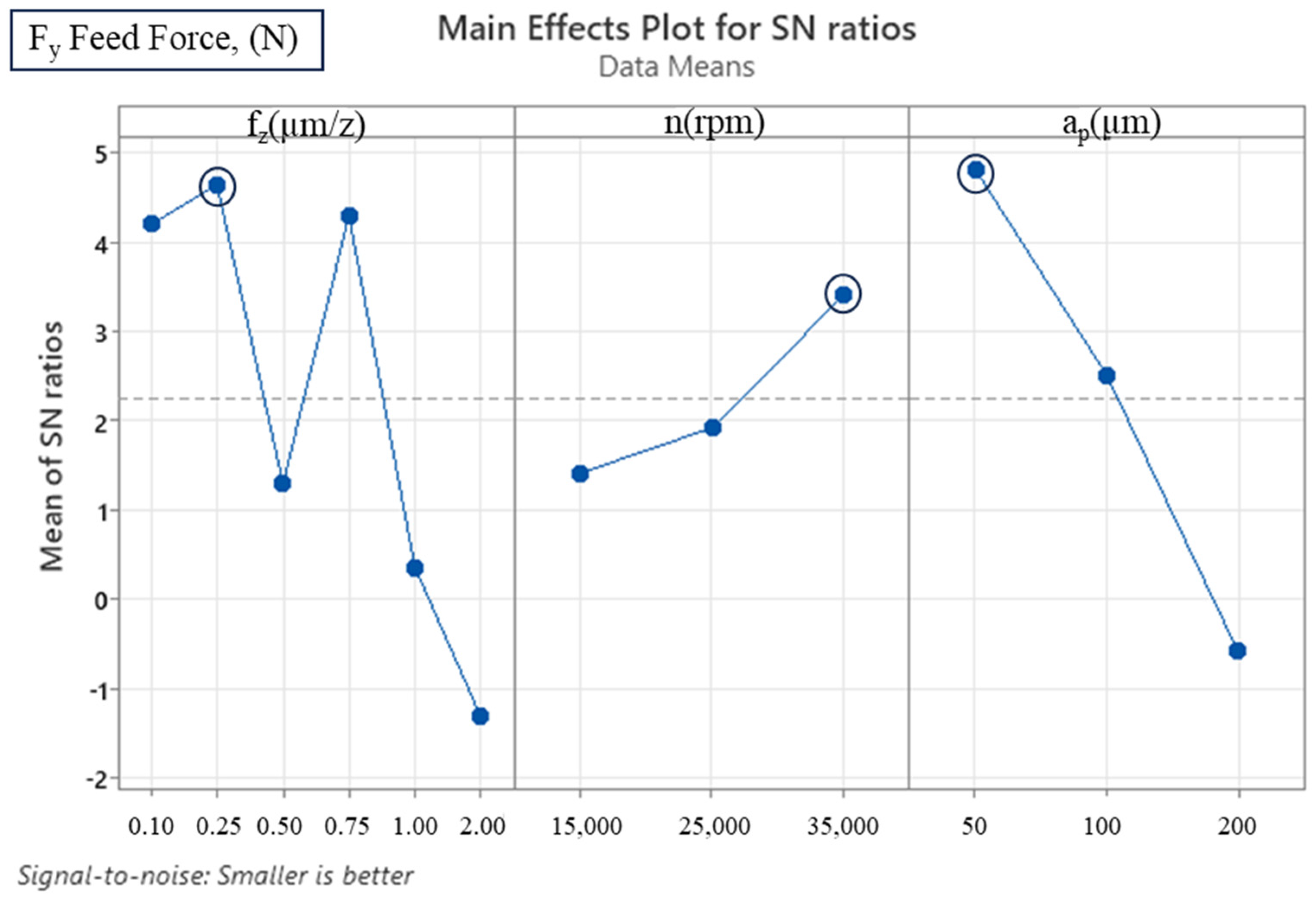
3.1. Signal-to-Noise (S/N) Ratio and ANOVA Analyses
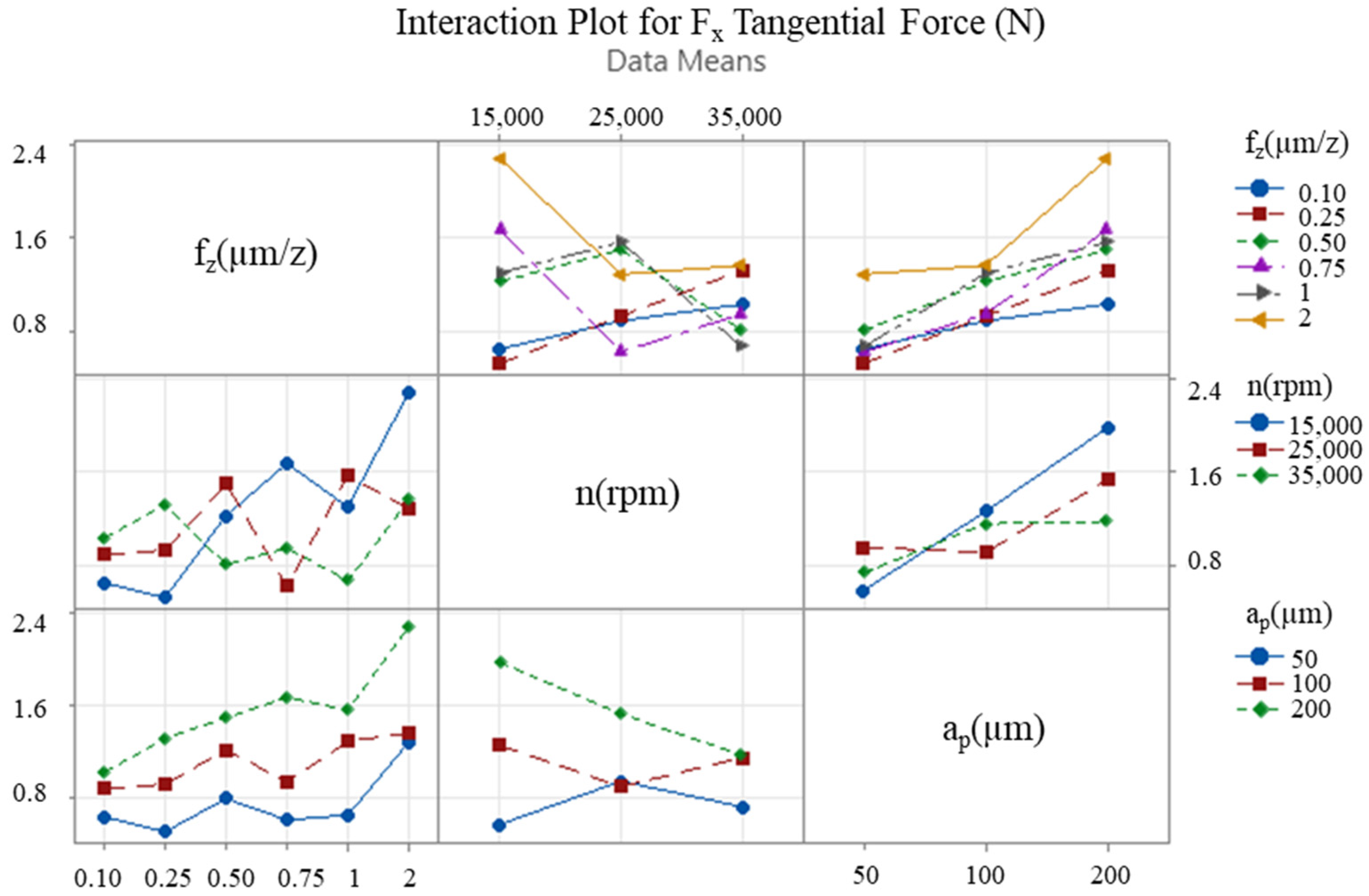
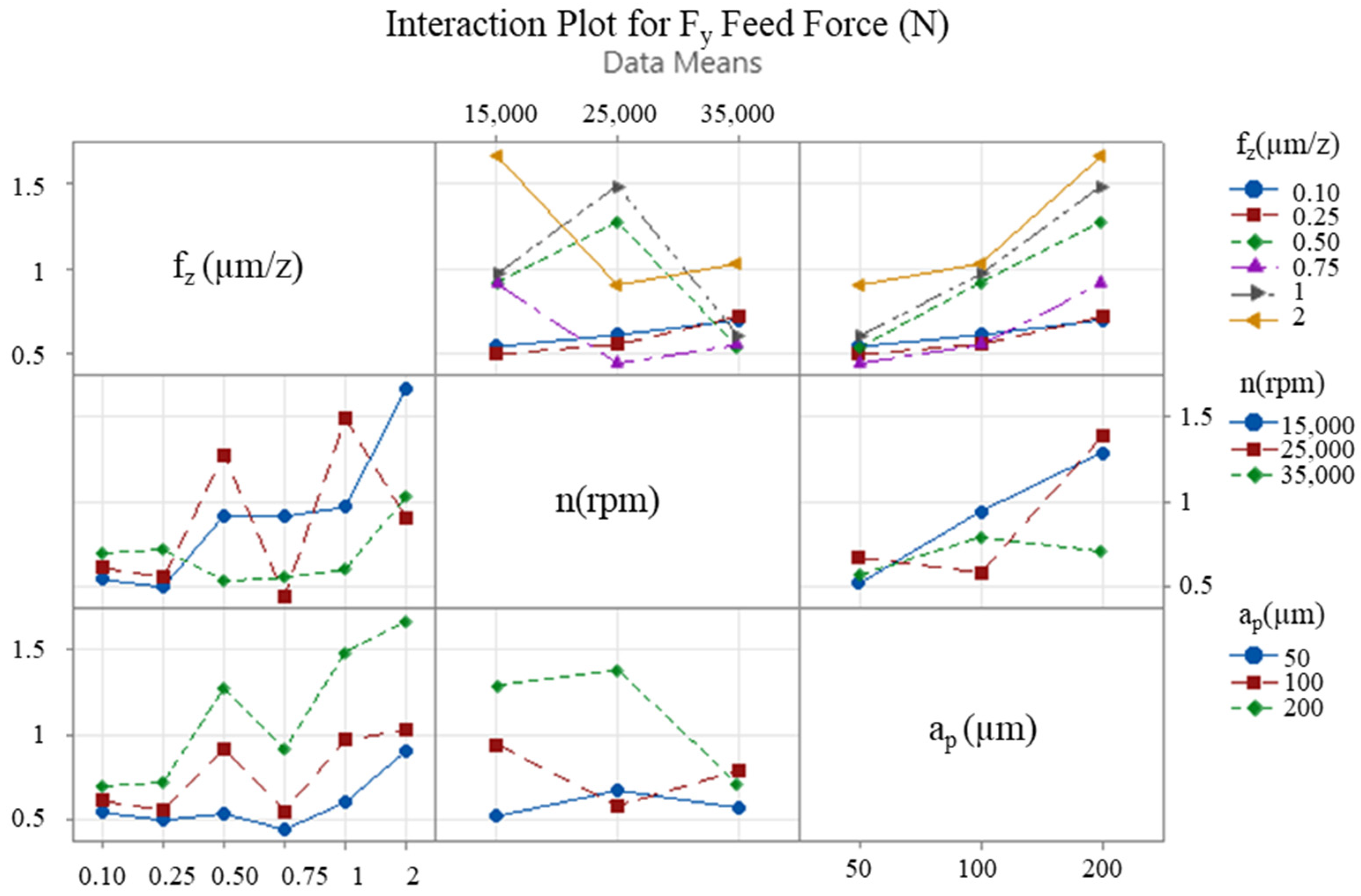
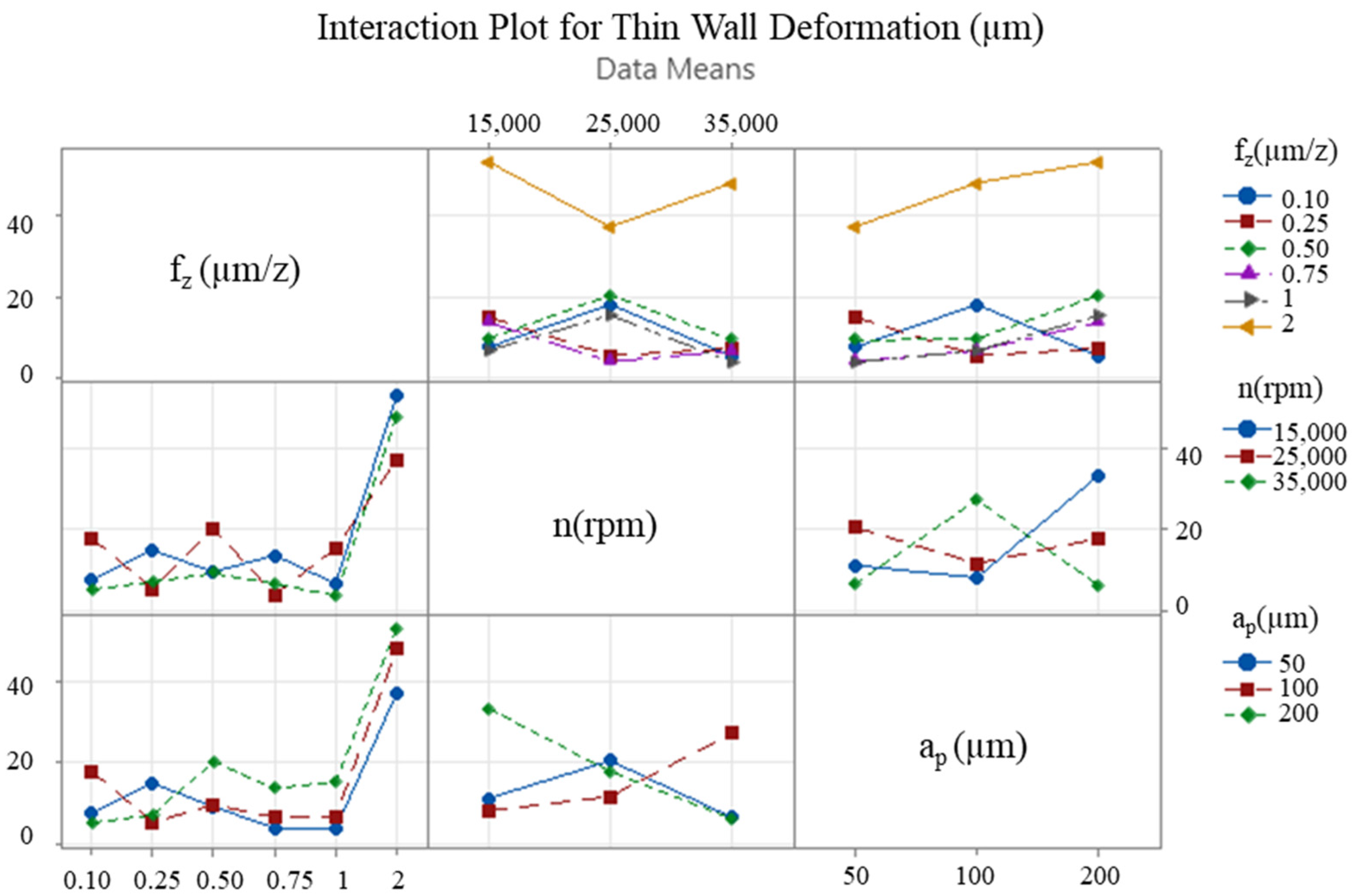
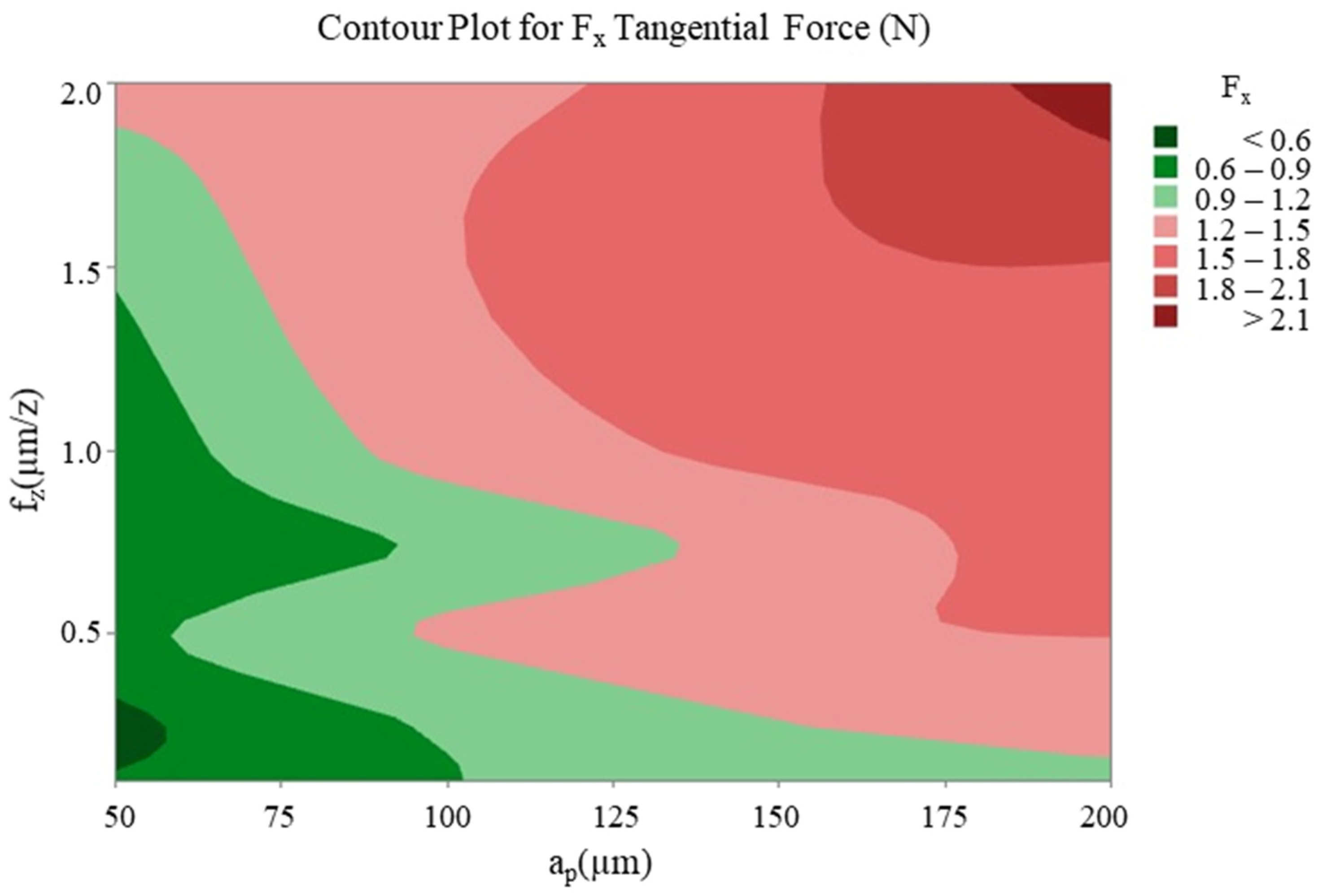
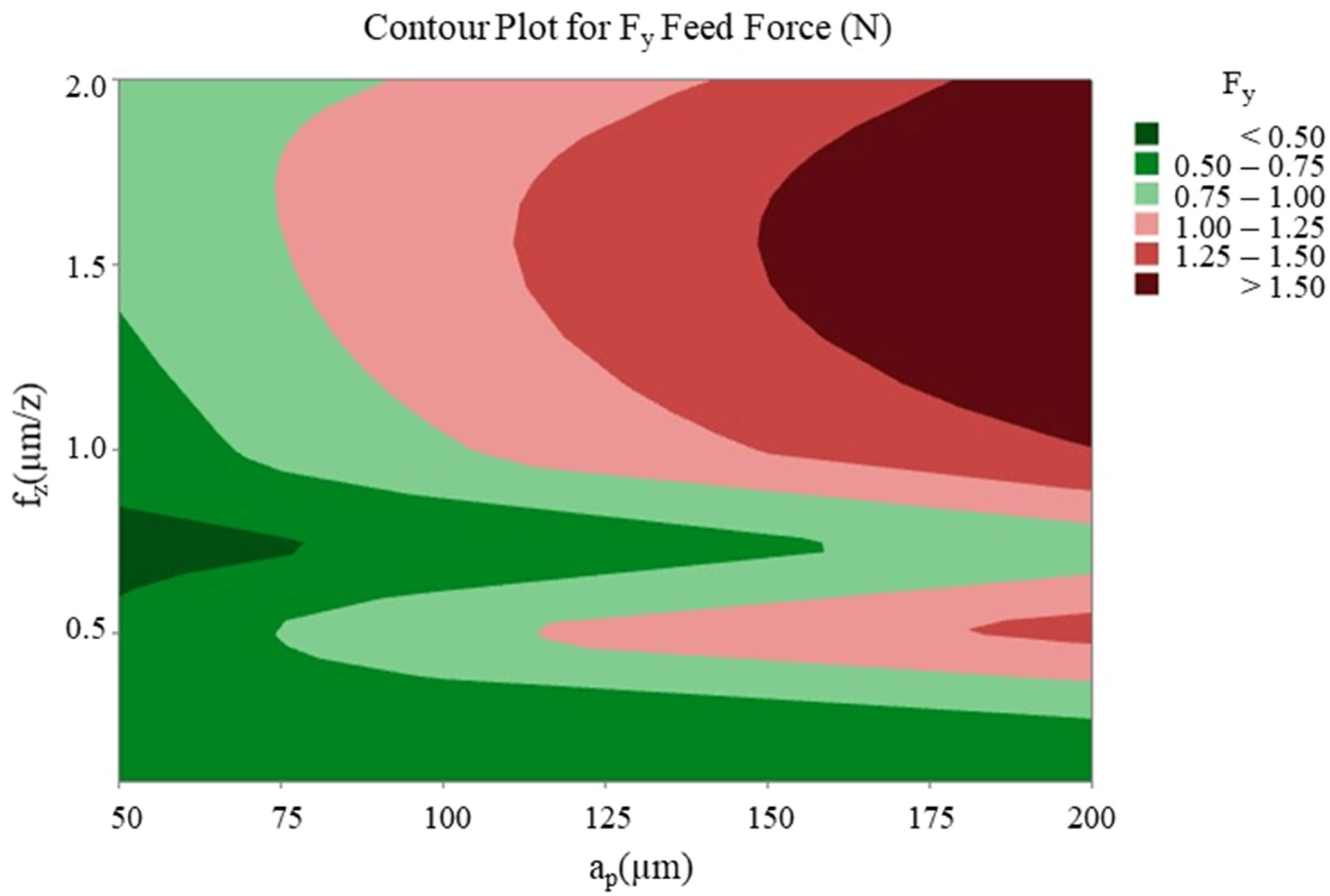
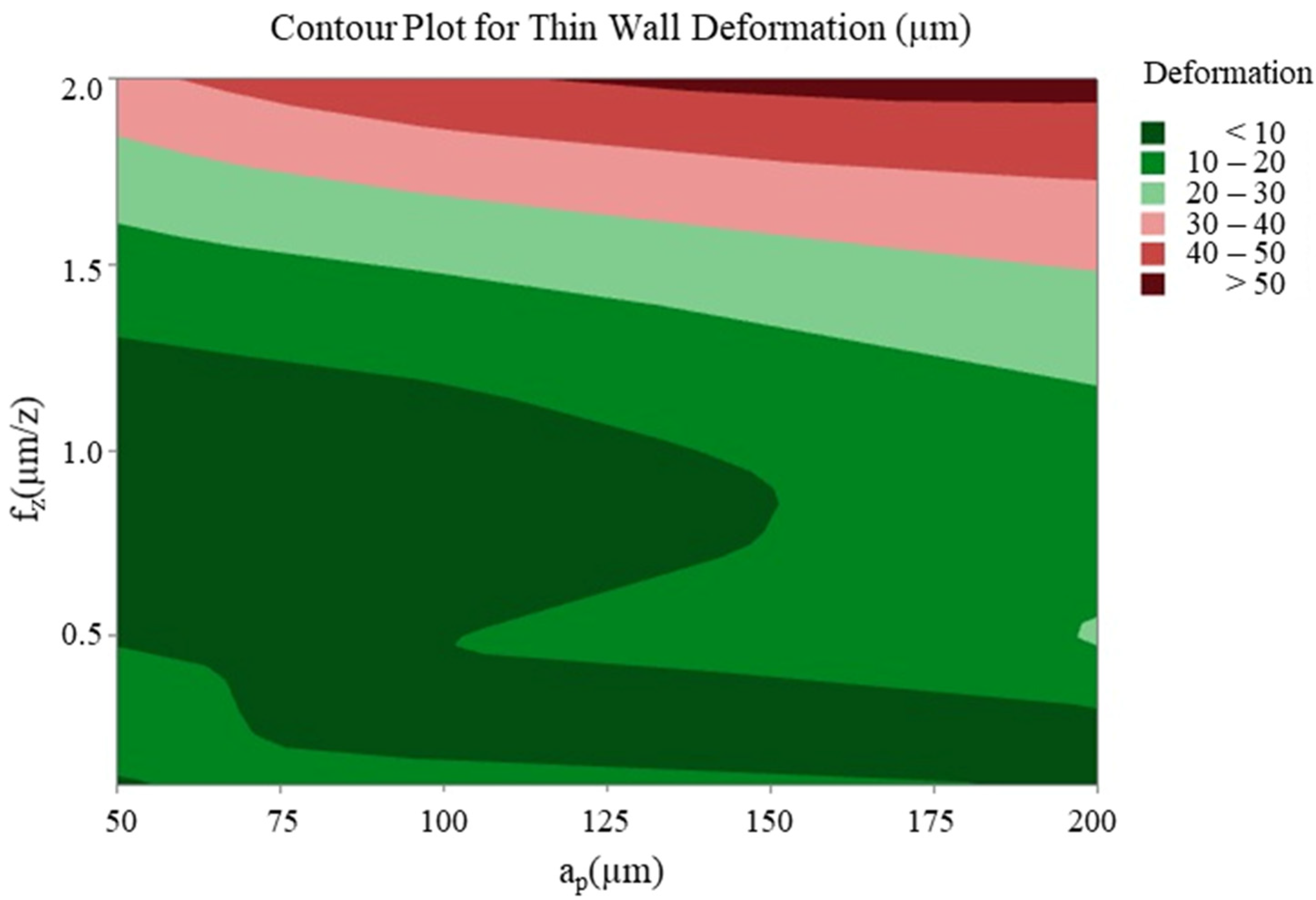
3.2. Interaction Between Significant Parameters
3.3. Regression Modeling Analysis
3.4. Optimization Results’ Verification
4. Conclusions
- The Taguchi approach, utilised for the optimisation of the cutting parameters, yielded highly accurate results and demonstrated a high level of performance. The effects of cutting parameters on tangential force (Fx), feed force (Fy) and thin-wall deformation were analysed with a confidence level of 96.55%, 96.06%, 92.19% (R-sq), respectively.
- It is evident that a decrease in the number of revolutions and an increase in the feed rate and depth of cut will result in an increase in cutting forces and thin-wall deformation.
- The findings of this study indicated that the most effective parameter on Fx tangential cutting force was depth of cut, with a percentage of 56.94%, and that the most effective parameter on Fy feed force was the feed rate, with a percentage of 45.3%. In the case of machined thin-wall deformation, the most effective parameter was identified as the feed rate, with an impact factor of 87.36%.
- The impact of depth of cut and machine speed on the micro-milled thin-wall deformation was found to be limited to 3.26% and 1.58%, respectively.
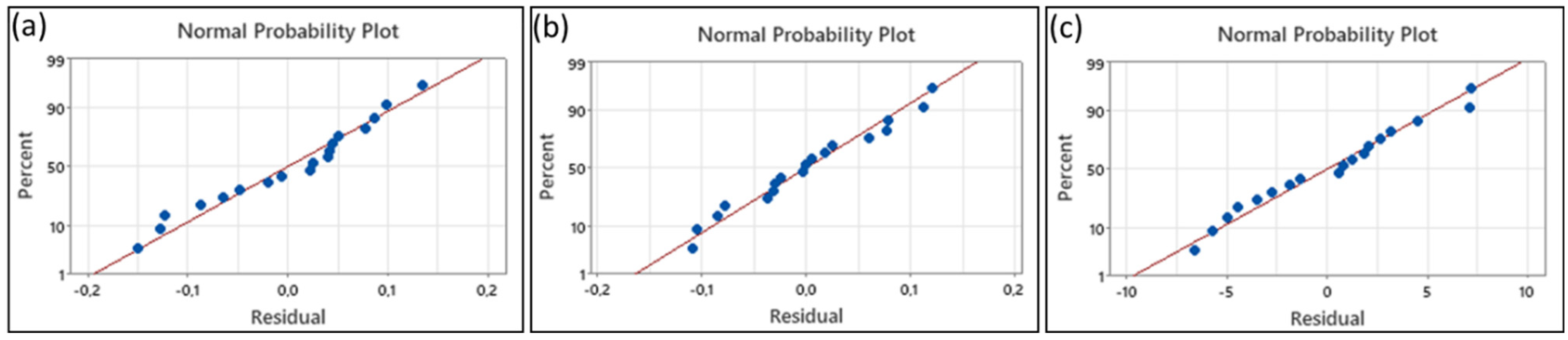
- In analyses of variance (ANOVA) determining the effect of control parameters on the output parameters, high residual plot values of 92.19%, 96.55% and 96.06% were obtained for micro-milled wall deformation, Fx tangential force and Fy feed force, respectively.
- It was determined that the ploughing mechanism exhibited enhanced efficacy in inducing thin-wall deformation through micro-milling when compared to conventional cutting forces. The predominant factor contributing to this phenomenon is hypothesised to be the substantial influence of the feed rate on thin-wall deformation.
- The optimal cutting parameters for micro-milled thin-wall deformation were determined as fz = 0.75 µm/z, n = 35,000 rpm, ap = 50 µm. Taguchi analysis estimated these with an average error of 19.44%.
- First-order mathematical models for micro-milled thin-wall deformation (1) and cutting forces (2) and (3) were developed using regression analyses.
- Optimised cutting parameters minimised deformation in the micro-milling of thin-walled structures. These results are seen as a guide for precision manufacturing in the aerospace, electronics and medical device industries.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Izamshah, R.A.R.; Mo, J.P.T.; Ding, S. Finite element analysis of machining thin-wall parts. Key Eng. Mater. 2011, 458, 283–288. [Google Scholar] [CrossRef]
- Khandagale, P.; Bhakar, G.; Kartik, V.; Joshi, S.S. Modelling time-domain vibratory deflection response of thin-walled cantilever workpieces during flank milling. J. Manuf. Process. 2018, 33, 278–290. [Google Scholar] [CrossRef]
- Xiang, J.; Yi, J. Deformation mechanism in wax supported milling of thin-walled structures based on milling forces stability. CIRP J. Manuf. Sci. Technol. 2021, 32, 356–369. [Google Scholar] [CrossRef]
- Annoni, M.; Rebaioli, L.; Semeraro, Q. Thin wall geometrical quality improvement in micromilling. Int. J. Adv. Manuf. Technol. 2015, 79, 881–895. [Google Scholar] [CrossRef]
- Liu, X.; DeVor, R.E.; Kapoor, S.G.; Ehmann, K.F. The mechanics of machining at the microscale: Assessment of the current state of the science. J. Manuf. Sci. Eng. 2004, 126, 666–678. [Google Scholar] [CrossRef]
- Wu, G.; Li, G.; Pan, W.; Wang, X.; Ding, S. A prediction model for the milling of thin-wall parts considering thermal-mechanical coupling and tool wear. Int. J. Adv. Manuf. Technol. 2020, 107, 4645–4659. [Google Scholar] [CrossRef]
- Dang, X.-B.; Wan, M.; Yang, Y.; Zhang, W.-H. Efficient prediction of varying dynamic characteristics in thin-wall milling using freedom and mode reduction methods. Int. J. Mech. Sci. 2019, 150, 202–216. [Google Scholar] [CrossRef]
- Dornfeld, D.; Min, S.; Takeuchi, Y. Recent Advances in Mechanical Micromachining. CIRP Ann. 2006, 55, 745–768. [Google Scholar] [CrossRef]
- Campos, F.d.O.; Mougo, A.L.; Araujo, A.C. Study of the cutting forces on micromilling of an aluminum alloy. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1289–1296. [Google Scholar] [CrossRef]
- Kou, D.J.; Wan, Y.; Liu, Z.Q.; Cai, Y.K.; Liang, X.C. Deformation control in micro-milling of thin-walled structures. Int. J. Adv. Manuf. Technol. 2015, 81, 967–974. [Google Scholar] [CrossRef]
- Hasçelik, A.; Aslantas, K. Mikro-Frezeleme Yöntemi ile İşlenen İnce Duvarlı Yapılarda Deformasyonun İncelenmesi. J. Mater. Mechatron. A 2023, 4, 134–146. [Google Scholar] [CrossRef]
- Izamshah, R.; Yuhazri, M.; Hadzley, M.; Ali, M.A.; Subramonian, S. Effects of End Mill Helix Angle on Accuracy for Machining Thin-Rib Aerospace Component. Appl. Mech. Mater. 2013, 315, 773–777. [Google Scholar] [CrossRef]
- Wojciechowski, S. The estimation of cutting forces and specific force coefficients during finishing ball end milling of inclined surfaces. Int. J. Mach. Tools Manuf. 2015, 89, 110–123. [Google Scholar] [CrossRef]
- Budak, E.; Tunç, L.; Alan, S.; Özgüven, H.N. Prediction of workpiece dynamics and its effects on chatter stability in milling. CIRP Ann. 2012, 61, 339–342. [Google Scholar] [CrossRef]
- Del Sol, I.; Rivero, A.; de Lacalle, L.N.L.; Gamez, A.J. Thin-Wall Machining of Light Alloys: A Review of Models and Industrial Approaches. Materials 2019, 12, 2012. [Google Scholar] [CrossRef]
- Wang, F.; Cheng, X.; Zheng, G.; Yang, X.; Guo, Q.; Sun, Q. Study of micromilling parameters and processes for thin wall fabrications. Precis. Eng. 2018, 56, 246–254. [Google Scholar] [CrossRef]
- Wang, H.; Huang, L.; Yao, C.; Kou, M.; Wang, W.; Huang, B.; Zheng, W. Integrated analysis method of thin-walled turbine blade precise machining. Int. J. Precis. Eng. Manuf. 2015, 16, 1011–1019. [Google Scholar] [CrossRef]
- Fu, M.; Wang, J. Size effects in multi-scale materials processing and manufacturing. Int. J. Mach. Tools Manuf. 2021, 167, 103755. [Google Scholar] [CrossRef]
- Wu, X.; Li, L.; He, N.; Hao, X.; Yao, C.; Zhong, L. Investigation on the ploughing force in microcutting considering the cutting edge radius. Int. J. Adv. Manuf. Technol. 2016, 86, 2441–2447. [Google Scholar] [CrossRef]
- Aslantas, K.; Alatrushi, L.K.; Bedir, F.; Kaynak, Y.; Yılmaz, N. An experimental analysis of minimum chip thickness in micro-milling of two different titanium alloys. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1486–1498. [Google Scholar] [CrossRef]
- Yalçın, B.; Yüksel, A.; Aslantaş, K.; Der, O.; Ercetin, A. Optimization of Micro-Drilling of Laminated Aluminum Composite Panel (Al–PE) Using Taguchi Orthogonal Array Design. Materials 2023, 16, 4528. [Google Scholar] [CrossRef]
- Sredanovic, B.; Cica, D.; Borojevic, S.; Tesic, S.; Kramar, D. Optimization of superalloy Inconel 718 micro-milling process by combined Taguchi and multi-criteria decision making method. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 423. [Google Scholar] [CrossRef]
- Khan, M.A.; Jaffery, S.H.I.; Khan, M.A.; Faraz, M.I.; Mufti, S. Multi-Objective Optimization of Micro-Milling Titanium Alloy Ti-3Al-2.5V (Grade 9) Using Taguchi-Grey Relation Integrated Approach. Metals 2023, 13, 1373. [Google Scholar] [CrossRef]
- Aslantas, K.; Ekici, E.; Çiçek, A. Optimization of process parameters for micro milling of Ti-6Al-4V alloy using Taguchi-based gray relational analysis. Measurement 2018, 128, 419–427. [Google Scholar] [CrossRef]
- Ali, S.; Abdallah, S.; Pervaiz, S. Predicting Cutting Force and Primary Shear Behavior in Micro-Textured Tools Assisted Machining of AISI 630: Numerical Modeling and Taguchi Analysis. Micromachines 2022, 13, 91. [Google Scholar] [CrossRef]
- Yu, H.; Zheng, M.; Zhang, W.; Nie, W.; Bian, T. Optimal design of helical flute of irregular tooth end milling cutter based on particle swarm optimization algorithm. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 236, 3323–3339. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.; Zhang, M. Modeling and Multi-objective Optimization Method of Machine Tool Energy Consumption Considering Tool Wear. Int. J. Precis. Eng. Manuf. Technol. 2021, 9, 127–141. [Google Scholar] [CrossRef]
- Kahya, M.; Ozbayoglu, M.; Unver, H.O. Precision and energy-efficient ball-end milling of Ti6Al4V turbine blades using particle swarm optimization. Int. J. Comput. Integr. Manuf. 2021, 34, 110–133. [Google Scholar] [CrossRef]
- Jain, A.; Bajpai, V. Introduction to high-speed machining (HSM). In High-Speed Machining; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–25. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Kuczmaszewski, J.; Legutko, S.; Pieśko, P. Techniques for Thin-Walled Element Milling with Respect to Minimising Post-Machining Deformations. Materials 2020, 13, 4723. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhang, L.; Wang, P.; Chang, Y. Experimental investigation on local buckling behaviors of stiffened closed-section thin-walled aluminum alloy columns under compression. Thin-Walled Struct. 2015, 94, 188–198. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Pieśko, P.; Józwik, J.; Legutko, S.; Kukiełka, L. A Comparison of the Geometrical Accuracy of Thin-Walled Elements Made of Different Aluminum Alloys. Materials 2021, 14, 7242. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhou, J.; Li, P. Simulations and Experiments on the Micro-Milling Process of a Thin-Walled Structure of Al6061-T6. Materials 2022, 15, 3568. [Google Scholar] [CrossRef] [PubMed]
- Samuel, A.U.; O Araoyinbo, A.; Elewa, R.R.; Biodun, M.B. Effect of Machining of Aluminium Alloys with Emphasis on Aluminium 6061 Alloy—A Review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1107, 012157. [Google Scholar] [CrossRef]
- Karakılınç, U.; Ergene, B.; Yalçın, B.; Aslantaş, K.; Erçetin, A. Comparative Analysis of Minimum Chip Thickness, Surface Quality and Burr Formation in Micro-Milling of Wrought and Selective Laser Melted Ti64. Micromachines 2023, 14, 1160. [Google Scholar] [CrossRef] [PubMed]
- Aslantas, K.; Hascelik, A.; Çiçek, A. Performance evaluation of DLC and NCD coatings in micro-milling of Al7075-T6 alloy. J. Manuf. Process. 2022, 81, 976–990. [Google Scholar] [CrossRef]




| Control Factors | Levels | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Feed Rate, fz (µm/z) | 0.1 | 0.25 | 0.5 | 0.75 | 1 | 2 |
| Spindle Speed, n (rpm) Cutting Speed, Vc (m/min) | 15,000 (47.1) | 25,000 (78.5) | 35,000 (109.9) | |||
| Depth of cut, ap (µm) | 50 | 100 | 200 |
| Control Factors | L18 Orthogonal Experimental Design | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Feed rate (fz) | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 6 | 6 | 6 |
| Spindle speed (n) | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| Depth of cut (ap) | 1 | 2 | 3 | 1 | 2 | 3 | 2 | 3 | 1 | 3 | 1 | 2 | 2 | 3 | 1 | 3 | 1 | 2 |
| Source | DF | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Feed rate (µm/z) | 5 | 34.020% | 1.1754 | 0.23507 | 15.79 | 0.001 |
| Spindle speed (rpm) | 2 | 5.589% | 0.1931 | 0.09657 | 6.49 | 0.021 |
| Depth of cut (µm) | 2 | 56.944% | 1.9674 | 0.98372 | 66.09 | 0.000 |
| Error | 8 | 3.447% | 0.1191 | 0.01488 | ||
| Total | 17 | 100% | 3.4550 |
| Source | DF | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Feed rate (µm/z) | 5 | 45.201% | 0.96380 | 0.19276 | 18.34 | 0.00034 |
| Spindle speed (rpm) | 2 | 8.423% | 0.17961 | 0.08980 | 8.54 | 0.01034 |
| Depth of cut (µm) | 2 | 42.432% | 0.90476 | 0.45238 | 43.03 | 0.00005 |
| Error | 8 | 3.944% | 0.08410 | 0.01051 | ||
| Total | 17 | 100% | 2.13226 |
| Level | 1 | 2 | 3 | 4 | 5 | 6 | Delta | Rank |
|---|---|---|---|---|---|---|---|---|
| Feed rate (µm/z) | 1.48020 | 1.25830 | 1.16376 | 0.00275 | 0.90571 | 4.05702 | 5.53722 | 2 |
| Spindle speed (rpm) | 1.07151 | 0.67022 | 0.04912 | 1.12063 | 3 | |||
| Depth of cut (µm) | 2.76866 | 0.80309 | 3.65818 | 6.42684 | 1 |
| Level | 1 | 2 | 3 | 4 | 5 | 6 | Delta | Rank |
|---|---|---|---|---|---|---|---|---|
| Feed rate (µm/z) | 4.1981 | 4.6374 | 1.3044 | 4.2915 | 0.3653 | −1.3039 | 5.9413 | 1 |
| Spindle speed (rpm) | 1.4169 | 1.9249 | 3.4046 | 1.9876 | 3 | |||
| Depth of cut (µm) | 4.8085 | 2.5112 | 0.5732 | 5.3817 | 2 |
| Source | DF | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| Feed rate (µm/z) | 5 | %87.362 | 3307.14 | 661.43 | 17.89 | 0.0004 |
| Spindle speed (rpm) | 2 | %1.588 | 60.11 | 30.06 | 0.81 | 0.4771 |
| Depth of cut (µm) | 2 | %3.236 | 122.49 | 61.25 | 1.66 | 0.2501 |
| Error | 8 | %7.814 | 295.8 | 36.98 | ||
| Total | 17 | %100 | 3785.56 |
| Level | 1 | 2 | 3 | 4 | 5 | 6 | Delta | Rank |
|---|---|---|---|---|---|---|---|---|
| Feed rate (µm/z) | −19.24 | −18.7 | −21.87 | −17.38 | −17.6 | −33.2 | 15.82 | 1 |
| Spindle speed (rpm) | −22.58 | −22.37 | −19.04 | 3 | ||||
| Depth of cut (µm) | −19.48 | −21.24 | −23.28 | 2 |
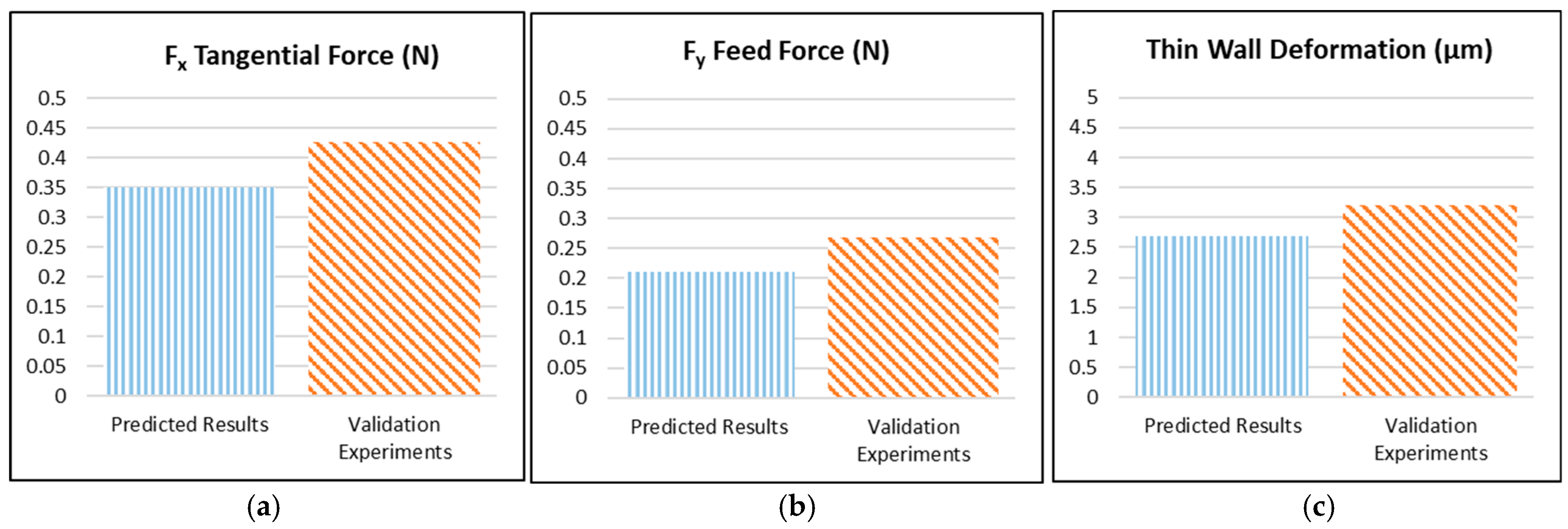
| Output Parameters | Parameter Setting Level | Predicted Results | Validation Experiments | Error % |
|---|---|---|---|---|
| Fx tangential force (N) | fz = 0.1 µm/z, n = 35,000 rpm, ap = 50 µm | 0.35 | 0.428 | 22.28 |
| Fy feed force (N) | fz = 0.25 µm/z, n = 35,000 rpm, ap = 50 µm | 0.21 | 0.268 | 27.62 |
| Thin-wall deformation (µm) | fz = 0.75 µm/z, n = 35,000 rpm, ap = 50 µm | 2.69 | 3.213 | 19.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasçelik, A.; Aslantas, K.; Yalçın, B. Optimization of Cutting Parameters to Minimize Wall Deformation in Micro-Milling of Thin-Wall Geometries. Micromachines 2025, 16, 310. https://doi.org/10.3390/mi16030310
Hasçelik A, Aslantas K, Yalçın B. Optimization of Cutting Parameters to Minimize Wall Deformation in Micro-Milling of Thin-Wall Geometries. Micromachines. 2025; 16(3):310. https://doi.org/10.3390/mi16030310
Chicago/Turabian StyleHasçelik, Ahmet, Kubilay Aslantas, and Bekir Yalçın. 2025. "Optimization of Cutting Parameters to Minimize Wall Deformation in Micro-Milling of Thin-Wall Geometries" Micromachines 16, no. 3: 310. https://doi.org/10.3390/mi16030310
APA StyleHasçelik, A., Aslantas, K., & Yalçın, B. (2025). Optimization of Cutting Parameters to Minimize Wall Deformation in Micro-Milling of Thin-Wall Geometries. Micromachines, 16(3), 310. https://doi.org/10.3390/mi16030310







