6DOF Aircraft Landing Gear System with Magnetorheological Damper in Various Taxing and Touchdown Scenarios
Abstract
:1. Introduction
2. Aircraft Landing Gear System
3. Touchdown Phase
3.1. Three-Point Touchdown
3.2. Two-Point Touchdown
3.3. One-Point Touchdown
4. Taxing Phase
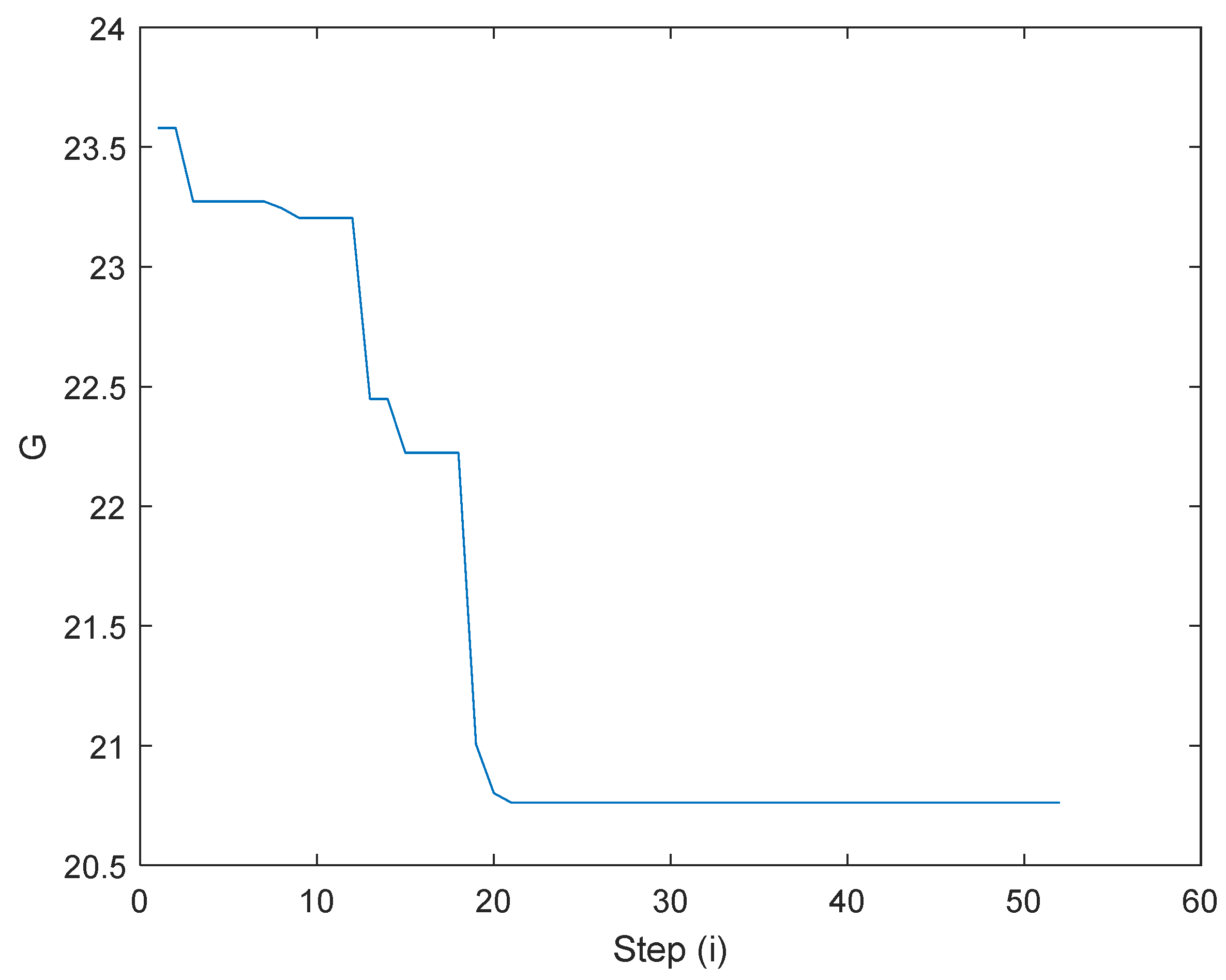
5. Q-Learning Neural Network Controller
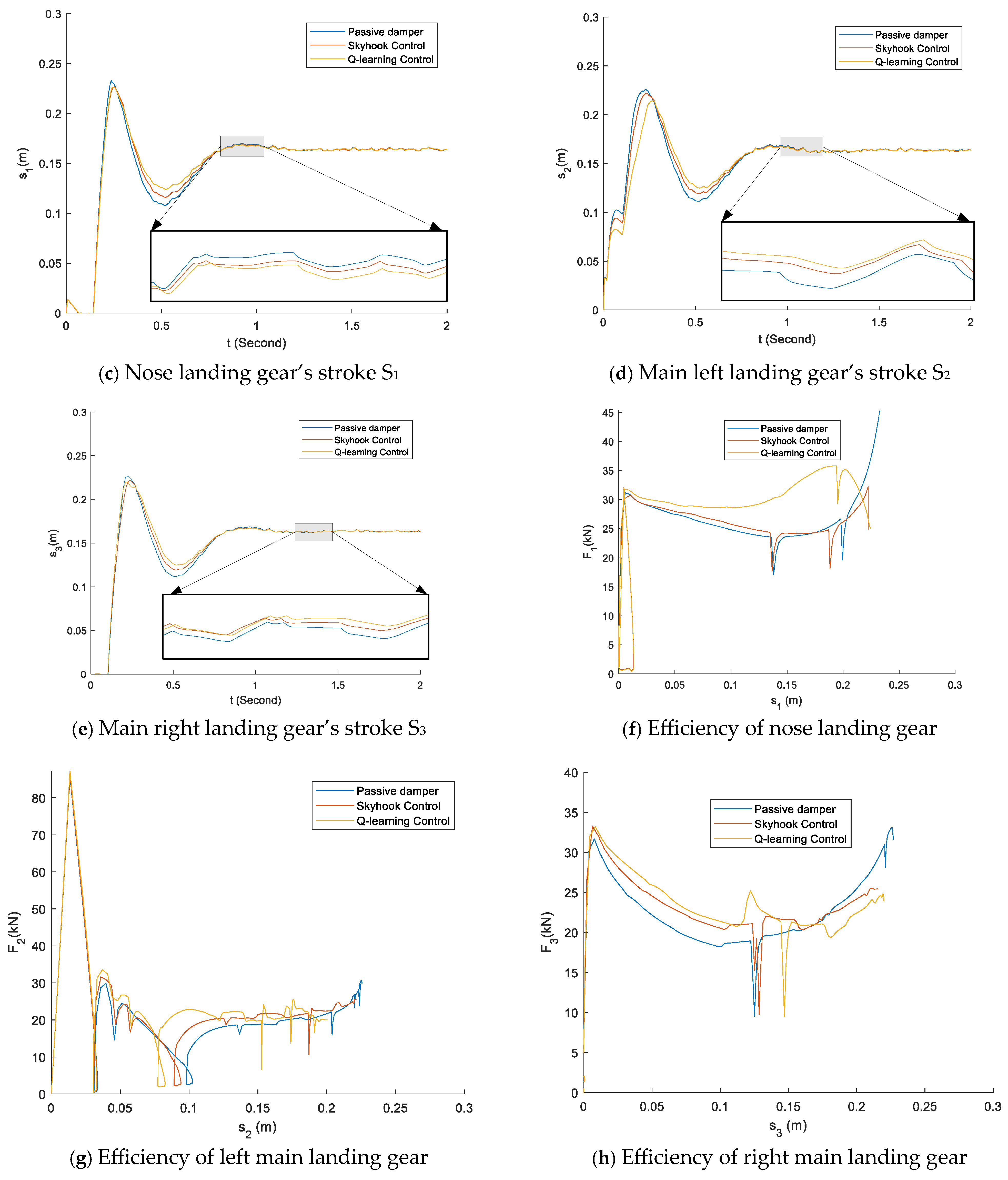
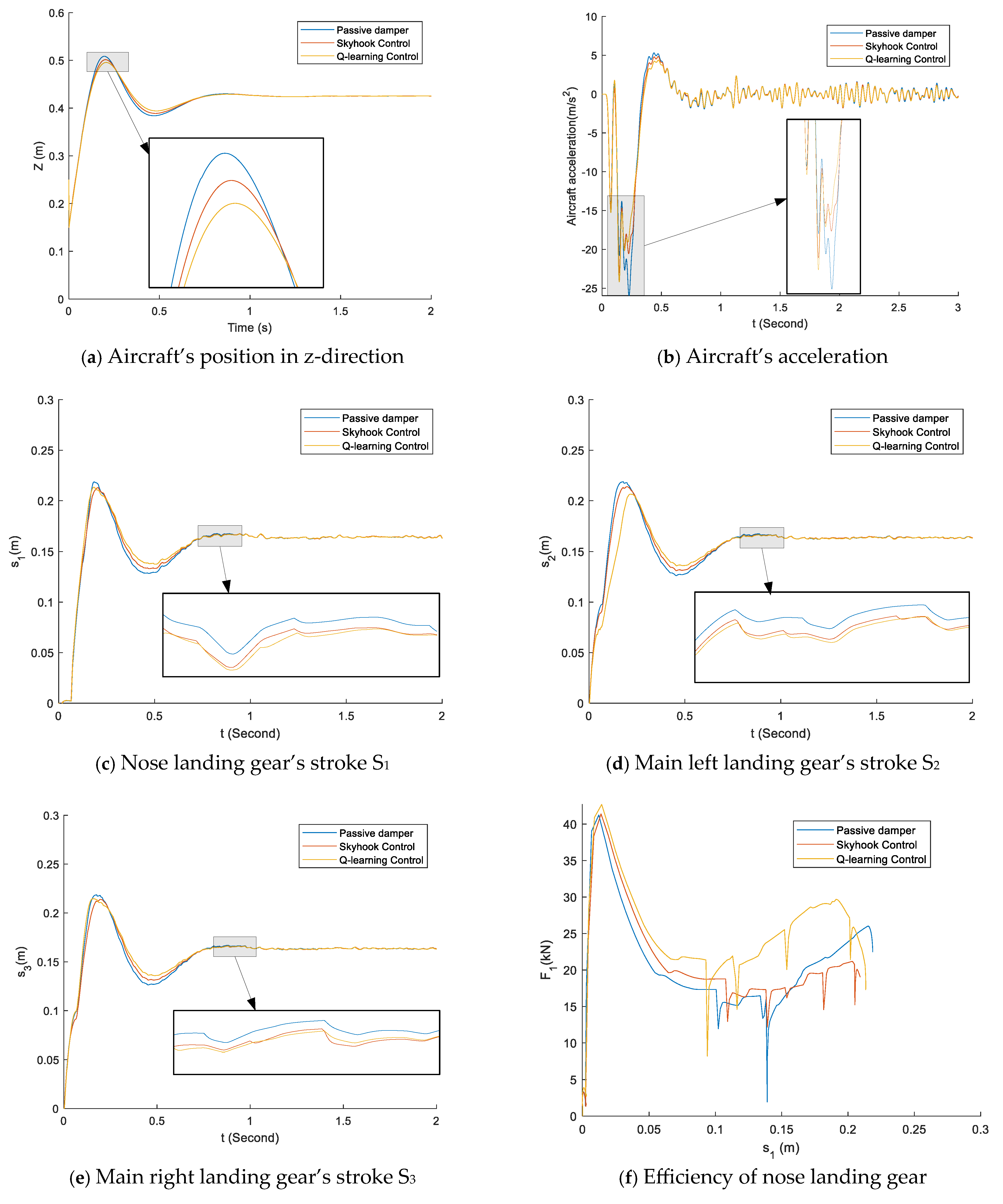
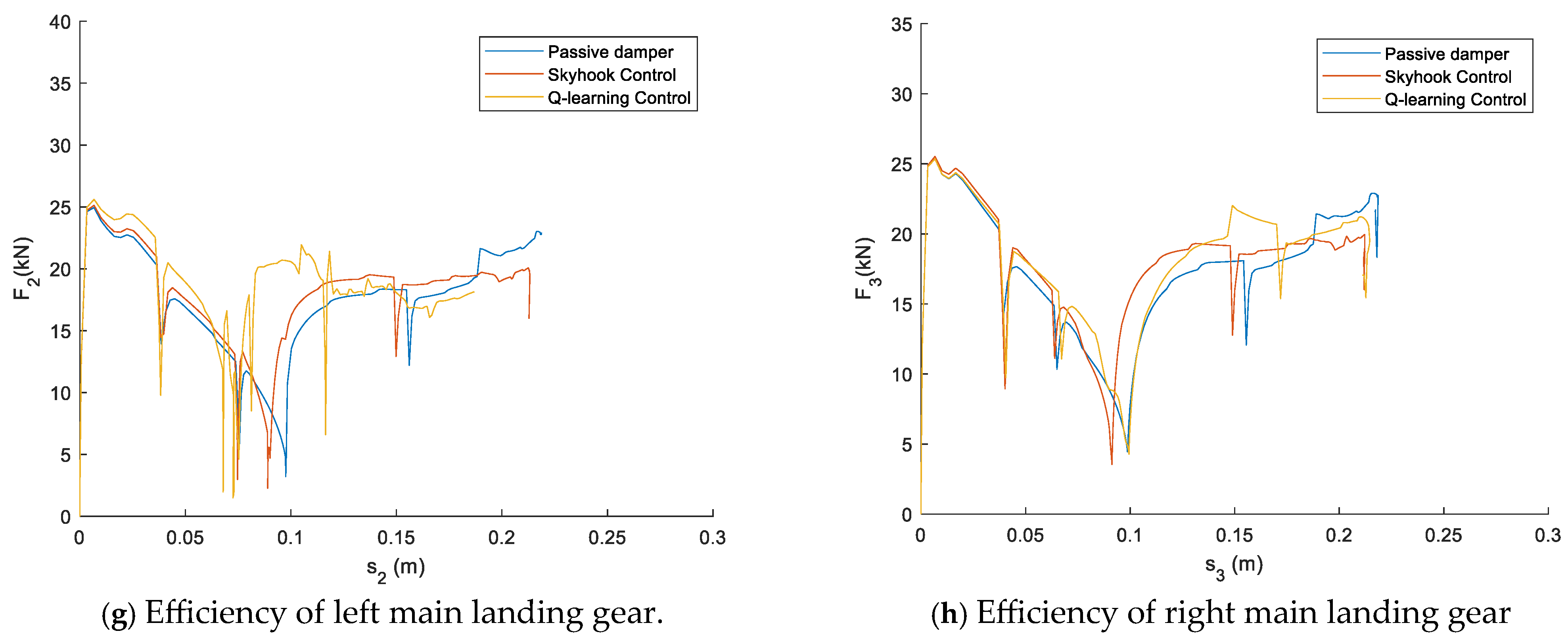
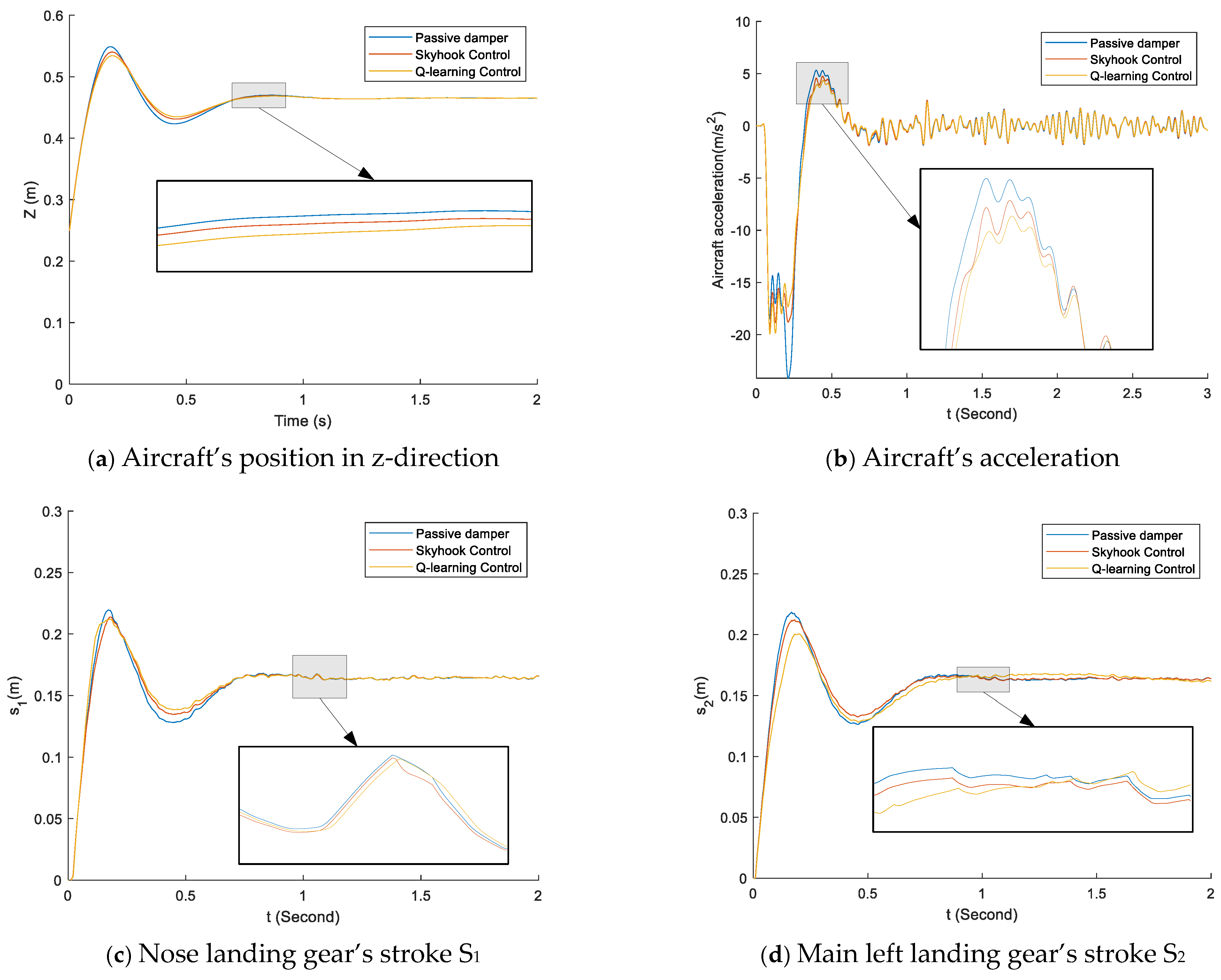
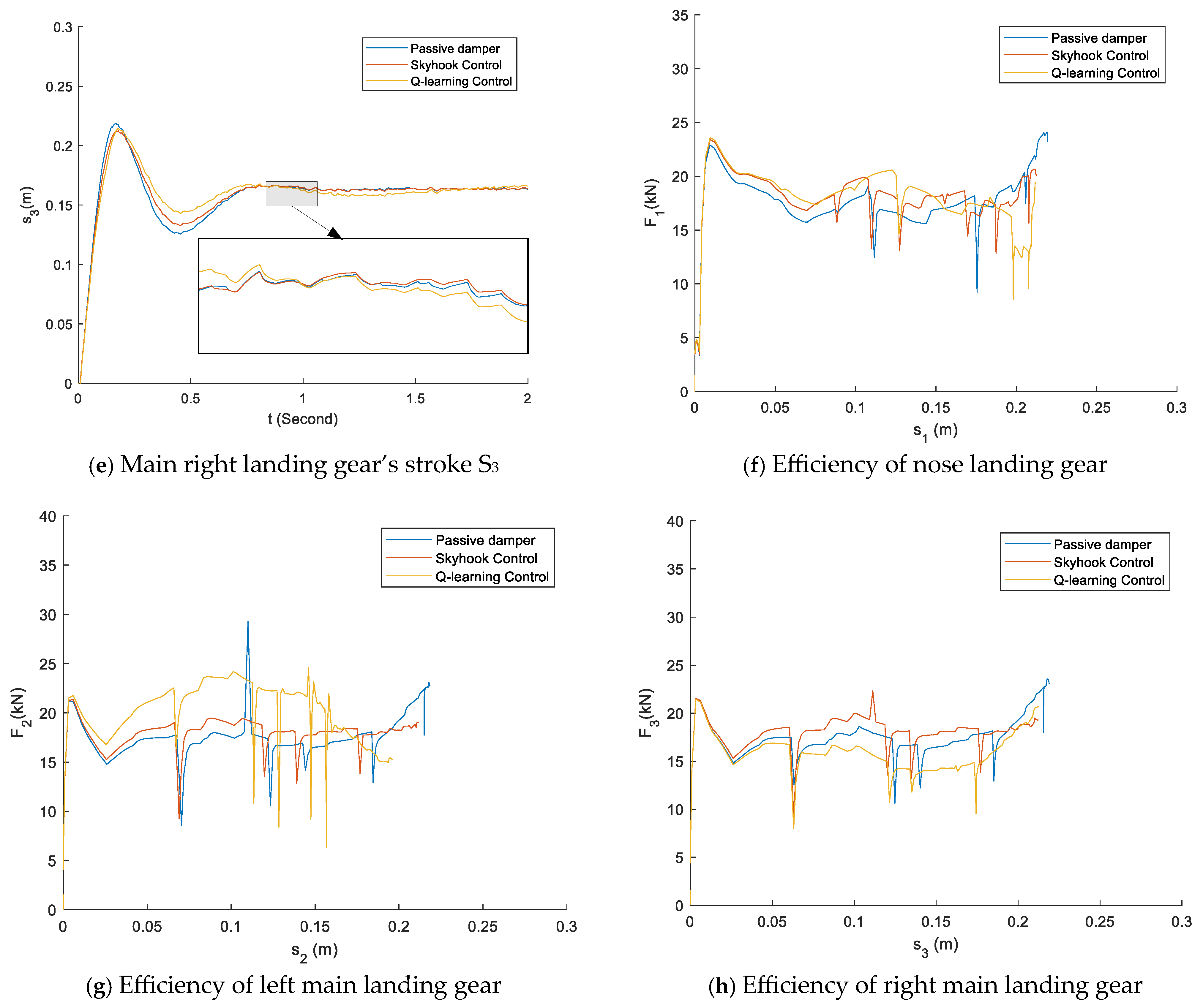
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Stroke velocity | |
| Aircraft body’s acceleration | |
| Ap | Cross-area of the piston |
| b, bf | Bias vector |
| C | Viscous damping coefficient |
| Csky | Skyhook factor |
| D | Draft force |
| Fa | Pneumatic force |
| Fd, FMRd, FMLd, FNd | Damping force |
| Fmax | Maximum damping force |
| FMR | MR force |
| FT1; FT2; FT3 | Reaction tired force |
| Fv | Viscous force |
| g | Gravitational acceleration |
| G, Gpassive | Cost function |
| I | Electrical current |
| Ixx | Roll mass moment of inertia |
| Iyy | Pitch mass moment of inertia |
| Izz | Yaw mass moment of inertia |
| kE | MR force factor |
| kT | Tire force constant |
| L | Lift force |
| la | Distance between the nose landing gear interface and the aircraft’s center of gravity |
| lb | Distance between the main landing gear interface and the aircraft’s center of gravity |
| ll | Distance between the left main landing gear interface and the aircraft’s center of gravity |
| lr | Distance between the right main landing gear interface and the aircraft’s center of gravity |
| M | Aircraft mass |
| m | Landing gear mass |
| n | Polytropic process index |
| N, Nrepeat | Number of the simulation loops |
| nstep | Number of sample signals |
| RMS | Root mean square |
| s | Landing gear stroke |
| smax | Maximum stroke |
| T | Engine thrust |
| u | Control input (electrical current) |
| v(0) | Initial sink speed |
| V0 | Initial air chamber volume |
| W, Wf | Weight matrix |
| Wg | Aircraft gravity force |
| z1, z1, z3 | Tire deformation |
| η, η1, η2, η3 | Shock absorber efficiency |
| θ | Pitch angle |
| φ | Roll angle |
References
- Pytka, J.; Budzyński, P.; Łyszczyk, T.; Józwik, J.; Michałowska, J.; Tofil, A.; Błażejczak, D.; Laskowski, J. Determining Wheel Forces and Moments on Aircraft Landing Gear with a Dynamometer Sensor. Sensors 2019, 20, 227. [Google Scholar] [CrossRef]
- Pecora, R. A Rational Numerical Method for Simulation of Drop-Impact Dynamics of Oleo-Pneumatic Landing Gear. Appl. Sci. 2021, 11, 4136. [Google Scholar] [CrossRef]
- Sonowal, P.; Pandey, K.M.; Sharma, K.K. Design and Static Analysis of Landing Gear Shock Absorber of Commercial Aircraft. Mater. Today Proc. 2021, 45, 6712–6717. [Google Scholar] [CrossRef]
- Wang, H.; Xing, J.T.; Price, W.G.; Li, W. An Investigation of an Active Landing Gear System to Reduce Aircraft Vibrations Caused by Landing Impacts and Runway Excitations. J. Sound Vib. 2008, 317, 50–66. [Google Scholar] [CrossRef]
- Gharapurkar, A.A.; Jahromi, A.F.; Bhat, R.B.; Xie, W.-F. Semi-Active Control of Aircraft Landing Gear System Using H-Infinity Control Approach. In Proceedings of the 2013 International Conference on Connected Vehicles and Expo (ICCVE), Las Vegas, NV, USA, 2–6 December 2013; pp. 679–686. [Google Scholar]
- Zarchi, M.; Attaran, B. Improved Design of an Active Landing Gear for a Passenger Aircraft Using Multi-Objective Optimization Technique. Struct. Multidisc. Optim. 2019, 59, 1813–1833. [Google Scholar] [CrossRef]
- Koutsoloukas, L.; Nikitas, N.; Aristidou, P. Passive, Semi-Active, Active and Hybrid Mass Dampers: A Literature Review with Associated Applications on Building-like Structures. Dev. Built Environ. 2022, 12, 100094. [Google Scholar] [CrossRef]
- Zoccolini, L.; Bruschi, E.; Cattaneo, S.; Quaglini, V. Current Trends in Fluid Viscous Dampers with Semi-Active and Adaptive Behavior. Appl. Sci. 2023, 13, 10358. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, C.; Zheng, X.; Zhao, L.; Qiu, Y. Advancements in Semi-Active Automotive Suspension Systems with Magnetorheological Dampers: A Review. Appl. Sci. 2024, 14, 7866. [Google Scholar] [CrossRef]
- Yang, J.; Ning, D.; Sun, S.S.; Zheng, J.; Lu, H.; Nakano, M.; Zhang, S.; Du, H.; Li, W.H. A Semi-Active Suspension Using a Magnetorheological Damper with Nonlinear Negative-Stiffness Component. Mech. Syst. Signal Process. 2021, 147, 107071. [Google Scholar] [CrossRef]
- Kang, B.-H.; Choi, S.-B. Design, Structure Analysis and Shock Control of Aircraft Landing Gear System with MR Damper. Smart Mater. Struct. 2024, 33, 055049. [Google Scholar] [CrossRef]
- Kang, B.-H.; Jo, B.-H.; Kim, B.-G.; Hwang, J.-H.; Choi, S.-B. Linear and Nonlinear Models for Drop Simulation of an Aircraft Landing Gear System with MR Dampers. Actuators 2023, 12, 287. [Google Scholar] [CrossRef]
- Kang, B.-H.; Hwang, J.-H.; Choi, S.-B. A New Design Model of an MR Shock Absorber for Aircraft Landing Gear Systems Considering Major and Minor Pressure Losses: Experimental Validation. Appl. Sci. 2021, 11, 7895. [Google Scholar] [CrossRef]
- Jo, B.-H.; Jang, D.-S.; Hwang, J.-H.; Choi, Y.-H. Experimental Validation for the Performance of MR Damper Aircraft Landing Gear. Aerospace 2021, 8, 272. [Google Scholar] [CrossRef]
- Dong, L.; Chen, Z.; Sun, M.; Sun, Q.; Yu, Z. Study on Magneto-Rheological Damper Control of Aircraft Landing Gear Based on LADRC. In Proceedings of 2021 Chinese Intelligent Systems Conference, Fuzhou, China, 16–17 October 2021; Jia, Y., Zhang, W., Fu, Y., Yu, Z., Zheng, S., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2022; Volume 803, pp. 830–840. ISBN 978-981-16-6327-7. [Google Scholar]
- Hao, J.; Wang, Y.; Peng, Y.; Ma, H.; Wei, X. Design and Structure Optimization of Arresting Gear Based on Magnetorheological Damper. Aerospace 2023, 10, 1019. [Google Scholar] [CrossRef]
- Yoon, J.-Y.; Kang, B.-H.; Kim, J.-H.; Choi, S.-B. New Control Logic Based on Mechanical Energy Conservation for Aircraft Landing Gear System with Magnetorheological Dampers. Smart Mater. Struct. 2020, 29, 084003. [Google Scholar] [CrossRef]
- Kang, B.-H.; Yoon, J.-Y.; Kim, G.-W.; Choi, S.-B. Landing Efficiency Control of a Six-Degree-of-Freedom Aircraft Model with Magnetorheological Dampers: Part 1—Modeling. J. Intell. Mater. Syst. Struct. 2021, 32, 1290–1302. [Google Scholar] [CrossRef]
- Liu, G.; Pei, L.; Feng, L.; Wu, Z. A Mathematical Model for Dynamic Vibration Analysis of a Landing Aircraft. J. Vib. Eng. Technol. 2024, 12, 4149–4162. [Google Scholar] [CrossRef]
- Currey, N.S. Aircraft Landing Gear Design: Principles and Practices; AIAA Education Series; American Institute of Aeronautics & Astronautics: Reston, VA, USA, 1988; ISBN 978-1-60086-018-8. [Google Scholar]
- Luong, Q.-V.; Jo, B.-H.; Hwang, J.-H.; Jang, D.-S. A Supervised Neural Network Control for Magnetorheological Damper in an Aircraft Landing Gear. Appl. Sci. 2021, 12, 400. [Google Scholar] [CrossRef]
- Han, C.; Kim, B.-G.; Kang, B.-H.; Choi, S.-B. Effects of Magnetic Core Parameters on Landing Stability and Efficiency of Magnetorheological Damper-Based Landing Gear System. J. Intell. Mater. Syst. Struct. 2020, 31, 198–208. [Google Scholar] [CrossRef]
- Yıldız, A.S.; Eker, S.B. Semi-Active Control Implementation in Aircraft Landing Gear Systems Using Hardware-in-the-Loop Test Bench. Eng. Res. Express 2024, 6, 035529. [Google Scholar] [CrossRef]
- Han, C.; Kang, B.-H.; Choi, S.-B.; Tak, J.M.; Hwang, J.-H. Control of Landing Efficiency of an Aircraft Landing Gear System With Magnetorheological Dampers. J. Aircr. 2019, 56, 1980–1986. [Google Scholar] [CrossRef]
- Kang, B.-H.; Han, C.; Choi, S.-B. A Sky-Ground Hook Controller for Efficiency Enhancement of Aircraft Landing Gear with MR Damper. In Active and Passive Smart Structures and Integrated Systems XIII; Erturk, A., Ed.; SPIE: Denver, CO, USA, 2019; p. 3. [Google Scholar]
- Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Robust Adaptive Control for an Aircraft Landing Gear Equipped with a Magnetorheological Damper. Appl. Sci. 2020, 10, 1459. [Google Scholar] [CrossRef]
- Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Intelligent Control Based on a Neural Network for Aircraft Landing Gear with a Magnetorheological Damper in Different Landing Scenarios. Appl. Sci. 2020, 10, 5962. [Google Scholar] [CrossRef]
- Le, Q.-N.; Park, H.-M.; Kim, Y.; Pham, H.-H.; Hwang, J.-H.; Luong, Q.-V. An Intelligent Control and a Model Predictive Control for a Single Landing Gear Equipped with a Magnetorheological Damper. Aerospace 2023, 10, 951. [Google Scholar] [CrossRef]
- Lee, H.; Hwang, J. Study on the Taxing Mode Control of MR Damper Landing Gear. J. Aerosp. Syst. Eng. 2019, 13, 43–51. [Google Scholar] [CrossRef]
- Textron Aviation Baron G58. Available online: https://beechcraft.txtav.com/en/baron-g58 (accessed on 17 December 2024).
- Lord-MAR. Available online: https://www.shoplordmr.com/mr-products/mrf-140cg-magneto-rheological-fluid-250ml (accessed on 17 December 2024).
- Airplane Flying Handbook. Available online: https://www.faa.gov/regulations_policies/handbooks_manuals/aviation/airplane_handbook (accessed on 17 December 2024).
- FAA AC 25.723-1—Shock Absorption Tests. Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentid/22663 (accessed on 19 December 2024).
- FAA Airport Pavement Roughness Research. Available online: https://www.airporttech.tc.faa.gov/Airport-Pavement/Nondestructive-Pavement-Testing/AirportPavementRoughnessResearch (accessed on 24 November 2024).
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; ISBN 978-0-262-19398-6. [Google Scholar]
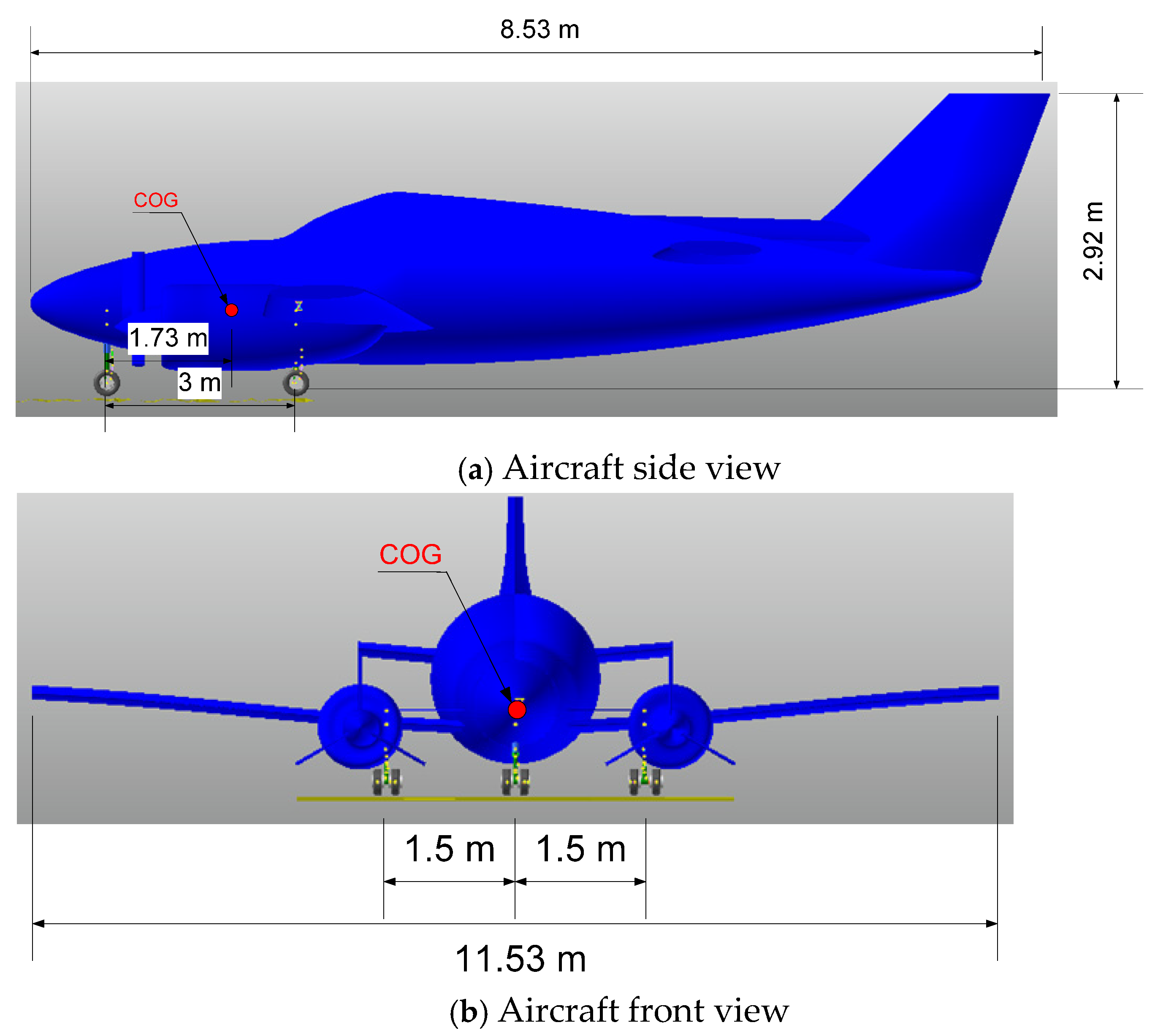

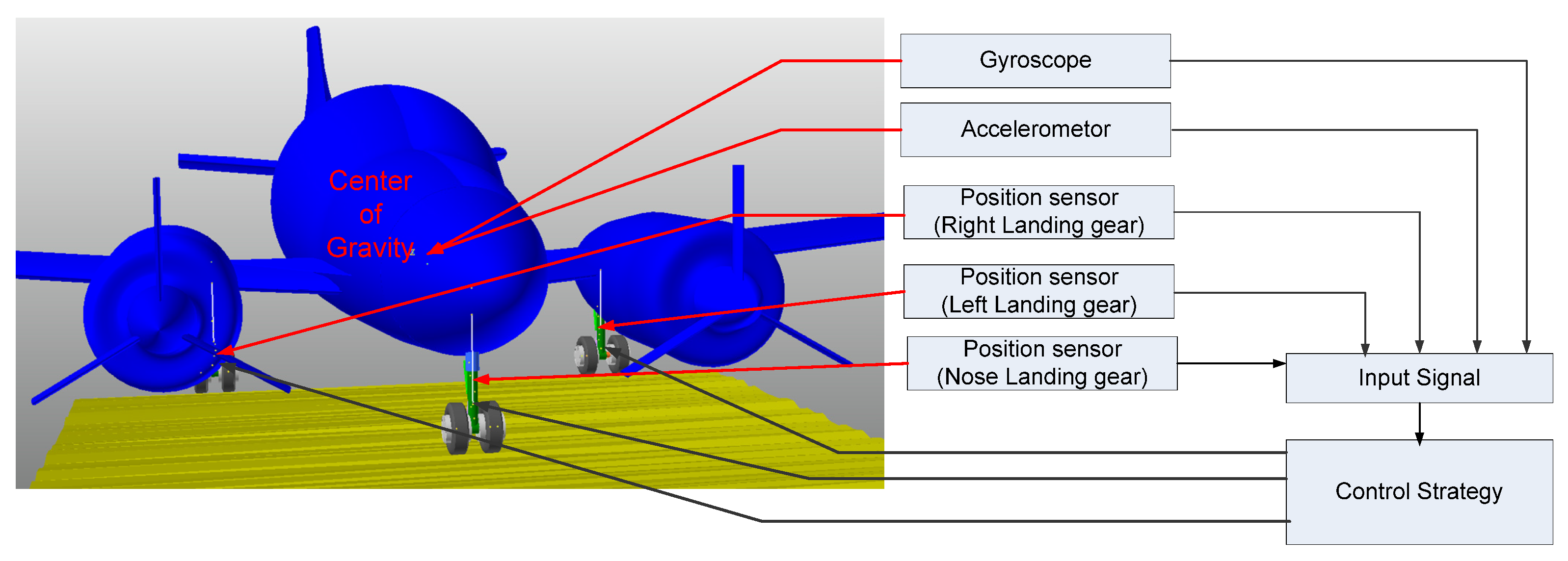


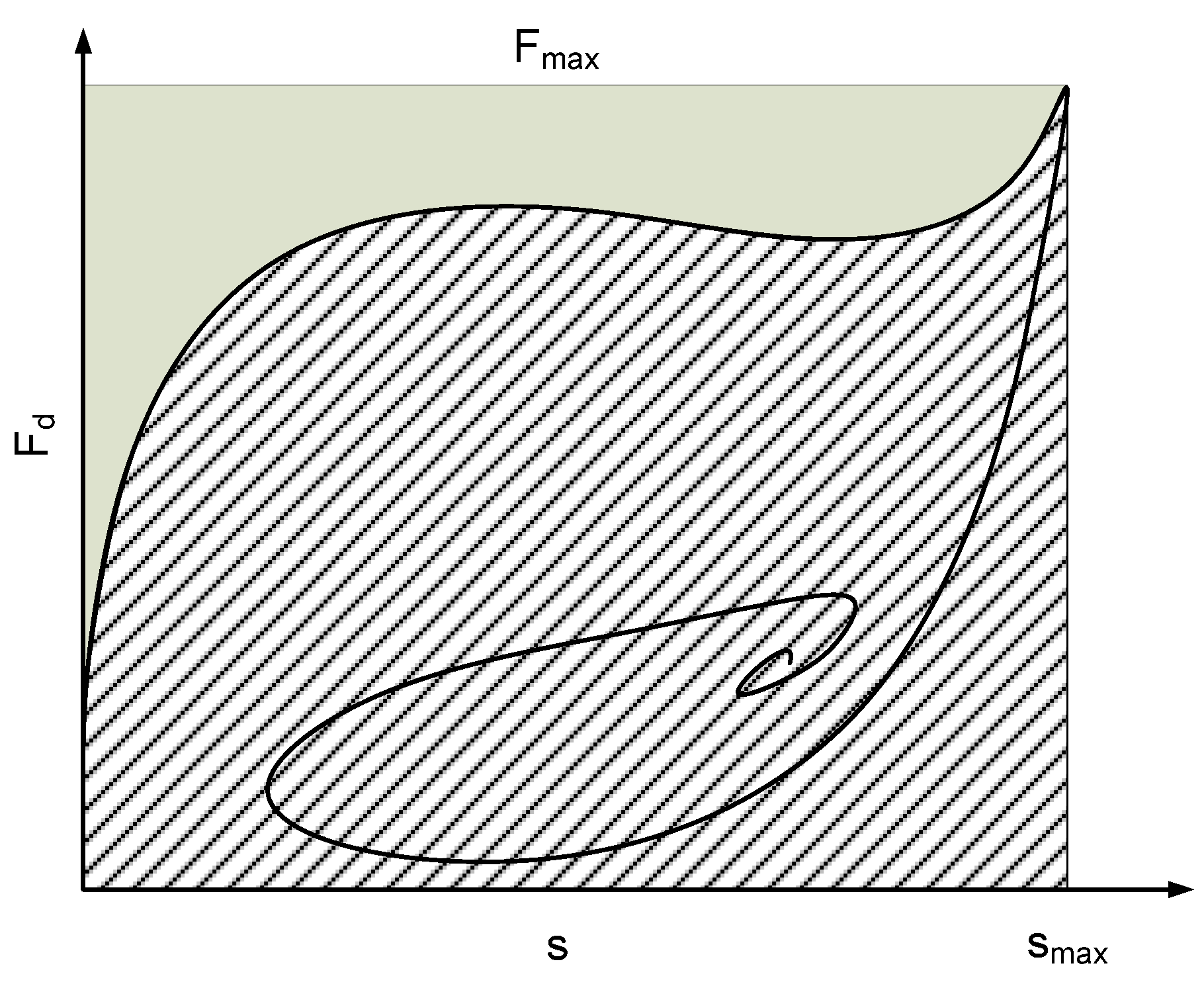
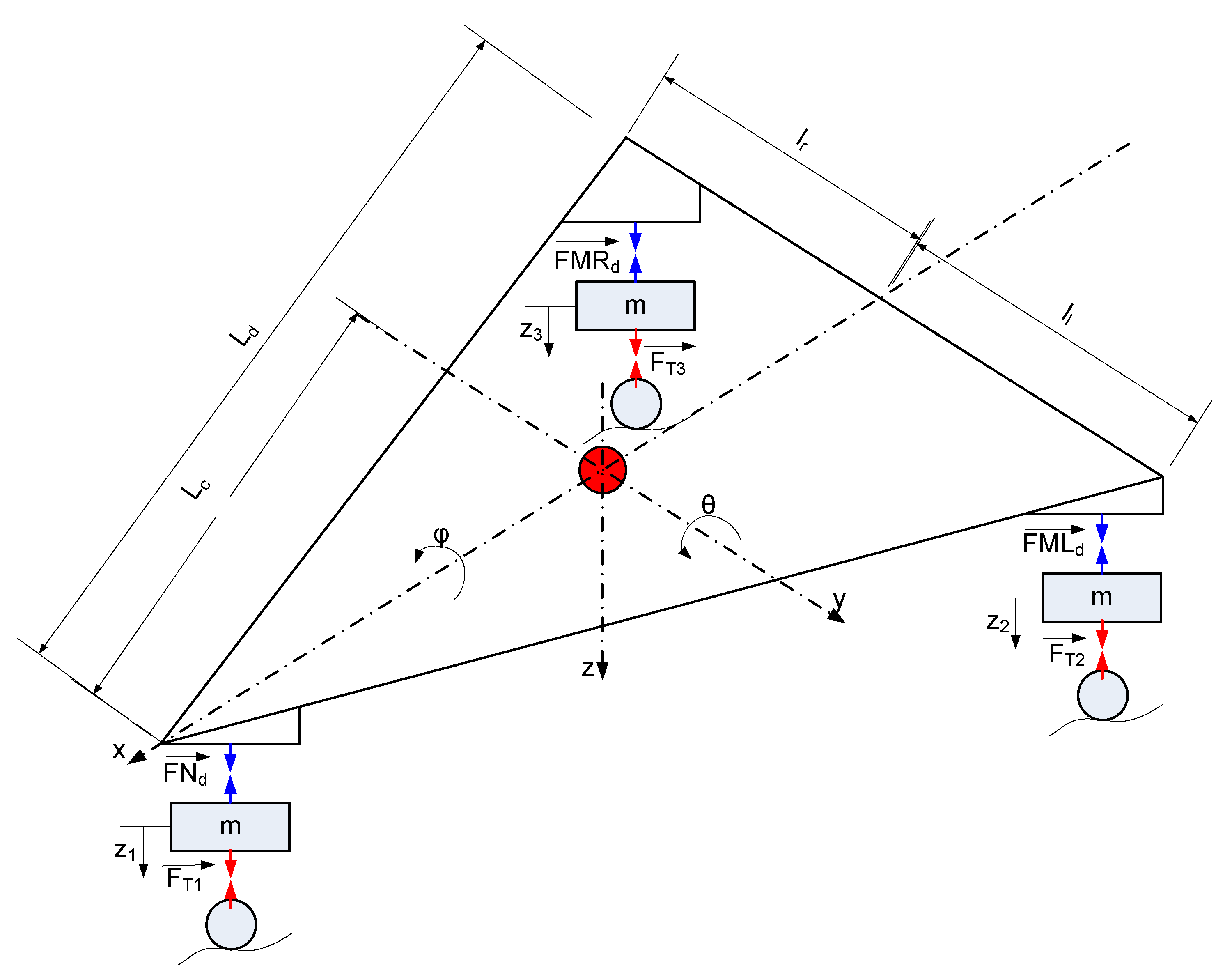
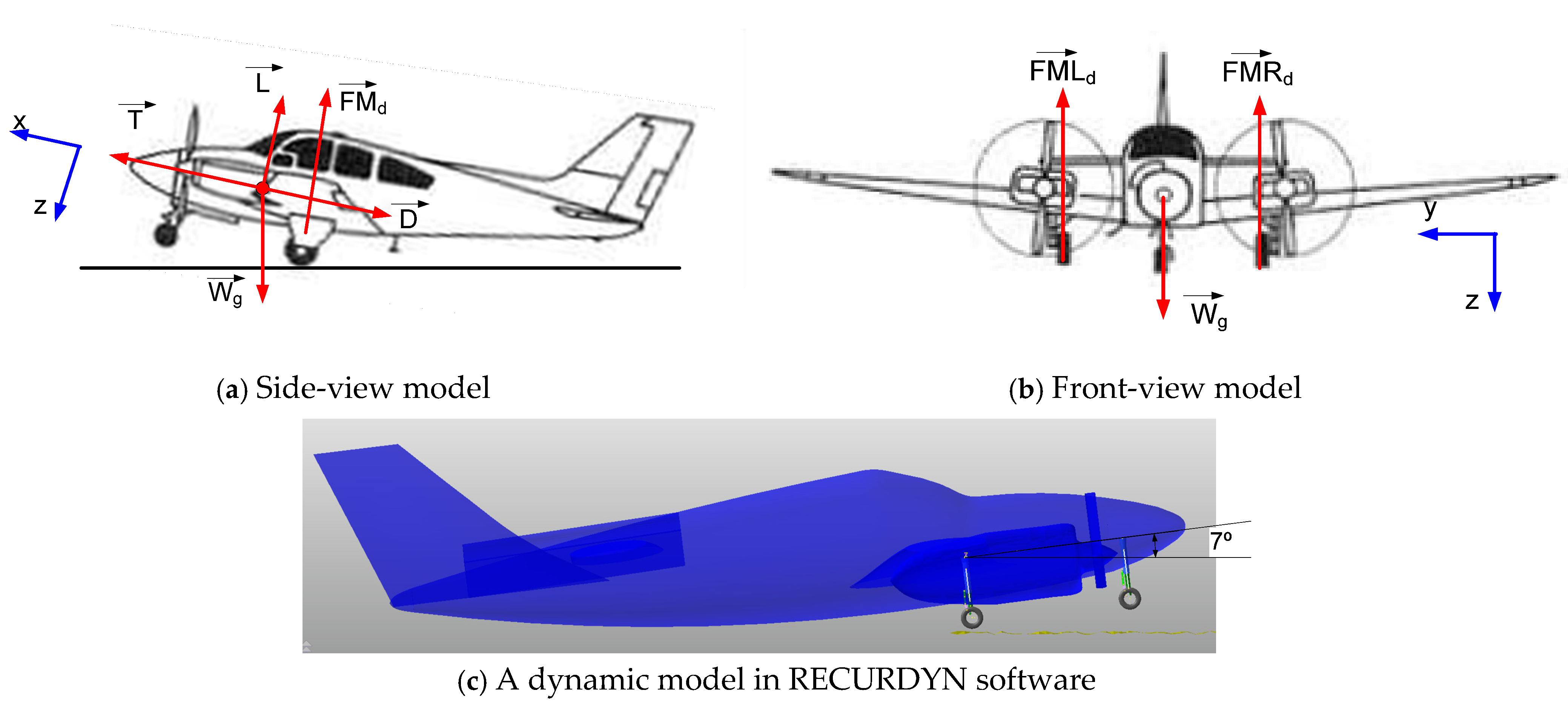
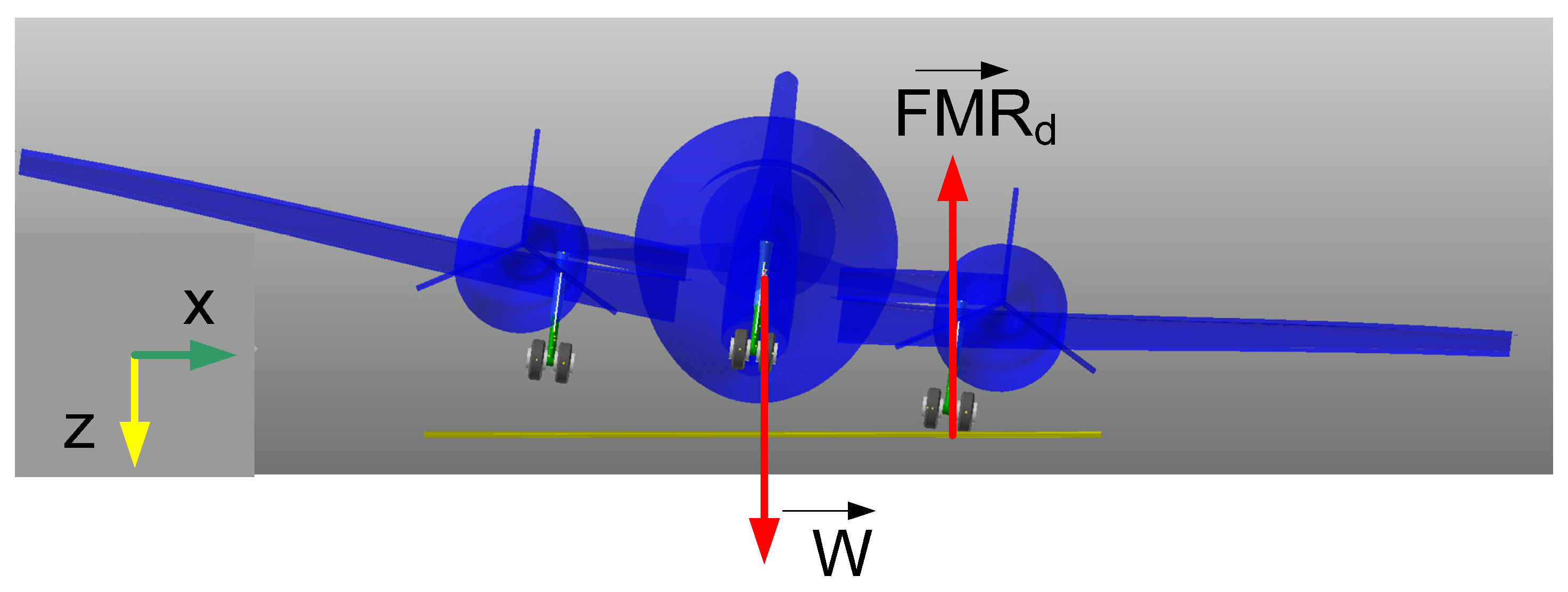


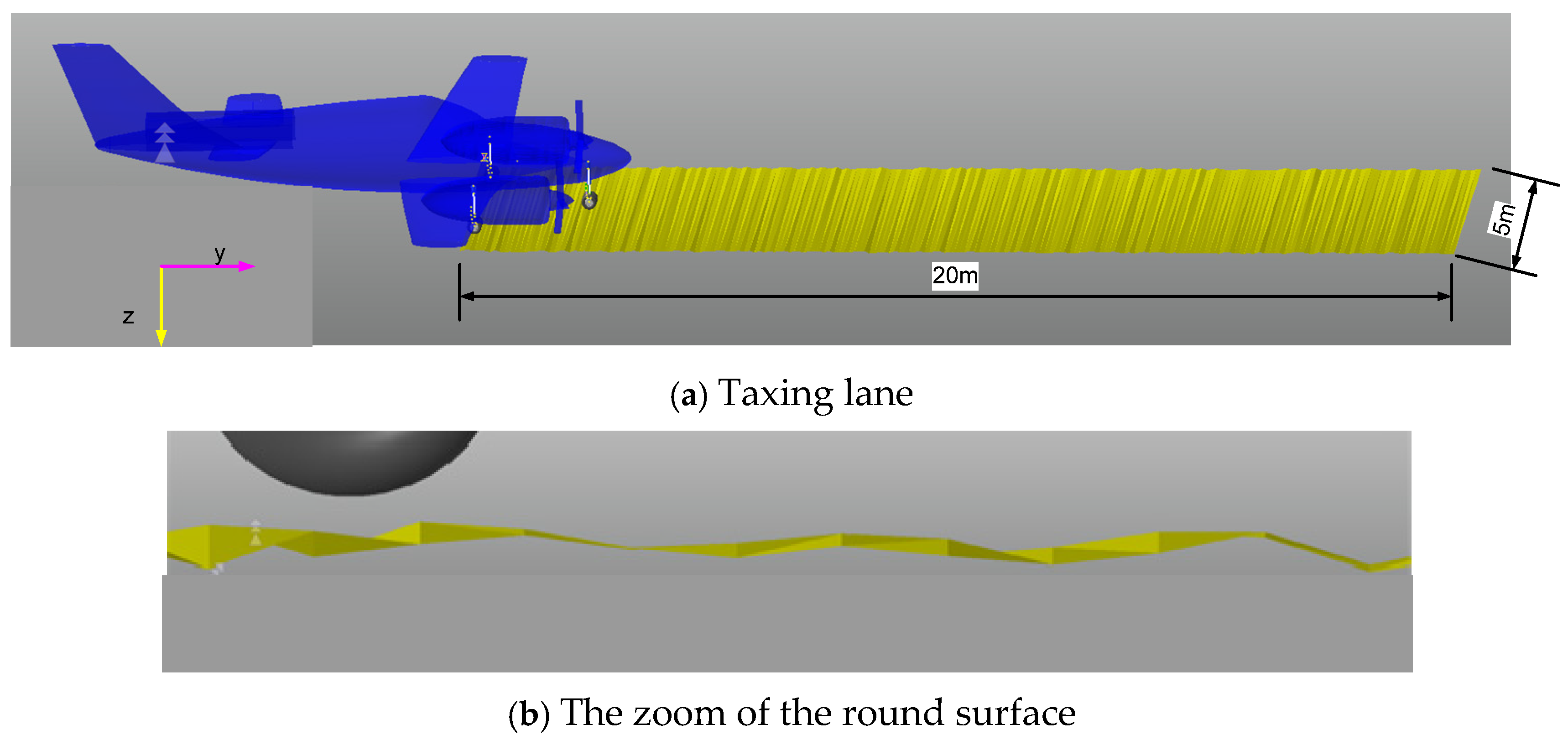
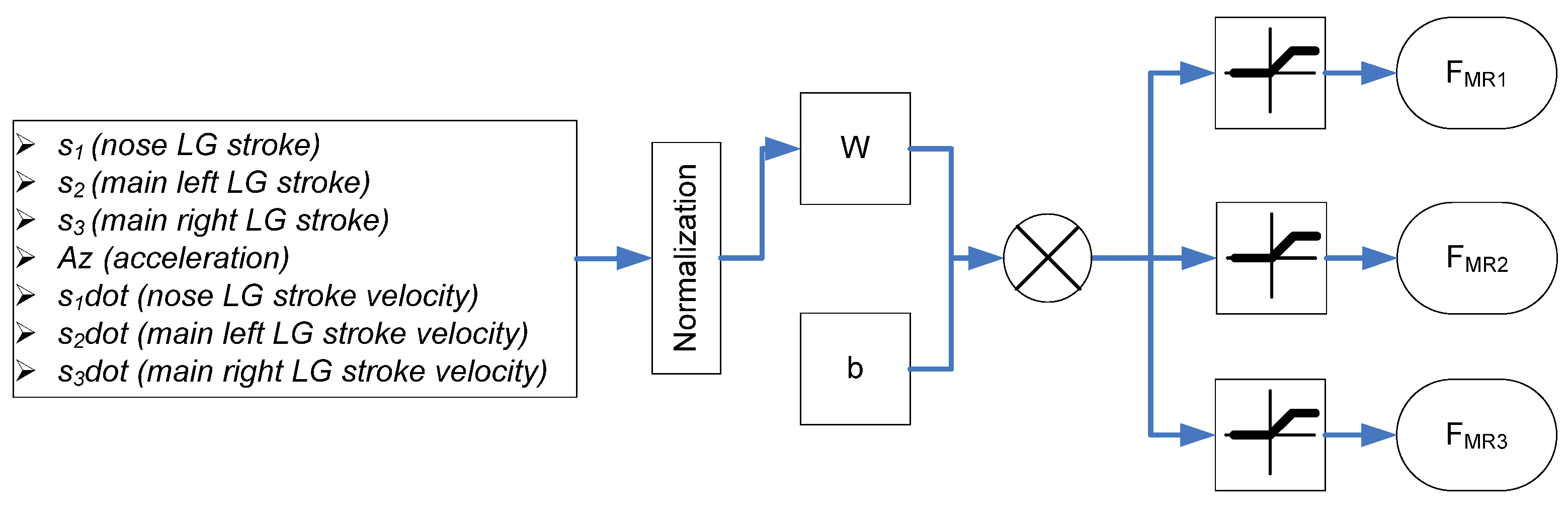

| Author | Article | Scope of Study of MR Landing Gear | Control Strategies | Year |
|---|---|---|---|---|
| Jo et al. | [14] | Single landing gear, touchdown phase | On–off control, skyhook control, hybrid control | 2021 |
| Kang and Choi | [11] | Single landing gear, touchdown phase | On–off control, skyhook control, hybrid control | 2024 |
| Han et al. | [24] | Single landing gear, touchdown phase | On–off control, skyhook control, | 2019 |
| Kang et al. | [12,13,18,25] | Single landing gear, 6-DOF aircraft landing gear system, touchdown phase | On–off control, skyhook control, hybrid control, landing efficiency control, | 2019–2023 |
| Hao et al. | [16] | Single landing gear, touchdown phase | 2023 | |
| QV Luong et al. | [21,26,27] | Single landing gear, touchdown phase | Supervise learning, genetic algorithm neural network, robust adaptive SMC | 2020–2021 |
| Yoon et al. | [17] | Single landing gear, touchdown phase | Energy conservation control, | 2020 |
| Le et al. | [28] | Single landing gear, touchdown phase | Model predicted control | 2024 |
| Lee et al. | [29] | Single landing gear, taxing phase | Skyhook control | 2019 |
| Present work | 6-DOF aircraft landing gear system involving both touchdown phase and taxing phase | Q-learning neural network | ||
| Symbol | Value | Unit |
|---|---|---|
| Ap | 2.6 × 10−3 | m2 |
| C | 7.0 | kNs/m |
| g | 9.81 | m/s2 |
| M | 2250 | kg |
| m | 18 | kg |
| n | 1.3 | |
| kT | 412 | kN/m |
| V0 | 6.29 × 10−4 | m3 |
| u | 0~1 | A |
| v(0) | 1–3 | m/s |
| lr | 1.5 | m |
| ll | 1.5 | m |
| la | 1.73 | m |
| lb | 0.87 | m |
| Ixx | 79.1 | kgm2 |
| Iyy | 2030.6 | kgm2 |
| Izz | 2317.2 | kgm2 |
| φ | 0–7 | ° |
| θ | 0–7 | ° |
| W | 0.07 | 0.01 | 0.18 | −0.05 | 0.01 | −0.10 | −0.12 | 0.40 | −0.09 | 0.06 | 0.00 | 0.25 | 0.06 | −0.21 | −0.04 |
| −0.11 | 0.25 | 0.20 | −0.35 | 0.14 | 0.30 | 0.05 | −0.31 | −0.38 | −0.45 | 0.24 | −0.08 | 0.03 | −0.04 | −0.10 | |
| 0.09 | −0.31 | −0.15 | −0.39 | 0.08 | 0.18 | −0.09 | −0.26 | −0.10 | −0.13 | −0.08 | 0.34 | −0.27 | −0.35 | −0.33 | |
| 0.01 | 0.45 | 0.15 | −0.37 | −0.20 | −0.11 | 0.28 | −0.17 | −0.10 | 0.33 | 0.19 | −0.52 | 0.27 | 0.10 | 0.18 | |
| 0.18 | −0.19 | −0.14 | 0.21 | −0.14 | 0.35 | −0.02 | 0.38 | −0.20 | 0.10 | −0.40 | −0.45 | −0.34 | 0.19 | −0.02 | |
| −0.10 | −0.22 | 0.33 | −0.09 | −0.14 | −0.14 | 0.47 | 0.04 | 0.38 | 0.09 | 0.15 | 0.47 | 0.44 | −0.42 | −0.01 | |
| −0.11 | −0.06 | 0.01 | 0.21 | −0.42 | 0.34 | 0.37 | 0.17 | 0.21 | 0.18 | 0.48 | −0.10 | −0.27 | 0.38 | −0.28 | |
| b | −0.51 | 0.02 | −0.09 |
| Case | Sink Speed (m/s) | Passive Damper | Skyhook Controller | Q-Learning Controller | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| η1 | η2 | η3 | RMS | η1 | η2 | η3 | RMS | η1 | η2 | η3 | RMS | ||
| 1-P | 1 | 0.80 | 0.61 | 0.73 | 4.23 | 0.65 | 0.5 | 0.54 | 3.59 | 0.8 | 0.81 | 0.75 | 3.85 |
| 2 | 0.70 | 0.43 | 0.74 | 5.3 | 0.69 | 0.46 | 0.6 | 4.39 | 0.82 | 0.61 | 0.76 | 4.78 | |
| 3 | 0.62 | 0.40 | 0.68 | 7.0 | 0.76 | 0.47 | 0.66 | 5.83 | 0.78 | 0.60 | 0.75 | 6.3 | |
| 2-P | 1 | 0.73 | 0.84 | 0.83 | 2.11 | 0.45 | 0.60 | 0.60 | 2.16 | 0.73 | 0.78 | 0.85 | 2.10 |
| 2 | 0.63 | 0.79 | 0.77 | 3.11 | 0.49 | 0.60 | 0.60 | 2.97 | 0.66 | 0.73 | 0.78 | 2.87 | |
| 3 | 0.69 | 0.75 | 0.75 | 4.93 | 0.55 | 0.69 | 0.68 | 4.19 | 0.65 | 0.77 | 0.80 | 4.4 | |
| 3-P | 1 | 0.80 | 0.83 | 0.81 | 1.66 | 0.47 | 0.53 | 0.53 | 1.59 | 0.8 | 0.83 | 0.86 | 1.59 |
| 2 | 0.76 | 0.86 | 0.87 | 2.84 | 0.5 | 0.6 | 0.6 | 2.88 | 0.78 | 0.77 | 0.85 | 2.68 | |
| 3 | 0.73 | 0.75 | 0.73 | 4.83 | 0.64 | 0.75 | 0.75 | 4.36 | 0.86 | 0.82 | 0.75 | 4.4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luong, Q.-V.; Le, Q.-N.; Hwang, J.-H.; Ho, T.-M.-N. 6DOF Aircraft Landing Gear System with Magnetorheological Damper in Various Taxing and Touchdown Scenarios. Micromachines 2025, 16, 355. https://doi.org/10.3390/mi16030355
Luong Q-V, Le Q-N, Hwang J-H, Ho T-M-N. 6DOF Aircraft Landing Gear System with Magnetorheological Damper in Various Taxing and Touchdown Scenarios. Micromachines. 2025; 16(3):355. https://doi.org/10.3390/mi16030355
Chicago/Turabian StyleLuong, Quoc-Viet, Quang-Ngoc Le, Jai-Hyuk Hwang, and Thi-My-Nu Ho. 2025. "6DOF Aircraft Landing Gear System with Magnetorheological Damper in Various Taxing and Touchdown Scenarios" Micromachines 16, no. 3: 355. https://doi.org/10.3390/mi16030355
APA StyleLuong, Q.-V., Le, Q.-N., Hwang, J.-H., & Ho, T.-M.-N. (2025). 6DOF Aircraft Landing Gear System with Magnetorheological Damper in Various Taxing and Touchdown Scenarios. Micromachines, 16(3), 355. https://doi.org/10.3390/mi16030355






