Methods for Designing High-Precision Relaxation Oscillator
Abstract
:1. Introduction
- (1)
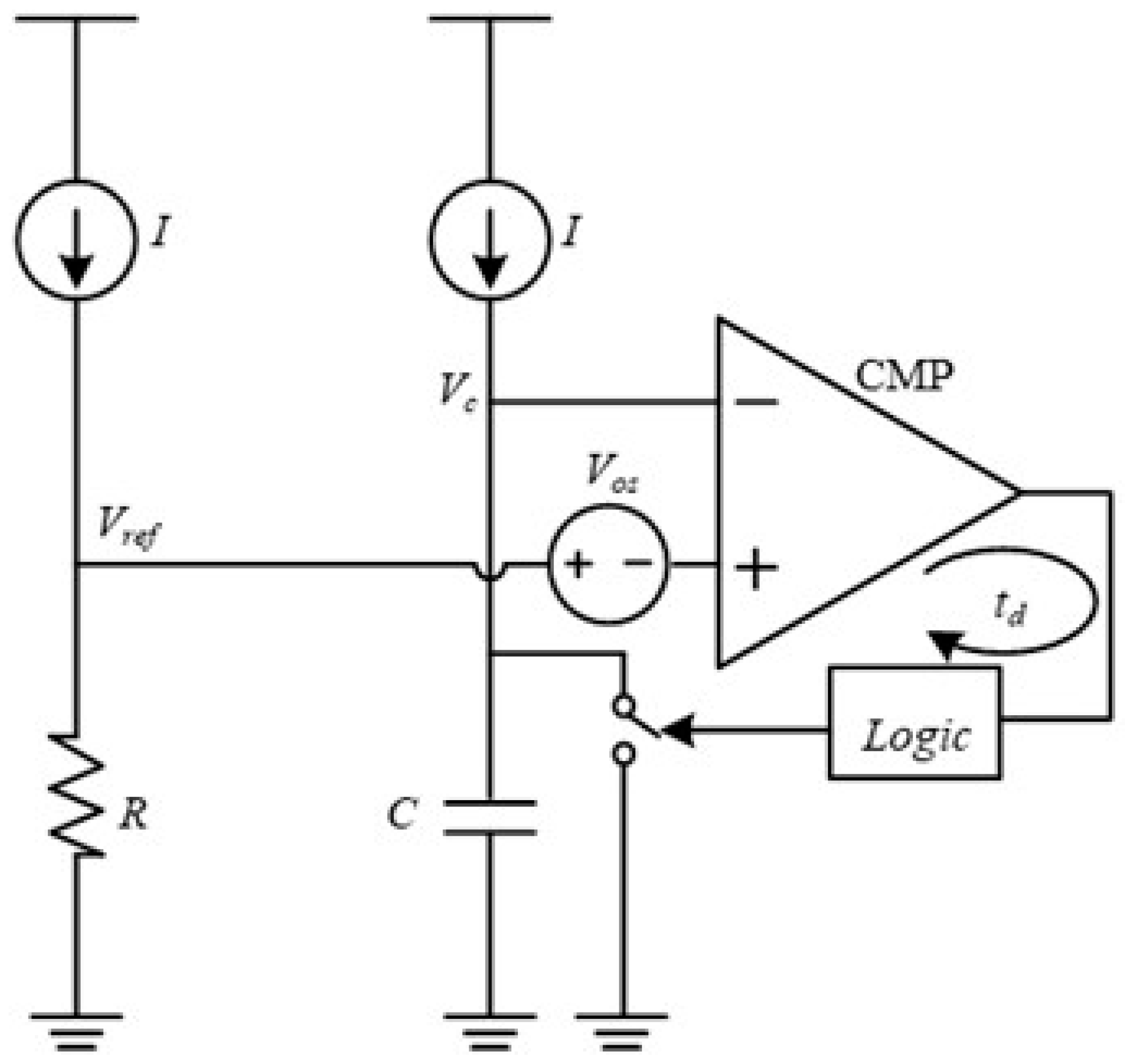
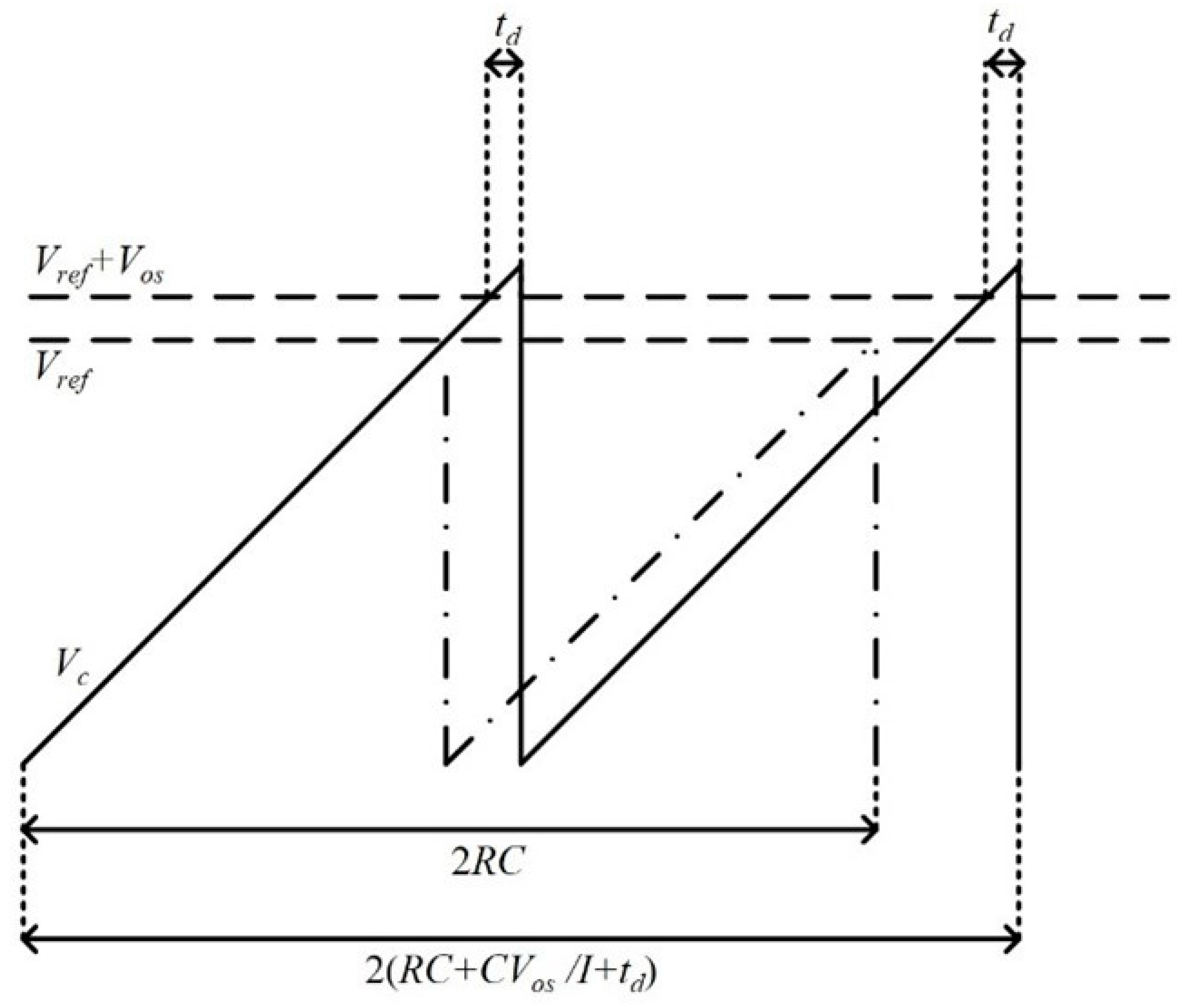
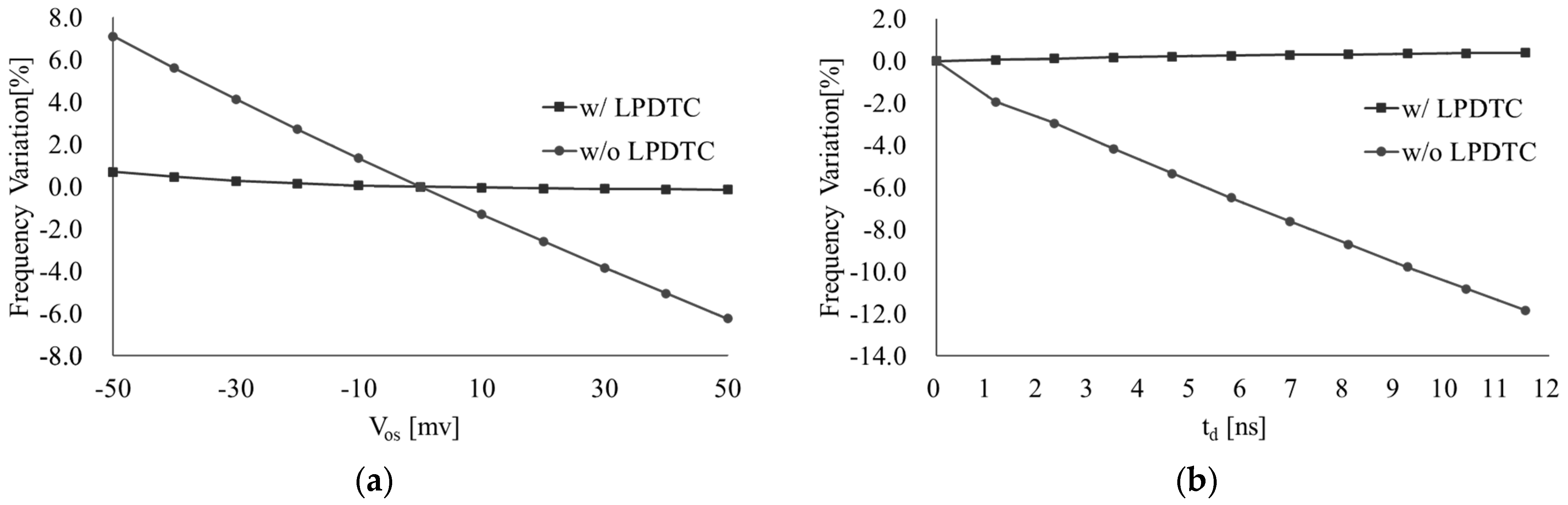
- Low-power delay time cancellation (LPDTC) technique: This innovative technique minimizes the impact of the comparator delay time and offsets voltage while maintaining low current consumption by utilizing only two comparators.
- (2)
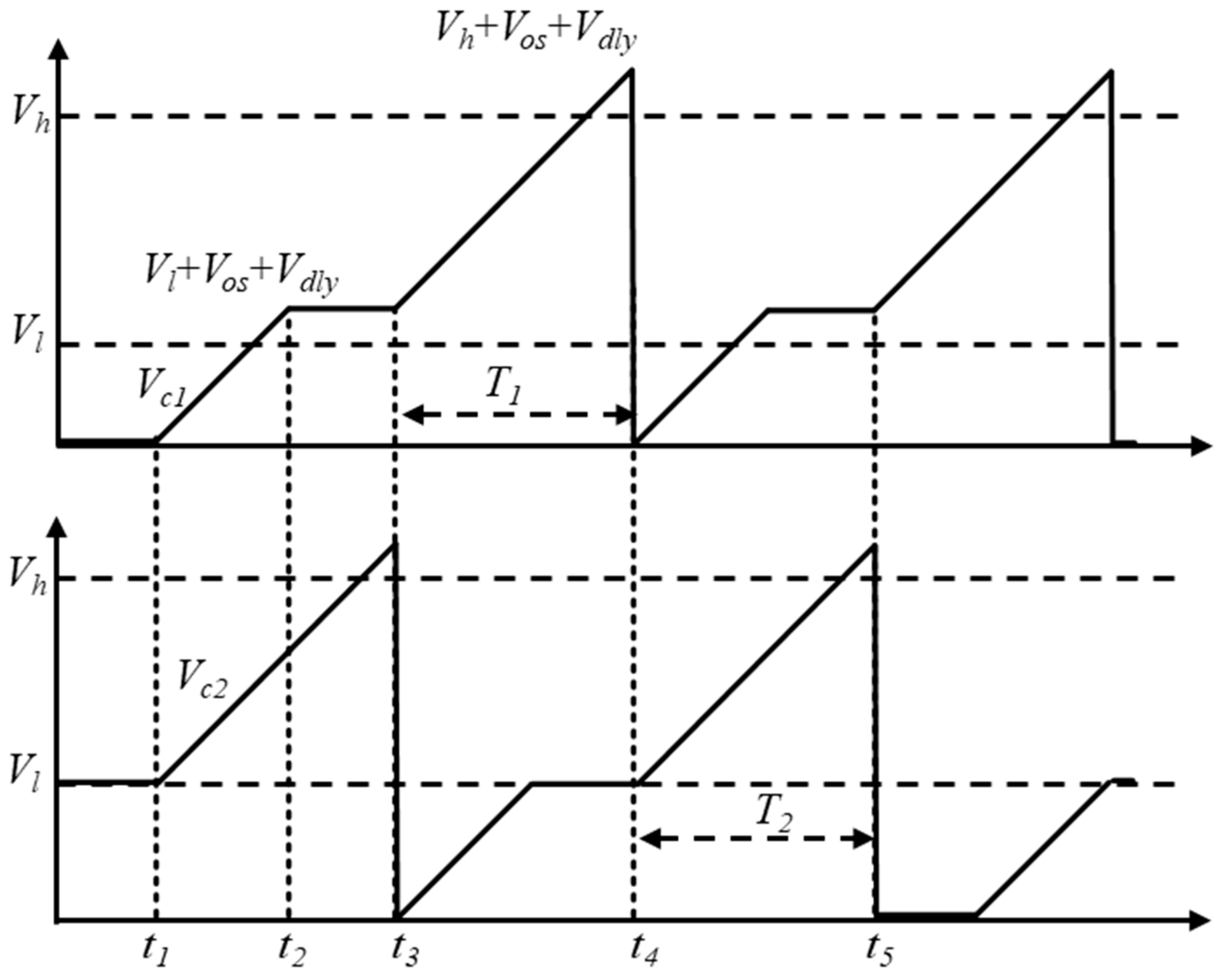
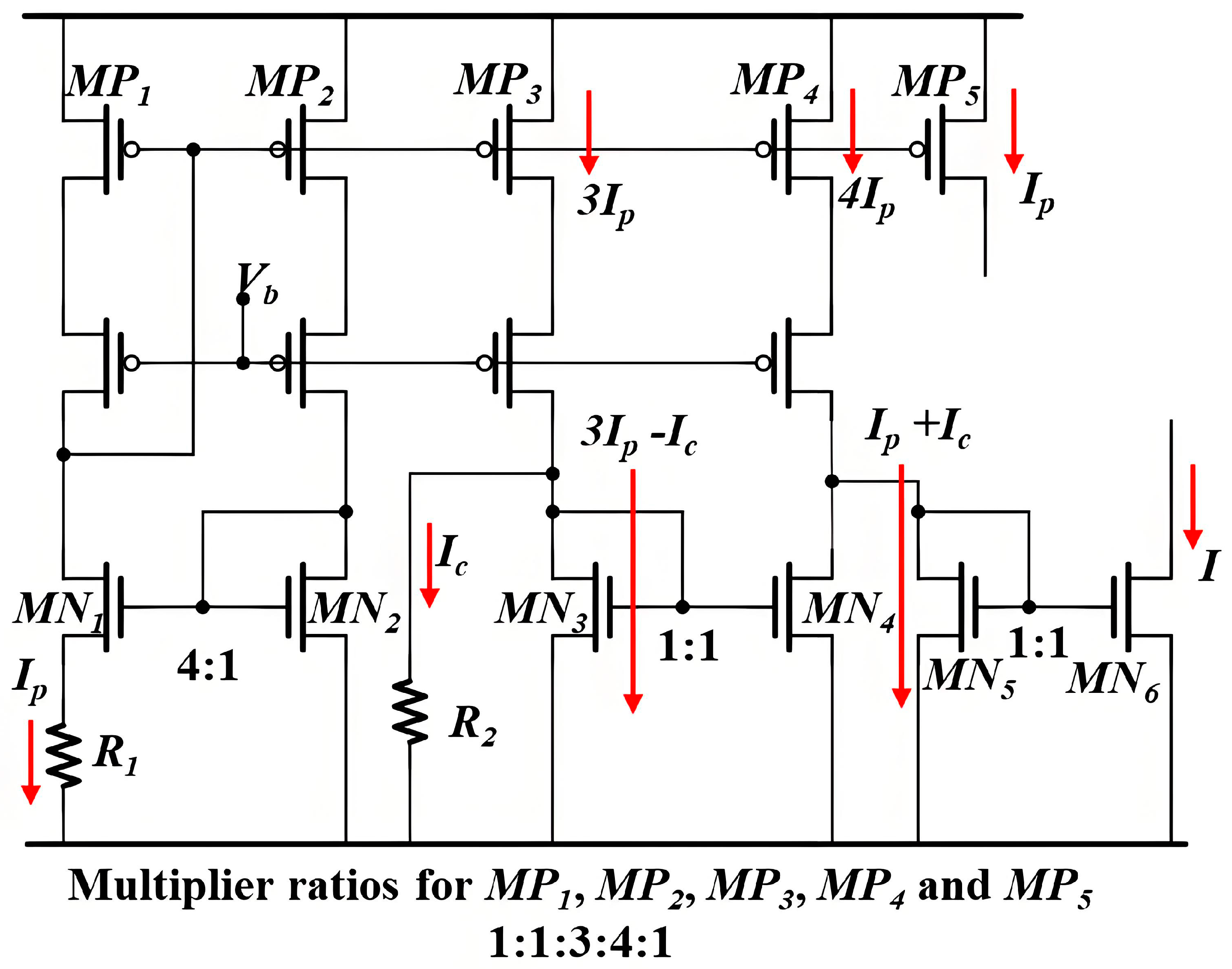
- Current ratio adjustment (CRA) method: This method mitigates temperature-induced variations in resistors by adjusting the ratio of the reference currents in the relaxation oscillators.
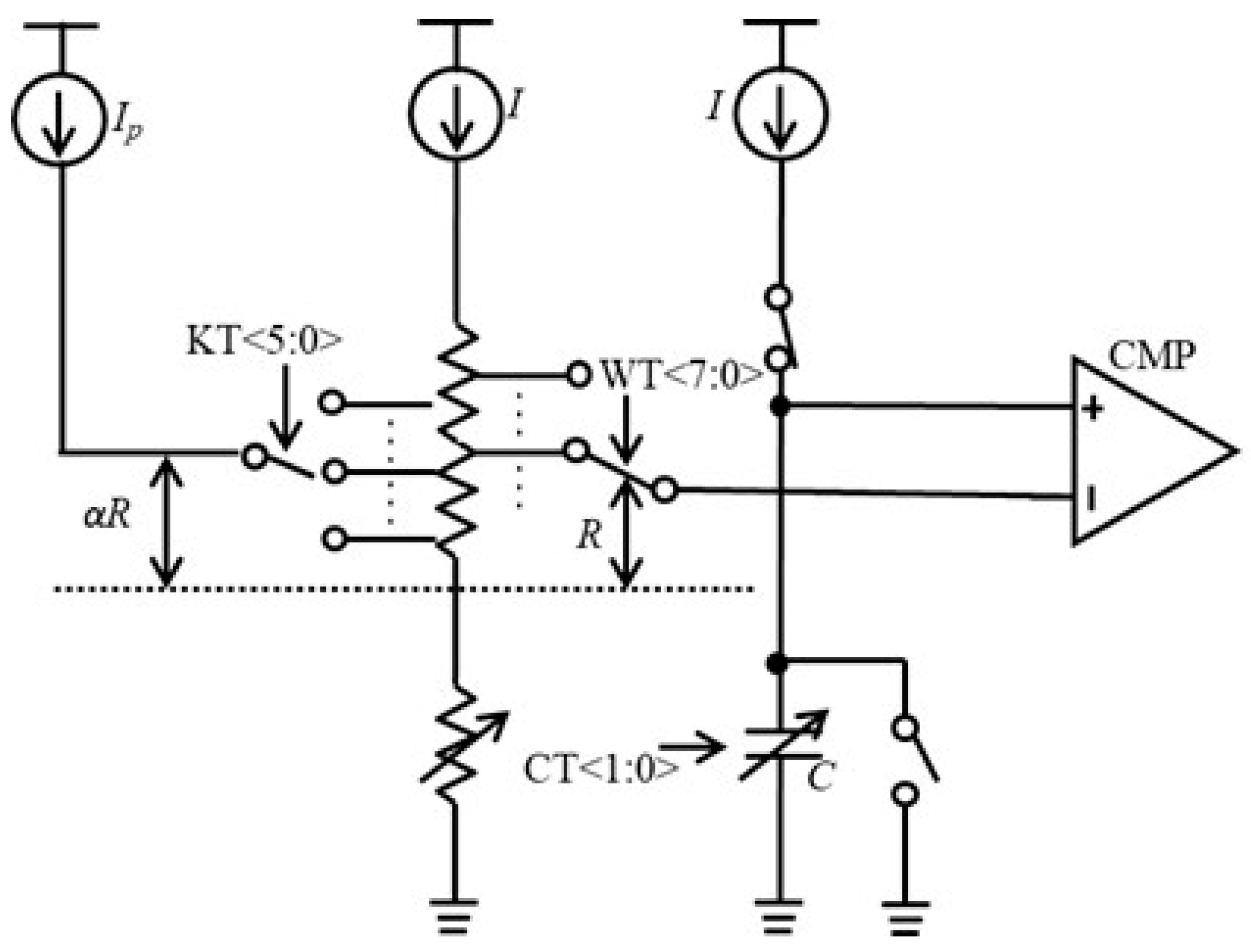
2. Delay Time Cancellation Technique
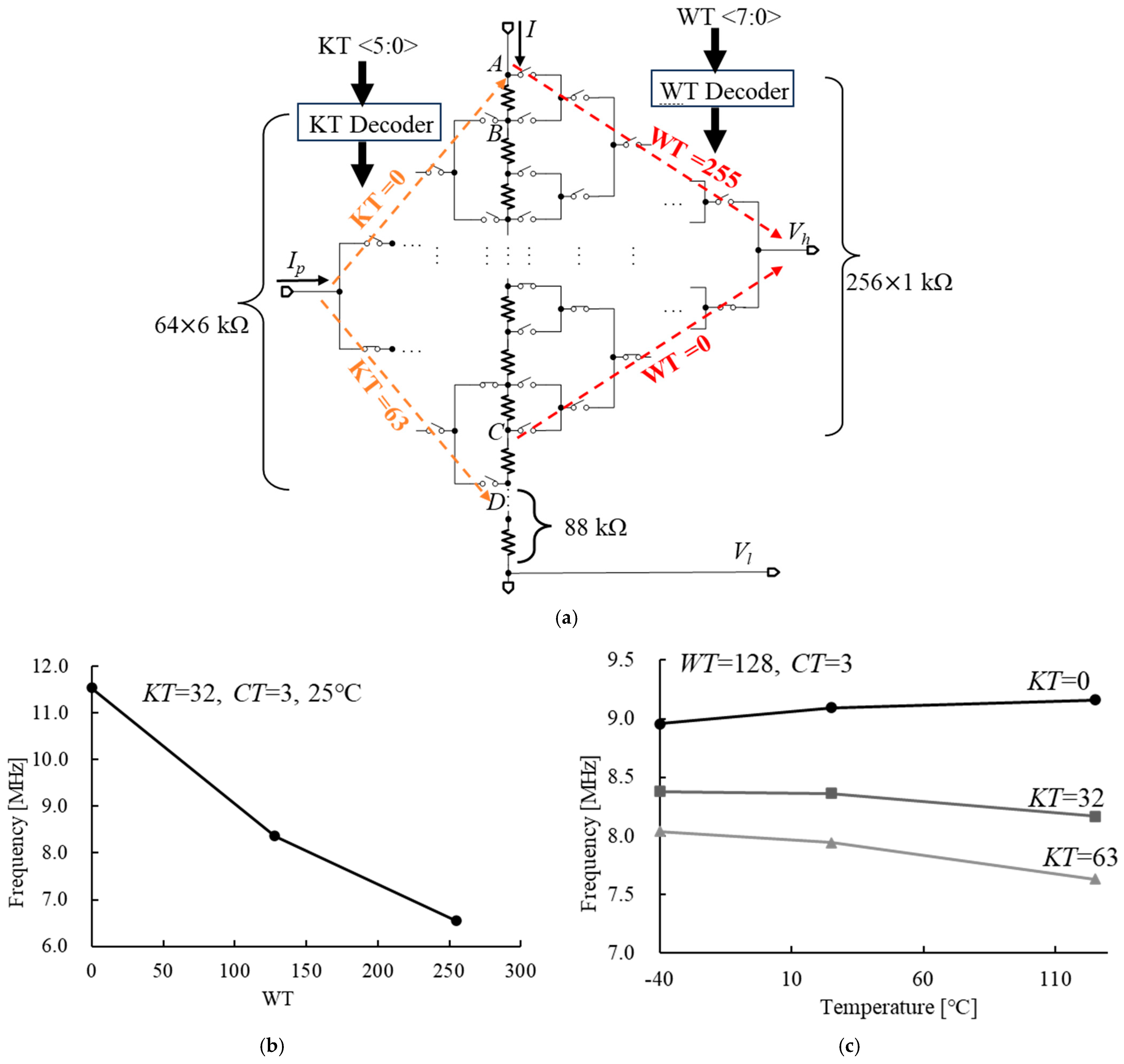
3. Current Ratio Adjustment Method
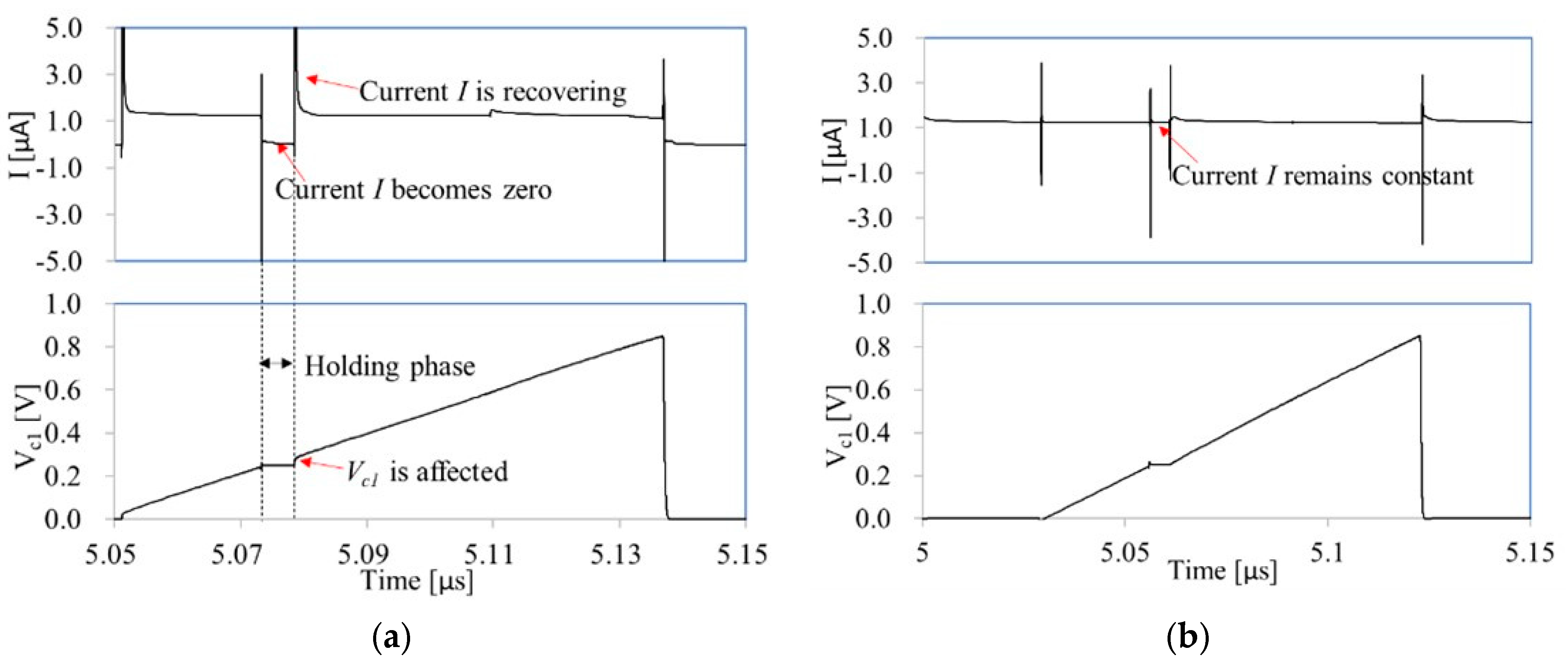
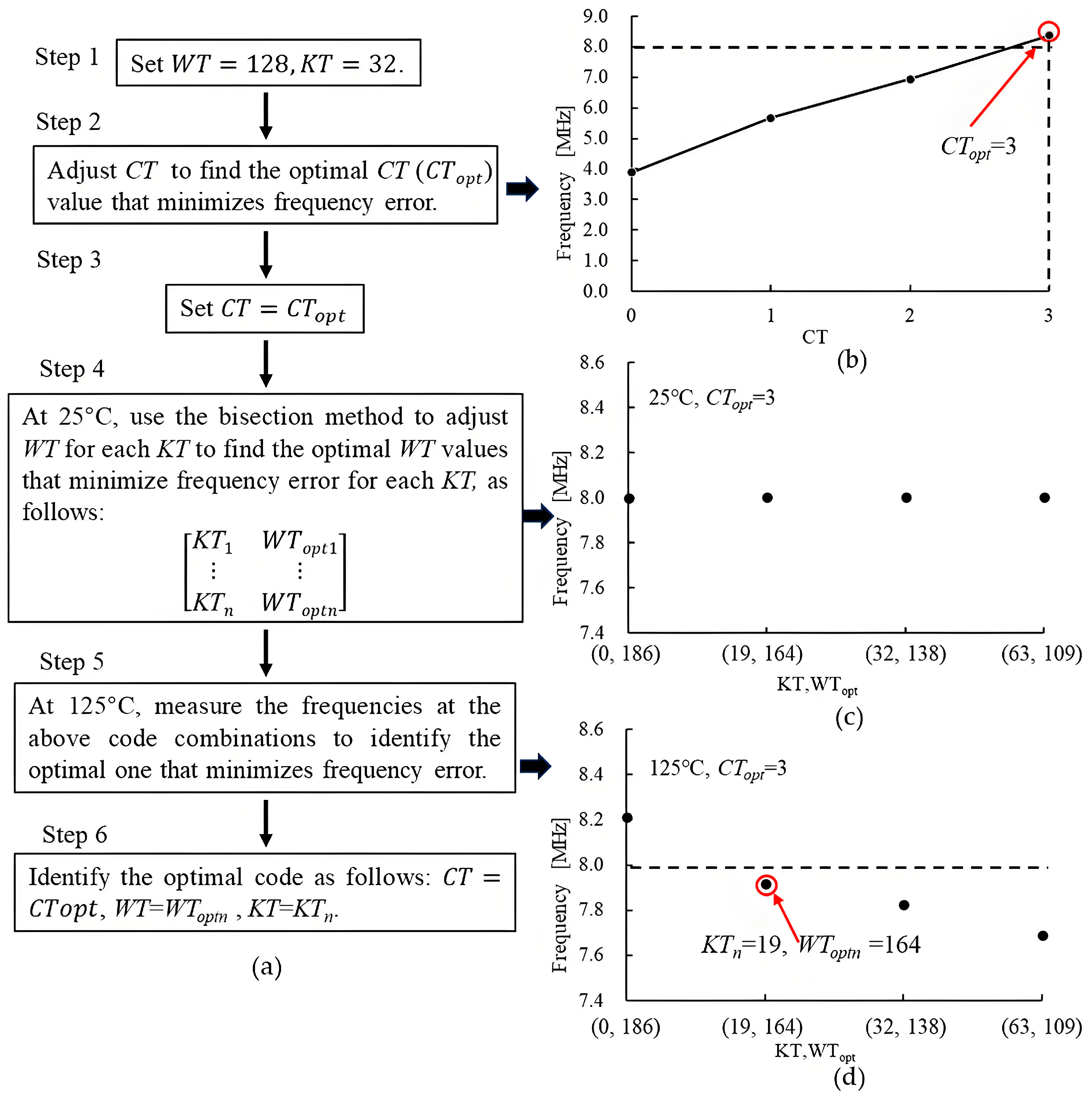
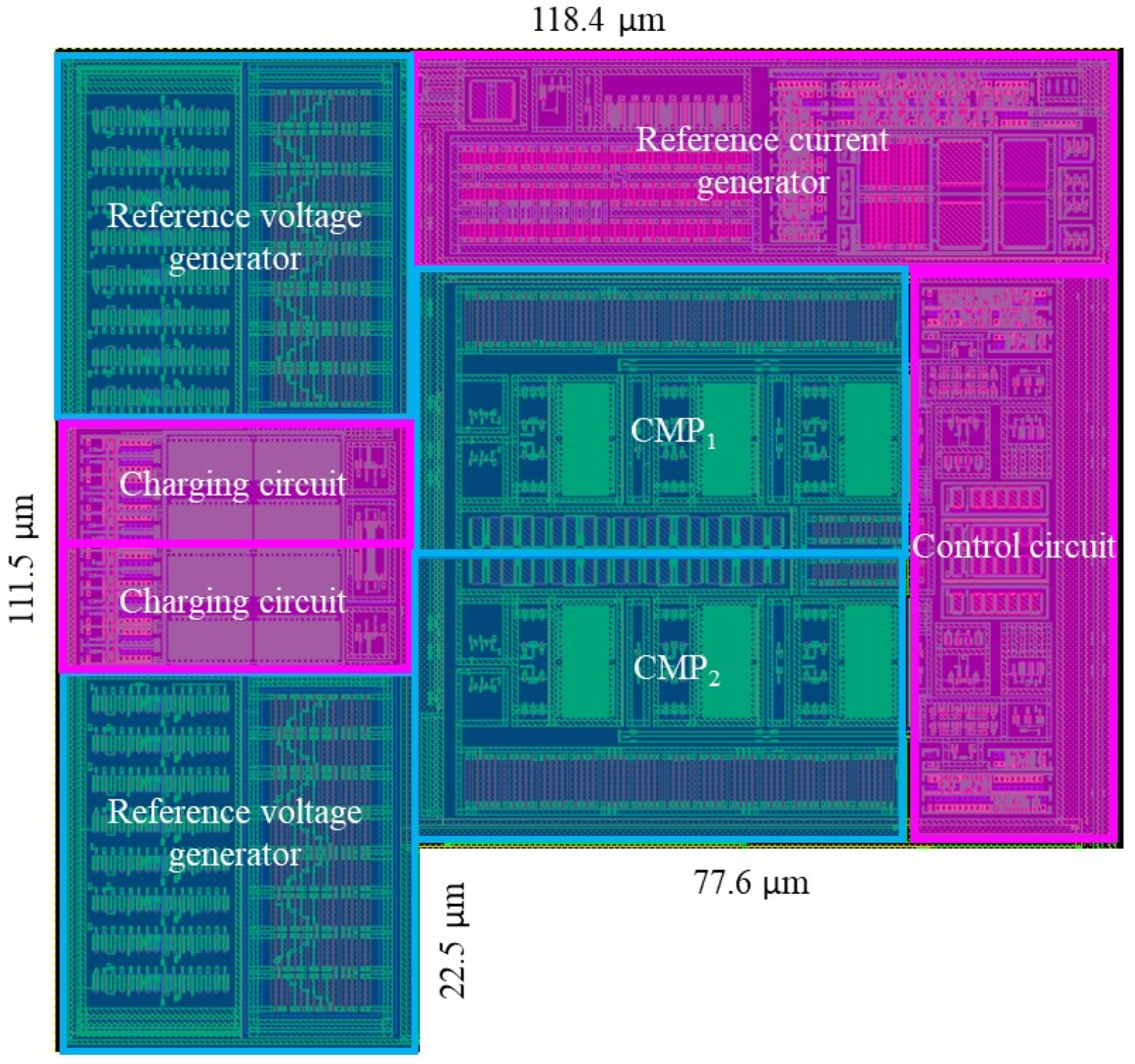
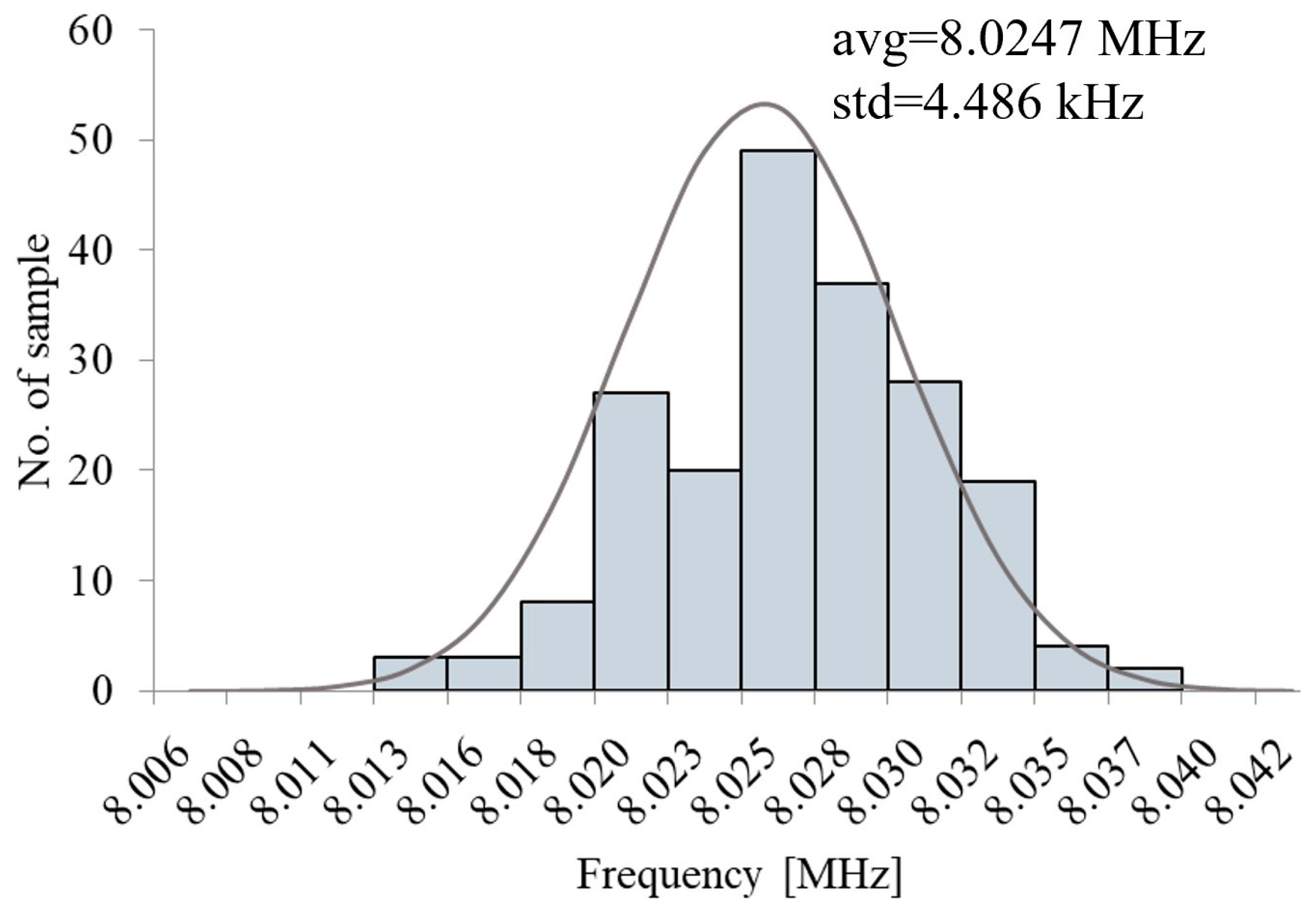
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, H.; Dai, F. Design of smart home security system based on 52 MCU. J. Adv. Artif. Life Robot. 2021, 1, 199–203. [Google Scholar]
- Otani, S.; Kondo, H. RX v2: Renesas’s new-generation MCU processor. IEICE Trans. Electron. 2015, 98, 544–549. [Google Scholar] [CrossRef]
- Kawamura, Y.; Okada, N.; Matsuda, Y.; Matsumura, T.; Makino, H.; Arimoto, K. A Field Programmable Sequencer and Memory with Middle Grained Programmability Optimized for MCU Peripherals. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, 99, 917–928. [Google Scholar] [CrossRef]
- Takashi, K.; Taito, Y.; Hidaka, H. Essential Roles, Challenges and Development of Embedded MCU Micro-Systems to Innovate Edge Computing for the IoT/AI Age. IEICE Trans. Electron. 2020, 103, 132–143. [Google Scholar]
- Liu, Y.; Zhu, Z.; Bao, R.; Yang, S.; Liu, J.; Zhou, X.; Li, Q. A Low-Power RC Oscillator with Offset and Path Delay Cancellation. In Proceedings of the 2021 IEEE International Conference on Integrated Circuits, Technologies and Applications, Zhuhai, China, 24–26 November 2021. [Google Scholar]
- Chang, Y.-A.; Adiono, T.; Hamidah, A.; Liu, S.-I. An on-chip relaxation oscillator with comparator delay compensation. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 969–973. [Google Scholar] [CrossRef]
- Hsiao, K. A 32.4 ppm/°C 3.2-1.6 V self-chopped relaxation oscillator with adaptive supply generation. In Proceedings of the 2012 Symposium on VLSI Circuits, Honolulu, HI, USA, 13–15 June 2012. [Google Scholar]
- Truesdell, D.S.; Li, S.; Calhoun, B.H. A 0.5V 560kHz 18.8fJ/Cycle Ultra-Low Energy Oscillator in 65nm CMOS with 96.1ppm/°C Stability using a Duty-Cycled Digital Frequency-Locked Loop. In Proceedings of the 2020 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 16–19 June 2020. [Google Scholar]
- Wang, J.; Goh, W.L. A 13.5-MHz relaxation oscillator with ±0.5% temperature stability for RFID application. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems, Montreal, QC, Canada, 22–25 May 2016. [Google Scholar]
- Cao, Y.; Leroux, P.; De Cock, W.; Steyaert, M. A 63,000 Q-factor relaxation oscillator with switched-capacitor integrated error feedback. In Proceedings of the 2013 IEEE International Solid-State Circuits Conference Digest of Technical Papers, San Francisco, CA, USA, 17–21 February 2013. [Google Scholar]
- Paidimarri, A.; Griffith, D.; Wang, A.; Burra, G.; Chandrakasan, A.P. An RC Oscillator with Comparator Offset Cancellation. IEEE J. Solid-State Circuits 2016, 51, 1866–1877. [Google Scholar] [CrossRef]
- Chiang, Y.-H.; Liu, S.-I. A Submicrowatt 1.1-MHz CMOS Relaxation Oscillator with Temperature Compensation. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 837–841. [Google Scholar] [CrossRef]
- Lee, J.; George, A.K.; Je, M. An ultra-low-noise swing-boosted differential relaxation oscillator in 0.18-µm CMOS. IEEE J. Solid-State Circuits 2020, 55, 2489. [Google Scholar] [CrossRef]
- Sun, J.; Hana, Y. A low power low supply sensitivity current-mode relaxation oscillator. IEICE Electron. Express 2014, 11, 23. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Zhao, H.; Zhao, H.; Yin, J.; Yin, J.; Qiao, S.; Qiao, S.; Zhou, Y.; Zhou, Y. A fully integrated RC oscillator with adaptive-body-biasing. IEICE Electron. Express 2022, 19, 20220102. [Google Scholar] [CrossRef]
- Xie, Z.; Zou, Z.; Lv, Z.; Yi, Y.; Zhang, J.; Tong, Q.; Liu, D. A 2.9 MHz low power RC relaxation oscillator with delay equivalent electric charges storage and fully covered trimming strategy. Microelectron. J. 2024, 143, 106062. [Google Scholar]
- Hu, Y.; Li, Z.; Hou, J.; Ma, W.; Lu, C.; Xiao, Z.; Liu, H.; Hu, W. A constant charging-current relaxation oscillator with a duty-cycled main comparator and an adaptive auxiliary comparator. Microelectron. J. 2022, 128, 105566. [Google Scholar]
- Mikulić, J.; Schatzberger, G.; Barić, A. A 1-MHz on-chip relaxation oscillator with comparator delay cancelation. In Proceedings of the 2017 43rd IEEE European Solid State Circuits Conference (ESSCIRC), Leuven, Belgium, 11–14 September 2017. [Google Scholar]
- Ge, R.; Chen, C.; Jiang, D. A Digitally Controlled Output Adjustable High Stability Relaxation Oscillator. In Proceedings of the 2024 36th Chinese Control and Decision Conference, Xi’an, China, 25–27 May 2024. [Google Scholar]
- Lee, J.; Cho, S. A 10MHz 80μW 67 ppm/°C CMOS reference clock oscillator with a temperature compensated feedback loop in 0.18μm CMOS. In Proceedings of the 2009 Symposium on VLSI Circuits, Kyoto, Japan, 16–18 June 2009. [Google Scholar]
- Jang, T.; Choi, M.; Jeong, S.; Bang, S.; Sylvester, D.; Blaauw, D. A 4.7nW 13.8ppm/°C self-biased wakeup timer using a switched-resistor scheme. In Proceedings of the 2016 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 31 January–4 February 2016. [Google Scholar]
- Zhou, R.; Wang, L.; Yang, J.; Li, Z.; Zhao, X.; Liu, S. A 8.1-nW, 4.22-kHz, −40–85 °C relaxation oscillator with subthreshold leakage current compensation and forward body bias buffer for low power IoT applications. Microelectron. J. 2024, 144, 106090. [Google Scholar] [CrossRef]
- Gürleyük, Ç.; Pedalà, L.; Pan, S.; Sebastiano, F.; Makinwa, K.A.A. A CMOS Dual-RC Frequency Reference with ±200-ppm Inaccuracy from −45 °C to 85 °C. IEEE J. Solid-State Circuits 2018, 53, 3386–3395. [Google Scholar]
- Gürleyük, Ç.; Pan, S.; Makinwa, K.A.A. A 16MHz CMOS RC Frequency Reference with ±400ppm Inaccuracy from −45°C to 85°C After Digital Linear Temperature Compensation. IEEE J. Solid-State Circuits 2020, 53, 64–66. [Google Scholar]
- Ge, G.; Zhang, C.; Hoogzaad, G.; Makinwa, K.A.A. A Single-Trim CMOS Bandgap Reference with a 3σ Inaccuracy of ± 0.15% from −40 °C to 125 °C. IEEE J. Solid-State Circuits 2011, 46, 2693–2701. [Google Scholar]
- Lee, T.-J.; Tu, K.-H. High-Sensitivity PTAT Current Generator Using PTAT and CTAT Current Subtraction Method for Temperature Sensor with Frequency Output. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3922–3926. [Google Scholar]
- Amaravati, A.; Dave, M.; Baghini, M.S.; Sharma, D.K. 800-nA Process-and-Voltage-Invariant 106-dB PSRR PTAT Current Reference. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 577–581. [Google Scholar]
- Sabharwal, S.; Kaur, J.; Shahi, A. Various Current Mirror Topologies: A Survey. In Proceedings of the 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering, Greater Noida, India, 28–29 April 2022. [Google Scholar]
- Bonteanu, G.; Cracan, A. A high-gain programmable current mirror for large bias currents generation. In Proceedings of the 2017 5th International Symposium on Electrical and Electronics Engineering, Galati, Romania, 20–22 October 2017. [Google Scholar]
- Huang, K.-K.; Wentzloff, D.D. A 1.2-MHz 5.8-μW Temperature-Compensated Relaxation Oscillator in 130-nm CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 334–338. [Google Scholar]
- Zhou, W.; Goh, W.L.; Gao, Y. A 3-MHz 17.3-μW 0.015% Period Jitter Relaxation Oscillator with Energy Efficient Swing Boosting. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1745–1749. [Google Scholar]
- Lei, K.-M.; Mak, P.-I.; Martins, R.P. A 0.35-V 5,200-μm2 2.1-MHz Temperature-Resilient Relaxation Oscillator with 667 fJ/Cycle Energy Efficiency Using an Asymmetric Swing-Boosted RC Network and a Dual-Path Comparator. IEEE J. Solid-State Circuits 2021, 56, 2701–2710. [Google Scholar]
- Choe, K.; Bernal, O.D.; Nuttman, D.; Je, M. A precision relaxation oscillator with a self-clocked offset-cancellation scheme for implantable biomedical SoCs. In Proceedings of the 2009 IEEE International Solid-State Circuits Conference-Digest of Technical Papers, San Francisco, CA, USA, 8–12 February 2009. [Google Scholar]






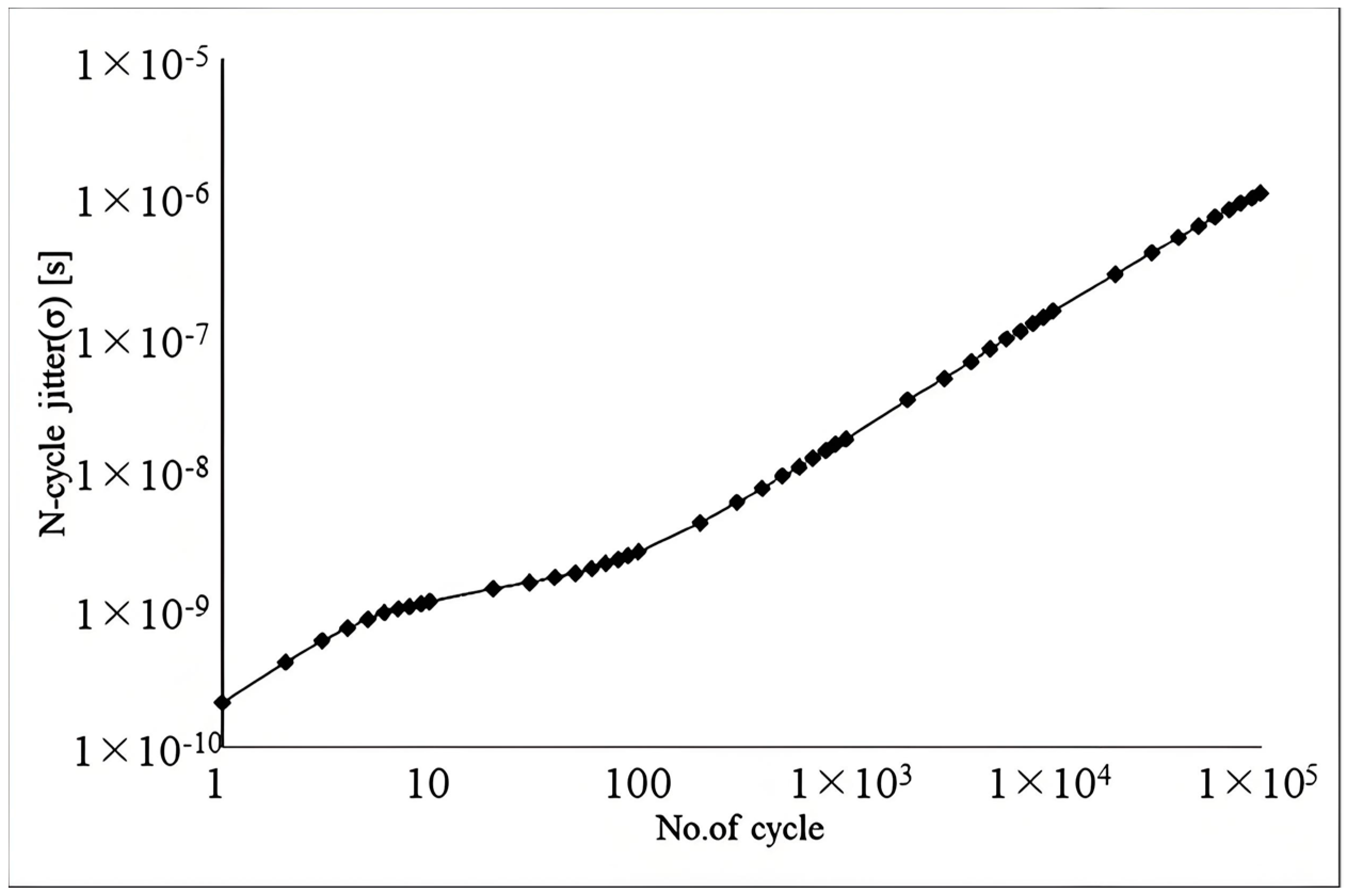
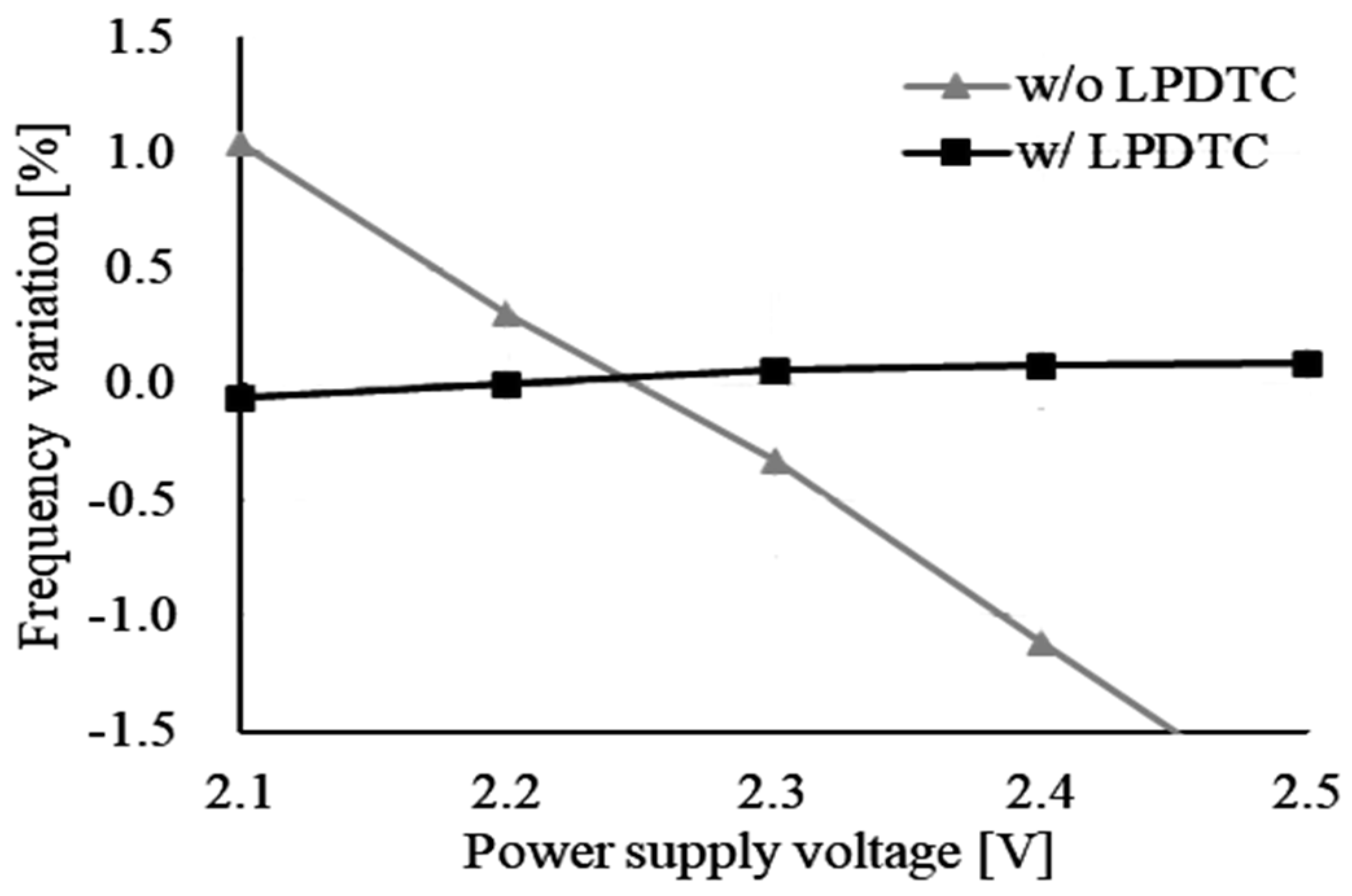
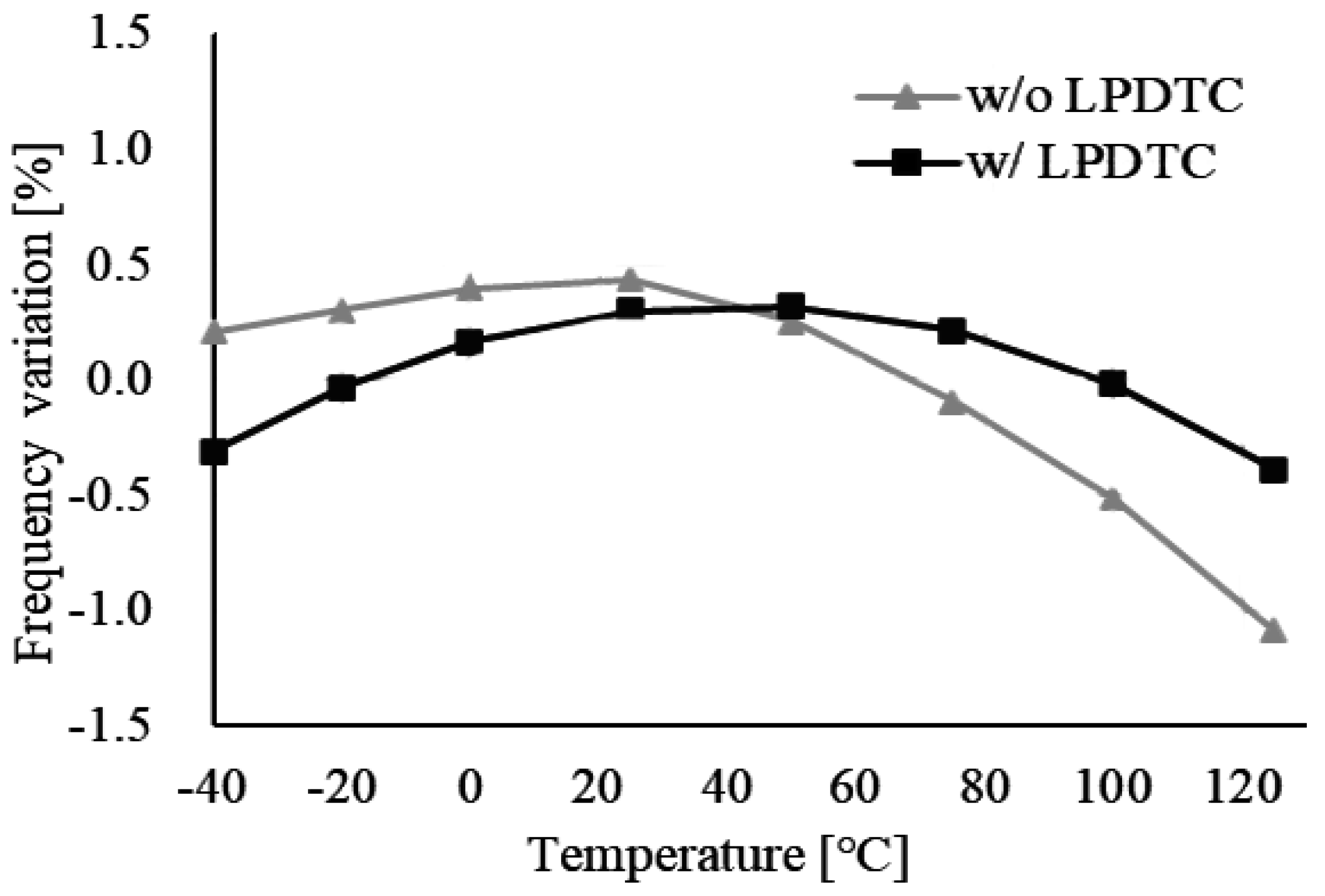
| Reference | [11] | [12] | [14] | [15] | [16] | [17] | [18] | [22] | |
|---|---|---|---|---|---|---|---|---|---|
| Process [nm] | 65 | 180 | 180 | 55 | 180 | 500 | 350 | 65 | |
| Supply Voltage [V] | 0.95~1.05 | 1.2~2.4 | 1.0~2.0 | 0.6~1.1 | 1.15~1.25 | 3~5.5 | 3~4.5 | 0.35~0.8 | |
| Temp. Range [°C] | −40~90 | −20~80 | −40~85 | −40~125 | −40~125 | −55~125 | −40~125 | −40~85 | |
| Frequency [Hz] | 18.5 k | 1.1 M | 100 k | 33 k | 2.9 M | 1 M | 1 M | 4.2 k | |
| Current Eff. [μA/MHz] | 7 | 0.4 | 5.4 | 9.24 | 2.1 | - | 63.6 | 4.88 | |
| Temp. Sen. [ppm/°C] | 85 | 64 | 51 | 58 | 45 | 124 | 48 | 114 | |
| Line Sen. [%/V] | 5 | 3 | 0.4 | 0.75 | 1.245 | 0.16 | 0.28 | 5.45 | |
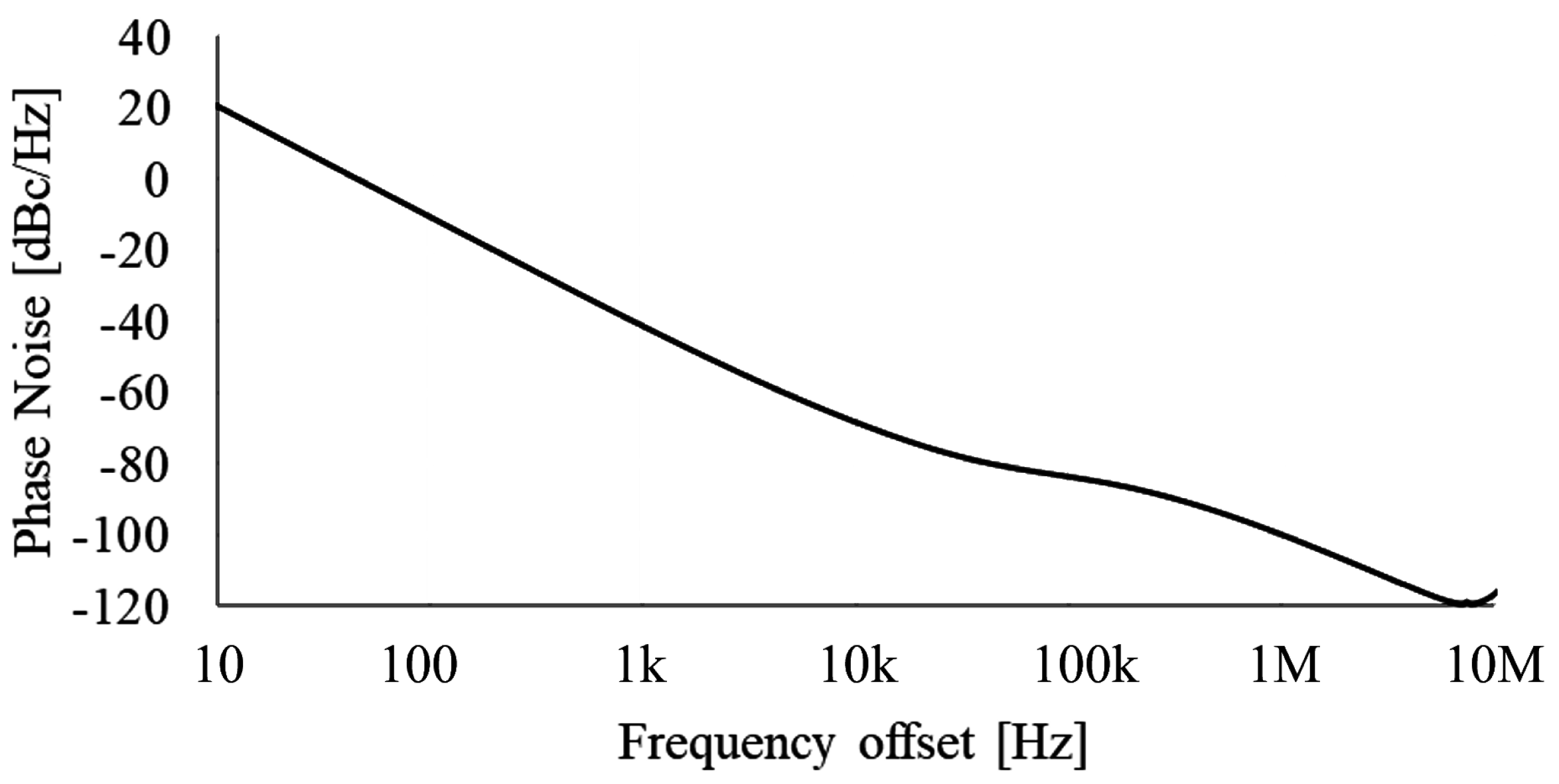
| Phase Noise @ 100 kHz [dBc/Hz] | - | −79.48 | - | - | - | −115.07 | - | - | |
| Period Jitter (σ) [ps] | - | - | - | - | 88.96 | 170 | - | - | |
| Allen Floor [ppm] | 20 | - | - | - | - | - | - | - | |
| FoM1 [dB] | 111.5 | 121.1 | 112.7 | 112.6 | 116.1 | 110.2 | 96.8 | 117.1 | |
| FoM2 [dB] | 173.4 | 183.0 | 176.6 | 177.1 | 181.7 | 171.8 | 162.1 | 177.5 | |
| FoM3 [dB] | - | 131.0 | - | - | 155.3 | 155.3 | - | - | |
| Area [mm2] | 0.105 | 0.075 | - | 0.052 | - | - | 0.04 | 0.34 | |
| Result Type | Measured | Measured | Pre-sim | Post-sim | Post-sim | Measured | Measured | Measured | |
| Reference | [19] | [30] | [31] | [32] | [13] | [33] | This Work | ||
| Process [nm] | 110 | 130 | 65 | 28 | 180 | 130 | 40 | ||
| Supply Voltage [V] | 3.3 | 0.99~1.01 | 0.95~1.45 | 0.35~0.38 | 1.4~2 | 1.4~1.6 | 2.1~2.5 | ||
| Temp. Range [°C] | −40~125 | 40~80 | 0~90 | −20~120 | −40~125 | 20~60 | −40~125 | ||
| Frequency [Hz] | 10 M | 1.2 M | 3 M | 2.1 M | 10.5 M | 3.2 M | 8 M | ||
| Current Eff. [μA/MHz] | - | 4.83 | 5.77 | 1.85 | 14.95 | 8.48 | 4.1 | ||
| Temp. Sen. [ppm/°C] | 133.3 | 296 | 133 | 158 | 137 | 1253 | 43 | ||
| Line Sen. [%/V] | - | 3.6 | 0.6 | 26.8 | 4.4 | 0.4 | 0.38 | ||
| Phase Noise @ 100 kHz [dBc/Hz] | - | - | −114 | - | −115.6 | - | −83.5 | ||
| Period Jitter (σ) [ps] | - | - | 50 | 800 | 9.86 | 455 | 214 | ||
| Allen Floor [ppm] | - | - | - | - | - | 140 | - | ||
| 1 FoM1 [dB] | - | 113.2 | 112.4 | 121.8 | 106.8 | 109.2 | 110.4 | ||
| 1 FoM2 [dB] | - | 169.2 | 170.7 | 181.2 | 167.6 | 154.2 | 176.2 | ||
| 1 FoM3 [dB] | - | - | 161.2 | - | 162.6 | - | 132.9 | ||
| Area [mm2] | - | 0.016 | 0.044 | 0.005 | 0.015 | 0.073 | 0.011 | ||
| Result Type | Pre-sim | Measured | Measured | Measured | Measured | Measured | Post-sim | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Xu, K.; Dai, H.; Wu, Z.; Yu, X.; Zhang, G. Methods for Designing High-Precision Relaxation Oscillator. Micromachines 2025, 16, 364. https://doi.org/10.3390/mi16040364
Huang Z, Xu K, Dai H, Wu Z, Yu X, Zhang G. Methods for Designing High-Precision Relaxation Oscillator. Micromachines. 2025; 16(4):364. https://doi.org/10.3390/mi16040364
Chicago/Turabian StyleHuang, Zhibo, Kunpeng Xu, Hongguang Dai, Zhanxia Wu, Xiaopeng Yu, and Guoqiang Zhang. 2025. "Methods for Designing High-Precision Relaxation Oscillator" Micromachines 16, no. 4: 364. https://doi.org/10.3390/mi16040364
APA StyleHuang, Z., Xu, K., Dai, H., Wu, Z., Yu, X., & Zhang, G. (2025). Methods for Designing High-Precision Relaxation Oscillator. Micromachines, 16(4), 364. https://doi.org/10.3390/mi16040364







