Numerical Simulation in Microvessels for the Design of Drug Carriers with the Immersed Boundary-Lattice Boltzmann Method
Abstract
:1. Introduction
2. Numerical Methods
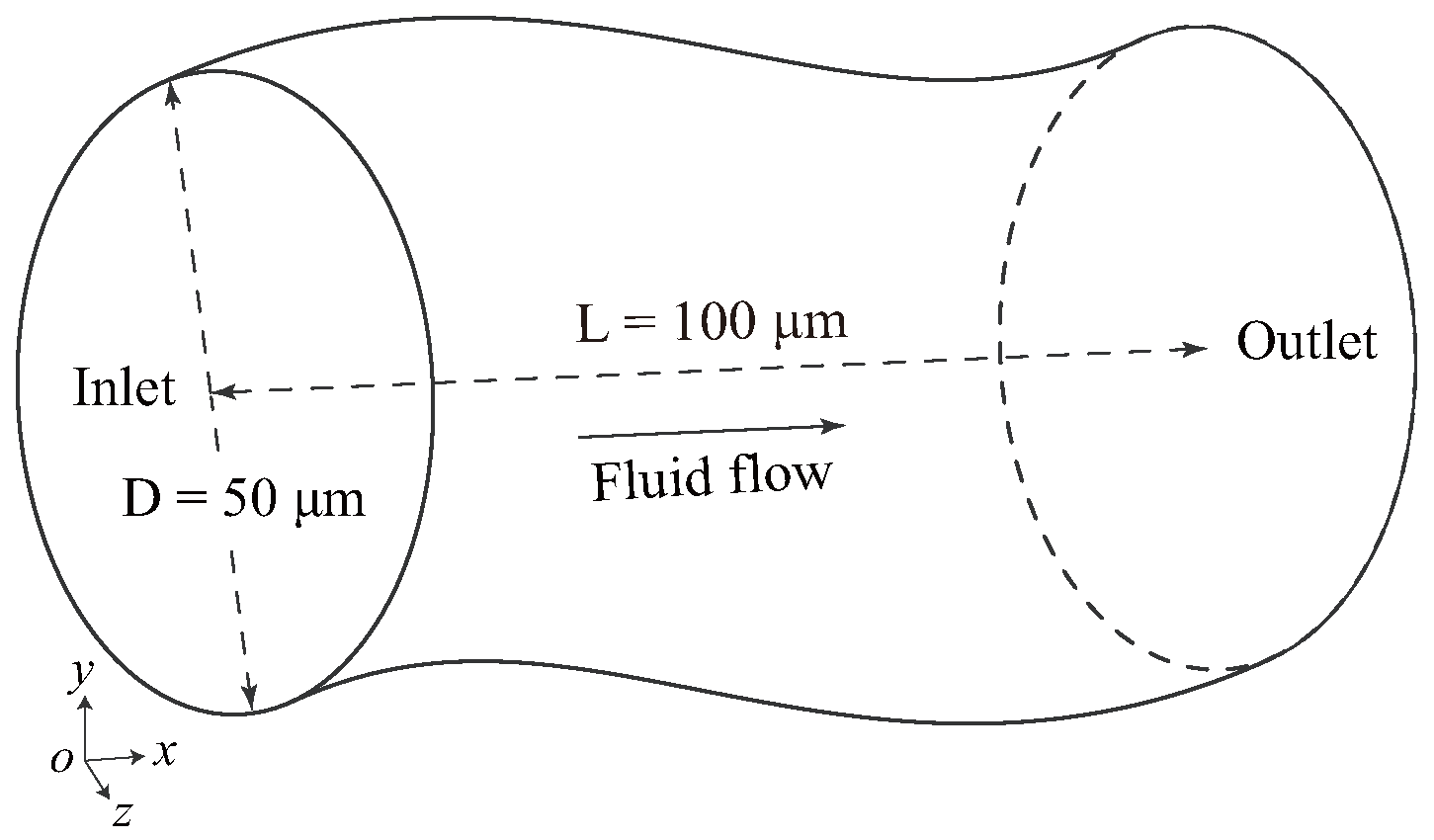
2.1. Problem Statement
2.2. Lattice Boltzmann Method for Blood Flow
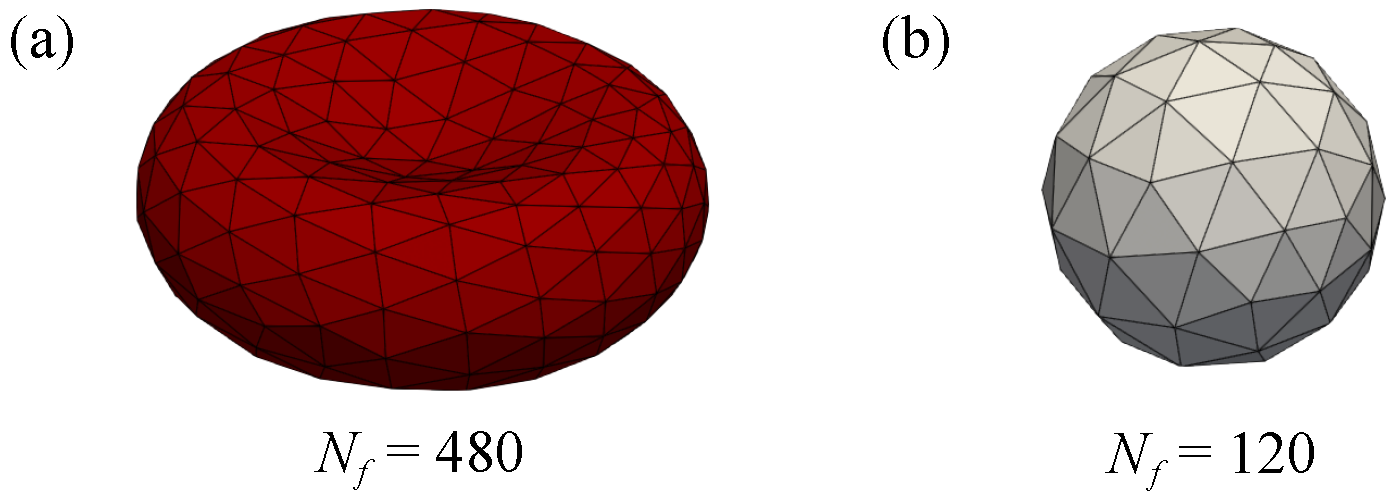
2.3. Model of Red Blood Cells and Drug Carriers
2.4. Immersed Boundary Method for Fluid–Solid Coupling
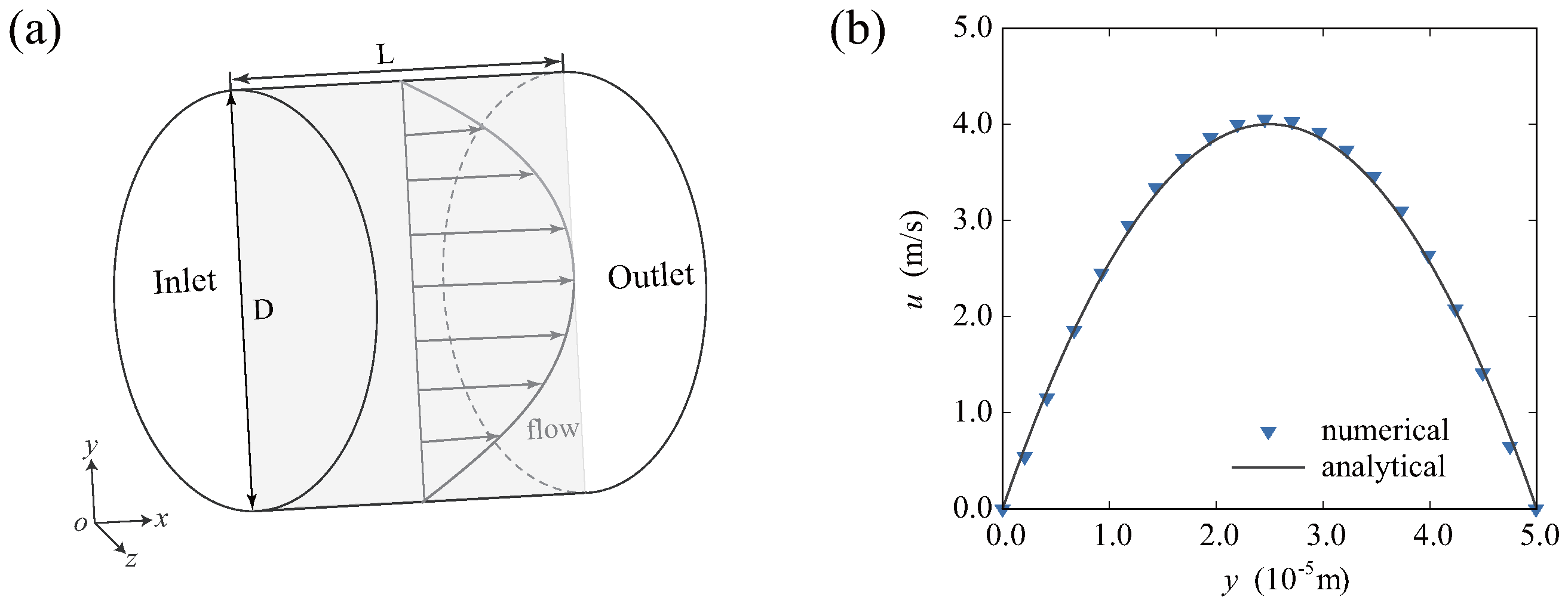
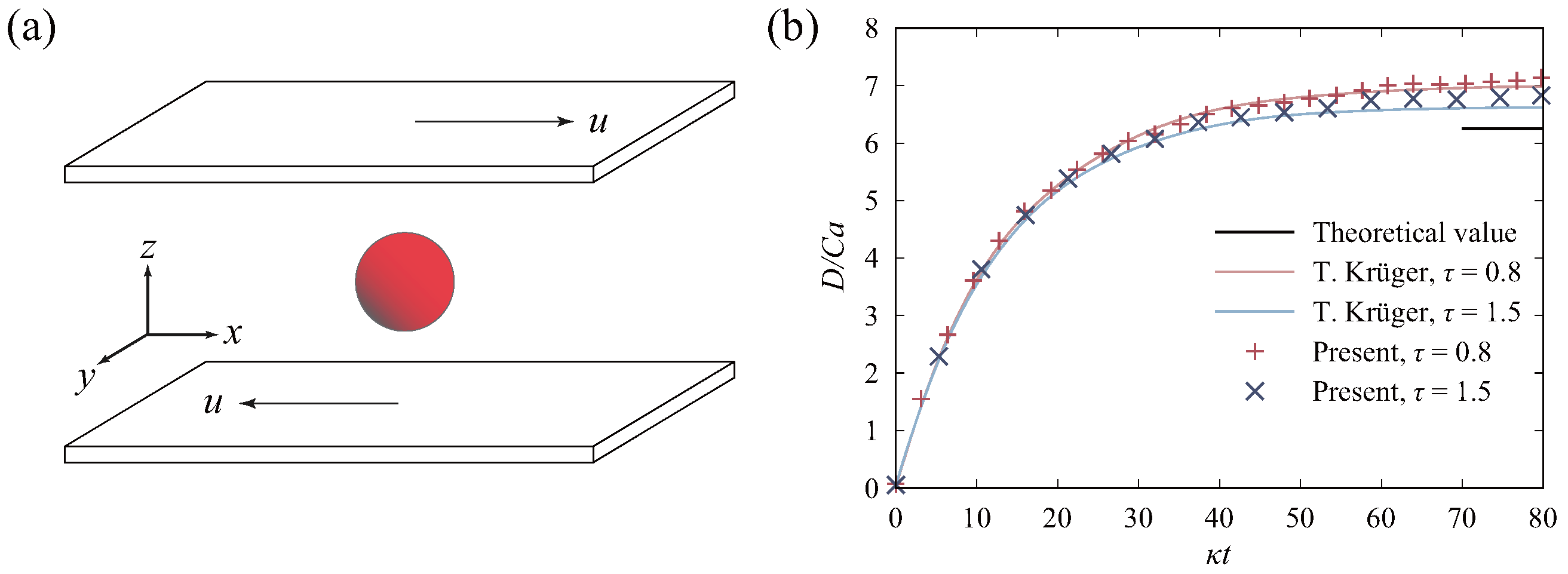
2.5. Validation of the Model
3. Results and Discussion
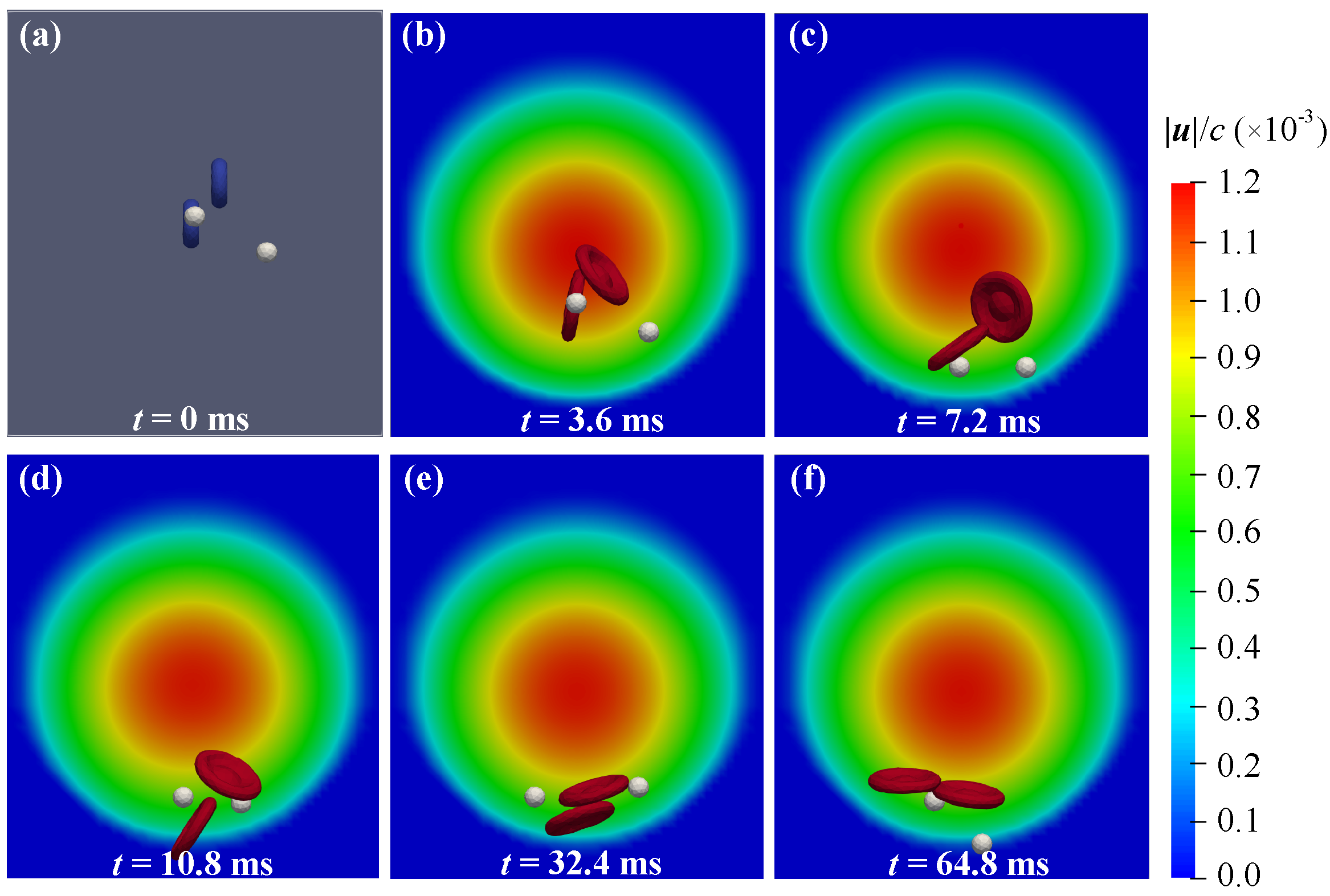
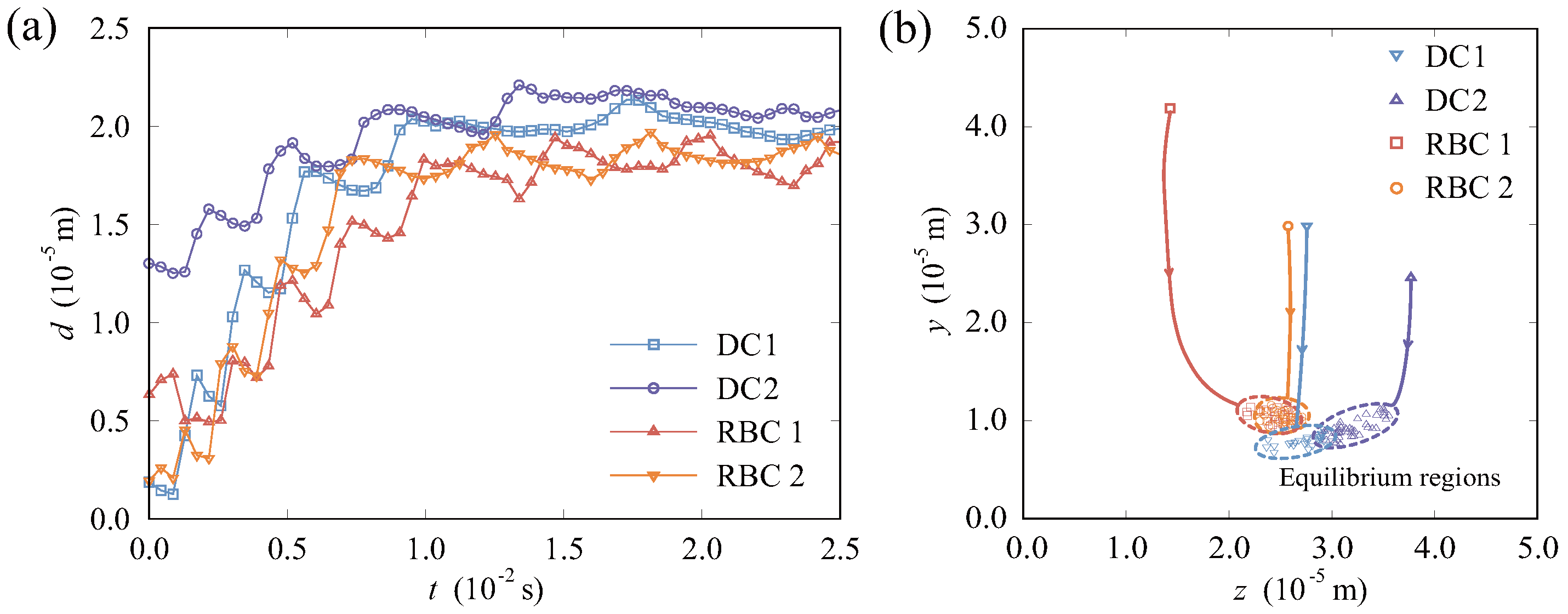
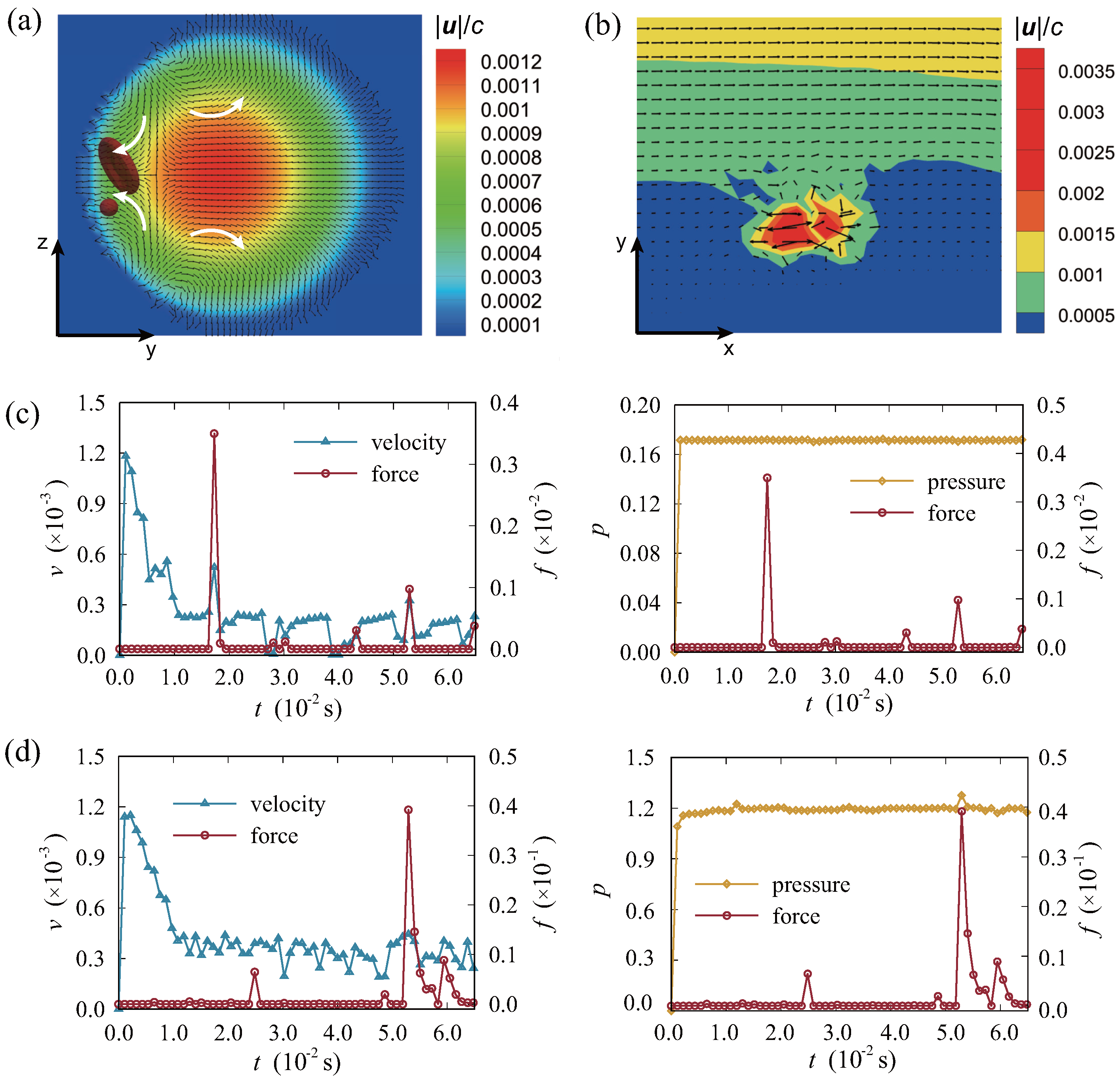
3.1. Migration and Distribution of Particles in the Vessel
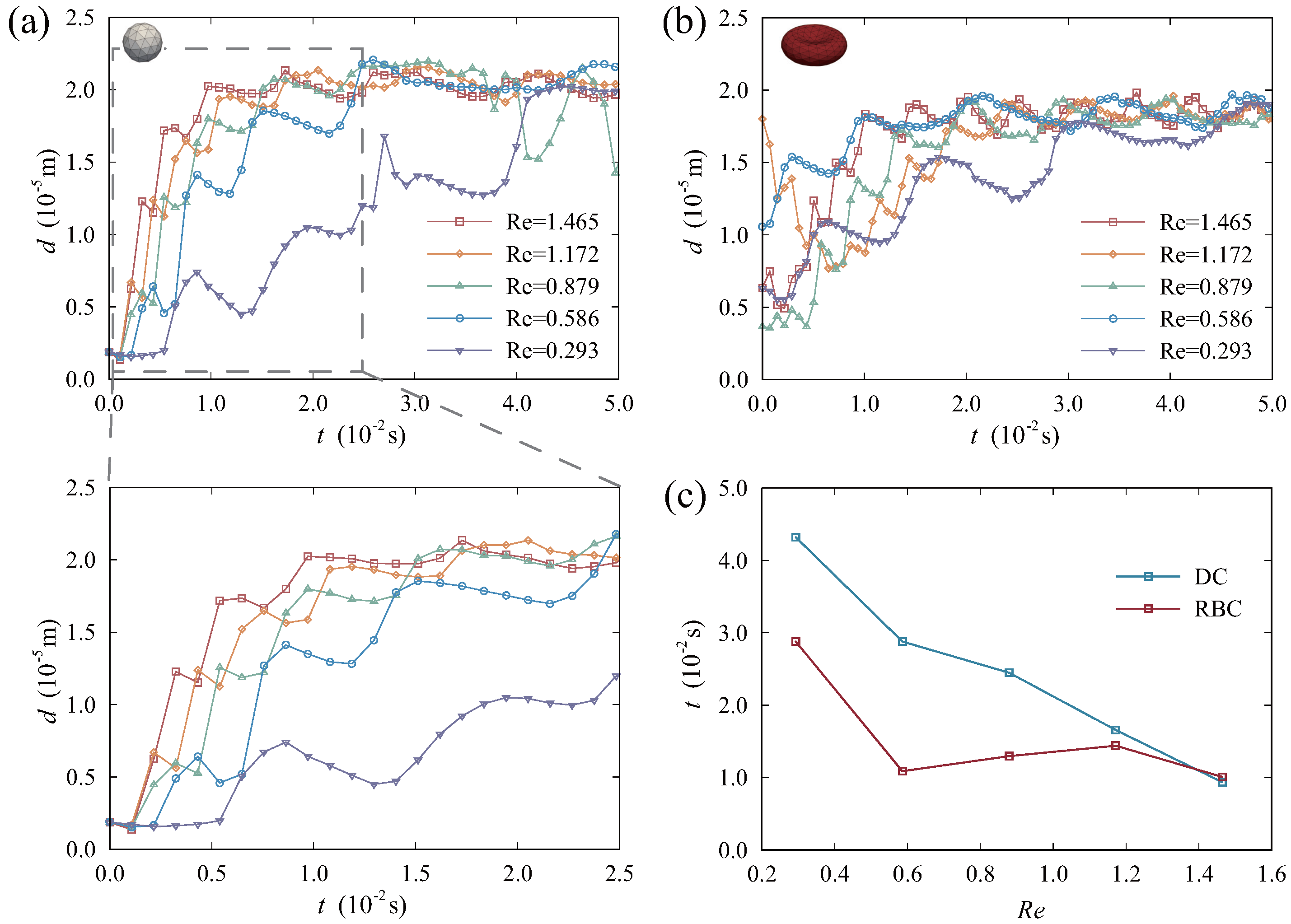
3.2. Effect of Reynolds Number
3.3. Effect of Drug Carrier Size
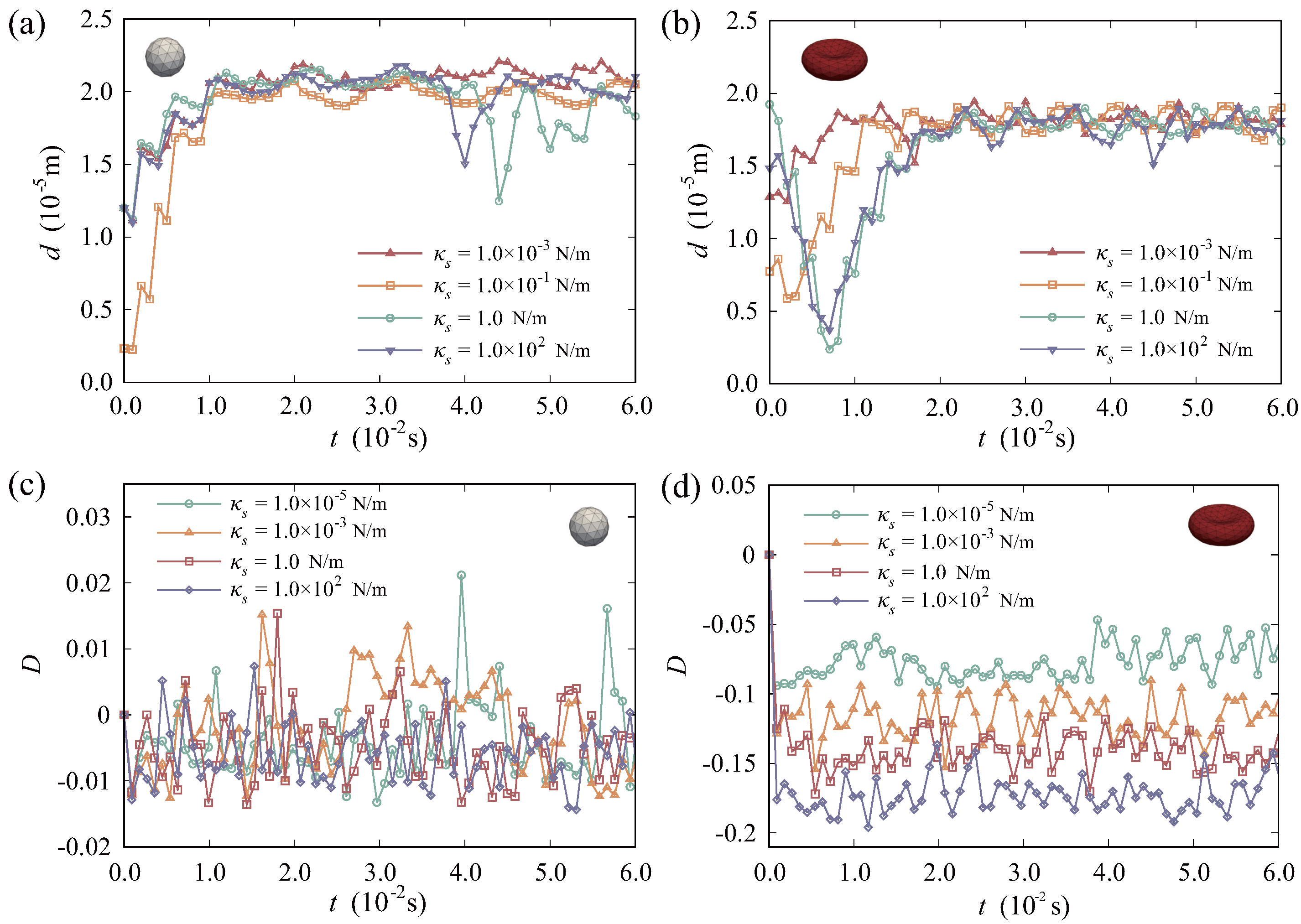
3.4. Effect of Drug Carrier Stiffness
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haq Khan, Z.U.; Khan, T.M.; Khan, A.; Shah, N.S.; Muhammad, N.; Tahir, K.; Iqbal, J.; Rahim, A.; Khasim, S.; Ahmad, I.; et al. Brief review: Applications of nanocomposite in electrochemical sensor and drugs delivery. Front. Chem. 2023, 11, 1152217. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, M.J.; Billingsley, M.M.; Haley, R.M.; Wechsler, M.E.; Peppas, N.A.; Langer, R. Engineering precision nanoparticles for drug delivery. Nat. Rev. Drug Discov. 2021, 20, 101–124. [Google Scholar] [CrossRef]
- Sharma, M.; Dev, S.K.; Kumar, M.; Shukla, A.K. Microspheres as suitable drug carrier in sustained release drug delivery: An overview. Asian J. Pharm. Pharmacol. 2018, 4, 102–108. [Google Scholar]
- Medina-Sánchez, M.; Xu, H.; Schmidt, O.G. Micro-and nano-motors: The new generation of drug carriers. Ther. Deliv. 2018, 9, 303–316. [Google Scholar]
- Avsievich, T.; Popov, A.; Bykov, A.; Meglinski, I. Mutual interaction of red blood cells influenced by nanoparticles. Sci. Rep. 2019, 9, 5147. [Google Scholar]
- Sun, Y.; Su, J.; Liu, G.; Chen, J.; Zhang, X.; Zhang, R.; Jiang, M.; Qiu, M. Advances of blood cell-based drug delivery systems. Eur. J. Pharm. Sci. 2017, 96, 115–128. [Google Scholar]
- Lenders, V.; Escudero, R.; Koutsoumpou, X.; Armengol Álvarez, L.; Rozenski, J.; Soenen, S.J.; Zhao, Z.; Mitragotri, S.; Baatsen, P.; Allegaert, K.; et al. Modularity of RBC hitchhiking with polymeric nanoparticles: Testing the limits of non-covalent adsorption. J. Nanobiotechnol. 2022, 20, 333. [Google Scholar] [CrossRef]
- Muzykantov, V.R. Drug delivery by red blood cells: Vascular carriers designed by mother nature. Expert Opin. Drug Deliv. 2010, 7, 403–427. [Google Scholar] [PubMed]
- Forouzandehmehr, M.; Ghoytasi, I.; Shamloo, A.; Ghosi, S. Particles in coronary circulation: A review on modelling for drug carrier design. Mater. Des. 2022, 216, 110511. [Google Scholar] [CrossRef]
- Sahai, N.; Gogoi, M.; Ahmad, N. Mathematical modeling and simulations for developing nanoparticle-based cancer drug delivery systems: A review. Curr. Pathobiol. Rep. 2021, 9, 1–8. [Google Scholar] [CrossRef]
- Mircioiu, C.; Voicu, V.; Anuta, V.; Tudose, A.; Celia, C.; Paolino, D.; Fresta, M.; Sandulovici, R.; Mircioiu, I. Mathematical modeling of release kinetics from supramolecular drug delivery systems. Pharmaceutics 2019, 11, 140. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; An, L.; Wu, X. Modeling drug-carrier interaction in the drug release from nanocarriers. J. Drug Deliv. 2011, 2011, 370308. [Google Scholar] [PubMed]
- Hamilton, S.; Kingston, B.R. Applying artificial intelligence and computational modeling to nanomedicine. Curr. Opin. Biotechnol. 2024, 85, 103043. [Google Scholar] [CrossRef]
- Pushkaran, A.C.; Arabi, A.A. From understanding diseases to drug design: Can artificial intelligence bridge the gap? Artif. Intell. Rev. 2024, 57, 86. [Google Scholar] [CrossRef]
- Kibria, M.R.; Akbar, R.I.; Nidadavolu, P.; Havryliuk, O.; Lafond, S.; Azimi, S. Predicting efficacy of drug-carrier nanoparticle designs for cancer treatment: A machine learning-based solution. Sci. Rep. 2023, 13, 547. [Google Scholar] [CrossRef]
- Pavel, D.G.; Zimmer, A.M.; Patterson, V.N. In vivo labeling of red blood cells with 99mTc: A new approach to blood pool visualization. J. Nucl. Med. 1977, 18, 305–308. [Google Scholar] [PubMed]
- Shah, R.; Bag, A.; Chapman, P.; Curé, J. Imaging manifestations of progressive multifocal leukoencephalopathy. Clin. Radiol. 2010, 65, 431–439. [Google Scholar] [CrossRef]
- Tarakanchikova, Y.; Stelmashchuk, O.; Seryogina, E.; Piavchenko, G.; Zherebtsov, E.; Dunaev, A.; Popov, A.; Meglinski, I. Allocation of rhodamine-loaded nanocapsules from blood circulatory system to adjacent tissues assessed in vivo by fluorescence spectroscopy. Laser Phys. Lett. 2018, 15, 105601. [Google Scholar] [CrossRef]
- Pérez-López, A.; Torres-Suárez, A.I.; Martín-Sabroso, C.; Aparicio-Blanco, J. An overview of in vitro 3D models of the blood–brain barrier as a tool to predict the in vivo permeability of nanomedicines. Adv. Drug Deliv. Rev. 2023, 196, 114816. [Google Scholar] [CrossRef]
- Koonyosying, P.; Srichairatanakool, S.; Tiwananthagorn, S.; Sthitmatee, N. Measurement of Babesia bovis infected red blood cells using flow cytometry. J. Microbiol. Methods 2023, 204, 106641. [Google Scholar] [CrossRef]
- Ye, T.; Phan-Thien, N.; Lim, C.T.; Peng, L.; Shi, H. Hybrid smoothed dissipative particle dynamics and immersed boundary method for simulation of red blood cells in flows. Phys. Rev. E 2017, 95, 063314. [Google Scholar] [CrossRef] [PubMed]
- Dzwinel, W.; Boryczko, K.; Yuen, D.A. A discrete-particle model of blood dynamics in capillary vessels. J. Colloid Interface Sci. 2003, 258, 163–173. [Google Scholar] [CrossRef]
- Soleimani, M.; Sahraee, S.; Wriggers, P. Red blood cell simulation using a coupled shell–fluid analysis purely based on the SPH method. Biomech. Model. Mechanobiol. 2019, 18, 347–359. [Google Scholar] [PubMed]
- Polwaththe-Gallage, H.N.; Saha, S.C.; Sauret, E.; Flower, R.; Gu, Y. A coupled SPH-DEM approach to model the interactions between multiple red blood cells in motion in capillaries. Int. J. Mech. Mater. Des. 2016, 12, 477–494. [Google Scholar] [CrossRef]
- Wang, S.; Ma, S.; Li, R.; Qi, X.; Han, K.; Guo, L.; Li, X. Probing the interaction between supercarrier rbc membrane and nanoparticles for optimal drug delivery. J. Mol. Biol. 2023, 435, 167539. [Google Scholar] [CrossRef]
- Djukic, T.; Filipovic, N.D. Modeling the Motion of Rigid and Deformable Objects in Fluid Flow. In Computational Modeling and Simulation Examples in Bioengineering; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 33–86. [Google Scholar]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar]
- Sun, C.; Munn, L.L. Particulate nature of blood determines macroscopic rheology: A 2-D lattice Boltzmann analysis. Biophys. J. 2005, 88, 1635–1645. [Google Scholar]
- Sun, C.; Munn, L.L. Lattice-Boltzmann simulation of blood flow in digitized vessel networks. Comput. Math. Appl. 2008, 55, 1594–1600. [Google Scholar]
- Skorczewski, T.; Erickson, L.C.; Fogelson, A.L. Platelet motion near a vessel wall or thrombus surface in two-dimensional whole blood simulations. Biophys. J. 2013, 104, 1764–1772. [Google Scholar]
- Kaoui, B. Computer simulations of drug release from a liposome into the bloodstream. Eur. Phys. J. E 2018, 41, 20. [Google Scholar]
- Ye, H.; Shen, Z.; Li, Y. Cell stiffness governs its adhesion dynamics on substrate under shear flow. IEEE Trans. Nanotechnol. 2017, 17, 407–411. [Google Scholar]
- Ye, H.; Shen, Z.; Li, Y. Shear rate dependent margination of sphere-like, oblate-like and prolate-like micro-particles within blood flow. Soft Matter 2018, 14, 7401–7419. [Google Scholar] [PubMed]
- Ye, H.; Shen, Z.; Li, Y. Shape-dependent transport of microparticles in blood flow: From margination to adhesion. J. Eng. Mech. 2019, 145, 04019021. [Google Scholar]
- Ye, H.; Shen, Z.; Li, Y. Interplay of deformability and adhesion on localization of elastic micro-particles in blood flow. J. Fluid Mech. 2019, 861, 55–87. [Google Scholar]
- Ye, H.; Shen, Z.; Wei, M.; Li, Y. Red blood cell hitchhiking enhances the accumulation of nano-and micro-particles in the constriction of a stenosed microvessel. Soft Matter 2021, 17, 40–56. [Google Scholar]
- Yue, K.; You, Y.; Yang, C.; Niu, Y.; Zhang, X. Numerical simulation of transport and adhesion of thermogenic nano-carriers in microvessels. Soft Matter 2020, 16, 10345–10357. [Google Scholar]
- Nikfar, M.; Razizadeh, M.; Paul, R.; Muzykantov, V.; Liu, Y. A numerical study on drug delivery via multiscale synergy of cellular hitchhiking onto red blood cells. Nanoscale 2021, 13, 17359–17372. [Google Scholar]
- Venier-Julienne, M.; Benoit, J. Preparation, purification and morphology of polymeric nanoparticles as drug carriers. Pharm. Acta Helv. 1996, 71, 121–128. [Google Scholar] [PubMed]
- Scioli Montoto, S.; Muraca, G.; Ruiz, M.E. Solid lipid nanoparticles for drug delivery: Pharmacological and biopharmaceutical aspects. Front. Mol. Biosci. 2020, 7, 587997. [Google Scholar] [CrossRef]
- Trucillo, P. Drug carriers: Classification, administration, release profiles, and industrial approach. Processes 2021, 9, 470. [Google Scholar] [CrossRef]
- Kavita, K.; Ashvini, V.; Ganesh, N. Albumin microspheres. Unique system as drug delivery carriers for non steroidal anti inflammatory drugs. Int. J. Pharm. Sci. Rev. Res. 2010, 5, 10. [Google Scholar]
- García, M.C. Nano-and microparticles as drug carriers. In Engineering Drug Delivery Systems; Elsevier: Amsterdam, The Netherlands, 2020; pp. 71–110. [Google Scholar]
- Krüger, T.; Varnik, F.; Raabe, D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 2011, 61, 3485–3505. [Google Scholar] [CrossRef]
- Ramanujan, S.; Pozrikidis, C. Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: Large deformations and the effect of fluid viscosities. J. Fluid Mech. 1998, 361, 117–143. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.; Chien, S. Strain Energy Function of Red Blood Cell Membranes. Biophys. J. 1973, 13, 245–264. [Google Scholar] [CrossRef] [PubMed]
- Krüger, H. Computer Simulation Study of Collective Phenomena in Dense Suspensions of Red Blood Cells Under Shear; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Gompper, G.; Schick, M. Soft Matter: Lipid Bilayers and Red Blood Cells; Wiley-VCH: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sun, D.K.; Wang, Y.; Dong, A.P.; Sun, B.D. A three-dimensional quantitative study on the hydrodynamic focusing of particles with the immersed boundary–Lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 94, 306–315. [Google Scholar] [CrossRef]
- Jiang, D.; Ni, C.; Tang, W.; Xiang, N. Numerical simulation of elasto-inertial focusing of particles in straight microchannels. J. Phys. D Appl. Phys. 2020, 54, 065401. [Google Scholar] [CrossRef]
- Wiggers, C.J. The dynamics of hypertension. Am. Heart J. 1938, 16, 515–543. [Google Scholar] [CrossRef]
- Secomb, T.W. Blood flow in the microcirculation. Annu. Rev. Fluid Mech. 2017, 49, 443–461. [Google Scholar] [CrossRef]
- Nguyen, P.H.D.; Jayasinghe, M.K.; Le, A.H.; Peng, B.; Le, M.T.N. Advances in Drug Delivery Systems Based on Red Blood Cells and Their Membrane-Derived Nanoparticles. ACS Nano 2023, 17, 5187–5210. [Google Scholar] [CrossRef]
- Chambers, E.; Mitragotri, S. Prolonged circulation of large polymeric nanoparticles by non-covalent adsorption on erythrocytes. J. Control Release 2004, 100, 111–119. [Google Scholar] [CrossRef]
- Chambers, E.; Mitragotri, S. Long Circulating Nanoparticles via Adhesion on Red Blood Cells: Mechanism and Extended Circulation. Exp. Biol. Med. 2007, 232, 958–966. [Google Scholar]


| Classification | Methodologies | Strengths | Limitations |
|---|---|---|---|
| In vivo experiments | Magnetic resonance imaging (MRI), computed tomography (CT) [16,17,18] |
|
|
| In vitro experiments | Dye marking, fluorescence imaging, flow cytometry [19,20] |
|
|
| Computational fluid dynamics | Dissipative particle dynamics (DPD), smoothed particle hydrodynamics (SPH), lattice Boltzmann method (LBM) |
|
|
| Parameter | Physical Value | LB Value | References |
|---|---|---|---|
| RBC radius () | m | 3.5 | [46] |
| RBC elastic shear modulus () | N/m | [47,48] | |
| RBC area dilation modulus () | N/m | [47,48] | |
| RBC bending modulus () | N·m | [47,48] | |
| RBC surface modulus () | 0.5 N/m | 0.108 | [47,48] |
| RBC volume modulus () | N/m2 | 0.216 | [47,48] |
| DC radius () | 1.3–2.0 × m | 0.8–1.5 | — |
| DC elastic shear modulus () | 1.0 N/m | 0.216 | [49] |
| DC area dilation modulus () | 0.1 N/m | 0.0216 | [49] |
| DC bending modulus () | N·m | 0.0216 | [49] |
| DC surface modulus () | 1.0 N/m | 0.216 | [49] |
| DC volume modulus () | N/m2 | 0.216 | [49] |
| (N/m) | (N/m) | (N·m) | (N/m) | (N/m2) | |
|---|---|---|---|---|---|
| Case 1 | |||||
| Case 2 | |||||
| Case 3 | 1.0 | 1.0 | |||
| Case 4 | 1.0 | ||||
| Case 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, Y.; Hu, M.; Sun, D.; Sun, Y. Numerical Simulation in Microvessels for the Design of Drug Carriers with the Immersed Boundary-Lattice Boltzmann Method. Micromachines 2025, 16, 389. https://doi.org/10.3390/mi16040389
Hou Y, Hu M, Sun D, Sun Y. Numerical Simulation in Microvessels for the Design of Drug Carriers with the Immersed Boundary-Lattice Boltzmann Method. Micromachines. 2025; 16(4):389. https://doi.org/10.3390/mi16040389
Chicago/Turabian StyleHou, Yulin, Mengdan Hu, Dongke Sun, and Yueming Sun. 2025. "Numerical Simulation in Microvessels for the Design of Drug Carriers with the Immersed Boundary-Lattice Boltzmann Method" Micromachines 16, no. 4: 389. https://doi.org/10.3390/mi16040389
APA StyleHou, Y., Hu, M., Sun, D., & Sun, Y. (2025). Numerical Simulation in Microvessels for the Design of Drug Carriers with the Immersed Boundary-Lattice Boltzmann Method. Micromachines, 16(4), 389. https://doi.org/10.3390/mi16040389





