Design of Piezoelectric Ultrasonic Composite Vibration System for Precision Grinding
Abstract
1. Introduction
2. Materials and Methods
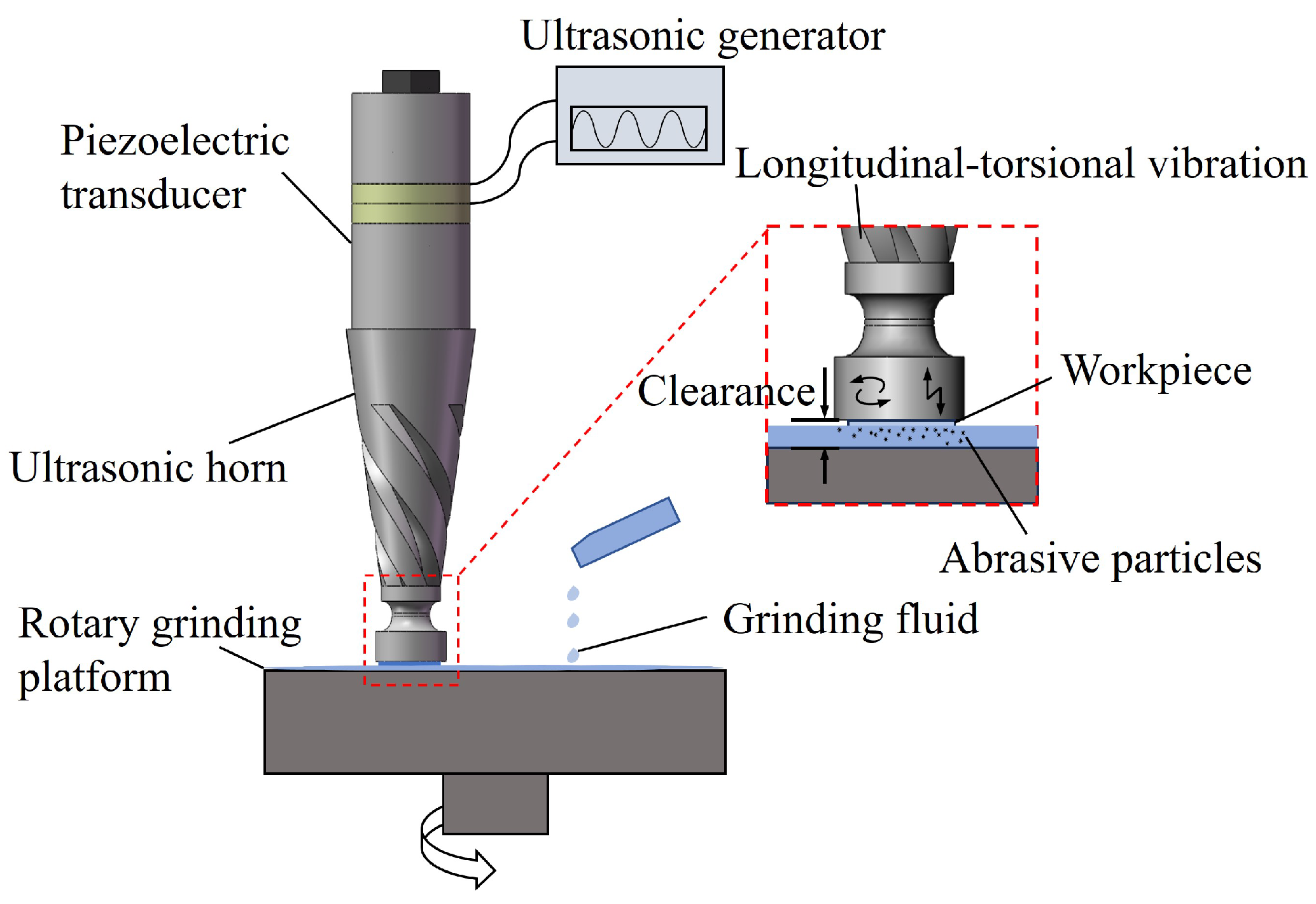
2.1. Design of Ultrasonic Vibration Grinding System
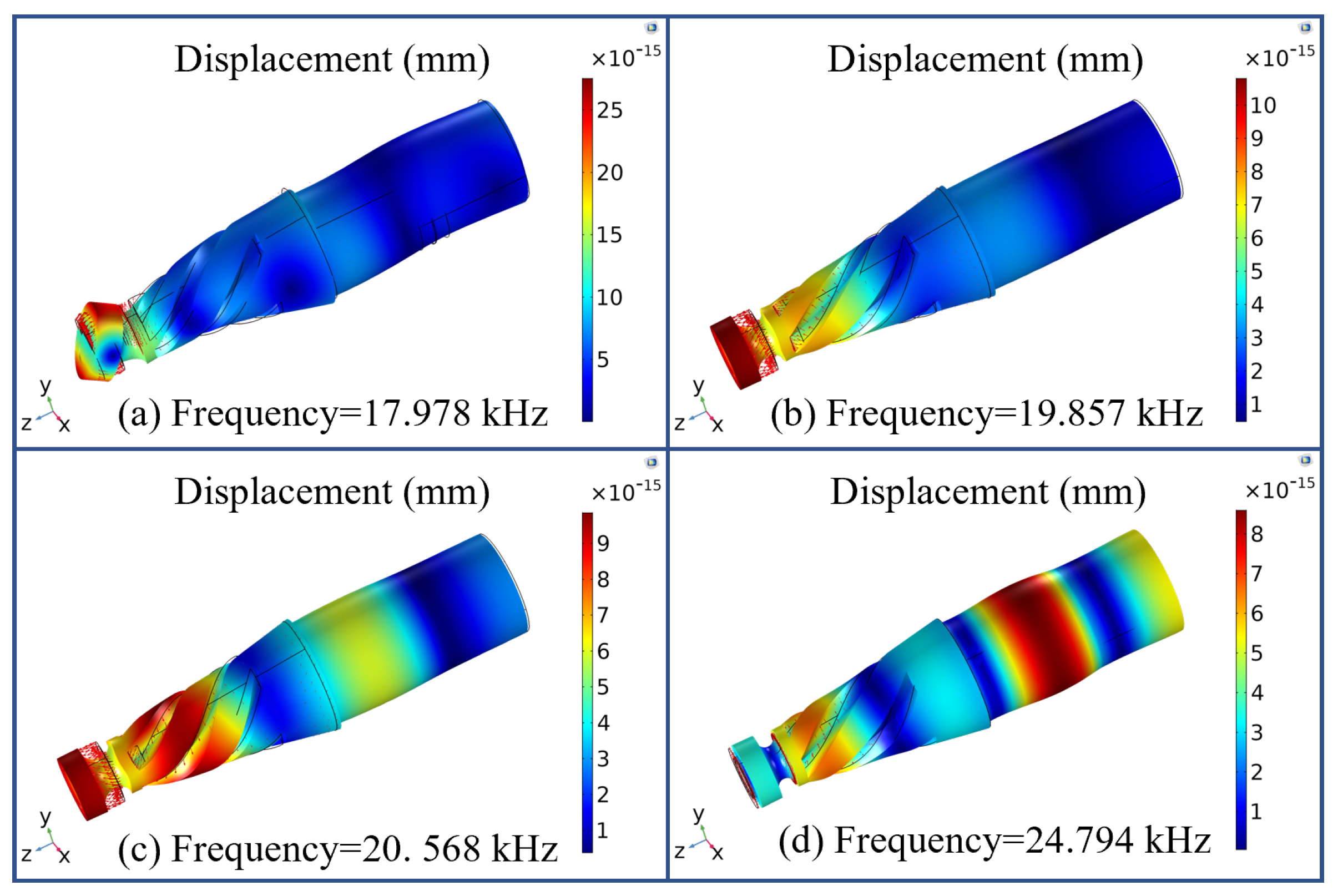
2.2. Finite Element Analysis of Vibration System
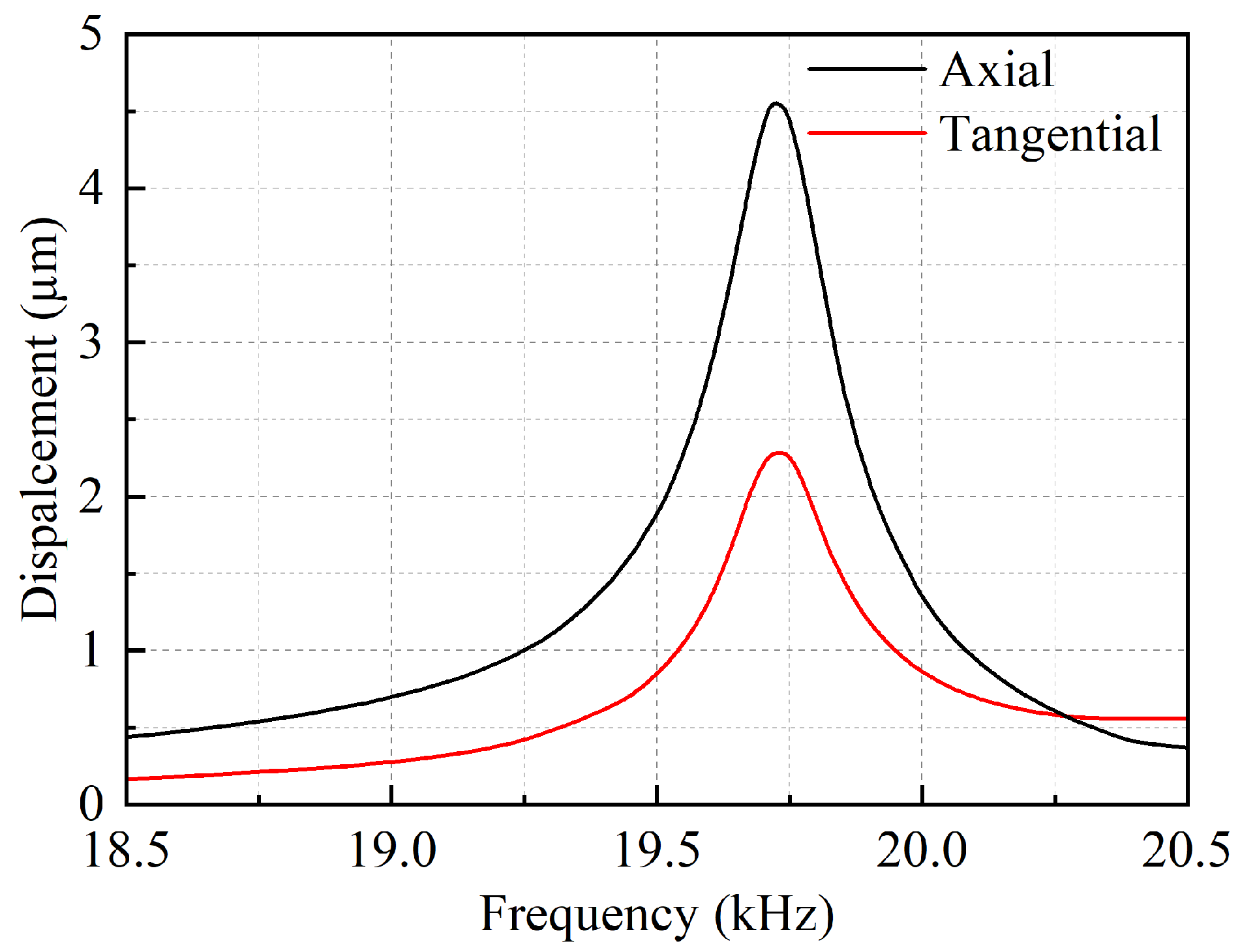
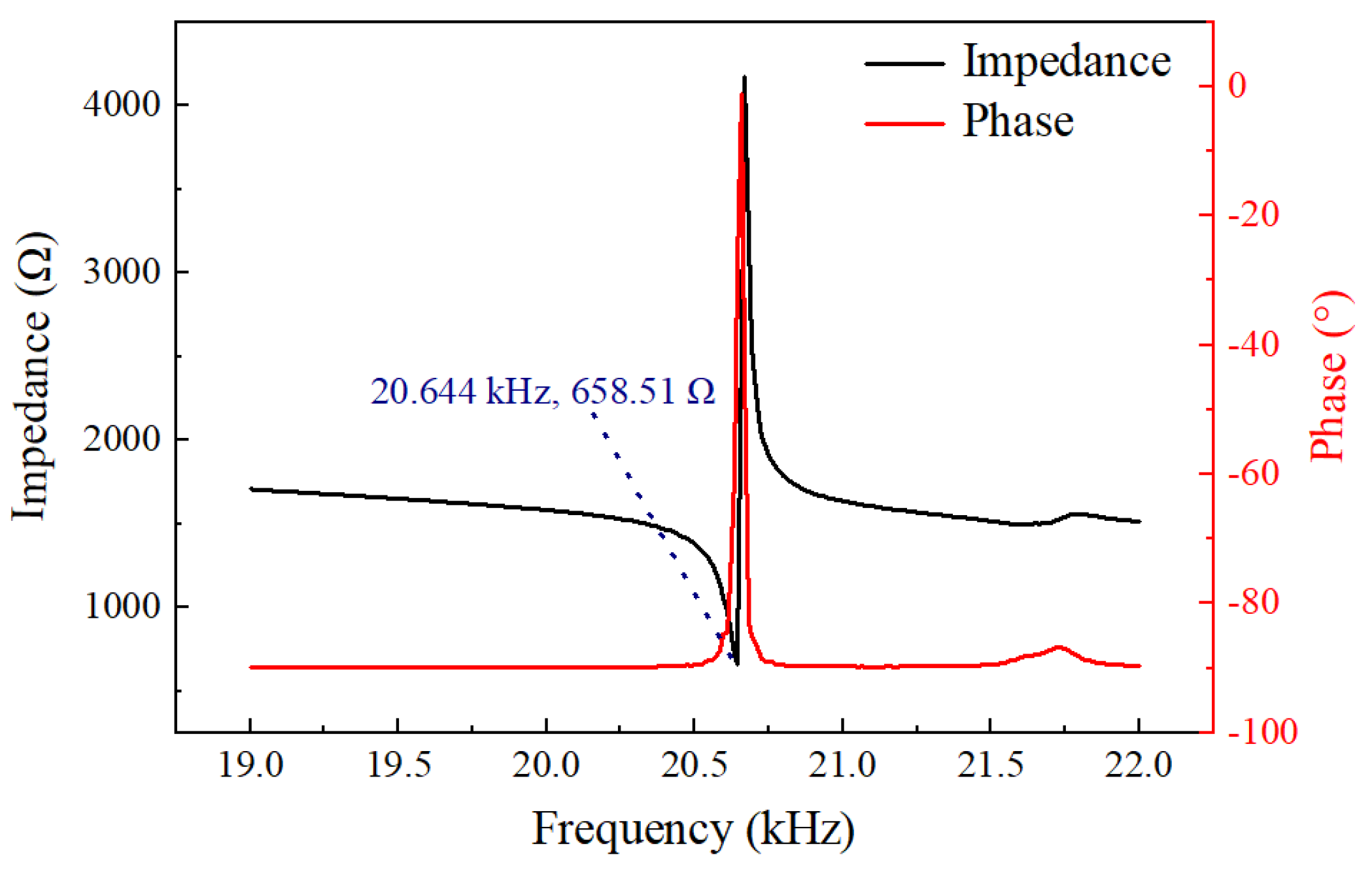
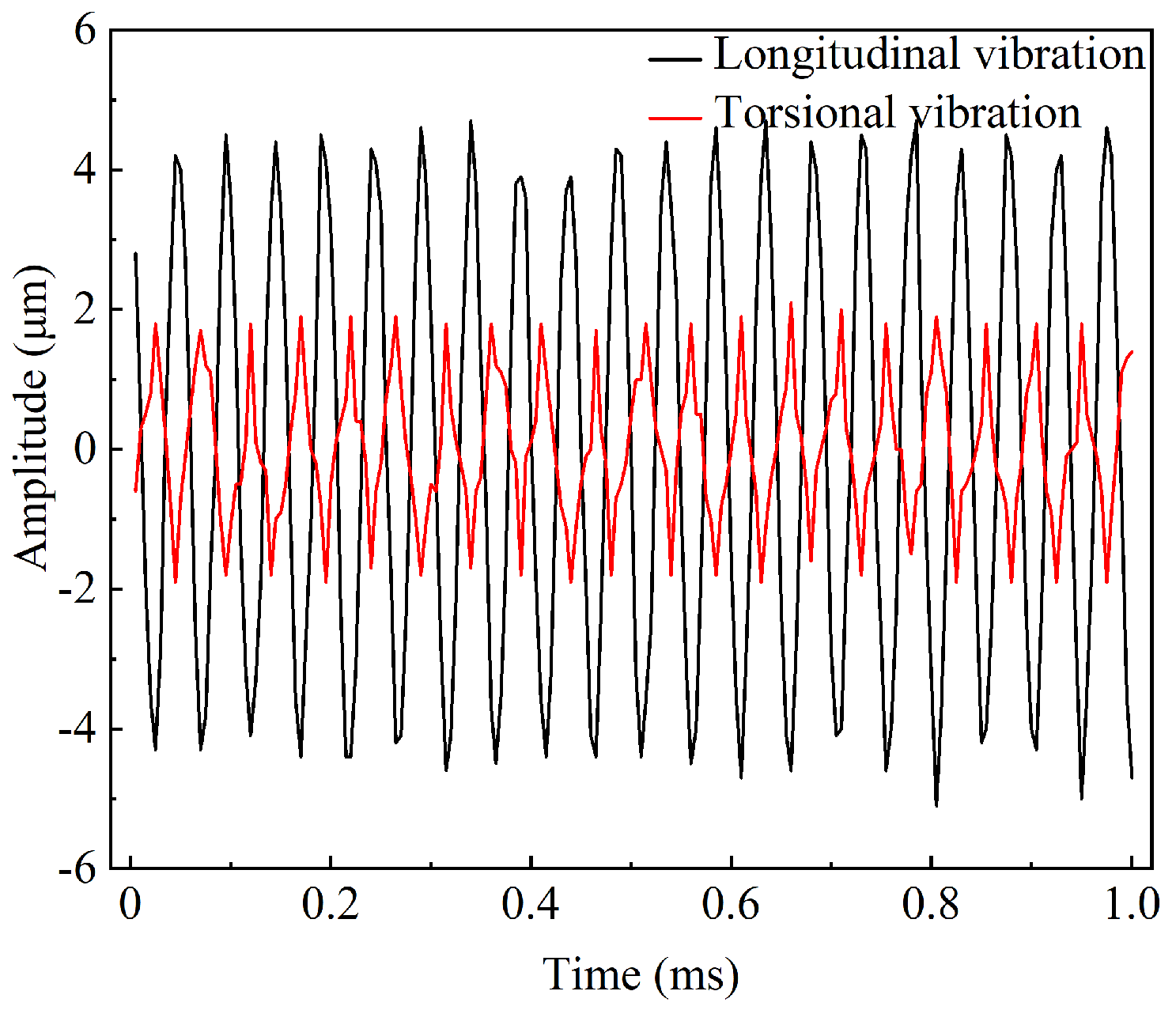
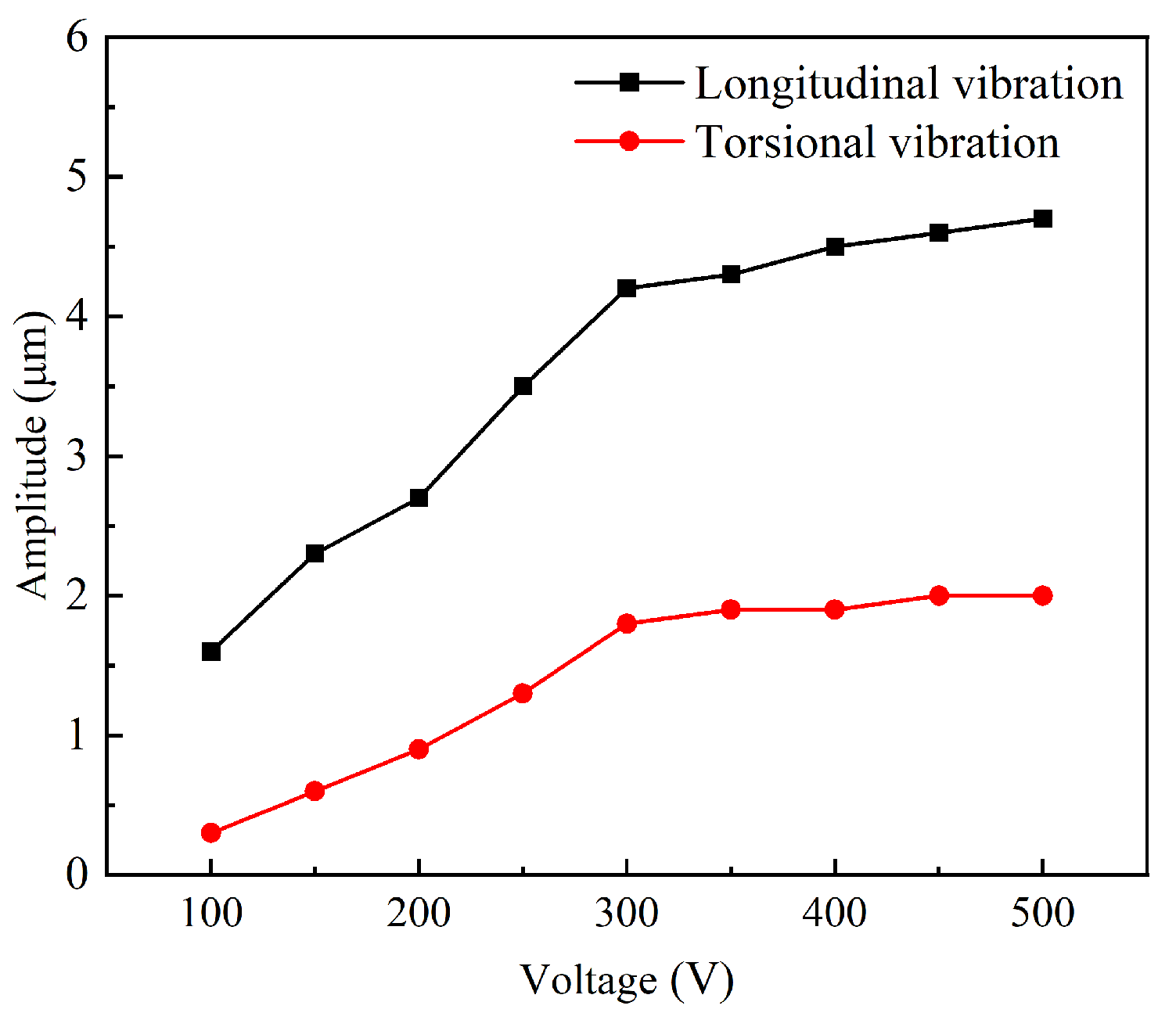
2.3. Performance Test of the Vibration System
2.4. Experimental Apparatus and Procedures
3. Results and Discussion
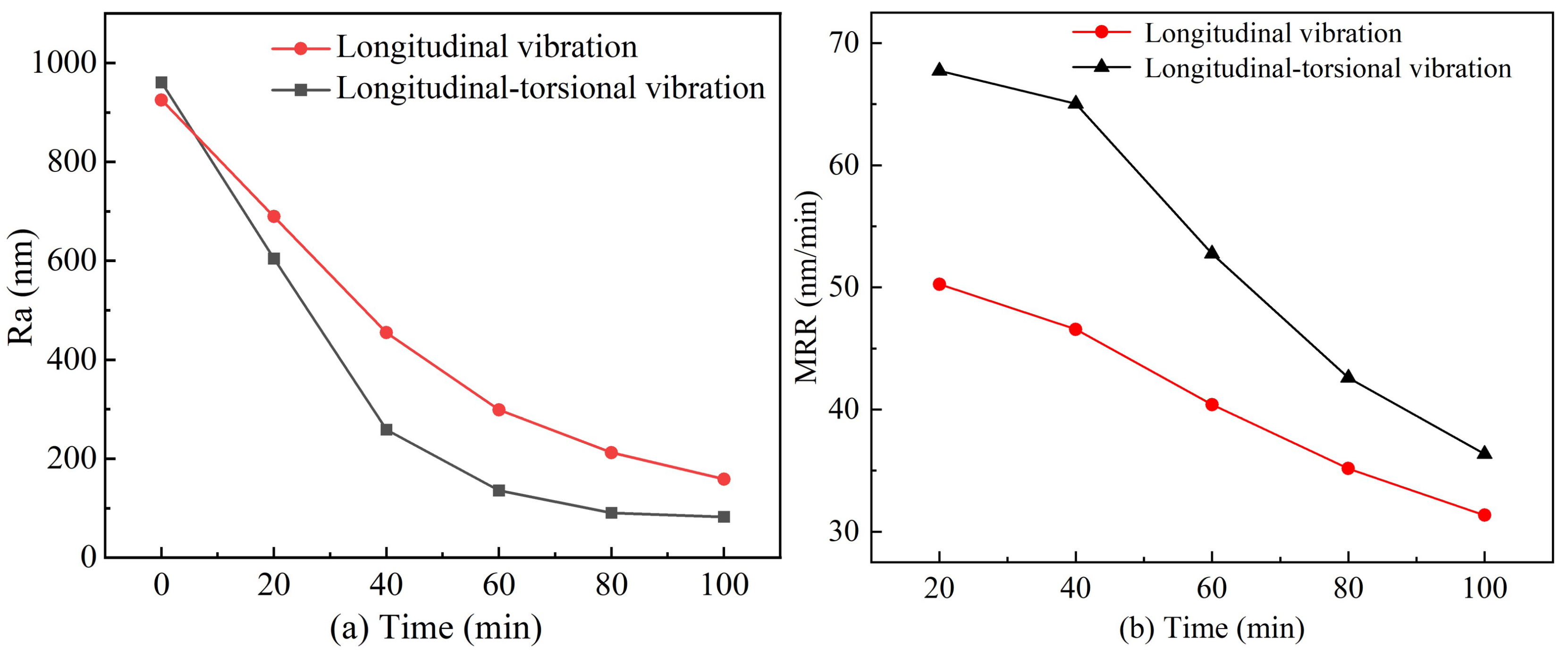
3.1. Surface Roughness Reduction and Material Removal Rate
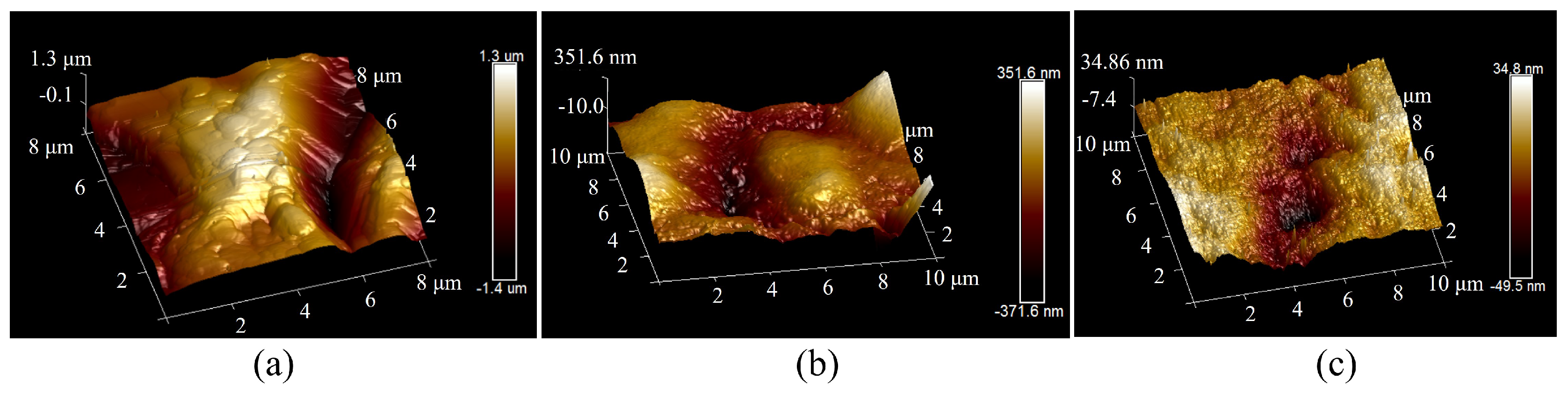
3.2. Surface Morphology of Sapphire
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Zhang, Q.; Chen, M.; Liu, Y.; Zhu, J.; Yang, J.; Wang, F.; Tang, Y.; Zhao, X. Multiphysics modeling and analysis of Sc-doped AlN thin film based piezoelectric micromachined ultrasonic transducer by finite element method. Micromachines 2023, 14, 1942. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Wu, Z.; Gu, Y.A.; Lou, L. Effect of humid environment on electromechanical performance of piezoelectric micromachined ultrasonic transducers (PMUTs). Sens. Actuators A Phys. 2024, 366, 114821. [Google Scholar] [CrossRef]
- Wang, D.-A.; Chuang, W.-Y.; Hsu, K.; Pham, H.-T. Design of a Bézier-profile horn for high displacement amplification. Ultrasonics 2011, 51, 148–156. [Google Scholar] [CrossRef]
- Yang, H.; Ji, M.; Xiu, X.; Lv, H.; Gu, A.; Zhang, S. AlScN film based piezoelectric micromechanical ultrasonic transducer for an extended long-range detection. Micromachines 2022, 13, 1942. [Google Scholar] [CrossRef] [PubMed]
- Munir, M.M.; Mughal, K.H.; Qureshi, M.A.M.; Qaiser, A.A.; Khalid, F.A. Design of Novel Longitudinally–Torsionally Coupled Ultrasonic Bezier Horns for Machining Advanced Hard and Brittle Materials. J. Vib. Eng. Technol. 2024, 12, 4881–4898. [Google Scholar]
- Satpute, V.; Huo, D.; Hedley, J.; Elgendy, M. Design of a novel 2D ultrasonic transducer for 2D high-frequency vibration-assisted micro-machining. Int. J. Adv. Manuf. Technol. 2023, 126, 1035–1053. [Google Scholar]
- Baraya, M.; Yan, J.; Hossam, M. Improving and Predicting the Surface Roughness and the Machining Accuracy in Ultrasonic Vibration-Assisted Milling. J. Vib. Eng. Technol. 2024, 12, 127–140. [Google Scholar]
- Choi, Y.-J.; Park, K.-H.; Hong, Y.-H.; Kim, K.-T.; Lee, S.-W.; Choi, H.-Z. Effect of ultrasonic vibration in grinding; horn design and experiment. Int. J. Precis. Eng. Manuf. 2013, 14, 1873–1879. [Google Scholar] [CrossRef]
- Chen, F.; Bie, W.; Wang, X.; Zhao, B. Longitudinal-torsional coupled rotary ultrasonic machining of ZrO2 ceramics: An experimental study. Ceram. Int. 2022, 48, 28154–28162. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, L.; Zhang, G.; Ni, C.; Lin, B. Review of ultrasonic vibration-assisted machining in advanced materials. Int. J. Mach. Tools Manuf. 2020, 156, 103594. [Google Scholar]
- Ye, Z.; Wen, X.; Wan, W.; Liu, F.; Bai, W.; Xu, C.; Chen, H.; Gong, P.; Han, G. Precision grinding technology of silicon carbide (SiC) ceramics by longitudinal torsional ultrasonic vibrations. Materials 2023, 16, 5572. [Google Scholar] [CrossRef]
- An, D.; Huang, Y.; Li, J.; Huang, W. Design and Characteristics Study of Longitudinal-Torsional Piezoelectric Ultrasonic Transducers. Int. J. Precis. Eng. Manuf. 2024, 26, 559–568. [Google Scholar] [CrossRef]
- Wu, C.; Chen, S.; Cheng, K.; Ding, H.; Xiao, C. Innovative Design and Analysis of a Longitudinal-Torsional Transducer with the Shared Node Plane Applied for Ultrasonic Assisted Milling. J. Mech. Eng. Sci. 2019, 233, 4128–4139. [Google Scholar] [CrossRef]
- Huang, S.; Li, X.; Zhao, Y.; Sun, Q.; Huang, H. A novel lapping process for single-crystal sapphire using hybrid nanoparticle suspensions. Int. J. Mech. Sci. 2021, 191, 106099. [Google Scholar] [CrossRef]
- Wang, S.; Tie, G.; Shi, F.; Tian, Y.; Yang, X. Effect of different grinding strategies on subsequent polishing processes of sapphire. J. Manuf. Process. 2024, 112, 339–357. [Google Scholar] [CrossRef]
- Cheng, Z.; Qin, S.; Fang, Z. Numerical modeling and experimental study on the material removal process using ultrasonic vibration-assisted abrasive water jet. Front. Mater. 2022, 9, 895271. [Google Scholar] [CrossRef]
- Sharma, A.K.; Venkatesh, G.; Rajesha, S.; Kumar, P. Experimental investigations into ultrasonic-assisted abrasive flow machining (UAAFM) process. Int. J. Adv. Manuf. Technol. 2015, 80, 477–493. [Google Scholar] [CrossRef]
- Zarepour, H.; Yeo, S.H. Single abrasive particle impingements as a benchmark to determine material removal modes in micro ultrasonic machining. Wear 2012, 288, 1–8. [Google Scholar] [CrossRef]
- Qu, S.; Yu, T.; Meng, F.; Zhang, C.; Zhang, X.; Ma, Z.; Wang, Z.; Yu, T.; Zhao, J. Material removal rate prediction and surface quality study for ultrasonic vibration polishing of monocrystalline silicon. Int. J. Adv. Manuf. Technol. 2023, 127, 4789–4802. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Q.; Chen, Z.; Li, Y.; Zhou, X.; Wang, R.; Xu, P. Study on abrasive belt grinding process assisted by ultrasonic elliptic vibration. Int. J. Adv. Manuf. Technol. 2022, 120, 4647–4661. [Google Scholar] [CrossRef]
- Wu, B.; Zhao, B.; Ding, W.; Su, H. Investigation of the wear characteristics of microcrystal alumina abrasive wheels during the ultrasonic vibration-assisted grinding of PTMCs. Wear 2021, 477, 203844. [Google Scholar] [CrossRef]
- Agarwal, S. On the mechanism and mechanics of material removal in ultrasonic machining. Int. J. Mach. Tools Manuf. 2015, 96, 1–14. [Google Scholar]
- Xiang, D.; Li, B.; Zhao, C.; Lei, X.; Peng, P.; Yuan, Z.; Gao, G.; Jiao, F.; Zhao, B. Mechanism and experimental evaluation on surface morphology of GCr15SiMn with ultrasonic vibration grinding. Int. J. Adv. Manuf. Technol. 2024, 131, 2377–2387. [Google Scholar]
- An, D.; Xian, J.; Zhang, Y.; Cheng, G.; Huang, Y.; Liang, Z.; Huang, W. Piezoelectric Ultrasonic Local Resonant Ultra-Precision Grinding for Hard-Brittle Materials. Micromachines 2024, 15, 1216. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Yin, Z.; Miao, Q.; Dai, C.; Cheng, J.; Li, H.; Liang, Z.; Li, Z. Longitudinal-torsional compound ultrasonic vibration end grinding sapphire: A study on surface topography and roughness. Mater. Sci. Semicond. Process. 2024, 171, 107990. [Google Scholar] [CrossRef]
- Zarepour, H.; Yeo, S.H. Predictive modeling of material removal modes in micro ultrasonic machining. Int. J. Mach. Tools Manuf. 2012, 62, 13–23. [Google Scholar]
- Ichida, Y.; Sato, R.; Morimoto, Y.; Kobayashi, K. Material removal mechanisms in non-contact ultrasonic abrasive machining. Wear 2005, 258, 107–114. [Google Scholar]
- Pandey, H.; Apurva, A.; Dixit, P. Investigations into velocity decay, initial tool-workpiece gap, and material removal behaviour in ultrasonic micromachining. J. Manuf. Process. 2024, 124, 52–67. [Google Scholar]
- Zhao, B.; Bie, W.; Wang, X.; Chen, F.; Chang, B. Design and experimental investigation on longitudinal-torsional composite horn considering the incident angle of ultrasonic wave. Int. J. Adv. Manuf. Technol. 2019, 105, 325–341. [Google Scholar]
- Al-Budairi, H.; Lucas, M.; Harkness, P. A design approach for longitudinal–torsional ultrasonic transducers. Sens. Actuators A Phys. 2013, 198, 99–106. [Google Scholar]
- Liu, Y.; Ozaki, R.; Morita, T. Investigation of Nonlinearity in Piezoelectric Transducers. Sens. Actuators A Phys. 2015, 227, 31–38. [Google Scholar] [CrossRef]
- Li, Z.; Tang, L.; Yang, W.; Zhao, R.; Liu, K.; Mace, B. Transient Response of a Nonlinear Energy Sink-Based Piezoelectric Vibration Energy Harvester Coupled to a Synchronized Charge Extraction Interface. Nano Energy 2021, 87, 106179. [Google Scholar] [CrossRef]
- Xu, J.; He, Q.; Zhang, X.; Yi, X.; Yu, Y.; Li, Y.; Zhang, L.; Gu, R.; Zhang, F. Investigation into the Role of Si and SiC Phases in RB-SiC Ceramics Surface Modified Ultra-Precision Grinding. Mater. Sci. Semicond. Process. 2024, 184, 108786. [Google Scholar]
- Chen, Y.; Su, H.; Qian, N.; He, J.; Gu, J.; Xu, J.; Ding, K. Ultrasonic Vibration-Assisted Grinding of Silicon Carbide Ceramics Based on Actual Amplitude Measurement: Grinding Force and Surface Quality. Ceram. Int. 2021, 47, 15433–15441. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Z.; Yu, Y.; Lai, Z.; Zhu, J.; Xu, X.; Peng, Q. Processing and Machining Mechanism of Ultrasonic Vibration-Assisted Grinding on Sapphire. Mater. Sci. Semicond. Process. 2022, 142, 106470. [Google Scholar] [CrossRef]




| Component | Material | Diameter (mm) | Length/Thickness (mm) |
|---|---|---|---|
| Ceramic Ring | PZT-8 | 50 | 41 |
| Rear Cover | Stainless Steel | 50 (OD) 17 (ID) | 6.5 |
| Front Cover | Aluminum Alloy | 50 | 45 |
| Horn | 45 Steel | 55 | 85 (Conical) |
| 25 | 5 (Cylindrical) | ||
| 30 | 10 (Tool) |
| Experimental Parameters | Constant | Variable |
|---|---|---|
| Workpiece material | Sapphire | |
| Dimension (mm) | ||
| Particles material | SiC | |
| Density (kg/m3) | 3950 | |
| Initial surface roughness (μm) | 0.9–1 | |
| Clearance (mm) | 30 r/min, 3.5 μm | 0.3, 0.5, 0.7, 0.9, 1.1 |
| Rotational speed (r/min) | 3 mm, 3.5 μm | 20, 30, 40, 50, 60 |
| Particles size (μm) | 3 mm, 30 r/min | 1.5, 3.5, 5, 7, 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Huang, K.; Zhong, Q.; Wu, J.; An, D. Design of Piezoelectric Ultrasonic Composite Vibration System for Precision Grinding. Micromachines 2025, 16, 408. https://doi.org/10.3390/mi16040408
Huang W, Huang K, Zhong Q, Wu J, An D. Design of Piezoelectric Ultrasonic Composite Vibration System for Precision Grinding. Micromachines. 2025; 16(4):408. https://doi.org/10.3390/mi16040408
Chicago/Turabian StyleHuang, Weiqing, Kaijie Huang, Qunyou Zhong, Jialun Wu, and Dawei An. 2025. "Design of Piezoelectric Ultrasonic Composite Vibration System for Precision Grinding" Micromachines 16, no. 4: 408. https://doi.org/10.3390/mi16040408
APA StyleHuang, W., Huang, K., Zhong, Q., Wu, J., & An, D. (2025). Design of Piezoelectric Ultrasonic Composite Vibration System for Precision Grinding. Micromachines, 16(4), 408. https://doi.org/10.3390/mi16040408








