Performing MHz-Level Repetition Rate Tuning for Coherent Dual-Microcomb Interferometry
Abstract
:1. Introduction
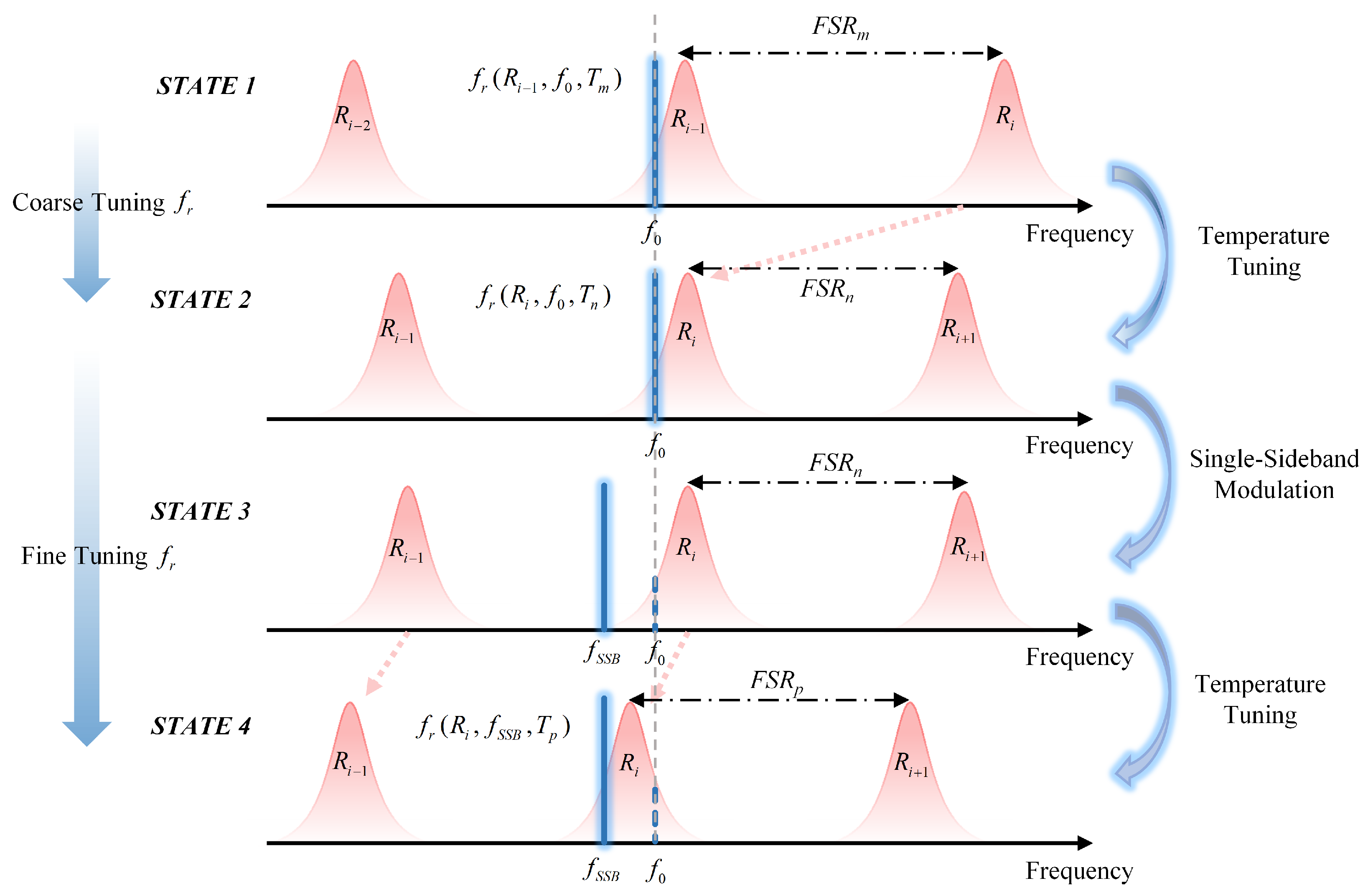
2. Method and Principle
3. Experimental Results
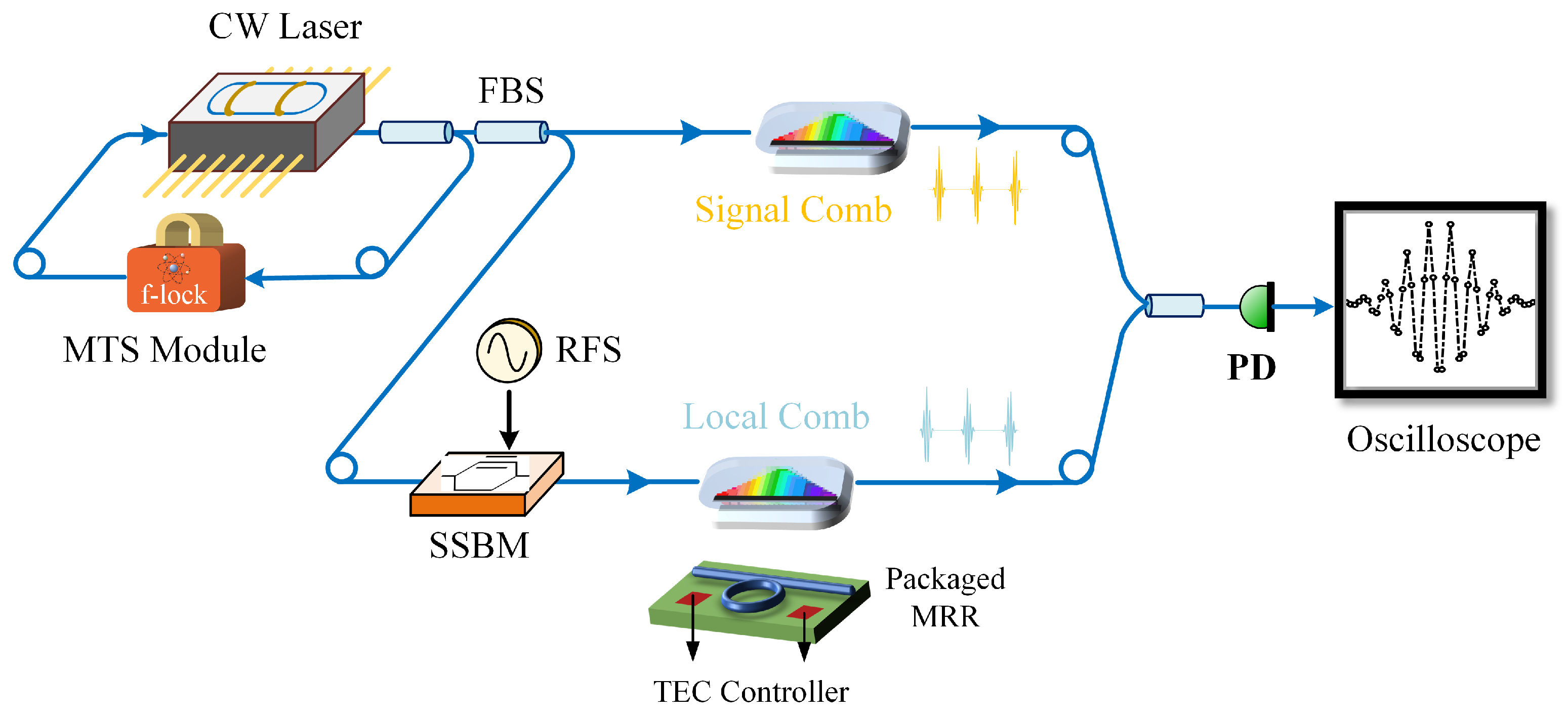
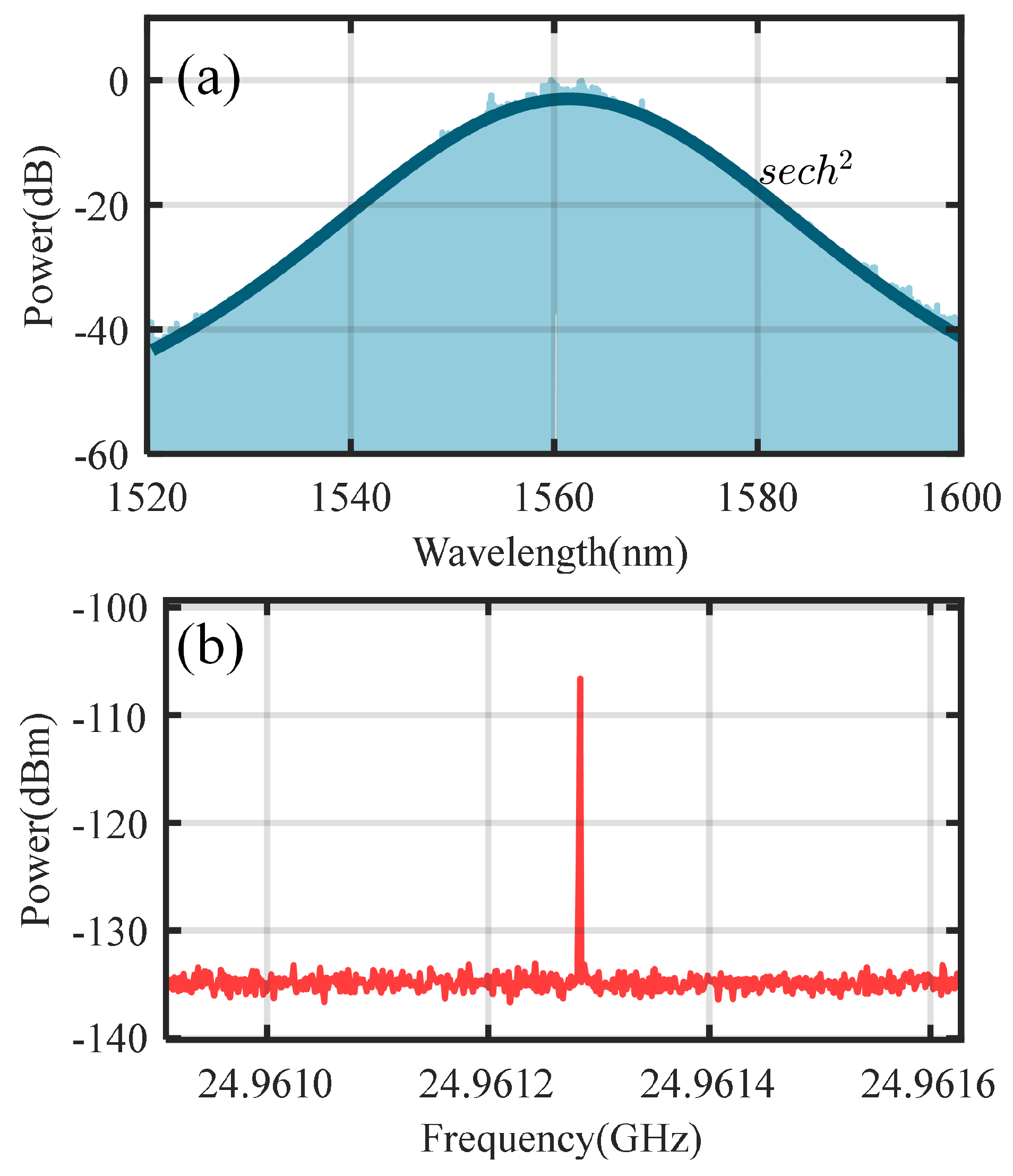
3.1. Experimental Setup
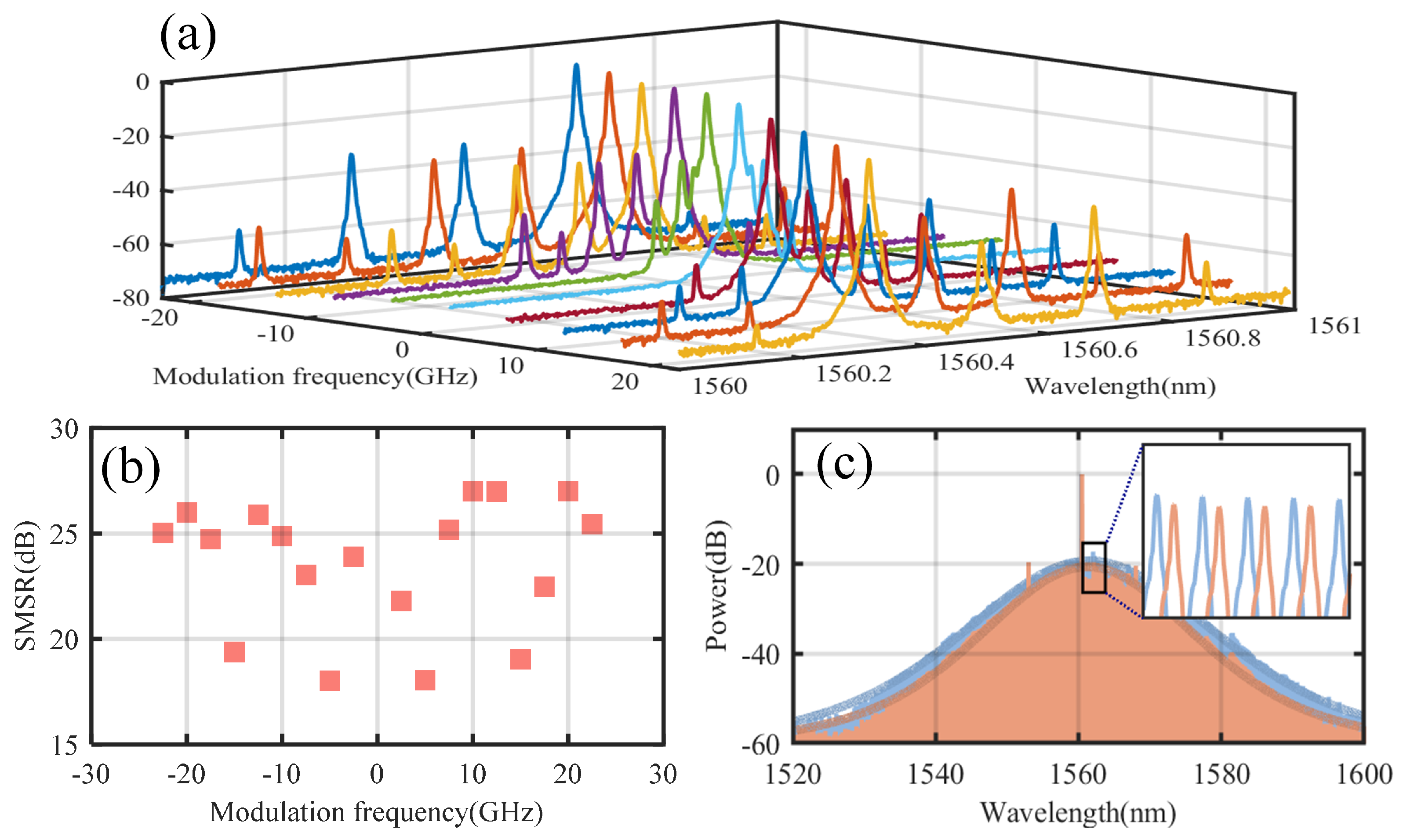
3.2. Single Sideband Modulation and Generation of SMC
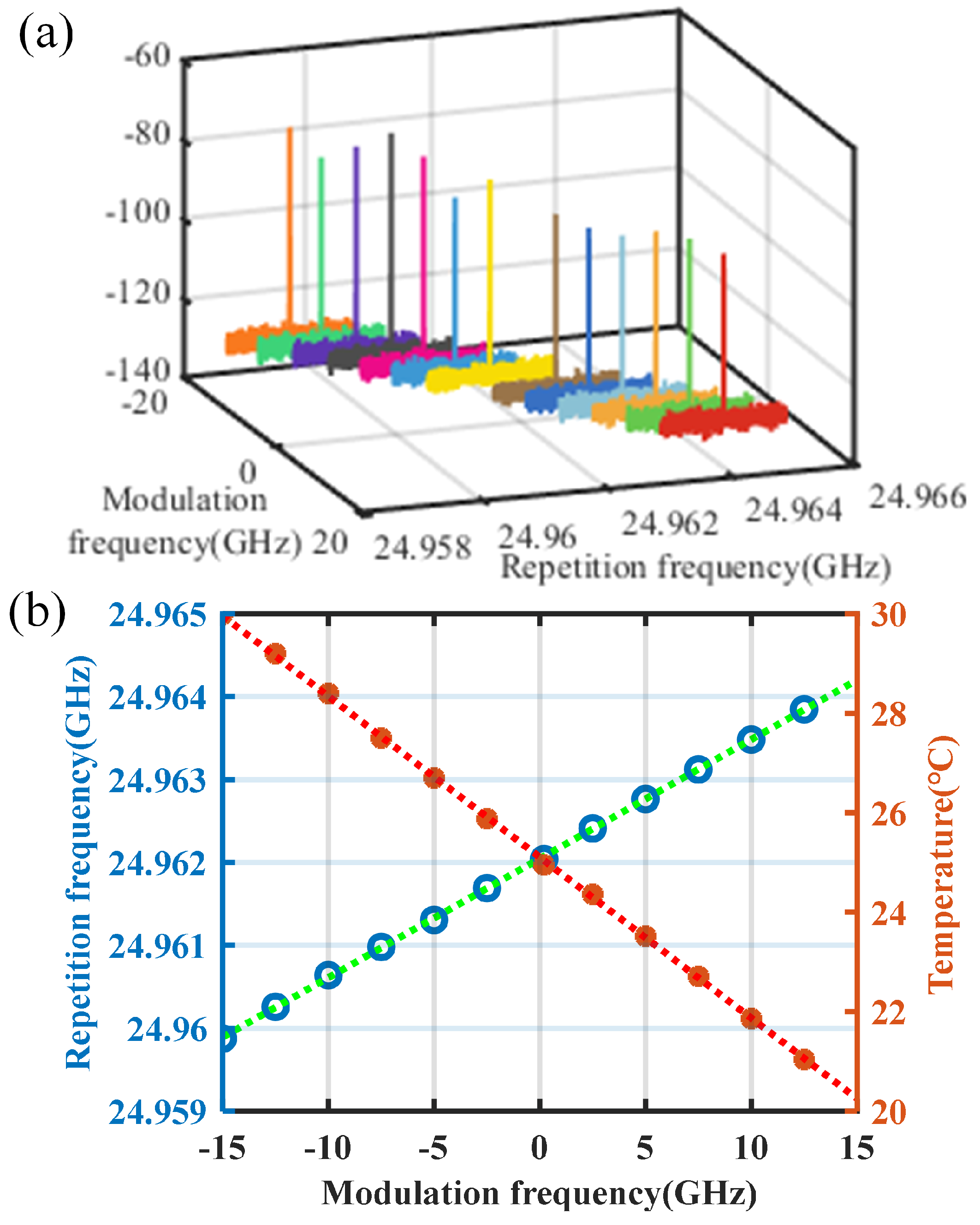
3.3. Results of Repetition Rate Tuning
3.4. Dual-Microcomb Interferograms with Different Repetition Rate Differences
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Minoshima, K.; Arai, K.; Inaba, H. High-accuracy self-correction of refractive index of air using two-color interferometry of optical frequency combs. Opt. Express 2011, 19, 26095–26105. [Google Scholar] [CrossRef] [PubMed]
- Jang, Y.S.; Kim, S.W. Distance measurements using mode-locked lasers: A review. Nanomanuf. Metrol. 2018, 1, 131–147. [Google Scholar] [CrossRef]
- Huang, G.; Cui, C.; Lei, X.; Li, Q.; Yan, S.; Li, X.; Wang, G. A Review of Optical Interferometry for High-Precision Length Measurement. Micromachines 2025, 16, 6. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Bouchand, R.; Nicolodi, D.; Giunta, M.; Hänsel, W.; Lezius, M.; Joshi, A.; Datta, S.; Alexandre, C.; Lours, M.; et al. Photonic microwave signals with zeptosecond-level absolute timing noise. Nat. Photonics 2017, 11, 44–47. [Google Scholar] [CrossRef]
- Bouchand, R.; Xie, X.; Giunta, M.; Hänsel, W.; Lezius, M.; Holzwarth, R.; Alexandre, C.; Tremblin, P.A.; Santarelli, G.; Le Coq, Y. Compact low-noise photonic microwave generation from commercial low-noise lasers. IEEE Photonics Technol. Lett. 2017, 29, 1403–1406. [Google Scholar] [CrossRef]
- Muraviev, A.; Smolski, V.O.; Loparo, Z.E.; Vodopyanov, K.L. Massively parallel sensing of trace molecules and their isotopologues with broadband subharmonic mid-infrared frequency combs. Nat. Photonics 2018, 12, 209–214. [Google Scholar] [CrossRef]
- Martín-Mateos, P.; Khan, F.U.; Bonilla-Manrique, O.E. Direct hyperspectral dual-comb imaging. Optica 2020, 7, 199–202. [Google Scholar] [CrossRef]
- Lisdat, C.; Grosche, G.; Quintin, N.; Shi, C.; Raupach, S.; Grebing, C.; Nicolodi, D.; Stefani, F.; Al-Masoudi, A.; Dörscher, S.; et al. A clock network for geodesy and fundamental science. Nat. Commun. 2016, 7, 12443. [Google Scholar] [CrossRef]
- Guéna, J.; Weyers, S.; Abgrall, M.; Grebing, C.; Gerginov, V.; Rosenbusch, P.; Bize, S.; Lipphardt, B.; Denker, H.; Quintin, N.; et al. First international comparison of fountain primary frequency standards via a long distance optical fiber link. Metrologia 2017, 54, 348. [Google Scholar] [CrossRef]
- Vicentini, E.; Wang, Z.; Van Gasse, K.; Hänsch, T.W.; Picqué, N. Dual-comb hyperspectral digital holography. Nat. Photonics 2021, 15, 890–894. [Google Scholar] [CrossRef]
- Ycas, G.; Giorgetta, F.R.; Baumann, E.; Coddington, I.; Herman, D.; Diddams, S.A.; Newbury, N.R. High-coherence mid-infrared dual-comb spectroscopy spanning 2.6 to 5.2 μm. Nat. Photonics 2018, 12, 202–208. [Google Scholar] [CrossRef]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photonics 2009, 3, 351–356. [Google Scholar] [CrossRef]
- Zhu, Z.; Wu, G. Dual-comb ranging. Engineering 2018, 4, 772–778. [Google Scholar] [CrossRef]
- Yan, E.; Wang, G.; Lei, X.; Tang, J.; Yang, M.; Tian, D.; Meng, Z.; Liu, S.; Guo, X.; Li, X.; et al. Rapid and high-precise ranging with a frequency-locked and coherent dual-microcomb source. J. Light. Technol. 2025, 1–7. [Google Scholar] [CrossRef]
- Ye, Z.; Jia, H.; Huang, Z.; Shen, C.; Long, J.; Shi, B.; Luo, Y.H.; Gao, L.; Sun, W.; Guo, H.; et al. Foundry manufacturing of tight-confinement, dispersion-engineered, ultralow-loss silicon nitride photonic integrated circuits. Photonics Res. 2023, 11, 558–568. [Google Scholar] [CrossRef]
- Dutt, A.; Joshi, C.; Ji, X.; Cardenas, J.; Okawachi, Y.; Luke, K.; Gaeta, A.L.; Lipson, M. On-chip dual-comb source for spectroscopy. Sci. Adv. 2018, 4, e1701858. [Google Scholar] [CrossRef]
- Li, J.T.; Chang, B.; Du, J.T.; Tan, T.; Geng, Y.; Zhou, H.; Liang, Y.P.; Zhang, H.; Yan, G.F.; Ma, L.M.; et al. Coherently parallel fiber-optic distributed acoustic sensing using dual Kerr soliton microcombs. Sci. Adv. 2024, 10, eadf8666. [Google Scholar] [CrossRef]
- Yi, X.; Yang, Q.F.; Yang, K.Y.; Vahala, K. Theory and measurement of the soliton self-frequency shift and efficiency in optical microcavities. Opt. Lett. 2016, 41, 3419–3422. [Google Scholar] [CrossRef]
- Bao, C.; Xuan, Y.; Wang, C.; Jaramillo-Villegas, J.A.; Leaird, D.E.; Qi, M.; Weiner, A.M. Soliton repetition rate in a silicon-nitride microresonator. Opt. Lett. 2017, 42, 759–762. [Google Scholar] [CrossRef]
- He, Y.; Lopez-Rios, R.; Javid, U.A.; Ling, J.; Li, M.; Xue, S.; Vahala, K.; Lin, Q. High-speed tunable microwave-rate soliton microcomb. Nat. Commun. 2023, 14, 3467. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.F.; Yi, X.; Yang, K.Y.; Vahala, K. Counter-propagating solitons in microresonators. Nat. Photonics 2017, 11, 560–564. [Google Scholar] [CrossRef]
- Niu, R.; Li, M.; Wan, S.; Sun, Y.R.; Hu, S.M.; Zou, C.L.; Guo, G.C.; Dong, C.H. kHz-precision wavemeter based on reconfigurable microsoliton. Nat. Commun. 2023, 14, 169. [Google Scholar] [CrossRef]
- Liu, J.; Tian, H.; Lucas, E.; Raja, A.S.; Lihachev, G.; Wang, R.N.; He, J.; Liu, T.; Anderson, M.H.; Weng, W.; et al. Monolithic piezoelectric control of soliton microcombs. Nature 2020, 583, 385–390. [Google Scholar] [CrossRef]
- Niu, R.; Wan, S.; Sun, S.M.; Ma, T.G.; Chen, H.J.; Wang, W.Q.; Lu, Z.; Zhang, W.F.; Guo, G.C.; Zou, C.L.; et al. Repetition rate tuning and locking of solitons in a microrod resonator. Opt. Lett. 2024, 49, 570–573. [Google Scholar] [CrossRef]
- Joshi, C.; Jang, J.K.; Luke, K.; Ji, X.; Miller, S.A.; Klenner, A.; Okawachi, Y.; Lipson, M.; Gaeta, A.L. Thermally controlled comb generation and soliton modelocking in microresonators. Opt. Lett. 2016, 41, 2565–2568. [Google Scholar] [CrossRef]
- Wang, G.; Gao, L.; Huang, G.; Lei, X.; Cui, C.; Wang, S.; Yang, M.; Zhu, J.; Yan, S.; Li, X. A Wavelength-Stabilized and Quasi-Common-Path Heterodyne Grating Interferometer With Sub-Nanometer Precision. IEEE Trans. Instrum. Meas. 2024, 73, 1–9. [Google Scholar] [CrossRef]
- Xue, X.; Xuan, Y.; Wang, C.; Wang, P.H.; Liu, Y.; Niu, B.; Leaird, D.E.; Qi, M.; Weiner, A.M. Thermal tuning of Kerr frequency combs in silicon nitride microring resonators. Opt. Express 2016, 24, 687–698. [Google Scholar] [CrossRef]
- Arbabi, A.; Goddard, L.L. Measurements of the refractive indices and thermo-optic coefficients of Si3N4 and SiOx using microring resonances. Opt. Lett. 2013, 38, 3878–3881. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, E.; Peng, M.; Tang, J.; Huang, J.; Tian, D.; Liu, S.; Meng, Z.; Li, X.; Zhu, L.; Yan, S.; et al. Performing MHz-Level Repetition Rate Tuning for Coherent Dual-Microcomb Interferometry. Micromachines 2025, 16, 448. https://doi.org/10.3390/mi16040448
Yan E, Peng M, Tang J, Huang J, Tian D, Liu S, Meng Z, Li X, Zhu L, Yan S, et al. Performing MHz-Level Repetition Rate Tuning for Coherent Dual-Microcomb Interferometry. Micromachines. 2025; 16(4):448. https://doi.org/10.3390/mi16040448
Chicago/Turabian StyleYan, Enqi, Mingliang Peng, Jian Tang, Jiyuan Huang, Donglai Tian, Suyang Liu, Zhijun Meng, Xianbin Li, Lingxiao Zhu, Shuhua Yan, and et al. 2025. "Performing MHz-Level Repetition Rate Tuning for Coherent Dual-Microcomb Interferometry" Micromachines 16, no. 4: 448. https://doi.org/10.3390/mi16040448
APA StyleYan, E., Peng, M., Tang, J., Huang, J., Tian, D., Liu, S., Meng, Z., Li, X., Zhu, L., Yan, S., & Wang, G. (2025). Performing MHz-Level Repetition Rate Tuning for Coherent Dual-Microcomb Interferometry. Micromachines, 16(4), 448. https://doi.org/10.3390/mi16040448






