A Hybrid GRA-TOPSIS-RFR Optimization Approach for Minimizing Burrs in Micro-Milling of Ti-6Al-4V Alloys
Abstract
:1. Introduction
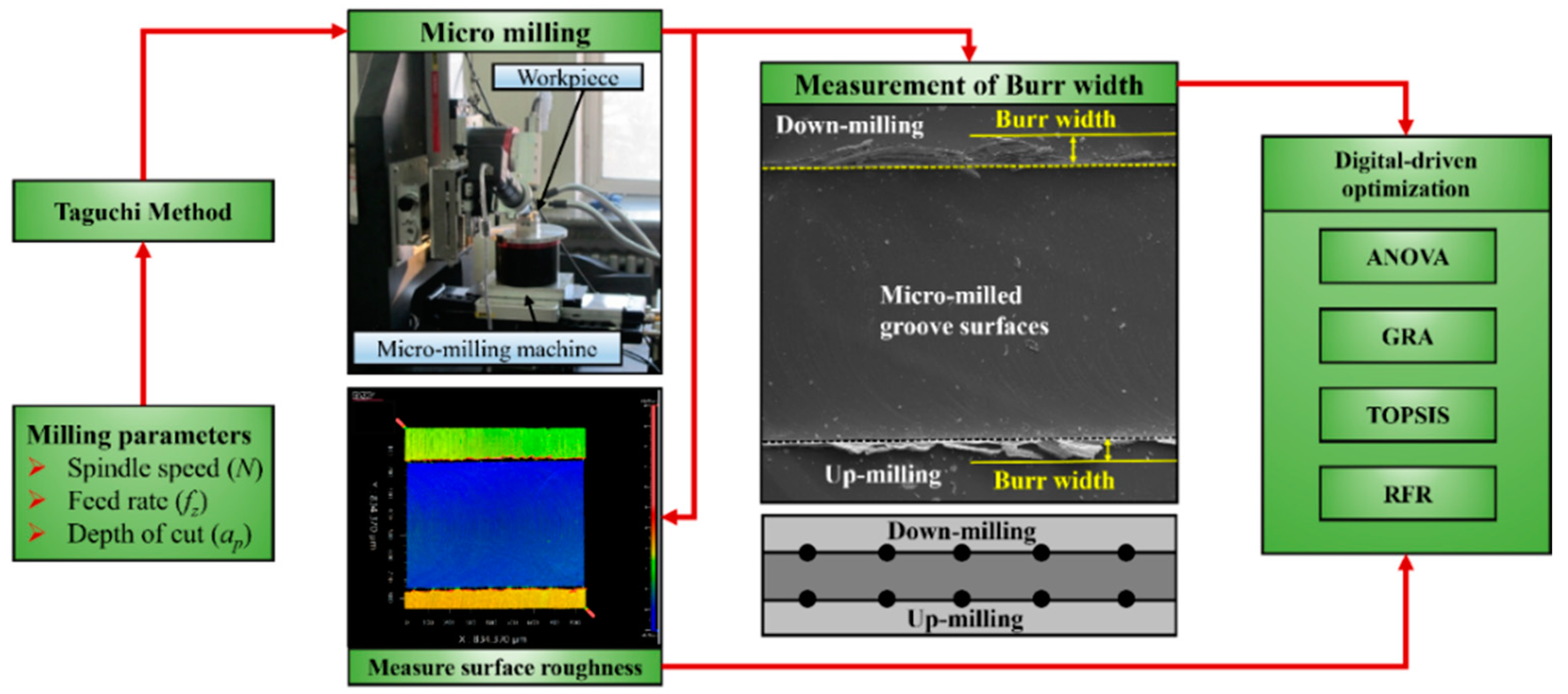
2. Experimental Design and Analysis Methods
2.1. Materials and Machining Set-Up
2.2. Experimental Design
3. Analysis Methods for Optimizing the Milling Parameters
3.1. GRA-TOPSIS Method
- (1)
- A decision matrix is developed considering all the responses and their alternatives. gives the response of alternative; also, and are the number of alternatives and responses, respectively.
- (2)
- The normalization of the decision matrix with the following formula:
- (3)
- The computation of the weighted normal decision matrix by choosing appropriate response weights. Weights are chosen based on relative importance. In the case of equal response significance, each weight , as shown in the following:
- (4)
- The selection of best and worst solution candidates among the weighed normalized matrix. The best value for a “lower is better” solution like surface roughness is the lowest value among the weighted normal responses and vice versa. The equations for best and worst solutions are as follows:
- (5)
- The positive grey relational coefficients with respect to the “best solution” are computed as
- (6)
- Positive and negative grey relational grades are computed as average positive and negative grey relational coefficients, respectively.
- (7)
- Calculating an alternative’s relative closeness compared to the ideal solution is given by
- (8)
- Ranking the alternatives based on the descending order of Pi.
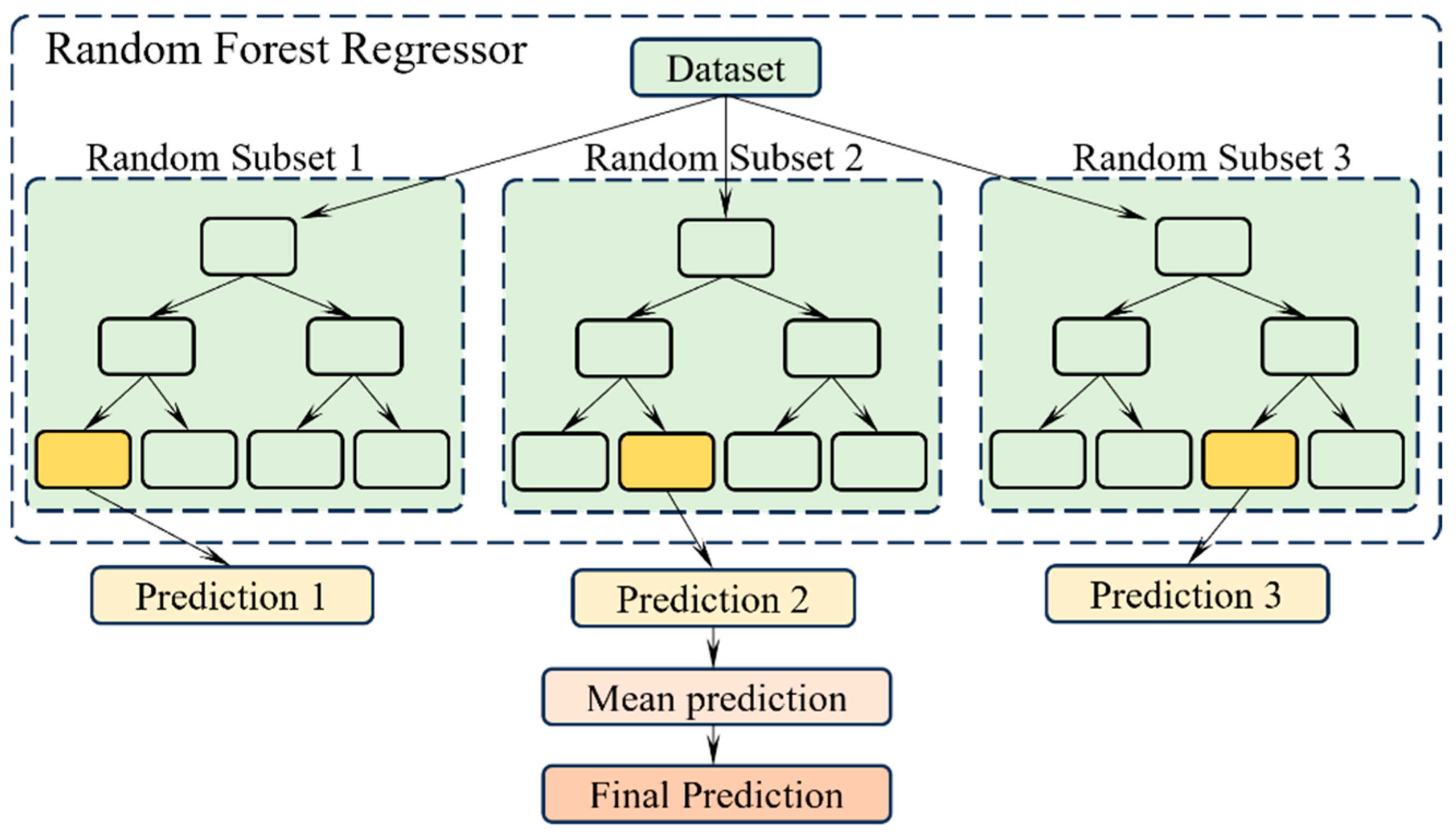
3.2. Random Forest Regression (RFR) Methods
- (1)
- In RFR, the “n” number of random data subsets are generated from the original dataset with replacement.
- (2)
- Next, “n” decision tree models are trained by considering each generated data sample.
- (3)
- The individual decision tree model predictions are recorded.
- (4)
- The final prediction is the mean of all individual model predictions.
4. Results and Discussion
4.1. ANOVA
4.1.1. ANOVA of the Surface Roughness
4.1.2. ANOVA of the Burr Width in Down-Milling
4.1.3. ANOVA of the Burr Width in Up-Milling
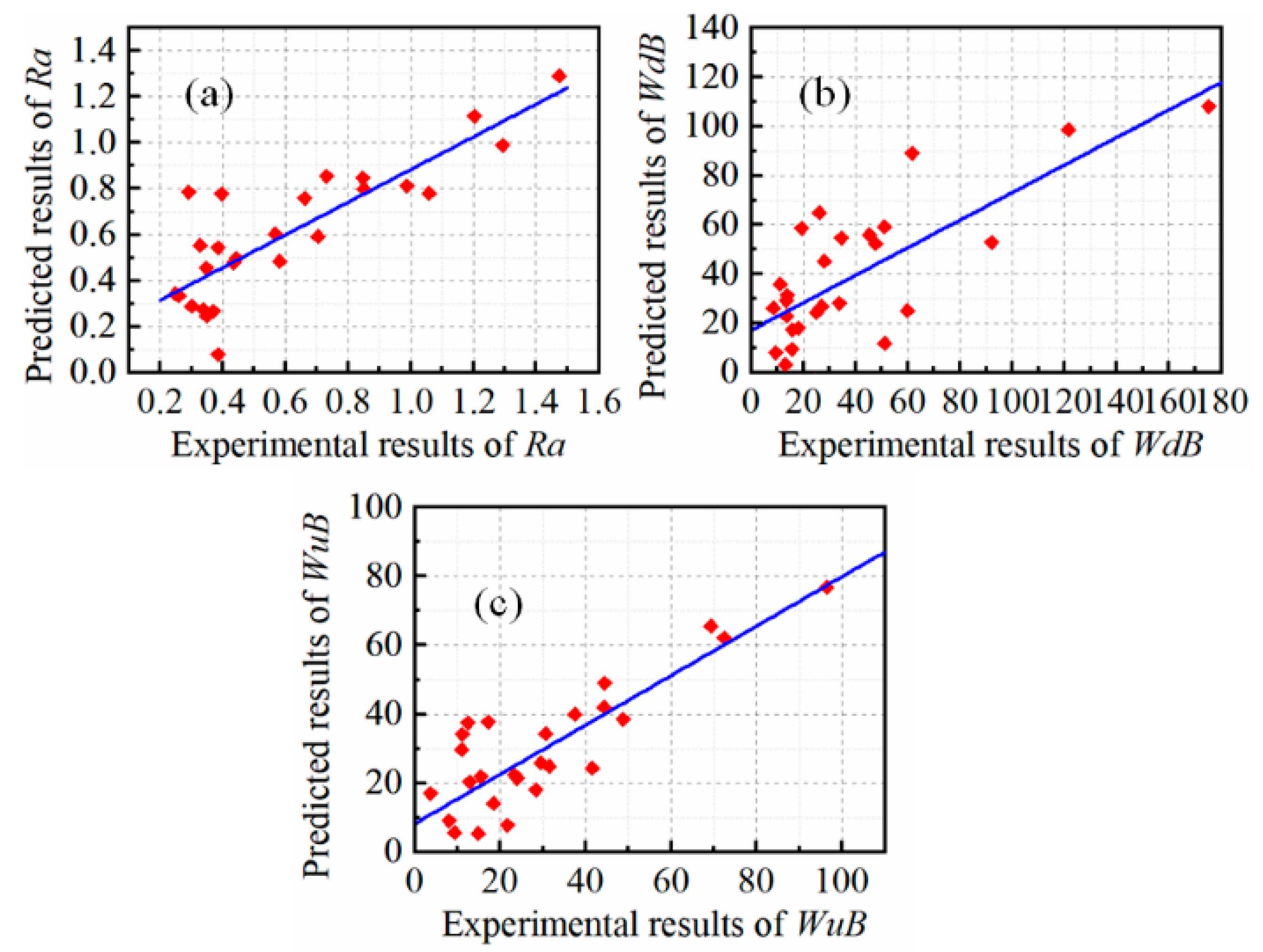
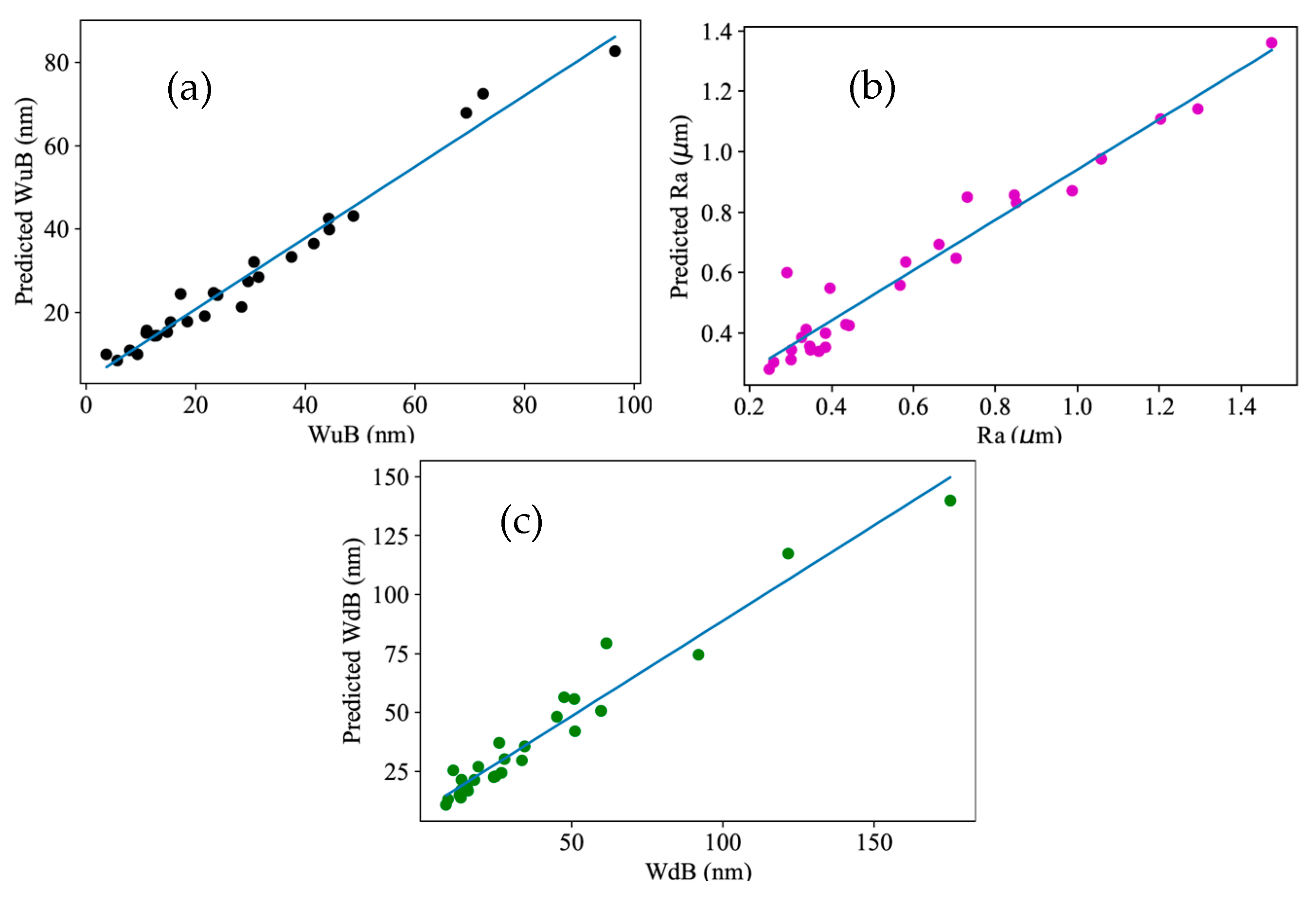
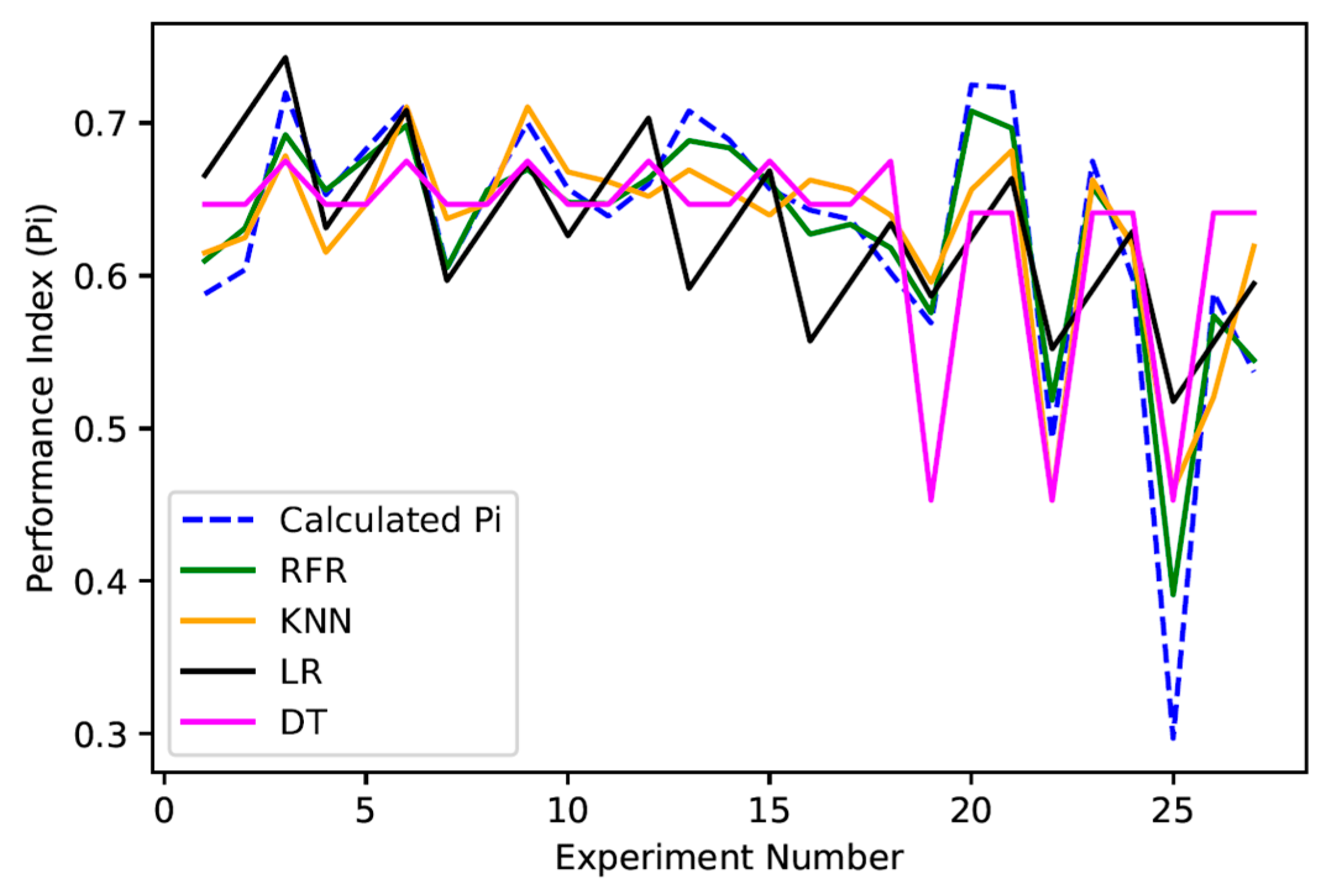
4.2. Machine Learning-Based Response Prediction
4.3. Multi-Objective Optimization Using GRA-TOPSIS
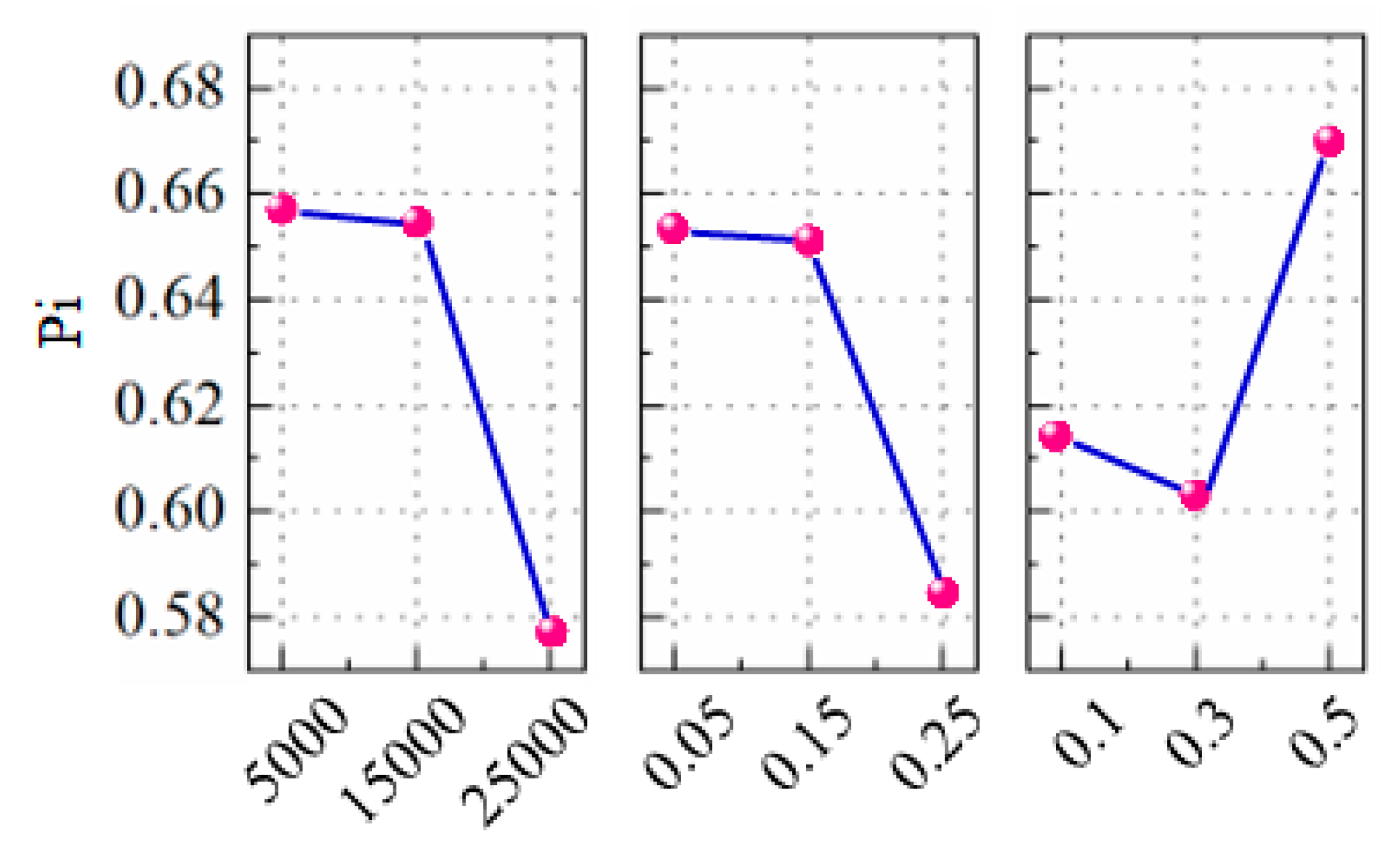
4.4. Confirmation of the Optimzied Paramters in Experments
5. Conclusions
- (1)
- The hybrid GRA-TOPSIS-RFR optimization algorithm proposed in this work can leverage the strengths of RFR models to handle complex, nonlinear relationships between micro-milling parameters and the optimization performance index. RFR being more accurate, robust, and explainable can be integrated effectively with GRA-TOPSIS to model and optimize challenging manufacturing problems.
- (2)
- Linear regression and RFR models were built for predicting the surface roughness (Ra), burr widths on the down-milling side (WdB), and burr widths on the up-milling side (WuB). For the given dataset, the RFR model outperformed the linear regression models with R2 values of 0.93, 0.93, and 0.96 against 0.7009, 0.5591, and 0.7164 for Ra, WdB, and WuB, respectively.
- (3)
- The surface roughness has a positive correlation with the spindle speed and depth of cut, while Ra was found to increase with a small feed rate due to the ploughing effect. Both burr widths (i.e., WuB and WdB) were found to first decrease and then increase with the rise in the spindle speed and depth of cut, while burr widths always showed a decreasing trend with the increase in feed rate.
- (4)
- The depth of cut has the largest influence on the surface roughness, while the feed rate per tooth plays the most important role in burr formation in both down- and up-milling processes.
- (5)
- Based on the GRA-TOPSIS-RFR approach, the optimal parameter combination for micro-milling Ti-6Al-4V was given as spindle speed N = 25,000 RPM, depth of cut ap = 0.05 mm, and feed rate per tooth fz = 0.3 μm/tooth. Overall, the GRA-RFR hybrid model offers a promising approach for data analysis and decision-making in smart manufacturing, especially for complex precision manufacturing applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pimenov, D.Y.; Mia, M.; Gupta, M.K.; Machado, A.R.; Tomaz, Í.V.; Sarikaya, M.; Wojciechowski, S.; Mikolajczyk, T.; Kapłonek, W. Improvement of machinability of Ti and its alloys using cooling-lubrication techniques: A review and future prospect. J. Mater. Res. Technol. 2021, 11, 719–753. [Google Scholar] [CrossRef]
- Xiao, G.; Liu, Z.; Li, C.; He, Y. Efficient and low-damage machining of Ti6Al4V: Laser-assisted CBN belt grinding. Mater. Manuf. Process. 2024, 39, 110–122. [Google Scholar] [CrossRef]
- Najafizadeh, M.; Yazdi, S.; Bozorg, M.; Ghasempour-Mouziraji, M.; Hosseinzadeh, M.; Zarrabian, M.; Cavaliere, P. Classification and applications of titanium and its alloys: A review. J. Alloys Compd. Commun. 2024, 3, 100019. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Sabirov, I.; Zemtsova, E.G.; Parfenov, E.V.; Dluhoš, L.; Lowe, T.C. 4.3—Nanostructured commercially pure titanium for development of miniaturized biomedical implants. In Titanium in Medical and Dental Applications; Woodhead Publishing: Cambridge, UK, 2018. [Google Scholar]
- Chen, N.; Li, H.N.; Wu, J.; Li, Z.; Li, L.; Liu, G.; He, N. Advances in micro milling: From tool fabrication to process outcomes. Int. J. Mach. Tools Manuf. 2021, 160, 103670. [Google Scholar] [CrossRef]
- Hashmi, A.W.; Mali, H.S.; Meena, A.; Saxena, K.K.; Ahmad, S.; Agrawal, M.K.; Sagbas, B.; Valerga Puerta, A.P.; Khan, M.I. A comprehensive review on surface post-treatments for freeform surfaces of bio-implants. J. Mater. Res. Technol. 2023, 23, 4866–4908. [Google Scholar] [CrossRef]
- Hourmand, M.; Sarhan, A.A.D.; Sayuti, M.; Hamdi, M. A Comprehensive Review on Machining of Titanium Alloys. Arab. J. Sci. Eng. 2021, 46, 7087–7123. [Google Scholar] [CrossRef]
- Tan, R.; Jin, S.; Wei, S.; Wang, J.; Zhao, X.; Wang, Z.; Liu, Q.; Sun, T. Evolution mechanism of microstructure and microhardness of Ti–6Al–4V alloy during ultrasonic elliptical vibration assisted ultra-precise cutting. J. Mater. Res. Technol. 2024, 30, 1641–1649. [Google Scholar] [CrossRef]
- Tan, R.; Zhao, X.; Guo, S.; Zou, X.; He, Y.; Geng, Y.; Hu, Z.; Sun, T. Sustainable production of dry-ultra-precision machining of Ti–6Al–4V alloy using PCD tool under ultrasonic elliptical vibration-assisted cutting. J. Clean. Prod. 2020, 248, 119254. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, N.; Bian, R.; He, N.; Li, Z.; Li, L. Investigations on burr formation mechanisms in micro milling of high-aspect-ratio titanium alloy ti-6al-4 v structures. Int. J. Mech. Sci. 2020, 185, 105884. [Google Scholar] [CrossRef]
- Chen, M.; Ni, H.; Wang, Z.; Jiang, Y. Research on the modeling of burr formation process in micro-ball end milling operation on Ti–6Al–4V. Int. J. Adv. Manuf. Technol. 2012, 62, 901–912. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, J.; Xiao, Y.; Yang, H.; Chen, M. Effect of milling modes on surface integrity of KDP crystal processed by micro ball-end milling. Procedia CIRP 2018, 71, 260–266. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, S.-H. Optimisation of cutting parameters for burr minimization in face-milling operations. Int. J. Prod. Res. 2010, 41, 497–511. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, J.; Yang, H.; Xu, Y.; Zhao, L.; Tan, C.; Chen, M. Modeling of residual tool mark formation and its influence on the optical performance of KH2PO4 optics repaired by micro-milling. Opt. Mater. Express 2019, 9, 3789–3807. [Google Scholar] [CrossRef]
- Zhang, Y.; Bai, Q. Microstructure effects on surface integrity in slot micro-milling multiphase titanium alloy Ti6Al4V. J. Mater. Res. Technol. 2023, 25, 6684–6701. [Google Scholar] [CrossRef]
- ul hasan, S.; Ali, S.; Jaffery, S.H.I.; ud Din, E.; Mubashir, A.; Khan, M. Study of burr width and height using ANOVA in laser hybrid micro milling of titanium alloy (Ti6Al4V). J. Mater. Res. Technol. 2022, 21, 4398–4408. [Google Scholar] [CrossRef]
- Ziberov, M.; de Oliveira, D.; da Silva, M.B.; Hung, W.N. Wear of TiAlN and DLC coated microtools in micromilling of Ti-6Al-4V alloy. J. Manuf. Process. 2020, 56, 337–349. [Google Scholar] [CrossRef]
- Thepsonthi, T.; Özel, T. Experimental and finite element simulation based investigations on micro-milling Ti-6Al-4V titanium alloy: Effects of cBN coating on tool wear. J. Mater. Process. Technol. 2013, 213, 532–542. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, P.; Xu, X. Digitalisation and servitisation of machine tools in the era of Industry 4.0: A review. Int. J. Prod. Res. 2021, 61, 4069–4101. [Google Scholar] [CrossRef]
- Shen, N.; Wu, Y.; Li, J.; He, T.; Lu, Y.; Xu, Y. Research on procedure optimisation for composite grinding based on Digital Twin technology. Int. J. Prod. Res. 2022, 61, 1736–1754. [Google Scholar] [CrossRef]
- Abbas, A.T.; Sharma, N.; Anwar, S.; Hashmi, F.H.; Jamil, M.; Hegab, H. Towards optimization of surface roughness and productivity aspects during high-speed machining of Ti–6Al–4V. Materials 2019, 12, 3749. [Google Scholar] [CrossRef]
- Khan, M.A.; Jaffery, S.H.I.; Khan, M.; Younas, M.; Butt, S.I.; Ahmad, R.; Warsi, S.S. Multi-objective optimization of turning titanium-based alloy Ti-6Al-4V under dry, wet, and cryogenic conditions using gray relational analysis (GRA). Int. J. Adv. Manuf. Technol. 2020, 106, 3897–3911. [Google Scholar] [CrossRef]
- Wang, J.; Mao, T.; Tu, Y. Simultaneous multi-response optimisation for parameter and tolerance design using Bayesian modelling method. Int. J. Prod. Res. 2020, 59, 2269–2293. [Google Scholar] [CrossRef]
- Dhuria, G.K.; Singh, R.; Batish, A. Application of a hybrid Taguchi-entropy weight-based GRA method to optimize and neural network approach to predict the machining responses in ultrasonic machining of Ti–6Al–4V. J. Braz. Soc. Mech. Sci. Eng. 2016, 39, 2619–2634. [Google Scholar] [CrossRef]
- Pradhan, M.K. Estimating the effect of process parameters on MRR, TWR and radial overcut of EDMed AISI D2 tool steel by RSM and GRA coupled with PCA. Int. J. Adv. Manuf. Technol. 2013, 68, 591–605. [Google Scholar] [CrossRef]
- Kharwar, P.K.; Verma, R.K. Machining performance optimization in drilling of multiwall carbon nano tube/epoxy nanocomposites using GRA-PCA hybrid approach. Measurement 2020, 158, 107701. [Google Scholar] [CrossRef]
- Umamaheswarrao, P.; Raju, D.R.; Suman, K.N.S.; Sankar, B.R. Multi objective optimization of process parameters for hard turning of AISI 52100 steel using Hybrid GRA-PCA. Procedia Comput. Sci. 2018, 133, 703–710. [Google Scholar] [CrossRef]
- Mat Deris, A.; Mohd Zain, A.; Sallehuddin, R. Hybrid GR-SVM for prediction of surface roughness in abrasive water jet machining. Meccanica 2013, 48, 1937–1945. [Google Scholar] [CrossRef]
- Dewangan, S.; Gangopadhyay, S.; Biswas, C.K. Multi-response optimization of surface integrity characteristics of EDM process using grey-fuzzy logic-based hybrid approach. Eng. Sci. Technol. Int. J. 2015, 18, 361–368. [Google Scholar] [CrossRef]
- Rajamani, D.; Siva Kumar, M.; Balasubramanian, E.; Tamilarasan, A. Nd: YAG laser cutting of Hastelloy C276: ANFIS modeling and optimization through WOA. Mater. Manuf. Process. 2021, 36, 1746–1760. [Google Scholar] [CrossRef]
- Manikandan, N.; Balasubramanian, K.; Palanisamy, D.; Gopal, P.M.; Arulkirubakaran, D.; Binoj, J.S. Machinability Analysis and ANFIS modelling on Advanced Machining of Hybrid Metal Matrix Composites for Aerospace Applications. Mater. Manuf. Process. 2019, 34, 1866–1881. [Google Scholar] [CrossRef]
- Latha, B.; Senthilkumar, V.S. Modeling and Analysis of Surface Roughness Parameters in Drilling GFRP Composites Using Fuzzy Logic. Mater. Manuf. Process. 2010, 25, 817–827. [Google Scholar] [CrossRef]
- Arisoy, Y.M.; Özel, T. Machine Learning Based Predictive Modeling of Machining Induced Microhardness and Grain Size in Ti–6Al–4V Alloy. Mater. Manuf. Process. 2014, 30, 425–433. [Google Scholar] [CrossRef]
- Prashanth, G.S.; Sekar, P.; Bontha, S.; Balan, A.S.S. Grinding parameters prediction under different cooling environments using machine learning techniques. Mater. Manuf. Process. 2022, 38, 235–244. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, J.; Xiao, Y.; Chen, M.; Yang, H.; Wang, J. Effect of tool inclination on surface quality of KDP crystal processed by micro ball-end milling. Int. J. Adv. Manuf. Technol. 2018, 99, 2777–2788. [Google Scholar] [CrossRef]
- Liu, Q.; Liao, Z.; Cheng, J.; Xu, D.; Chen, M. Mechanism of chip formation and surface-defects in orthogonal cutting of soft-brittle potassium dihydrogen phosphate crystals. Mater. Des. 2021, 198, 109327. [Google Scholar] [CrossRef]
- García-Cascales, M.S.; Lamata, M.T. On rank reversal and TOPSIS method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Sanayei, A.; Farid Mousavi, S.; Yazdankhah, A. Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst. Appl. 2010, 37, 24–30. [Google Scholar] [CrossRef]
- Liu, Q.; Cheng, J.; Zhao, L.; Tan, R.; Lei, H.; Chen, M. Invesitgation on characterizing the surface topography of KH2PO4 optics repaired by different milling modes. J. Manuf. Process. 2025, 141, 1–16. [Google Scholar] [CrossRef]
- Liu, Q.; Liao, Z.; Axinte, D. Temperature effect on the material removal mechanism of soft-brittle crystals at nano/micron scale. Int. J. Mach. Tools Manuf. 2020, 159, 103620. [Google Scholar] [CrossRef]
- Tan, R.; Zhao, X.; Liu, Q.; Guo, X.; Lin, F.; Yang, L.; Sun, T. Investigation of Surface Integrity of Selective Laser Melting Additively Manufactured AlSi10Mg Alloy under Ultrasonic Elliptical Vibration-Assisted Ultra-Precision Cutting. Materials 2022, 15, 8910. [Google Scholar] [CrossRef]
- Chen, N.; Li, L.; Wu, J.; Qian, J.; He, N.; Reynaerts, D. Research on the ploughing force in micro milling of soft-brittle crystals. Int. J. Mech. Sci. 2019, 155, 315–322. [Google Scholar] [CrossRef]




| Chemical Elements | V | Al | Sn | Zr | Mo | C | Si | Cr | Fe | Cu | Nb | Ti |
| Weight (%) | 4.22 | 5.48 | 0.0625 | 0.0025 | 0.005 | 0.369 | 0.022 | 0.0099 | 0.112 | <0.02 | 0.0386 | 90 |
| Parameter | Value |
|---|---|
| Tensile strength (MPa) | 950 |
| Elastic modulus (GPa) | 114 |
| Density (g/cm3) | 4.42 |
| Vickers hardness (kgf/mm2) | 330 |
| Symbol | Factors | Level | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | Spindle speed N (RPM) | 5000 | 15,000 | 25,000 |
| B | Depth of cut ap (mm) | 0.05 | 0.15 | 0.25 |
| C | Feed per tooth fz (μm/tooth) | 0.1 | 0.3 | 0.5 |
| Exp. | Group | Factors | Response Results | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | Ra (μm) | WdB (μm) | WuB (μm) | ||
| 1 | A1B1C1 | 5000 | 0.05 | 0.1 | 0.349 | 92.05 | 44.25 |
| 2 | A1B1C2 | 5000 | 0.05 | 0.3 | 0.385 | 59.83 | 48.76 |
| 3 | A1B1C3 | 5000 | 0.05 | 0.5 | 0.338 | 13.56 | 11.03 |
| 4 | A1B2C1 | 5000 | 0.15 | 0.1 | 0.347 | 45.23 | 31.45 |
| 5 | A1B2C2 | 5000 | 0.15 | 0.3 | 0.302 | 33.68 | 23.95 |
| 6 | A1B2C3 | 5000 | 0.15 | 0.5 | 0.581 | 8.53 | 3.65 |
| 7 | A1B3C1 | 5000 | 0.25 | 0.1 | 0.662 | 50.95 | 29.53 |
| 8 | A1B3C2 | 5000 | 0.25 | 0.3 | 0.704 | 13.68 | 23.24 |
| 9 | A1B3C3 | 5000 | 0.25 | 0.5 | 0.291 | 13.45 | 28.35 |
| 10 | A2B1C1 | 15,000 | 0.05 | 0.1 | 0.259 | 47.62 | 37.46 |
| 11 | A2B1C2 | 15,000 | 0.05 | 0.3 | 0.301 | 51.18 | 41.53 |
| 12 | A2B1C3 | 15,000 | 0.05 | 0.5 | 0.567 | 24.35 | 21.62 |
| 13 | A2B2C1 | 15,000 | 0.15 | 0.1 | 0.385 | 19.23 | 10.95 |
| 14 | A2B2C2 | 15,000 | 0.15 | 0.3 | 0.443 | 17.92 | 18.45 |
| 15 | A2B2C3 | 15,000 | 0.15 | 0.5 | 0.987 | 12.98 | 5.67 |
| 16 | A2B3C1 | 15,000 | 0.25 | 0.1 | 0.846 | 26.13 | 12.45 |
| 17 | A2B3C2 | 15,000 | 0.25 | 0.3 | 0.851 | 24.89 | 15.39 |
| 18 | A2B3C3 | 15,000 | 0.25 | 0.5 | 1.203 | 15.56 | 14.78 |
| 19 | A3B1C1 | 25,000 | 0.05 | 0.1 | 0.369 | 61.58 | 69.35 |
| 20 | A3B1C2 | 25,000 | 0.05 | 0.3 | 0.248 | 10.96 | 17.22 |
| 21 | A3B1C3 | 25,000 | 0.05 | 0.5 | 0.396 | 9.24 | 7.95 |
| 22 | A3B2C1 | 25,000 | 0.15 | 0.1 | 0.435 | 121.65 | 72.42 |
| 23 | A3B2C2 | 25,000 | 0.15 | 0.3 | 0.327 | 27.89 | 30.61 |
| 24 | A3B2C3 | 25,000 | 0.15 | 0.5 | 1.294 | 15.8 | 9.35 |
| 25 | A3B3C1 | 25,000 | 0.25 | 0.1 | 1.058 | 175.32 | 96.48 |
| 26 | A3B3C2 | 25,000 | 0.25 | 0.3 | 0.731 | 34.58 | 44.35 |
| 27 | A3B3C3 | 25,000 | 0.25 | 0.5 | 1.474 | 26.88 | 12.86 |
| Sour. | Fre. | Seq SS | Adj SS | Adj MS | F | p | Cont. (%) |
|---|---|---|---|---|---|---|---|
| A | 2 | 0.3488 | 0.3488 | 0.1744 | 8.75 | 0.010 | 11.1 |
| B | 2 | 1.1924 | 1.1924 | 0.5962 | 29.92 | 0.000 | 37.8 |
| C | 2 | 0.5221 | 0.5221 | 0.2610 | 13.10 | 0.003 | 16.6 |
| A∗B | 4 | 0.2466 | 0.2466 | 0.0616 | 3.09 | 0.082 | 7.8 |
| A∗C | 4 | 0.4200 | 0.4200 | 0.1050 | 5.27 | 0.022 | 13.3 |
| B∗C | 4 | 0.2594 | 0.2594 | 0.0648 | 3.25 | 0.073 | 8.24 |
| RE | 8 | 0.1594 | 0.1594 | 0.0199 | 5.1 | ||
| Total | 26 | 3.1486 |
| Sour. | Fre. | Seq SS | Adj SS | Adj MS | F | p | Cont. (%) |
|---|---|---|---|---|---|---|---|
| A | 2 | 3379.5 | 3379.5 | 1689.7 | 4.52 | 0.049 | 9.0 |
| B | 2 | 401.5 | 401.5 | 200.7 | 0.54 | 0.604 | 1.1 |
| C | 2 | 14,843.4 | 14,843.4 | 7421.7 | 19.83 | 0.001 | 39.5 |
| A∗B | 4 | 6122.6 | 6122.6 | 1530.7 | 4.09 | 0.043 | 16.3 |
| A∗C | 4 | 8944.5 | 8944.5 | 2236.1 | 5.98 | 0.016 | 23.8 |
| B∗C | 4 | 930.3 | 930.3 | 232.6 | 0.62 | 0.660 | 2.5 |
| RE | 8 | 2993.5 | 2993.5 | 374.2 | 8.0 | ||
| Total | 26 | 37,615.2 |
| Sour. | Fre. | Seq SS | Adj SS | Adj MS | F | p | Cont. (%) |
|---|---|---|---|---|---|---|---|
| A | 2 | 88.73 | 88.73 | 44.37 | 4.72 | 0.044 | 7.2 |
| B | 2 | 106.76 | 106.76 | 53.38 | 5.68 | 0.029 | 8.6 |
| C | 2 | 537.53 | 537.53 | 268.76 | 28.58 | 0.001 | 43.4 |
| A∗B | 4 | 157.66 | 157.66 | 39.41 | 4.19 | 0.040 | 12.7 |
| A∗C | 4 | 187.91 | 187.91 | 46.98 | 4.99 | 0.026 | 15.2 |
| B∗C | 4 | 83.95 | 83.95 | 20.99 | 2.23 | 0.155 | 6.8 |
| RE | 8 | 75.24 | 75.24 | 9.41 | 1 | ||
| Total | 26 | 1237.8 |
| S. No. | N-Ra | N-WdB | N-WuB | W-N-Ra | W-N-WdB | W-N-WuB | GRC+ Ra |
|---|---|---|---|---|---|---|---|
| 1 | 0.10 | 0.33 | 0.23 | 0.03 | 0.11 | 0.08 | 0.86 |
| 2 | 0.11 | 0.21 | 0.26 | 0.04 | 0.07 | 0.09 | 0.82 |
| 3 | 0.09 | 0.05 | 0.06 | 0.03 | 0.02 | 0.02 | 0.87 |
| 4 | 0.10 | 0.16 | 0.17 | 0.03 | 0.05 | 0.06 | 0.86 |
| 5 | 0.08 | 0.12 | 0.13 | 0.03 | 0.04 | 0.04 | 0.92 |
| 6 | 0.16 | 0.03 | 0.02 | 0.05 | 0.01 | 0.01 | 0.65 |
| 7 | 0.19 | 0.18 | 0.16 | 0.06 | 0.06 | 0.05 | 0.60 |
| 8 | 0.20 | 0.05 | 0.12 | 0.07 | 0.02 | 0.04 | 0.57 |
| 9 | 0.08 | 0.05 | 0.15 | 0.03 | 0.02 | 0.05 | 0.93 |
| 10 | 0.07 | 0.17 | 0.20 | 0.02 | 0.06 | 0.07 | 0.98 |
| 11 | 0.08 | 0.18 | 0.22 | 0.03 | 0.06 | 0.07 | 0.92 |
| 12 | 0.16 | 0.09 | 0.11 | 0.05 | 0.03 | 0.04 | 0.66 |
| 13 | 0.11 | 0.07 | 0.06 | 0.04 | 0.02 | 0.02 | 0.82 |
| 14 | 0.12 | 0.06 | 0.10 | 0.04 | 0.02 | 0.03 | 0.76 |
| 15 | 0.28 | 0.05 | 0.03 | 0.09 | 0.02 | 0.01 | 0.45 |
| 16 | 0.24 | 0.09 | 0.07 | 0.08 | 0.03 | 0.02 | 0.51 |
| 17 | 0.24 | 0.09 | 0.08 | 0.08 | 0.03 | 0.03 | 0.50 |
| 18 | 0.34 | 0.06 | 0.08 | 0.11 | 0.02 | 0.03 | 0.39 |
| 19 | 0.10 | 0.22 | 0.37 | 0.03 | 0.07 | 0.12 | 0.84 |
| 20 | 0.07 | 0.04 | 0.09 | 0.02 | 0.01 | 0.03 | 1.00 |
| 21 | 0.11 | 0.03 | 0.04 | 0.04 | 0.01 | 0.01 | 0.81 |
| 22 | 0.12 | 0.43 | 0.38 | 0.04 | 0.14 | 0.13 | 0.77 |
| 23 | 0.09 | 0.10 | 0.16 | 0.03 | 0.03 | 0.05 | 0.89 |
| 24 | 0.36 | 0.06 | 0.05 | 0.12 | 0.02 | 0.02 | 0.37 |
| 25 | 0.30 | 0.62 | 0.51 | 0.10 | 0.21 | 0.17 | 0.43 |
| 26 | 0.20 | 0.12 | 0.23 | 0.07 | 0.04 | 0.08 | 0.56 |
| 27 | 0.41 | 0.10 | 0.07 | 0.14 | 0.03 | 0.02 | 0.33 |
| S. No. | GRC+ Ra | GRC+ WdB | GRC+ WdC | GRC− Ra | GRC− WdB | GRC− WdC | GRG+ | GRG− | Pi | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.86 | 0.50 | 0.53 | 0.35 | 0.50 | 0.47 | 0.63 | 0.44 | 0.588 | 23 |
| 2 | 0.82 | 0.62 | 0.51 | 0.36 | 0.42 | 0.49 | 0.65 | 0.42 | 0.604 | 19 |
| 3 | 0.87 | 0.94 | 0.86 | 0.35 | 0.34 | 0.35 | 0.89 | 0.35 | 0.720 | 3 |
| 4 | 0.86 | 0.69 | 0.63 | 0.35 | 0.39 | 0.42 | 0.73 | 0.39 | 0.653 | 14 |
| 5 | 0.92 | 0.77 | 0.70 | 0.34 | 0.37 | 0.39 | 0.79 | 0.37 | 0.683 | 8 |
| 6 | 0.65 | 1.00 | 1.00 | 0.41 | 0.33 | 0.33 | 0.88 | 0.36 | 0.712 | 4 |
| 7 | 0.60 | 0.66 | 0.64 | 0.43 | 0.40 | 0.41 | 0.63 | 0.41 | 0.605 | 18 |
| 8 | 0.57 | 0.94 | 0.70 | 0.44 | 0.34 | 0.39 | 0.74 | 0.39 | 0.654 | 13 |
| 9 | 0.93 | 0.94 | 0.65 | 0.34 | 0.34 | 0.41 | 0.84 | 0.36 | 0.700 | 6 |
| 10 | 0.98 | 0.68 | 0.58 | 0.34 | 0.40 | 0.44 | 0.75 | 0.39 | 0.657 | 11 |
| 11 | 0.92 | 0.66 | 0.55 | 0.34 | 0.40 | 0.46 | 0.71 | 0.40 | 0.639 | 16 |
| 12 | 0.66 | 0.84 | 0.72 | 0.40 | 0.36 | 0.38 | 0.74 | 0.38 | 0.660 | 10 |
| 13 | 0.82 | 0.89 | 0.86 | 0.36 | 0.35 | 0.35 | 0.86 | 0.35 | 0.708 | 5 |
| 14 | 0.76 | 0.90 | 0.76 | 0.37 | 0.35 | 0.37 | 0.81 | 0.36 | 0.689 | 7 |
| 15 | 0.45 | 0.95 | 0.96 | 0.56 | 0.34 | 0.34 | 0.79 | 0.41 | 0.657 | 12 |
| 16 | 0.51 | 0.83 | 0.84 | 0.49 | 0.36 | 0.36 | 0.72 | 0.40 | 0.643 | 15 |
| 17 | 0.50 | 0.84 | 0.80 | 0.50 | 0.36 | 0.36 | 0.71 | 0.41 | 0.637 | 17 |
| 18 | 0.39 | 0.92 | 0.81 | 0.69 | 0.34 | 0.36 | 0.71 | 0.47 | 0.602 | 20 |
| 19 | 0.84 | 0.61 | 0.41 | 0.36 | 0.42 | 0.63 | 0.62 | 0.47 | 0.569 | 24 |
| 20 | 1.00 | 0.97 | 0.77 | 0.33 | 0.34 | 0.37 | 0.92 | 0.35 | 0.725 | 1 |
| 21 | 0.81 | 0.99 | 0.92 | 0.36 | 0.33 | 0.34 | 0.90 | 0.35 | 0.723 | 2 |
| 22 | 0.77 | 0.42 | 0.40 | 0.37 | 0.61 | 0.66 | 0.53 | 0.55 | 0.493 | 26 |
| 23 | 0.89 | 0.81 | 0.63 | 0.35 | 0.36 | 0.41 | 0.78 | 0.37 | 0.675 | 9 |
| 24 | 0.37 | 0.92 | 0.89 | 0.77 | 0.34 | 0.35 | 0.73 | 0.49 | 0.598 | 21 |
| 25 | 0.43 | 0.33 | 0.33 | 0.60 | 1.00 | 1.00 | 0.37 | 0.87 | 0.297 | 27 |
| 26 | 0.56 | 0.76 | 0.53 | 0.45 | 0.37 | 0.47 | 0.62 | 0.43 | 0.589 | 22 |
| 27 | 0.33 | 0.82 | 0.83 | 1.00 | 0.36 | 0.36 | 0.66 | 0.57 | 0.537 | 25 |
| S. No. | ML Models | Prediction Accuracy (R2) |
|---|---|---|
| 1 | Linear regression (LR) | 0.5016 |
| 2 | Decision tree (DT) | 0.7236 |
| 4 | K nearest neighbours (KNNs) | 0.866 |
| 5 | Random forest regression (RFR) | 0.947 |
| Parameters | A | B | C |
|---|---|---|---|
| Level 1 | 0.6577 | 0.6539 | 0.6178 |
| Level 2 | 0.6547 | 0.6520 | 0.6030 |
| Level 3 | 0.5784 | 0.5849 | 0.6700 |
| Delta | 0.0792 | 0.0690 | 0.0670 |
| Rank | 1 | 2 | 3 |
| Sour. | Fre. | Seq SS | Adj SS | Adj MS | F | p | Cont. (%) |
|---|---|---|---|---|---|---|---|
| A | 2 | 88.73 | 88.73 | 44.37 | 4.72 | 0.044 | 7.2 |
| B | 2 | 106.76 | 106.76 | 53.38 | 5.68 | 0.029 | 8.6 |
| C | 2 | 537.53 | 537.53 | 268.76 | 28.58 | 0.001 | 43.4 |
| A∗B | 4 | 157.66 | 157.66 | 39.41 | 4.19 | 0.040 | 12.7 |
| A∗C | 4 | 187.91 | 187.91 | 46.98 | 4.99 | 0.026 | 15.2 |
| B∗C | 4 | 83.95 | 83.95 | 20.99 | 2.23 | 0.155 | 6.8 |
| RE | 8 | 75.24 | 75.24 | 9.41 | 1 | ||
| Total | 26 | 1237.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, R.; Madathil, A.P.; Liu, Q.; Cheng, J.; Lin, F. A Hybrid GRA-TOPSIS-RFR Optimization Approach for Minimizing Burrs in Micro-Milling of Ti-6Al-4V Alloys. Micromachines 2025, 16, 464. https://doi.org/10.3390/mi16040464
Tan R, Madathil AP, Liu Q, Cheng J, Lin F. A Hybrid GRA-TOPSIS-RFR Optimization Approach for Minimizing Burrs in Micro-Milling of Ti-6Al-4V Alloys. Micromachines. 2025; 16(4):464. https://doi.org/10.3390/mi16040464
Chicago/Turabian StyleTan, Rongkai, Abhilash Puthanveettil Madathil, Qi Liu, Jian Cheng, and Fengtao Lin. 2025. "A Hybrid GRA-TOPSIS-RFR Optimization Approach for Minimizing Burrs in Micro-Milling of Ti-6Al-4V Alloys" Micromachines 16, no. 4: 464. https://doi.org/10.3390/mi16040464
APA StyleTan, R., Madathil, A. P., Liu, Q., Cheng, J., & Lin, F. (2025). A Hybrid GRA-TOPSIS-RFR Optimization Approach for Minimizing Burrs in Micro-Milling of Ti-6Al-4V Alloys. Micromachines, 16(4), 464. https://doi.org/10.3390/mi16040464









